Estimation of Uncertainty in Airborne LiDAR Inventories Using Approaches Based on Bootstrapping-Pairs Methods
Abstract
1. Introduction
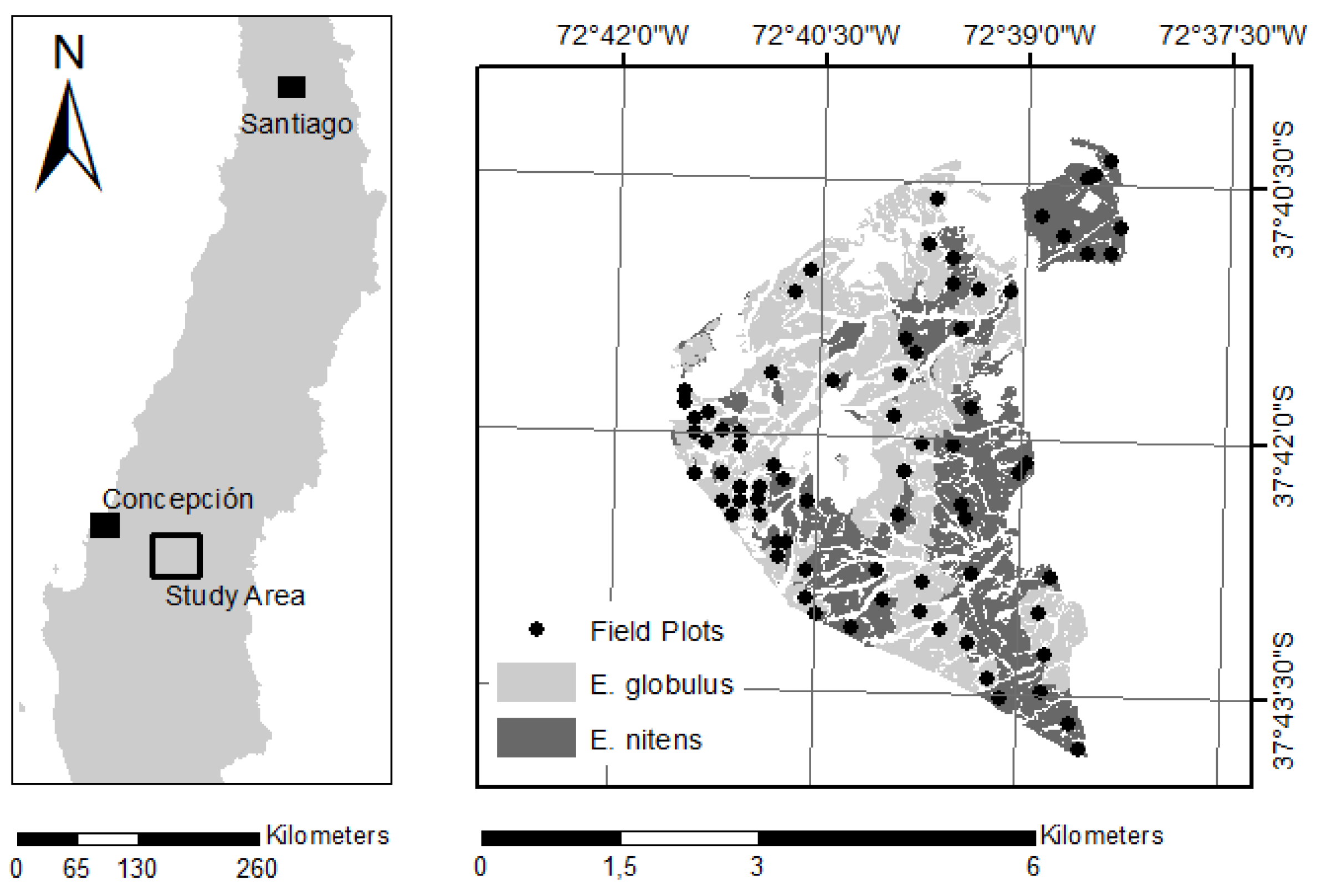
2. Materials and Methods
2.1. Data
2.2. Method Development
2.3. Modeling
3. Results
3.1. Models Performance
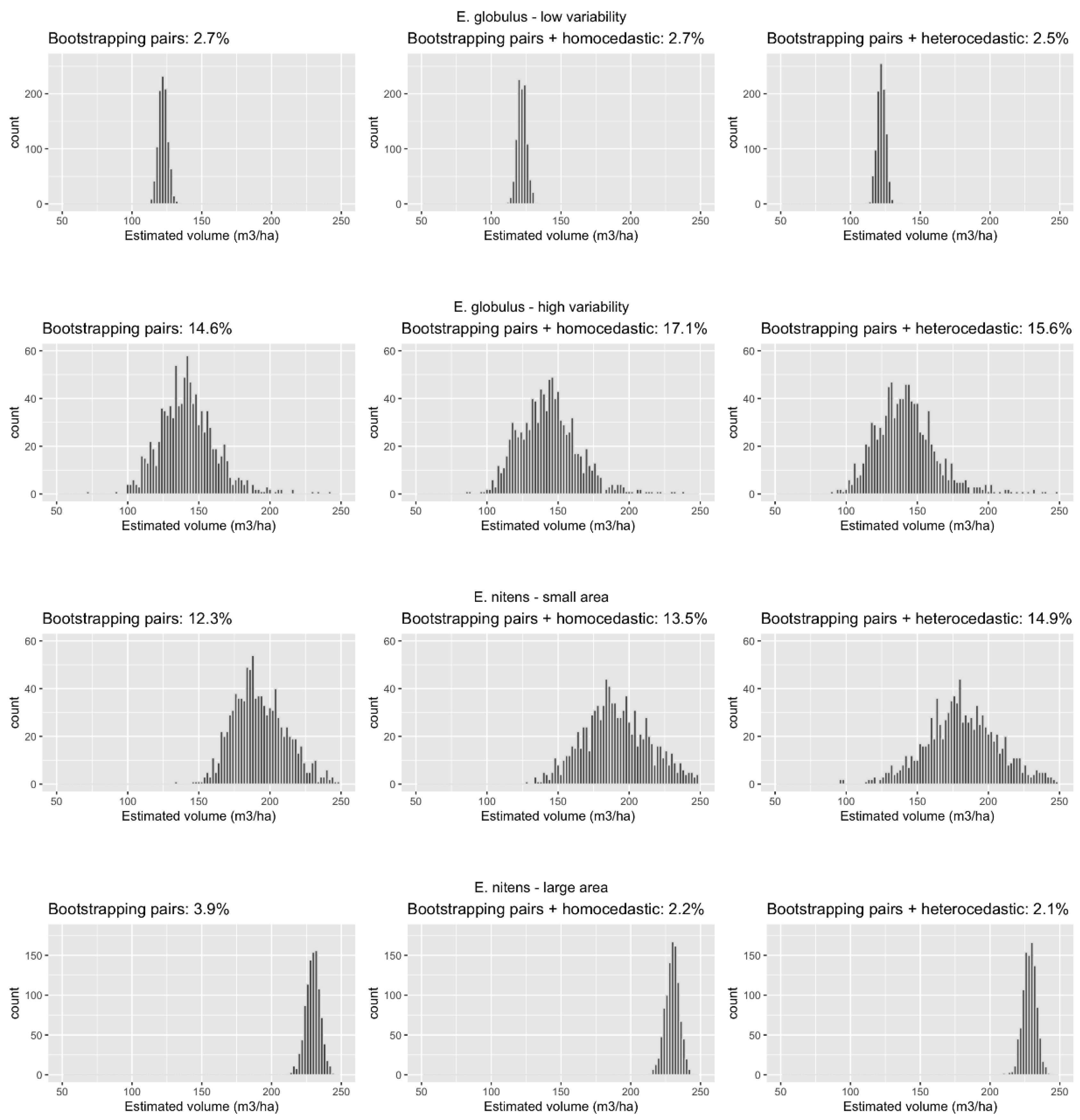
3.2. Methods Performance
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mielcarek, M.; Stereńczak, K.; Khosravipour, A. Testing and evaluating different LiDAR-derived canopy height model generation methods for tree height estimation. Int. J. Appl. Earth Obs. Geoinf. 2018, 71, 132–143. [Google Scholar] [CrossRef]
- Pearse, G.D.; Watt, M.S.; Dash, J.P.; Stone, C.; Caccamo, G. Comparison of models describing forest inventory attributes using standard and voxel-based lidar predictors across a range of pulse densities. Int. J. Appl. Earth Obs. Geoinf. 2019, 78, 341–351. [Google Scholar] [CrossRef]
- Watt, M.S.; Meredith, A.; Watt, P.; Gunn, A. Use of LiDAR to estimate stand characteristics for thinning operations in young Douglas-fir plantations. N. Z. J. For. Sci. 2013, 43, 18. [Google Scholar] [CrossRef]
- Hu, B.; Li, J.; Jing, L.; Judah, A. Improving the efficiency and accuracy of individual tree crown delineation from high-density LiDAR data. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 145–155. [Google Scholar] [CrossRef]
- Massey, A.; Mandallaz, D.; Lanz, A. Integrating remote sensing and past inventory data under the new annual design of the Swiss National Forest Inventory using three-phase design-based regression estimation. Can. J. For. Res. 2014, 44, 1177–1186. [Google Scholar] [CrossRef]
- White, J.C.; Coops, N.C.; Wulder, M.A.; Vastaranta, M.; Hilker, T.; Tompalski, P. Remote Sensing Technologies for Enhancing Forest Inventories: A Review. Can. J. Remote Sens. 2016, 42, 619–641. [Google Scholar] [CrossRef]
- Breidenbach, J.; McRoberts, R.E.; Astrup, R. Empirical coverage of model-based variance estimators for remote sensing assisted estimation of stand-level timber volume. Remote Sens. Environ. 2016, 173, 274–281. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Næsset, E.; Gobakken, T.; Chirici, G.; Condés, S.; Hou, Z.; Saarela, S.; Chen, Q.; Ståhl, G.; Walters, B.F. Assessing components of the model-based mean square error estimator for remote sensing assisted forest applications. Can. J. For. Res. 2018, 48, 642–649. [Google Scholar] [CrossRef]
- Thomson, S. Sampling, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2012; p. 436. [Google Scholar]
- Gregoire, T.G. Design-based and model-based inference in survey sampling: Appreciating the difference. Can. J. For. Res. 1998, 28, 1429–1447. [Google Scholar] [CrossRef]
- Puliti, S.; Dash, J.P.; Watt, M.S.; Breidenbach, J.; Pearse, G.D. A comparison of UAV laser scanning, photogrammetry and airborne laser scanning for precision inventory of small-forest properties. For. Int. J. For. Res. 2020, 93, 150–162. [Google Scholar] [CrossRef]
- Næsset, E. Predicting forest stand characteristics with airborne scanning laser using a practical two-stage procedure and field data. Remote Sens. Environ. 2002, 80, 88–99. [Google Scholar] [CrossRef]
- Næsset, E.; Gobakken, T. Estimation of above- and below-ground biomass across regions of the boreal forest zone using airborne laser. Remote Sens. Environ. 2008, 112, 3079–3090. [Google Scholar] [CrossRef]
- Zhao, K.; Popescu, S.; Nelson, R. Lidar remote sensing of forest biomass: A scale-invariant estimation approach using airborne lasers. Remote Sens. Environ. 2009, 113, 182–196. [Google Scholar] [CrossRef]
- Frazer, G.W.; Magnussen, S.; Wulder, M.A.; Niemann, K.O. Simulated impact of sample plot size and co-registration error on the accuracy and uncertainty of LiDAR-derived estimates of forest stand biomass. Remote Sens. Environ. 2011, 115, 636–649. [Google Scholar] [CrossRef]
- Martín-García, S.; Diéguez-Aranda, U.; Álvarez González, J.G.; Pérez-Cruzado, C.; Buján, S.; González-Ferreiro, E. Estimación de las existencias maderables de Pinus radiata a escala provincial utilizando datos LiDAR de baja resolución. Bosque 2017, 38, 17–28. [Google Scholar] [CrossRef]
- Chambers, R.; Clark, R. An Introduction to Model-Based Survey Sampling with Applications; Oxford University Press Inc.: New York, NY, USA, 2012. [Google Scholar]
- McRoberts, R.E. Probability- and model-based approaches to inference for proportion forest using satellite imagery as ancillary data. Remote Sens. Environ. 2010, 114, 1017–1025. [Google Scholar] [CrossRef]
- McRoberts, R.E. A model-based approach to estimating forest area. Remote Sens. Environ. 2006, 103, 56–66. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Næsset, E.; Gobakken, T. Inference for lidar-assisted estimation of forest growing stock volume. Remote Sens. Environ. 2013, 128, 268–275. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; Taylor & Francis: London, UK, 1994. [Google Scholar]
- Rapidlasso, G. LAStools. 2018. Available online: https://rapidlasso.com/lastools/ (accessed on 15 April 2020).
- McGaughey, R. FUSION/LDV: Software for LiDAR Data Analysis and Visualization; FUSION Version 3.80; USDA: Seattle, WA, USA, 2018.
- McConville, K.S.; Moisen, G.G.; Frescino, T.S. A Tutorial on Model-Assisted Estimation with Application to Forest Inventory. Forests 2020, 11, 244. [Google Scholar] [CrossRef]
- McConville, K.S.; Breidt, F.J. Survey design asymptotics for the model-assisted penalised spline regression estimator. J. Nonparametr. Stat. 2013, 25, 745–763. [Google Scholar] [CrossRef]
- Mashreghi, Z.; Haziza, D.; Léger, C. A survey of bootstrap methods in finite population sampling. Stat. Surv. 2016, 10, 1–52. [Google Scholar] [CrossRef]
- Tompalski, P.; White, J.C.; Coops, N.C.; Wulder, M.A. Demonstrating the transferability of forest inventory attribute models derived using airborne laser scanning data. Remote Sens. Environ. 2019, 227, 110–124. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Gobakken, T.; Næsset, E. Post-stratified estimation of forest area and growing stock volume using lidar-based stratifications. Remote Sens. Environ. 2012, 125, 157–166. [Google Scholar] [CrossRef]
- Rahlf, J.; Breidenbach, J.; Solberg, S.; Astrup, R. Forest Parameter Prediction Using an Image-Based Point Cloud: A Comparison of Semi-ITC with ABA. Forests 2015, 6, 4059–4071. [Google Scholar] [CrossRef]
- A Language and Environment for Statistical Computing. In R Foundation for Statistical Computing; R Version 4.0.1; The R Development Core Team: Vienna, Austria, 2020.
- Gobakken, T.; Naesset, E. Assessing effects of laser point density on biophysical stand properties derived from air-borne laser scanner data in mature forest. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2007, 36, 150–155. [Google Scholar]


| Model | Method | RMSE (m3/ha) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| E. globulus | ||||||||||||
| 1 | 1 | 0.0770 | 1.5303 | 0.8342 | 0.2720 | 0.1954 | 0.1971 | 22.8 | ||||
| 2 | 0.0772 | 1.5304 | 0.8339 | 0.3846 | 0.1995 | 0.2072 | 22.8 | |||||
| 3 | 0.0632 | 1.5415 | 0.8480 | 0.1934 | 0.2102 | 0.1887 | 21.6170 | 0.0330 | 21.7 | |||
| 2 | 1 | 216.4260 | 5.8486 | −0.2275 | −0.0262 | 13.8212 | 1.3731 | 0.0524 | 0.0098 | 22.2 | ||
| 2 | 216.4229 | 5.8464 | −0.2265 | −0.0265 | 13.7925 | 1.3586 | 0.0566 | 0.0098 | 22.2 | |||
| 3 | 217.2242 | 5.9792 | −0.2301 | −0.0276 | 22.3504 | 1.4129 | 0.0578 | 0.0098 | 42.3884 | −0.1546 | 21.9 | |
| E. nitens | ||||||||||||
| 1 | 1 | 0.3080 | 1.5217 | 0.4918 | 0.7323 | 0.9643 | 1.3233 | 34.2 | ||||
| 2 | 0.3004 | 1.5437 | 0.5419 | 0.3068 | 0.1525 | 0.1611 | 34.1 | |||||
| 3 | 0.1594 | 1.5830 | 0.6602 | 0.2043 | 0.1234 | 0.1785 | 3.2637 | 1.3250 | 32.4 | |||
| 2 | 1 | 267.7107 | 3.5054 | −11.1531 | −43.0304 | 12.4449 | 0.0369 | 0.8298 | 3.3628 | 85.7 | ||
| 2 | 266.8452 | 3.5065 | −11.1256 | −42.9084 | 11.9852 | 0.0343 | 0.7606 | 3.1181 | 86.0 | |||
| 3 | 319.4280 | 8.4594 | −0.3437 | −0.0495 | 34.7860 | 4.8668 | 0.7278 | 0.2793 | 0.3066 | 2.5574 | 71.1 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sandoval, S.; Bustamante-Ortega, R. Estimation of Uncertainty in Airborne LiDAR Inventories Using Approaches Based on Bootstrapping-Pairs Methods. Forests 2020, 11, 1305. https://doi.org/10.3390/f11121305
Sandoval S, Bustamante-Ortega R. Estimation of Uncertainty in Airborne LiDAR Inventories Using Approaches Based on Bootstrapping-Pairs Methods. Forests. 2020; 11(12):1305. https://doi.org/10.3390/f11121305
Chicago/Turabian StyleSandoval, Simón, and Ramón Bustamante-Ortega. 2020. "Estimation of Uncertainty in Airborne LiDAR Inventories Using Approaches Based on Bootstrapping-Pairs Methods" Forests 11, no. 12: 1305. https://doi.org/10.3390/f11121305
APA StyleSandoval, S., & Bustamante-Ortega, R. (2020). Estimation of Uncertainty in Airborne LiDAR Inventories Using Approaches Based on Bootstrapping-Pairs Methods. Forests, 11(12), 1305. https://doi.org/10.3390/f11121305






