Determination of Elastic Properties of Beech Plywood by Analytical, Experimental and Numerical Methods
Abstract
:1. Introduction
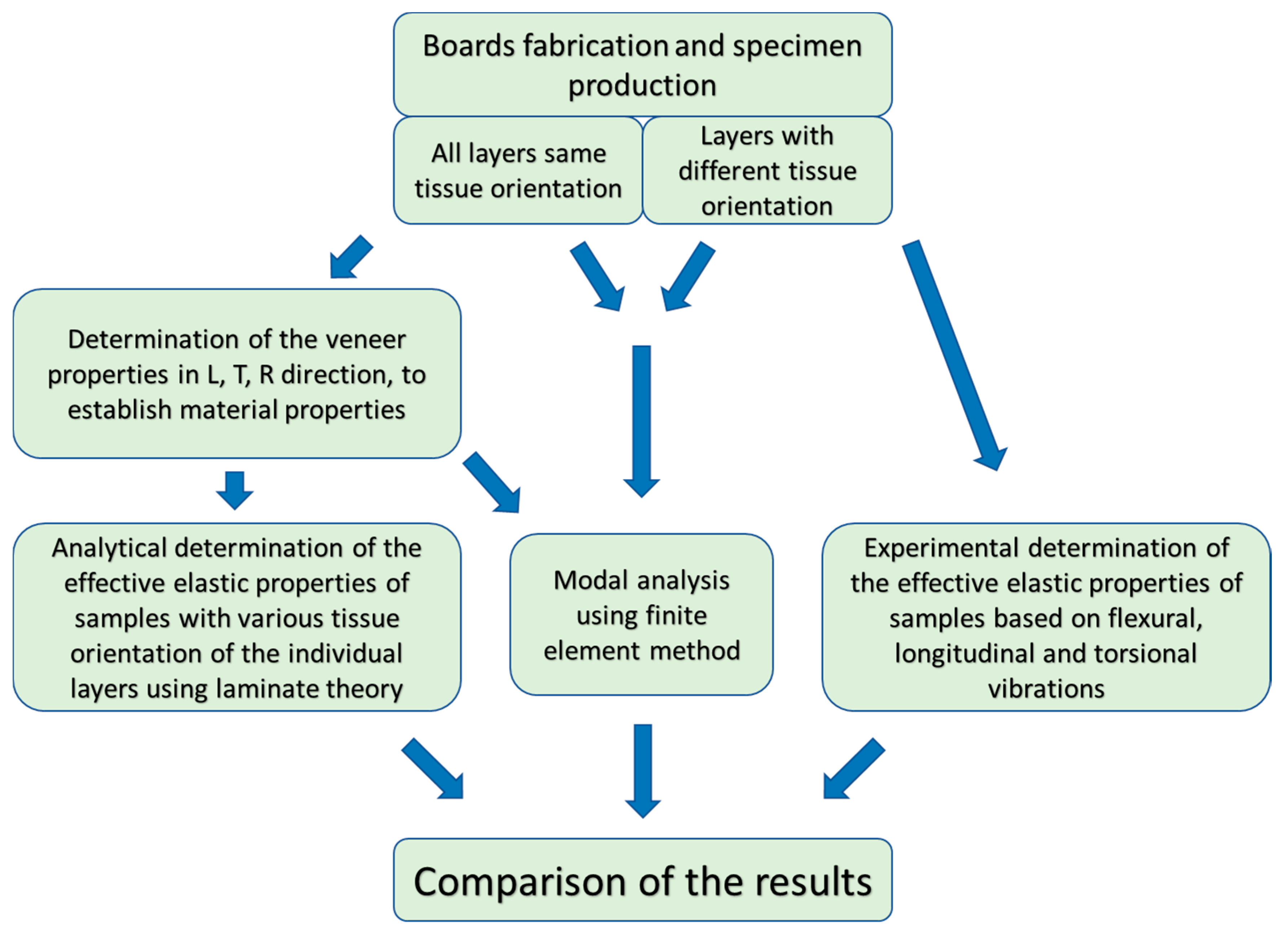
2. Materials and Methods
2.1. Plyboards Fabricaton
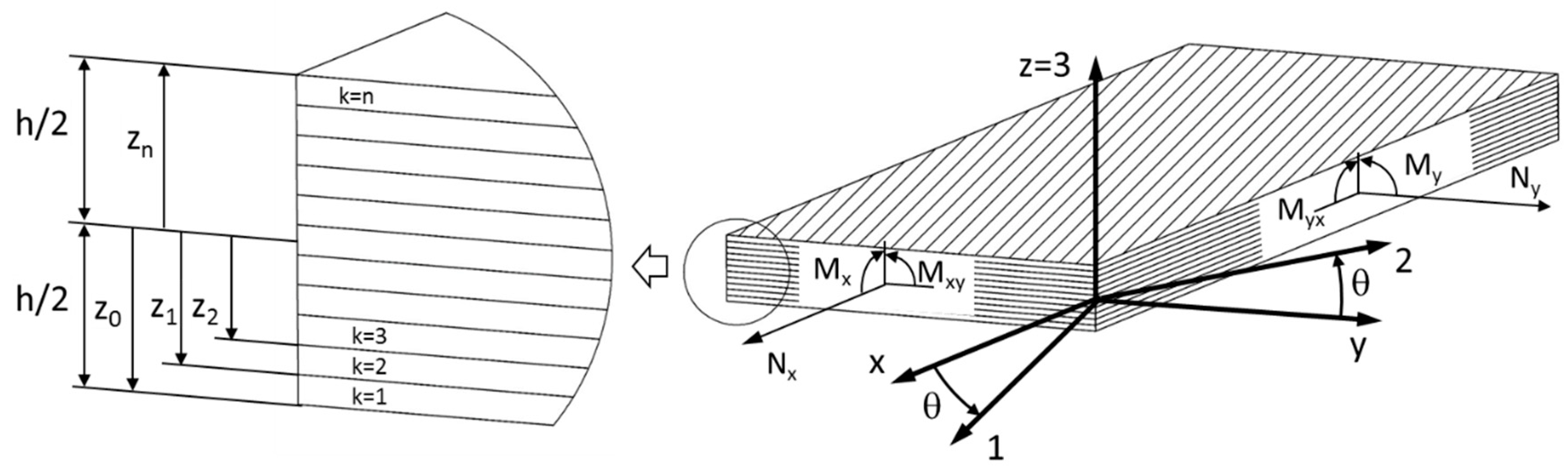
2.2. Determination of Elastic Properties
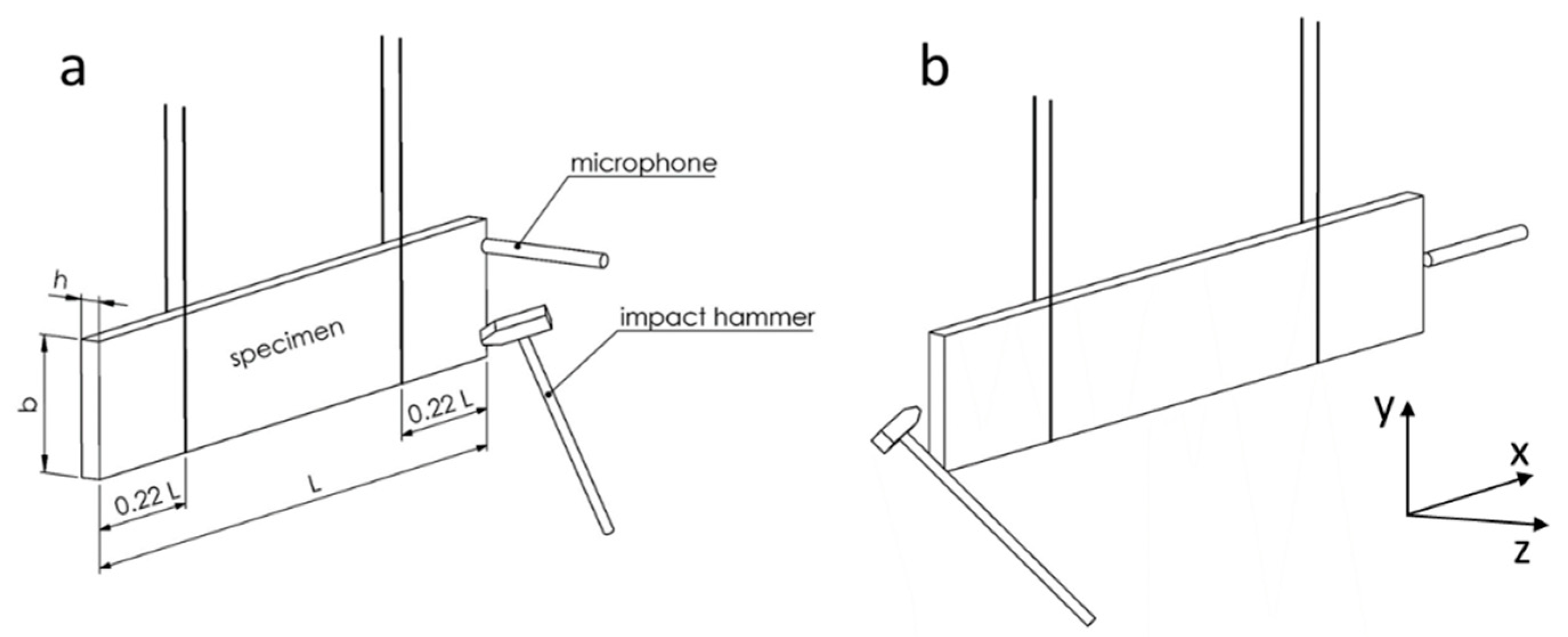
2.2.1. Determination of Elastic Properties of Beech Veneer in Principal (L—Longitudinal, T—Tangential, R—Radial) Directions by Flexural and Torsional Vibrations
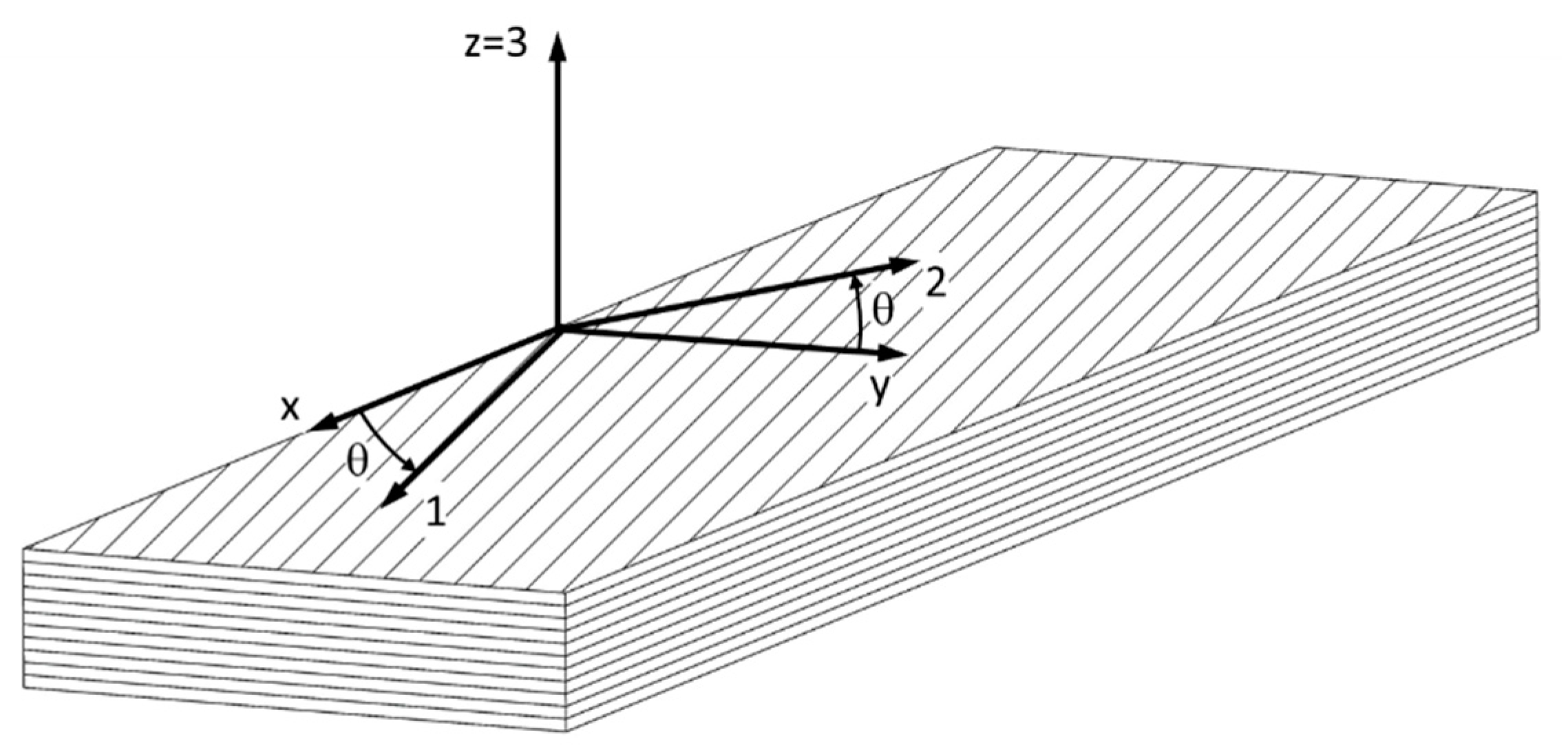
2.2.2. Determination of Effective Elastic Properties in x and y Directions from Specimens with Different Tissue Orientation of Individual Layers
2.2.3. Determination of Effective Elastic Properties Using Laminate Theory
2.2.4. Modal Analysis Using the Finite Element Method
3. Results and Discussion
3.1. Elastic Properties in Principal Material Directions in Specimens with the Same Layer Orientation
3.2. Effective Elastic Properties in Specimen with Various Layer Orientations
4. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Norris, C.B.; McKinnon, P.F. Compression, Tension, and Shear Tests on Yellow-Poplar Plywood Panels of Sizes that do not Buckle with Tests Made at Various Angles to the Face Grain; U.S. Dept. of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 1956.
- Norris, C.B. Strength of Orthotropic Materials Subjected to Combined Stresses; U.S. Dept. of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 1962; p. 40.
- Kallakas, H.; Rohumaa, A.; Vahermets, H.; Kers, J. Effect of different hardwood species and lay-up schemes on the mechanical properties of plywood. Forests 2020, 11, 649. [Google Scholar] [CrossRef]
- Biadała, T.; Czarnecki, R.; Dukarska, D. Water resistant plywood of increased elasticity produced from European wood species. Wood Res. 2020, 65, 111–123. [Google Scholar] [CrossRef]
- Bal, B.C. Some physical and mechanical properties of reinforced laminated veneer lumber. Constr. Build. Mater. 2014, 68, 120–126. [Google Scholar] [CrossRef]
- Svoboda, T.; Sikora, A.; Zaborsky, V.; Gaffova, Z. Laminated Veneer Lumber with Non-Wood Components and the Effects of Selected Factors on Its Bendability. Forests 2019, 10, 470. [Google Scholar] [CrossRef] [Green Version]
- Sikora, A.; Svoboda, T.; Zaborsky, V.; Gaffova, Z. Effect of Selected Factors on the Bending Deflection at the Limit of Proportionality and at the Modulus of Rupture in Laminated Veneer Lumber. Forests 2019, 10, 401. [Google Scholar] [CrossRef] [Green Version]
- Salca, E.A.; Bekhta, P.; Seblii, Y. The effect of veneer densification temperature and wood species on the plywood properties made from alternate layers of densified and non-densified veneers. Forests 2020, 11, 700. [Google Scholar] [CrossRef]
- Yu, X.; Xu, D.; Sun, Y.; Geng, Y.; Fan, J.; Dai, X.; He, Z.; Dong, X.; Dong, Y.; Li, Y. Preparation of wood-based panel composites with poplar veneer as the surface layer modified by in-situ polymerization of active monomers. Forests 2020, 11, 893. [Google Scholar] [CrossRef]
- Král, P.; Klímek, P.; Mishra, P.K.; Rademacher, P.; Wimmer, R. Preparation and characterization of cork layered composite plywood boards. BioResources 2014, 9, 1977–1985. [Google Scholar] [CrossRef] [Green Version]
- Hao, J.; Wu, X.; Oporto-Velasquez, G.; Wang, J.; Dahle, G. Compression properties and its prediction of wood-based sandwich panels with a novel taiji honeycomb core. Forests 2020, 11, 886. [Google Scholar] [CrossRef]
- Zhou, H.Y.; Wei, X.; Smith, L.M.; Wang, G.; Chen, F.M. Evaluation of Uniformity of Bamboo Bundle Veneer and Bamboo Bundle Laminated Veneer Lumber (BLVL). Forests 2019, 10, 921. [Google Scholar] [CrossRef] [Green Version]
- Wilczyński, M.; Warmbier, K. Elastic moduli of veneers in pine and beech plywood. Drewno 2012, 188, 47–56. [Google Scholar]
- Yoshihara, H. Influence of the specimen depth to length ratio and lamination construction on Young’s modulus and in-plane shear modulus of plywood measured by flexural vibration. BioResources 2012, 7, 1337–1351. [Google Scholar]
- Yoshihara, H. Edgewise shear modulus of plywood measured by square-plate twist and beam flexure methods. Constr. Build. Mater. 2009, 23, 3537–3545. [Google Scholar] [CrossRef]
- Guan, C.; Liu, J.; Zhang, H.; Wang, X.; Zhou, L. Evaluation of modulus of elasticity and modulus of rupture of full-size wood composite panels supported on two nodal-lines using a vibration technique. Constr. Build. Mater. 2019, 218, 64–72. [Google Scholar] [CrossRef]
- Guan, C.; Zhang, H.; Zhou, L.; Wang, X. Dynamic determination of modulus of elasticity of full-size wood composite panels using a vibration method. Constr. Build. Mater. 2015, 100, 201–206. [Google Scholar] [CrossRef]
- Park, H.M.; Fushitani, M.; Byeon, H.S. Derivation and application of an equation for calculating shear modulus of three-ply laminated material beam from shear moduli of individual laminae. J. Wood Sci. 2009, 55, 181–189. [Google Scholar] [CrossRef]
- Sanne, M.; Ahn-Ercan, G.; Pfriem, A. A mathematical solution for calculating the springback of laminated beech stacks molded within the elastic range. Forests 2020, 11, 725. [Google Scholar] [CrossRef]
- Brancheriau, L.; Bailleres, H.; Guitard, D. Comparison between modulus of elasticity values calculated using 3 and 4 point bending tests on wooden samples. Wood Sci. Technol. 2002, 36, 367–383. [Google Scholar] [CrossRef]
- Krüger, R.; Wagenführ, A. Comparison of methods for determining shear modulus of wood. Eur. J. Wood Wood Prod. 2020. [Google Scholar] [CrossRef]
- Merhar, M.; Bučar, B. Determination of correction coefficient for dynamic modulus of elasticity obtained by analysing the frequency response of a clamped cantilever specimen. Holz Als Roh Und Werkst. 2008, 66, 233–235. [Google Scholar] [CrossRef]
- Hoffmann, J.A.; Wertheimer, T. Cantilever beam vibration. J. Sound Vib. 2000, 229, 1269–1276. [Google Scholar] [CrossRef]
- Roohnia, M. An estimation of dynamic modulus of elasticity in cantilever flexural timber beams. Drv. Ind. 2014, 65, 3–10. [Google Scholar] [CrossRef]
- Huang, T.C. The effect of rotatory inertia and of shear deformation on the frequency and normal mode equations of uniform beams with simple end conditions. J. Appl. Mech. Trans. Asme 1960, 28, 579–584. [Google Scholar] [CrossRef]
- Hearmon, R.F.S. The influence of shear and rotatory inertia on the free flexural vibration of wooden beams. Br. J. Appl. Phys. 1958, 9, 381–388. [Google Scholar] [CrossRef]
- Chui, Y.H.; Smith, I. Influence of rotatory inertia, shear deformation and support condition on natural frequencies of wooden beams. Wood Sci. Technol. 1990, 24, 233–245. [Google Scholar] [CrossRef]
- Ip, K.H.; Tse, P.C. Determination of dynamic flexural and shear moduli of thick composite beams using natural frequencies. J. Compos. Mater. 2001, 35, 1553–1569. [Google Scholar] [CrossRef]
- Brancheriau, L. Influence of cross section dimensions on Timoshenko’s shear factor—Application to wooden beams in free-free flexural vibration. Ann. For. Sci. 2006, 63, 319–321. [Google Scholar] [CrossRef]
- Brancheriau, L.; Bailleres, H. Natural vibration analysis of clear wooden beams: A theoretical review. Wood Sci. Technol. 2002, 36, 347–365. [Google Scholar] [CrossRef]
- Kollmann, F.F.P.; Côte, W.A. Principles of Wood Science and Technology. Solid Wood.; Springer: Berlin, Germany, 1975; p. 592. [Google Scholar]
- Arriaga, F.; Monton, J.; Segues, E.; Íñiguez-Gonzalez, G. Determination of the mechanical properties of radiata pine timber by means of longitudinal and transverse vibration methods. Holzforschung 2014, 68, 299–305. [Google Scholar] [CrossRef]
- Haines, D.W.; Leban, J.M.; Herbé, C. Determination of Young’s modulus for spruce, fir and isotropic materials by the resonance flexure method with comparisons to static flexure and other dynamic methods. Wood Sci. Technol. 1996, 30, 253–263. [Google Scholar] [CrossRef]
- Boruvka, V.; Novák, D.; Šedivka, P. Comparison and Analysis of Radial and Tangential Bending of Softwood and Hardwood at Static and Dynamic Loading. Forests 2020, 11, 896. [Google Scholar] [CrossRef]
- Pang, S.; Liang, Y.; Tao, W.; Liu, Y.; Huan, S.; Qin, H. Effect of the strain rate and fiber direction on the dynamic mechanical properties of beechwood. Forests 2019, 10, 881. [Google Scholar] [CrossRef] [Green Version]
- Hu, N. Composites and Their Properties; InTech: Rijeka, Croatia, 2012. [Google Scholar]
- Herakovich, C.T. Mechanics of Fibrous Composites; John and Wiley and Sons: New York, NY, USA, 1998; p. 450. [Google Scholar]
- Isaac, M.D.; Ishai, O. Engineering Mechanics of Composite Materials, 2nd ed.; Oxford University Press: New York, NY, USA, 2006. [Google Scholar]
- Mohammadabadi, M.; Jarvis, J.; Yadama, V.; Cofer, W. Predictive models for elastic bending behavior of a wood composite sandwich panel. Forests 2020, 11, 624. [Google Scholar] [CrossRef]
- Fortino, S.; Hradil, P.; Salminen, L.I.; De Magistris, F. A 3D micromechanical study of deformation curves and cell wall stresses in wood under transverse loading. J. Mater. Sci. 2016, 50, 482–492. [Google Scholar] [CrossRef]
- Contemporary Plywood Furniture Designs. Available online: https://www.architectureartdesigns.com/27-contemporary-plywood-furniture-designs/ (accessed on 3 October 2020).
- Ross, R.J. Wood Handbook: Wood as an Engineering Material; The Forest Products Laboratory: Forest Products Society: Madison, WI, USA, 2010; p. 508.
- Aicher, S.; Dill-Langer, G. Effect of lamination anysotropy and lay-up in glued-laminated timbers. J. Struct. Eng. 2005, 131, 1095–1103. [Google Scholar] [CrossRef]
- Fortino, S.; Mirianon, F.; Toratti, T. A 3D moisture-stress FEM analysis for time dependent problems in timber structures. Mech. Time-Depend. Mater. 2009, 13, 333–356. [Google Scholar] [CrossRef]
- Hein, P.R.G.; Lima, J.T.; Gril, J.; Rosado, A.M.; Brancheriau, L. Resonance of scantlings indicates the stiffness even of small specimens of Eucalyptus from plantations. Wood Sci. Technol. 2012, 46, 621–635. [Google Scholar] [CrossRef]
- Yoshihara, H.; Maruta, M. Shear moduli in the longitudinal-radial and radial-tangential planes of Sitka spruce measured by torsional vibration tests. Holzforschung 2018, 72, 507–512. [Google Scholar] [CrossRef]
- Nakao, T.; Okano, T.; Asano, I. Measurement of the anisotropic-shear modulus by the torsional-vibration method for free-free wooden beams. Mokuzai Gakkaishi 1984, 30, 877–885. [Google Scholar]
- Love, A. A Treatise on the Mathematical Theory of Elasticity; Cambridge University Press: Cambridge, UK, 1892. [Google Scholar]
- Yoshihara, H. Off-axis Young’s modulus and off-axis shear modulus of wood measured by flexural vibration tests. Holzforschung 2012, 66, 207–213. [Google Scholar] [CrossRef]
- Kubojima, Y.; Tonosaki, M. Young’s and shear moduli of glued laminated timber composed of different species obtained by a flexural vibration test. Holzforschung 2012, 66, 871–875. [Google Scholar] [CrossRef]
- Bodig, J.; Jayne, B.A. Mechanics of Wood and Wood Composites; Van Nostrand Reinhold: New York, NY, USA, 1982. [Google Scholar]
- Hering, S.; Keunecke, D.; Niemz, P. Moisture-dependent orthotropic elasticity of beech wood. Wood Sci. Technol. 2012, 46, 927–938. [Google Scholar] [CrossRef] [Green Version]
- Ozyhar, T.; Hering, S.; Niemz, P. Moisture-dependent elastic and strength anisotropy of European beech wood in tension. J. Mater. Sci. 2012, 47, 6141–6150. [Google Scholar] [CrossRef]
- Milch, J.; Tippner, J.; Sebera, V.; Brabec, M. Determination of the elasto-plastic material characteristics of Norway spruce and European beech wood by experimental and numerical analyses. Holzforschung 2016, 70, 1081–1092. [Google Scholar] [CrossRef]
- Boruvka, V.; Zeidler, A.; Holecek, T.; Dudik, R. Elastic and Strength Properties of Heat-Treated Beech and Birch Wood. Forests 2018, 9, 197. [Google Scholar] [CrossRef] [Green Version]
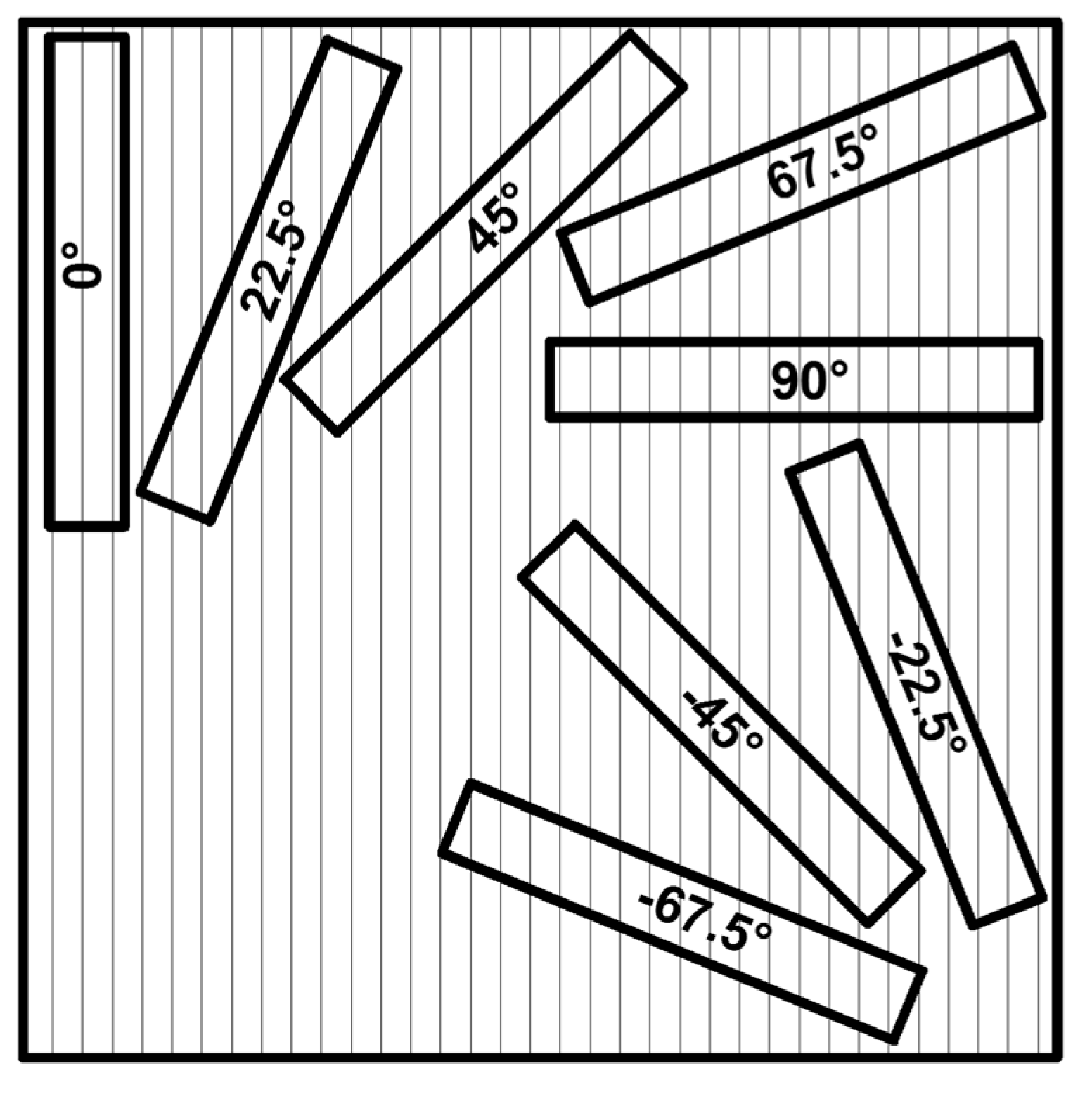
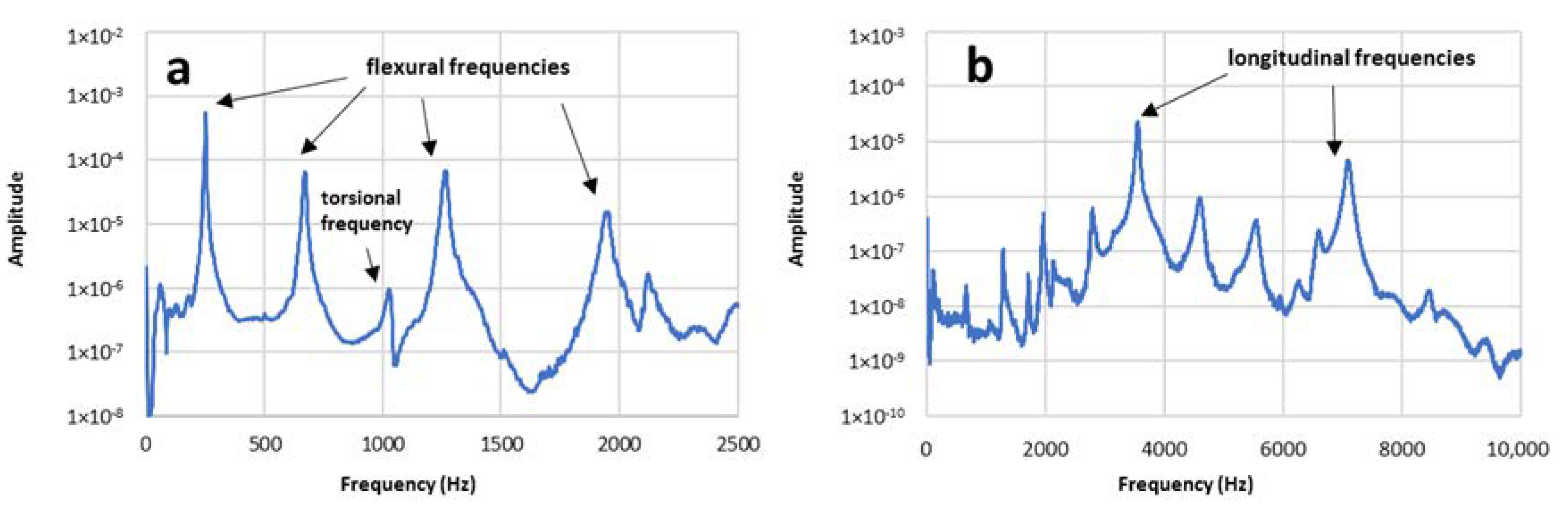
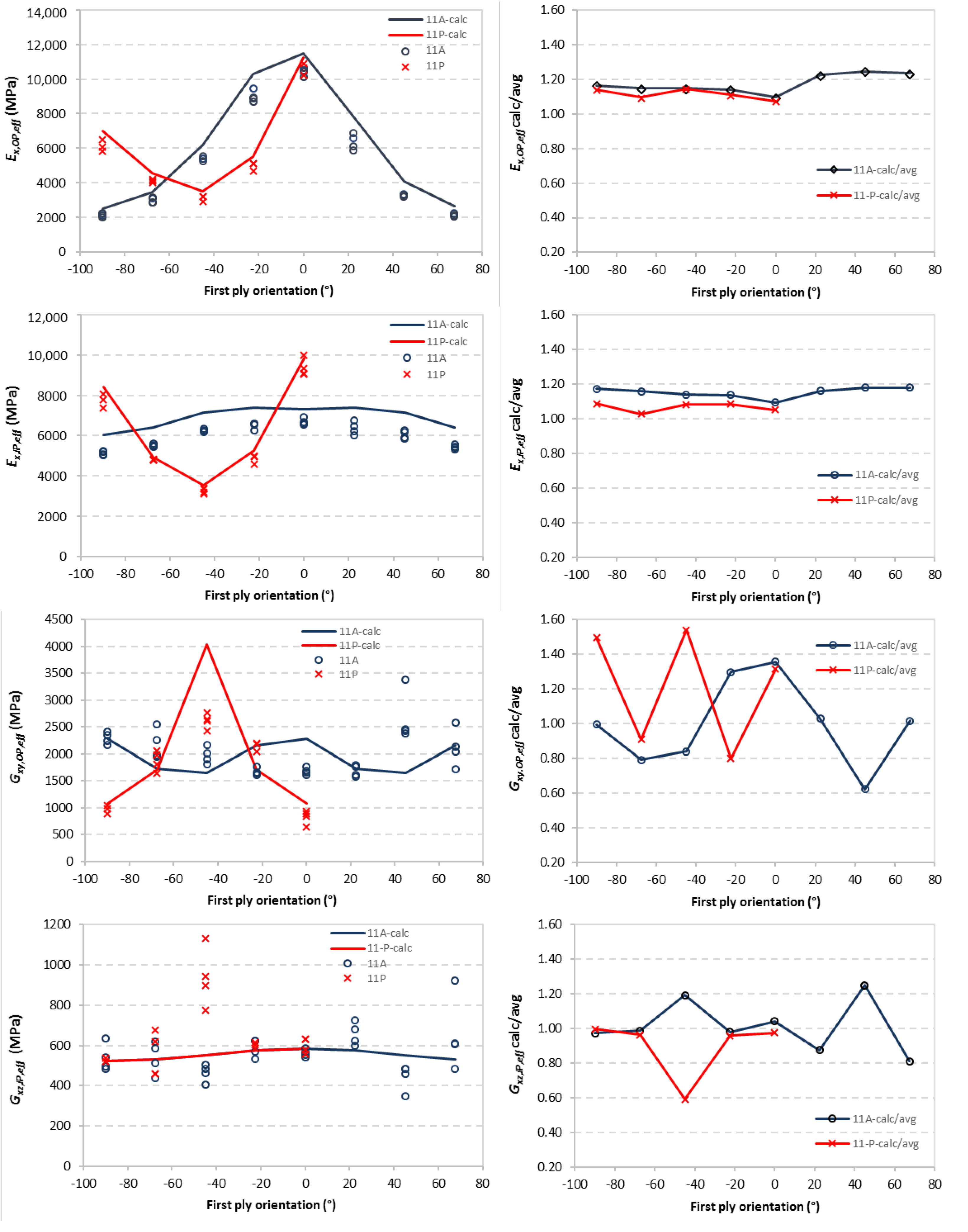

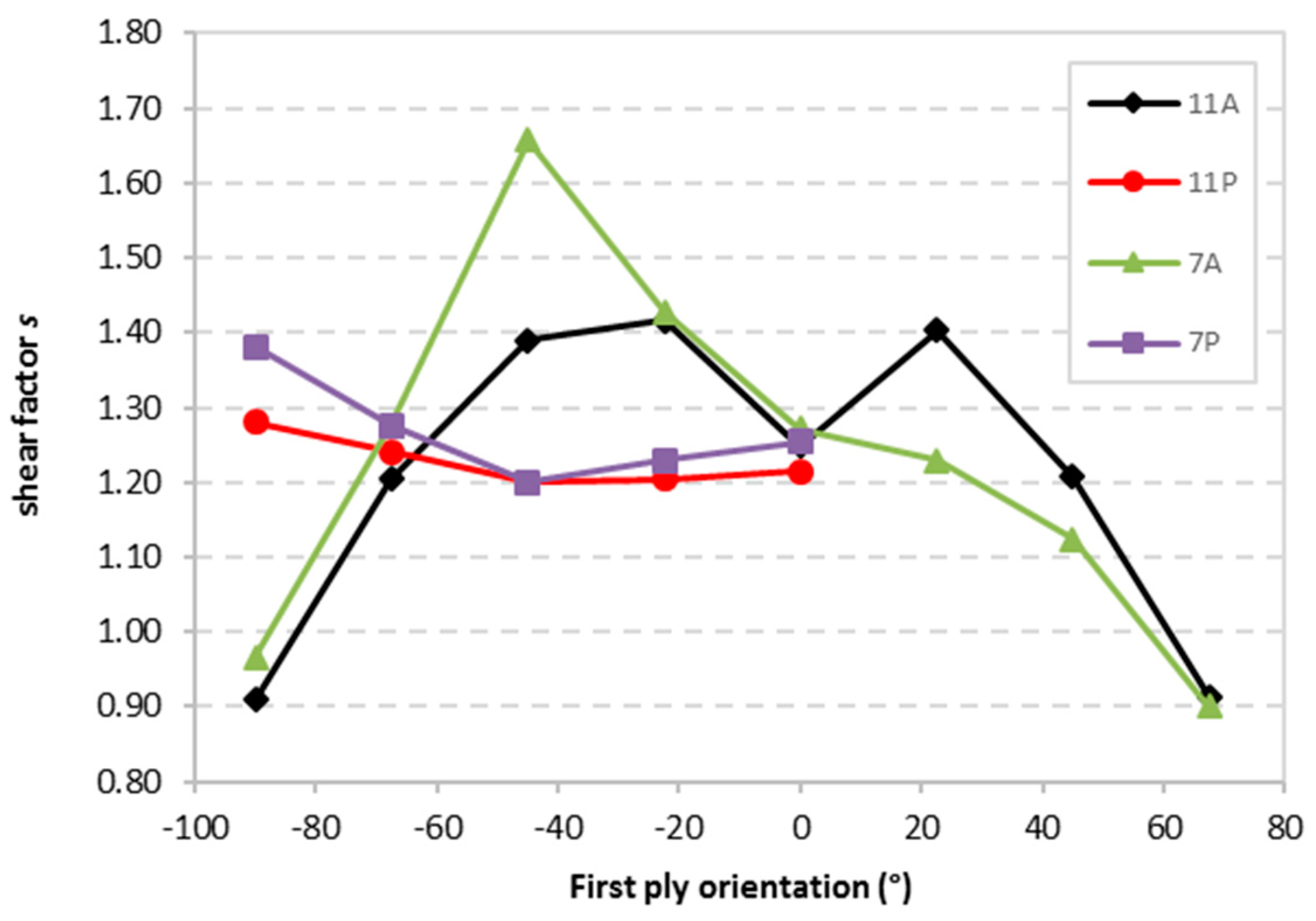

| 7 Layers | 11 Layers | ||||
|---|---|---|---|---|---|
| Ply No. | 7A (°) | 7P (°) | 11E (°) | 11A (°) | 11P (°) |
| 1 | 0 | 0 | 0 | 0 | 0 |
| 2 | 45 | 90 | 0 | 30 | 90 |
| 3 | −45 | 0 | 0 | −30 | 0 |
| 4 | 90 | 90 | 0 | 60 | 90 |
| 5 | −45 | 0 | 0 | −60 | 0 |
| 6 | 45 | 90 | 0 | 90 | 90 |
| 7 | 0 | 0 | 0 | −60 | 0 |
| 8 | - | - | 0 | 60 | 90 |
| 9 | - | - | 0 | −30 | 0 |
| 10 | - | - | 0 | 30 | 90 |
| 11 | - | - | 0 | 0 | 0 |
| Modulus of Elasticity (MPa) | Shear Modulus (MPa) | Poisson’s Ratio | ||||||
|---|---|---|---|---|---|---|---|---|
| E1 = EL | E2 = ET | E3 = ER | G12 = GLT | G23 = GTR | G13 = GLR | ν12 = νLT | ν23 = νTR | ν13 = νLR |
| 13,739 | 1138 | 2240 | 1056 | 456 | 1608 | 0.52 | 0.36 | 0.45 |
| Source | Property | Specimen No. | Avg | Stdev | Cov (%) | ||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | |||||
| Flexural vibration | E1 = EL | 16,803 | 16,861 | 16,916 | 16,860 | 57 | 0.34 |
| Flexural vibration | E2 = ET | 1202 | 1210 | 1199 | 1204 | 6 | 0.47 |
| Longitudinal vibration | EL | 15,977 | 16,225 | 16,665 | 16,289 | 348 | 2.14 |
| ET | 1139 | 1216 | 1166 | 1174 | 39 | 3.31 | |
| Kollman [31] | E3 = ER | - | - | - | 2737 | ||
| Torsional vibration | G12 = GLT | 1055 | 1070 | 1124 | 1083 | 37 | 3.39 |
| Torsional vibration | G23 = GTR | 365 | 341 | 383 | 363 | 21 | 5.81 |
| Torsional vibration | G13 = GLR | 1416 | 1442 | 1428 | 1429 | 13 | 0.89 |
| Kollman [31] | ν12 = νLT | - | - | - | 0.52 | ||
| Kollman [31] | ν23 = νTR | - | - | - | 0.36 | ||
| Kollman [31] | ν13 = νLR | - | - | - | 0.45 | ||
| Experiment—Average Value | Modal Analysis—Finite Element Method | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Flexural | Tors | Long | Flexural | Tors | Long | ||||||||
| Specimen | First Ply Orientation (°) | f1 | f2 | f3 | f4 | f1 | f1 | f1 | f2 | f3 | f4 | fi | f1 |
| 11E | 0 | 445 | 1188 | 2230 | 3491 | 938 | 5662 | 445 | 1192 | 2243 | 3526 | 953 | 5755 |
| 11E | 90 | 120 | 327 | 630 | 1021 | 781 | 1524 | 120 | 328 | 634 | 1028 | 808 | 1547 |
| 11A | 0 | 352 | 924 | 1700 | 2612 | 1016 | 3662 | 363 | 954 | 1751 | 2681 | 1053 | 3732 |
| 11A | 22.5 | 278 | 741 | 1389 | 2252 | 1046 | 3593 | 297 | 790 | 1477 | 2328 | 1084 | 3705 |
| 11A | 45 | 199 | 540 | 1015 | 1661 | 1106 | 3494 | 218 | 589 | 1098 | 1786 | 1098 | 3648 |
| 11A | 67.5 | 162 | 443 | 855 | 1386 | 1117 | 3322 | 174 | 474 | 914 | 1483 | 1173 | 3488 |
| 11A | −90 | 160 | 440 | 845 | 1368 | 1110 | 3207 | 169 | 460 | 888 | 1441 | 1161 | 3354 |
| 11A | −22.5 | 329 | 865 | 1592 | 2453 | 1022 | 3625 | 342 | 900 | 1656 | 2543 | 1070 | 3730 |
| 11A | −45 | 253 | 678 | 1275 | 1957 | 1034 | 3556 | 266 | 711 | 1338 | 2051 | 1090 | 3647 |
| 11A | −67.5 | 189 | 516 | 982 | 1575 | 1089 | 3328 | 200 | 542 | 1029 | 1658 | 1137 | 3471 |
| 11P | 0 | 351 | 925 | 1704 | 2634 | 779 | 4314 | 362 | 954 | 1759 | 2703 | 869 | 4412 |
| 11P | −22.5 | 242 | 656 | 1262 | 1952 | 1108 | 3103 | 254 | 684 | 1313 | 2024 | 1143 | 3214 |
| 11P | −45 | 191 | 525 | 1010 | 1628 | 1273 | 2551 | 204 | 554 | 1063 | 1711 | 1293 | 2638 |
| 11P | −67.5 | 221 | 596 | 1143 | 1792 | 1034 | 3094 | 231 | 623 | 1192 | 1873 | 1070 | 3114 |
| 11P | −90 | 271 | 721 | 1355 | 2113 | 824 | 3945 | 286 | 763 | 1426 | 2226 | 868 | 4078 |
| 7A | 0 | 527 | 1395 | 2585 | 3989 | 1163 | 5618 | 547 | 1442 | 2661 | 4094 | 1189 | 5787 |
| 7A | 22.5 | 400 | 1072 | 2030 | 3003 | 1210 | 5729 | 411 | 1101 | 2082 | 3295 | 1238 | 5743 |
| 7A | 45 | 286 | 779 | 1511 | 2362 | 1306 | 5632 | 293 | 797 | 1552 | 2425 | 1328 | 0 |
| 7A | 67.5 | 233 | 639 | 1231 | 2007 | 1296 | 5036 | 245 | 671 | 1293 | 2116 | 1342 | 5180 |
| 7A | −90 | 238 | 658 | 1278 | 2039 | 1207 | 4770 | 250 | 682 | 1329 | 2138 | 1261 | 4901 |
| 7A | −22.5 | 476 | 1270 | 2345 | 3625 | 1282 | 5590 | 497 | 1312 | 2425 | 3735 | 1309 | 5792 |
| 7A | −45 | 395 | 1047 | 1958 | 3055 | 1368 | 5577 | 408 | 1085 | 2028 | 3166 | 1225 | 5665 |
| 7A | −67.5 | 297 | 802 | 1536 | 2489 | 1157 | 5051 | 308 | 832 | 1595 | 2589 | 1200 | 5148 |
| 7P | 0 | 542 | 1435 | 2665 | 4090 | 909 | 6718 | 559 | 1471 | 2711 | 4164 | 960 | 6837 |
| 7P | −22.5 | 349 | 949 | 1840 | 3038 | 1352 | 4721 | 378 | 1021 | 1963 | 3181 | 1361 | 4914 |
| 7P | −45 | 278 | 770 | 1496 | 2435 | 1495 | 3862 | 297 | 814 | 1583 | 2560 | 1526 | 3992 |
| 7P | −67.5 | 310 | 842 | 1617 | 2600 | 1123 | 4610 | 324 | 877 | 1679 | 2701 | 1194 | 4675 |
| 7P | −90 | 366 | 989 | 1866 | 2926 | 900 | 5895 | 383 | 1027 | 1932 | 3039 | 956 | 6040 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Merhar, M. Determination of Elastic Properties of Beech Plywood by Analytical, Experimental and Numerical Methods. Forests 2020, 11, 1221. https://doi.org/10.3390/f11111221
Merhar M. Determination of Elastic Properties of Beech Plywood by Analytical, Experimental and Numerical Methods. Forests. 2020; 11(11):1221. https://doi.org/10.3390/f11111221
Chicago/Turabian StyleMerhar, Miran. 2020. "Determination of Elastic Properties of Beech Plywood by Analytical, Experimental and Numerical Methods" Forests 11, no. 11: 1221. https://doi.org/10.3390/f11111221
APA StyleMerhar, M. (2020). Determination of Elastic Properties of Beech Plywood by Analytical, Experimental and Numerical Methods. Forests, 11(11), 1221. https://doi.org/10.3390/f11111221





