Development of Crown Ratio and Height to Crown Base Models for Masson Pine in Southern China
Abstract
:1. Introduction
2. Materials and Methods
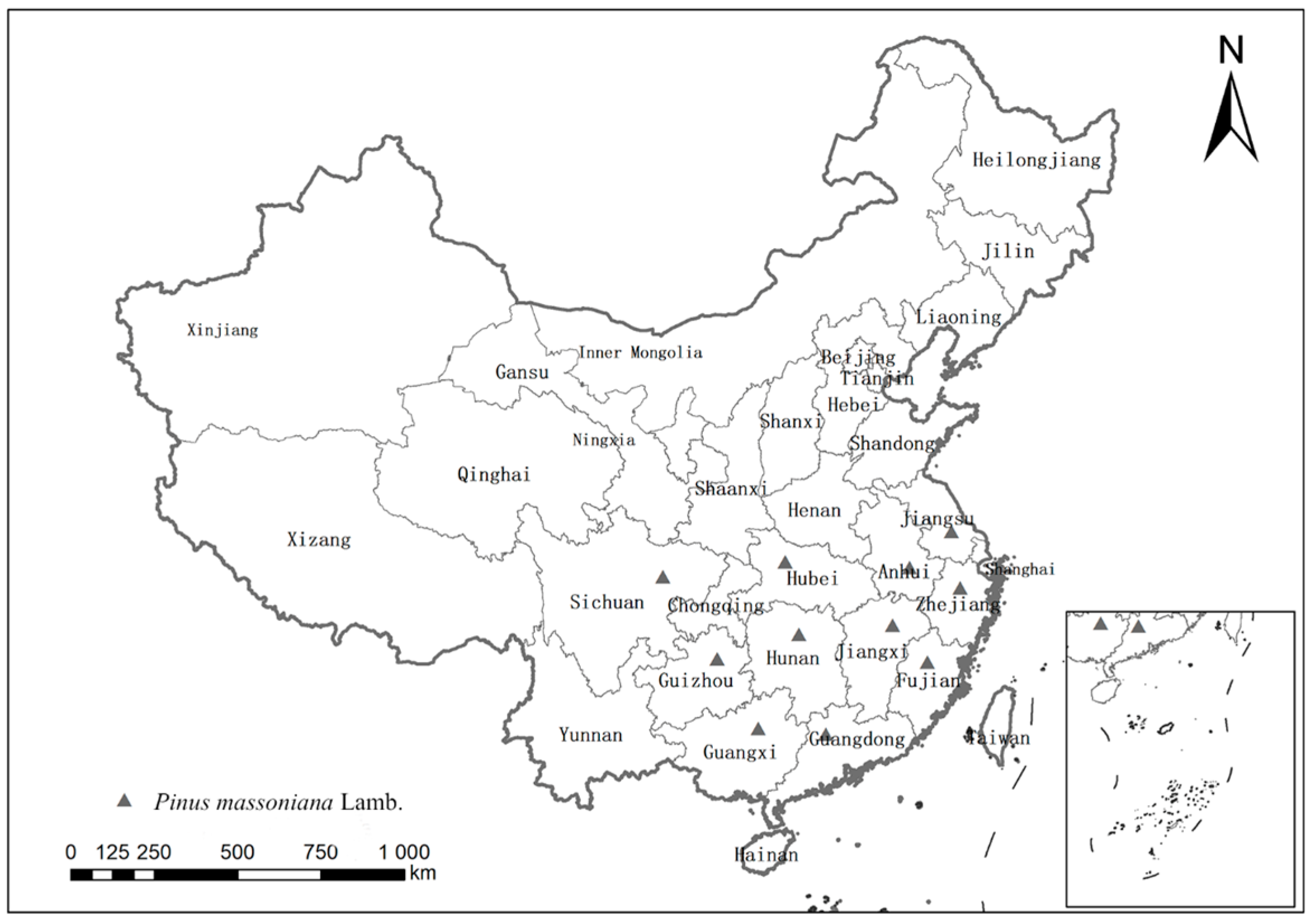
2.1. Data
2.2. Model Development
2.2.1. Basic Model Selection
2.2.2. Additional Variable Selection
2.2.3. Parameter Estimation and Evaluation
2.3. Model Validation
3. Results
3.1. Basic Model Selection
3.2. Inclusion of Additional Covariates
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Muth, C.C.; Bazzaz, F.A. Tree canopy displacement and neighborhood interactions. Can. J. For. Res. 2003, 33, 1323–1330. [Google Scholar] [CrossRef]
- Carreiras, J.M.B.; Pereira, J.M.C.; Pereira, J.S. Estimation of tree canopy cover in evergreen oak woodlands using remote sensing. For. Ecol. Manag. 2006, 223, 45–53. [Google Scholar] [CrossRef]
- Terashima, I.; Hikosaka, K. Comparative ecophysiology of leaf and canopy photosynthesis. Plant Cell Environ. 1995, 18, 1111–1128. [Google Scholar] [CrossRef]
- Ma, S.Y.; Osuna, J.; Verfaillie, J.; Baldocchi, D. Photosynthetic responses to temperature across leaf–canopy–ecosystem scales: A 15-year study in a Californian oak-grass savanna. Photosynth. Res. 2017, 132. [Google Scholar] [CrossRef]
- Turnbull, M.H.; Whitehead, D.; Tissue, D.T.; Schuster, W.S.F.; Brown, K.J.; Griffin, K.L. Scaling Foliar Respiration in Two Contrasting Forest Canopies. Funct. Ecol. 2003, 17, 101–114. [Google Scholar] [CrossRef]
- Drake, J.; Tjoelker, M.; Aspinwall, M.; Reich, P.; Barton, C.; Medlyn, B.; Duursma, R. Does physiological acclimation to climate warming stabilize the ratio of canopy respiration to photosynthesis? New Phytol. 2016, 211, 850–863. [Google Scholar] [CrossRef]
- Schulze, E.D.; Čermák, J.; Matyssek, M.; Penka, M.; Zimmermann, R.; Vasícek, F.; Gries, W.; Kučera, J. Canopy transpiration and water fluxes in the xylem of the trunk of Larix and Picea trees—A comparison of xylem flow, porometer and cuvette measurements. Oecologia 1985, 66, 475–483. [Google Scholar] [CrossRef]
- Köstner, B.M.M.; Schulze, E.D.; Kelliher, F.M.; Hollinger, D.Y.; Byers, J.N.; Hunt, J.E.; McSeveny, T.M.; Meserth, R.; Weir, P.L. Transpiration and canopy conductance in a pristine broad-leaved forest of Nothofagus: An analysis of xylem sap flow and eddy correlation measurements. Oecologia 1992, 91, 350–359. [Google Scholar] [CrossRef]
- Meinzer, F.C.; Andrade, J.L.; Goldstein, G.; Holbrook, N.M.; Cavelier, J.; Wright, S.J. Partitioning of soil water among canopy trees in a seasonally dry tropical forest. Oecologia 1999, 121, 293–301. [Google Scholar] [CrossRef]
- Zhang, X.; Luo, L.; Jing, W.; Wang, S.; Wang, R.; Che, Z. Study on the Distribution Effect of Canopy Interception of Picea Crassifolia Forest in Qilian Mountains. J. Mt. Sci. 2007, 25, 678–683. [Google Scholar] [CrossRef]
- Scott, J.H.; Reinhardt, E.D.; Station, R.M.R. Assessing Crown Fire Potential by Linking Models of Surface and Crown Fire Behavior; U.S. Department of Agriculture, Forest Service, Rocky Mountain Research Station: Fort Collins, CO, USA, 2001. [CrossRef] [Green Version]
- Peterson, D.L.; Johnson, M.C.; Agee, J.K.; Jain, T.B.; McKenzie, D.; Reinhardt, E.D. Forest Structure and Fire Hazard in Dry Forests of the Western United States; U.S. Department of Agriculture, Forest Service, Pacific Northwest Research Station: Portland, OR, USA, 2005. [CrossRef]
- Lentile, L.; Smith, F.; Shepperd, W. Influence of topography and forest structure on patterns of mixed severity fire in ponderosa pine forests of the South Dakota Black Hills, USA. Int. J. Wildland Fire 2006, 15, 557–566. [Google Scholar] [CrossRef]
- Cruz, M.; Alexander, M.; WakimotoC, R. Assessing canopy fuel stratum characteristics in crown fire prone fuel types of western North America. Int. J. Wildland Fire 2003, 12. [Google Scholar] [CrossRef] [Green Version]
- Fernández-Alonso, J.M.; Alberdi, I.; Álvarez-González, J.G.; Vega, J.A.; Cañellas, I.; Ruiz-González, A.D. Canopy fuel characteristics in relation to crown fire potential in pine stands: Analysis, modelling and classification. Eur. J. For. Res. 2013, 132, 363–377. [Google Scholar] [CrossRef]
- Mitsopoulos, I.D.; Dimitrakopoulos, A.P. Estimation of canopy fuel characteristics of Aleppo pine (Pinus halepensis Mill.) forests in Greece based on common stand parameters. Eur. J. For. Res. 2014, 133, 73–79. [Google Scholar] [CrossRef]
- Keyes, C.; O’Hara, K. Quantifying Stand Targets for Silvicultural Prevention of Crown Fires. West. J. Appl. For. 2002, 17, 101–109. [Google Scholar] [CrossRef] [Green Version]
- Ruiz-González, A.; Álvarez-González, J. Canopy bulk density and canopy base height equations for assessing crown fire hazard in Pinus radiata plantations. Can. J. For. Res. 2011, 41, 839–850. [Google Scholar] [CrossRef]
- Sherlock, J.W. Integrating stand density management with fuel reduction. In Restoring Fire-Adapted Ecosystems: Proceedings of the 2005 National Silviculture Workshop; Powers, R.F., Ed.; PSW-GTR-203; Pacific Southwest Research Station, Forest Service, U.S. Department of Agriculture: Albany, CA, USA, 2007; pp. 55–66. [Google Scholar]
- López-Sánchez, C.; Rodríguez-Soalleiro, R. A Density Management Diagram Including Stand Stability and Crown Fire Risk for Pseudotsuga Menziesii (Mirb.) Franco in Spain. Mt. Res. Dev. 2009, 29, 169–176. [Google Scholar] [CrossRef]
- Gómez-Vázquez, I.; Fernandes, P.; Arias-Rodil, M.; Anta, M.; Castedo-Dorado, F. Using density management diagrams to assess crown fire potential in Pinus pinaster Ait. stands. Ann. For. Sci. 2014, 473–484. [Google Scholar] [CrossRef] [Green Version]
- Härkönen, S.; Neumann, M.; Mues, V.; Berninger, F.; Bronisz, K.; Cardellini, G.; Chirici, G.; Hasenauer, H.; Koehl, M.; Lang, M.; et al. A climate-sensitive forest model for assessing impacts of forest management in Europe. Environ. Model. Softw. 2019, 115, 128–143. [Google Scholar] [CrossRef]
- Mitchell, K.J. Dynamics and Simulated Yieldof Douglas-fir. For. Sci. 1975, 21, a0001–z0001. [Google Scholar] [CrossRef]
- Wykoff, W.; Crookston, N.L.; Stage, A.; Forest, I.; Station, R.E. User’s Guide to the Stand Prognosis Model; U.S. Dept. of Agriculture, Forest Service, Intermountain Forest and Range Experiment Station: Ogden, UT, USA, 1982.
- Ritchie, M.; Hann, D. Equations for predicting basal area increment in Douglas-fir and grand fir. Or. State Univ. For. Res. Lab. Res. Bull. 1985, 51. Available online: https://ir.library.oregonstate.edu/downloads/wd375x45s (accessed on 11 November 2020).
- Wykoff, W.R. A Basal Area Increment Model for Individual Conifers in the Northern Rocky Mountains. For. Sci. 1990, 36, 1077–1104. [Google Scholar] [CrossRef]
- Biging, G.S.; Dobbertin, M. A Comparison of Distance-Dependent Competition Measures for Height and Basal Area Growth of Individual Conifer Trees. For. Sci. 1992, 38, 695–720. [Google Scholar] [CrossRef]
- Monserud, R.A.; Sterba, H. A basal area increment model for individual trees growing in even- and uneven-aged forest stands in Austria. For. Ecol. Manag. 1996, 80, 57–80. [Google Scholar] [CrossRef]
- Cole, W.G.; Lorimer, C.G. Predicting tree growth from crown variables in managed northern hardwood stands. For. Ecol. Manag. 1994, 67, 159–175. [Google Scholar] [CrossRef]
- Zarnoch, S.; Bechtold, W.A.; Stolte, K. Using crown condition variables as indicators of forest health. Can. J. For. Res.-Rev. Can. De Rech. For. Can J For. Res 2004, 34, 1057–1070. [Google Scholar] [CrossRef]
- Sharma, R.; Vacek, Z.; Vacek, S. Generalized Nonlinear Mixed-Effects Individual Tree Crown Ratio Models for Norway Spruce and European Beech. Forests 2018, 9, 555. [Google Scholar] [CrossRef] [Green Version]
- Cameron, I.; Parish, R.; Goudie, J.; Statland, C. Modelling the Crown Profile of Western Hemlock (Tsuga heterophylla) with a Combination of Component and Aggregate Measures of Crown Size. Forests 2020, 11, 281. [Google Scholar] [CrossRef] [Green Version]
- Fu, L.; Zhang, H.; Lu, J.; Zang, H.; Lou, M.; Wang, G.; Wang, L. Multilevel Nonlinear Mixed-Effect Crown Ratio Models for Individual Trees of Mongolian Oak (Quercus mongolica) in Northeast China. PLoS ONE 2015, 10, e0133294. [Google Scholar] [CrossRef]
- Leites, L.; Robinson, A.; Crookston, N. Accuracy and equivalence testing of crown ratio models and assessment of their impact on diameter growth and basal area increment predictions of two variants of the Forest Vegetation Simulator. Can. J. For. Res. 2009, 39, 655–665. [Google Scholar] [CrossRef]
- Wilson, J.S.; Oliver, C.D. Stability and density management in Douglas-fir plantations. Can. J. For. Res. 2000, 30, 910–920. [Google Scholar] [CrossRef]
- Hasenauer, H.; Monserud, R.A. A crown ratio model for Austrian forests. For. Ecol. Manag. 1996, 84, 49–60. [Google Scholar] [CrossRef]
- Fu, L.; Zhang, H.; Sharma, R.; Lifeng, P.; Wang, G. A generalized nonlinear mixed-effects height to crown base model for Mongolian oak in northeast China. For. Ecol. Manag. 2016, 384, 34–43. [Google Scholar] [CrossRef]
- Petersson, H. Functions for predicting crown height of Pinus sylvestris and Picea abies in Sweden. Scand. J. For. Res. 1997, 12, 179–188. [Google Scholar] [CrossRef]
- Jiménez, E.; Vega, J.; Fernández-Alonso, J.; Vega-Nieva, D.; González, J.; Ruiz-González, A. Allometric equations for estimating canopy fuel load and distribution of pole-size maritime pine trees in five Iberian provenances. Can. J. For. Res. 2013, 43, 149. [Google Scholar] [CrossRef]
- Wagner, C.E.V. Conditions for the start and spread of crown fire. Can. J. For. Res. 1977, 7, 23–34. [Google Scholar] [CrossRef]
- McAlpine, R.S.; Hobbs, M.W. Predicting the height to live crown base in plantations of four boreal forest species. Int. J. Wildland Fire 1994, 4, 103–106. [Google Scholar] [CrossRef]
- Butler, B.W.; Finney, M.A.; Andrews, P.L.; Albini, F.A. A radiation-driven model for crown fire spread. Can. J. For. Res. 2004, 34, 1588–1599. [Google Scholar] [CrossRef]
- Fernandes, P.M. Combining forest structure data and fuel modelling to classify fire hazard in Portugal. Ann. For. Sci. 2009, 66, 415. [Google Scholar] [CrossRef] [Green Version]
- Short Iii, E.A.; Burkhart, H.E. Predicting Crown-Height Increment for Thinned and Unthinned Loblolly Pine Plantations. For. Sci. 1992, 38, 594–610. [Google Scholar] [CrossRef]
- Monserud, R.A.; Sterba, H. Modeling individual tree mortality for Austrian forest species. For. Ecol. Manag. 1999, 113, 109–123. [Google Scholar] [CrossRef]
- Hann, D.J.O.S.U. ORGANON user’s Manual Edition 8.2 [Computer Manual]; Department of Forest Resources: Corvallis, OR, USA, 2006.
- Kuprevicius, A.; Auty, D.; Achim, A.; Caspersen, J.P. Quantifying the influence of live crown ratio on the mechanical properties of clear wood. For. Int. J. For. Res. 2013, 86, 361–369. [Google Scholar] [CrossRef] [Green Version]
- Sharma, R.; Vacek, Z.; Vacek, S. Modelling tree crown-to-bole diameter ratio for Norway spruce and European beech. Silva Fenn. 2017, 51, 1740. [Google Scholar] [CrossRef] [Green Version]
- Rijal, B.; Weiskittel, A.; Kershaw, J. Development of height to crown base models for thirteen tree species of the North American Acadian Region. For. Chron. 2012, 88, 60–73. [Google Scholar] [CrossRef] [Green Version]
- Administration, C.S.F. China Forest Resource Report (2014–2018); China Forestry Press: Beijing, China, 2019. [Google Scholar]
- Meng, J.; Lu, Y.; Zeng, J. Transformation of a Degraded Pinus massoniana Plantation into a Mixed-Species Irregular Forest: Impacts on Stand Structure and Growth in Southern China. Forests 2014, 5, 3199–3221. [Google Scholar] [CrossRef]
- Wu, D.; Yi, S.; Liu, A.; Liu, S.; Cai, M. Understory Burning In Stands Of Masson’s Pine. Fire Saf. Sci. 2003, 7, 545–556. [Google Scholar] [CrossRef]
- Molina, J.R.; Silva, F.R.Y.; Herrera, M.Á. Potential crown fire behavior in Pinus pinea stands following different fuel treatments. For. Syst. 2011, 20, 266–267. [Google Scholar] [CrossRef] [Green Version]
- Xue, L.; Li, Q.; Chen, H. Effects of a Wildfire on Selected Physical, Chemical and Biochemical Soil Properties in a Pinus massoniana Forest in South China. Forests 2014, 5, 2947–2966. [Google Scholar] [CrossRef] [Green Version]
- Fernandes, P.; Luz, A.L.; Loureiro, C.; Godinho-Ferreira, P.; Botelho, H. Fuel modelling and fire hazard assessment based on data from the Portuguese National Forest Inventory. For. Ecol. Manag. 2006, 234. [Google Scholar] [CrossRef]
- Fajvan, M.A. The Role of Silvicultural Thinning in Eastern Forests Threatened by Hemlock Woolly Adelgid (Adelges tsugae). In Proceedings of USDA Forest Service-General Technical Report PNW-GTR; U.S. Department of Agriculture, Forest Service, Pacific Northwest Research Station: Portland, OR, USA, 2007; pp. 247–256. [Google Scholar]
- Azuma, D.; Monleon, V.; Gedney, D. Equations for Predicting Uncompacted Crown Ratio Based on Compacted Crown Ratio and Tree Attributes. West. J. Appl. For. 2004, 19, 260–267. [Google Scholar] [CrossRef] [Green Version]
- Mitsopoulos, I.D.; Dimitrakopoulos, A.P. Canopy fuel characteristics and potential crown fire behavior in Aleppo pine (Pinus halepensis Mill.) forests. Ann. For. Sci. 2007, 64, 287–299. [Google Scholar] [CrossRef] [Green Version]
- Keyser, T.; Smith, F. Influence of Crown Biomass Estimators and Distribution on Canopy Fuel Characteristics in Ponderosa Pine Stands of the Black Hills. For. Sci. 2010, 56, 156–165. [Google Scholar]
- Zeng, W. Modeling Crown Biomass for Four Pine Species in China. Forests 2015, 6, 433–449. [Google Scholar] [CrossRef] [Green Version]
- Soares, P.; Tomé, M. A tree crown ratio prediction equation for eucalypt plantations. Ann. For. Sci. 2001, 58, 193–202. [Google Scholar] [CrossRef] [Green Version]
- Temesgen, H.; LeMay, V.; Mitchell, S.J. Tree crown ratio models for multi-species and multi-layered stands of southeastern British Columbia. For. Chron. 2005, 81, 133–141. [Google Scholar] [CrossRef]
- Popoola, F.S.; Adesoye, P. Crown Ratio Models for Tectona grandis (Linn. f) Stands in Osho Forest Reserve, Oyo State, Nigeria. J. For. Sci. 2012, 28, 63–67. [Google Scholar] [CrossRef]
- Dyer, M.E.; Burkhart, H.E. Compatible crown ratio and crown height models. Can. J. For. Res. 1987, 17, 572–574. [Google Scholar] [CrossRef]
- Walters, D.; Hann, D. Taper equations for six conifer species in southwest Oregon. Or. State Univ. For. Res. Lab. Res. Bull. 1986, 56, 1–41. [Google Scholar]
- Duan, G.; Li, X.; Feng, Y.; Fu, L. Generalized nonlinear mixed-effects crown base height model of Larix principis-rupprechtii natural secondary forests. J. Nanjing For. Univ. 2018, 42, 170–176. [Google Scholar] [CrossRef]
- Garber, S.M.; Monserud, R.A.; Maguire, D.A. Crown recession patterns in three conifer species of the northern Rocky Mountains. For. Sci. 2008, 54, 633–646. [Google Scholar]
- Sumida, A.; Miyaura, T.; Torii, H. Relationships of tree height and diameter at breast height revisited: Analyses of stem growth using 20-year data of an even-aged Chamaecyparis obtusa stand. Tree Physiol. 2013, 33, 106–118. [Google Scholar] [CrossRef] [PubMed]
- Sharma, R.; Vacek, Z.; Vacek, S.; Podrázský, V.; Jansa, V. Modelling individual tree height to crown base of Norway spruce (Picea abies (L.) Karst.) and European beech (Fagus sylvatica L.). PLoS ONE 2017, 12, e0186394. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zumrawi, A.; Hann, D. Equations for predicting the height to crown base of six tree species in the central Willamette Valley of Oregon. Or. State Univ. For. Res. Lab. 1989, 52, 1–9. [Google Scholar]
- Wang, Y.; Titus, S.J.; LeMay, V.M. Relationships between tree slenderness coefficients and tree or stand characteristics for major species in boreal mixedwood forests. Can. J. For. Res. 1998, 28, 1171–1183. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, H.; Chhin, S.; Zhang, J. Effects of competition, age and climate on tree slenderness of Chinese fir plantations in southern China. For. Ecol. Manag. 2020, 458, 117815. [Google Scholar] [CrossRef]
- Kahriman, A.; Şahin, A.; Sonmez, T.; Yavuz, M. A novel approach to selecting a competition index: The effect of competition on individual tree diameter growth of Calabrian pine. Can. J. For. Res. 2018, 48, 1217–1226. [Google Scholar] [CrossRef]
- Krajicek, J.E.; Brinkman, K.A.; Gingrich, S.F. Crown Competition-A Measure of Density. For. Sci. 1961, 7, 35–42. [Google Scholar] [CrossRef]
- Yang, Y.; Huang, S. Allometric modelling of crown width for white spruce by fixed- and mixed-effects models. For. Chron. 2017, 93, 138–147. [Google Scholar] [CrossRef] [Green Version]
- Lu, J.; Li, F.; Zhang, H.; Zhang, S. A crown ratio model for dominant species in secondary forests in Mao’er Mountain. Sci. Silvae Sin. 2011, 47, 70–76. [Google Scholar] [CrossRef]
- Uzoh, F.; Oliver, W. Individual tree diameter increment model for managed even-aged stands of ponderosa pine throughout the western United States using a multilevel linear mixed effects model. For. Ecol. Manag. 2008, 256, 438–445. [Google Scholar] [CrossRef]
- Fu, L.; Sun, H.; Sharma, R.; Lei, Y.; Zhang, H.; Tang, S. Nonlinear mixed-effects crown width models for individual trees of Chinese fir (Cunninghamia lanceolata) in south-central China. For. Ecol. Manag. 2013, 302, 210–220. [Google Scholar] [CrossRef]
- Montgomery, D.C.; Peck, E.A.; Vining, G.G. Introduction to Linear Regression Analysis; Wiley: Hoboken, NJ, USA, 2001. [Google Scholar]
- Sharma, R.; Bílek, L.; Vacek, Z.; Vacek, S. Modelling crown width–diameter relationship for Scots pine in the central Europe. Trees 2017. [Google Scholar] [CrossRef]
- Li, X.; Dong, L. Building height to crown base models for Mongolian pine plantation based on simultaneous equations in Heilongjiang Province of northeastern China. J. Beijing For. Univ. 2018, 40, 9–18. [Google Scholar] [CrossRef]
- Wang, W.; Chen, X.; Zeng, W.-S.; Wang, J.; Meng, J. Development of a Mixed-Effects Individual-Tree Basal Area Increment Model for Oaks (Quercus spp.) Considering Forest Structural Diversity. Forests 2019, 10, 474. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Bai, Y.; Jiang, C.; Yang, H.; Meng, J. Development of a linear mixed-effects individual-tree basal area increment model for masson pine in Hunan Province, South-central China. J. Sustain. For. 2019, 39, 526–541. [Google Scholar] [CrossRef]
- Ritz, C.; Streibig, J.C. Nonlinear Regression with R; Springer: New York, NY, USA, 2008; Volume 148. [Google Scholar] [CrossRef]
- Straub, C.; Stepper, C.; Seitz, R.; Waser, L. Potential of UltraCamX stereo images for estimating timber volume and basal area at the plot level in mixed European forests. Can. J. For. Res. 2013, 43, 731–741. [Google Scholar] [CrossRef]
- Ahmadi, K.; Alavi, S.J. Generalized height-diameter models for Fagus orientalis Lipsky in Hyrcanian forest, Iran. J. For. Sci. 2016, 62, 413–421. [Google Scholar] [CrossRef]
- De Brogniez, D.; Ballabio, C.; Stevens, A.; Jones, R.; Montanarella, L.; Wesemael, B. A map of the topsoil organic carbon content of Europe generated by a generalized additive model. Eur. J. Soil Sci. 2014, 66, 121–134. [Google Scholar] [CrossRef]
- Quan, N.T. The prediction sum of squares as a general measure for regression diagnostics. J. Bus. Econ. Stat. 1988, 6, 501–504. [Google Scholar]
- Team, C. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2017. [Google Scholar]
- Pinheiro, J.; Bates, D.; DebRoy, S.; Sarkar, D.; Team, R.C. nlme: Linear and Nonlinear Mixed Effects Models. 2020. Available online: https://CRAN.R-project.org/package=nlme (accessed on 17 November 2020).
- Hadley, W. ggplot2: Elegant Graphics for Data Analysis; Springer New York: New York, NY, USA, 2016. [Google Scholar]
- Meng, J.; Bai, Y.; Zeng, W.-S.; Ma, W. A management tool for reducing the potential risk of windthrow for coastal Casuarina equisetifolia L. stands on Hainan Island, China. Eur. J. For. Res. 2017, 136, 543–554. [Google Scholar] [CrossRef]
- Ritchie, M.; Hann, D. Equations for Predicting Height to Crown Base for Fourteen Tree Species in Southwest Oregon. Or. State Univ. For. Res. Lab. 1987, 50, 1–14. [Google Scholar]
- Kiernan, D.H.; Bevilacqua, E.; Nyland, R.D. Individual-tree diameter growth model for sugar maple trees in uneven-aged northern hardwood stands under selection system. For. Ecol. Manag. 2008, 256, 1579–1586. [Google Scholar] [CrossRef]
- Subedi, N.; Sharma, M. Individual-tree diameter growth models for black spruce and jack pine plantations in northern Ontario. For. Ecol. Manag. 2011, 261, 2140–2148. [Google Scholar] [CrossRef]
- Zhao, L.; Li, C.; Tang, S. Individual-tree diameter growth model for fir plantations based on multi-level linear mixed effects models across southeast China. J. For. Res. 2013, 18, 305–315. [Google Scholar] [CrossRef]
- Bohora, S.B.; Cao, Q. Prediction of tree diameter growth using quantile regression and mixed-effects models. For. Ecol. Manag. 2014, 319, 62–66. [Google Scholar] [CrossRef]
- Hao, X.; Yujun, S.; Xinjie, W.; Jin, W.; Yao, F. Linear mixed-effects models to describe individual tree crown width for China-fir in Fujian province, southeast China. PLoS ONE 2015, 10, e0122257. [Google Scholar] [CrossRef] [Green Version]
- Sharma, R.P.; Vacek, Z.; Vacek, S. Individual tree crown width models for Norway spruce and European beech in Czech Republic. For. Ecol. Manag. 2016, 366, 208–220. [Google Scholar] [CrossRef]
- Perin, J.; Hébert, J.; Brostaux, Y.; Lejeune, P.; Claessens, H.J. Modelling the top-height growth and site index of Norway spruce in Southern Belgium. For. Ecol. Manag. 2013, 298, 62–70. [Google Scholar] [CrossRef]
- Wang, Y.; LeMay, V.M.; Baker, T.G. Modelling and prediction of dominant height and site index of Eucalyptus globulus plantations using a nonlinear mixed-effects model approach. Can. J. For. Res. 2007, 37, 1390–1403. [Google Scholar] [CrossRef]
- Zhu, G.; Hu, S.; Chhin, S.; Zhang, X.; He, P.J. Modelling site index of Chinese fir plantations using a random effects model across regional site types in Hunan province, China. For. Ecol. Manag. 2019, 446, 143–150. [Google Scholar] [CrossRef]
- Fu, L.; Zeng, W.; Zhang, H.; Wang, G.; Lei, Y.; Tang, S. Generic linear mixed-effects individual-tree biomass models for Pinus massoniana in southern China. South. For. A J. For. Sci. 2014, 76, 47–56. [Google Scholar]
- Huber, J.A.; May, K.; Hülsbergen, K.-J. Allometric tree biomass models of various species grown in short-rotation agroforestry systems. Eur. J. For. Res. 2017, 136, 75–89. [Google Scholar] [CrossRef]
- Huff, S.; Poudel, K.P.; Ritchie, M.; Temesgen, H. Quantifying aboveground biomass for common shrubs in northeastern California using nonlinear mixed effect models. For. Ecol. Manag. 2018, 424, 154–163. [Google Scholar] [CrossRef]
- Nong, M.; Leng, Y.; Xu, H.; Li, C.; Ou, G.J. Incorporating competition factors in a mixed-effect model with random effects of site quality for individual tree above-ground biomass growth of Pinus kesiya var. langbianensis. N. Zeal. J. For. Sci. 2019, 49. [Google Scholar] [CrossRef] [Green Version]
- Pokharel, B.; Dech, J.P. Mixed-effects basal area increment models for tree species in the boreal forest of Ontario, Canada using an ecological land classification approach to incorporate site effects. For. Int. J. For. Res. 2012, 85, 255–270. [Google Scholar] [CrossRef] [Green Version]

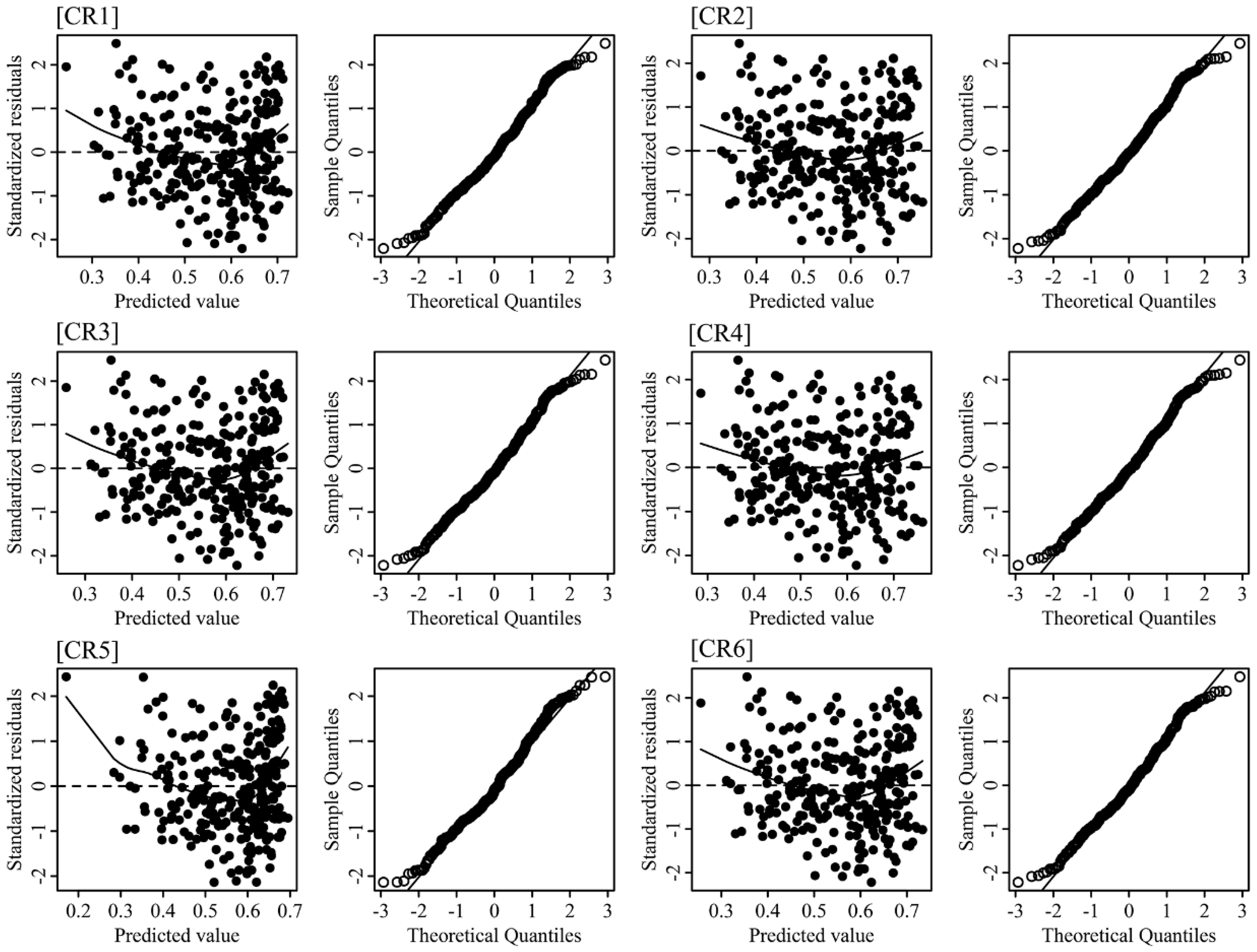
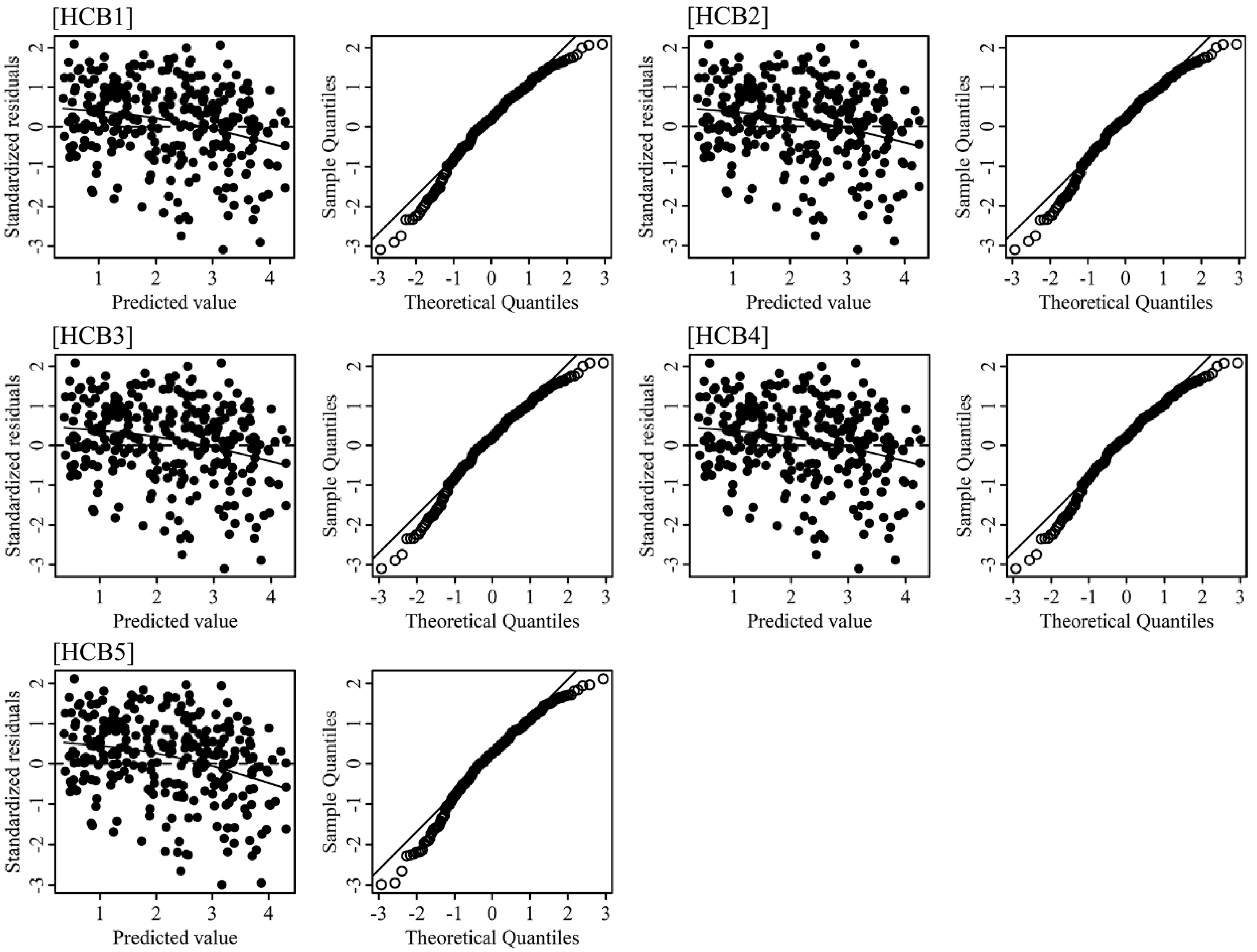

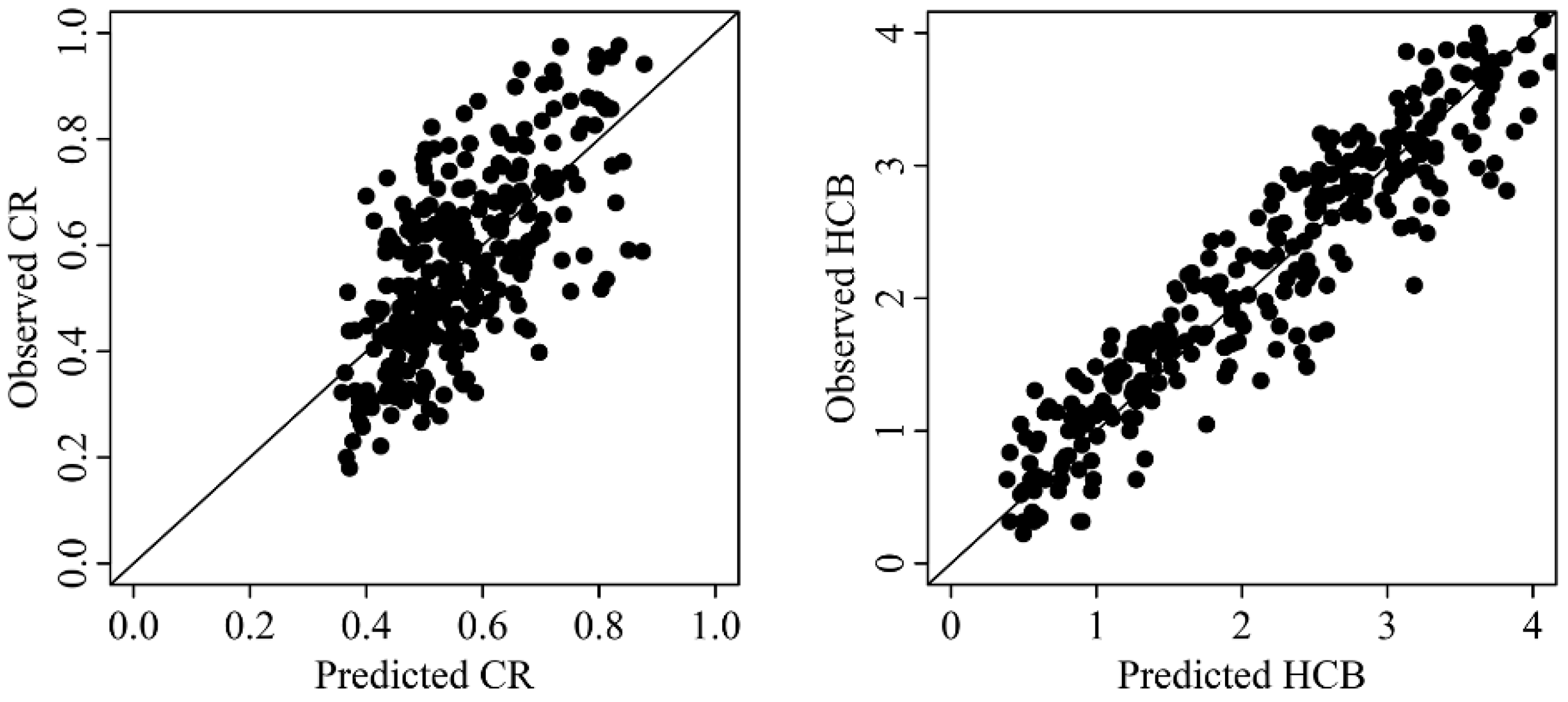
| Model | Equation | Model Form | Range of Function Value | Reference |
|---|---|---|---|---|
| CR1 | Logistic | (0, 1) | [62] | |
| CR2 | Richards | (0, 1) | [61] | |
| CR3 | Richards | (0, 1) | [63] | |
| CR4 | Exponential | (0, +) | [34] | |
| CR5 | Exponential | (−, 1) | [64] | |
| CR6 | Weibull | (−, 1) | [61] | |
| HCB1 | Logistic | (0, H) | [65] | |
| HCB2 | Richards | (0, H) | [49] | |
| HCB3 | Richards | (0, H) | [66] | |
| HCB4 | Exponential | (0, +) | [64] | |
| HCB5 | Exponential | (−, H) | [37] |
| Model | Fitting Statistics of the CR Candidate Models | Cross-Validation | ||||
|---|---|---|---|---|---|---|
| AIC | BIC | RMSE | NMSEte | PRESS | ||
| CR1 | −333.3678 | −318.5928 | 0.1369 | 0.3763 | 0.6726 | 0.5607 |
| CR2 | −344.0376 | −329.2626 | 0.1345 | 0.3983 | 0.6454 | 0.5408 |
| CR3 | −337.2242 | −322.4493 | 0.1360 | 0.3843 | 0.6623 | 0.5533 |
| CR4 | −346.0108 | −331.2359 | 0.1340 | 0.4023 | 0.6409 | 0.5375 |
| CR5 | −319.7976 | −305.0226 | 0.1401 | 0.3471 | 0.7161 | 0.5908 |
| CR6 | −337.3960 | −322.6210 | 0.1360 | 0.3847 | 0.6624 | 0.5531 |
| Model | Fitting Statistics of the HCB Candidate Models | Cross-Validation | ||||
|---|---|---|---|---|---|---|
| AIC | BIC | RMSE | NMSEte | PRESS | ||
| HCB1 | 225.2464 | 236.3275 | 0.3512 | 0.8803 | 0.1246 | 3.7029 |
| HCB2 | 222.4478 | 233.5290 | 0.3495 | 0.8814 | 0.1233 | 3.6683 |
| HCB3 | 223.3159 | 234.3971 | 0.3500 | 0.8811 | 0.1238 | 3.6790 |
| HCB4 | 222.4446 | 233.5258 | 0.3495 | 0.8814 | 0.1234 | 3.6683 |
| HCB5 | 237.8585 | 248.9397 | 0.3587 | 0.8751 | 0.1305 | 3.8639 |
| Variables | DBH | DBH2 | DBH0.5 | ln(DBH) | H | ln(H) | HDR | CW | ln(CW) |
|---|---|---|---|---|---|---|---|---|---|
| CR | −0.38 ** | −0.29 ** | −0.42 ** | −0.46 ** | −0.54 ** | −0.59 ** | −0.04 | −0.28 ** | −0.31 ** |
| HCB | 0.75 ** | 0.67 ** | 0.77 ** | 0.76 ** | 0.92 ** | 0.87 ** | −0.19 ** | 0.61 ** | 0.63 ** |
| Model | Submodel | Number of Variables | The Best Combinations of Variables | ||
|---|---|---|---|---|---|
| c1 | c2 | c3 | |||
| CR2 | CR2_1 | 2 | DBH0.5 | HDR | |
| CR2_2 | 3 | DBH2 | DBH0.5 | HDR | |
| HCB2 | HCB2_1 | 1 | ln(CW) | ||
| HCB2_2 | 2 | H | ln(CW) | ||
| HCB2_3 | 3 | HDR | CW | ln(CW) | |
| Model | Parameter Values | Fitting Statistics | Cross-Validation | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| b0 | b1 | b2 | c1 | c2 | c3 | AIC | BIC | RMSE | NMSEte | PRESS | ||
| CR2 | −1.287 | 0.097 | −0.313 | — | — | — | −344.0376 | −329.2626 | 0.1345 | 0.3983 | 0.6454 | 0.5408 |
| CR2_1 | 5.217 | 0.274 | −0.097 | −2.603 | −2.504 | — | −372.1724 | −350.0100 | 0.1278 | 0.4563 | 0.5821 | 0.4928 |
| CR2_2 | 7.625 | 0.714 | −0.104 | −0.005 | −4.606 | −2.614 | −376.0822 | −350.2261 | 0.1268 | 0.4652 | 0.5813 | 0.4893 |
| Model | Parameter Values | Fitting Statistics | Cross-Validation | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| b0 | b1 | c1 | c2 | c3 | AIC | BIC | RMSE | NMSEte | PRESS | ||
| HCB2 | 8.441 | 0.084 | — | — | — | 222.4478 | 233.5290 | 0.3495 | 0.8814 | 0.1233 | 3.6683 |
| HCB2_1 | 7.980 | 0.064 | 0.584 | — | — | 213.9222 | 228.6972 | 0.3440 | 0.8851 | 0.1189 | 3.5479 |
| HCB2_2 | 7.304 | 0.024 | 0.083 | 0.689 | — | 179.3343 | 197.8029 | 0.3240 | 0.8981 | 0.1059 | 3.1647 |
| HCB2_3 | 6.494 | 0.077 | 0.736 | −0.258 | 1.816 | 198.3975 | 220.5599 | 0.3340 | 0.8917 | 0.1131 | 3.3735 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Wang, W.; Zeng, W.; Wang, J.; Meng, J. Development of Crown Ratio and Height to Crown Base Models for Masson Pine in Southern China. Forests 2020, 11, 1216. https://doi.org/10.3390/f11111216
Li Y, Wang W, Zeng W, Wang J, Meng J. Development of Crown Ratio and Height to Crown Base Models for Masson Pine in Southern China. Forests. 2020; 11(11):1216. https://doi.org/10.3390/f11111216
Chicago/Turabian StyleLi, Yao, Wei Wang, Weisheng Zeng, Jianjun Wang, and Jinghui Meng. 2020. "Development of Crown Ratio and Height to Crown Base Models for Masson Pine in Southern China" Forests 11, no. 11: 1216. https://doi.org/10.3390/f11111216
APA StyleLi, Y., Wang, W., Zeng, W., Wang, J., & Meng, J. (2020). Development of Crown Ratio and Height to Crown Base Models for Masson Pine in Southern China. Forests, 11(11), 1216. https://doi.org/10.3390/f11111216





