Next Article in Journal
Pinus spp. Somatic Embryo Conversion under High Temperature: Effect on the Morphological and Physiological Characteristics of Plantlets
Previous Article in Journal
The Complete Plastid Genome of Artocarpus camansi: A High Degree of Conservation of the Plastome Structure in the Family Moraceae
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Forests
Volume 11
Issue 11
10.3390/f11111180
forests-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Estimates of Tree Canopy Closure and Basal Area as Proxies for Tree Crown Volume at a Stand Scale

by
Guntis Brūmelis
1,*,
Iluta Dauškane
1,
Didzis Elferts
1,
Linda Strode
1,
Tatjana Krama
2,3 and
Indrikis Krams
1,2,4
1
Faculty of Biology, University of Latvia, Jelgavas iela 1, LV1004 Riga, Latvia
2
Department of Biotechnology, Daugavpils University, LV5401 Daugavpils, Latvia
3
Chair of Plant Health, Estonian University of Life Sciences, 51006 Tartu, Estonia
4
Institute of Ecology and Earth Sciences, University of Tartu, 51014 Tartu, Estonia
*
Author to whom correspondence should be addressed.
Forests 2020, 11(11), 1180; https://doi.org/10.3390/f11111180
Submission received: 6 October 2020 / Revised: 3 November 2020 / Accepted: 6 November 2020 / Published: 8 November 2020
(This article belongs to the Section Forest Inventory, Modeling and Remote Sensing)
Browse Figures
Versions Notes

Abstract

:
Research Highlights: Studies on tree canopy dwelling species often require simple proxies of tree canopy volume estimated at a stand level. These include allometrically related tree crown parameters such as crown area and basal area, and canopy cover. Background and Objectives: In monoculture Scot’s pine and mixed pine/Norway spruce forest, we aimed to test the relationships between tree diameter at breast height (DBH) and tree crown volume at a tree level and between densitometer canopy closure estimates and tree crown volume at a stand level. Materials and Methods: The study was carried out in eastern Latvia (hemiboreal zone) in monoculture pine and mixed coniferous stands. On a subset of trees in 22 forest stands (88 100 m2 plots), we determined the best regression model that described the relationship between tree DBH and crown volume for spruce and pine. Tree crown volume at a stand level was determined from the individual tree volume estimates calculated from these regression models. On a stand level, we also calculated regression models for densitometer closure estimates versus total crown volume for pine and mixed stands. Results: Linear mixed effects models showed significant relationships between DBH and crown volume for pine (R2 = 0.63) and spruce (R2 = 0.40), indicating that basal area could be used as a predictor of crown volume at a stand level. Variance explained by a regression model of canopy closure versus tree crown volume at a stand level was R2 = 0.52. Conclusions: Tree basal area and crown closure can be used as proxies of tree crown volume at a stand scale in monoculture stands. In mixed stands estimates of crown volume based on basal area need to be calculated separately for each tree species, while canopy closure will provide an estimate of total crown volume.

1. Introduction

Species richness and survival, and the fitness of individual organisms, are often determined by the quality of their habitats. Forest habitat selection is mostly a function of a vegetation structure [1]. Safety and food availability are among the contested resources and belong to the most important habitat requirements affecting patterns of tree canopy use. Tree crown volume of habitat available in a tree canopy is related to the amount of available resources, which often lack a pronounced vertical gradient in arthropod communities in temperate forest, in contrast to tropical forest [2]. The upper canopy of coniferous trees is a foraging site most preferred by dominant members of the mixed-species groups composed by small passerine birds because of better availability of food and increased safety there. It has been found that sparrowhawks (Accipiter nisus) and pygmy owls (Glaucidium passerinum) are less successful in the upper canopy than in the lower parts. In the canopy of conifers, arthropod biomass is found to be highest in the upper part of the tree [3,4]. This pattern for coniferous trees is explained by preferences of arthropods for branches with needles [5], and thus arthropod density in a stand should be related to canopy crown volume. Thus, foraging niche distribution and foraging niche separation in many forest passerine birds can be interpreted not only in terms of depredation risk, food availability, and social dominance but also as the variation in the canopy structure and crown volume. Although all of these factors can be equally important to habitat selection in birds, food resources, safety, inter- and intra-specific competition, and tree crown size are rarely considered together because the latter requires extra time/effort for appropriate measurement, which usually falls out of the focus of zoological research.
Estimation of tree crown dimensions is important in understanding biological processes such as photosynthesis, growth, and competition [6] and has vast importance in forest management [7]. The structure and geometry of tree crowns also determine canopy carbon and water fluxes [8]. Tree crown area differs within species due to climatic and soil factors and competition [9]. For example, Norway spruce (Picea abies (L.) H.Karst.) has an efficient vertical tree crown with a low crown projection area [10] compared to Scot’s pine (Pinus sylvestris L.) [6]. Knowledge of the tree crown radii is also required to determine the growing space required by trees in urban parks [11]. The crown projection area occupied by trees can be used to estimate growth efficiency on a tree and stand level [12].
While tree dimensions have great importance in studies of biological processes, forest inventory is focused on tree diameter at breast height (DBH), tree height, basal area, and wood volume, but not on tree crown dimensions. However, crown area, which can be estimated as a circle when symmetrical and an ellipse when asymmetrical, is allometrically related with DBH [13,14]. Estimates of tree crown projection area from remote sensing data can be used to estimate tree DBH [15]. Crown maximum radius is also well correlated with tree DBH [16,17]. Other tree crown parameters such as tree leaf area can also be modelled by basal area [18]. Precise estimation of tree crown volume requires the use of crown vertical profile models, which require a large number of field measurements [19,20]. This has been developed for silver birch (Betula pendula Roth) and Scots pine, and the models included a competition factor [21]. Estimation of tree crown volume as truncated cones can be accomplished with, for example, applied terrestrial 3D scanning technology [22]. Without such technologies, the field time needed for estimation of crown width of a profile increases with the number of points where measurements are needed, and repeatability will decline due to the observer effect and visibility of the crown profile from the ground from an oblique position. For practical purposes, pine and spruce crown volume can be estimated as ellipsoids, which is much simpler than estimating crown area along a vertical profile [6], as only the crown depth and maximum crown radius need to be measured in one direction as a circle, two directions as an ellipse, or in more directions as a convex hull. Estimating crown volume as an ellipsoid, a good correlation was found for pine between field and LIDAR remote sensing estimates at a plot level [23].
Estimates of the vertical projection of crown cover represent the area of ground covered by foliage, which might not exhibit a linear relationship with the summed crown area of tree layers, i.e., overlap of tree crowns [24]. There are various methods of determining crown cover (vertical projection) using visual estimation, processing of hemispherical images with a narrow angle of view, and the transect method with a siting tube (GRS densitometer) [25]. Canopy closure, which estimates the proportion of a wider hemisphere taken up by leaves of trees and tall shrubs, and thus takes into account forest layering, can be estimated using hemispherical images with a wide angle of view, and a handheld spherical densitometer with a gridded convex mirror [25]. It seems intuitive that crown volume at a stand level would be better related to canopy closure than canopy cover, as the latter to a lesser extent accounts for the overlap of canopy layers.
Considering the need for simple easy-to-measure proxies (variables that serve in place of an unobservable or immeasurable variable) that can represent crown volume at a stand level, we first tested the relationships between tree DBH and crown volume for spruce and pine at a tree level. Then, on a stand level, we determined the relationships between canopy closure estimated by a spherical densitometer and tree crown volume. The study was conducted within a larger study of factors affecting fitness in cavity-nesting birds.

2. Materials and Methods

2.1. Site Description

The study was conducted in the eastern part of Latvia, in the Augšdaugavas lowland. Mean annual precipitation in the area is 650 mm; mean temperature in July is 17.6 °C and −5 °C in February [26]. The landscape of the study territory is a mosaic of agricultural land, forests dominated by Norway spruce, Scot’s pine, silver birch, and aspen (Populus tremula L.). Two sites were chosen for the study: Scot’s pine forest on dry sand near Daugavpils and mixed Scot’s pine and Norway spruce coniferous forest on mesic soil near Krāslava. In the latter site, the proportion of spruce by basal area ranged from 3.3%–91.7% (mean 32.8%). Mean tree height of pine in Daugavpils and Krāslava sites was 25.8 m (range 11.1–33.2 m) and 26.6 m (range 9.9–38.1 m), respectively. Mean tree height of spruce in the Krāslava site was 21.1 (range 11.2–35.3); most of the trees were in the sapling to subcanopy tree layers. Monoculture spruce stands were lacking at the studied sites.

2.2. Field Methods

At each site, 11 forest stands were selected. The stand selection was based on another study (submitted) in which bird nest boxes had been established to study the effect of stand structure on nesting success and of winter survival of small passerine birds. From central locations in each stand, circular plots with size 100 m2 were set up in azimuth direction at distances of 50 m, giving four plots per stand. In each plot, the diameter of all trees at a height of 1.3 m (DBH) was measured. In each plot, for each species, three trees with different sizes (or less if not available) and lacking stem deformities were selected for canopy measurements, altogether 158 pine and 73 spruce. The selection method was chosen to provide a balanced size distribution. Measurements of the tree crown were made as an ellipsoid, as previously suggested for practical purposes [6]. Furthermore, visual observations in the stands confirmed that the vertical profile of both pine and spruce resembled an ellipsoid, rather than a cone. Height to base and top of the tree crown was measured with a Haglof VL5 Vertex. The maximum and minimum width of the crown was estimated with a measuring tape and an angled siting mirror (GRS densitometer) to precisely locate the edge of the crown. In each plot, canopy closure was estimated with a gridded concave mirror (spherical crown densitometer) in each of four azimuth directions at a central point offset at least 2 m distance from the nearest tree. Briefly, the grid on the mirror is used to count points at crossing lines that coincide with the tree canopy on the mirror, calculated as percentage canopy closure.

2.3. Data Analyses

Canopy volume was calculated as a simple ellipsoid for the selected trees. For this set of trees, linear mixed effects models as implemented in R library nlme were used to determine the relationships between tree DBH and crown volume for each species [27]. The second set of models also included stand density (number of trees per plot) as an additional explanatory variable. As there were multiple trees in each stand, stand ID was used as a random variable. Model performance was assessed by AIC and marginal R2 values. As residual plots of initial models’ showed problems with variance homogeneity, canopy volume was log-transformed for further models. The Pearson Correlation between observed and expected crown volumes was also determined. Stand level total crown volume and crown volume by each species was calculated from the individual tree crown volume estimates obtained from the best-selected models. Analysis of covariance (ANCOVA) was performed on a stand level to estimate the relationships between canopy closure and total tree crown volume for mixed and pine stands, the testing interaction effect of stand type (pine or mixed) and canopy closure. Assumptions of models were checked by inspection of residuals plots. The analyses were conducted using R 4.0.2 [27].

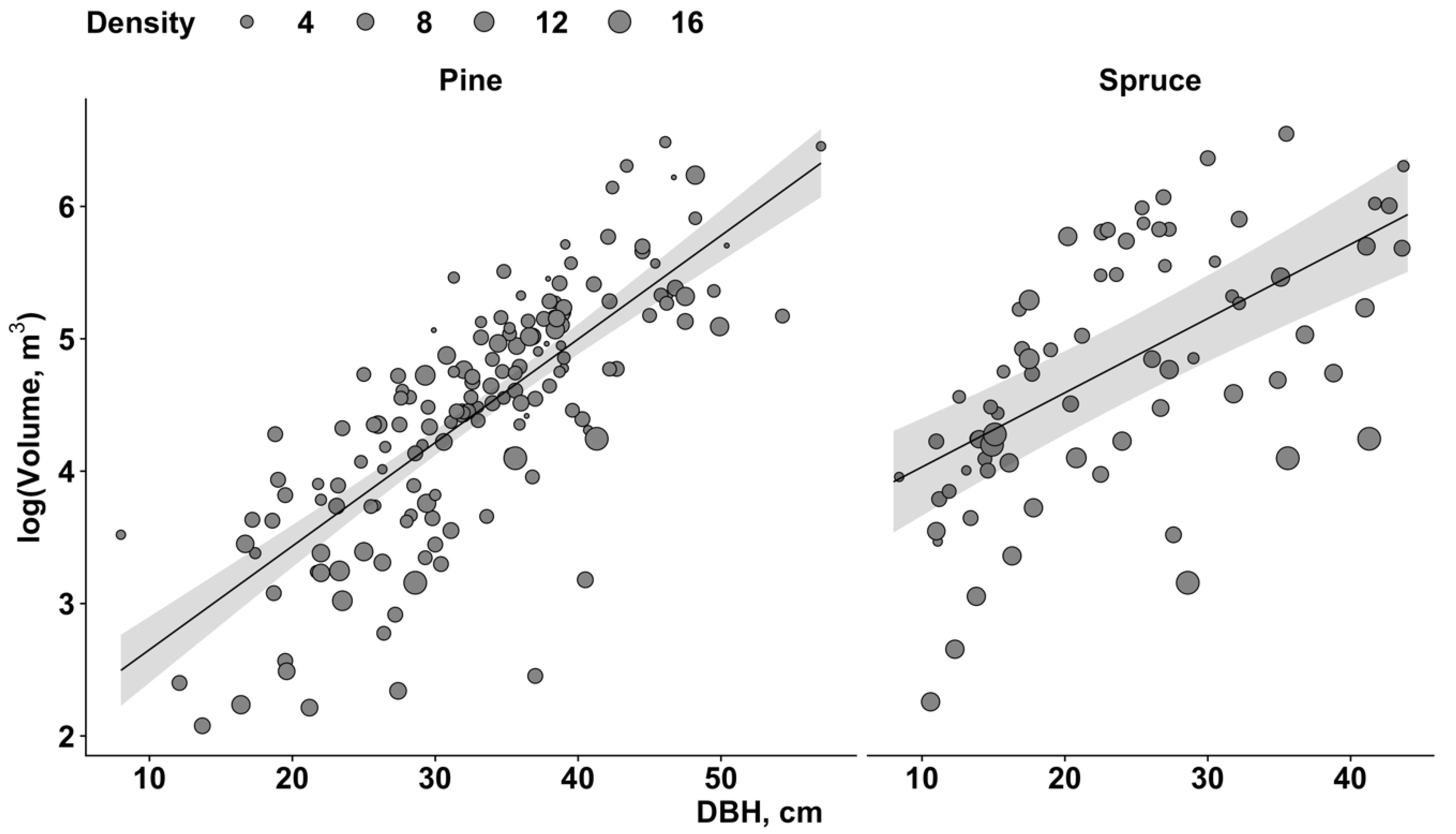
3. Results

3.1. Tree-Level Models

The modelled regression equations for DBH versus crown volume of trees explained more variation for pine compared to spruce, and for both species explained variation increased when stand density was added additional explanatory variable (Table 1, Figure 1 and Figure 2). The AIC value was lower for the model with both variables in the case of pine but higher in the case of spruce (although both variables had significant coefficients). Of these models, for further analyses, we chose the model with DBH and stand density for both pine (R2 = 0.63) and spruce (R2 = 0.40). Using these models, Pearson correlation coefficients (r) for observed (calculated from field measurements) and expected (modelled) were 0.85 for spruce and 0.79 for pine. There was a linear relationship between DBH and log-tree crown volume, while plot density remained constant around a mean value Figure 1. The residual plots showed a random pattern (Figure 2).

3.2. Stand-Level Models

There was also a significant linear relationship between estimated canopy closure in the stands and total crown volume (F = 24.179, p < 0.001) (Table 2), estimated by the sum of pine and spruce crown volume (Figure 3). There was no significant difference between the calculated slopes for pine monoculture and mixed coniferous stands (F = 0.001, p = 0.981). There appeared to be a wider spread (variability) of crown volume estimates at higher canopy closure in mixed stands. The variance explained by the model for all stands was R2 = 0.52.

4. Discussion

4.1. Estimation of Tree Crown Volume

As the relationship between tree DBH and crown radius is linear [11], the logarithmic relationship between tree DBH and crown volume was not surprising. In our study, DBH was a significant predictor of canopy volume, but with a large residual effect, and the variance explained by the models for spruce was less than for pine. This can be due to the simplistic model of tree architecture used and tree-level effects such as position in the canopy [28]. Estimating crown volume as an ellipsoid, a good correlation was found for pine between field and LIDAR estimates at a plot level [23]. However, at a tree level, the correlation was significant but poor [23], likely due to variation in shape between individuals. Equations have been developed for several tree species to estimate tree crown width in relation to height in the crown, and these were used to describe stand structure, which can have relevance for understanding the habitat requirements of many canopy dwelling species [29]. However, derivation of equations for tree crown volume that incorporate the shape of the vertical profile will generally be out of the realm of studies focusing on species using the tree canopy as a habitat due to time and financial expenses required for measuring trees compared to that needed for the study of the target organisms. Furthermore, the importance of crown shape in potential allometric models used in applications, such as physiological or functional processes, is not known [16], but likely would not be warranted or financially possible. The issue becomes even more problematic considering that crown profiles differ due to differing age and growing space, i.e., competition, as shown for Norway spruce [30]. The effect of competition on the relationship between tree DBH and crown volume was indicated by the additional effect of tree density in the regression model for spruce. Therefore, when using DBH as a proxy for tree crown volume, the variability of tree crown profiles for a species within stands needs to be considered.

4.2. Stand-Level Tree Crown Parameters

Use of DBH at the tree level and basal area at a stand level as proxies of crown volume depends on knowing that allometric relationships with sufficient explanatory power do exist for each tree species. The stand-level crown volume was calculated from individual tree volumes, which would lack precision if tree architecture for a species differed within a stand. However, the observed significant relationships between DBH and crown volume at a tree level, and the amounts of variance explained, do show that it is reasonable to use basal area (a function of DBH) as a predictor of crown volume at a stand level, but to a lesser extent for tree species with a variable crown profile, such as spruce. The basal area of tree species in stands can be determined quickly, and therefore could be used as proxies of crown volume (without calculating crown volumes) in modeling relationships with resource supply for species utilizing tree canopies as a habitat. The effect of crown-height variability on arthropod diversity was shown to be explained by differing tree architecture among tree species [31]. In pine stands, older trees, which had greater crown volume, support larger abundance of arthropods [32], and the species found in the communities of canopies of smaller trees can be a subset of those found in larger trees [33].
The selection of tree species for foraging differs between bird species [2], which might partly be explained by tree crown characteristics. Therefore, estimation of crown parameters at a stand level (total canopy closure and crown volume) across all tree species in mixed stands might not be suitable. A regression model to predict canopy closure from the total basal area of all tree species in mixed stands was shown to be improved when the proportion of Norway spruce was accounted for [34]. In our case, the higher variability of calculated crown volume with greater canopy closure in mixed stands can be explained by greater variability of the vertical profile of spruce. However, the regressions between canopy closure and crown volume did not significantly differ between pine and mixed coniferous stands, suggesting that canopy closure could be used as a proxy for total canopy crown volume in cases where the proportion of crown volume contributed by each tree species is not of interest. For example, total arthropod density in the canopy might be expected to be related to total crown volume. Canopy closure, which is due to canopy density and volume, will provide an estimate of light conditions, which is an important factor for the diversity and composition of epiphytic lichen communities [35]. It is simple to estimate crown closure in the field using a handheld densitometer, and these estimates could be used as proxies of canopy crown volume or to calculate these values.
We have recently shown in the Krāslava study area that wintering in the older mixed stands, compared to disturbed stands, enhances the survival of members of bird social groups [36]. Poorer habitat quality in younger pine stands increases the competition for food leading to the escalation of intra-and inter-specific aggression which may result in higher exposure to predators. Further study will determine if bird survival is associated with total crown volume and/or a higher proportion of spruce in the canopy. In the studied pine monoculture stands, we found that the fledgling number of breeding great tits (Parus major) was lower in stands with lower canopy closure and tree crown volume, which could be explained by lower larval biomass in tree crowns affected by an insect pest outbreak (submitted). This indeed showed the relevance of simple canopy proxies of crown volume in studies of food resource availability in tree canopies. Arthropod diversity was also related to canopy density estimated by airborne LIDAR, but the relationship was positive at a tree level and negative at a stand level, with higher arthropod diversity in open spruce stands with broad-leaved tree species [31].

5. Conclusions

While acknowledging that tree shape should be included in precise models for the estimation of tree crown volume, tree size parameters do have allometric relationships, and simple-to-measure canopy parameters can be used to successfully study their relationships with plant and animal communities. The tree-level models based on DBH and stand density can be used to calculate crown volume on a stand level by tree species. This further suggests that the basal area of a stand could also be a good predictor of tree crown volume and could be estimated separately for each tree species to determine the importance of each in resource supply. Tree canopy closure estimated by a spherical densitometer can be a useful easy way to measure proxy for tree crown volume or to estimate the predicted values.

Author Contributions

Conceptualization, G.B., I.D., D.E., L.S., I.K. and T.K.; methodology, G.B., I.D., D.E., L.S., I.K. and T.K.; validation, G.B., I.D. and L.S.; formal analysis, G.B. and D.E.; investigation, G.B., I.D., D.E., and L.S.; writing —original draft preparation, G.B.; writing—review and editing, G.B., I.D., D.D., L.S., I.K., and T.K.; visualization, D.E.; supervision, G.B. and T.K.; project administration, G.B. and T.K.; funding acquisition, T.K. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Latvian Council of Science, grant number lzp-2018/2-0057.

Acknowledgments

The authors acknowledge the support of the staff of the Department of Botany and Ecology of the Faculty of Biology, University of Latvia, for logistic support. The comments of three anonymous reviewers much helped to improve the manuscript.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Cody, M.L. Habitat selection in birds: The roles of vegetation structure, competitors, and productivity. Bioscience 1981, 31, 107–113. [Google Scholar] [CrossRef]
  2. Basset, Y.; Hammond, P.M.; Barrios, H.; Holloway, J.D.; Miller, S.E. Vertical stratification of arthropod assemblages. In Arthropods of Tropical Forests; Basset, Y., Novotny, V., Miller, S.E., Kitching, R.L., Eds.; Cambridge University Press: Cambridge, UK, 2003; pp. 17–27. [Google Scholar]
  3. Suhonen, J.; Alatalo, R.V.; Carlson, A.; Höglund, J. Food resource distribution and the organization of the Parus guild in a spruce forest. Ornis Scand. 1992, 23, 467–474. [Google Scholar] [CrossRef]
  4. Krams, I.A.; Krams, T.; Cernihovics, J. Selection of foraging sites in mixed willow and crested tit flocks: Rank-dependent survival strategies. Ornis Fenn. 2001, 78, 1–11. [Google Scholar]
  5. Gunnarsson, B. Vegetation structure and the abundance and size distribution of spruce-living spiders. J. Anim. Ecol. 1990, 59, 743–752. [Google Scholar] [CrossRef]
  6. Rautiainen, M.; Mõttus, M.; Stenberg, P.; Ervasti, S. Crown envelope shape measurements and models. Silva Fenn. 2008, 42, 19–33. [Google Scholar] [CrossRef] [Green Version]
  7. Sharma, R.P.; Vacek, Z.; Vacek, S. Individual tree crown width models for Norway spruce and European beech in Czech Republic. For. Ecol. Manage. 2016, 366, 208–220. [Google Scholar] [CrossRef]
  8. Cermák, J.; Riguzzi, F.; Ceulemans, R. Scaling up from the Individual Tree to the Stand Level in Scots Pine. I. Needle Distribution, Overall Crown and Root Geometry. Ann. For. Sci. 1998, 55, 63–88. [Google Scholar]
  9. Pokorný, R.; Tomášková, I. Allometric relationships for surface area and dry mass of young Norway spruce aboveground organs. J. For. Sci. 2007, 53, 548–554. [Google Scholar] [CrossRef] [Green Version]
  10. Pretzsch, H.; Schütze, G. Crown allometry and growing space efficiency of Norway spruce (Picea abies [L.] Karst.) and European beech (Fagus sylvatica L.) in pure and mixed stands. Plant Biol. 2005, 7, 628–639. [Google Scholar] [CrossRef] [Green Version]
  11. Pretzsch, H.; Biber, P.; Uhl, E.; Dahlhausen, J.; Rötzer, T.; Caldentey, J.; Koike, T.; Van Con, T.; Chavanne, A.; Seifert, T. Crown size and growing space requirement of common tree species in urban centres, parks, and forests. Urban For. Urban Green. 2015, 14, 466–479. [Google Scholar] [CrossRef] [Green Version]
  12. Dirnberger, G.; Sterba, H.; Condés, S.; Ammer, C.; Annighöfer, P.; Avdagić, A.; Bielak, K.; Brazaitis, G.; Coll, L.; Heym, M. Species proportions by area in mixtures of Scots pine (Pinus sylvestris L.) and European beech (Fagus sylvatica L.). Eur. J. For. Res. 2017, 136, 171–183. [Google Scholar] [CrossRef] [Green Version]
  13. Blanchard, E.; Birnbaum, P.; Ibanez, T.; Boutreux, T.; Antin, C.; Ploton, P.; Vincent, G.; Pouteau, R.; Vandrot, H.; Hequet, V. Contrasted allometries between stem diameter, crown area, and tree height in five tropical biogeographic areas. Trees 2016, 30, 1953–1968. [Google Scholar] [CrossRef]
  14. Svoboda, M.; Pouska, V. Structure of a Central-European mountain spruce old-growth forest with respect to historical development. For. Ecol. Manag. 2008, 255, 2177–2188. [Google Scholar] [CrossRef]
  15. Verma, N.K.; Lamb, D.W.; Reid, N.; Wilson, B. An allometric model for estimating DBH of isolated and clustered eucalyptus trees from measurements of crown projection area. For. Ecol. Manag. 2014, 326, 125–132. [Google Scholar] [CrossRef]
  16. Rautiainen, M.; Stenberg, P. Simplified tree crown model using standard forest mensuration data for Scots pine. Agric. For. Meteorol. 2005, 128, 123–129. [Google Scholar] [CrossRef]
  17. Gill, S.J.; Biging, G.S.; Murphy, E.C. Modeling conifer tree crown radius and estimating canopy cover. For. Ecol. Manag. 2000, 126, 405–416. [Google Scholar] [CrossRef] [Green Version]
  18. Laubhann, D.; Eckmüllner, O.; Sterba, H. Applicability of non-destructive substitutes for leaf area in different stands of Norway spruce (Picea abies L. Karst.) focusing on traditional forest crown measures. For. Ecol. Manag. 2010, 260, 1498–1506. [Google Scholar] [CrossRef] [Green Version]
  19. Crecente-Campo, F.; Marshall, P.; LeMay, V.; Diéguez-Aranda, U. A crown profile model for Pinus radiata D. Don in northwestern Spain. For. Ecol. Manag. 2009, 257, 2370–2379. [Google Scholar] [CrossRef]
  20. Crecente-Campo, F.; Álvarez-González, J.G.; Castedo-Dorado, F.; Gómez-García, E.; Diéguez-Aranda, U. Development of crown profile models for Pinus pinaster Ait. and Pinus sylvestris L. in northwestern Spain. Forestry 2013, 86, 481–491. [Google Scholar] [CrossRef] [Green Version]
  21. Lintunen, A.; Sievänen, R.; Kaitaniemi, P.; Perttunen, J. Models of 3d crown structure for Scots pine (Pinus sylvestris) and silver birch (Betula pendula) grown in mixed forest. Can. J. For. Res. 2011, 41, 1779–1794. [Google Scholar] [CrossRef]
  22. Lin, W.; Meng, Y.; Qiu, Z.; Zhang, S.; Wu, J. Measurement and calculation of crown projection area and crown volume of individual trees based on 3d laser-scanned point-cloud data. Int. J. Remote Sens. 2017, 38, 1083–1100. [Google Scholar] [CrossRef]
  23. Riano, D.; Chuvieco, E.; Condés, S.; González-Matesanz, J.; Ustin, S.L. Generation of crown bulk density for Pinus sylvestris L. From lidar. Remote Sens. Environ. 2004, 92, 345–352. [Google Scholar] [CrossRef]
  24. Fiala, A.C.; Garman, S.L.; Gray, A.N. Comparison of five canopy cover estimation techniques in the western oregon cascades. For. Ecol. Manage. 2006, 232, 188–197. [Google Scholar] [CrossRef]
  25. Paletto, A.; Tosi, V. Forest canopy cover and canopy closure: Comparison of assessment techniques. Eur. J. For. Res. 2009, 128, 265–272. [Google Scholar] [CrossRef]
  26. Briede, A.; Avotniece, Z.; Dravniece, A.; Kalvāne, G.; Kļaviņš, M.; Koreļska, L. Atmosfēra. Latvija. Zeme, Daba, Tauta, Valsts; Nikodemus, O., Māris, K., Zaiga, K., Vitālijs, Z., Eds.; Latvijas Universitātes Akadēmiskais apgāds: Rīga, Latvia, 2018; pp. 225–271. [Google Scholar]
  27. R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020; Available online: https://www.R-project.org/ (accessed on 10 August 2020).
  28. Sharma, R.P.; Bílek, L.; Vacek, Z.; Vacek, S. Modelling crown width–diameter relationship for Scots pine in the central Europe. Trees 2017, 31, 1875–1889. [Google Scholar] [CrossRef]
  29. Dubrasich, M.E.; Hann, D.W.; Tappeiner, J.C., II. Methods for evaluating crown area profiles of forest stands. Can. J. For. Res. 1997, 27, 385–392. [Google Scholar] [CrossRef]
  30. Kantola, A.; Mäkelä, A. Crown development in Norway spruce [Picea abies (L.) Karst.]. Trees 2004, 18, 408–421. [Google Scholar] [CrossRef]
  31. Müller, J.; Bae, S.; Röder, J.; Chao, A.; Didham, R.K. Airborne Lidar reveals context dependence in the effects of canopy architecture on arthropod diversity. For. Ecol. Manag. 2014, 312, 129–137. [Google Scholar] [CrossRef]
  32. Thunes, K.H.; Skarveit, J.; Gjerde, I. The canopy arthropods of old and mature pine Pinus sylvestris in Norway. Ecography 2003, 26, 490–502. [Google Scholar] [CrossRef] [Green Version]
  33. Campos, R.I.; Vasconcelos, H.L.; Ribeiro, S.P.; Neves, F.S.; Soares, J.P. Relationship between tree size and insect assemblages associated with Anadenanthera Macrocarpa. Ecography 2006, 29, 442–450. [Google Scholar] [CrossRef]
  34. Kuusipalo, J. On the use of tree stand parameters in estimating light conditions below the canopy. Silva Fenn. 1985, 19, 185–196. [Google Scholar] [CrossRef] [Green Version]
  35. Nascimbene, J.; Marini, L.; Motta, R.; Nimis, P.L. Influence of tree age, tree size and crown structure on lichen communities in mature alpine spruce forests. Biodivers. Conserv. 2009, 18, 1509. [Google Scholar] [CrossRef]
  36. Krams, I.A.; Luoto, S.; Krama, T.; Sieving, K.; Trakimas, G.; Elferts, D.; Rantala, M.J.; Goodale, E. Egalitarian mixed-species bird groups enhance winter survival of subordinate group members but only in high-quality forests. Sci. Rep. 2020, 10, 4005. [Google Scholar] [CrossRef] [Green Version]
Forests 11 01180 g001 550
Figure 1. Scatterplots of DBH versus log-transformed crown volume for spruce and pine. Point size shows plot density. Lines show predicted values for the linear mixed effects.
Figure 1. Scatterplots of DBH versus log-transformed crown volume for spruce and pine. Point size shows plot density. Lines show predicted values for the linear mixed effects.
Forests 11 01180 g001
Forests 11 01180 g002 550
Figure 2. Residuals plots for the mixed effects models for crown volume: (A) Pine model with DBH, (B) Pine model with DBH and density, (C) Spruce model with DBH, (D) Spruce model with DBH and density.
Figure 2. Residuals plots for the mixed effects models for crown volume: (A) Pine model with DBH, (B) Pine model with DBH and density, (C) Spruce model with DBH, (D) Spruce model with DBH and density.
Forests 11 01180 g002
Forests 11 01180 g003 550
Figure 3. The relationship between canopy closure and tree crown volume estimated from individual tree volumes for pine stands and mixed pine/spruce stands as estimated by the ANCOVA model. Regression equations: mixed stands crown volume = 25,080.80 + 922.16 * canopy closure; pine stand crown volume = 14,201.64 + 935.83 * canopy closure.
Figure 3. The relationship between canopy closure and tree crown volume estimated from individual tree volumes for pine stands and mixed pine/spruce stands as estimated by the ANCOVA model. Regression equations: mixed stands crown volume = 25,080.80 + 922.16 * canopy closure; pine stand crown volume = 14,201.64 + 935.83 * canopy closure.
Forests 11 01180 g003
Table
Table 1. Tested linear mixed effects models for the relationship between tree diameter at breast height (DBH), stand density and log-transformed crown volume.
Table 1. Tested linear mixed effects models for the relationship between tree diameter at breast height (DBH), stand density and log-transformed crown volume.
ModelVariableEstimateStd. Errort-Valuep-ValueMarginal R2AIC
Pine, model 1Intercept1.7940.17810.055<0.0010.60295.243
DBH0.0810.00515.458<0.001
Pine, model 2Intercept2.1910.20710.563<0.0010.63291.410
DBH0.0780.00515.314<0.001
Density−0.0560.016−3.576<0.001
Spruce, model 1Intercept3.6170.24814.575<0.0010.30152.541
DBH0.0510.0076.967<0.001
Spruce, model 2Intercept3.9040.25615.269<0.0010.40154.325
DBH0.0560.0077.617<0.001
Density−0.0580.023−2.5640.013
Table
Table 2. Anova type table for the tested linear covariance model (ANCOVA) between canopy closure, stand type and total crown volume.
Table 2. Anova type table for the tested linear covariance model (ANCOVA) between canopy closure, stand type and total crown volume.
VariableSum Sq.F-Valuep-Value
Canopy closure943232524.179<0.001
Stand type6182971.5850.224
Canopy closure:Stand type2190.0010.981
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Brūmelis, G.; Dauškane, I.; Elferts, D.; Strode, L.; Krama, T.; Krams, I. Estimates of Tree Canopy Closure and Basal Area as Proxies for Tree Crown Volume at a Stand Scale. Forests 2020, 11, 1180. https://doi.org/10.3390/f11111180

AMA Style

Brūmelis G, Dauškane I, Elferts D, Strode L, Krama T, Krams I. Estimates of Tree Canopy Closure and Basal Area as Proxies for Tree Crown Volume at a Stand Scale. Forests. 2020; 11(11):1180. https://doi.org/10.3390/f11111180

Chicago/Turabian Style

Brūmelis, Guntis, Iluta Dauškane, Didzis Elferts, Linda Strode, Tatjana Krama, and Indrikis Krams. 2020. "Estimates of Tree Canopy Closure and Basal Area as Proxies for Tree Crown Volume at a Stand Scale" Forests 11, no. 11: 1180. https://doi.org/10.3390/f11111180

APA Style

Brūmelis, G., Dauškane, I., Elferts, D., Strode, L., Krama, T., & Krams, I. (2020). Estimates of Tree Canopy Closure and Basal Area as Proxies for Tree Crown Volume at a Stand Scale. Forests, 11(11), 1180. https://doi.org/10.3390/f11111180

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop