Study on the Diurnal Dynamic Changes and Prediction Models of the Moisture Contents of Two Litters
Abstract
1. Introduction
2. Methods
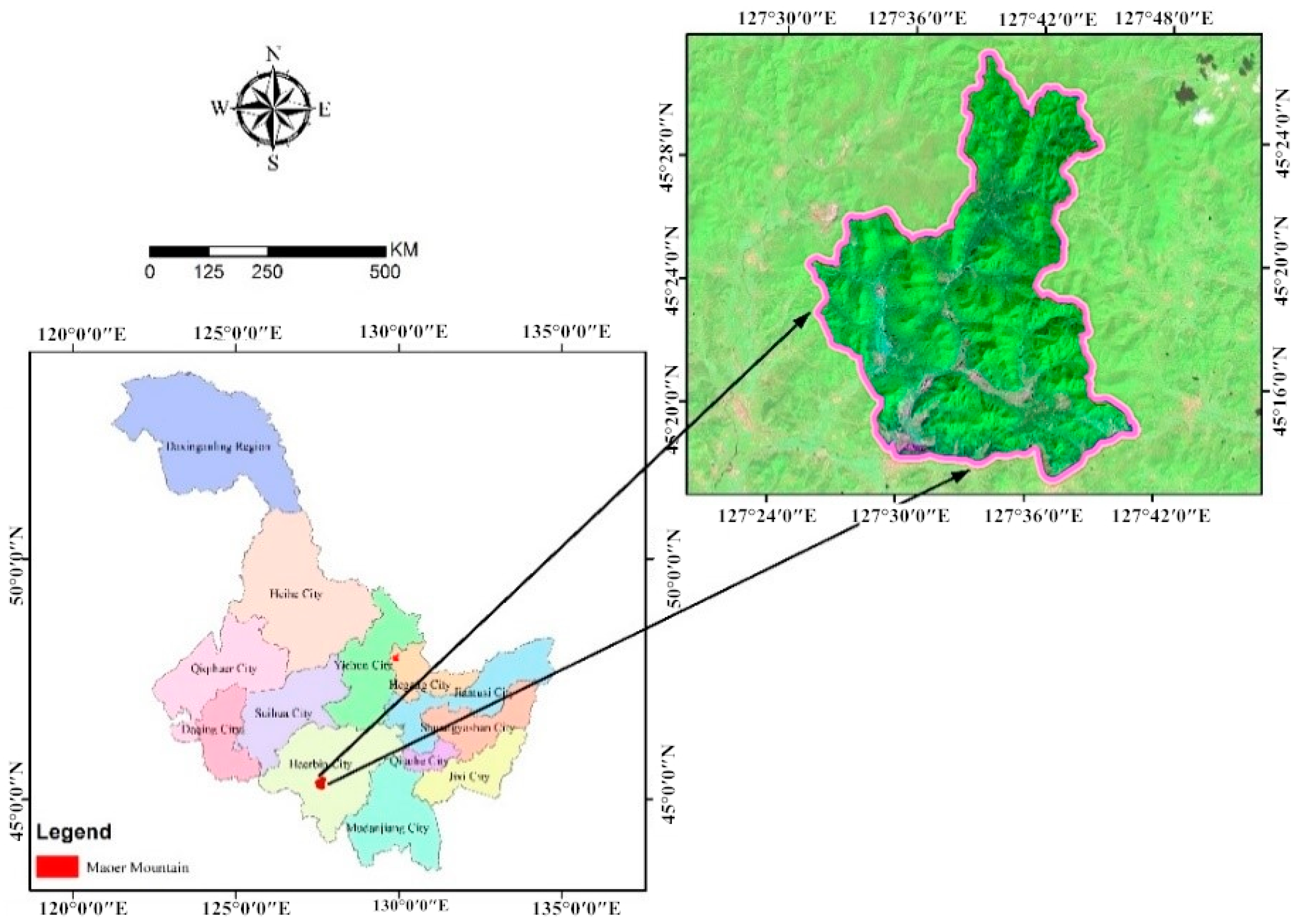
2.1. Study Area
2.2. Field Experiment
2.3. Model Description
2.3.1. Direct Estimation Method
2.3.2. Meteorological Factor Regression Method
2.4. Data Analysis
2.4.1. Basic Statistics
2.4.2. Correlation Analysis
2.4.3. Model
3. Results
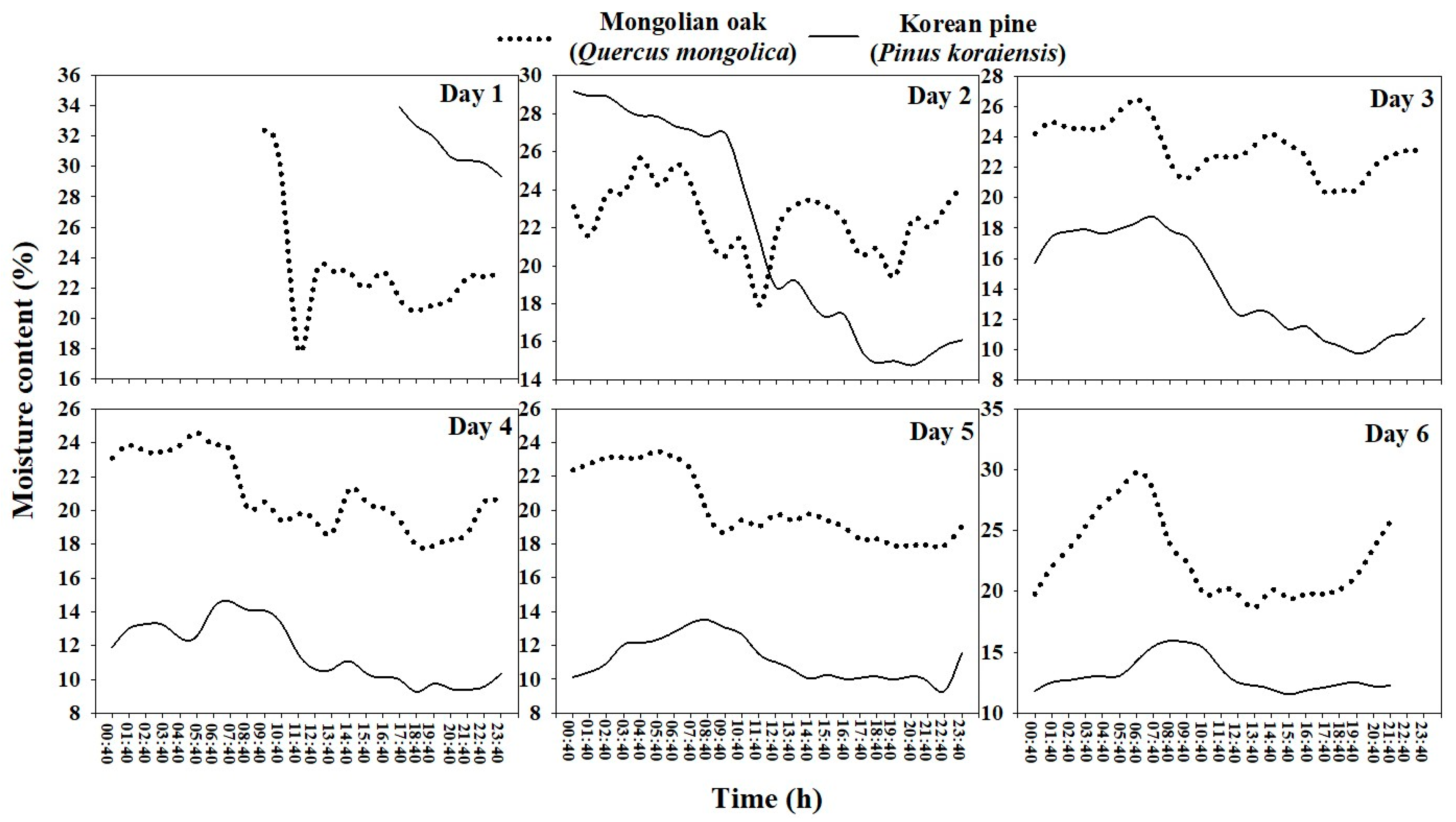
3.1. Diurnal Variation in the Litter Moisture Content
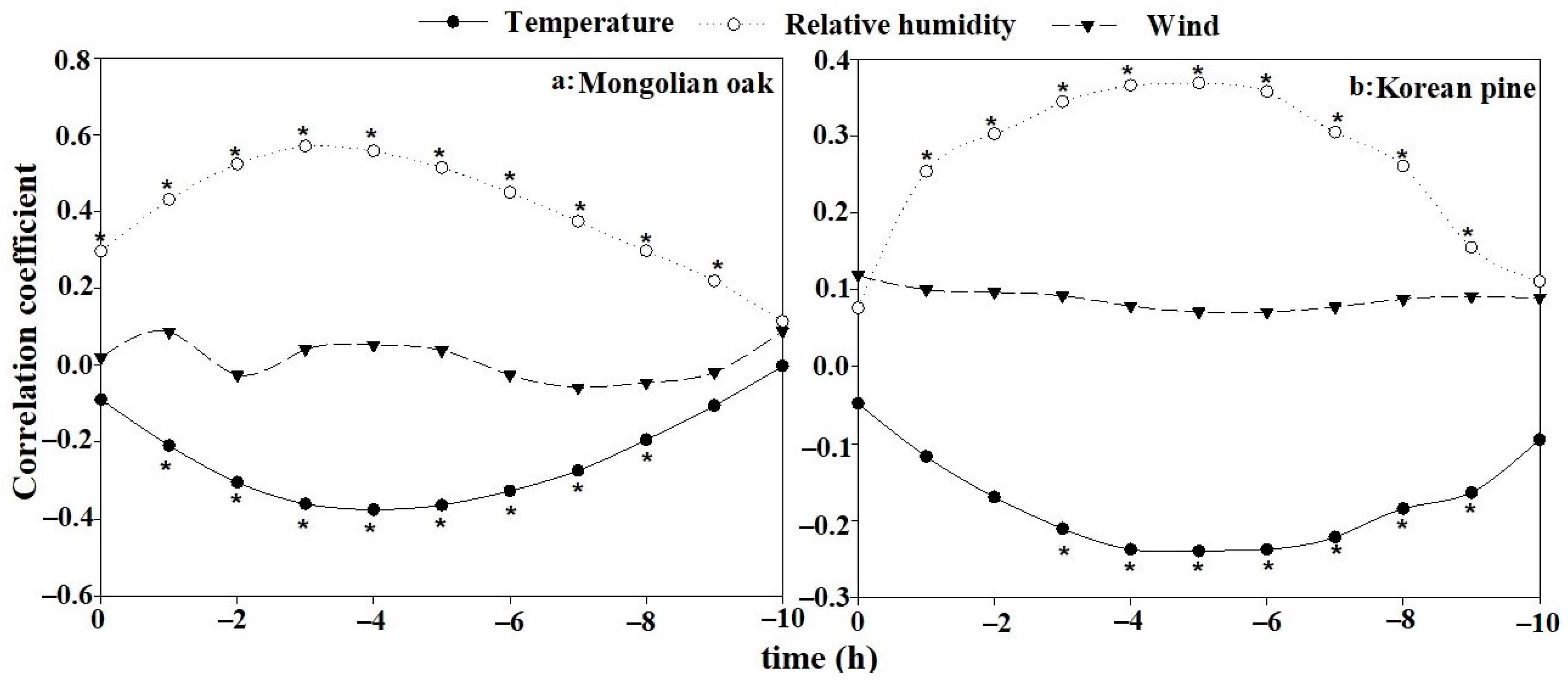
3.2. Correlation Analysis
3.3. Model
3.3.1. Model Parameters
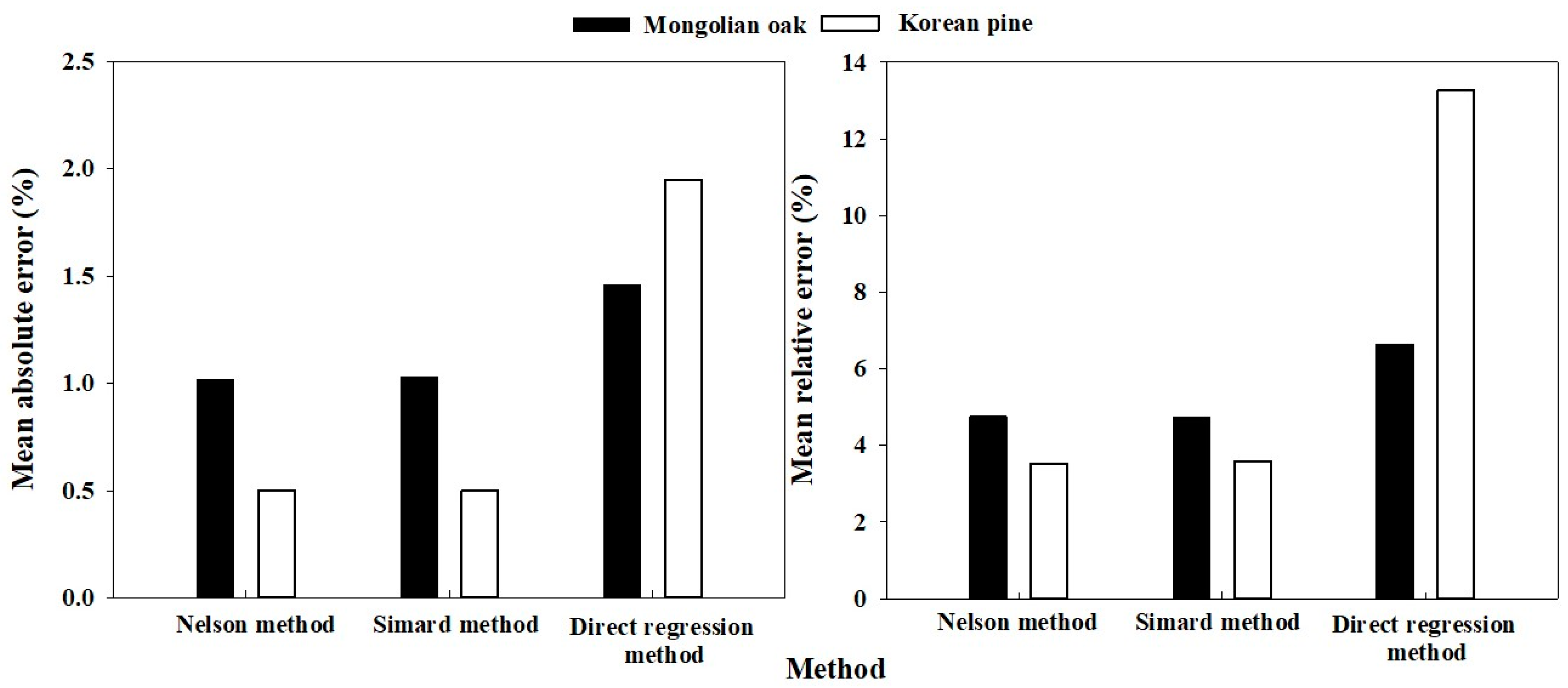
3.3.2. Model Error Comparison
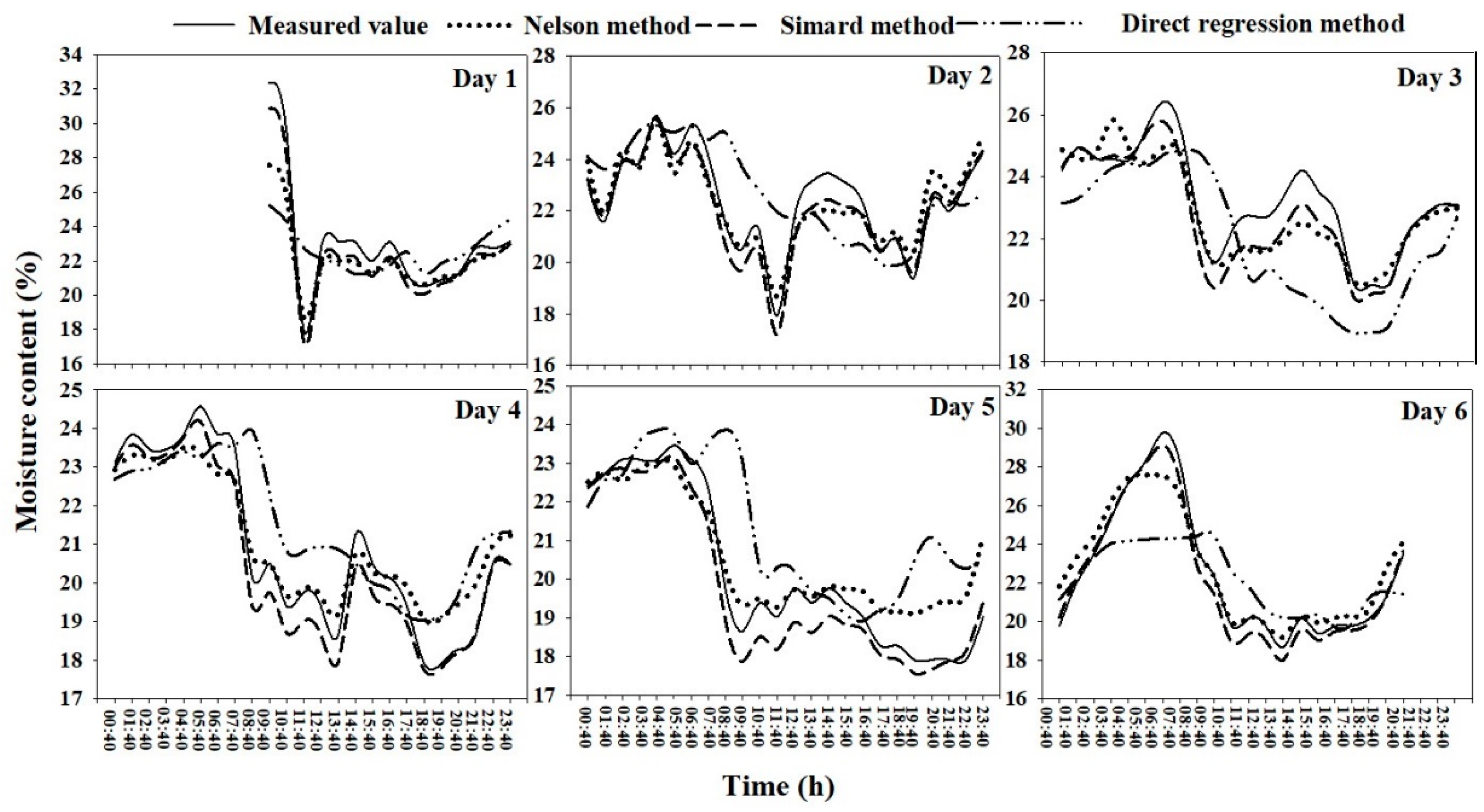
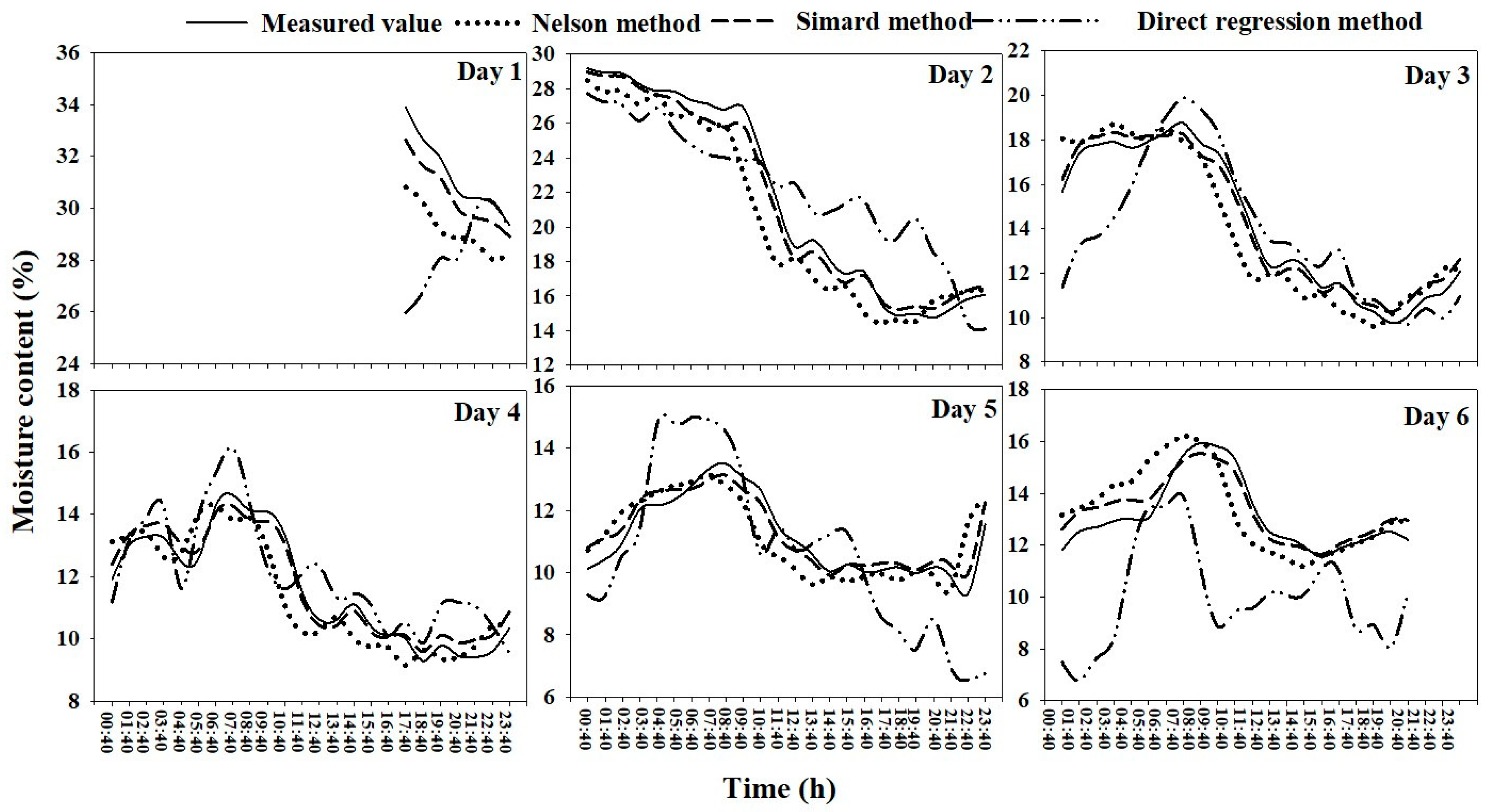
3.3.3. Comparison of Measured and Predicted Values of Diurnal Variation
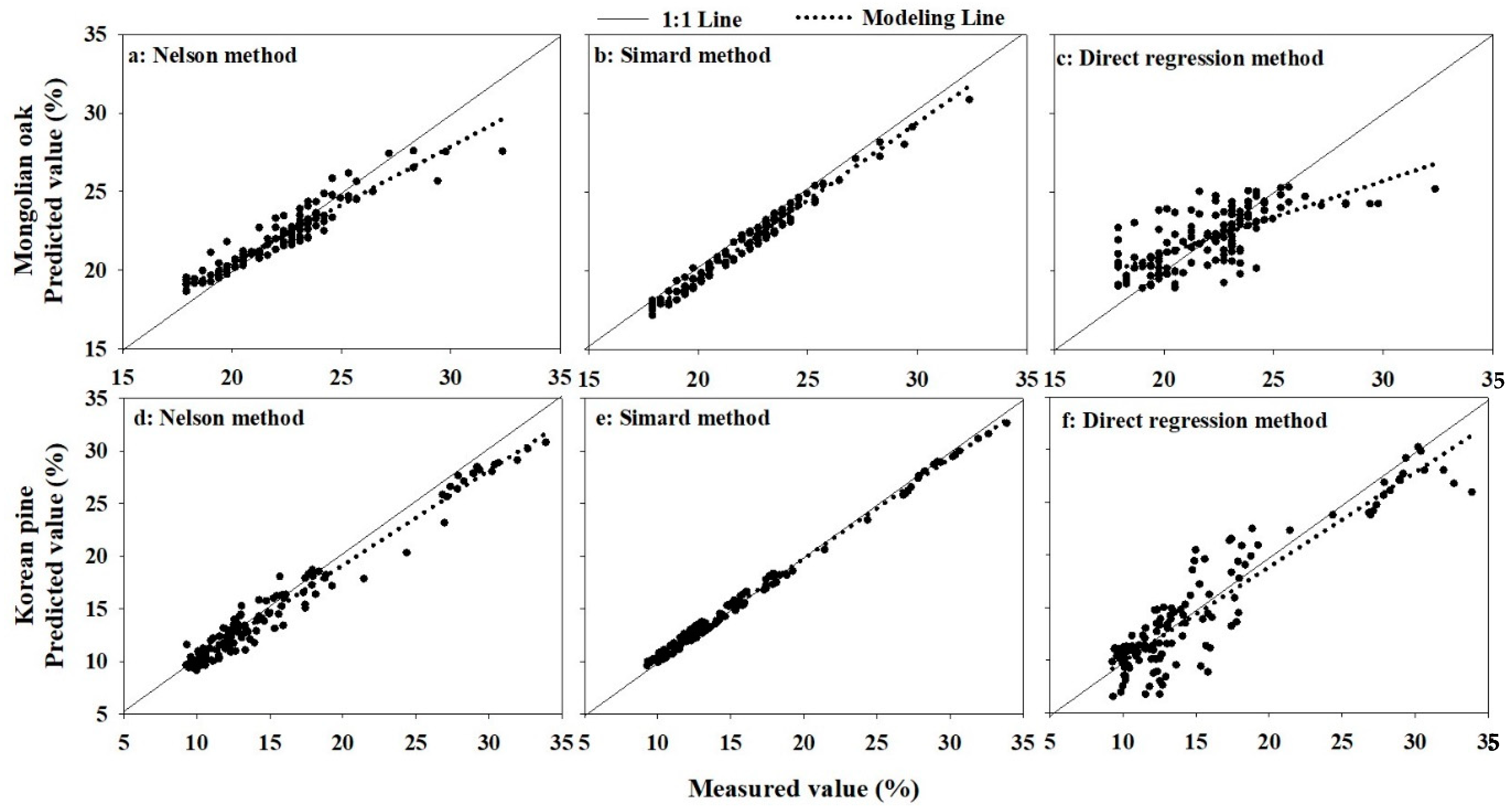
3.3.4. 1:1 Comparison of Measured and Predicted Values
4. Discussion
4.1. Correlation Analysis
4.2. Model Parameters
4.3. Time Lag
4.4. Model Accuracy
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chuvieco, E.; Aguado, I.; Yebra, M.; Nieto, H.; Salas, J.; Martín, M.P.; Vilar, L.; Martínez, J.; Martín, S.; Ibarra, P.; et al. Development of a framework for fire risk assessment using remote sensing and geographic information system technologies. Ecol. Model. 2010, 221, 46–58. [Google Scholar] [CrossRef]
- Finney, M.A. The challenge of quantitative risk analysis for wildland fire. For. Ecol. Manag. 2005, 211, 97–108. [Google Scholar] [CrossRef]
- Shu, L.F.; Tian, X.R. Current Status and Prospects of Forest Fire Prevention work abroad. World For. Res. 1997, 2, 28–36. [Google Scholar]
- Ager, A.; Vaillant, N.; Finney, M. A comparison of landscape fuel treatment strategies to mitigate wildland fire risk in the urban interface and preserve old forest structure. For. Ecol. Manag. 2010, 259, 1556–1570. [Google Scholar] [CrossRef]
- Turco, M.; Marcos-Matamoros, R.; Castro, X.; Canyameras, E.; Llasat, M. Seasonal prediction of climate-driven fi re risk for decision-making and operational applications in a Mediterranean region. Sci. Total Environ. 2019, 676, 577–583. [Google Scholar] [CrossRef]
- Chowdhury, E.H.; Hassan, Q.K. Operational Perspective of Remote Sensing-based Forest Fire Danger Forecasting Systems. ISPRS J. Photogramm. Remote Sens. 2015, 104, 224–236. [Google Scholar] [CrossRef]
- Sokolova, G.V.; Makogonov, S.V. Development of the Forest Fire Forecast Method (a Case Study for the Far East). Russ. Meteorol. Hydrol. 2013, 38, 222–226. [Google Scholar] [CrossRef]
- Deeeming, J.E.; Burgan, R.E.; Cohen, J.D. The Nation Fire Danger Rating System-1978. USDA For. Serv. GTR 1978. [Google Scholar] [CrossRef]
- Bradshaw, L.S.; Deeming, J.E.; Burgan, R.E. The 1978 National Fire-Danger Rating System: Technical documentation; General Technical Report INT-169; United States Department of Agriculture, Forest Service, Intermountain Research Station: Ogden, UT, USA, 1983; p. 44.
- Van Wagner, C.E. Development and Structure of the Canadian Forest Fire Weather Index System; Forestry Technical Report; Canadian Forestry Service: Ottawa, ON, Canada, 1987; pp. 35–37.
- Hu, H.Q. Forest Ecology and Management; China Forestry Press: Beijing, China, 2005. [Google Scholar]
- Sun, P.; Zhang, Y.L. A Probabilistic Method Predicting Forest Fire Occurrence Combining Firebrands and the Weather-Fuel Complex in the Northern Part of the Daxinganling Region, China. Forests 2018, 9, 428. [Google Scholar] [CrossRef]
- Rothermel, R.C.; Wilson, R.A.J.; Morris, G.A.; Scatett, S.S. Modeling Moisture Content of Fine Dead Wildland Fuels: Input to the BEHAVE Fire Prediction System. Usda For. Serv. Intermt. Res. Stn. Res. Pap. 1986, 11, 1–61. [Google Scholar] [CrossRef]
- Marsdensmedley, J.B.; Catchpole, W.R.; Marsdensmedley, J.B.; Catchpole, W.R. Fire Modelling in Tasmanian Buttongrass Moorlands. III. Dead Fuel Moisture. Int. J. Wildland Fire 2001, 10, 241–253. [Google Scholar] [CrossRef]
- Chuvieco, E.; Aguado, I.; Dimitrakopoulos, A.P. Conversion of Fuel Moisture Content Values to Ignition Potential for Integrated Fire Danger Assessment. Can. J. For. Res. 2004, 34, 2284–2293. [Google Scholar] [CrossRef]
- Trevitt, A.C.F. Weather parameters and fuel moisture content: Standards for fire model inputs. In Proceedings of the Conference on Bushfire Modeling and Fire Danger Rating Systems, Canberra, ACT, Australia, 11–12 July 1988. [Google Scholar]
- Nelson, R.M.J. Prediction of Diurnal Change in 10-h Fuel Stick Moisture Content. Can. J. For. Res. 2000, 30, 1071–1087. [Google Scholar] [CrossRef]
- Matthews, S.; Mccaw, W.L. A Next-generation Fuel Moisture Content Model for Fire Behavior Prediction. For. Ecol. Manag. 2006, 234, s27–s30. [Google Scholar] [CrossRef]
- Matthews, S.; Mccaw, W.L.; Neal, J.E.; Smith, R.H. Testing a Process-based Fine Fuel Moisture Model in Two Forest Types. Can. J. For. Res. 2007, 37, 23–35. [Google Scholar] [CrossRef]
- Matthews, S.; Gould, J.; Mccaw, L. Simple models for predicting dead fuel moisture in eucalyptus forests. Int. J. Wildland Fire 2010, 19, 459–467. [Google Scholar] [CrossRef]
- Wang, C.; Gao, H.Z.; Cheng, S.; Lu, D.L.; Chang, W.Q. Study on water content of Forest Fuel and Forest Fire Risk Prediction in Saihanba Forest Area. For. Sci. Technol. Dev. 2009, 23, 59–61. [Google Scholar] [CrossRef]
- Pook, E.W.; Gill, A.M. Variation of live and dead fine fuel moisture in Pinus radiata plantations of the Autralian Capital Territory. Int. J. Wildland Fire 1993, 3, 155–168. [Google Scholar] [CrossRef]
- Li, S.Y.; Shu, Q.T.; Ma, A.L.; Zhang, Q.R.; Liu, Y.; Wang, X.Q. Modeling on Moisture Content Predicting of Surface Fuel of Litter- fall Layer in Pinus armandii Plantations. For. Resour. Manag. 2009, 1, 84–88. [Google Scholar] [CrossRef]
- Sun, P.; Yu, H.Z.; Jin, S. Predicting hourly litter moisture content of larch stands in daxinganling region, china using three vapour-exchange methods. Int. J. Wildland Fire 2015, 24, 114–119. [Google Scholar] [CrossRef]
- Jin, S.; Li, L. Validation of the Method for Direct Estimation of Timelag and Equilibrium Moisture Content of Forest Fuel. Sci. Silvae Sin. 2010, 46, 98–105. [Google Scholar]
- Catchpole, E.A.; Catchpole, W.R.; Viney, N.R.; McCaw, W.L.; Marsden-Smedley, J.B. Estimating Fuel Response Time and Predicting Fuel Moisture Content From Field Data. Int. J. Wildland Fire 2001, 10, 215–222. [Google Scholar] [CrossRef]
- Nelson, R.M. A method for describing equilibrium moisture content of forest fuels. Can. J. For. Res. 1984, 14, 597–600. [Google Scholar] [CrossRef]
- Ruiz, A.D.; Maseda, C.M.; Lourido, C.; Viegas, D.X. Possibilities of dead fine fuels moisture prediction in Pinus pinaster Ait. stands at “Cordal de Ferreiros” (Lugo, north-western of Spain). In Proceedings of the Forest Fire Research & Wildland Fire Safety: IV International Conference on Forest Fire Research Wildland Fire Safety Summit, Coimbra, Portugal, 18–23 November 2002. [Google Scholar]
- Slijepcevic, A.; Anderson, W. Hourly variation in fine fuel moisture in eucalypt forests in tasmania. For. Ecol. Manag. 2006, 234. [Google Scholar] [CrossRef]
- Simard, A.J.; Main, W.A. Comparing methods of predicting jack pine slash moisture. Can. J. For. Res. 1982, 12, 793–802. [Google Scholar] [CrossRef]
- Simard, A.J.; Eenigenburg, J.E.; Blank, R.W. Predicting fuel moisture in jack pine slash: A test of two systems. Can. J. For. Res. 1984, 14, 68–76. [Google Scholar] [CrossRef]
- Groot, W.J.; Wardati Wang, Y. Calibrating the fine fuel moisture code for grass ignition potential in sumatra, indonesia. Int. J. Wildland Fire 2005, 14, 161–168. [Google Scholar] [CrossRef]
- Wang, H.Y.; Li, L.; Liu, Y.; Jin, S. Suitability of Canadian Forest Fire Danger Rating System in Tahe Forestry Bureau, Heilongjiang Province. J. Northeast For. Univ. 2008, 36, 47–49. [Google Scholar]
- Wotton, B.M.; Stocks, B.J.; Martell, D.L. An index for tracking sheltered forest floor moisture within the canadian forest fire weather index system. Int. J. Wildland Fire 2005, 14, 169–182. [Google Scholar] [CrossRef]
- Wotton, B.K.; Beverly, J.L. Stand-specific litter moisture content calibrations for the Canadian Fine Fuel Moisture Code. Int. J. Wildland Fire 2007, 16, 463–472. [Google Scholar] [CrossRef]
- Mao, W.X.; Tong, D.H.; Zhang, C.; Zhao, D.D.; Ding, Y.Y.; Jin, S. Spatial Heterogeneity of Moisture Content of Land Surface Dead Fuel in Larch Stand and Effects of Sampling Methods on Moisture Estimation. J. Northeast For. Univ. 2012, 40, 29–33. [Google Scholar] [CrossRef]
- Bülent, S.; Bilgili, E.; KuUk, O.; Durmaz, B.D. Determination of surface fuels moisture contents based on weather conditions. For. Ecol. Manag. 2006, 234, S75–S81. [Google Scholar] [CrossRef]
- Viegas, D.X.; Piñol, J.; Viegas, M.T.; Ogaya, R. Estimating live fine fuels moisture content using meteorologically-based indices. Int. J. Wildland Fire 2001, 10, 223–240. [Google Scholar] [CrossRef]
- Van Wagner, C.E. Equilibrium Moisture Contents of some Fine Forest Fuels in Eastern Canada. Inf. Rep. Petawawa For. Exp. Stn. 1972, PS-X-36. [Google Scholar]
- Lawson, B.D.; Armitage, O.B.; Hoskins, W.D. Diurnal variation in the fine fuel moisture code: Tables and computer source code. FRDA Rep. 1996, 245. (Pacific Forestry Centre and Research Branch: Victoria, BC). [Google Scholar]
- Sun, P.; Zhang, Y.L.; Sun, L.; Hu, H.H.; Guo, F.T.; Wang, G.Y.; Zhang, H. Influence of Fuel Moisture Content, Packing Ratio and Wind Velocity on the Ignition Probability of Fuel Beds Composed of Mongolian Oak Leaves via Cigarette Butts. Forests 2018, 9, 507. [Google Scholar] [CrossRef]
- Byram, G.M.; Nelson, R.M. An Analysis of the drying Process in Forest Fuel Material. In General Technical Report; Southern Research Station, USDA Forest Service: Blacksburg, VA, USA, 1963; pp. 1–38. [Google Scholar]
- Simard, A.J. The moisture content of forest fuels-1. In A Review of the Basic Concepts; Information Report FF-X-14; Canadian Department of Forest and Rural Development, Forest Fire Research Institute: Ottawa, ON, Canada, 1968; p. 47. [Google Scholar]
- Liu, X.; Jin, S. Development of Dead Forest Fuel Moisture Prediction Based on Equilibrium Moisture Content. Sci. Silvae Sin. 2007, 43, 126–133. [Google Scholar] [CrossRef]
- Viney, N.R. A Review of Fine Fuel Moisture Modelling. Int. J. Wildland Fire 1991, 1, 215–234. [Google Scholar] [CrossRef]
- Luke, R.H.; Mcarthur, A.G.; Brown, A.G.; Mcarthur, A.G.; Hillis, W.E. Bushfires in Australia; Australian Government Publishing Service: Canberra, Australia, 1978.
- Pixton, S.W.; Warburton, S. Moisture Content/Relative Humidity Equilibrium of Some Cereal Grains at Different Temperatures. J. Stored Prod. Res. 1971, 6, 283–293. [Google Scholar] [CrossRef]
- Britton, C.M.; Countryman, C.M.; Wright, H.A.; Walvekar, A.G. The Effect of Humidity, Air Temperature, and Wind Speed on Fine Fuel Moisture Content. Fire Technol. 1973, 9, 46–55. [Google Scholar] [CrossRef]
- Anderson Hal, E. Moisture Diffusivity and Response Time in Fine Forest Fuels. Can. J. For. Res. 1990, 20, 315–325. [Google Scholar] [CrossRef]
- Zhang, H. Influencing Factors of Dead Surface Fuel Moisture Prediction in Great Xing’an Region. Ph.D. Thesis, Northeast Forestry University, Harbin, China, 2014. [Google Scholar]
- Slijepcevic, A.; Anderson, W.R.; Matthews, S. Testing existing models for predicting hourly variation in fine fuel moisture in eucalypt forests. For. Ecol. Manag. 2013, 306, 202–215. [Google Scholar] [CrossRef]
- Zhang, Y.L. Study on Influencing Factors and Prediction Model of Dynamic Change of Litter Moisture Content of Mongolian Oak and Pinus Koraiensis. Ph.D. Thesis, Northeast Forestry University, Harbin, China, 2019. [Google Scholar] [CrossRef]
- Yu, H.Z.; Jin, S.; Di, X.Y. Prediction Models for Ground Surface Fuels Moisture Content of Larix gmelinii Stand in Daxing’anling of China Based on One-hour Time Step. Chin. J. Appl. Ecol. 2013, 24, 1565–1571. [Google Scholar]
- Yu, H.Z.; Jin, S.; Di, X.Y. Models for Predicting the Hourly Fuel Moisture Content on the Forest Floor of Birch Stands in Tahe Forestry Bureau. Sci. Silvae Sin. 2013, 49, 108–113. [Google Scholar] [CrossRef]
- Lu, X. Research on Dynamic and Prediction Model of Dead Fuel Moisture Content of Typical Stands in Great Xing’an Mountains. Ph.D. Thesis, Northeast Forestry University, Harbin, China, 2016. [Google Scholar]
- Liu, X. Effects of Temperature and Humidity on Fuel Equilibrium Moisture Content. Master’s Thesis, Northeast Forestry University, Harbin, China, 2007. [Google Scholar]
- Carlson, J.D.; Bradshaw, L.S.; Nelson, R.M. Application of the Nelson Model to Four Timelag Fuel Classes Using Oklahoma Field Observations: Model Evaluation and Comparison with National Fire Danger Rating System Algorithms. Int. J. Wildland Fire 2007, 16, 204–216. [Google Scholar] [CrossRef]
| Forest Type | Location | Elevation (m) | Mean Height (m) | Mean Diameter at Breast Height (cm) | Canopy Density | Litter Load (t·ha−1) |
|---|---|---|---|---|---|---|
| Mongolian oak (Quercus mongolica) | Upper slope | 544 | 12 | 23 | 0.45 | 3.68 |
| Korean pine (Pinus koraiensis) | Middle slope | 382 | 15 | 21 | 0.55 | 6.22 |
| Litter Type | N | Mean (%) | Minimum (%) | Maximum (%) | Mean Change in 1 h (%) | Minimum Change in 1 h (%) | Maximum Change in 1 h (%) |
|---|---|---|---|---|---|---|---|
| Mongolian oak | 134 | 22.02 | 17.91 | 32.37 | 1.06 | 0.00 | 11.49 |
| Korean pine | 125 | 15.35 | 9.28 | 33.89 | 0.58 | 0.00 | 2.94 |
| Method | Parameters | Mongolian Oak | MAE (%) | MRE (%) | Korean Pine | MAE (%) | MRE (%) |
|---|---|---|---|---|---|---|---|
| Nelson method | 0.2458 | 1.02 | 4.76 | 0.0039 | 0.50 | 3.53 | |
| −0.0261 | −0.0023 | ||||||
| 0.7813 | 0.9600 | ||||||
| 2.0261 | 12.2335 | ||||||
| Simard method | 0.9694 | 1.03 | 4.73 | 0.9732 | 0.50 | 3.59 | |
| 16.0968 | 18.4463 | ||||||
| Direction regression method | 19.7130 | 1.46 | 6.65 | 15.009 | 1.95 | 13.26 | |
| 0.0630 | −08400 | ||||||
| −0.1211 | 0.4130 | ||||||
| - | 0.079 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Sun, P. Study on the Diurnal Dynamic Changes and Prediction Models of the Moisture Contents of Two Litters. Forests 2020, 11, 95. https://doi.org/10.3390/f11010095
Zhang Y, Sun P. Study on the Diurnal Dynamic Changes and Prediction Models of the Moisture Contents of Two Litters. Forests. 2020; 11(1):95. https://doi.org/10.3390/f11010095
Chicago/Turabian StyleZhang, Yunlin, and Ping Sun. 2020. "Study on the Diurnal Dynamic Changes and Prediction Models of the Moisture Contents of Two Litters" Forests 11, no. 1: 95. https://doi.org/10.3390/f11010095
APA StyleZhang, Y., & Sun, P. (2020). Study on the Diurnal Dynamic Changes and Prediction Models of the Moisture Contents of Two Litters. Forests, 11(1), 95. https://doi.org/10.3390/f11010095




