Temporal Evolution of Carbon Stocks, Fluxes and Carbon Balance in Pedunculate Oak Chronosequence under Close-To-Nature Forest Management
Abstract
:1. Introduction
2. Materials and Methods
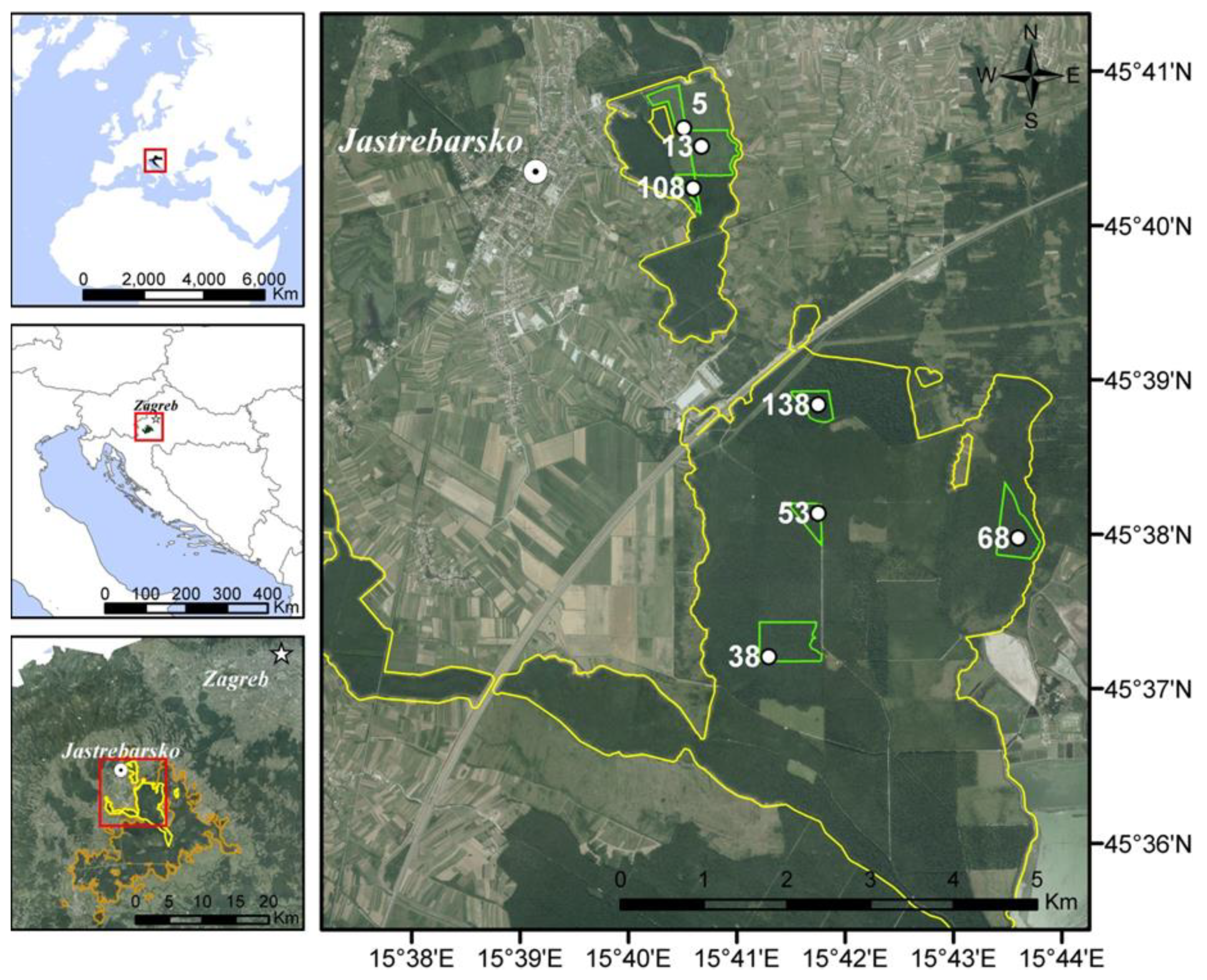
2.1. Study Area and Forest Management Practice
2.2. Experimental Design and Field Measurements
2.2.1. Aboveground Live Biomass Stocks
2.2.2. Dead Wood, Litterfall and Soil
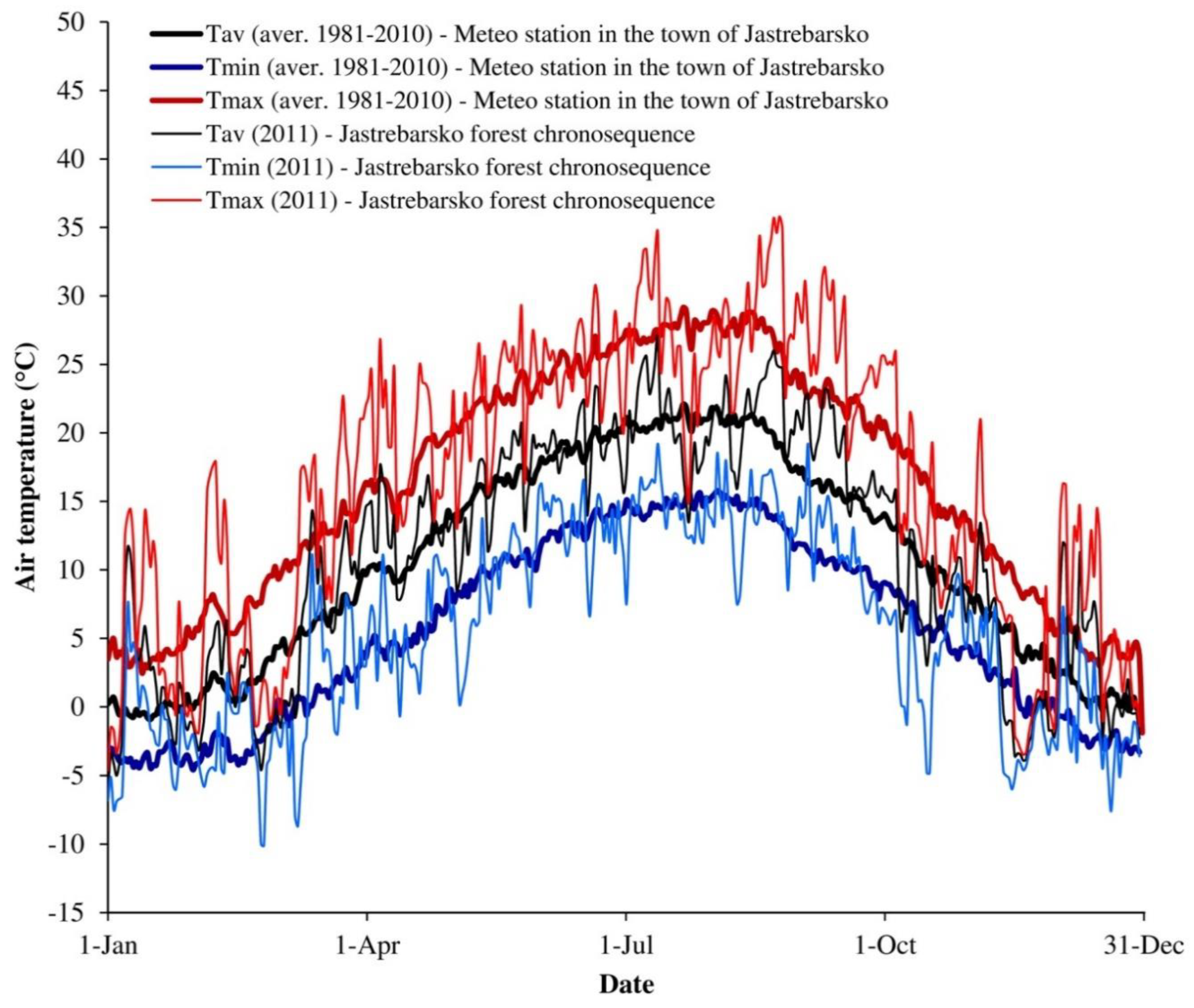
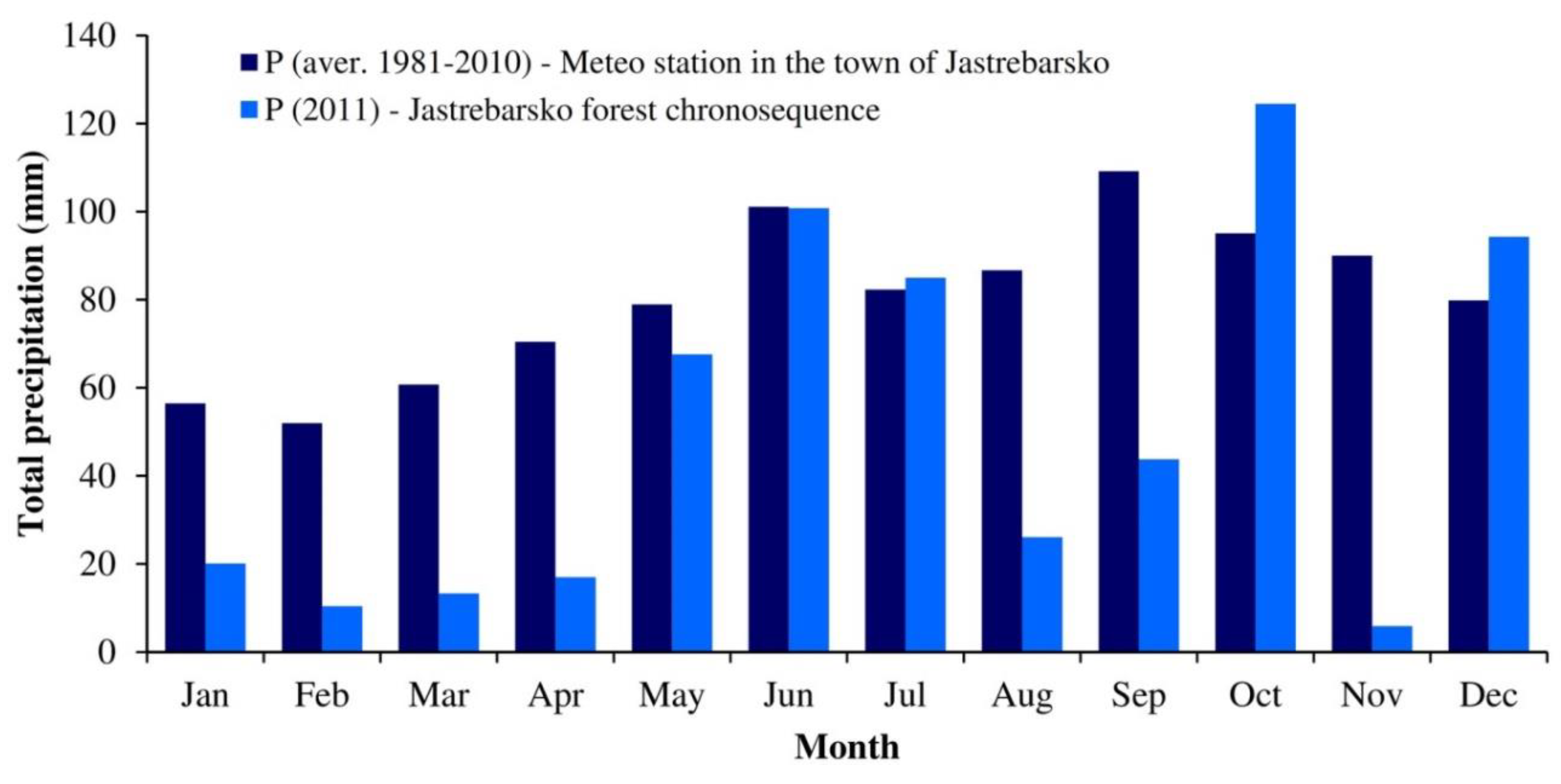
2.2.3. Meteorological Measurements, Soil Respiration and Dead Wood Decomposition Flux
2.3. Laboratory Analysis
2.4. Carbon Stocks Calculations
2.5. Carbon Fluxes Calculations and Modelling
2.6. Harvest Carbon Losses and Net Ecosystem Carbon Balance
2.7. Statistical Analysis
3. Results
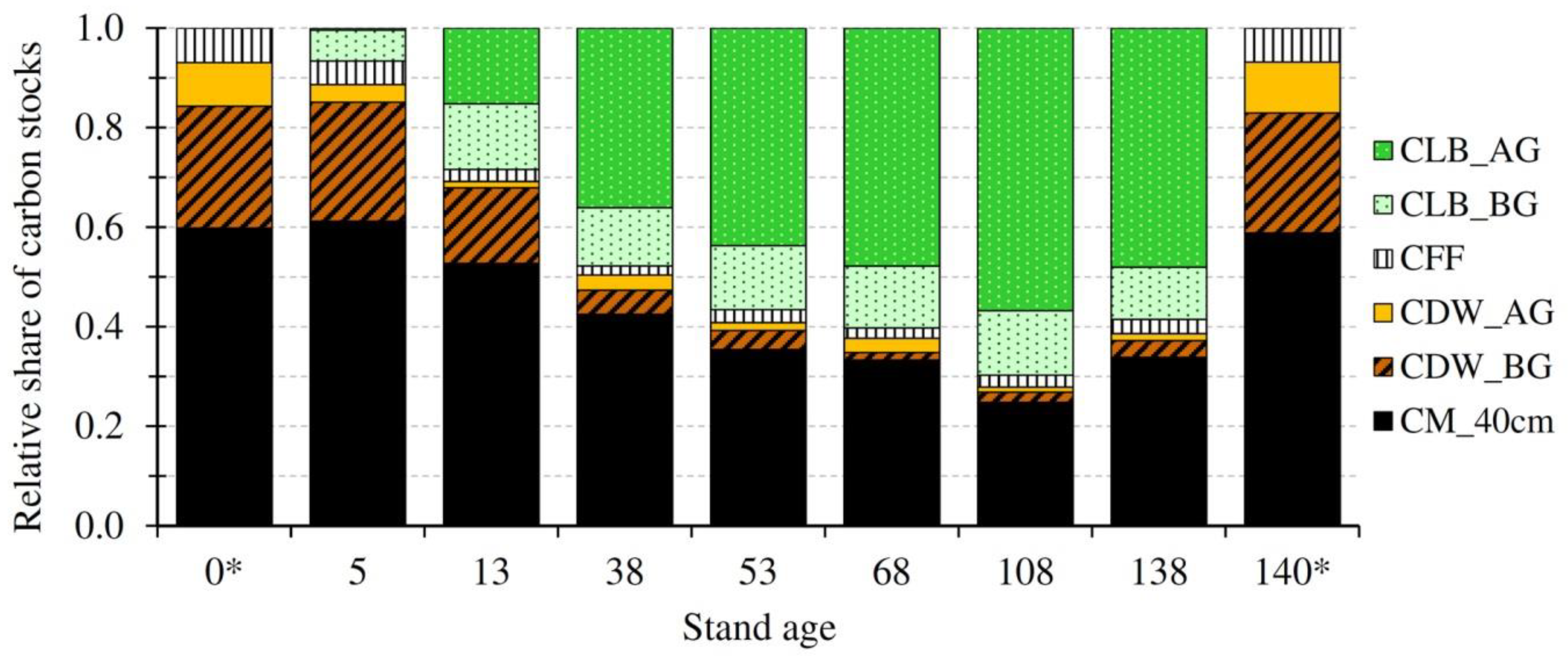
3.1. Carbon Stocks and Their Temporal Evolution
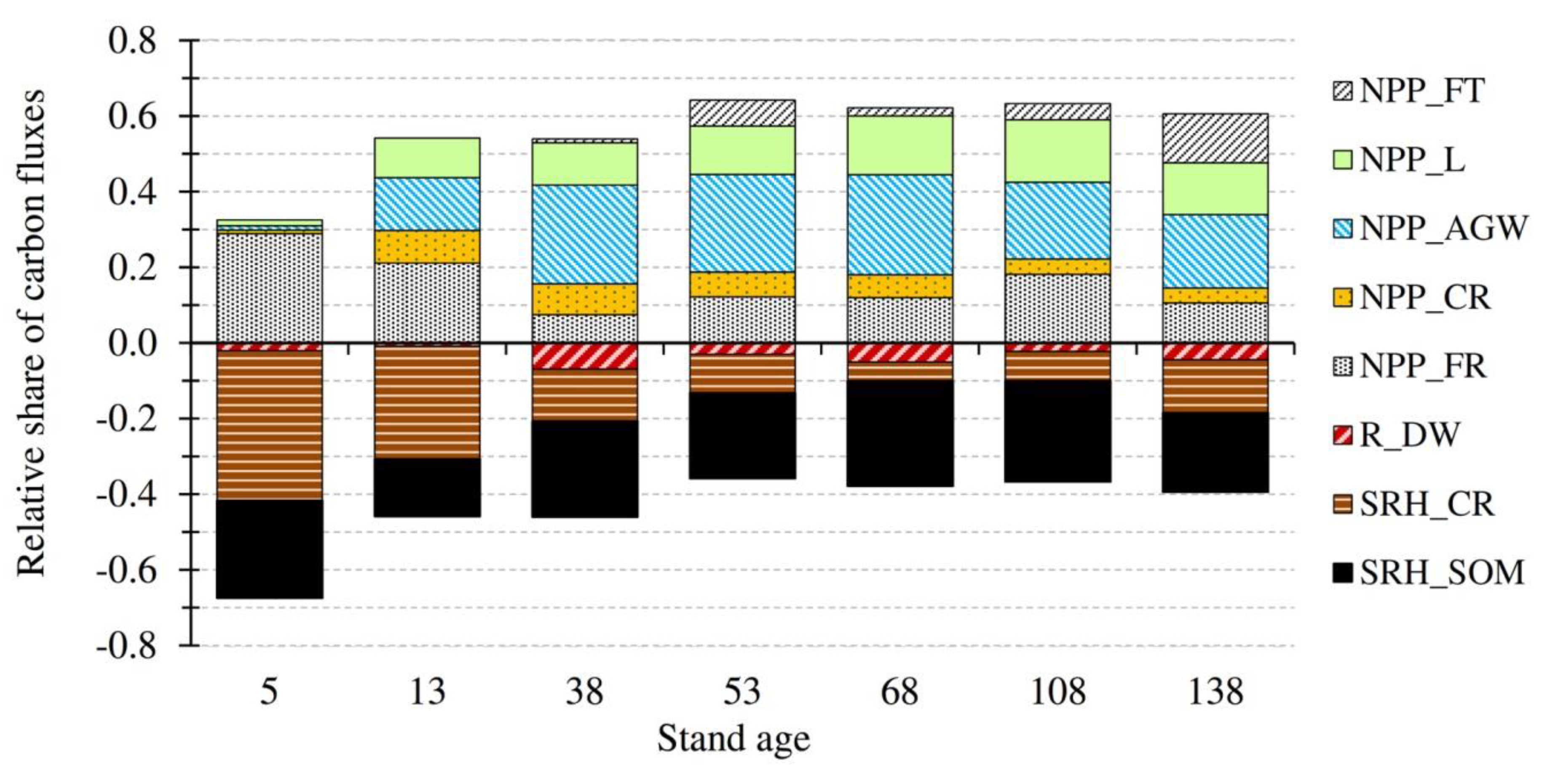
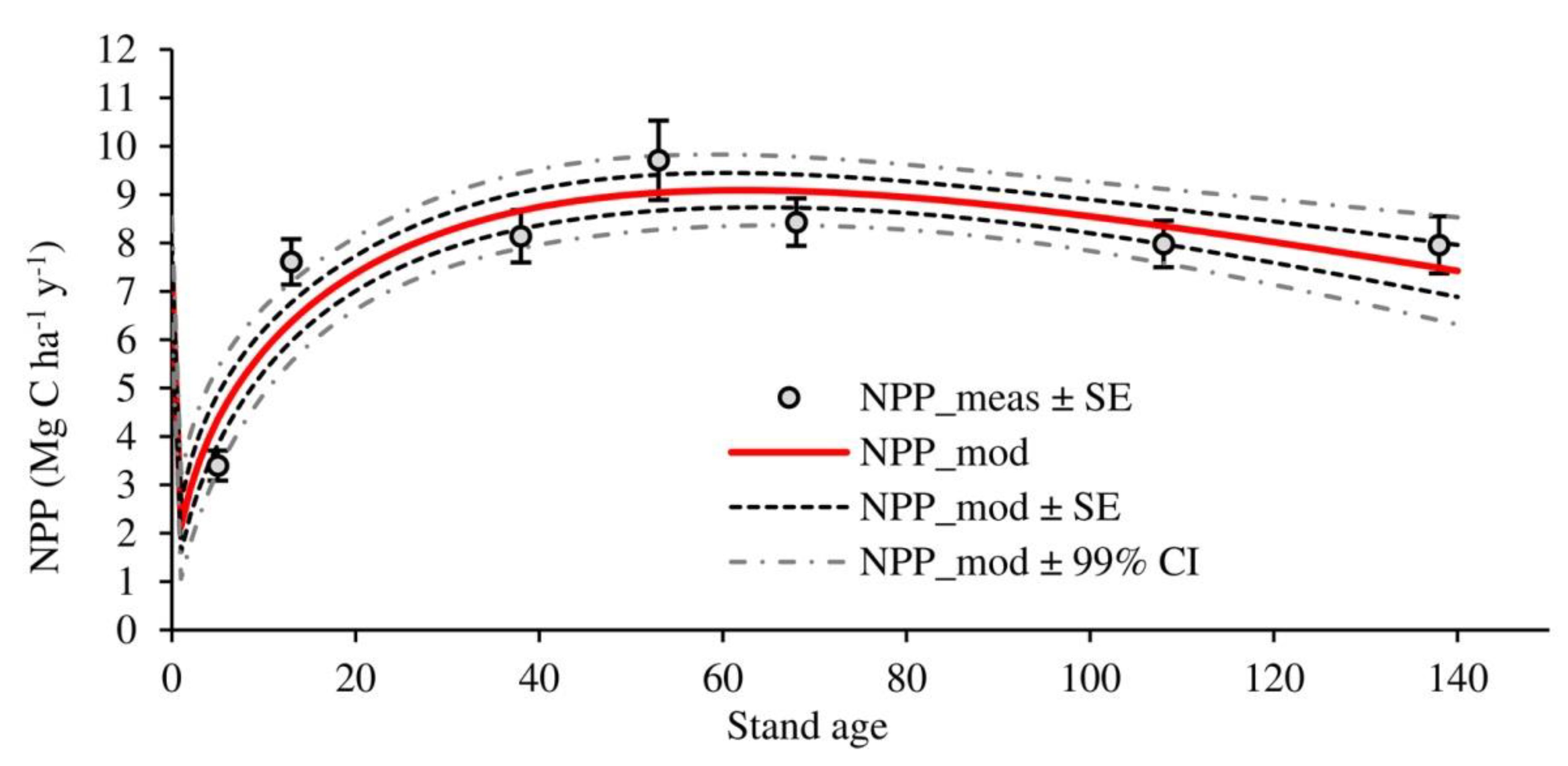
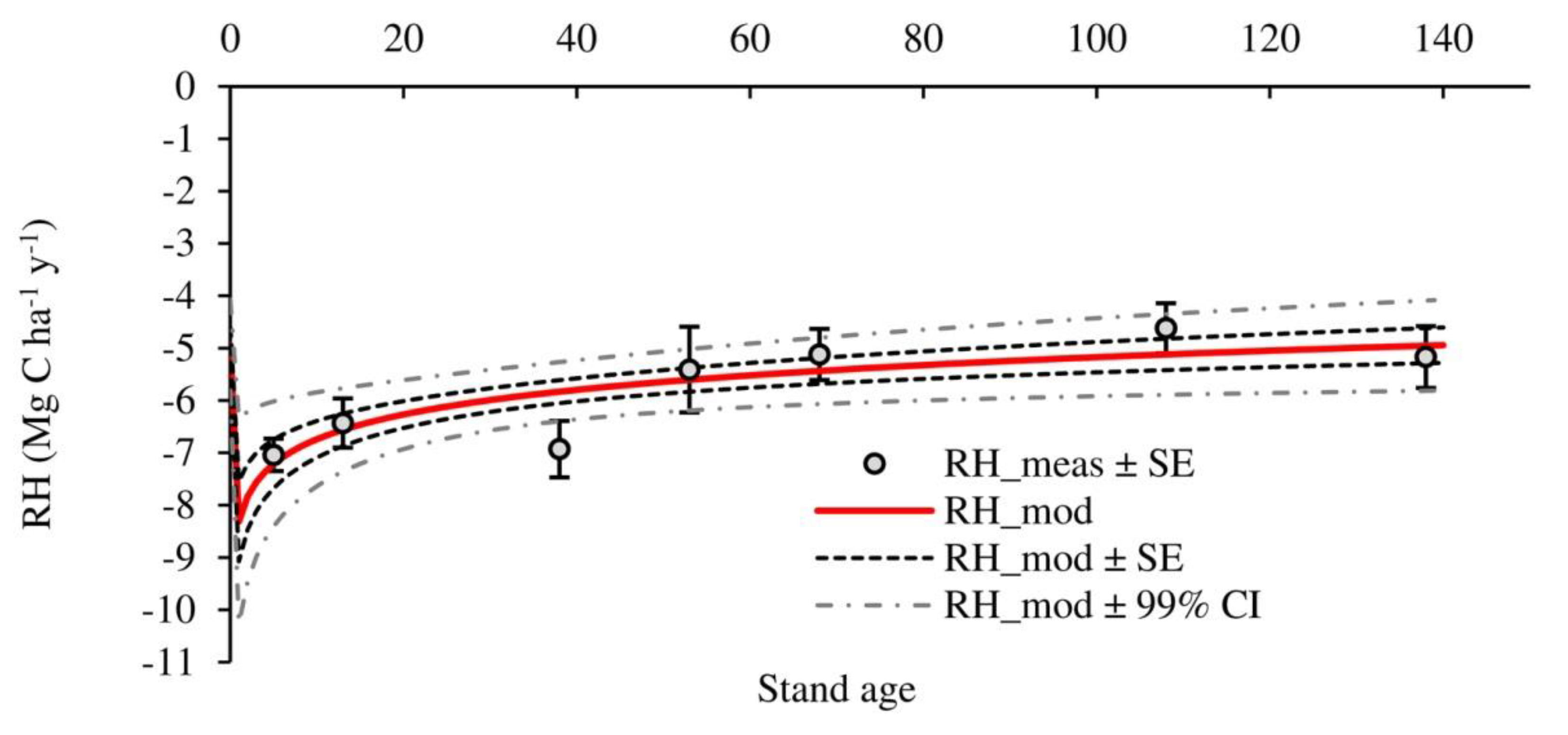
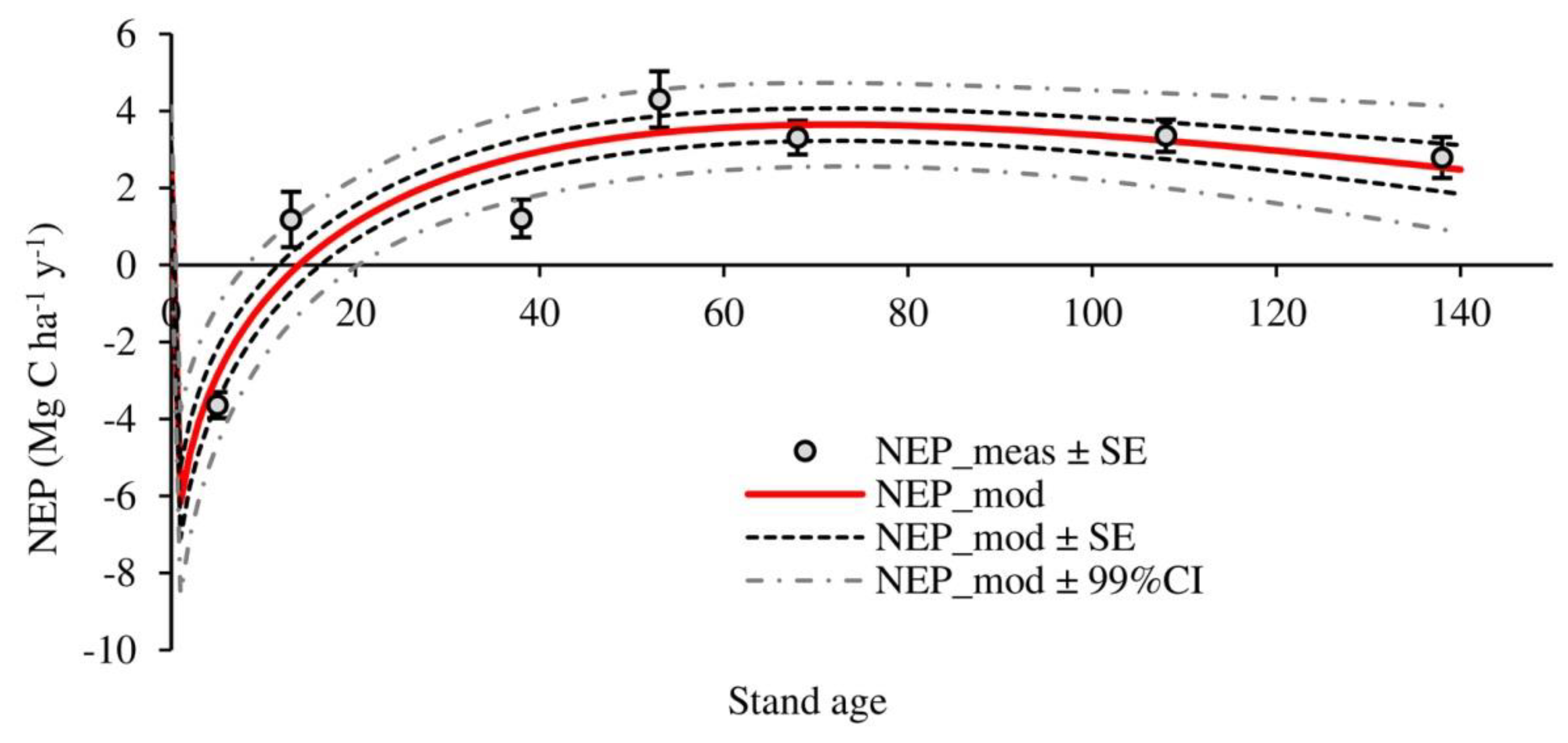
3.2. Temporal Evolution of Carbon Fluxes and Net Ecosystem Productivity
3.3. Harvest Carbon Losses and Net Ecosystem Carbon Balance throughout the Rotation
4. Discussion
4.1. Carbon Stocks in Different Ecosystem Pools and Their Temporal Evolution
4.2. Carbon Fluxes and Net Ecosystem Productivity
4.3. Net Ecosystem Carbon Balance throughout the Rotation Estimated by Different Approaches
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| DBH (cm) | Age Class * | |||||
|---|---|---|---|---|---|---|
| I. (1–20 y) | II. (21–40 y) | III. (41–60 y) | IV. (61–80 y) | VI. (101–120) | VII. (121–140) | |
| 2–5 | 2 | 2 | 2 | 2 | 2 | 2 |
| 6–10 | 3.5 | 3.5 | 3.5 | 3.5 | 3.5 | 3.5 |
| 11–30 | 7 | 8 | 10 | 12 | 16 | 17 |
| 31–50 | 7 | 8 | 13 | 13 | 16 | 17 |
| 51–80 | 7 | 8 | 13 | 13 | 16 | 17 |
| >80 | 56.4 (1 ha) | 56.4 | 56.4 | 56.4 | 56.4 | 56.4 |
| Parameter | Value | Standard Error | t Value | p Value | Lower Conf. Limit | Upper Conf. Limit |
|---|---|---|---|---|---|---|
| R = 0.9069; R2 = 0.8225; n = 1313 | ||||||
| aAGE | 2.7652 | 0.0922 | 29.98 | <0.0001 | 2.5843 | 2.9461 |
| bAGE | −0.0047 | 0.0004 | −11.16 | <0.0001 | −0.0055 | −0.0039 |
| aREW | 157.0005 | 21.3813 | 7.34 | <0.0001 | 115.0550 | 198.9459 |
| bREW | 376.0356 | 30.0037 | 12.53 | <0.0001 | 317.1749 | 434.8963 |
| RSWC1/2 | 0.0985 | 0.0227 | 4.34 | <0.0001 | 0.0540 | 0.1430 |
| Parameter | Value | Standard Error | t Value | p Value | Lower Conf. Limit | Upper Conf. Limit |
|---|---|---|---|---|---|---|
| R = 0.9096; R2 = 0.8274; n = 192 | ||||||
| Rref | 4.8274 | 0.7813 | 6.18 | <0.0001 | 3.2863 | 6.3685 |
| E0 | 507.8437 | 25.1566 | 20.19 | <0.0001 | 458.2199 | 557.4675 |
| RSWC1/2 | 1.0342 | 0.2886 | 3.58 | 0.0004 | 0.4650 | 1.6035 |
| Age Class | Harvest (m3 ha−1) | Cum. Harvest (m3 ha−1) | Harvest C Loss (Mg C ha−1) | Cum. Harvest C Loss (Mg C ha−1) | Source |
|---|---|---|---|---|---|
| 20 | 0 | 0 | 0.00 | 0.00 | Local species-specific yield tables (Špiranec 1975) Pedunculate Oak II site class |
| 30 | 5 | 5 | 1.55 | 1.55 | |
| 40 | 17 | 22 | 5.27 | 6.82 | |
| 50 | 34 | 56 | 10.54 | 17.36 | |
| 60 | 50 | 106 | 15.50 | 32.86 | |
| 70 | 62 | 168 | 19.22 | 52.08 | |
| 80 | 71 | 239 | 22.01 | 74.09 | |
| 90 | 75 | 314 | 23.25 | 97.34 | |
| 100 | 76 | 390 | 23.56 | 120.90 | |
| 110 | 75 | 465 | 23.25 | 144.15 | |
| 120 | 72 | 537 | 22.32 | 166.47 | |
| 130 | 67 | 604 | 20.77 | 187.24 | |
| 140 | 477 | 1081 | 147.94 | 335.18 | Estimated * |
References
- Pan, Y.D.; Birdsey, R.A.; Fang, J.Y.; Houghton, R.; Kauppi, P.E.; Kurz, W.A.; Phillips, O.L.; Shvidenko, A.; Lewis, S.L.; Canadell, J.G.; et al. A Large and Persistent Carbon Sink in the World’s Forests. Science 2011, 333, 988–993. [Google Scholar] [CrossRef] [PubMed]
- FAO. State of the World’s Forests; Food and Agriculture Organization of the United Nations: Rome, Italy, 2009. [Google Scholar]
- Fisher, B.; Turner, R.K. Ecosystem services: Classification for valuation. Biol. Conserv. 2008, 141, 1167–1169. [Google Scholar] [CrossRef]
- Ciais, P.; Schelhaas, M.J.; Zaehle, S.; Piao, S.L.; Cescatti, A.; Liski, J.; Luyssaert, S.; Le-Maire, G.; Schulze, E.D.; Bouriaud, O.; et al. Carbon accumulation in European forests. Nat. Geosci. 2008, 1, 425–429. [Google Scholar] [CrossRef]
- Law, B.E.; Sun, O.J.; Campbell, J.; Van Tuyl, S.; Thornton, P.E. Changes in carbon storage and fluxes in a chronosequence of ponderosa pine. Glob. Chang. Biol. 2003, 9, 510–524. [Google Scholar] [CrossRef]
- Mund, M. Carbon Pools of European Beech Forests (Fagus sylvatica) Under Different Silvicultural Management. Doctoral Dissertation, University of Göttingen, Göttingen, Germany, 2004. [Google Scholar]
- Campbell, J.L.; Sun, O.J.; Law, B.E. Disturbance and net ecosystem production across three climatically distinct forest landscapes. Glob. Biogeochem. Cycles 2004, 18. [Google Scholar] [CrossRef] [Green Version]
- Hedde, M.; Aubert, M.; Decaens, T.; Bureau, F. Dynamics of soil carbon in a beechwood chronosequence forest. For. Ecol. Manag. 2008, 255, 193–202. [Google Scholar] [CrossRef]
- Marjanović, H.; Alberti, G.; Balogh, J.; Czóbel, S.; Horváth, L.; Jagodics, A.; Nagy, Z.; Ostrogović, M.Z.; Peressotti, A.; Führer, E. Measurements and estimations of biosphere-atmosphere exchange of greenhouse gases—Forests. In Atmospheric Greenhouse Gases: The Hungarian Perspective; Haszpra, L., Ed.; Springer: New York, NY, USA, 2010; pp. 121–156. [Google Scholar]
- Tupek, B.; Zanchi, G.; Verkerk, P.J.; Churkina, G.; Viovy, N.; Hughes, J.K.; Lindner, M. A comparison of alternative modelling approaches to evaluate the European forest carbon fluxes. For. Ecol. Manag. 2010, 260, 241–251. [Google Scholar] [CrossRef]
- Bruckman, V.J.; Yan, S.; Hochbichler, E.; Glatzel, G. Carbon pools and temporal dynamics along a rotation period in Quercus dominated high forest and coppice with standards stands. For. Ecol. Manag. 2011, 262, 1853–1862. [Google Scholar] [CrossRef]
- De Simon, G.; Alberti, G.; Delle Vedove, G.; Zerbi, G.; Peressotti, A. Carbon stocks and net ecosystem production changes with time in two Italian forest chronosequences. Eur. J. For. Res. 2012, 131, 1297–1311. [Google Scholar] [CrossRef]
- Hale, K. Long-Term Carbon Storage in a Semi-Natural British Woodland. Doctoral Dissertation, University of Liverpool, Liverpool, UK, 2015. [Google Scholar]
- Lundmark, T.; Bergh, J.; Nordin, A.; Fahlvik, N.; Poudel, B.C. Comparison of carbon balances between continuous-cover and clear-cut forestry in Sweden. Ambio 2016, 45, S203–S213. [Google Scholar] [CrossRef]
- Pregitzer, K.S.; Euskirchen, E.S. Carbon cycling and storage in world forests: Biome patterns related to forest age. Glob. Chang. Biol 2004, 10, 2052–2077. [Google Scholar] [CrossRef]
- Hlasny, T.; Barcza, Z.; Fabrika, M.; Balazs, B.; Churkina, G.; Pajtik, J.; Sedmak, R.; Turcani, M. Climate change impacts on growth and carbon balance of forests in Central Europe. Clim. Res. 2011, 47, 219–236. [Google Scholar] [CrossRef]
- Vicca, S.; Luyssaert, S.; Penuelas, J.; Campioli, M.; Chapin, F.S.; Ciais, P.; Heinemeyer, A.; Hogberg, P.; Kutsch, W.L.; Law, B.E.; et al. Fertile forests produce biomass more efficiently. Ecol. Lett. 2012, 15, 520–526. [Google Scholar] [CrossRef] [PubMed]
- Alberti, G.; Vicca, S.; Inglima, I.; Belelli-Marchesini, L.; Genesio, L.; Miglietta, F.; Marjanović, H.; Martinez, C.; Matteucci, G.; D’Andrea, E.; et al. Soil C: N stoichiometry controls carbon sink partitioning between above-ground tree biomass and soil organic matter in high fertility forests. Iforest 2015, 8, 195–206. [Google Scholar] [CrossRef]
- Luyssaert, S.; Inglima, I.; Jung, M.; Richardson, A.D.; Reichstein, M.; Papale, D.; Piao, S.L.; Schulzes, E.D.; Wingate, L.; Matteucci, G.; et al. CO2 balance of boreal, temperate, and tropical forests derived from a global database. Glob. Chang. Biol. 2007, 13, 2509–2537. [Google Scholar] [CrossRef]
- Campioli, M.; Vicca, S.; Luyssaert, S.; Bilcke, J.; Ceschia, E.; Chapin, F.S.; Ciais, P.; Fernandez-Martinez, M.; Malhi, Y.; Obersteiner, M.; et al. Biomass production effciency controlled by management in temperate and boreal ecosystems. Nat. Geosci. 2015, 8, 843–846. [Google Scholar] [CrossRef]
- Verlinden, M.S.; Broeckx, L.S.; Zona, D.; Berhongaray, G.; De Groote, T.; Serrano, M.C.; Janssens, I.A.; Ceulemans, R. Net ecosystem production and carbon balance of an SRC poplar plantation during its first rotation. Biomass Bioenerg. 2013, 56, 412–422. [Google Scholar] [CrossRef] [Green Version]
- Price, D.T.; Halliwell, D.H.; Apps, M.J.; Kurz, W.A.; Curry, S.R. Comprehensive assessment of carbon stocks and fluxes in a Boreal-Cordilleran forest management unit. Can. J. For. Res. 1997, 27, 2005–2016. [Google Scholar] [CrossRef]
- Scott, N.A.; Rodrigues, C.A.; Hughes, H.; Lee, J.T.; Davidson, E.A.; Dail, D.B.; Malerba, P. Changes in carbon storage and net carbon exchange one year after an initial shelterwood harvest at Howland Forest, ME. Environ. Manag. 2004, 33, S9–S22. [Google Scholar] [CrossRef]
- Chapin, F.S.; Woodwell, G.M.; Randerson, J.T.; Rastetter, E.B.; Lovett, G.M.; Baldocchi, D.D.; Clark, D.A.; Harmon, M.E.; Schimel, D.S.; Valentini, R.; et al. Reconciling carbon-cycle concepts, terminology, and methods. Ecosystems 2006, 9, 1041–1050. [Google Scholar] [CrossRef]
- Schulze, E.D. Biological control of the terrestrial carbon sink. Biogeosciences 2006, 3, 147–166. [Google Scholar] [CrossRef] [Green Version]
- Teets, A.; Fraver, S.; Hollinger, D.Y.; Weiskittel, A.R.; Seymour, R.S.; Richardson, A.D. Linking annual tree growth with eddy-flux measures of net ecosystem productivity across twenty years of observation in a mixed conifer forest. Agric. For. Meteorol. 2018, 249, 479–487. [Google Scholar] [CrossRef]
- Pretzsch, H.; Biber, P.; Schutze, G.; Uhl, E.; Rotzer, T. Forest stand growth dynamics in Central Europe have accelerated since 1870. Nat. Commun 2014, 5. [Google Scholar] [CrossRef] [PubMed]
- Lindner, M.; Maroschek, M.; Netherer, S.; Kremer, A.; Barbati, A.; Garcia-Gonzalo, J.; Seidl, R.; Delzon, S.; Corona, P.; Kolstrom, M.; et al. Climate change impacts, adaptive capacity, and vulnerability of European forest ecosystems. For. Ecol. Manag. 2010, 259, 698–709. [Google Scholar] [CrossRef]
- Mund, M.; Kummetz, E.; Hein, M.; Bauer, G.A.; Schulze, E.D. Growth and carbon stocks of a spruce forest chronosequence in central Europe. For. Ecol. Manag. 2002, 171, 275–296. [Google Scholar] [CrossRef]
- Johnson, E.A.; Miyanishi, K. Testing the assumptions of chronosequences in succession. Ecol. Lett. 2008, 11, 419–431. [Google Scholar] [CrossRef]
- Walker, L.R.; Wardle, D.A.; Bardgett, R.D.; Clarkson, B.D. The use of chronosequences in studies of ecological succession and soil development. J. Ecol. 2010, 98, 725–736. [Google Scholar] [CrossRef]
- Löf, M.; Brunet, J.; Filyushkina, A.; Lindbladh, M.; Skovsgaard, J.P.; Felton, A. Management of oak forests: Striking a balance between timber production, biodiversity and cultural services. Int. J. Biodivers. Sci. Ecosyst. Serv. Manag. 2016, 12, 59–73. [Google Scholar] [CrossRef]
- Haavik, L.J.; Billings, S.A.; Guldin, J.M.; Stephen, F.M. Emergent insects, pathogens and drought shape changing patterns in oak decline in North America and Europe. For. Ecol. Manag. 2015, 354, 190–205. [Google Scholar] [CrossRef]
- Mayer, B. Hidropedološki odnosi na području nizinskih šuma Pokupskog bazena. Radovi Šumar. Inst. Jastrebar. 1996, 31, 37–89. (In Croatian) [Google Scholar]
- Marjanović, H.; Ostrogović, M.Z.; Alberti, G.; Balenović, I.; Paladinić, E.; Indir, K.; Peressotti, A.; Vuletić, D. Carbon Dynamics in Younger Stands of Pedunculate Oak during Two Vegetation Periods. Sumar. List 2011, 135, 59–73. [Google Scholar]
- Croatian Forests Ltd. Forest Management Area Plan for the Republic of Croatia for the Period 2016–2025; Croatian Forests Ltd: Zagreb, Croatia, 2016. Available online: https://poljoprivreda.gov.hr/istaknute-teme/sume-112/sumarstvo/sumskogospodarska-osnova-2016-2025/250 (accessed on 17 July 2019). (In Croatian)
- Ordinance on Forest Management; Official Gazette 97; Narodne novine: Zagreb, Croatia, 2018; Available online: https://narodne-novine.nn.hr/clanci/sluzbeni/2018_11_97_1875.html (accessed on 17 July 2019).
- Klepac, D.; Fabijanić, G. Management of Pedunculate oak forest. In Monography: Pedunculate Oak in Croatia; Klepac, D., Ed.; Croatian Academy of Science and Art and Croatian Forests Ltd.: Zagreb, Croatia, 1996; pp. 257–272. (In Croatian) [Google Scholar]
- Meštrović, Š. Pravilnik o izradi šumskoprivrednih osnova, osnova gospodarenja i programa za unapređenja šuma u svjetlu šumarske znanosti. Šumar. List. 1978, 102, 352–364. (In Croatian) [Google Scholar]
- Duncker, P.S.; Barreiro, S.M.; Hengeveld, G.M.; Lind, T.; Mason, W.L.; Ambrozy, S.; Spiecker, H. Classification of Forest Management Approaches: A New Conceptual Framework and Its Applicability to European Forestry. Ecol. Soc. 2012, 17. [Google Scholar] [CrossRef]
- Law, B.E.; Arkebauer, T.; Campbell, J.L.; Chen, J.; Sun, O.; Schwartz, M.; van Ingen, C.; Verma, S. Terrestrial Carbon Observing Protocols for Vegetation Sampling and Data Submission; Food and Agriculture Organization of the United Nations: Rome, Italy, 2008. [Google Scholar]
- Anić, M.; Sever, M.Z.O.; Alberti, G.; Balenović, I.; Paladinić, E.; Peressotti, A.; Tijan, G.; Večenaj, Z.; Vuletić, D.; Marjanović, H. Eddy Covariance vs. Biometric Based Estimates of Net Primary Productivity of Pedunculate Oak (Quercus robur L.) Forest in Croatia during Ten Years. Forests 2018, 9. [Google Scholar] [CrossRef]
- Van Wagner, C.E. The Line Intersect Method in Forest Fuel Sampling. For. Sci. 1968, 14, 20–26. [Google Scholar]
- Hunter, M.L. Wildlife, Forest, and Forestry: Principles of Managing Forests for Biological Diversity; Prentice-Hall: Englewood Cliffs, NJ, USA, 1990. [Google Scholar]
- Cools, N.; De Vos, B. Part X: Sampling and Analysis of Soil. In Manual on Methods and Criteria for Harmonized Sampling, Assessment, Monitoring and Analysis of the Effects of Air Pollution on Forests, 1st ed.; UNECE ICP Forests Programme Co-Ordinating Centre, Ed.; Thünen Institute of Forest Ecosystems: Eberswalde, Germany, 2016; p. 115. [Google Scholar]
- Matić, S.; Anić, I. One year since the establishment of a research station for intensive monitoring of carbon cycling in a Pedunculate oak stand—What have we learned? In Proceedings of the Scientific Symposium Forests of Pedunculate Oak in Changed Site and Management Conditions; Croatian Academy of Science and Art: Zagreb, Croatia, 2008; pp. 193–207. [Google Scholar]
- Delle Vedove, G.; Alberti, G.; Peressotti, A.; Inglima, I.; Zuliani, M.; Zerbi, G. Automated monitoring of soil respiration: An improved automatic chamber system. Italian J Agron. 2007, 2, 377–382. [Google Scholar] [CrossRef]
- Reichstein, M.; Rey, A.; Freibauer, A.; Tenhunen, J.; Valentini, R.; Banza, J.; Casals, P.; Cheng, Y.F.; Grunzweig, J.M.; Irvine, J.; et al. Modeling temporal and large-scale spatial variability of soil respiration from soil water availability, temperature and vegetation productivity indices. Glob. Biogeochem. Cycle 2003, 17. [Google Scholar] [CrossRef]
- Ostrogović, M.Z.; Marjanović, H.; Balenović, I.; Sever, K.; Jazbec, A. Decomposition of fine woody debris from main tree species in lowland oak forests. Pol. J. Ecol. 2015, 63, 247–259. [Google Scholar] [CrossRef]
- Špiranec, M. Allometric equations. Rad Šumar. Inst. Jastrebar. 1975, 22, 1–262. (In Croatian) [Google Scholar]
- Cestar, D.; Kovačić, D.J. Wood volume tables for Black Alder and Black Locust. Rad Šumar. Inst. Jastrebar. 1982, 49, 1–149, (In Croatian with English Summary). [Google Scholar]
- Cestar, D.; Kovačić, D.J. Wood volume tables for Narrow-leaved Ash (Fraxinus parvifolia Auct.). Rad Šumar. Inst. Jastrebar. 1984, 60, 1–178, (In Croatian with English Summary). [Google Scholar]
- Ugrenović, A. Forestry Encyclopaedia I; Miroslav Krleža Institute of Lexicography: Zagreb, Croatia, 1959. (In Croatian) [Google Scholar]
- Balboa-Murias, M.A.; Rojo, A.; Alvarez, J.G.; Merino, A. Carbon and nutrient stocks in mature Quercus robur L. stands in NW Spain. Ann. For. Sci. 2006, 63, 557–565. [Google Scholar] [CrossRef]
- Cairns, M.A.; Brown, S.; Helmer, E.H.; Baumgardner, G.A. Root biomass allocation in the world’s upland forests. Oecologia 1997, 111, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Genet, H.; Breda, N.; Dufrene, E. Age-related variation in carbon allocation at tree and stand scales in beech (Fagus sylvatica L.) and sessile oak (Quercus petraea (Matt.) Liebl.) using a chronosequence approach. Tree Physiol. 2010, 30, 177–192. [Google Scholar] [CrossRef] [PubMed]
- Joslin, J.D.; Gaudinski, J.B.; Torn, M.S.; Riley, W.J.; Hanson, P.J. Fine-root turnover patterns and their relationship to root diameter and soil depth in a C-14-labeled hardwood forest. New Phytol. 2006, 172, 523–535. [Google Scholar] [CrossRef] [PubMed]
- Jackson, R.B.; Mooney, H.A.; Schulze, E.D. A global budget for fine root biomass, surface area, and nutrient contents. Proc. Natl. Acad. Sci. USA 1997, 94, 7362–7366. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pietsch, S.A.; Hasenauer, H.; Thornton, P.E. BGC-model parameters for tree species growing in central European forests. For. Ecol. Manag. 2005, 211, 264–295. [Google Scholar] [CrossRef]
- Tang, J.W.; Luyssaert, S.; Richardson, A.D.; Kutsch, W.; Janssens, I.A. Steeper declines in forest photosynthesis than respiration explain age-driven decreases in forest growth. Proc. Natl. Acad. Sci. USA 2014, 111, 8856–8860. [Google Scholar] [CrossRef] [Green Version]
- Ostrogović, M.Z. Carbon Stocks and Carbon Balance of an Even Aged Pedunculate Oak (Quercus robur L.) Forest in Kupa River Basin. Doctoral Dissertation, Faculty of Forestry, University of Zagreb, Zagreb, Croatia, 2013. [Google Scholar]
- Bond-Lamberty, B.P.; Thomson, A.M. A Global Database of Soil Respiration Data; Version 2.0; Oak Ridge National Laboratory Distributed Active Archive Center: Oak Ridge, TN, USA. Available online: http://daac.ornl.gov (accessed on 12 March 2018).
- Subke, J.A.; Inglima, I.; Cotrufo, M.F. Trends and methodological impacts in soil CO2 efflux partitioning: A meta-analytical review. Glob. Chang. Biol. 2006, 12, 1813. [Google Scholar] [CrossRef]
- Harmon, M.E.; Bond-Lamberty, B.; Tang, J.W.; Vargas, R. Heterotrophic respiration in disturbed forests: A review with examples from North America. J. Geophys. Res. Biogeosci. 2011, 116. [Google Scholar] [CrossRef]
- Liu, Q.; Zhao, C.Z.; Cheng, X.Y.; Yin, H.J. Soil respiration and carbon pools across a range of spruce stand ages, Eastern Tibetan Plateau. Soil Sci. Plant. Nutr. 2015, 61, 440–449. [Google Scholar] [CrossRef]
- Olson, J.S. Energy-Storage and Balance of Producers and Decomposers in Ecological-Systems. Ecology 1963, 44, 322–331. [Google Scholar] [CrossRef]
- Mattson, K.G.; Swank, W.T.; Waide, J.B. Decomposition of Woody Debris in a Regenerating, Clear-Cut Forest in the Southern Appalachians. Can. J. For. Res. 1987, 17, 712–721. [Google Scholar] [CrossRef]
- Špiranec, M. Yield tables. Rad Šumar. Inst. Jastrebar. 1975, 25, 1–103. (In Croatian) [Google Scholar]
- StataCorp. Stata Statistical Software; Release 14; StataCorp LP: College Station, TX, USA, 2015. [Google Scholar]
- Debeljak, M. Coarse woody debris in virgin and managed forest. Ecol. Indic. 2006, 6, 733–742. [Google Scholar] [CrossRef]
- Čavlović, J. First National Forest Inventory in Republic of Croatia; Ministry of Regional Development; Forestry and Water Management: Zagreb, Croatia, 2010. (In Croatian) [Google Scholar]
- Pernar, N.; Klimo, E.; Baksić, D.; Perković, I.; Rybnicek, M.; Vavrcik, H.; Gryc, V.H. Carbon and Nitrogen Accumulation in Common Alder Forest (Alnus glutinosa Gaertn.) in Plain of Drava River. Sumar. List 2012, 136, 431–444. [Google Scholar]
- Schulp, C.J.E.; Nabulars, G.J.; Verburg, P.H.; de Waal, R.W. Effect of tree species on carbon stocks in forest floor and mineral soil and implications for soil carbon inventories. For. Ecol. Manag. 2008, 256, 482–490. [Google Scholar] [CrossRef]
- Justine, M.F.; Yang, W.Q.; Wu, F.Z.; Tan, B.; Khan, M.N.; Zhao, Y.Y. Biomass Stock and Carbon Sequestration in a Chronosequence of Pinus massoniana Plantations in the Upper Reaches of the Yangtze River. Forests 2015, 6, 3665–3682. [Google Scholar] [CrossRef]
- Uri, V.; Varik, M.; Aosaar, J.; Kanal, A.; Kukumagi, M.; Lohmus, K. Biomass production and carbon sequestration in a fertile silver birch (Betula pendula Roth) forest chronosequence. For. Ecol. Manag. 2012, 267, 117–126. [Google Scholar] [CrossRef]
- Yuste, J.C.; Konopka, B.; Janssens, I.A.; Coenen, K.; Xiao, C.W.; Ceulemans, R. Contrasting net primary productivity and carbon distribution between neighboring stands of Quercus robur and Pinus sylvestris. Tree Physiol. 2005, 25, 701–712. [Google Scholar] [CrossRef]
- Luo, Y.; Zhou, X. Soil Respiration and the Environment, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Campbell, J.L.; Law, B.E. Forest soil respiration across three climatically distinct chronosequences in Oregon. Biogeochemistry 2005, 73, 109–125. [Google Scholar] [CrossRef]
- Hanson, P.J.; Wullschleger, S.D.; Bohlman, S.A.; Todd, D.E. Seasonal and Topographic Patterns of Forest Floor Co2 Efflux from an Upland Oak Forest. Tree Physiol. 1993, 13, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Yuste, J.C.; Nagy, M.; Janssens, I.A.; Carrara, A.; Ceulemans, R. Soil respiration in a mixed temperate forest and its contribution to total ecosystem respiration. Tree Physiol. 2005, 25, 609–619. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Luan, J.W.; Liu, S.R.; Wang, J.X.; Zhu, X.L.; Shi, Z.M. Rhizospheric and heterotrophic respiration of a warm-temperate oak chronosequence in China. Soil Biol. Biochem. 2011, 43, 503–512. [Google Scholar] [CrossRef]
- Sihi, D.; Davidson, E.A.; Chen, M.; Savage, K.E.; Richardson, A.D.; Keenan, T.F.; Hollinger, D.Y. Merging a mechanistic enzymatic model of soil heterotrophic respiration into an ecosystem model in two AmeriFlux sites of northeastern USA. Agric. For. Meteorol. 2018, 252, 155–166. [Google Scholar] [CrossRef] [Green Version]
- Ćirić, M. Soil Science (Pedologija); Svjetlost: Sarajevo, BIH, 1984. (In Croatian) [Google Scholar]
- Harmon, M.E.; Franklin, J.F.; Swanson, F.J.; Sollins, P.; Gregory, S.V.; Lattin, J.D.; Anderson, N.H.; Cline, S.P.; Aumen, N.G.; Sedell, J.R.; et al. Ecology of Coarse Woody Debris in Temperate Ecosystems. Adv. Ecol. Res. 1986, 15, 133–302. [Google Scholar] [CrossRef]
- Rustad, L.E.; Campbell, J.L.; Marion, G.M.; Norby, R.J.; Mitchell, M.J.; Hartley, A.E.; Cornelissen, J.H.C.; Gurevitch, J.; Gcte-News. A meta-analysis of the response of soil respiration, net nitrogen mineralization, and aboveground plant growth to experimental ecosystem warming. Oecologia 2001, 126, 543–562. [Google Scholar] [CrossRef]
- Boisvenue, C.; Running, S.W. Impacts of climate change on natural forest productivity–evidence since the middle of the 20th century. Glob. Chang. Biol. 2006, 12, 862–882. [Google Scholar] [CrossRef]
- McMahon, S.M.; Parker, G.G.; Miller, D.R. Evidence for a recent increase in forest growth. Proc. Natl. Acad. Sci. USA 2010, 107, 3611–3615. [Google Scholar] [CrossRef] [Green Version]
- Horak, R.; Borisev, M.; Pilipović, A.; Orlović, S.; Pajevio, S.; Nikolić, N. Drought Impact on Forest Trees in Four Nature Protected Areas in Serbia. Sumar. List 2014, 138, 301–308. [Google Scholar]
- Kern, A.; Marjanović, H.; Dobor, L.; Anić, M.; Hlásny, T.; Barcza, Z. Identification of Years with Extreme Vegetation State in Central Europe Based on Remote Sensing and Meteorological Data. South-East Eur. For. 2017, 8, 1–20. [Google Scholar] [CrossRef]
| Stand Age (y) | DBH (cm) b | H (m) b | N (Tree ha−1) | BA (m2 ha−1) | V (m3 ha−1) | Clay (%) | Silt (%) | Ts (°C) | SWC (m3 m−3) | FC (m3 m−3) |
|---|---|---|---|---|---|---|---|---|---|---|
| 5 a | [0.91] | [0.53] | [120,000 ± 12,217] | [7.96 ± 0.83] | [1.4 ± 0.1] | 0.22 | 0.48 | 11.05 | 0.392 | 0.52 |
| 13 | 4.7 ± 1.9 | 5.4 ± 0.8 | 8507 ± 1029 | 11.63 ± 1.42 | 36.7 ± 4.7 | 0.28 | 0.49 | 10.45 | 0.379 | 0.58 |
| 38 | 16.0 ± 5.4 | 17.6 ± 3.4 | 1684 ± 188 | 27.03 ± 1.49 | 267.0 ± 15.3 | 0.51 | 0.37 | 10.62 | 0.403 | 0.53 |
| 53 | 23.1 ± 7.6 | 21.2 ± 3.9 | 860 ± 215 | 26.24 ± 1.5 | 310.4 ± 13 | 0.33 | 0.44 | 10.31 | 0.394 | 0.54 |
| 68 | 28.2 ± 10.6 | 23.5 ± 5.2 | 406 ± 39 | 26.62 ± 1.53 | 376.5 ± 22.5 | 0.25 | 0.49 | n.a. | n.a. | n.a. |
| 108 | 37.5 ± 16.5 | 26.0 ± 6.3 | 390 ± 144 | 30.7 ± 2.79 | 492.3 ± 43.8 | 0.25 | 0.49 | 10.35 | 0.383 | 0.49 |
| 138 | 42.9 ± 23.2 | 24.3 ± 7.4 | 169 ± 22 | 28.57 ± 1.26 | 466.5 ± 20.1 | 0.26 | 0.50 | 10.63 | 0.437 | 0.58 |
| C Stocks | Stand Age (Years) | Average (Share) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0 * | 5 | 13 | 38 | 53 | 68 | 108 | 138 | 140 * | ||
| No # | − | 5 | 12 | 14 | 12 | 12 | 10 | 12 | − | − |
| CLBAGW | 0.0 | 0.4 ± 0 a | 25.2 ± 3.2 a | 93.8 ± 6.6 b | 106.2 ± 5.1 b,c | 129.9 ± 7.3 c | 164.7 ± 14.6 d | 158.5 ± 5.8 d | 0.0 | 97.0 (40%) |
| CLBL | 0.0 | 0.2 ± 0.1 a | 1.5 ± 0.1 b | 1.7 ± 0.1 b | 1.9 ± 0.2 b | 2.1 ± 0.1 b | 2.1 ± 0.1 b | 1.8 ± 0.3 b | 0.0 | 1.6 (1%) |
| CLBFT | 0.0 | 0 | 0 | 0.2 ± 0.1 a | 1.0 ± 0.2 a,b | 0.3 ± 0.1 a | 0.5 ± 0.2 a | 1.7 ± 0.4 b | 0.0 | 0.5 (0%) |
| CLBCR& | 0.0 | 0.5 ± 0.2 | 16.0 ± 1.8 | 28.2 ± 3.6 | 27.6 ± 3.2 | 30.5 ± 2.2 | 33.0 ± 3.0 | 31.8 ± 1.3 | 0.0 | 23.9 (10%) |
| CLBFR | 0.0 | 6.0 ± 0.5 a | 5.9 ± 0.3 a | 2.3 ± 0.3 c | 3.7 ± 0.5 b,c | 3.3 ± 0.3 b,c | 4.6 ± 0.3 a,b | 2.8 ± 0.2 c | 0.0 | 4.1 (2%) |
| CLB | 0.0 | 7.2 ± 0.6 a | 48.6 ± 4.8 b | 126.2 ± 16.7 c | 140.4 ± 15.8 c,d | 166.1 ± 11.7 d | 204.9 ± 18.1 e | 196.6 ± 7.8 e | 0.0 | 127.1 (53%) |
| CDWAG | 13.3 | 3.7 | 2.1 ± 0.4 a | 8.0 ± 1.2 b | 3.9 ± 0.7 a,b | 7.8 ± 2.4 a,b | 3.0 ± 0.8 a,b | 4.6 ± 1.3 a,b | 19.5 | 4.7 (2%) |
| CDWBG | 37.1 | 24.9 | 25.2 ± 3.6 a | 12.5 ± 0.8 b | 9.3 ± 1.1 b,c | 4.1 ± 0.8 c | 5.9 ± 0.6 b,c | 11.1 ± 1.0 b,c | 45.7 | 13.3 (6%) |
| CDW | 50.4 | 28.6 | 27.3 ± 4.0 a | 20.5 ± 1.8 a,b | 13.2 ± 1.4 b | 11.9 ± 2.3 b | 8.9 ± 1.0 c | 15.7 ± 2.0 b | 65.2 | 18.0 (8%) |
| CFFOL | 5.8 | 3.0 ± 0.4 a,b | 3.1 ± 0.3 a,b | 2.9 ± 0.3 a,b | 3.5 ± 0.3 a,b | 2.2 ± 0.1 a | 4.2 ± 0.6 b | 3.6 ± 0.3 a,b | 7.1 | 3.2 (1%) |
| CFFOFH | 4.7 | 1.9 ± 0.7 a | 0.9 ± 0.2 a | 1.8 ± 0.1a | 2.8 ± 0.5 a,b | 3.4 ± 0.8 a,b | 2.7 ± 0.3 a,b | 5.8 ± 1.6 b | 5.8 | 2.8 (1%) |
| CFF | 10.5 | 4.9 ± 0.8 a | 4.0 ± 0.4 a | 4.7 ± 0.3 a | 6.3 ± 0.6 a,b | 5.6 ± 0.8 a,b | 6.9 ± 0.7 a,b | 9.4 ± 1.6 b | 12.9 | 6.0 (2%) |
| CM_0–5 | 18.1 | 14.9 ± 1.2 | 12.1 ± 0.4 | 19.4 ± 1.2 | 16.7 ± 0.5 | 16.8 ± 1.9 | 17.7 ± 1.0 | 22.3 ± 0.9 | 22.3 | 17.1 (7%) |
| CM_5–10 | 15.7 | 12.3 ± 1.1 | 14.3 ± 1.3 | 20.9 ± 0.9 | 16.2 ± 0.2 | 15.4 ± 1.8 | 12.4 ± 0.7 | 19.4 ± 1.0 | 19.4 | 15.8 (7%) |
| CM_10–20 | 27.2 | 16.6 ± 0.7 | 25.4 ± 1.2 | 31.4 ± 1.2 | 25.2 ± 1.4 | 27.6 ± 3.1 | 18.3 ± 1.3 | 33.6 ± 2.2 | 33.6 | 25.4 (10%) |
| CM_20–40 | 29.6 | 20.0 ± 1.4 | 35.7 ± 3.8 | 38.9 ± 1.6 | 28.0 ± 3.3 | 30.7 ± 1.8 | 23.6 ± 1.3 | 36.4 ± 1.2 | 36.4 | 30.5 (13%) |
| CM40 | 90.6 | 63.8 ± 2.2 a | 87.5 ± 4.2 c | 110.6 ± 2.5 d | 86.1 ± 3.6 b,c | 90.5 ± 4.4 c | 72.0 ± 2.2 a,b | 111.7 ± 2.8 d | 111.7 | 88.9 (37%) |
| ΣC | 151.5 | 104.4 ± 2.4 a | 167.4 ± 6.7 a | 262.0 ± 8.0 b,c | 246.0 ± 7.1 b | 274.1 ± 9.2 b,c | 292.7 ± 6.0 c,d | 333.4 ± 7.0 e | 189.8 | 240.0 (100%) |
| C Fluxes | Stand Age (Years) | Average | ||||||
|---|---|---|---|---|---|---|---|---|
| 5 | 13 | 38 | 53 | 68 | 108 | 138 | ||
| NPPAGW | 0.12 ± 0.02 a | 1.96 ± 0.25 b | 3.94 ± 0.34 c | 3.90 ± 0.56c | 3.58 ± 0.29 c | 2.56 ± 0.30 b,c | 2.55 ± 0.16 b,c | 2.66 ± 0.51 |
| NPPL | 0.16 ± 0.10 a | 1.47 ± 0.13 b | 1.68 ± 0.09 b | 1.94 ± 0.20 b | 2.11 ± 0.14 b | 2.08 ± 0.10 b | 1.80 ± 0.25 b | 1.61 ± 0.26 |
| NPPFT | 0 | 0 | 0.16 ± 0.09 a | 1.03 ± 0.24 a,b | 0.29 ± 0.11 a | 0.54 ± 0.18 a | 1.70 ± 0.43 b | 0.53 ± 0.24 |
| NPPCR | 0.10 ± 0.01 | 1.21 ± 0.12 | 1.23 ± 0.12 | 0.99 ± 0.14 | 0.82 ± 0.07 | 0.51 ± 0.06 | 0.52 ± 0.04 | 0.77 ± 0.16 |
| NPPFR | 3.02 ± 0.23 a | 2.97 ± 0.15 a | 1.13 ± 0.16 c | 1.85 ± 0.26 b,c | 1.63 ± 0.16 bc | 2.29 ± 0.14 a,b | 1.39 ± 0.11 c | 2.04 ± 0.28 |
| NPP | 3.40 ± 0.23 a | 7.61 ± 0.32 b | 8.14 ± 0.40 b | 9.71 ± 0.68 b | 8.43 ± 0.36 b | 7.98 ± 0.38 b | 7.96 ± 0.47 b | 7.60 ± 0.75 |
| SR | −9.37 | −8.32 | −9.49 | −8.18 | n.a.(−8.00) # | −7.52 | −7.19 | −8.35 ± 0.38 |
| SRHCR | −4.14 ± 0.23 a | −4.19 ± 0.64 a | −2.08 ± 0.18 b | −1.55 ± 0.20 b,c | −0.68 ± 0.14 c | −0.98 ± 0.11 b,c | −1.85 ± 0.20 b,c | −2.21 ± 0.54 |
| SRHSOM | −2.69 ± 0.11 a,b | −2.12 ± 0.09 a | -3.81 ± 0.15 d | -3.41 ± 0.14 c,d | -3.76 ± 0.15 c,d | -3.36 ± 0.14 c,d | -2.74 ± 0.11 a,b | -3.13 ± 0.24 |
| RDW | −0.21 | −0.12 ± 0.03 a | −1.04 ± 0.15 d | −0.45 ± 0.08 a,b,c | −0.68 ± 0.16 c,d | −0.28 ± 0.05 a,b,c | −0.58 ± 0.11 b,c | −0.48 ± 0.12 |
| RH | −7.04 ± 0.25 a | −6.43 ± 0.65 a,b | −6.93 ± 0.28 a | −5.41 ± 0.26 b | −5.12 ± 0.26 b | −4.62 ± 0.18 b,c | −5.17 ± 0.25 b | −5.82 ± 0.37 |
| NEP | −3.64 ± 0.34 a | 1.18 ± 0.72 b | 1.21 ± 0.49 b | 4.30 ± 0.73 c | 3.31 ± 0.44 b,c | 3.36 ± 0.42 b,c | 2.79 ± 0.53 b,c | 1.79 ± 1.0 |
| Parameter | Value | SE | t-Value | p-Value | CI Lower (95%) | CI Upper (95%) |
|---|---|---|---|---|---|---|
| K0 | 2.1535 | 0.5246 | 4.10 | <0.001 | 1.0730 | 3.2340 |
| k1 | 0.4601 | 0.0870 | 5.29 | <0.001 | 0.2809 | 0.6393 |
| k2 | −0.0074 | 0.0018 | −4.12 | <0.001 | −0.0111 | −0.0037 |
| Parameter | Value | SE | t-Value | p-Value | CI Lower (95%) | CI Upper (95%) |
|---|---|---|---|---|---|---|
| a | 0.6555 | 0.2200 | 2.98 | 0.041 | 0.0447 | 1.2662 |
| b | −8.2702 | 0.8248 | −10.03 | 0.001 | −10.5603 | −5.9802 |
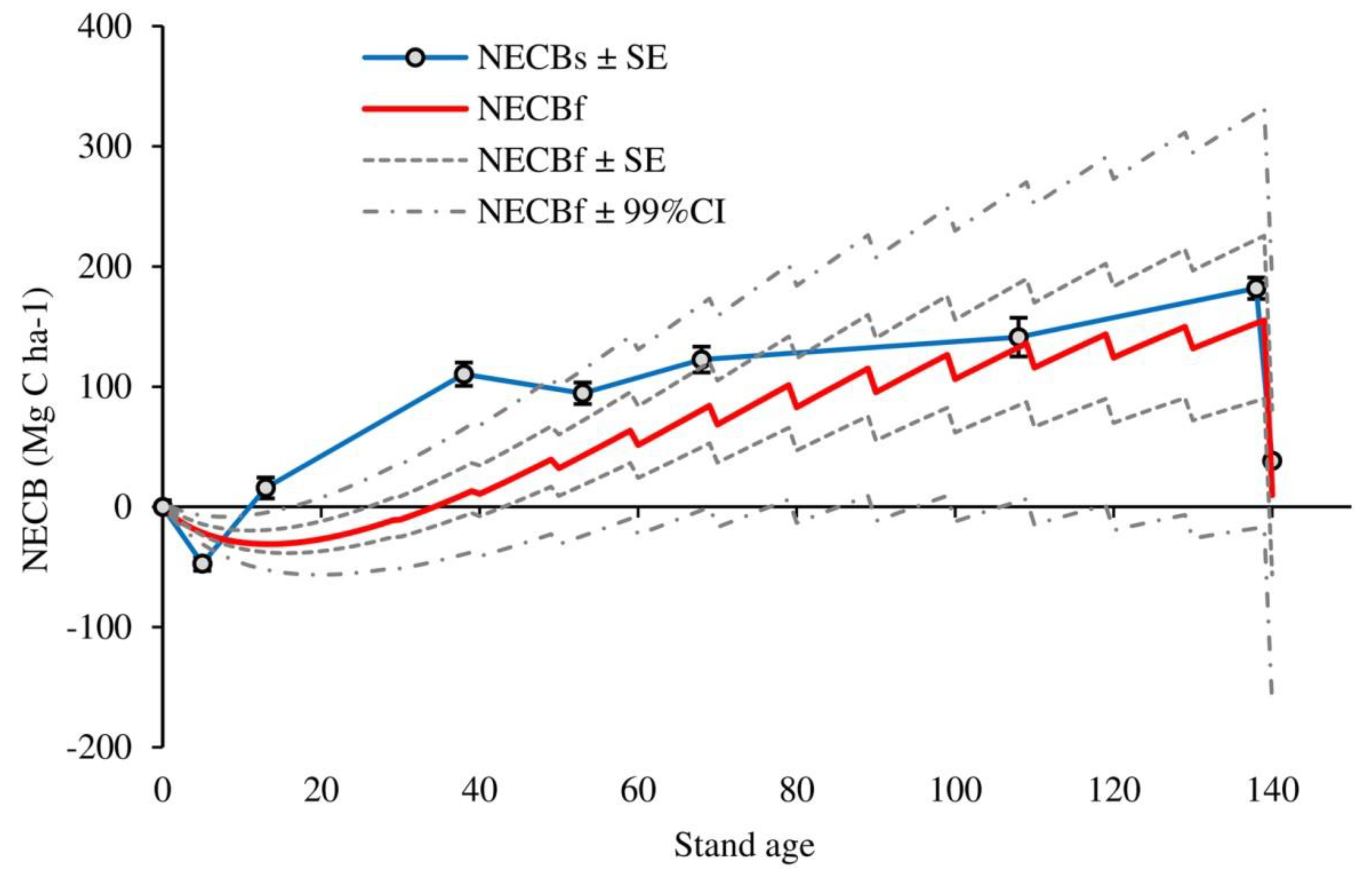
| Stand Age | ΣC (Mg C ha−1) | NECBs (Mg C ha−1) | Cum. Harvest C Loss (Mg C ha−1) | Cum. NEP (Mg C ha−1) | NECBf (Mg C ha−1) |
|---|---|---|---|---|---|
| 0 | 151.5 ± 5.5 | 0 | 0.0 | 0.0 | |
| 5 | 104.4 ± 2.4 | −47.1 ± 6.0 | 0 | −21.4 | −21.4 |
| 13 | 167.4 ± 6.7 | 15.8 ± 8.7 | 0 | −31.0 | −31.0 |
| 38 | 262.0 ± 8.0 | 110.4 ± 9.7 | 1.55 | 11.8 | 10.3 |
| 53 | 246.0 ± 7.1 | 94.5 ± 9.0 | 17.36 | 59.8 | 42.4 |
| 68 | 274.1 ± 9.2 | 122.6 ± 10.7 | 32.86 | 113.3 | 80.4 |
| 108 | 292.7 ± 6.0 | 141.2 ± 8.2 | 120.9 | 253.5 | 132.6 |
| 138 | 333.4 ± 7.0 | 181.9 ± 8.9 | 187.24 | 340.0 | 152.7 |
| 140 | 189.8 ± 6.9 | 38.3 ± 8.9 | 335.18 | 345.0 | 9.8 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ostrogović Sever, M.Z.; Alberti, G.; Delle Vedove, G.; Marjanović, H. Temporal Evolution of Carbon Stocks, Fluxes and Carbon Balance in Pedunculate Oak Chronosequence under Close-To-Nature Forest Management. Forests 2019, 10, 814. https://doi.org/10.3390/f10090814
Ostrogović Sever MZ, Alberti G, Delle Vedove G, Marjanović H. Temporal Evolution of Carbon Stocks, Fluxes and Carbon Balance in Pedunculate Oak Chronosequence under Close-To-Nature Forest Management. Forests. 2019; 10(9):814. https://doi.org/10.3390/f10090814
Chicago/Turabian StyleOstrogović Sever, Maša Zorana, Giorgio Alberti, Gemini Delle Vedove, and Hrvoje Marjanović. 2019. "Temporal Evolution of Carbon Stocks, Fluxes and Carbon Balance in Pedunculate Oak Chronosequence under Close-To-Nature Forest Management" Forests 10, no. 9: 814. https://doi.org/10.3390/f10090814
APA StyleOstrogović Sever, M. Z., Alberti, G., Delle Vedove, G., & Marjanović, H. (2019). Temporal Evolution of Carbon Stocks, Fluxes and Carbon Balance in Pedunculate Oak Chronosequence under Close-To-Nature Forest Management. Forests, 10(9), 814. https://doi.org/10.3390/f10090814






