Catering Information Needs from Global to Local Scales—Potential and Challenges with National Forest Inventories
Abstract
1. Introduction
2. Potential and Challenges within NFIs
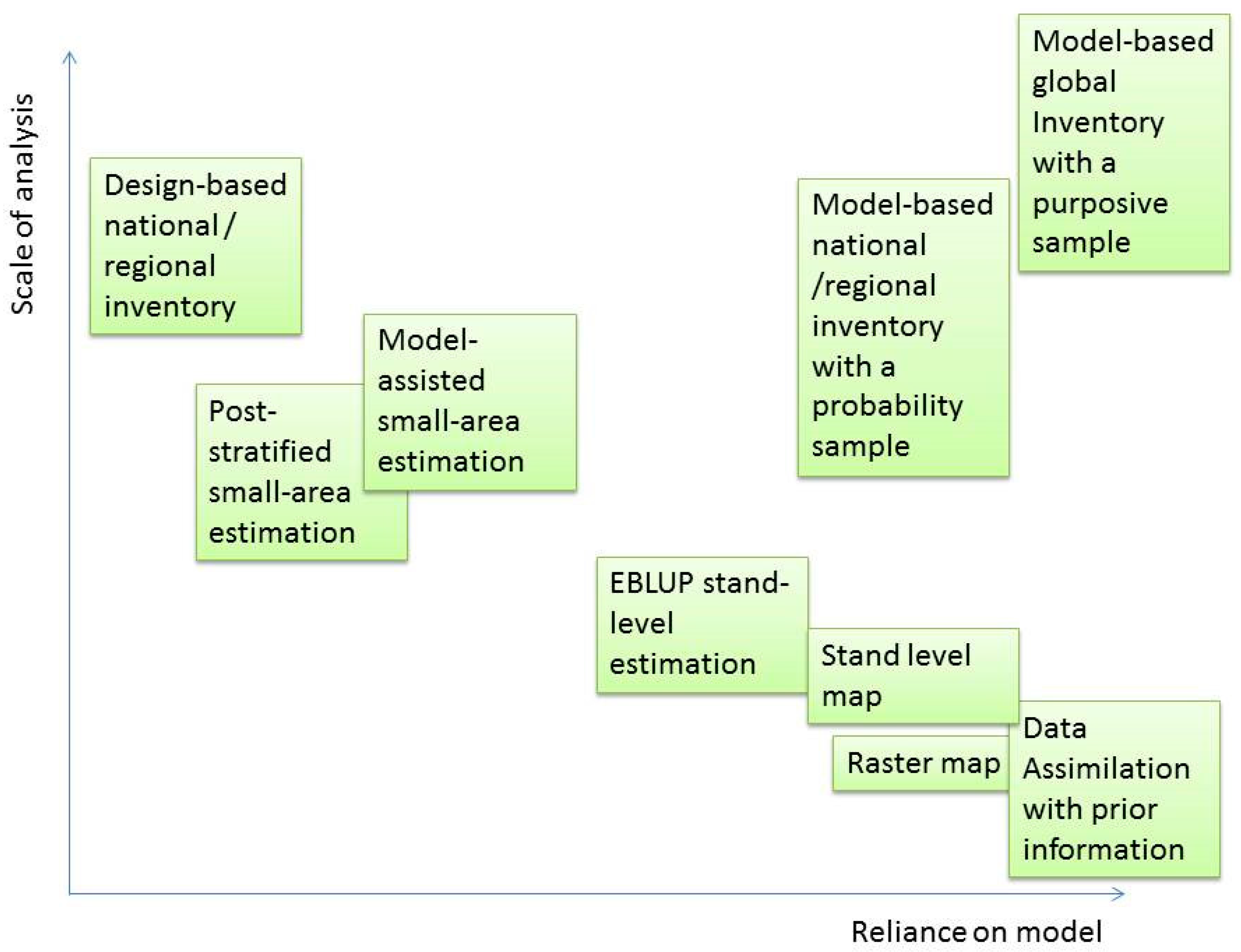
2.1. Dependence between Scale and Inference
2.2. Measurement and Model Errors
2.3. Change Detection
3. Harmonization between NFIs
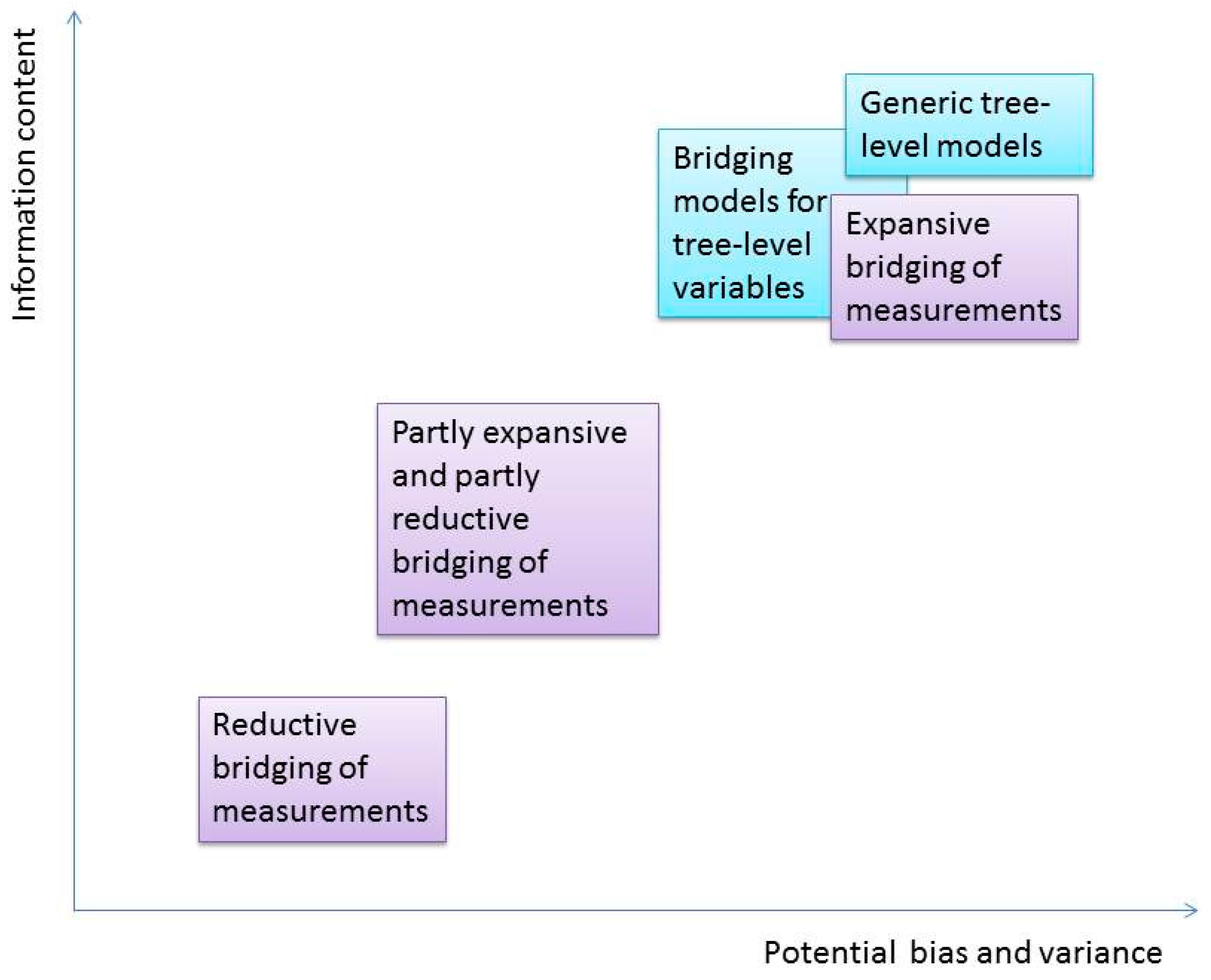
3.1. Implications on Measurements
3.2. Implications on Information Contents
3.3. Implications on Modelling
3.4. Implications on Mapping
3.5. Implications on Change Estimation
3.6. Implications on Future Projections
4. Discussion
4.1. Maintaining the Time Series of NFIs in Changing Demands
4.2. Models as a Part of Forest Inventory
4.3. Maintaining the Coherence of Results in Multiple Scales and Methodologies
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ni, X.; Zhou, Y.; Cao, C.; Wang, X.; Shi, Y.; Park, T.; Choi, S.; Myneni, R.B. Mapping forest canopy height over continental China using multi-source remote sensing data. Remote Sens. 2015, 7, 8436–8452. [Google Scholar] [CrossRef]
- Ståhl, G.; Saarela, S.; Schnell, S.; Holm, S.; Breidenbach, J.; Healey, S.P.; Patterson, P.L.; Magnussen, S.; Næsset, E.; McRoberts, R.E.; et al. Use of models in large-area forest surveys: Comparing model-assisted, model-based and hybrid estimation. For. Ecosyst. 2016, 3, 5. [Google Scholar] [CrossRef]
- Nedyalkova, D.; Tillé, Y. Bias-robustness and efficiency of model-based inference in survey sampling. Stat. Sin. 2012, 22, 777–794. [Google Scholar] [CrossRef]
- Magnussen, S. Arguments for a model-dependent inference? Forestry 2015, 88, 317–325. [Google Scholar] [CrossRef]
- National Forest Inventories—Pathways for Common Reporting; Tomppo, E., Gschwantner, T.H., Lawrence, M., McRoberts, R.E., Eds.; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- National Forest Inventories—Assessment of Wood Availability and Use; Vidal, C., Alberdi, I., Hernandez, L., Redmond, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; p. 845. [Google Scholar]
- Barreiro, S.; Schelhaas, M.-J.; Kändler, G.; Anton-Fernandez, C.; Colin, A.; Bontemps, J.-D.; Alberdi, I.; Condes, S.; Dumitru, M.; Ferezliev, A.; et al. Overview of methods and tools for evaluating future woody biomass availability in European countries. Ann. For. Sci. 2016, 73, 823–837. [Google Scholar] [CrossRef]
- Marchi, M.; Ducci, F. Some refinements on species distribution models using tree-level National Forest Inventories for supporting forest management and marginal forest population detection. iForest 2018, 11, 291–299. [Google Scholar] [CrossRef]
- Chirici, G.; McRoberts, R.E.; Winter, S.; Bertini, R.; Braendli, U.-B.; Asensio, I.A.; Bastrup-Birk, A.; Rondeux, J.; Barsoum, N.; Marchetti, M. National forest inventory contributions to forest biodiversity monitoring. For. Sci. 2012, 58, 257–268. [Google Scholar] [CrossRef]
- Fridman, J.; Holm, S.; Nilsson, M.; Nilsson, P.; Ringvall, A.H.; Ståhl, G. Adapting national forest inventories to changing requirements—The case of the Swedish National Forest Inventory at the turn of the 20th century. Silva Fennica 2016, 48, 1095. [Google Scholar] [CrossRef]
- Corona, P. Consolidating new paradigms in large-scale monitoring and assessment of forest ecosystems. Environ. Res. 2016, 144, 8–14. [Google Scholar] [CrossRef]
- Breidenbach, J.; Astrup, R. Small area estimation of forest attributes in the Norwegian National Forest Inventory. Eur. J. For. Res. 2012, 131, 1255–1267. [Google Scholar]
- Massey, A.; Mandallaz, D. Design-based regression estimation of net change for forest inventories. Can. J. Res. 2015, 45, 1775–1784. [Google Scholar] [CrossRef]
- Gregoire, T.G.; Ståhl, G.; Næsset, E.; Gobakken, T.; Nelson, R.; Holm, S. Model-assisted estimation of biomass in a LiDAR sample survey in Hedmark County, Norway. Can. J. Res. 2011, 41, 83–95. [Google Scholar] [CrossRef]
- Ståhl, G.; Holm, S.; Gregoire, T.G.; Gobakken, T.; Næsset, E.; Nelson, R. Model-based inference for biomass estimation in a LiDAR sample survey in Hedmark County, Norway. Can. J. Res. 2011, 41, 96–107. [Google Scholar] [CrossRef]
- Nord-Larsen, T.; Schumacher, J. Estimation of forest resources from a country wide laser scanning survey and national forest inventory data. Remote Sens. Environ. 2012, 119, 148–157. [Google Scholar] [CrossRef]
- Nilsson, M.; Nordkvist, K.; Jonzén, J.; Lindgren, N.; Axensten, P.; Wallerman, J.; Egberth, M.; Larsson, S.; Nilsson, L.; Eriksson, J.; et al. A nationwide forest attribute map of Sweden predicted using airborne laser scanning data and field data from the national forest inventory. Remote Sens. Environ. 2017, 194, 447–454. [Google Scholar] [CrossRef]
- Rahlf, J.; Breidenbach, J.; Solberg, S.; Næsset, E.; Astrup, R. Comparison of four types of 3D data for timber volume estimation. Remote Sens. Environ. 2014, 155, 325–333. [Google Scholar]
- Saarela, S.; Grafström, A.; Ståhl, G.; Kangas, A.; Holopainen, M.; Tuominen, S.; Nordkvist, K.; Hyyppä, J. Model-assisted estimation of forest resources using different combinations of LiDAR and Landsat data as auxiliary information. Remote Sens. Environ. 2015, 158, 431–440. [Google Scholar] [CrossRef]
- Kangas, A.; Myllymäki, M.; Gobakken, T.; Næsset, E. Model-assisted forest inventory with parametric, semi-parametric and non-parametric models. Can. J. Res. 2016, 46, 855–868. [Google Scholar] [CrossRef]
- Myllymäki, M.; Gobakken, T.; Næsset, E.; Kangas, A. The efficiency of post-stratification compared to model-assisted estimation. Can. J. Res. 2017, 47, 515–526. [Google Scholar] [CrossRef]
- Grafström, A.; Saarela, S.; Ene, L. Efficient sampling strategies for forest inventories by spreading the sample in auxiliary space. Can. J. Res. 2014, 44, 1156–1164. [Google Scholar] [CrossRef]
- Grafström, A.; Zhao, X.; Nylander, M.; Petersson, H. A new sampling strategy for forest inventories applied to the temporary clusters of the Swedish national forest inventory. Can. J. Res. 2017, 47, 1161–1167. [Google Scholar] [CrossRef]
- Räty, M.; Heikkinen, J.; Kangas, A. Assessment of sampling strategies utilizing auxiliary information in large-scale forest inventory. Can. J. Res. 2018, 48, 749–757. [Google Scholar] [CrossRef]
- Haakana, H.; Heikkinen, J.; Kangas, A. Efficiency of post-stratification for a large-scale forest inventory—Case Finnish NFI. Ann. For. Sci. 2019, 76, 9. [Google Scholar] [CrossRef]
- Corona, P. Integration of forest mapping and inventory to support forest management. Iforest Biogeosci. For. 2010, 3, 59–64. [Google Scholar] [CrossRef]
- Kangas, A.; Astrup, R.; Breidenbach, J.; Fridman, J.; Gobakken, T.; Korhonen, K.T.; Maltamo, M.; Nilsson, M.; Nord-Larsen, T.; Næsset, E.; et al. Remote sensing and forest inventories in Nordic countries—Roadmap for the future. Scand. J. For. Res. 2018, 33, 397–412. [Google Scholar] [CrossRef]
- Särndal, C.E.; Swensson, B.; Wretman, J. Model Assisted Survey Sampling; Springer: Berlin/Heidelberg, Germany, 1992; p. 694. [Google Scholar]
- Magnussen, S.; Mandallaz, D.; Breidenbach, J.; Lanz, A.; Ginzler, C. National forest inventories in the service of small area estimation of stem volume. Can. J. Res. 2014, 44, 1079–1090. [Google Scholar] [CrossRef]
- Pulkkinen, M.; Ginzler, C.; Traub, B.; Lanz, A. Stereo-imagery-based post-stratification by regression-tree modelling in Swiss National Forest Inventory. Remote Sens. Environ. 2018, 213, 182–194. [Google Scholar] [CrossRef]
- Lappi, J. Forest inventory of small areas combining the calibration estimator and a spatial model. Can. J. Res. 2001, 31, 1551–1560. [Google Scholar] [CrossRef]
- Goerndt, M.E.; Monleon, V.J.; Temesgen, H. Small-area estimation of county-level forest attributes using ground data and remote sensed auxiliary information. For. Sci. 2013, 59, 536–548. [Google Scholar] [CrossRef]
- Ehlers, S.; Grafström, A.; Nyström, K.; Olsson, H.; Ståhl, G. Data assimilation in stand-level forest inventories. Can. J. Res. 2013, 43, 1104–1113. [Google Scholar] [CrossRef]
- Nyström, M.; Lindgren, N.; Wallerman, J.; Grafström, A.; Muszta, A.; Nyström, K.; Bohlin, J.; Willén, E.; Fransson, J.E.S.; Ehlers, S.; et al. Data assimilation in forest inventory: First empirical results. Forests 2013, 6, 4540–4557. [Google Scholar] [CrossRef]
- Haakana, H.; Katila, M.; Heikkinen, J.; Kangas, A. Post-Stratification Based on Satellite Imagery for Downscaling Information on Forest Resources from the Finnish National Forest Inventory. Canadian J. For. Res. submitted for publication.
- Breidenbach, J.; McRoberts, R.E.; Astrup, R. Empirical coverage of model-based variance estimators for remote sensing assisted estimation of stand-level timber volume. Remote Sens. Environ. 2015, 173, 274–281. [Google Scholar] [CrossRef] [PubMed]
- Magnussen, S.; Frazer, G.; Penner, M. Alternative mean-squared error estimators for synthetic estimators of domain means. J. Appl. Stat. 2016, 1, 24. [Google Scholar] [CrossRef]
- Breidenbach, J.; Magnussen, S.; Rahlf, J.; Astrup, R. Unit-level and area-level small area estimation under heteroscedasticity using digital areal photogrammetry data. Remote Sens. Environ. 2018, 212, 199–211. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Næsset, E.; Gobakken, T.; Chirici, G.; Condés, S.; Hou, Z.; Saarela, S.; Chen, Q.; Ståhl, G.; Walters, B.F. Assessing components of model-based mean square error estimator for remote sensing assisted forest applications. Can. J. Res. 2018, 48, 642–649. [Google Scholar] [CrossRef]
- Chirici, G.; Mura, M.; McInerney, D.; Py, N.; Tomppo, E.O.; Waser, L.T.; Travaglini, D.; McRoberts, R.E. A meta-analysis and review of the literature on the k-Nearest Neighbors technique for forestry applications that use remotely sensed data. Remote Sens. Environ. 2016, 176, 282–294. [Google Scholar] [CrossRef]
- McInerney, D.; Barrett, F.; McRoberts, R.E.; Tomppo, E. Enhancing the Irish NFI using k-nearest neighbors and a genetic algorithm. Can. J. Res. 2018, 48, 1482–1494. [Google Scholar] [CrossRef]
- Opsomer, J.D.; Claeskens, G.; Ranalli, M.G.; Kauermann, G.; Breidt, F.J. Non-parametric small area estimation using penalized spline regression. J. R. Stat. Soc. 2008, 70, 265–286. [Google Scholar] [CrossRef]
- Salvati, N.; Tzavidis, N.; Pratesi, M.; Chambers, R. Small area estimation via M-quantile geographically weighted regression. Test 2012, 21, 1–28. [Google Scholar] [CrossRef]
- Chen, Q.; McRoberts, R.E.; Wang, C.; Radtke, P.J. Forest aboveground biomass mapping and estimation across multiple spatial scales using model-based inference. Remote Sens. Environ. 2016, 184, 350–360. [Google Scholar] [CrossRef]
- Ståhl, G.; Heikkinen, J.; Petersson, H.; Repola, J.; Holm, S. Sample-based estimation of greenhouse gas emissions from forests—A new approach to account for both sampling and model errors. Forest Sci. 2014, 60, 3–13. [Google Scholar] [CrossRef]
- Corona, P.; Fattorini, L.; Franceschi, S.; Scrinzi, G.; Torresan, C. Estimation of standing wood volume in forest compartments by exploiting airborne laser scanning information: Model-based, design-based, and hybrid perspectives. Can. J. For. Res. 2014, 44, 1303–1311. [Google Scholar] [CrossRef]
- Fortin, M.; Manso, R.; Schneider, R. Parametric bootstrap estimators for hybrid inference in forest inventories. Forestry 2018, 91, 354–365. [Google Scholar] [CrossRef]
- Melo, L.; Schneider, R.; Fortin, M. Estimating model-and sampling-related uncertainty in large-area growth predictions. Ecol. Model. 2018, 390, 62–69. [Google Scholar] [CrossRef]
- Shettles, M.; Temesgen, H.; Gray, A.N.; Hilker, T. Comparison of uncertainty per unit area estimates of aboveground biomass for two selected model sets. For. Ecol. Manag. 2015, 354, 18–25. [Google Scholar] [CrossRef]
- Päivinen, R.; Nousiainen, M.; Korhonen, K.T. Puutunnusten mittaamisen luotettavuus summary: Accuracy of certain tree measurements. Folia For. 1992, 787, 18, (In Finnish with English summary). [Google Scholar]
- Liang, X.; Hyyppä, J.; Kaartinen, H.; Lehtomäki, M.; Pyörälä, J.; Pfeifer, N.; Holopainen, M.; Brolly, G.; Francesco, P.; Hackenberg, J.; et al. International benchmarking of terrestrial laser scanning approaches for forest inventories. ISPRS J. Photogramm. Remote Sens. 2018, 144, 137–179. [Google Scholar] [CrossRef]
- Pitkänen, T.P.; Raumonen, P.; Kangas, A. Measuring TLS-based stem diameters in boreal forests by cylinder-based complementary fitting procedure. ISPRS J. Photogramm. Remote Sens. 2019, 147, 294–306. [Google Scholar] [CrossRef]
- Kuronen, M.; Henttonen, H.M.; Myllymäki, M. Correcting for nondetection in estimating forest characteristics from single-scan terrestrial laser measurements. Can. J. For. Res. 2019, 49, 96–103. [Google Scholar] [CrossRef]
- Chen, Q.; Laurin, G.V.; Valentini, R. Uncertainty of remotely sensed aboveground biomass over an Afrian tropical forest: Propagating errors from trees to plots to pixels. Remote Sens. Environ. 2015, 160, 134–143. [Google Scholar] [CrossRef]
- Kangas, A. On the bias and variance of tree volume predictions due to model and measurement errors. Scand. J. For. Res. 1996, 11, 281–290. [Google Scholar] [CrossRef]
- Päivinen, R. Metsän Inventoinnin Suunnittelumalli. Summary: A Planning Model for Forest Inventory. Joensuun Yliopiston Luonnontieteellisiä Julkaisuja; Joensuun Yliopisto: Joensuu, Finland, 1987; pp. 11–179. [Google Scholar]
- Räty, M.; Heikkinen, J.; Kangas, A. Kriging with External Drift in Model Localization. Math. Comput. For. Nat. Resour. Sci. 2011, 3, 1–14. [Google Scholar]
- Breidenbach, J.; Antón-Fernández, C.; Petersson, H.; McRoberts, R.E.; Astrup, R. Quantifying the model-related variability of biomass stock and change estimates in the Norwegian national forest inventory. For. Sci. 2014, 60, 25–33. [Google Scholar] [CrossRef]
- Saarela, S.; Schnell, S.; Tuominen, S.; Balazs, A.; Hyyppä, J.; Grafström, A.; Ståhl, G. Effects of positional errors in model-assisted and model-based estimation of growing stock volume. Remote Sens. Environ. 2016, 172, 101–108. [Google Scholar] [CrossRef]
- Holm, S.; Nelson, R.; Ståhl, G. Hybrid three-phased estimators for large-area forest inventory using ground plots, airborne lidar and space lidar. Remote Sens. Environ. 2017, 197, 85–97. [Google Scholar] [CrossRef]
- Saarela, S.; Holm, S.; Grafström, A.; Schnell, S.; Næsset, E.; Gregoire, T.G.; Nelson, R.F.; Ståhl, G. Hierarchical model-based inference for forest inventory utilizing three sources of information. Ann. For. Sci. 2016, 73, 895–910. [Google Scholar] [CrossRef]
- Ene, L.; Gobakken, T.; Andersen, H.-E.; Næsset, E.; Cook, B.D.; Morton, D.C.; Babcock, C.; Nelson, R. Large-area hybrid estimation of aboveground biomass in interior Alaska using airborne laser scanning data. Remote Sens. Environ. 2018, 204, 741–755. [Google Scholar] [CrossRef]
- Fortin, M.; Manso, R.; Calama, R. Hybrid estimation based on mixed-effects models in forest inventories. Can. J. For. Res. 2016, 46, 1310–1319. [Google Scholar] [CrossRef]
- Holopainen, M.; Vastaranta, M.; Hyyppä, J. Outlook for the next generation’s precision forestry in Finland. Forests 2014, 5, 1682–1694. [Google Scholar] [CrossRef]
- Gschwantner, T.; Lanz, A.; Vidal, C.; Bosela, M.; Di Cosmo, L.; Fridman, J.; Gasparini, P.; Kuliešis, A.; Tomter, S.; Schadauer, K. Comparison of methods used in European National Forest Inventories for the estimation of volume increment: Towards harmonization. Ann. For. Sci. 2016, 73, 807–821. [Google Scholar] [CrossRef]
- Vidal, C.; Alberdi, I.; Redmond, J.; Vestman, M.; Lanz, A.; Schadauer, K. The role of European National Forest Inventories for international forestry reporting. Ann. For. 2016, 73, 793–806. [Google Scholar]
- Gschwantner, T.; Schadauer, K.; Vidal, C.; Lanz, A.; Tomppo, E.; di Cosmo, L.; Robert, N.; Englert Duursma, D.; Lawrence, M. Common tree definitions for national forest inventories in Europe. Silva. Fenn. 2009, 43, 303–321. [Google Scholar] [CrossRef]
- Ståhl, G.; Cienciala, E.; Chirici, G.; Lanz, A.; Vidal, C.; Winter, S.; McRoberts, R.; Rondeusx, J.; Schadauer, K.; Tomppo, E. Bridging national and reference definitions for harmonizing forest statistics. For. Sci. 2012, 58, 214–223. [Google Scholar] [CrossRef]
- Köhl, M.; Traub, B.; Päivinen, R. Harmonisation and standardisation in multi-national environmental statistics—Mission impossible? Environ. Monit. Assess. 2000, 63, 361–380. [Google Scholar] [CrossRef]
- Vidal, C.; Lanz, A.; Tomppo, E.; Schadauer, K.; Gschwantner, T.; Di Cosmo, L.; Robert, N. Establishing forest inventory reference definitions for forest and growing stock: A study towards common reporting. Silva Fennica 2008, 42, 247–266. [Google Scholar] [CrossRef]
- Alberdi, I.; Condés, S.; McRoberts, R.; Winter, S. Mean species cover: A harmonized indicator of schrub cover for forest inventories. Eur. J. For. Res. 2018, 137, 265–278. [Google Scholar] [CrossRef]
- Gschwantner, T.; Alberdi, I.; Balázs, A.; Bauwens, S.; Bender, S.; Borota, D.; Bosela, M.; Bouriaud, O.; Cañellas, I.; Donis, J.; et al. Harmonisation of stem volume estimates in European National Forest Inventories. Ann. For. Sci. 2019, 76, 24. [Google Scholar] [CrossRef]
- Neumann, M.; Moreno, A.; Mues, V.; Härkönen, S.; Mura, M.; Bouriaud, O.; Lang, M.; Wouter, M.J.A.; Thivolle-Cazat, A.; Bronisz, K.; et al. Comparison of carbon estimation methods for European forests. For. Ecol. Manag. 2016, 361, 397–420. [Google Scholar] [CrossRef]
- Bouriaud, O.; Saint-André, L.; Santenoise, P.; Longuetaud, F.; Hervé, J.C.; Casella, E.; Freudenschuss, A.; Gschwantner, T.; Kändler, G.; Klatt, S.; et al. Deliverable 2.2 of the European Union’s Horizon 2020 Research and Innovation Programme Project DIABOLO—Distributed, Integrated and Harmonised Forest Information for Bioeconomy Outlooks; Technical Report No. 633464; European Commission: Brussels, Belgium, 2017. [Google Scholar]
- Genet, A.; Wernsdorfer, H.; Jonard, M.; Pretzsch, H.; Rauch, M.; Ponette, Q.; Nys, C.; Legout, A.; Ranger, J.; Vallet, P.; et al. Ontogeny partly explains the apparent heterogeneity of published biomass equations for Fagus sylvatica in central Europe. For. Ecol. Manag. 2011, 261, 1188–1202. [Google Scholar] [CrossRef]
- Bouriaud, O.; Saint-André, L.; Santenoise, P.; Longuetaud, F.; Hervé, J.C.; Bauwens, S.; Casella, E.; Freudenschuss, A.; Gschwantner, T.; Kändler, G.; et al. Deliverable 2.9 of the European Union’s Horizon 2020 Research and Innovation Programme Project DIABOLO—Distributed, Integrated and Harmonised Forest Information for Bioeconomy Outlooks; Technical Report No. 633464; European Commission: Brussels, Belgium, 2018. [Google Scholar]
- Kangas, A.; Korhonen, K.T.; Packalen, T.; Vauhkonen, J. Assessing the sources and types of uncertainties in the information on forest-related ecosystem services. For. Ecol. Manag. 2018, 427, 7–16. [Google Scholar] [CrossRef]
- Kosztra, B.; Büttner, G.; Hazeu, G.; Arnold, S. Updated CLC Illustrated Nomenclature Guidelines. European Environment Agency: Copenhagen, Denmark, 2017. [Google Scholar]
- Vizzardi, M.; Chiavetta, U.; Chirici, G.; Garfi, V.; Bastrup-Birk, A.; Marchetti, M. Comparing multisource harmonized forest types mapping: A case study from central Italy. iForest 2015, 8, 59–66. [Google Scholar] [CrossRef]
- Lind, T.; Trubins, R.; Lier, M.; Packalen, T. Harmonization of Definitions for Sustainable Biomass Supply in Terms of Sustainability Constraints in Relation to Experiences and Guidelines from International Processes and Projects e.g., Forest Europe, UNECE SFM, EU projects BEE and S2BIOM, as Well as Form the European Bioeconomy Observatory (BISO)—Guidelines for Harmonization of Biomass Supply Analyses. Deliverable 5.1 of the European Union’s Horizon 2020 Research and Innovation Programme Project DIABOLO—Distributed, Integrated and Harmonised Forest Information for Bioeconomy Outlooks; Technical Report No. 633464; European Commission: Brussels, Belgium, 2016; p. 31. [Google Scholar]
- Alberdi, I.; Michalak, R.; Fischer, C.; Gasparini, P.; Brändli, U.B.; Tomter, S.M.; Kuliesis, A.; Snorrason, A.; Redmond, J.; Hernández, L.; et al. Towards harmonized assessment of European forest availability for wood supply in Europe. For. Policy Econ. 2016, 70, 20–29. [Google Scholar] [CrossRef]
- Fischer, C.; Gasparini, P.; Nylander, M.; Redmond, J.; Hernandez, L.; Brändli, U.B.; Pastor, A.; Rizzo, M.; Alberdi, I. Joining criteria for harmonizing European Forest available for wood supply estimates. Case studies from National Forest Inventories. Forests 2016, 7, 104. [Google Scholar] [CrossRef]
- Vauhkonen, J.; Packalen, T. A Markov Chain Model for simulating wood supply from any-aged forest management based on national forest inventory (NFI) data. Forests 2017, 8, 307. [Google Scholar] [CrossRef]
- Vauhkonen, J.; Packalen, T. Uncertainties related to climate change and forest management with implications on climate regulation in Finland. Ecosyst. Serv. 2018, 33, 213–224. [Google Scholar] [CrossRef]
- Vauhkonen, J.; Packalen, T. Shifting from even-aged management to less intensive forestry in varying proportions of forest land in Finland: Impacts on carbon storage, harvest removals, and harvesting costs. Eur. J. For. Res. 2019, 138, 219–238. [Google Scholar] [CrossRef]
- UNECE/FAO. The European Forest Sector Outlook Study II 2010–2030. United Nations Economic Commission for Europe/Food and Agriculture Organization of the United Nations. 2011. Available online: https://www.unece.org/efsos2.html (accessed on 14 June 2019).
- Schelhaas, M.J.; Nabuurs, G.J.; Verkerk, P.J.; Hengeveld, G.; Packalen, T.; Sallnäs, O.; Pilli, R.; Grassi, G.; Forsell, N.; Frank, S.; et al. Forest resource projection tools at the European level. In Forest Inventory-Based Projection Systems for Wood and Biomass Availability, Managing Forest Ecosystems 29; Barreiro, S., Schelhaas, M.J., McRoberts, R.E., Kändler, G., Eds.; Springer: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Packalen, T.; Sallnäs, O.; Sirkiä, S.; Korhonen, K.T.; Salminen, O.; Vidal, C.; Robert, N.; Colin, A.; Belouard, T.; Schadauer, K.; et al. The European Forestry Dynamics Model: Concept, Design and Results of First Case Studies. JRC Science and Policy Reports; Technical Report No. EUR 27004; Publications Office of the European Union: Luxembourg, 2014; Volume 93450. [Google Scholar]
- Sallnäs, O.; Berger, A.; Räty, M.; Trubins, R. An area-based matrix model for uneven-aged forests. Forests 2015, 6, 1500–1515. [Google Scholar] [CrossRef]
- Vauhkonen, J.; Berger, A.; Gschwantner, T.; Schadauer, K.; Lejeune, P.; Perin, J.; Pitchugin, M.; Adolt, R.; Zeman, M.; Johannsen, V.K.; et al. Harmonised projections of future forest resources in Europe. Ann. For. Sci. 2019, 76, 79. [Google Scholar] [CrossRef]
- Henttonen, H.M.; Nöjd, P.; Suvanto, S.; Heikkinen, J.; Mäkinen, H. Large trees have increased greatly in Finland during 1921–2013, but recent observations on old trees tell a different story. Ecol. Indic. 2019, 99, 118–129. [Google Scholar] [CrossRef]
- Rocchini, D.; Marcantonio, M.; Da Re, D.; Chirici, G.; Galluzzi, G.; Lenoir, J.; Ricotta, C.; Torresani, M.; Ziv, G. Time-lapsing biodiversity: An open source method for measuring diversity changes by remote sensing. Remote Sens. Environ. 2019, 231, 111192. [Google Scholar] [CrossRef]
- Ayrey, E.; Hayes, D.J. The use of three-dimensional convolutional neural networks to interpret LiDAR for forest inventory. Remote Sens. 2018, 10, 649. [Google Scholar] [CrossRef]
- Massey, A.; Mandallaz, D.; Lanz, A. Integrating remote sensing and past inventory data under the new annual design of the Swiss National Forest Inventory using three-phase design-based regression estimation. Can. J. Res. 2014, 44, 1177–1186. [Google Scholar] [CrossRef]
- Ene, L.T.; Lanz, A.; Adolt, A.; Fejfar, J.; Kohn, I.; Riedel, T.; Morneau, F.; Pesty, B. Report on the Development of Imputations Techniques and Updating Algorithms, Including Concept and Implementation and Demonstration on Case Studies at Various Time Points and Spatial Scales. Deliverable 2.10 of the European Union’s Horizon 2020 Research and Innovation Programme Project DIABOLO—Distributed, Integrated and Harmonised Forest Information for Bioeconomy Outlooks; Technical Report No. 633464; European Commission: Brussels, Belgium, 2018. [Google Scholar]
- Schelhaas, M.J.; Fridman, J.; Hengeveld, G.M.; Henttonen, H.M.; Lehtonen, A.; Kies, U.; Krajnc, N.; Lerink, B.; Dhubháin, A.N.; Polley, H.; et al. Actual European forest management by region, tree species and owner based on 714,000 re-measured trees in national forest inventories. PLoS ONE 2018, 13, e0207151. [Google Scholar] [CrossRef] [PubMed]
- Grassi, G.; Pilli, R.; House, J.; Federici, S.; Kurz, W.A. Science-based approach for credible accounting of mitigation in managed forests. Carbon Balance Manag. 2018, 13, 8. [Google Scholar] [CrossRef] [PubMed]
- Nabuurs, G.J.; Arets, E.J.; Schelhaas, M.J. Understanding the implications of the EU-LULUCF regulation for the wood supply from EU forests to the EU. Carbon Balance Manag. 2018, 13, 18. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kangas, A.; Räty, M.; Korhonen, K.T.; Vauhkonen, J.; Packalen, T. Catering Information Needs from Global to Local Scales—Potential and Challenges with National Forest Inventories. Forests 2019, 10, 800. https://doi.org/10.3390/f10090800
Kangas A, Räty M, Korhonen KT, Vauhkonen J, Packalen T. Catering Information Needs from Global to Local Scales—Potential and Challenges with National Forest Inventories. Forests. 2019; 10(9):800. https://doi.org/10.3390/f10090800
Chicago/Turabian StyleKangas, Annika, Minna Räty, Kari T. Korhonen, Jari Vauhkonen, and Tuula Packalen. 2019. "Catering Information Needs from Global to Local Scales—Potential and Challenges with National Forest Inventories" Forests 10, no. 9: 800. https://doi.org/10.3390/f10090800
APA StyleKangas, A., Räty, M., Korhonen, K. T., Vauhkonen, J., & Packalen, T. (2019). Catering Information Needs from Global to Local Scales—Potential and Challenges with National Forest Inventories. Forests, 10(9), 800. https://doi.org/10.3390/f10090800




