Scaling Up Sap Flow Measurements from the Stem Scale to the Individual Scale for Multibranched Caragana Korshinskii on the Chinese Loess Plateau
Abstract
1. Introduction
2. Materials and Methods
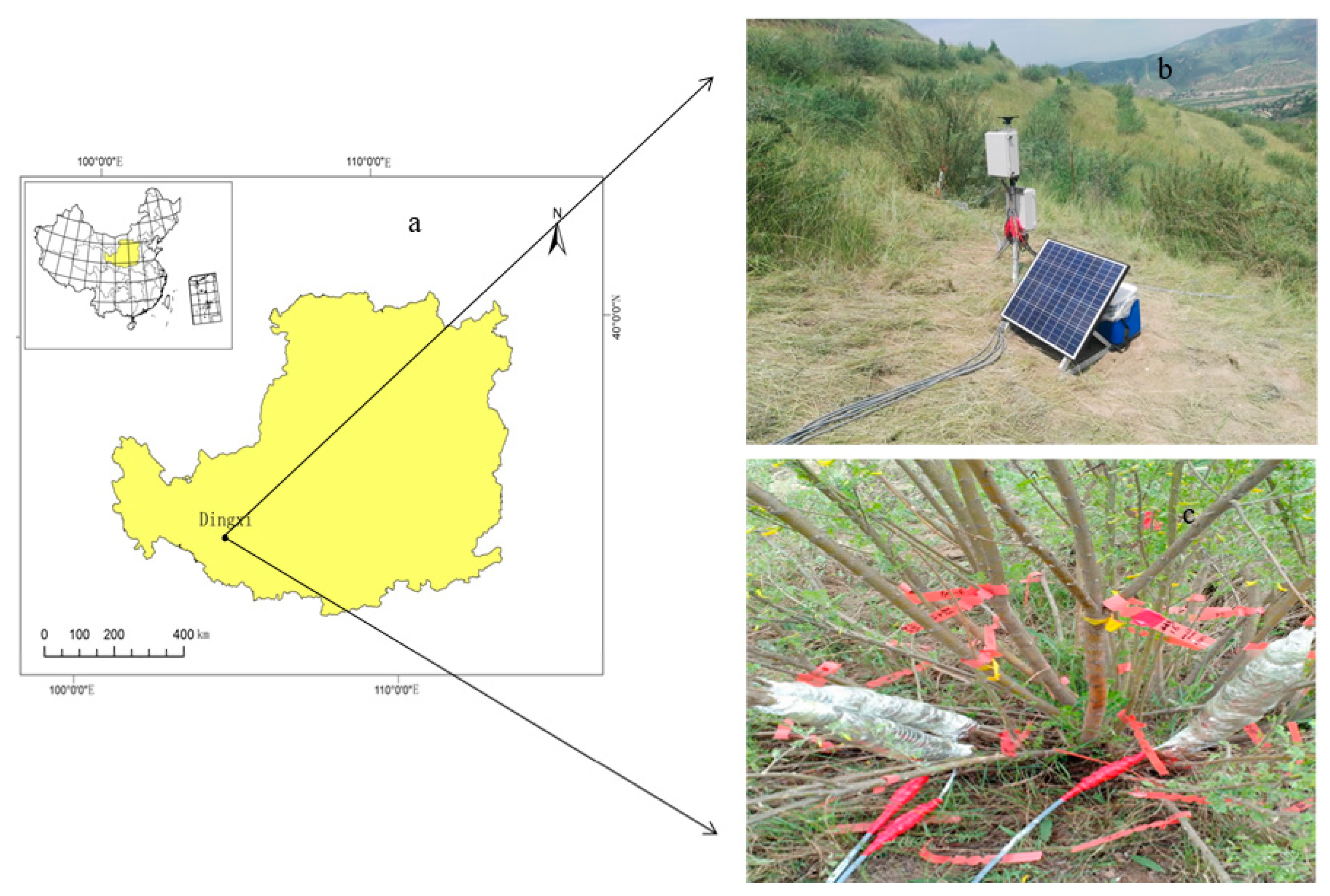
2.1. Study Area
2.2. Measurement of Sap Flow
2.3. Soil Water Content Measurement
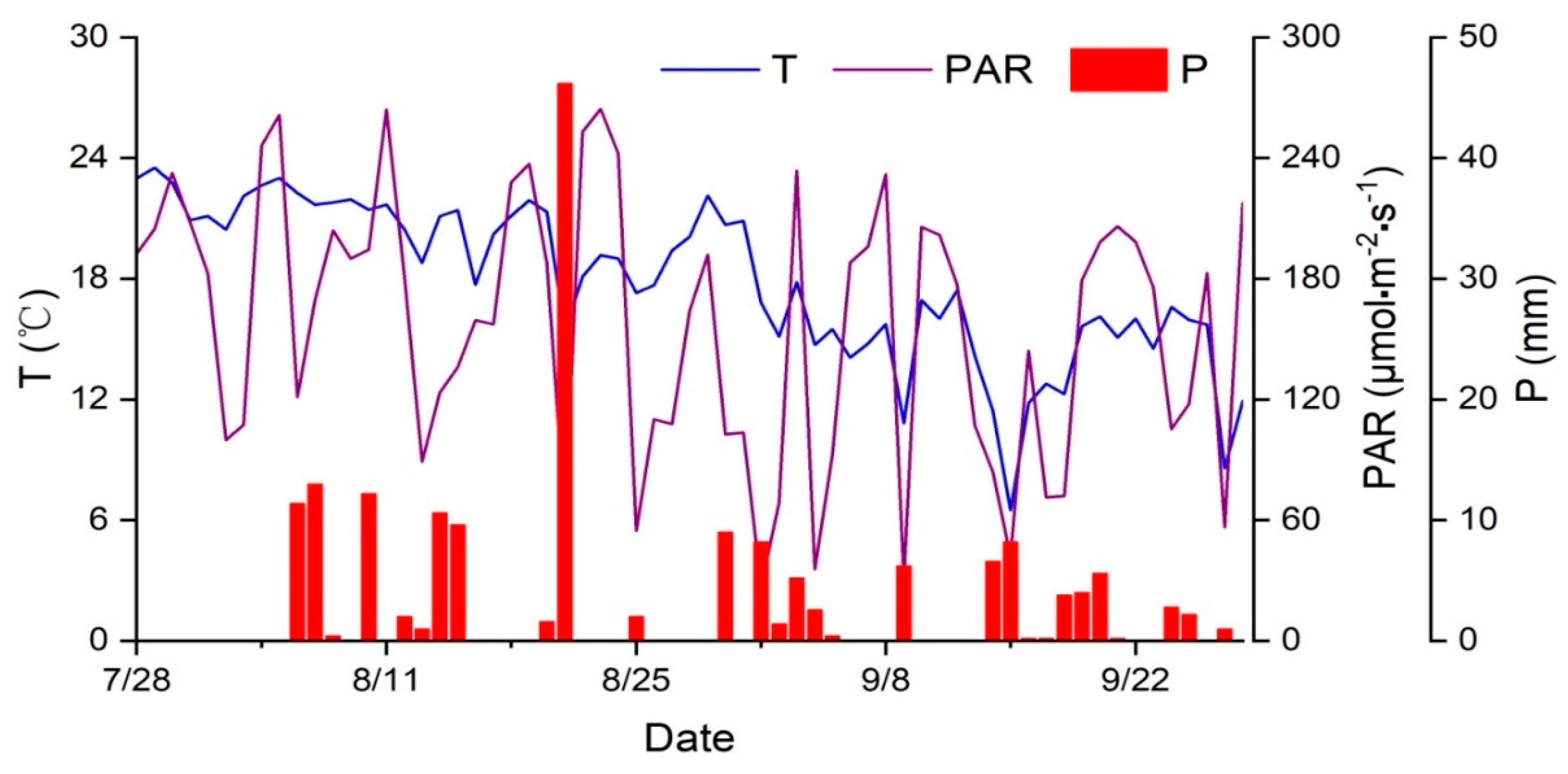
2.4. Measurement of Meteorological Variables
2.5. Model Establishment and Validation
2.6. Data Analysis
3. Results and Discussion
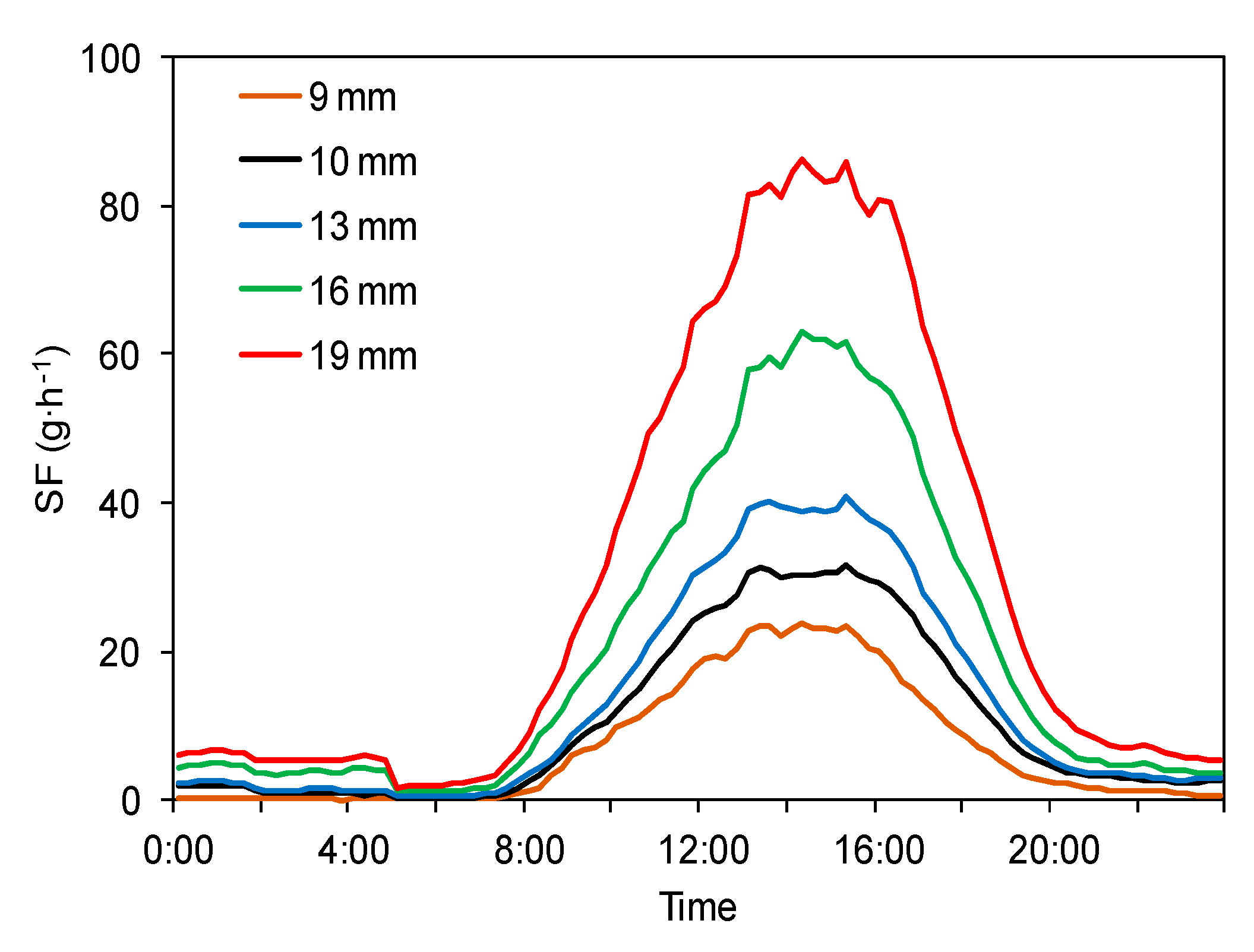
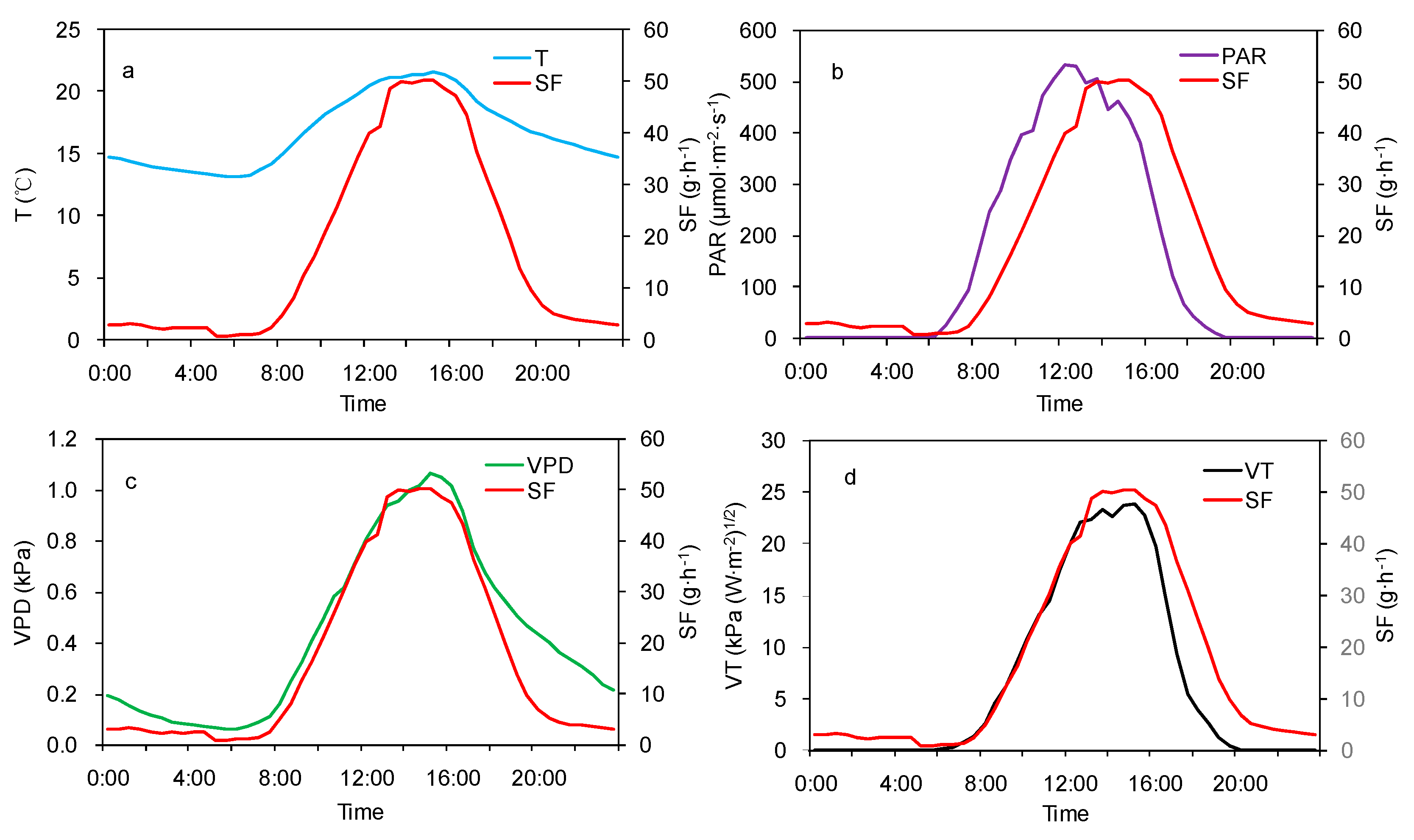
3.1. Diurnal Variations in Sap Flow
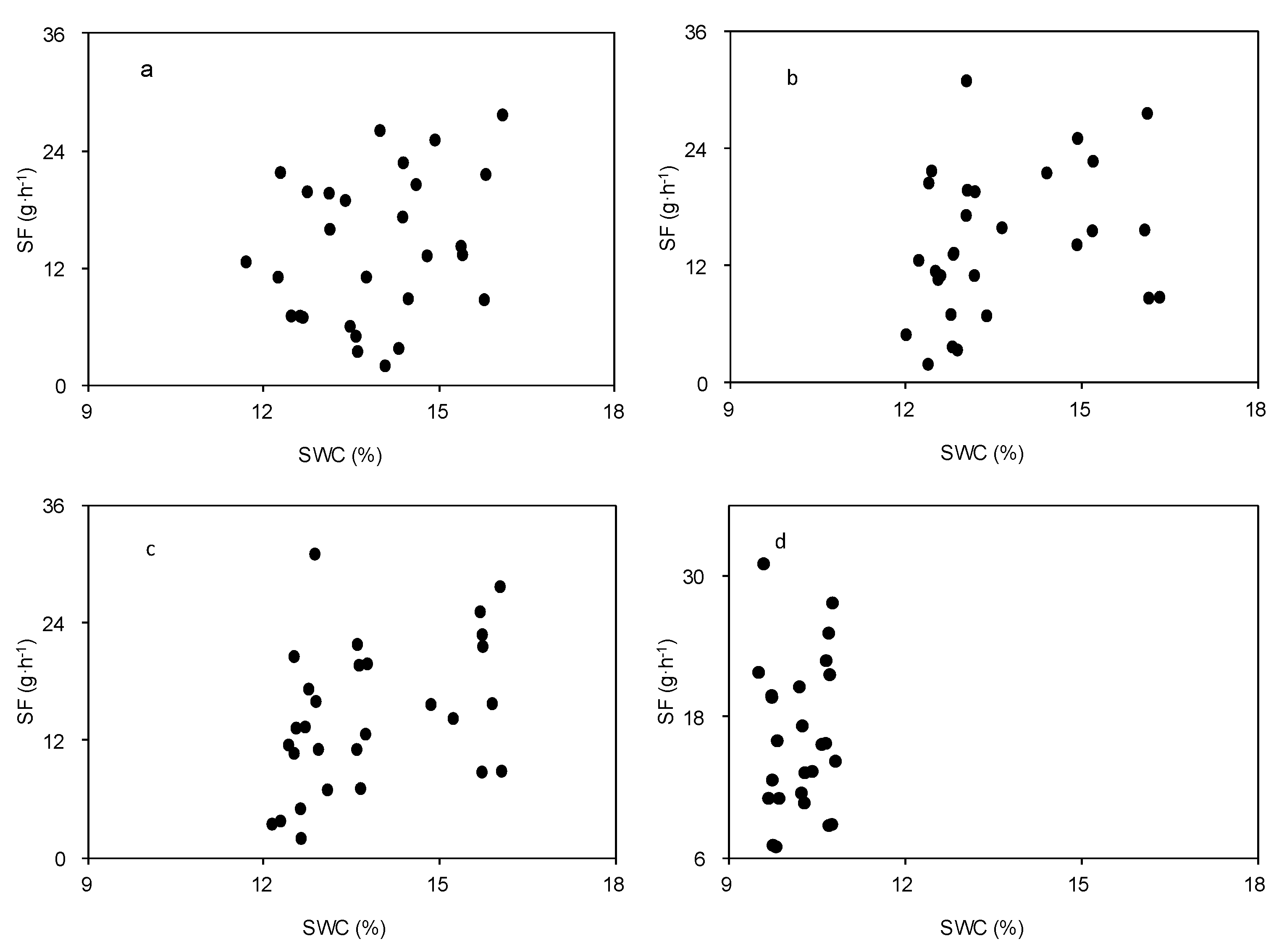
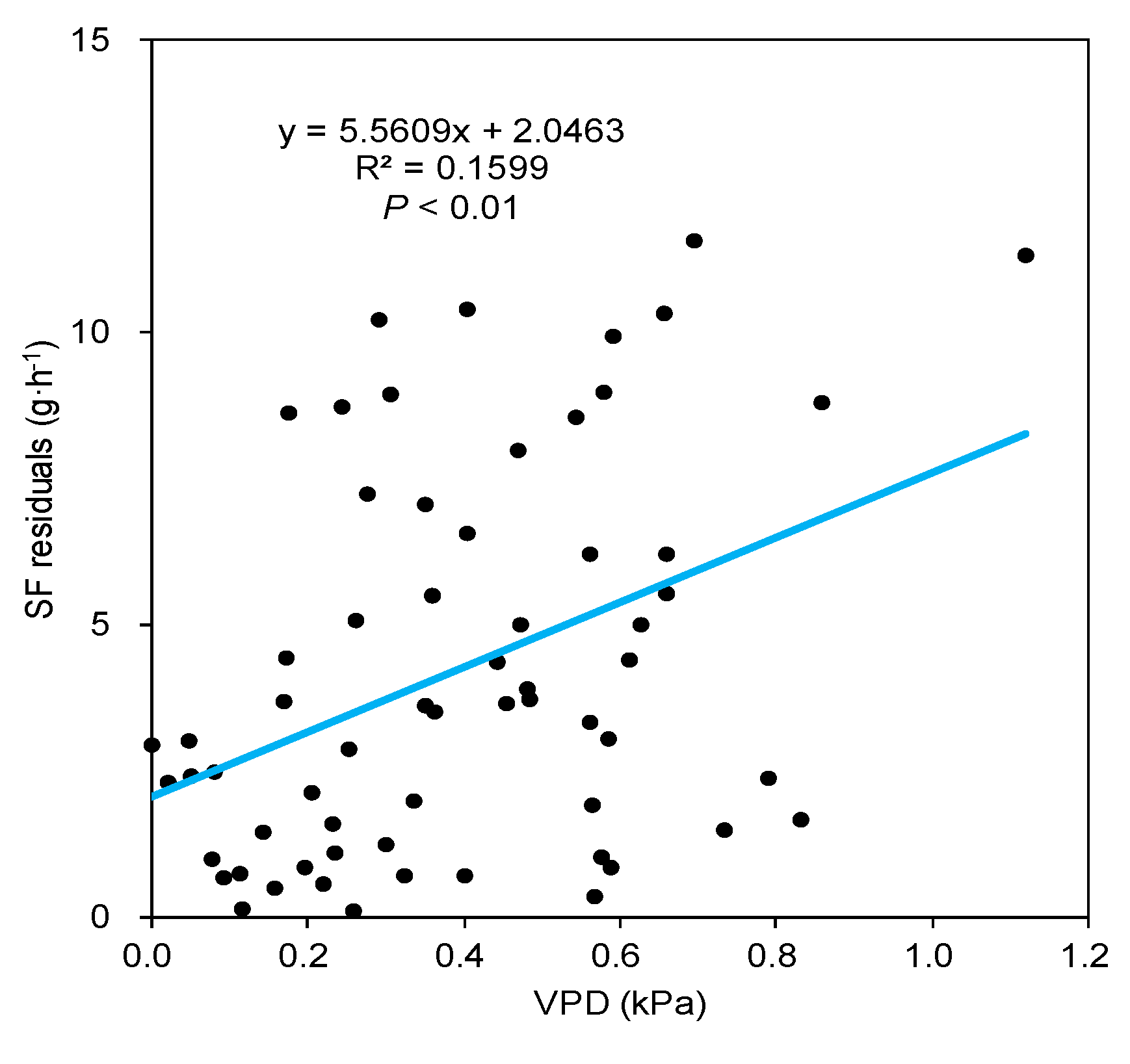
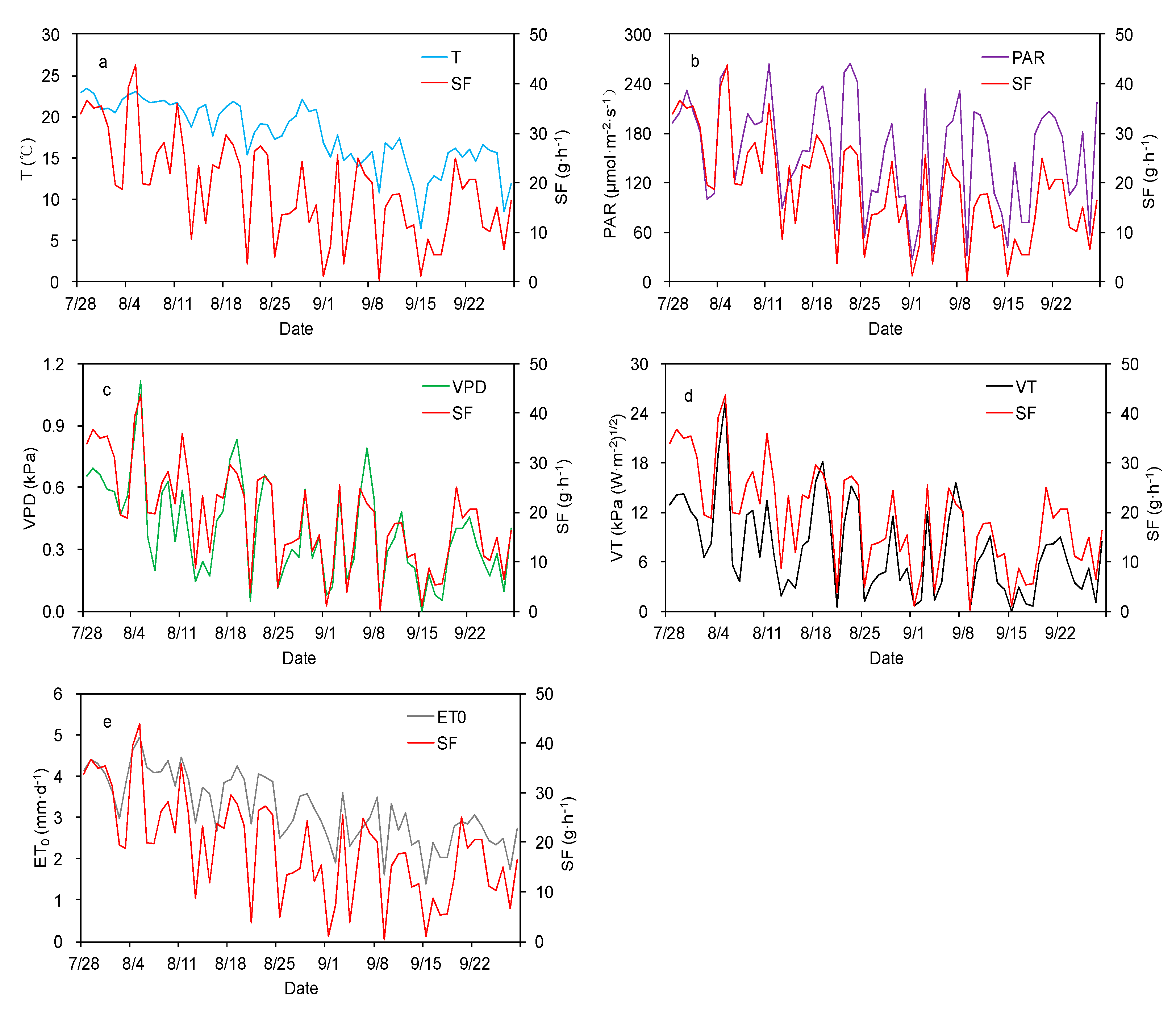
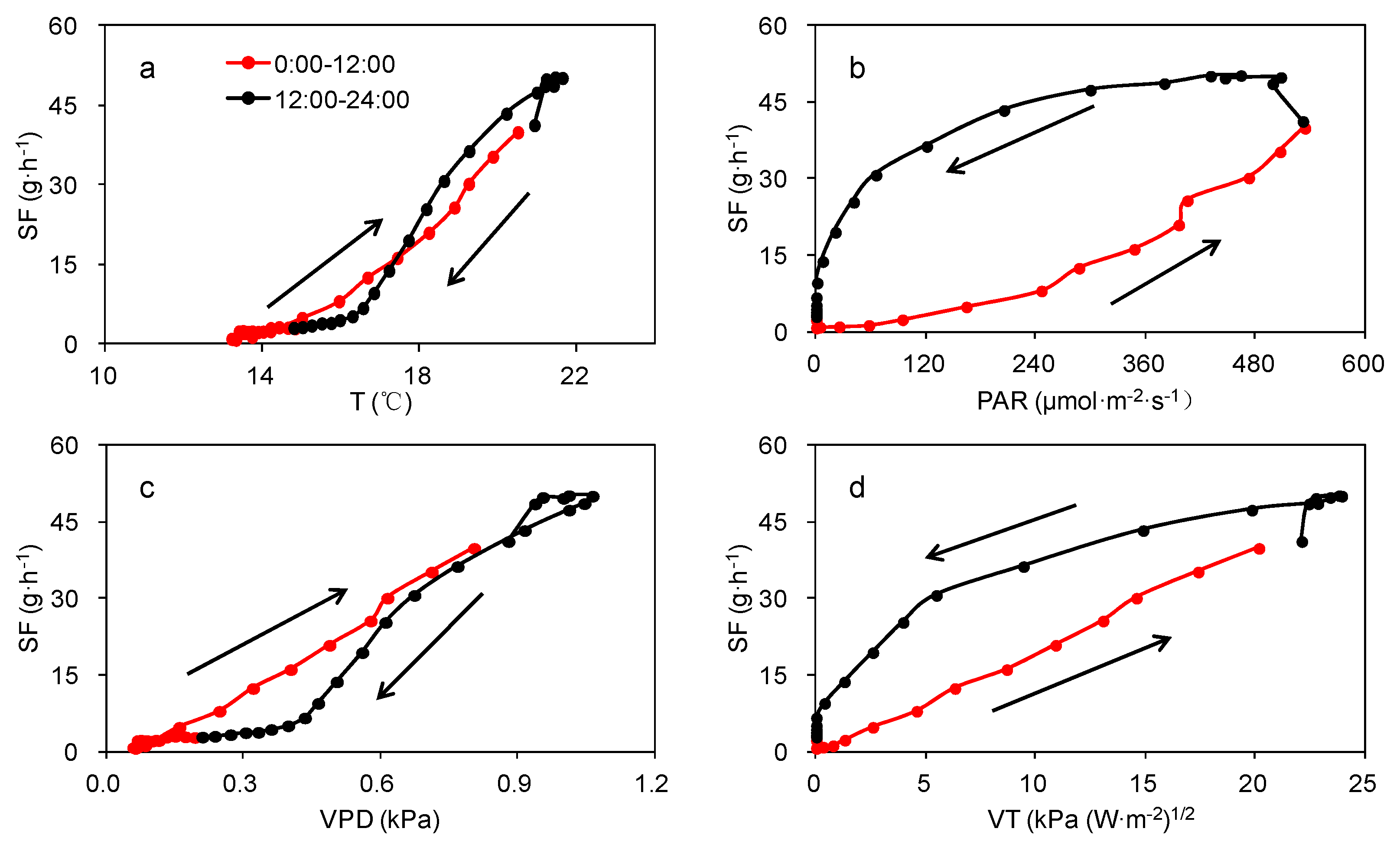
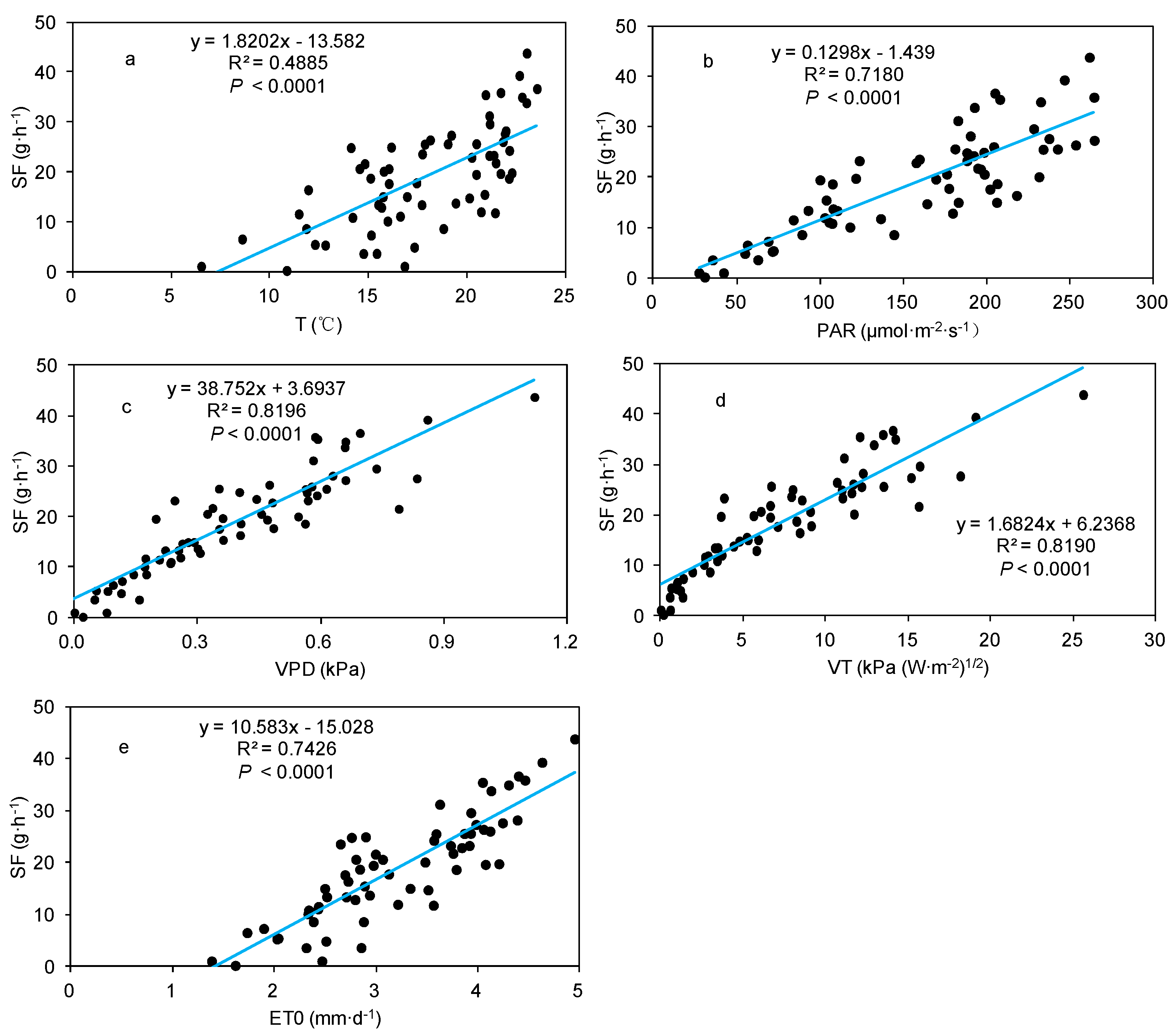
3.2. Effect of Meteorological Factors on SF
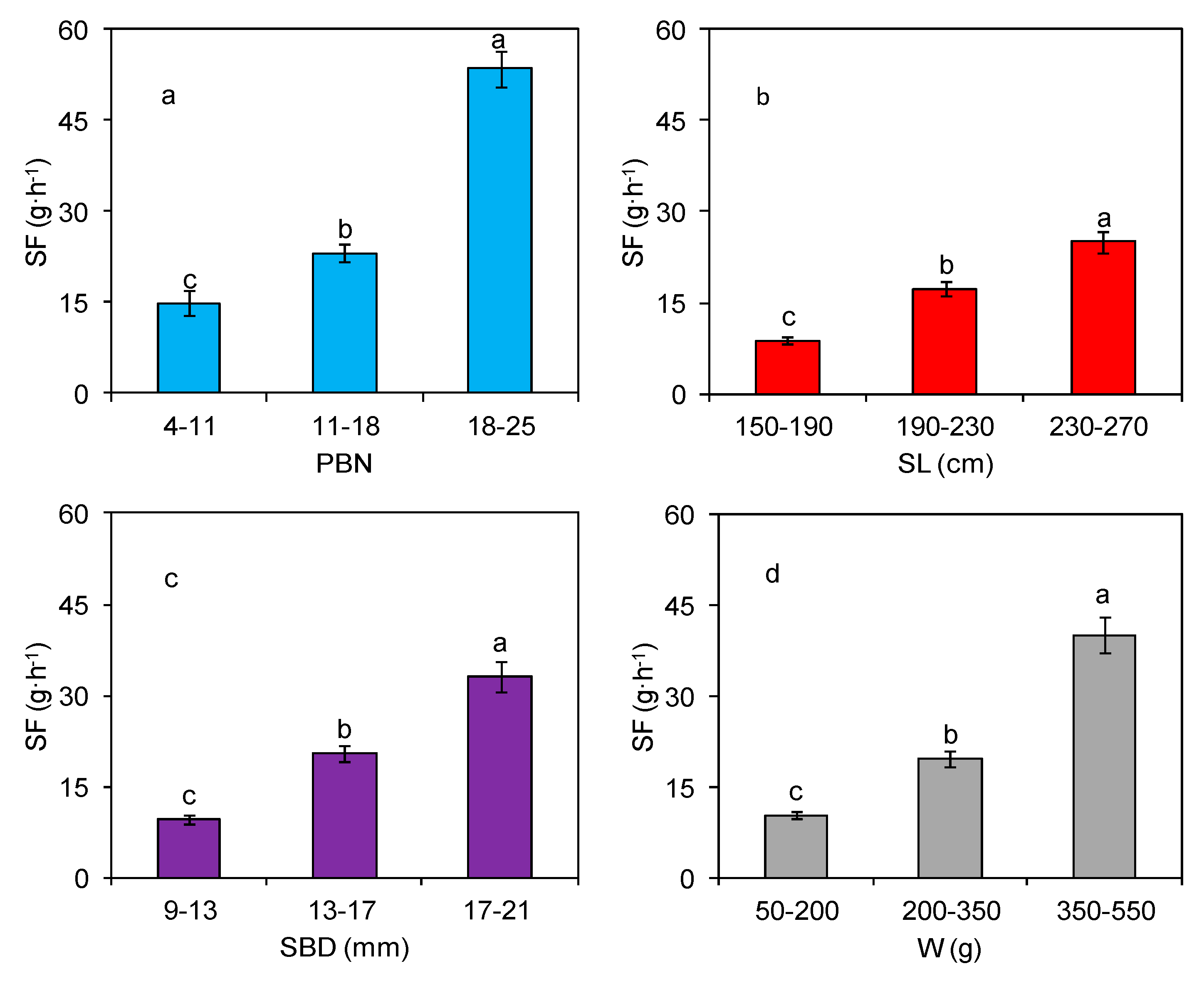
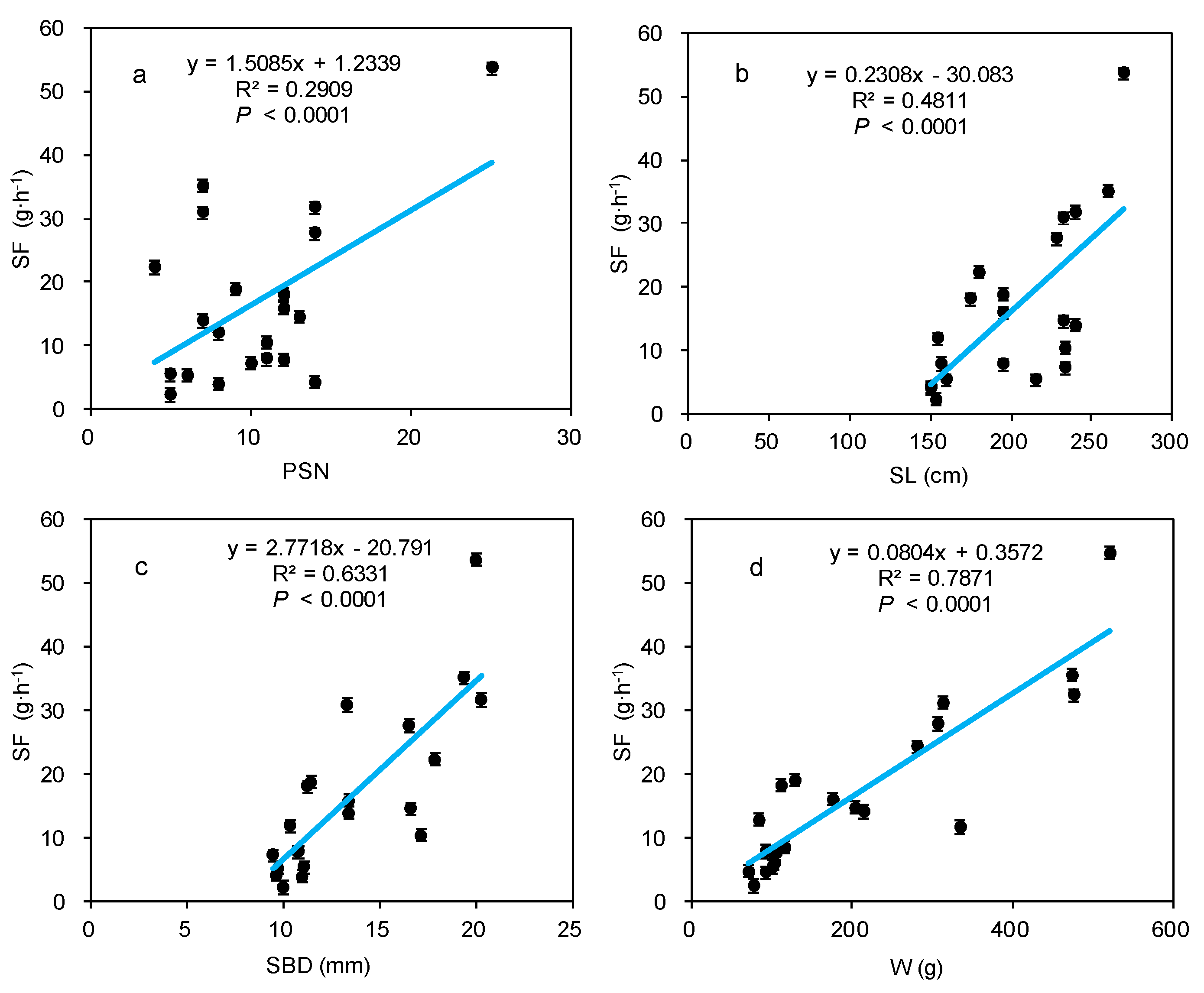
3.3. Effect of Morphological Traits on Stem-Scale SF
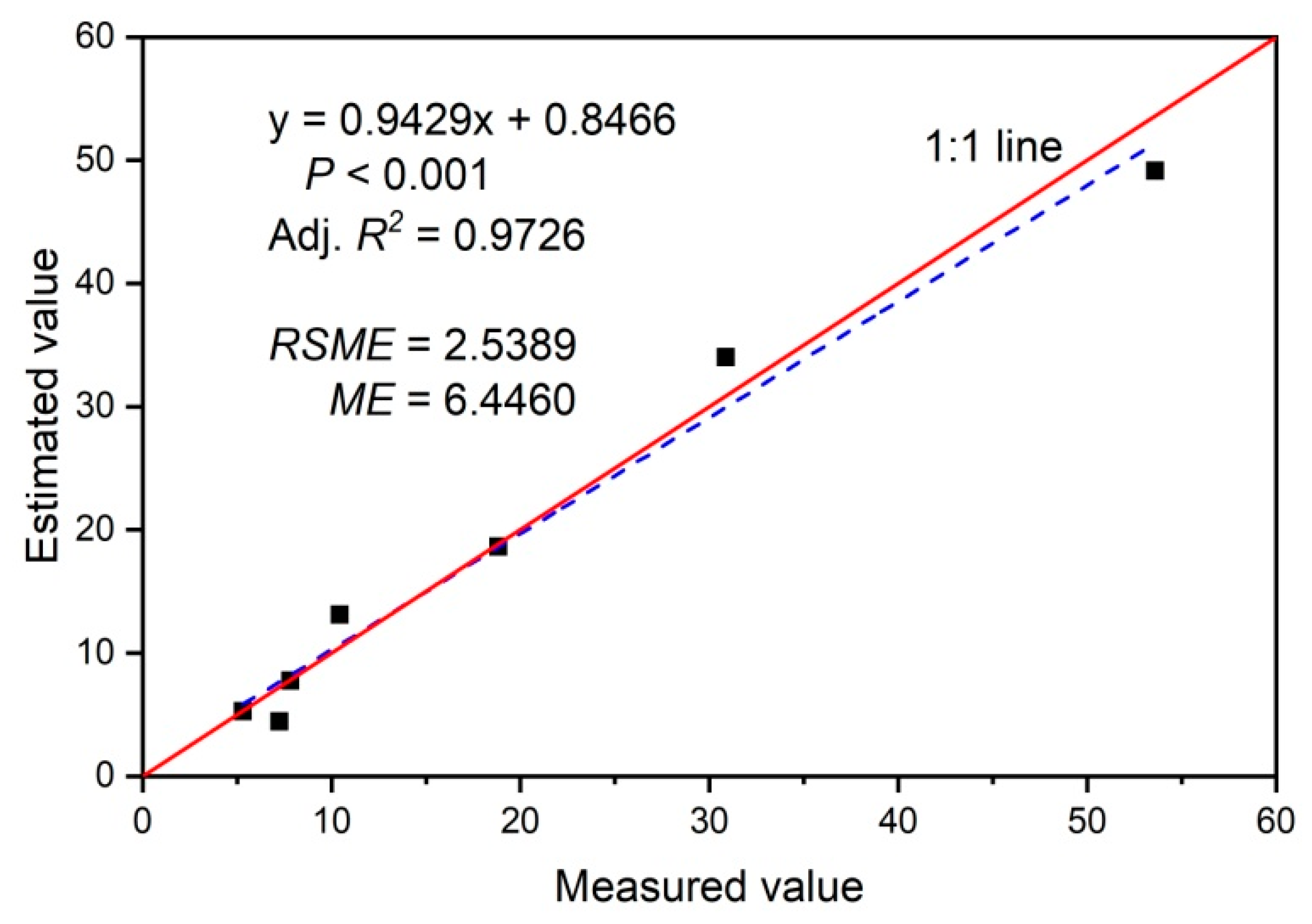
3.4. Established Models for Estimating Stem-Scale SF and Its Validation
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Potts, D.L.; Huxman, T.E.; Cable, J.M.; English, N.B.; Ignace, D.D.; Eilts, J.A.; Mason, M.J.; Weltzin, J.F.; Williams, D.G. Antecedent moisture and seasonal precipitation influence the response of canopy-scale carbon and water exchange to rainfall pulses in a semi-arid grassland. New Phytol. 2010, 170, 849–860. [Google Scholar] [CrossRef] [PubMed]
- Wilson, K.B.; Hanson, P.J.; Mulholland, P.J.; Baldocchi, D.D.; Wullschleger, S.D. A comparison of methods for determining forest evapotranspiration and its components: Sap-flow, soil water budget, eddy covariance and catchment water balance. Agric. For. Meteorol. 2001, 106, 153–168. [Google Scholar]
- Small, E.E.; Mcconnell, J.R. Comparison of soil moisture and meteorological controls on pine and spruce transpiration. Ecohydrology 2010, 1, 205–214. [Google Scholar] [CrossRef]
- Sun, S.J.; Meng, P.; Zhang, J.S.; Wan, X.; Zheng, N.; He, C. Partitioning oak woodland evapotranspiration in the rocky mountainous area of North China was disturbed by foreign vapor, as estimated based on non-steady-state 18 O isotopic composition. Agric. For. Meteorol. 2014, 184, 36–47. [Google Scholar] [CrossRef]
- Kume, T.; Takizawa, H.; Yoshifuji, N.; Tanaka, K.; Tantasirin, C.; Tanaka, N.; Suzuki, M. Impact of soil drought on sap flow and water status of evergreen trees in a tropical monsoon forest in northern Thailand. For. Ecol. Manag. 2007, 238, 220–230. [Google Scholar] [CrossRef]
- Miner, G.L.; Ham, J.M.; Kluitenberg, G.J. A heat-pulse method for measuring sap flow in corn and sunflower using 3D-printed sensor bodies and low-cost electronics. Agric. For. Meteorol. 2017, 246, 86–97. [Google Scholar] [CrossRef]
- Ghimire, C.P.; Lubczynski, M.W.; Bruijnzeel, L.A.; Chavarro-Rincón, D. Transpiration and canopy conductance of two contrasting forest types in the Lesser Himalaya of Central Nepal. Agric. For. Meteorol. 2014, 197, 76–90. [Google Scholar]
- Masmoudi, C.C.; Masmoudi, M.; Abid-Karray, J.E.N.; Mechlia, N.E.T.B. Sap flow measurements in young olive trees (Olea europaea L.) cv. Chetoui under Tunisian conditions. Sci. Hortic-Amst. 2011, 129, 520–527. [Google Scholar] [CrossRef]
- Tie, Q.; Hu, H.C.; Tian, F.Q.; Guan, H.D.; Lin, H. Environmental and physiological controls on sap flow in a subhumid mountainous catchment in North China. Agric. For. Meteorol. 2017, 240, 46–57. [Google Scholar] [CrossRef]
- Zhang, Y.; Kang, S.; Ward, E.J.; Ding, R.; Zhang, X.; Zheng, R. Evapotranspiration components determined by sap flow and microlysimetry techniques of a vineyard in northwest China: Dynamics and influential factors. Agric. Water Manag. 2011, 98, 1207–1214. [Google Scholar] [CrossRef]
- Zang, C.X.; Yang, J.; Yuan, J.; Liu, X. Transpiration characteristics of individual shrubs of Caragana intermedia in mu us sandy land of north-central china. Chin. J. Plant Ecol. 2009, 33, 719–727. (In Chinese) [Google Scholar]
- Huang, L.; Zhang, Z.S.; Li, X.R. Sap flow of Artemisia ordosica and the influence of environmental factors in a revegetated desert area: Tengger Desert, China. Hydrol. Process. 2010, 24, 1249–1253. [Google Scholar]
- Huang, L.; Zhang, Z. Effect of rainfall pulses on plant growth and transpiration of two xerophytic shrubs in a revegetated desert area: Tengger Desert, China. Catena 2016, 137, 269–276. [Google Scholar] [CrossRef]
- Zhao, W.; Liu, B. The response of sap flow in shrubs to rainfall pulses in the desert region of China. Agric. For. Meteorol. 2010, 150, 1297–1306. [Google Scholar] [CrossRef]
- Jian, S.; Wu, Z.; Hu, C.; Zhang, X. Sap flow in response to rainfall pulses for two shrub species in the semiarid Chinese Loess Plateau. J. Hydrol. Hydromech. 2016, 64, 121–132. [Google Scholar] [CrossRef]
- Hoelscher, M.; Kern, M.A.; Wessolek, G.; Nehls, T. A new consistent sap flow baseline-correction approach for the stem heat balance method using nocturnal water vapour pressure deficits and its application in the measurements of urban climbing plant transpiration. Agric. For. Meteorol. 2018, 248, 169–176. [Google Scholar] [CrossRef]
- Chabot, R.; Bouarfa, S.; Zimmer, D.; Chaumont, C.; Moreau, S. Evaluation of the sap flow determined with a heat balance method to measure the transpiration of a sugarcane canopy. Agric. Water Manag. 2005, 75, 10–24. [Google Scholar] [CrossRef]
- Yue, G.; Zhao, H.; Zhang, T.; Zhao, X.; Li, N.; Drake, S. Evaluation of water use of Caragana microphylla with the stem heat-balance method in Horqin Sandy Land, Inner Mongolia, China. Agric. For. Meteorol. 2008, 148, 1668–1678. [Google Scholar] [CrossRef]
- Zha, T.S.; Qian, D.; Jia, X.; Bai, Y.J.; Tian, Y.; Bourque, C.P.A.; Ma, J.Y.; Feng, W.; Wu, B.; Peltola, H. Soil moisture control of sap-flow response to biophysical factors in a desert-shrub species, Artemisia ordosica. Biogeosciences 2017, 14, 4533–4544. [Google Scholar] [CrossRef]
- Fu, W.; Huang, M.; Gallichand, J.; Shao, M. Optimization of plant coverage in relation to water balance in the Loess Plateau of China. Geoderma 2012, 173, 134–144. [Google Scholar] [CrossRef]
- Wei, X.; Huang, M.; Shao, M.; Li, L.; Zhang, X.; Horton, R. Shrubs increase soil resources heterogeneity along semiarid grass slopes in the Loess Plateau. J. Arid Environ. 2013, 88, 175–183. [Google Scholar] [CrossRef]
- Xu, M.; Zhang, J.; Liu, G.B.; Norikazu, Y. Soil properties in natural grassland, Caragana korshinskii planted shrubland, and Robinia pseudoacacia planted forest in gullies on the hilly Loess Plateau, China. Catena 2014, 119, 116–124. [Google Scholar]
- Duan, L.; Huang, M.; Zhang, L. Differences in hydrological responses for different vegetation types on a steep slope on the Loess Plateau, China. J. Hydrol. 2016, 537, 356–366. [Google Scholar] [CrossRef]
- Liu, J.; Li, S.; Ouyang, Z.; Tam, C.; Chen, X. Ecological and socioeconomic effects of China’s policies for ecosystem services. Proc. Natl. Acad. Sci. USA 2008, 105, 9477–9482. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Wei, W.; Chen, L.; Mo, B. Response of deep soil moisture to land use and afforestation in the semi-arid Loess Plateau, China. J. Hydrol. 2012, 475, 111–122. [Google Scholar] [CrossRef]
- Sun, G.; Zhou, G.; Zhang, Z.; Wei, X.; Mcnulty, S.G.; Vose, J.M. Potential water yield reduction due to forestation across China. J. Hydrol. 2006, 328, 548–558. [Google Scholar] [CrossRef]
- Mo, B.R.; Wang, Z.T.; Cai, G.J.; Yang, L.; Dang, H.Z.; Wang, D.F.; Xue, R. Soil water environment in different soil layers and influence factors of mature forest of Caragana korshinskii in semiarid loess area. Arid Land Geogr. 2014, 37, 1207–1215. (In Chinese) [Google Scholar]
- Valancogne, C.; Nasr, Z. A heat balance method for measuring the sap flow in s mall trees. Agronomie 1989, 24, 383–385. [Google Scholar]
- Yang, X.L.; Wei, X.R.; Shao, M.A. Stem biomass estimation models for dominant shrubs on the northern Loess Plateau of China. Chin. J. Appl. Ecol. 2016, 27, 3164–3172. (In Chinese) [Google Scholar]
- Campbell, G.S.; Norman, J.M. Introduction to Environmental Biophysics; Springer: New York, NY, USA, 1998. [Google Scholar]
- Du, S.; Wang, Y.L.; Kume, T.; Zhang, J.G.; Otsuki, K.; Yamanaka, N.; Liu, G.B. Sapflow characteristics and climatic responses in three forest species in the semiarid Loess Plateau region of China. Agric. For. Meteorol. 2011, 151, 1–10. [Google Scholar] [CrossRef]
- Chen, D.; Wang, Y.; Liu, S.; Wei, X.; Wang, X. Response of relative sap flow to meteorological factors under different soil moisture conditions in rainfed jujube (Ziziphus jujuba Mill.) plantations in semiarid Northwest China. Agric. Water Manag. 2014, 136, 23–33. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements-FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998; p. 300. [Google Scholar]
- Cai, G.; Vanderborght, J.; Langensiepen, M.; Schnepf, A.; Hüging, H.; Vereecken, H. Root growth, water uptake, and sap flow of winter wheat in response to different soil water conditions. Hydrol. Earth Syst. Sci. 2018, 22, 2449–2470. [Google Scholar] [CrossRef]
- Kigalu, J.M. Effects of planting density on the productivity and water use of tea (Camellia sinensis L.) clones: I. Measurement of water use in young tea using sap flow meters with a stem heat balance method. Agric. Water Manag. 2007, 90, 224–232. [Google Scholar] [CrossRef]
- Arneth, A.; Kelliher, F.M.; Bauer, G.; Hollinger, D.Y.; Byers, J.N.; Hunt, J.E.; Mcseveny, T.M.; Ziegler, W.; Vygodskaya, N.N.; Milukova, I.; et al. Environmental regulation of xylem sap flow and total conductance of Larix gmelinii trees in eastern Siberia. Tree Physiol. 1996, 16, 247–255. [Google Scholar] [CrossRef] [PubMed]
- Grady, O.A.P.; Worledge, D.; Battaglia, M. Constraints on transpiration of Eucalyptus globulus in southern Tasmania, Australia. Agric. For. Meteorol. 2008, 148, 453–465. [Google Scholar]
- Zeppel, M.; Macinnis-Ng, C.M.O.; Ford, C.R.; Eamus, D. The response of sap flow to pulses of rain in a temperate Australian woodland. Plant Soil 2008, 305, 121–130. [Google Scholar] [CrossRef]
- Pataki, D.E.; Oren, R.; Smith, W.K. Sap flux of co-occurring species in a western subalpine forest during seasonal soil drought. Ecology 2000, 81, 2557–2566. [Google Scholar] [CrossRef]
- Oren, R.; Pataki, D.E. Transpiration in response to variation in microclimate and soil moisture in southeastern deciduous forests. Oecologia 2001, 127, 549–559. [Google Scholar] [CrossRef] [PubMed]
- Ma, C.; Luo, Y.; Shao, M.; Li, X.; Sun, L.; Jia, X. Environmental controls on sap flow in black locust forest in Loess Plateau, China. Sci. Rep. 2017, 7, 13160. [Google Scholar] [CrossRef]
- Horna, V.; Schuldt, B.; Brix, S.; Leuschner, C. Environment and tree size controlling stem sap flux in a perhumid tropical forest of Central Sulawesi, Indonesia. Ann. For. Sci. 2011, 68, 1027–1038. [Google Scholar] [CrossRef]
- Ford, C.R.; Goranson, C.E.; Mitchell, R.J.; Will, R.E.; Teskey, R.O. Modeling canopy transpiration using time series analysis: A case study illustrating the effect of soil moisture deficit on Pinus taeda. Agric. For. Meteorol. 2005, 130, 163–175. [Google Scholar] [CrossRef]
- Aguilos, M.; Stahl, C.E.M.; Burban, B.; Herault, B.; Courtois, E.; Coste, S.; Wagner, F.; Ziegler, C.; Takagi, K.; Bonal, D. Interannual and seasonal variations in ecosystem transpiration and water use efficiency in a tropical rainforest. Forests 2019, 10, 14. [Google Scholar] [CrossRef]
- Schulze, E.; Kelliher, F.M.; Korner, C.; Lloyd, J.; Leuning, R. Relationships among maximum stomatal conductance, ecosystem surface conductance, carbon assimilation rate, and plant nitrogen nutrition: A global ecology scaling exercise. Annu. Rev. Ecol. Syst. 1994, 25, 629–662. [Google Scholar] [CrossRef]
- Chang, X.; Zhao, W.; He, Z. Radial pattern of sap flow and response to microclimate and soil moisture in Qinghai spruce (Picea crassifolia) in the upper Heihe River Basin of arid northwestern China. Agric. For. Meteorol. 2014, 187, 14–21. [Google Scholar] [CrossRef]
- Nagler, P.L.; Glenn, E.P.; Thompson, T.L. Comparison of transpiration rates among saltcedar, cottonwood and willow trees by sap flow and canopy temperature methods. Agric. For. Meteorol. 2003, 116, 73–89. [Google Scholar] [CrossRef]
- Xia, G.; Kang, S.; Li, F.; Zhang, J.; Zhou, Q. Diurnal and seasonal variations of sap flow of Caragana korshinskii in the arid desert region of north-west China. Hydrol. Process. 2007, 22, 1197–1205. [Google Scholar] [CrossRef]
- Cermák, J.; Kucera, J.; Bauerle, W.L.; Phillips, N.; Hinckley, T.M. Tree water storage and its diurnal dynamics related to sap flow and changes in stem volume in old-growth Douglas-fir trees. Tree Physiol. 2007, 27, 181–198. [Google Scholar] [CrossRef]
- Hatton, T.J.; Moore, S.J.; Reece, P.H. Estimating stand transpiration in a Eucalyptus populnea woodland with the heat pulse method: Measurement errors and sampling strategies. Tree Physiol. 1995, 15, 219–227. [Google Scholar] [CrossRef]
- Burgess, S.S.O.; Dawson, T.E. Using branch and basal trunk sap flow measurements to estimate whole-plant water capacitance: A caution. Plan Soil 2008, 305, 5–13. [Google Scholar] [CrossRef]
- Huang, L.; Zhang, Z.; Li, X. The extrapolation of the leaf area-based transpiration of two xerophytic shrubs in a revegetated desert area in the Tengger Desert, China. Hydrol. Res. 2015, 46, 389–399. [Google Scholar] [CrossRef]
- Zhang, J.G.; Guan, J.; Shi, W.; Yamanaka, N.; Du, S. Interannual variation in stand transpiration estimated by sap flow measurement in a semi-arid black locust plantation, Loess Plateau, China. Ecohydrology 2015, 8, 137–147. [Google Scholar] [CrossRef]
- Mcjannet, D.; Fitch, P.; Disher, M.; Wallace, J. Measurements of transpiration in four tropical rainforest types of north Queensland, Australia. Hydrol. Process. 2010, 21, 3549–3564. [Google Scholar] [CrossRef]
- Zimmermann, R.; Schulze, E.D.; Wirth, C.; Schulze, E.E.; Mcdonald, K.C.; Vygodskaya, N.N.; Ziegler, W. Canopy transpiration in a chronosequence of Central Siberian pine forests. Glob. Chang. Biol. 2010, 6, 25–37. [Google Scholar] [CrossRef]
| Shrub No. | Stem No. | PBN | SL (cm) | SBD (mm) | W (g) | Height (cm) | Canopy Size (cm) |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 5 | 153 | 10.0 | 77.8 | 310.0 | 410 × 374 |
| 2 | 6 | 215 | 9.7 | 103.5 | |||
| 3 | 12 | 175 | 11.2 | 115.9 | |||
| 4 | 9 | 195 | 11.5 | 84.4 | |||
| 5 | 7 | 240 | 13.4 | 104.9 | |||
| 6 | 13 | 232 | 16.6 | 71.3 | |||
| 7 | 7 | 260 | 19.4 | 111.6 | |||
| 2 | 8 | 12 | 195 | 10.8 | 91.9 | 280.0 | 340 × 340 |
| 9 | 8 | 155 | 10.3 | 99.7 | |||
| 10 | 11 | 157 | 10.7 | 92.5 | |||
| 11 | 12 | 195 | 13.4 | 128.9 | |||
| 12 | 14 | 228 | 16.6 | 213. 7 | |||
| 13 | 25 | 270 | 20.0 | 174.7 | |||
| 3 | 14 | 10 | 233 | 9.4 | 204.7 | 320.0 | 350 × 330 |
| 15 | 14 | 150 | 9.6 | 313.1 | |||
| 16 | 5 | 160 | 11.1 | 306.4 | |||
| 17 | 8 | 150 | 11.0 | 334.1 | |||
| 18 | 7 | 232 | 13.3 | 281.5 | |||
| 19 | 11 | 233 | 17.1 | 473.3 | |||
| 20 | 4 | 180 | 17.8 | 521.8 | |||
| 21 | 14 | 240 | 20.3 | 476.4 |
| No. | Function | R2-adj | p | pcon | pPBN | pSL | pSBD | pW | VIFPBN | VIFSL | VIFSBD | VIFW |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | SF = 0.166 PBN − 0.012 SL + 0.069 W + 1.691 | 0.766 | <0.0001 | 0.880 | 0.688 | 0.879 | 0.007 | 1.112 | 3.143 | 2.956 | ||
| 2 | SF = 0.229 PBN + 0.034 SL + 2.233 SBD − 24.086 | 0.766 | <0.0001 | 0.009 | 0.582 | 0.605 | 0.007 | 1.097 | 4.354 | 4.163 | ||
| 3 | SF = 0.151 PBN + 0.067 W + 0.119 | 0.541 | <0.0001 | 0.977 | 0.693 | <0.0001 | 1.079 | 1.079 | ||||
| 4 | SF = 0.293 PBN + 2.517 SBD − 21.931 | 0.781 | <0.0001 | 0.004 | 0.448 | <0.0001 | 1.015 | 1.015 | ||||
| 5 | SF = −0.007 PBN+0.212 SL − 25.610 | 0.781 | 0.005 | 0.031 | 0.990 | 0.002 | 1.032 | 1.032 | ||||
| 6 | SF = 0.045 SL + 2.169 SBD − 23.089 | 0.781 | <0.0001 | 0.007 | 0.464 | 0.005 | 2.868 | 2.868 | ||||
| 7 | SF = −0.004 SL + 0.068 W + 2.033 | 0.784 | <0.0001 | 0.849 | 0.954 | 0.005 | 4.096 | 4.096 | ||||
| 8 | SF = 1.0.597 PBN + 9.570 | 0.036 | 0.473 | 0.271 | 0.473 | 1.000 | ||||||
| 9 | SF = 0.218 SL − 25.644 | 0.579 | 0.001 | 0.020 | 0.001 | 1.000 | ||||||
| 10 | SF = 2.552 BD − 19.586 | 0.788 | <0.0001 | 0.002 | <0.0001 | 1.000 | ||||||
| 11 | SF = 0.0767 W + 7.429 | 0.802 | <0.0001 | 0.542 | <0.0001 | 1.000 |
| SF | Shrub 1 | Shrub 2 | Shrub 3 | Average | SD |
|---|---|---|---|---|---|
| SF (g∙h−1) | 1111.71 | 528.73 | 789.86 | 810.10 | 195.89 |
| SF (mm∙d−1) | 1.91 | 1.10 | 1.59 | 1.53 | 0.22 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, G.; Shen, Y.; Yang, X.; Chen, Z.; Mo, B. Scaling Up Sap Flow Measurements from the Stem Scale to the Individual Scale for Multibranched Caragana Korshinskii on the Chinese Loess Plateau. Forests 2019, 10, 785. https://doi.org/10.3390/f10090785
Wang G, Shen Y, Yang X, Chen Z, Mo B. Scaling Up Sap Flow Measurements from the Stem Scale to the Individual Scale for Multibranched Caragana Korshinskii on the Chinese Loess Plateau. Forests. 2019; 10(9):785. https://doi.org/10.3390/f10090785
Chicago/Turabian StyleWang, Guohui, Yuying Shen, Xianlong Yang, Zhixue Chen, and Baoru Mo. 2019. "Scaling Up Sap Flow Measurements from the Stem Scale to the Individual Scale for Multibranched Caragana Korshinskii on the Chinese Loess Plateau" Forests 10, no. 9: 785. https://doi.org/10.3390/f10090785
APA StyleWang, G., Shen, Y., Yang, X., Chen, Z., & Mo, B. (2019). Scaling Up Sap Flow Measurements from the Stem Scale to the Individual Scale for Multibranched Caragana Korshinskii on the Chinese Loess Plateau. Forests, 10(9), 785. https://doi.org/10.3390/f10090785





