Quantifying the Relationship among Impact Factors of Shrub Layer Diversity in Chinese Pine Plantation Forest Ecosystems
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
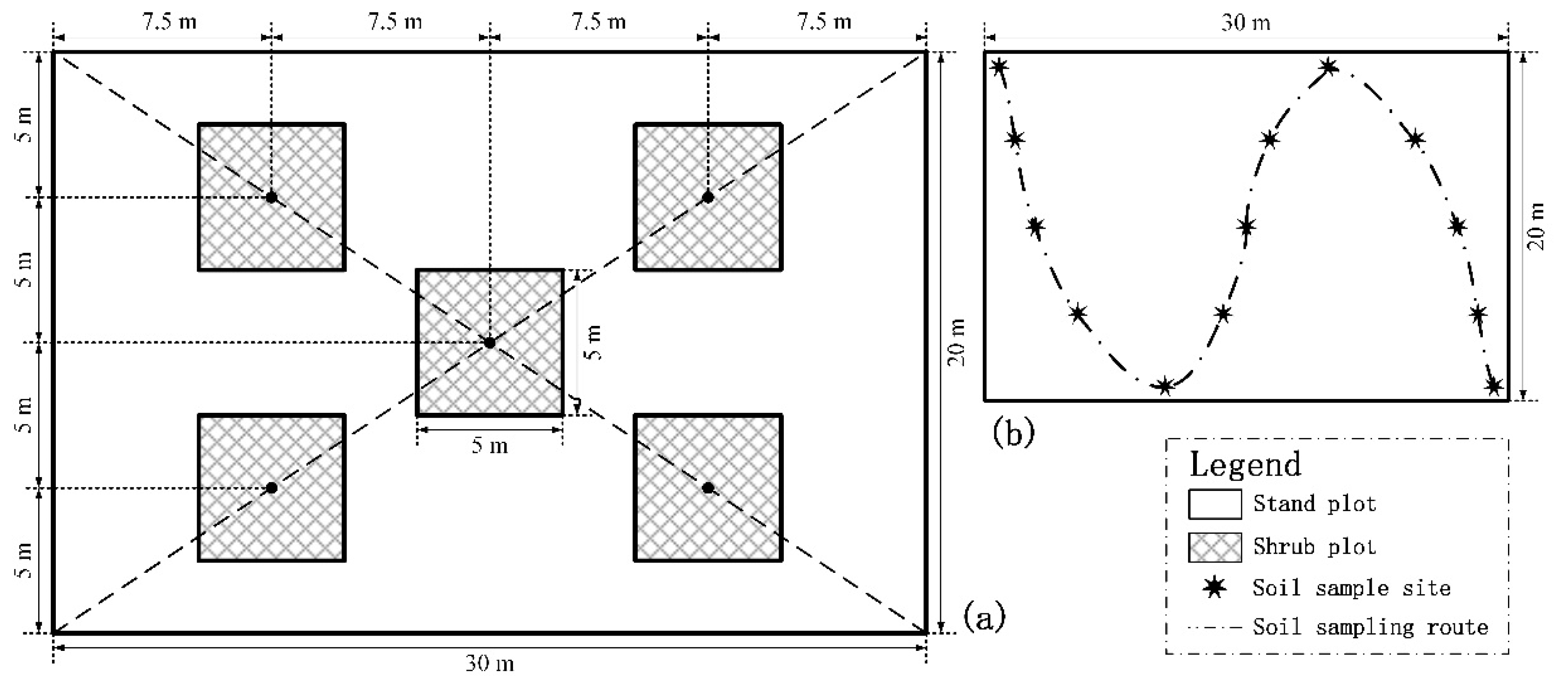
2.2. Forest Survey, Sample Collection, and Soil Sample Analysis
2.3. Variables
2.4. Selection of Variables
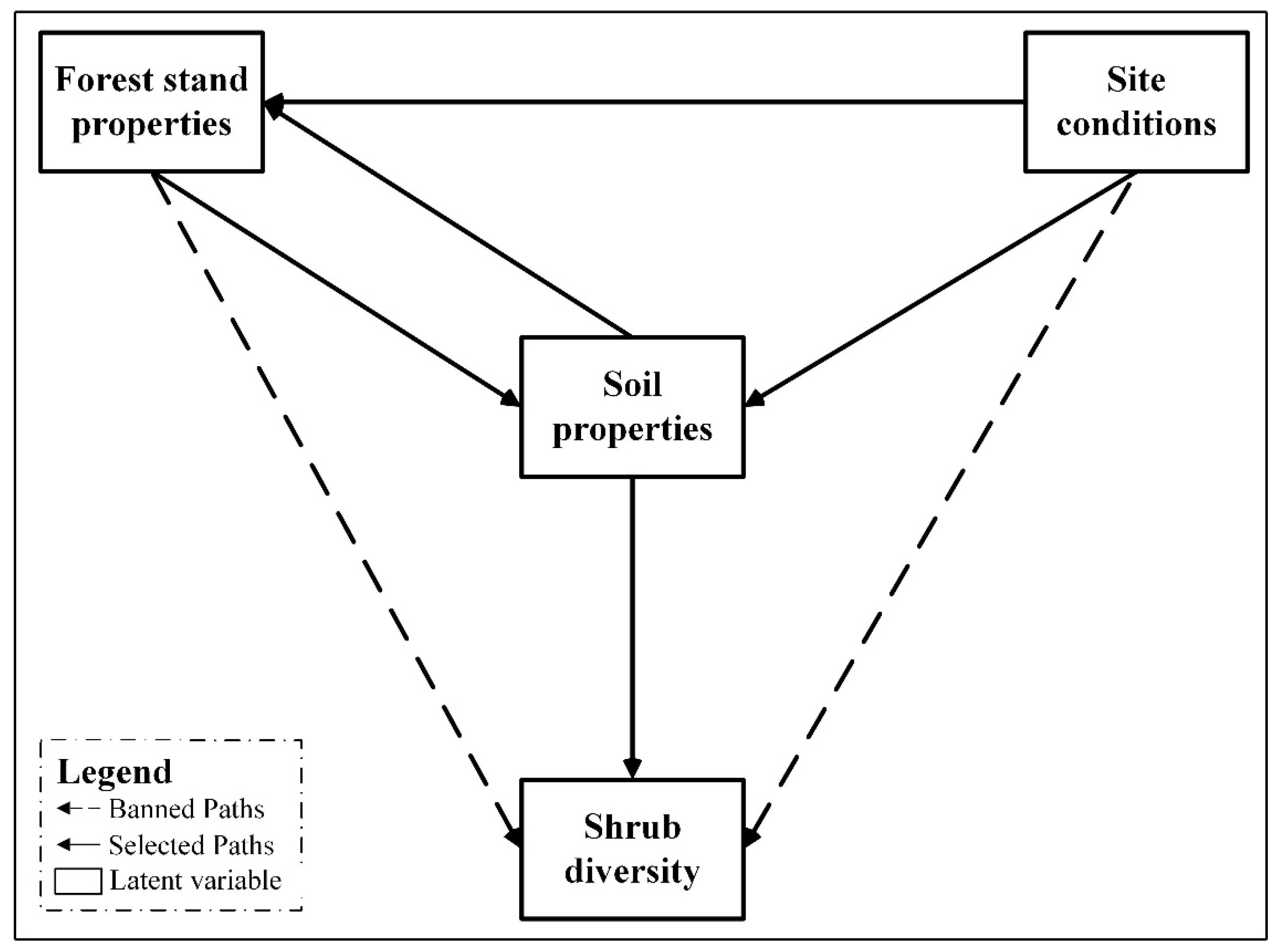
2.5. Establishment of Preliminary Model and Determination of Paths
2.6. Evaluation of PLS-SEM
3. Results
3.1. Observed Variables of Latent Variables of Shrub Diversity
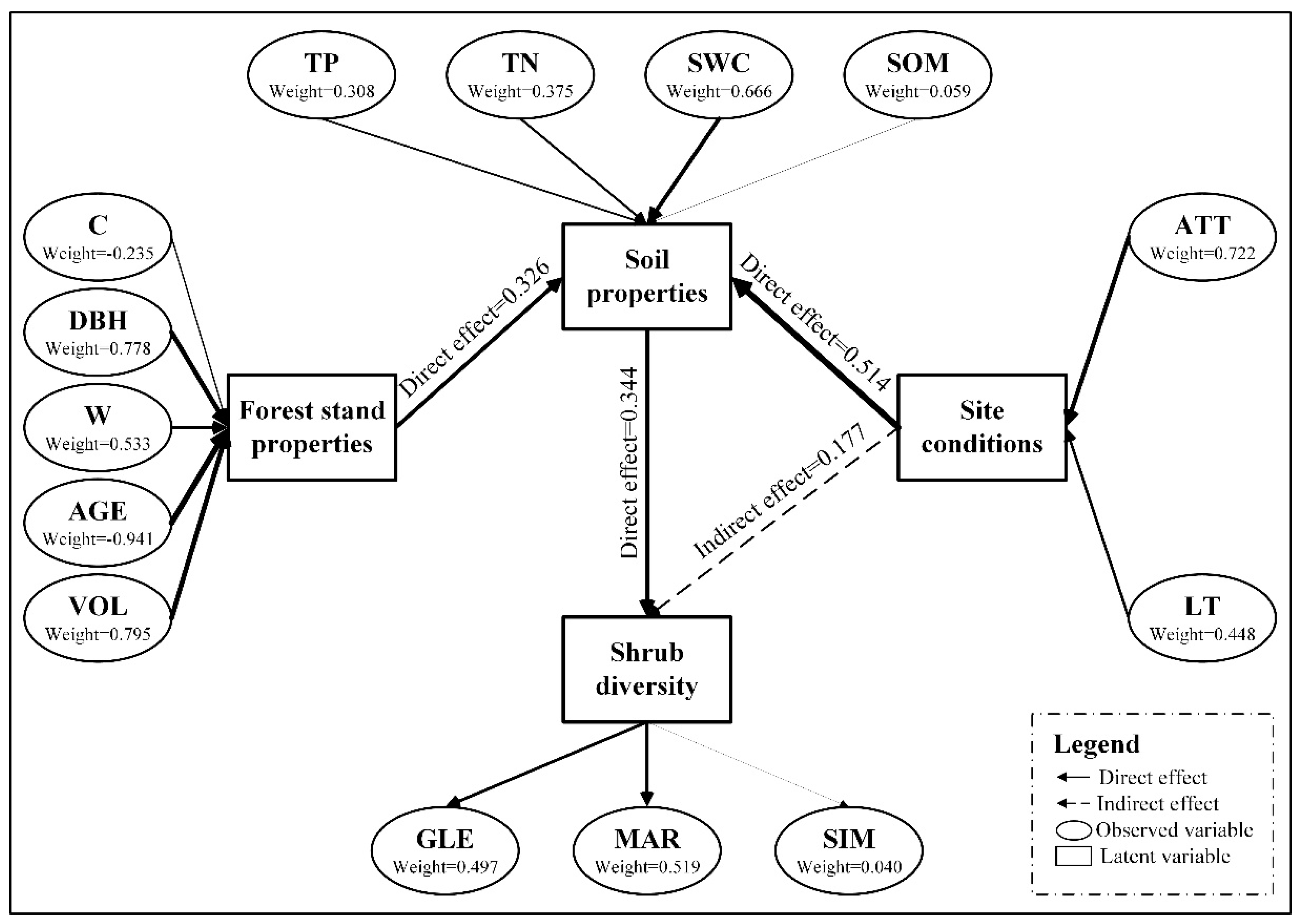
3.2. Possible Path and Model
3.3. Model Fit
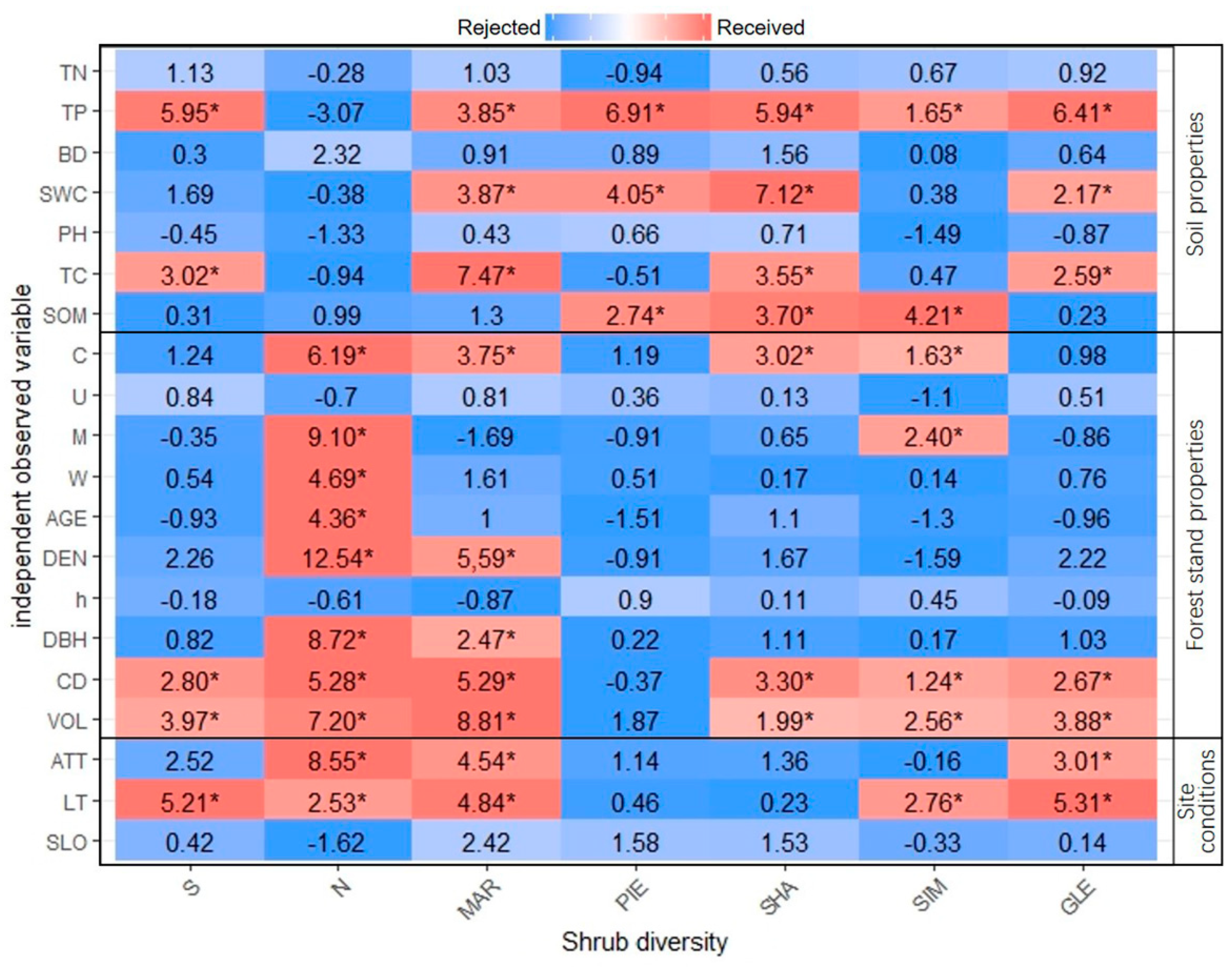
3.4. Evaluation of Shrub Diversity’s Effect Factor
4. Discussion
4.1. Direct Effect of Shrub Diversity
4.2. Site Condition Influence On Shrub Diversity as Demonstrated by the Effects on the Soil Properties
4.3. Effect of Tree Layers on Soil Properties
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- FAO. Global Forest Resources Assessment 2015: How are the World’s Forests Changing? Food and Agriculture Organization of United Nation: Rome, Italy, 2016. [Google Scholar]
- Kelty, M.J. The role of species mixtures in plantation forestry. For. Ecol. Manag. 2006, 233, 195–204. [Google Scholar] [CrossRef]
- Evans, J.; Turnbull, J.W. Plantation Forestry in the Tropics: The Role, Silviculture, and Use of Planted Forests for Industrial, Social, Environmental, and Agroforestry Purposes; Oxford University Press: Oxford, UK, 2004; p. 480. [Google Scholar]
- Gracia, M.; Montané, F.; Piqué, J.; Retana, J. Overstory structure and topographic gradients determining diversity and abundance of understory shrub species in temperate forests in central Pyrenees (NE Spain). For. Ecol. Manag. 2007, 242, 391–397. [Google Scholar] [CrossRef]
- De Groote, S.R.E.; Vanhellemont, M.; Baeten, L.; De Schrijver, A.; Martel, A.; Bonte, D.; Lens, L.; Verheyen, K. Tree species diversity indirectly affects nutrient cycling through the shrub layer and its high-quality litter. Plant Soil 2018, 427, 335–350. [Google Scholar] [CrossRef]
- Myers-Smith, I.H.; Forbes, B.C.; Wilmking, M.; Hallinger, M.; Lantz, T.; Blok, D.; Tape, K.D.; Macias-Fauria, M.; Sass-Klaassen, U.; Lévesque, E.; et al. Shrub expansion in tundra ecosystems: Dynamics, impacts and research priorities. Environ. Res. Lett. 2011, 6, 045509. [Google Scholar] [CrossRef]
- John, R.; Dalling, J.W.; Harms, K.E.; Yavitt, J.B.; Stallard, R.F.; Mirabello, M.; Hubbell, S.P.; Valencia, R.; Navarrete, H.; Vallejo, M.; et al. Soil nutrients influence spatial distributions of tropical tree species. Proc. Natl. Acad. Sci. USA 2007, 104, 864–869. [Google Scholar] [CrossRef]
- Small, C.J.; McCarthy, B.C. Spatial and temporal variability of herbaceous vegetation in an eastern deciduous forest. Plant Ecol. 2003, 164, 37–48. [Google Scholar] [CrossRef]
- Grandin, U. Dynamics of understory vegetation in boreal forests: Experiences from Swedish integrated monitoring sites. For. Ecol. Manag. 2004, 195, 45–55. [Google Scholar] [CrossRef]
- Légaré, S.; Bergeron, Y.; Paré, D. Influence of Forest Composition on Understory Cover in Boreal Mixedwood Forests of Western Quebec. Silva Fennica 2002, 36, 353–366. [Google Scholar] [CrossRef]
- Bergstedt, J.; Milberg, P. The impact of logging intensity on field-layer vegetation in Swedish boreal forests. For. Ecol. Manag. 2001, 154, 105–115. [Google Scholar] [CrossRef]
- Frelich, L.E.; Machado, J.-L.; Reich, P.B. Fine-scale environmental variation and structure of understorey plant communities in two old-growth pine forests. J. Ecol. 2003, 91, 283–293. [Google Scholar] [CrossRef]
- Légaré, S.; Bergeron, Y.; Leduc, A.; Paré, D. Comparison of the understory vegetation in boreal forest types of southwest Quebec. Can. J. Bot. 2001, 79, 1019–1027. [Google Scholar] [CrossRef]
- Shi, Y.; Xu, L.; Zhou, Y.; Ji, B.; Zhou, G.; Fang, H.; Yin, J.; Deng, X. Quantifying driving factors of vegetation carbon stocks of Moso bamboo forests using machine learning algorithm combined with structural equation model. For. Ecol. Manag. 2018, 429, 406–413. [Google Scholar] [CrossRef]
- Granados-Peláez, C.; Santibáñez-Andrade, G.; Guerra-Martínez, F.; Serrano-Giné, D.; García-Romero, A. Evaluation of multi-causal dynamics of variability composition of patch edges in temperate forest. For. Ecol. Manag. 2018, 429, 207–216. [Google Scholar] [CrossRef]
- Tin Kam, H. Random decision forests. In Proceedings of the 3rd International Conference on Document Analysis and Recognition, Montreal, QC, Canada, 14–16 August 1995; pp. 278–282. [Google Scholar]
- Kaplan, D. Structural Equation Modeling: Foundations and Extensions; Sage Publications: Thousand Oaks, CA, USA, 2008; Volume 10. [Google Scholar]
- Van Groenewoud, H. Methods and samplers for obtaining undisturbed soil samples in the forest. METHODS 1960, 90, 272–274. [Google Scholar] [CrossRef][Green Version]
- Walkley, A.; Black, I.A. An examination of the Degtjareff method for determining soil organic matter, and a proposed modification of the chromic acid titration method. Soil Sci. 1934, 37, 29–38. [Google Scholar] [CrossRef]
- Bremner, J.M. Nitrogen-total. In Methods of Soil Analysis, Part3; American Society of Agronomy-Soil Science Society of America: Madison, WI, USA, 1996; pp. 1085–1121. [Google Scholar]
- Parkinson, J.A.; Allen, S.E. A wet oxidation procedure suitable for the determination of nitrogen and mineral nutrients in biological material. Commun. Soil Sci. Plant Anal. 1975, 6, 1–11. [Google Scholar] [CrossRef]
- Gadow, K.V.; Huy, G.Y.; Albert, M. The uniform angle index—A structural parameter for describing tree distribution in forest stands. Forstwesen 1998, 115, 1–10. [Google Scholar]
- Hui, G.Y.; Albert, M.; Von Gadow, K. The measure of neighbourhood dimensions as a parameter to reproduce stand structures. Forstwiss. Cent. Bl. 1998, 117, 258–266. [Google Scholar] [CrossRef]
- Hui, G.; Gadow, K.V. The uniform angle index. Derivation of the optimal standard angle. Allg. Forst-U. J.-Ztg. 2002, 173, 173–177. [Google Scholar]
- Hu, Y.; Hui, G. How to describe the crowding degree of trees based on the relationship of neighboring trees. J. Beijing For. Univ 2015, 37, 1–8. [Google Scholar]
- Tuv, E.; Borisov, A.; Runger, G.; Torkkola, K. Feature selection with ensembles, artificial variables, and redundancy elimination. J. Mach. Learn. Res. 2009, 10, 1341–1366. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Kursa, M.B.; Rudnicki, W.R. Feature selection with the Boruta package. J. Stat. Softw. 2010, 36, 1–13. [Google Scholar] [CrossRef]
- Doncaster, C.P. Structural Equation Modeling and Natural Systems; Grace, J.B., Ed.; Cambridge University Press: Cambridge, UK, 2006; pp. 368–369. [Google Scholar]
- Samani, S. Steps in Research Process (Partial Least Square of Structural Equation Modeling (PLS-SEM) A Review). Int. J. Soc. Sci. Bus. 2016, 1, 55–66. [Google Scholar]
- Wong, K.K.-K. Partial least squares structural equation modeling (PLS-SEM) techniques using SmartPLS. Mark. Bull. 2013, 24, 1–32. [Google Scholar]
- Bacon, L.D. Using LISREL and PLS to measure customer satisfaction. In Proceedings of the Sawtooth Software Conference Proceedings, La Jolla, CA, USA, 2–5 February 1999; pp. 305–306. [Google Scholar]
- Wong, K. Handling small survey sample size and skewed dataset with partial least square path modelling. Vue Mag. Mark. Res. Intell. Assoc. Novemb. 2010, 20, 20–23. [Google Scholar]
- Hair, J.F.; Anderson, R.E.; Tatham, R.L.; Black, W.C. Multivariate Data Analysis, 5th ed.; Prentice Hall: New York, NY, USA, 1998. [Google Scholar]
- Fornell, C.; Larcker, D.F. Evaluating Structural Equation Models with Unobservable Variables and Measurement Error. J. Mark. Res. 1981, 18, 39–50. [Google Scholar] [CrossRef]
- Hair, J.F.; Sarstedt, M. PLS-SEM: Indeed a Silver Bullet. J. Mark. Theory Pract. 2011, 19, 139–152. [Google Scholar] [CrossRef]
- Henseler, J.; Dijkstra, T.K.; Sarstedt, M.; Ringle, C.M.; Diamantopoulos, A.; Straub, D.W.; Ketchen, D.J.; Hair, J.F.; Hult, G.T.M.; Calantone, R.J. Common Beliefs and Reality About PLS:Comments on Rönkkö and Evermann (2013). Organ. Res. Methods 2014, 17, 182–209. [Google Scholar] [CrossRef]
- Hu, L.t.; Bentler, P.M. Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Struct. Equ. Model. A Multidiscip. J. 1999, 6, 1–55. [Google Scholar] [CrossRef]
- Sang, W. Plant diversity patterns and their relationships with soil and climatic factors along an altitudinal gradient in the middle Tianshan Mountain area, Xinjiang, China. Ecol. Res. 2009, 24, 303–314. [Google Scholar] [CrossRef]
- Jia, X.; Shao, M.A.; Zhu, Y.; Luo, Y. Soil moisture decline due to afforestation across the Loess Plateau, China. J. Hydrol. 2017, 546, 113–122. [Google Scholar] [CrossRef]
- Li, X.; Tan, H.; He, M.; Wang, X.; Li, X. Patterns of shrub species richness and abundance in relation to environmental factors on the Alxa Plateau: Prerequisites for conserving shrub diversity in extreme arid desert regions. Sci. China Ser. D Earth Sci. 2009, 52, 669–680. [Google Scholar] [CrossRef]
- Goldberg, D.E.; Miller, T.E. Effects of Different Resource Additions of Species Diversity in an Annual Plant Community. Ecology 1990, 71, 213–225. [Google Scholar] [CrossRef]
- Condit, R.; Engelbrecht, B.M.J.; Pino, D.; Pérez, R.; Turner, B.L. Species distributions in response to individual soil nutrients and seasonal drought across a community of tropical trees. Proc. Natl. Acad. Sci. USA 2013, 110, 5064–5068. [Google Scholar] [CrossRef] [PubMed]
- Zemunik, G.; Turner, B.L.; Lambers, H.; Laliberté, E. Increasing plant species diversity and extreme species turnover accompany declining soil fertility along a long-term chronosequence in a biodiversity hotspot. J. Ecol. 2016, 104, 792–805. [Google Scholar] [CrossRef]
- Fu, B.J.; Liu, S.L.; Ma, K.M.; Zhu, Y.G. Relationships between soil characteristics, topography and plant diversity in a heterogeneous deciduous broad-leaved forest near Beijing, China. Plant Soil 2004, 261, 47–54. [Google Scholar] [CrossRef]
- Lu, N.N.; Gao, Z.X.; Zhang, P.; Xu, X.L.; Wang, X.J. Path Analysis between Soil Properties and Undergrowth Vegetation in Pure Chinese Fir Forest. J. Northeast For. Univ. 2015, 43, 73–77. [Google Scholar]
- Cleve, K.V.; Oliver, L.; Schlentner, R.; Viereck, L.A.; Dyrness, C.T. Productivity and nutrient cycling in taiga forest ecosystems. Can. J. For. Res. 1983, 13, 747–766. [Google Scholar] [CrossRef]
- Chawla, A.; Rajkumar, S.; Singh, K.N.; Lal, B.; Singh, R.D.; Thukral, A.K. Plant Species Diversity along an Altitudinal Gradient of Bhabha Valley in Western Himalaya. J. Mt. Sci. 2008, 5, 157–177. [Google Scholar] [CrossRef]
- Unger, M.; Leuschner, C.; Homeier, J. Variability of indices of macronutrient availability in soils at different spatial scales along an elevation transect in tropical moist forests (NE Ecuador). Plant Soil 2010, 336, 443–458. [Google Scholar] [CrossRef]
- Iii, F.S.C.; Matson, P.A.; Mooney, H.A. Principles of Terrestrial Ecosystem Ecology; Springer: New York, NY, USA, 2011. [Google Scholar]
- Sayer, E.J. Using experimental manipulation to assess the roles of leaf litter in the functioning of forest ecosystems. Biol. Rev. 2010, 81, 1–31. [Google Scholar] [CrossRef] [PubMed]
- Shaolin, P.; Hai, R.; Jianguo, W.; Hongfang, L. Effects of litter removal on plant species diversity: A case study in tropical Eucalyptus forest ecosystems in South China. J. Environ. Sci. 2003, 15, 367. [Google Scholar]
- Opedal, Ø.H.; Armbruster, W.S.; Graae, B.J. Linking small-scale topography with microclimate, plant species diversity and intra-specific trait variation in an alpine landscape. Plant Ecol. Divers. 2015, 8, 305–315. [Google Scholar] [CrossRef]
- Montgomery, R.A.; Chazdon, R.L. Forest structure, canopy architecture, and light transmittance in tropical wet forests. Ecology 2001, 82, 2707–2718. [Google Scholar] [CrossRef]
- Guomei, J.; Jing, C.; Chunyan, W.; Gang, W. Microbial biomass and nutrients in soil at the different stages of secondary forest succession in Ziwulin, northwest China. For. Ecol. Manag. 2005, 217, 117–125. [Google Scholar] [CrossRef]
- Högberg, M.N.; Chen, Y.; Högberg, P. Gross nitrogen mineralisation and fungi-to-bacteria ratios are negatively correlated in boreal forests. Biol. Fertil. Soils 2007, 44, 363–366. [Google Scholar] [CrossRef]
- Pötzelsberger, E.; Hasenauer, H. Forest–water dynamics within a mountainous catchment in Austria. Nat. Hazards 2015, 77, 625–644. [Google Scholar] [CrossRef]
- February, E.C.; Higgins, S.I. The distribution of tree and grass roots in savannas in relation to soil nitrogen and water. S. Afr. J. Bot. 2010, 76, 517–523. [Google Scholar] [CrossRef]
- Prescott, C.E. The influence of the forest canopy on nutrient cycling. Tree Physiol. 2002, 22, 1193. [Google Scholar] [CrossRef]
- Muscolo, A.; Sidari, M.; Mercurio, R. Influence of gap size on organic matter decomposition, microbial biomass and nutrient cycle in Calabrian pine (Pinus laricio, Poiret) stands. For. Ecol. Manag. 2007, 242, 412–418. [Google Scholar] [CrossRef]
- Li, H.; Zhao, J.; Zhou, C.; Merkle, S.A.; Zhang, J.-F. Morphologic characters and element content during development of Pinus tabuliformis seeds. J. For. Res. 2016, 27, 67–74. [Google Scholar] [CrossRef]
- Colin, F.; Drexhage, M. Estimating root system biomass from breast-height diameters. For. Int. J. For. Res. 2001, 74, 491–497. [Google Scholar] [CrossRef]
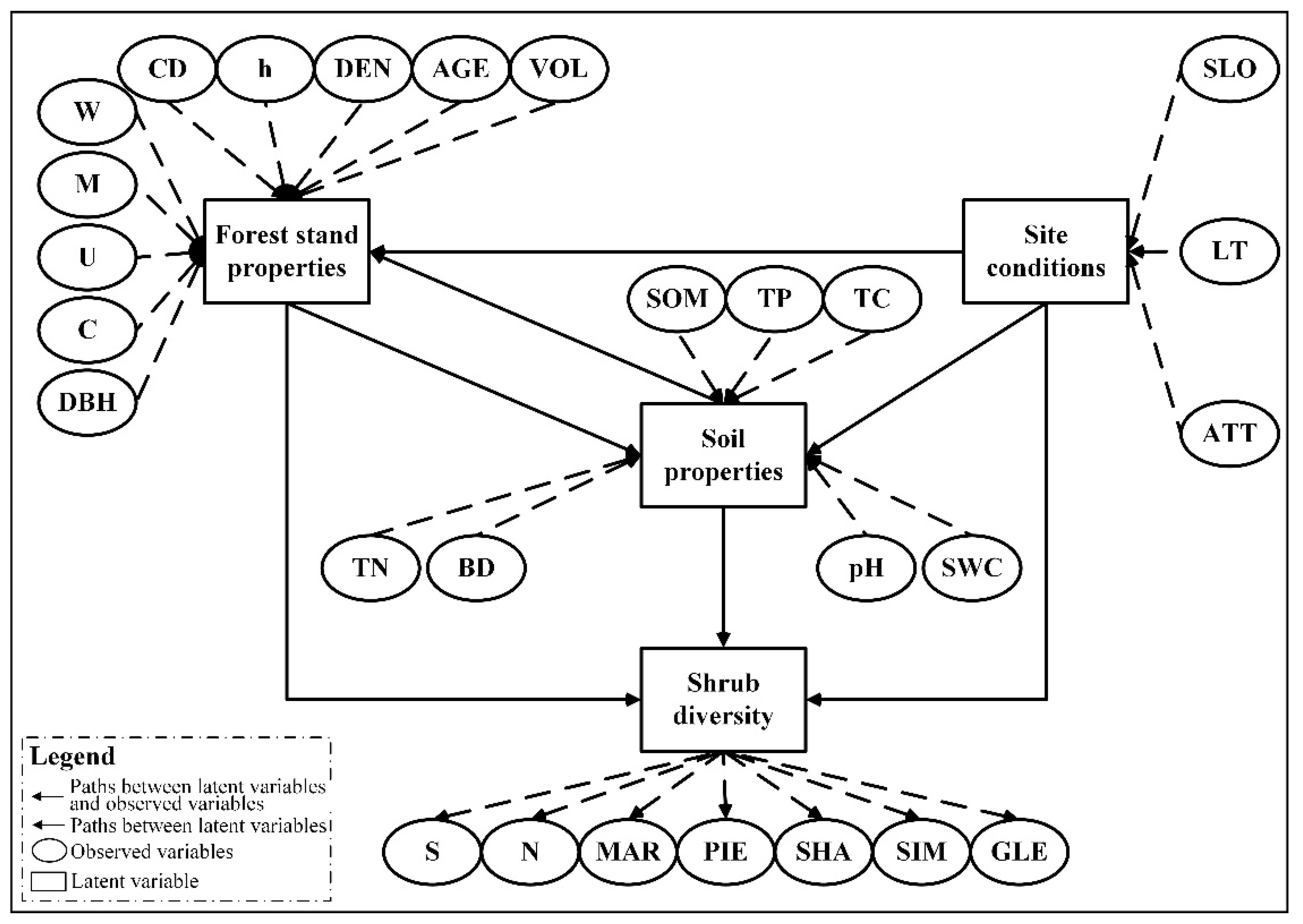
| Latent Variable | Observed Variable | Abbreviation | Detail |
|---|---|---|---|
| Forest stand properties | mingling | M | The mean fraction of trees among the k nearest neighbors of a given reference tree with heterospecific neighbors |
| dominance | U | The proportion of the n nearest neighbors of a given reference tree which are smaller than the reference tree | |
| uniform angle index | W | Characterize the spatial distribution of a forest community or of individual tree species within that community by gradually comparing the included 4 angles with the standard angle | |
| crowding | C | Crowding degree of a neighborhood unit according to the overlapping of the crown in spatial micro-environment which clearly define the crowding degree for a reference tree and its four nearest neighbors | |
| forest stock volume | VOL | The total volume of living trees in a stand that bigger than 3 m diameter at breast height | |
| canopy density | CD | The aggregate of all vertically projected tree crowns onto the ground surface | |
| diameter at breast height | DBH | The tree diameter measured at 1.3 m above the ground | |
| tree height | h | Mean height of all the tree in a stand | |
| stand density | DEN | the number of stems on a per hectare basis in relative terms | |
| average age of the tree | AGE | Average age of all trees in a stand | |
| Site conditions | slope | SLO | Mean angle of the site to the horizontal |
| litter thickness | LT | Mean thickness of litter in a stand | |
| altitude | ATT | Mean altitude of each plot | |
| Soil property | soil organic matter | SOM | The content of organic matter component of soil |
| total carbon content | TC | The content of total carbon of soil | |
| total phosphorus content | TP | The content of total phosphorus of soil | |
| total nitrogen content | TN | The content of total nitrogen of soil | |
| soil bulk density | BD | The weight of soil in a unit volume | |
| soil water content | SWC | The content of water in soil | |
| Pondus Hydrogenii | pH | the negative of the base 10 logarithm of the molar concentration of hydrogen ions in a solution | |
| Shrub diversity | total shrub species | S | Total number of shrub species |
| total number of shrubs | N | Total number of shrub individuals | |
| Margalef species richness index | MAR | ||
| Shannon diversity index | SHA | and | |
| Pielou’s evenness index | PIE | ||
| Simpson diversity index | SIM | and | |
| Gleason richness index | GLE |
| Latent Variables Group | Canonical Correlations 1 | p-Value | Wilk’s | Chi-SQ | DF |
|---|---|---|---|---|---|
| Site conditions vs. forest stand properties | 0.697 | 0.000 ★★★ | 0.273 | 63.664 | 30 |
| Site conditions vs. soil properties | 0.699 | 0.000 ★★★ | 0.291 | 62.42 | 21 |
| Site conditions vs. shrub diversity | 0.511 | 0.072 | 0.632 | 23.619 | 12 |
| Forest stand properties vs. soil properties | 0.845 | 0.000 ★★★ | 0.058 | 134.01 | 70 |
| Forest stand properties vs. shrub diversity | 0.768 | 0.080 | 0.260 | 64.645 | 50 |
| Soil properties vs. shrub diversity | 0.642 | 0.020 ★ | 0.333 | 54.36 | 35 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Bu, Y.; Li, Y.; Li, W.; Zhao, P.; Yang, Y.; Qi, N.; Gou, R. Quantifying the Relationship among Impact Factors of Shrub Layer Diversity in Chinese Pine Plantation Forest Ecosystems. Forests 2019, 10, 781. https://doi.org/10.3390/f10090781
Wang B, Bu Y, Li Y, Li W, Zhao P, Yang Y, Qi N, Gou R. Quantifying the Relationship among Impact Factors of Shrub Layer Diversity in Chinese Pine Plantation Forest Ecosystems. Forests. 2019; 10(9):781. https://doi.org/10.3390/f10090781
Chicago/Turabian StyleWang, Boheng, Yuankun Bu, Yanjie Li, Weizhong Li, Pengxiang Zhao, Yanzheng Yang, Ning Qi, and Ruikun Gou. 2019. "Quantifying the Relationship among Impact Factors of Shrub Layer Diversity in Chinese Pine Plantation Forest Ecosystems" Forests 10, no. 9: 781. https://doi.org/10.3390/f10090781
APA StyleWang, B., Bu, Y., Li, Y., Li, W., Zhao, P., Yang, Y., Qi, N., & Gou, R. (2019). Quantifying the Relationship among Impact Factors of Shrub Layer Diversity in Chinese Pine Plantation Forest Ecosystems. Forests, 10(9), 781. https://doi.org/10.3390/f10090781




