Removing the Scaling Error Caused by Allometric Modelling in Forest Biomass Estimation at Large Scales
Abstract
1. Introduction
2. Methods
2.1. Derivation
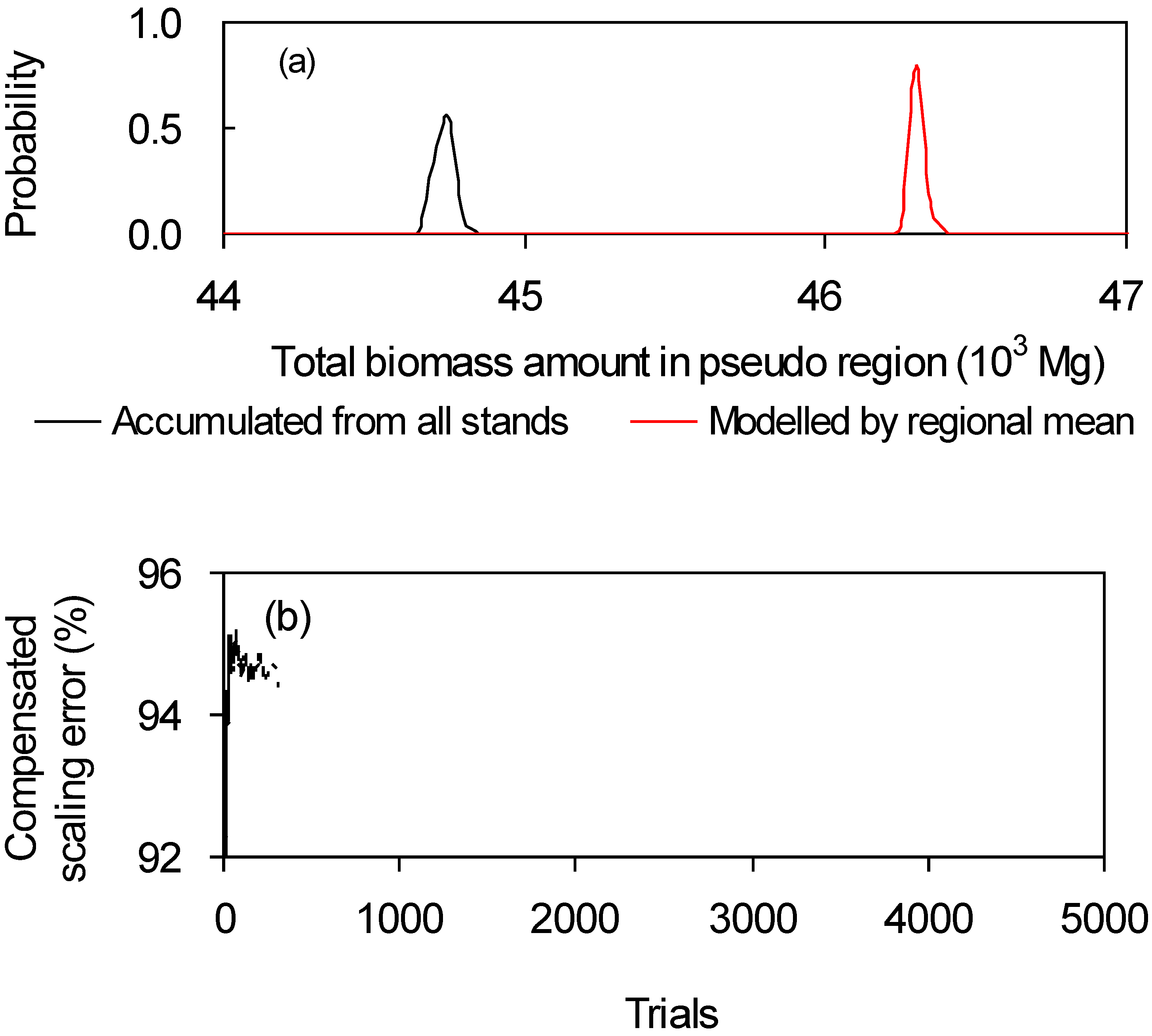
2.2. Simulation
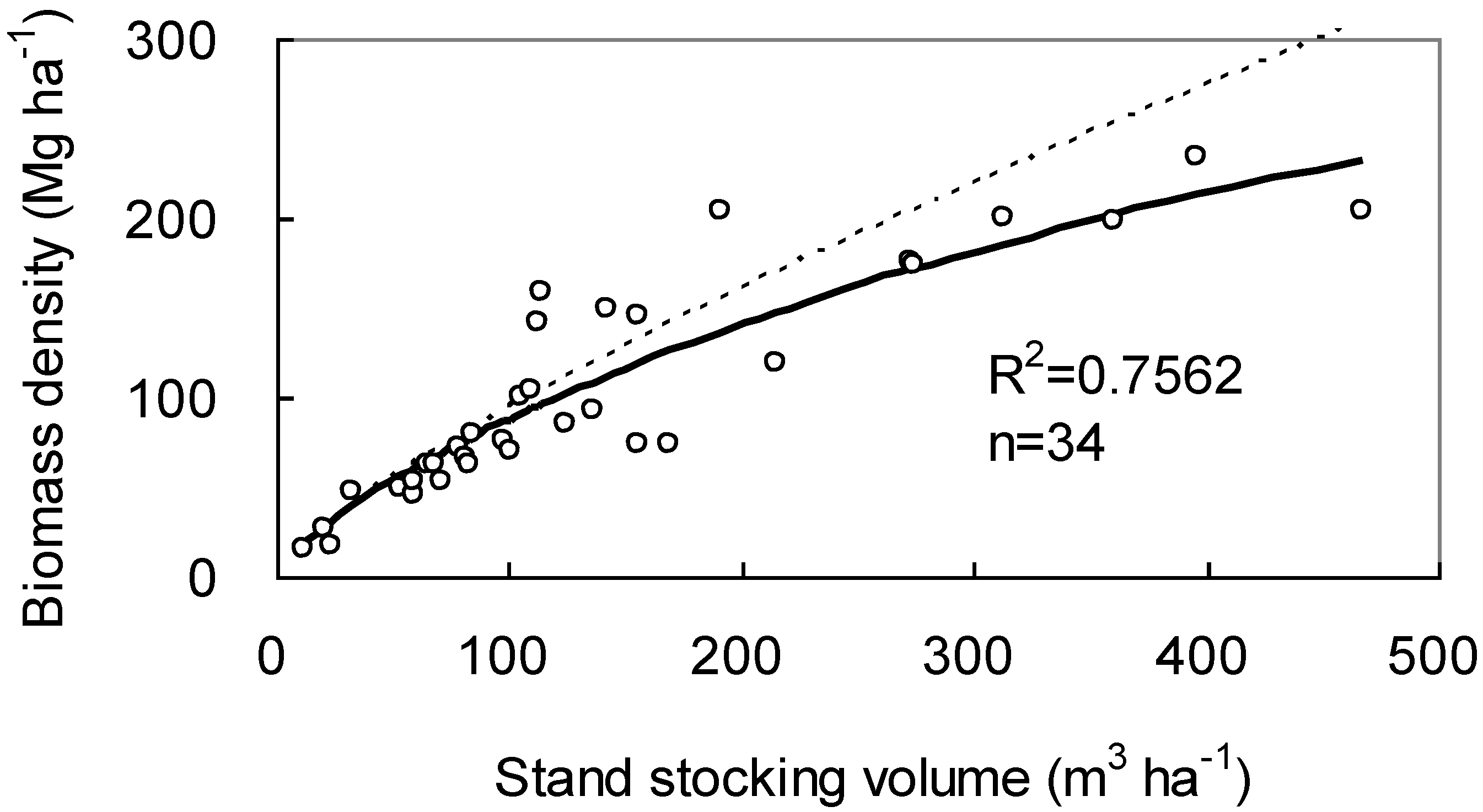
2.3. Data for Case Study
3. Results and Discussions
3.1. Error Compensator
3.2. Efficiency of Reducing the Error
3.3. Comparison
3.4. Uncertainty Analysis
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A1. Problem Background of Scaling Error
(a) Example
(b) Analysis
Appendix A2. Derivation of Dm
References
- Odum, E.P.; Barrett, G.W. Fundamentals of Ecology, 5th ed.; Thomoson Brooks/Cole: Belmont, CA, USA, 2005. [Google Scholar]
- Huxley, J.S.; Teissier, G. Terminology of Relative Growth. Nature 1936, 137, 780–781. [Google Scholar] [CrossRef]
- Anderson, B.G.; Busch, H.L. Allometry in antennal. Biol. Bull. 1941, 81, 119–126. [Google Scholar] [CrossRef]
- Cowin, S.C. The Specific Growth Rates of Tissues: A Review and a Re-Evaluation. J. Biomech. Eng. 2011, 133, 41001. [Google Scholar] [CrossRef] [PubMed]
- Kittredge, J. Estimation of the amount of foliage of trees and stands. J. For. 1944, 42, 905–912. [Google Scholar]
- Niklas, K.J. Plant allometry: Is there a grand unifying theory? Biol. Rev. 2004, 79, 871–889. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, S.E.; Bendoricchio, G. Fundamentals of Ecological Modelling, 3rd ed.; Elservier Science: Amsterdam, The Netherlands, 2001. [Google Scholar]
- Searle, E.B.; Chen, H.Y.H. Persistent and pervasive compositional shifts of western boreal forest plots in Canada. Glob. Chang. Biol. 2017, 23, 857–866. [Google Scholar] [CrossRef] [PubMed]
- Reich, P.B.; Luo, Y.; Bradford, J.B.; Poorter, H.; Perry, C.H.; Oleksyn, J. Temperature drives global patterns in forest biomass distribution in leaves, stems, and roots. Proc. Natl. Acad. Sci. USA 2014, 111, 13721–13726. [Google Scholar] [CrossRef]
- Michaletz, S.T.; Cheng, D.; Kerkhoff, A.J.; Enquist, B.J. Convergence of terrestrial plant production across global climate gradients. Nature 2014, 512, 39–43. [Google Scholar] [CrossRef]
- Chu, C.; Bartlett, M.; Wang, Y.; He, F.; Weiner, J.; Chave, J.; Sack, L. Does climate directly influence NPP globally? Glob. Chang. Biol. 2016, 22, 12–24. [Google Scholar] [CrossRef]
- Bettencourt, L.M.A.; Lobo, J.; Helbing, D.; Kühnert, C.; West, G.B. Growth, innovation, scaling, and the pace of life in cities. Proc. Natl. Acad. Sci. USA 2007, 104, 7301–7306. [Google Scholar] [CrossRef]
- Li, X.; Wang, X.; Zhang, J.; Wu, L. Allometric scaling, size distribution and pattern formation of natural cities. Palgrave Commun. 2015, 1, 1–11. [Google Scholar] [CrossRef]
- West, G.B.; Brown, J.H.; Enquist, B.J. A general model for the structure and allometry of plant vascular systems. Nature 1999, 400, 664–667. [Google Scholar] [CrossRef]
- Komiyama, A.; Ong, J.E.; Poungparn, S. Allometry, biomass, and productivity of mangrove forests: A review. Aquat. Bot. 2008, 89, 128–137. [Google Scholar] [CrossRef]
- Cannell, M.G.R. World Forest Biomass and Primary Production Data; Academic Press: London, UK, 1982. [Google Scholar]
- Usoltsev, V.A. Forest Biomass and Primary Production Database for Eurasia, 2nd ed.; CD-ve.; Ural State Forest Engineering University: Yekaterinburg, Russia, 2013. [Google Scholar]
- Luo, Y.; Wang, X.; Zhang, X.; Lu, F. Biomass and Its Allocation of Forest Ecosystems in China; Chinese Forestry Publishing House Press: Beijing, China, 2013. [Google Scholar]
- Duursma, R.A.; Robinson, A.P. Bias in the mean tree model as a consequence of Jensen’s inequality. For. Ecol. Manag. 2003, 186, 373–380. [Google Scholar] [CrossRef]
- Gertner, G. Prediction bias and response surface curvature. For. Sci. 1991, 37, 755–765. [Google Scholar]
- Gardner, R.H.; Cale, W.G.; O’Neill, R.V. Robust Analysis of Aggregation Error. Ecology 1982, 63, 1771–1779. [Google Scholar] [CrossRef]
- Sambakhe, D.; Fortin, M.; Renaud, J.P.; Deleuze, C.; Dreyfus, P.; Picard, N. Prediction bias induced by plot size in forest growth models. For. Sci. 2014, 60, 1050–1059. [Google Scholar] [CrossRef]
- Rastetter, E.B.; King, A.W.; Cosby, B.J.; Hornberger, G.M.; O’Neill, R.V.; Hobbie, J.E. Aggregating fine-scale ecological knowledge to model coarser-resolution attributes of ecosystems. Ecol. Appl. 1992, 2, 55–77. [Google Scholar] [CrossRef]
- Kangas, A. On the bias and variance in tree volume predictions due to model and measurement errors. Scand. J. For. Res. 1996, 11, 281–290. [Google Scholar] [CrossRef]
- Zhou, X.; Lei, X.; Peng, C.; Wang, W.; Zhou, C.; Liu, C.; Liu, Z. Correcting the overestimate of forest biomass carbon on the national scale. Methods Ecol. Evol. 2016, 7, 447–455. [Google Scholar] [CrossRef]
- Woodall, C.W.; Heath, L.S.; Domke, G.M.; Nichols, M.C. Methods and Equations for Estimating Aboveground Volume, Biomass, and Carbon for Trees in the U.S. Forest Inventory, 2010; Tech. Rep. NRS-88.; USDA, Forest Service, Northern Research Station: Newtown Square, PA, USA, 2011; p. p. 30.
- Lei, X.; Tang, M.; Lu, Y.; Hong, L.; Tian, D. Forest inventory in China: status and challenges. Int. For. Rev. 2009, 11, 52–63. [Google Scholar] [CrossRef]
- Eggleston, H.S.; Buendia, L.; Miwa, K.; Ngara, T.; Tanabe, K. 2006 IPCC Guidelines for National Greenhouse Gas Inventories. In Forest land; IGES: Kanagawa, Japan, 2006. [Google Scholar]
- Brown, S.L.; Lugo, A. Biomass of Tropical Forests: A New Estimate Based on Forest Volumes. Science 1984, 223, 1290–1293. [Google Scholar] [CrossRef] [PubMed]
- Smith, J.E.; Heath, L.S.; Jenkins, J.C. Forest volume-to-biomass models and estimates of mass for live and standing dead trees of U.S. forests. USDA For. Serv. 2003, 1–62. [Google Scholar] [CrossRef]
- Guo, Z.; Fang, J.; Pan, Y.; Birdsey, R. Inventory-based estimates of forest biomass carbon stocks in China: A comparison of three methods. For. Ecol. Manag. 2010, 259, 1225–1231. [Google Scholar] [CrossRef]
- Henry, M.; Bombelli, A.; Trotta, C.; Alessandrini, A.; Birigazzi, L.; Sola, G.; Vieilledent, G.; Santenoise, P.; Longuetaud, F.; Valentini, R.; et al. GlobAllomeTree: International platform for tree allometric equations to support volume, biomass and carbon assessment. IForest 2013, 6, 1–5. [Google Scholar] [CrossRef]
- Fang, J.; Chen, A.; Peng, C.; Zhao, S.; Ci, L. Changes in forest biomass carbon storage in China between 1949 and 1998. Science 2001, 292, 2320–2322. [Google Scholar] [CrossRef]
- Boudewyn, P.; Song, X.; Magnussen, S.; Gillis, M.D. Model-Based, Volume-to-Biomass Conversion for Forested and Vegetated Land in Canada; Natural Resources Canada, Canadian Forest Service Pacific Forestry Centre Natural: Victoria, BC, Canada, 2007; p. 124. [Google Scholar]
- Ruark, G.; Bockheim, J.G.; Martin, G.L. Comparison of constant and variable allometric ratios for estimating Populus tremuloides biomass. For. Sci. 1987, 33, 294–300. [Google Scholar]
- Geron, C.D. Comparison of constant and variable allometric ratios for predicting foliar biomass of various tree genera. Can. J. For. Res 1988, 18, 1298–1340. [Google Scholar] [CrossRef]
- Berton, A.J.; Pregitzer, K.S.; Reed, D.D. Leaf area and foliar biomass relationships in northern hardwood forests located along an 800 km acid deposition gradient. For. Sci. 1991, 37, 1041–1059. [Google Scholar]
- Mather, A.S. Assessing the world’s forests. Glob. Environ. Chang. 2005, 15, 267–280. [Google Scholar] [CrossRef]
- Deng, X.; Huang, B.; Wen, Q.; Hua, C.; Tao, J.; Zheng, J. Dynamic of Pinus yunnanensis Forest Resources in Yunnan. J. Nat. Resour. 2014, 29, 1411–1419, (In Chinese with English abstract). [Google Scholar]
- Chinese Ministry of Forestry. Forest Resource Report of China for Periods 2003–2007; Department of Forest Resource and Management, Chinese Ministry of Forestry: Beijing, China, 2008. [Google Scholar]
- Lu, H. Preliminary estimation of forest carbon reserves of Pinus yunnanensis. For. Invent. Plan. 2010, 35, 91–93. [Google Scholar]
- Li, X. A review of researches on Pinus yunnanensis. J. Sichuan Agric. Univ. 1995, 13, 309–314. [Google Scholar]
- Wang, B.; Mao, J.F.; Zhao, W.; Wang, X.R. Impact of Geography and Climate on the Genetic Differentiation of the Subtropical Pine Pinus yunnanensis. PLoS ONE 2013, 8, e67345. [Google Scholar] [CrossRef] [PubMed]
- Dan, C.; Wu, Z. Studies on the biomass of Pinus yunnanensis forest. Acta Bot. Yunnanica 1991, 13, 59–64. [Google Scholar]
- Matasci, G.; Hermosilla, T.; Wulder, M.A.; White, J.C.; Coops, N.C.; Hobart, G.W.; Bolton, D.K.; Tompalski, P.; Bater, C.W. Three decades of forest structural dynamics over Canada’s forested ecosystems using Landsat time-series and lidar plots. Remote Sens. Environ. 2018, 216, 697–714. [Google Scholar] [CrossRef]

| Symbol | Description | Unit |
|---|---|---|
| A | Total forested area in a region, A = ∑ai. | ha |
| ai | The area of ith stand. | ha |
| The combination. = j!/[s!(j − s)!]. j represents the total number of elements, and s is the number of elements being chosen at a time. | - | |
| Dm | The maximum variance, which is a function of expectation. | m6 ha−2 |
| E | The mathematical expectation operator. | - |
| g(x) | The function of random variable x, g(x) = xke−ux. | - |
| i | Stand number, i = 1, 2, …, n. | - |
| k | Parameter, 0 < k ≤ 1. | - |
| n | The number of stands. | - |
| q | Derivative order, q is set up to 4 in this study. | - |
| r | Parameter, r > 0. | - |
| u | Parameter, u > 0. | m−3 ha |
| wi | Weight or the probability of occurrence of ith stand, wi = ai/A. | - |
| x | Stocking volume of a fine-scale area, e.g., a stand. | m3 ha−1 |
| xi | Stand stocking volume of ith stand. | m3 ha−1 |
| xmax | The maximum possible value of x in the forest inventory. | m3 ha−1 |
| xmin | The minimum possible value of x in the forest inventory. | m3 ha−1 |
| Y1 | Regional total biomass ideally supposed to accumulate from all stands. | Mg |
| Y2 | Regional total biomass calculated from A and μ, Y2 = Arμke−ux. | Mg |
| yi | Stand biomass density of ith stand or sample plot, yi = r xik e−ux. | Mg ha−1 |
| z | Intermediate parameter (0~1), the percentage of the samples at the point of xmax to total samples. | - |
| Φ(μ, σ2) | The compensator of scaling-up error. | Mg ha−1 |
| η(μ, σ2) | The compensation rate; η(μ, σ2) = Φ(μ, σ2)/(Y2/A) = Φ(μ, σ2)/(rμke−ux). | - |
| μ (xs) | The expectation of xs, μ (xs) = E(xs), s = 1, 2. | - |
| μ | The expectation of x. It denotes regional stocking volume. μ = ∑wixi = E(x). | m3 ha−1 |
| μg | The expectation of g(x), μg = E[g(x)]. | - |
| νs | sth-order central moment, νs = E[(x − μ)s]= ∑ μ(xj) (−μ)s−j, sigma from j = 0 to s, s = 1, 2. | - |
| σ2 | Variance of random variable x. | m6 ha−2 |
| Forest Age Groups | Sum or Ave. | ||||||
|---|---|---|---|---|---|---|---|
| Unit | Young | Middle | Near-Mature | Mature | Over-Mature | ||
| Total forested area A (data) | 106 ha | 1.051 | 0.955 | 0.480 | 0.341 | 0.096 | 2.92 |
| Total volume V (data) | 106 m3 | 41.18 | 68.62 | 45.62 | 44.56 | 22.45 | 222.4 |
| Area proportion (p) | - | 0.360 | 0.327 | 0.164 | 0.117 | 0.033 | 1.0 |
| Mean stocking volume x and μ | m3 ha−1 | 39.2 | 71.9 | 95.1 | 130.8 | 233.8 | 76.1 |
| p(x − 76.1)2 for calculating * | m6 ha−2 | 490.3 | 5.9 | 59.0 | 348.7 | 817.3 | 1721 |
| Mean biomass Y † | Mg ha−1 | 71.7 | |||||
| Total biomass (71.7 × A) | 106 Mg | 209.5 | |||||
| Corrected Y | Mg ha−1 | 69.1 | |||||
| Removable scaling error ‡ | % | 3.6 | |||||
| Total biomass (69.1 × A) | 106 Mg | 201.8 | |||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, C.; Zhou, X. Removing the Scaling Error Caused by Allometric Modelling in Forest Biomass Estimation at Large Scales. Forests 2019, 10, 602. https://doi.org/10.3390/f10070602
Zhou C, Zhou X. Removing the Scaling Error Caused by Allometric Modelling in Forest Biomass Estimation at Large Scales. Forests. 2019; 10(7):602. https://doi.org/10.3390/f10070602
Chicago/Turabian StyleZhou, Carl, and Xiaolu Zhou. 2019. "Removing the Scaling Error Caused by Allometric Modelling in Forest Biomass Estimation at Large Scales" Forests 10, no. 7: 602. https://doi.org/10.3390/f10070602
APA StyleZhou, C., & Zhou, X. (2019). Removing the Scaling Error Caused by Allometric Modelling in Forest Biomass Estimation at Large Scales. Forests, 10(7), 602. https://doi.org/10.3390/f10070602




