Juniper Tree-Ring Data from the Kuramin Range (Northern Tajikistan) Reveals Changing Summer Drought Signals in Western Central Asia
Abstract
1. Introduction
2. Material and Methods
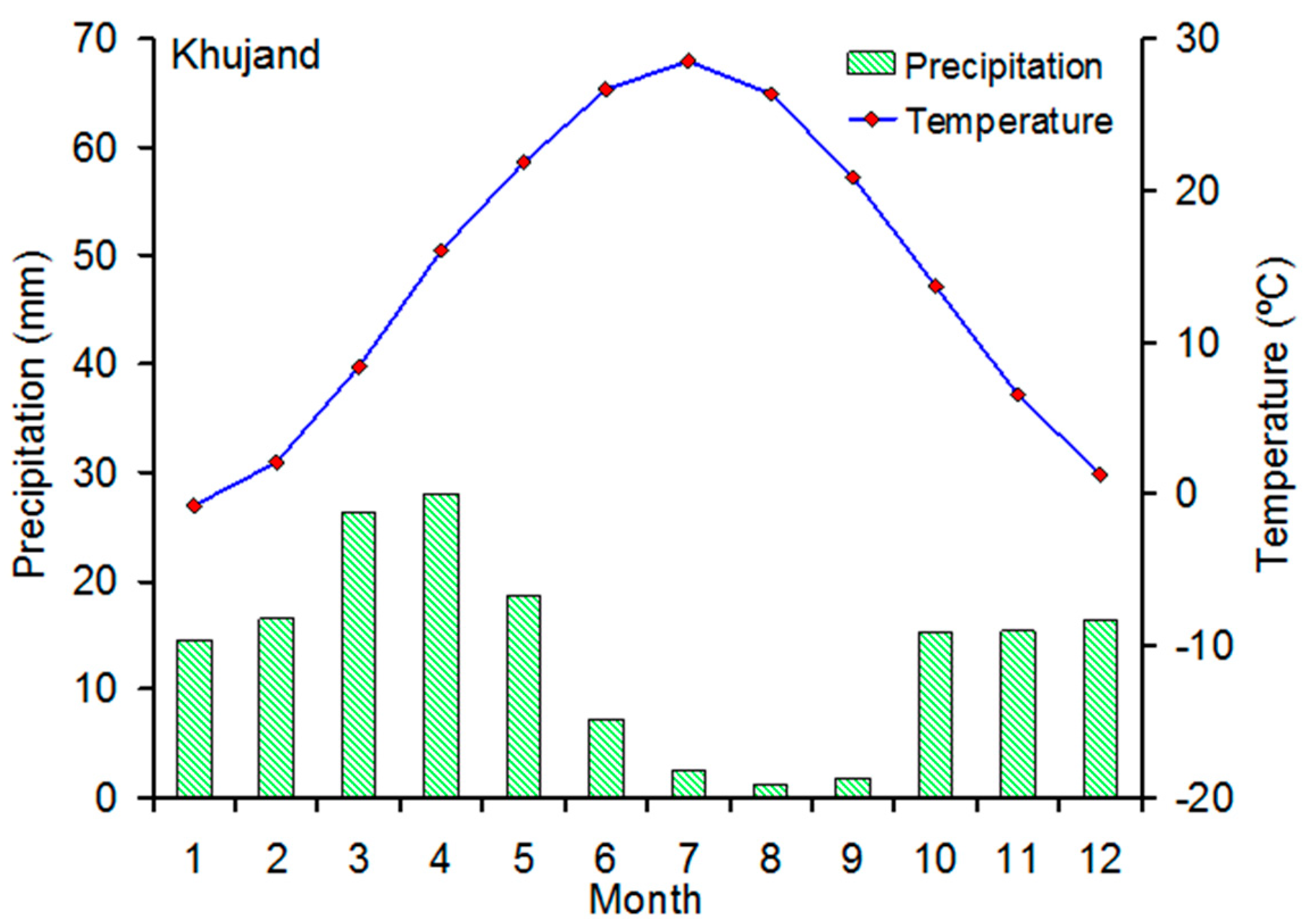
2.1. Geographical Settings and Chronology Development
2.2. Statistical Analysis
3. Results
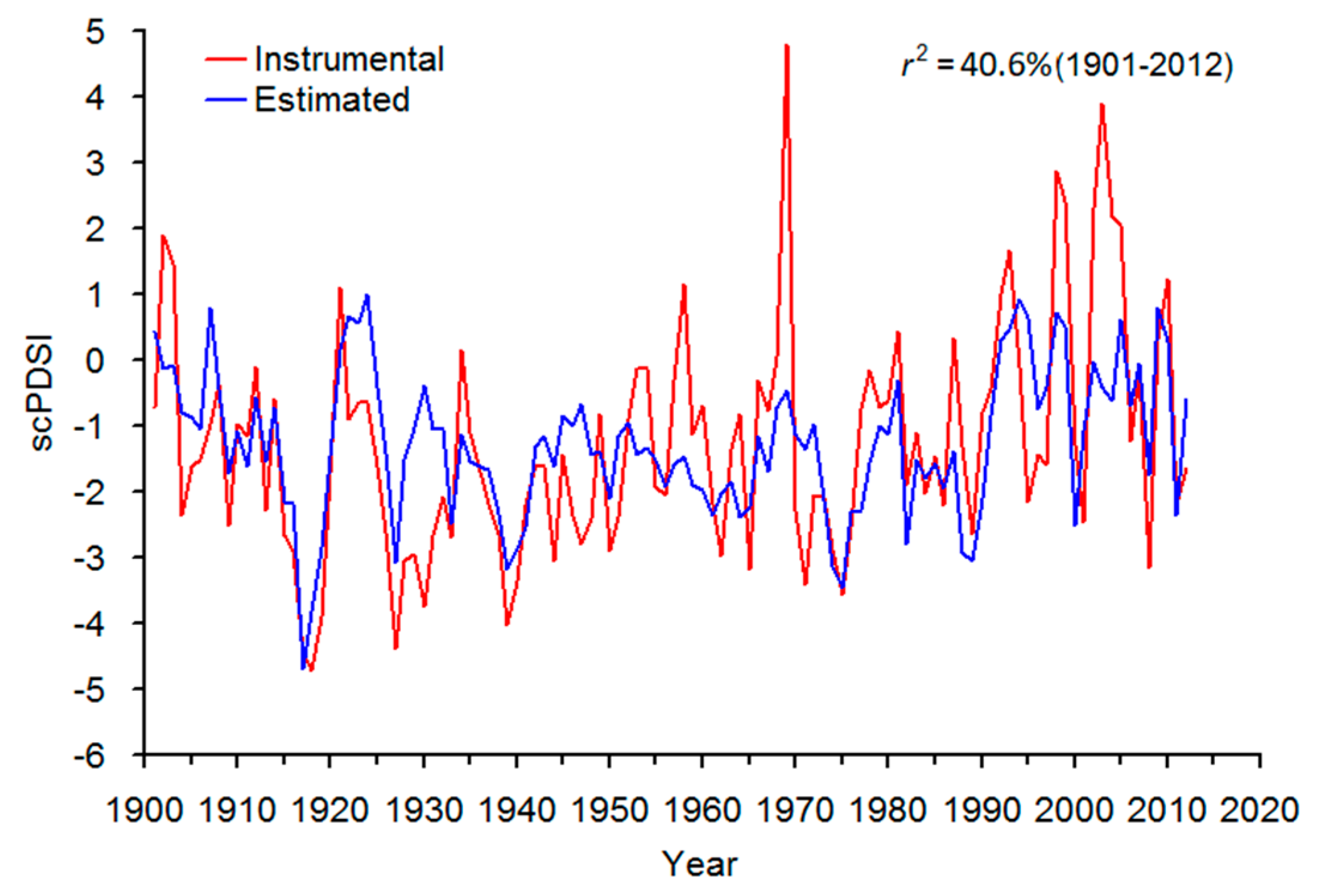
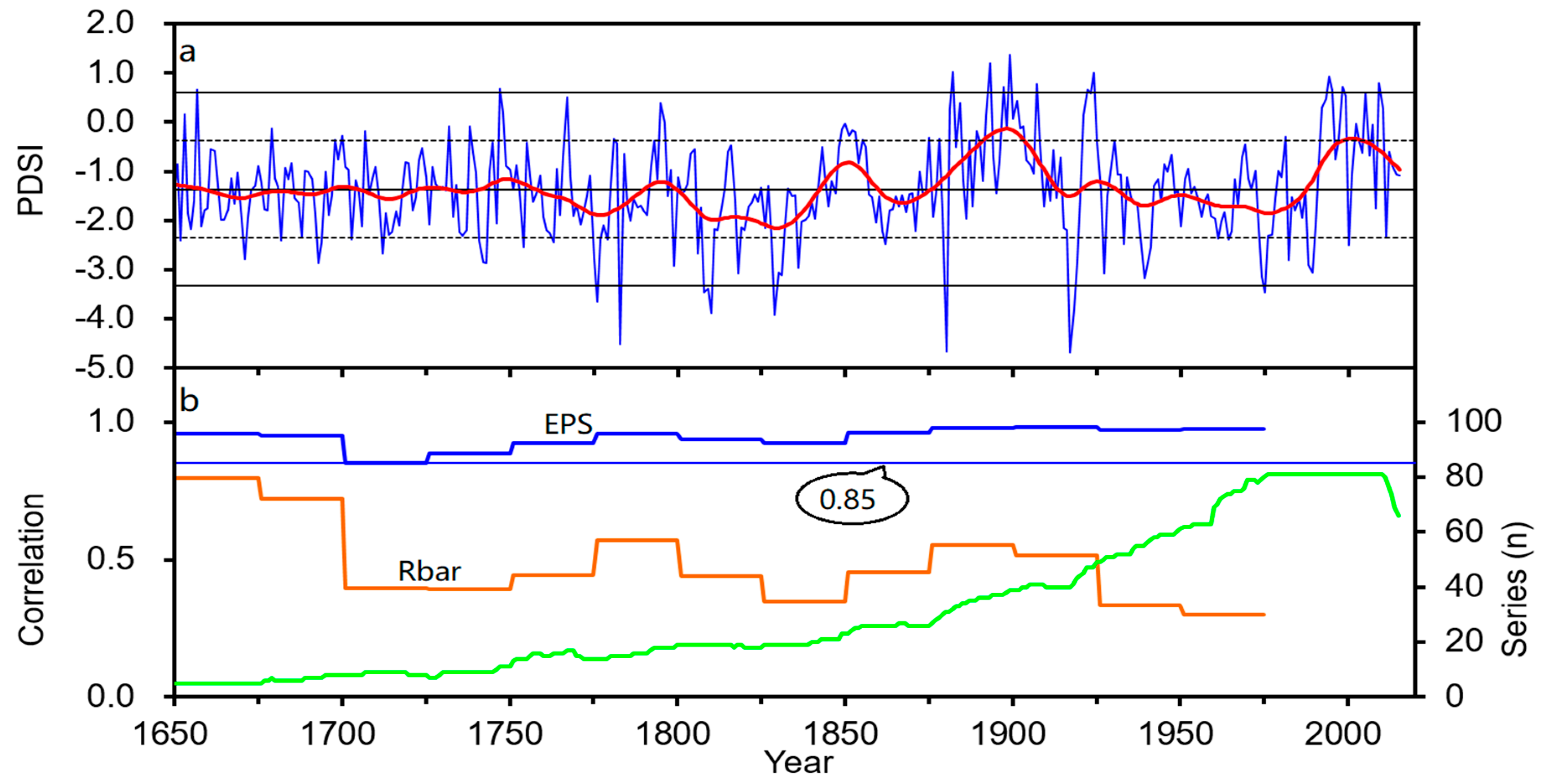
3.1. The scPDSI Reconstruction
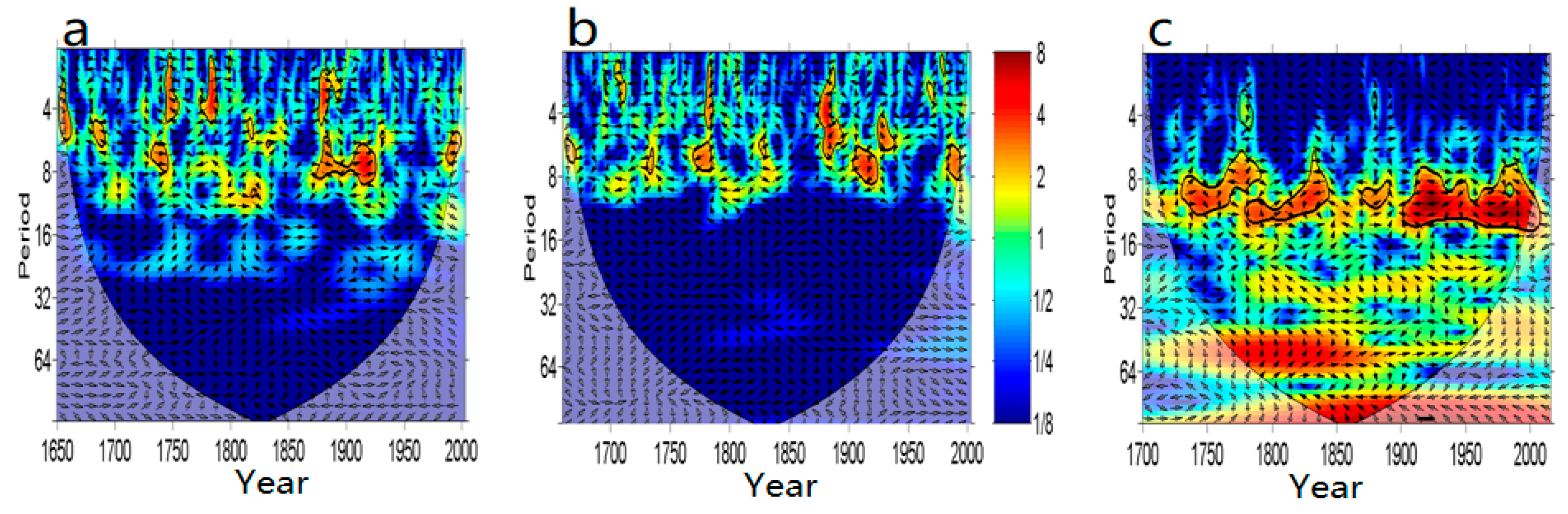
3.2. Analyses of Drought Variation in the Kuramin Range
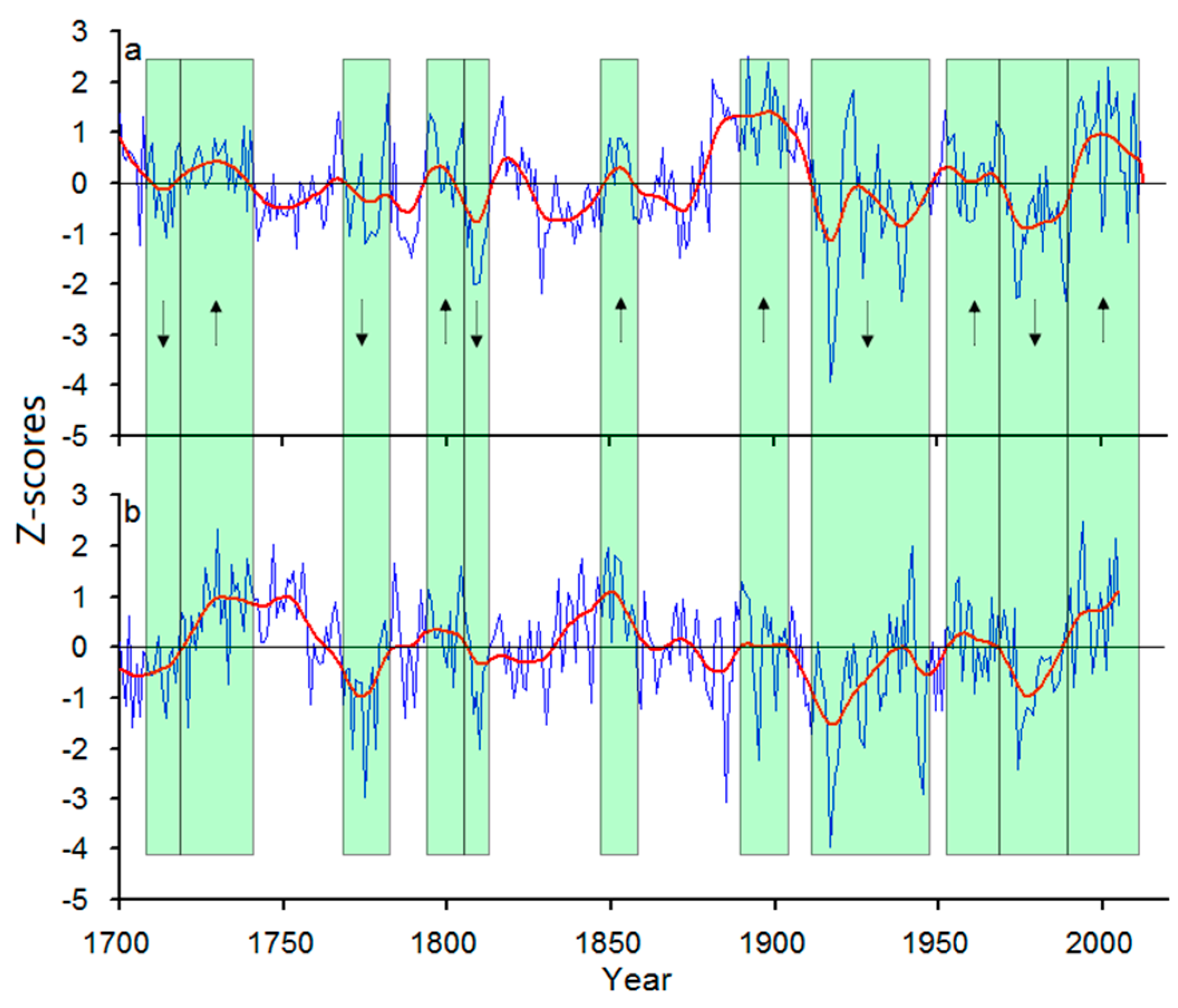
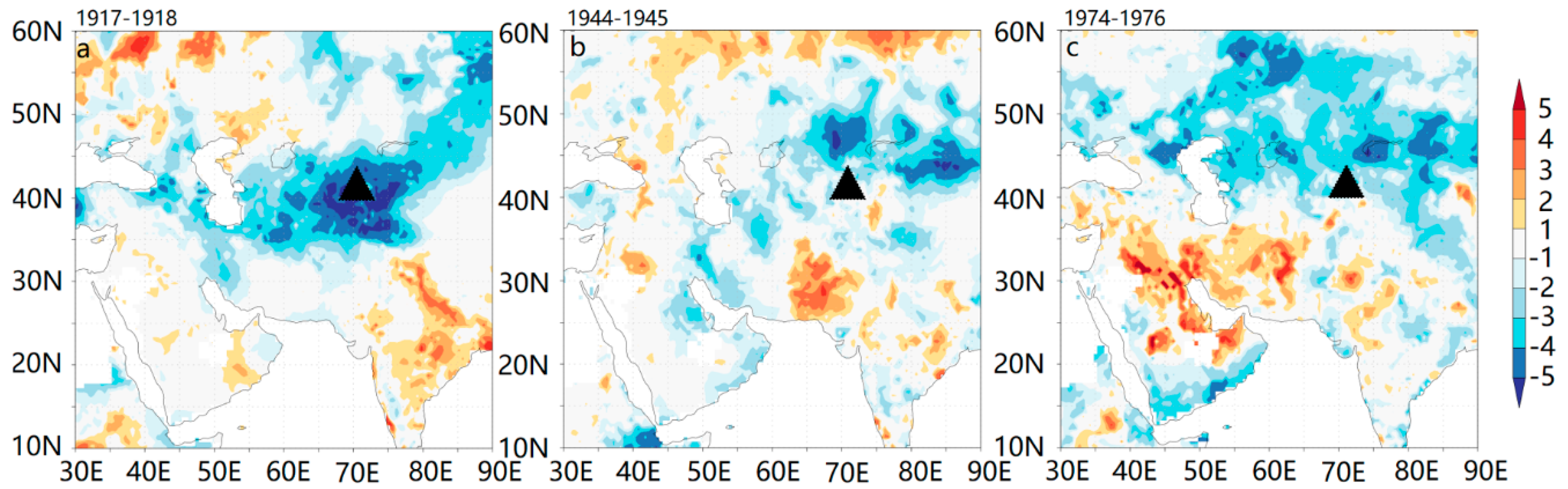
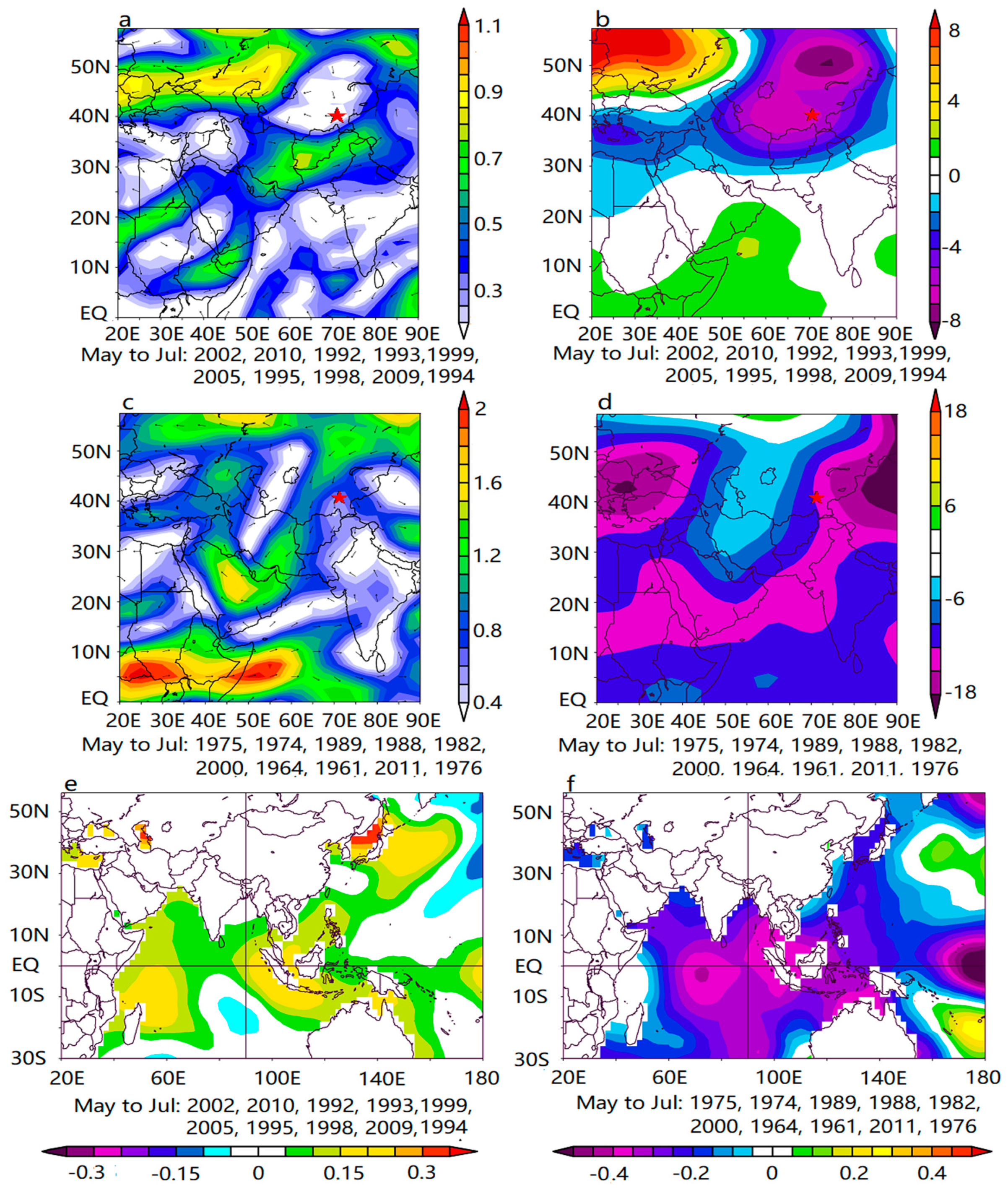
4. Discussion
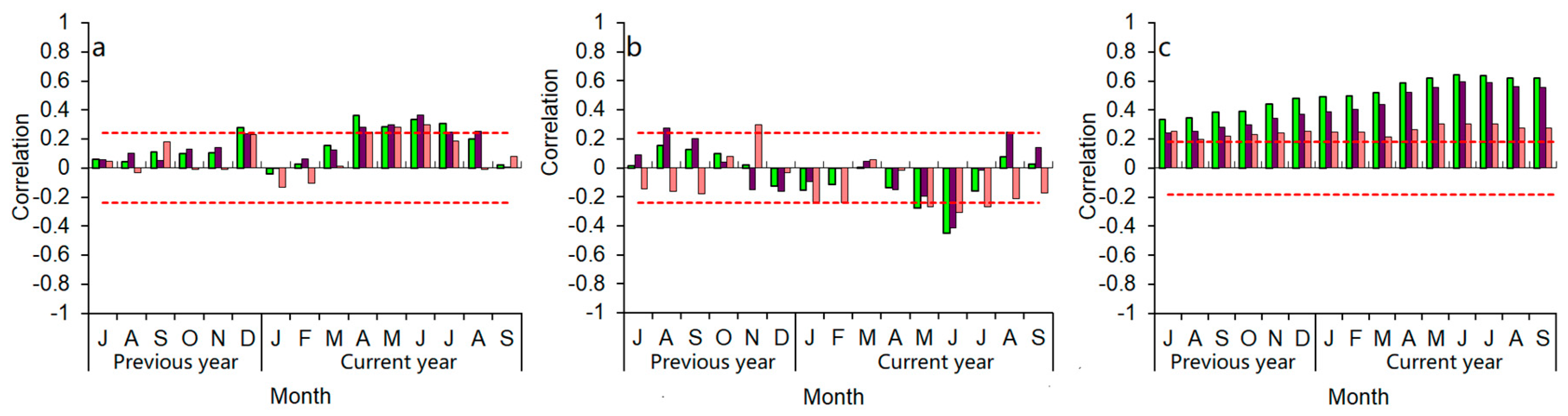
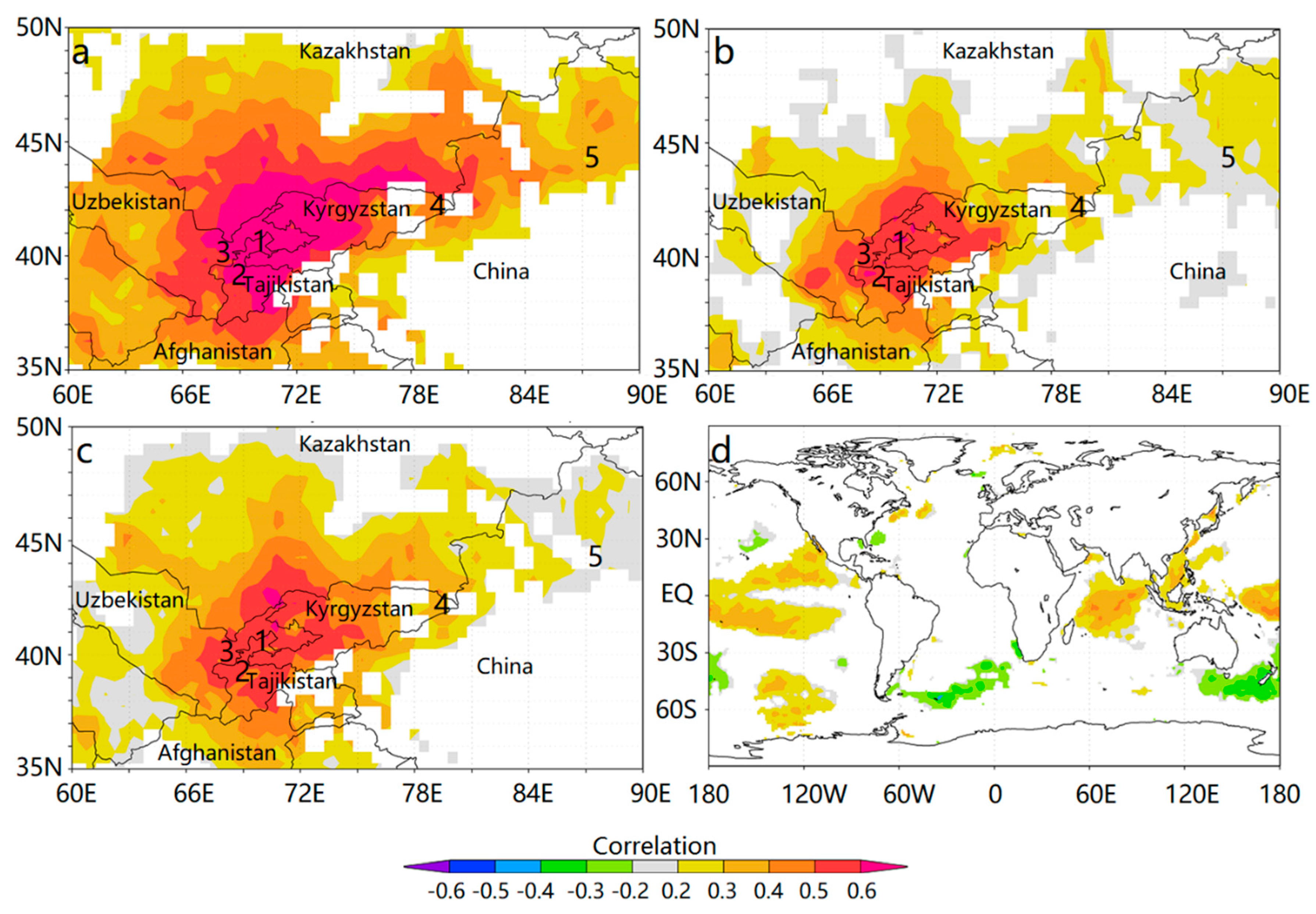
4.1. Climate–Growth Relationships
4.2. Comparing Reconstructed Drought in Central Asia
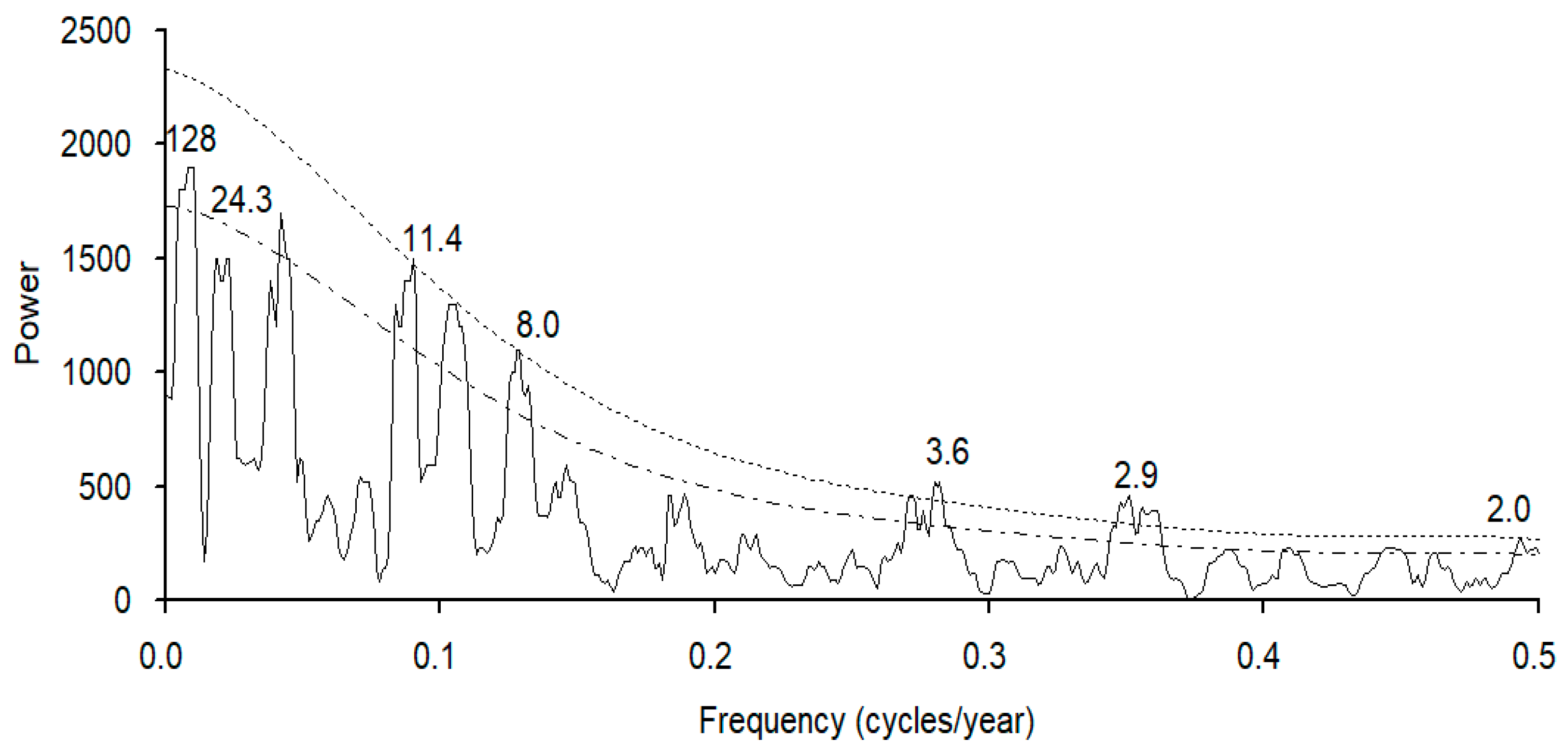
4.3. Possible Climate Drivers
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Easterling, D.R.; Evans, J.; Groisman, P.Y.; Karl, T.; Kunkel, K.E.; Ambenje, P. Observed variability and trends in extreme climate events: a brief review. Bull. Amer. Meteorol. Soc. 2000, 81, 417–425. [Google Scholar] [CrossRef]
- Dai, A. Drought under global warming: A review. Wiley Interdiscip. Rev. Clim. Chang. 2011, 2, 45–65. [Google Scholar] [CrossRef]
- Schrier, G.; Barichivich, J.; Briffa, K.; Jones, P. A scPDSI-based global data set of dry and wet spells for 1901–2009. J. Geophy. Res. Atmos. 2013, 118, 4025–4048. [Google Scholar] [CrossRef]
- Huang, J.; Yu, H.; Guan, X.; Wang, G.; Guo, R. Accelerated dryland expansion under climate change. Nature Clim. Chang. 2015, 6, 166–171. [Google Scholar] [CrossRef]
- Huang, W.; Feng, S.; Liu, C.; Chen, J.; Chen, J.H.; Chen, F.H. Changes of climate regimes during the last millennium and the twenty-first century simulated by the Community Earth System Model. Quat. Sci. Rev. 2018, 180, 42–56. [Google Scholar] [CrossRef]
- Ososkova, T.; Gorelkin, N.; Chub, V. Water resources of central Asia and adaptation measures for climate change. Environ. Monit. Assess. 2000, 61, 161–166. [Google Scholar] [CrossRef]
- Siegfried, T.; Bernauer, T.; Guiennet, R.; Sellars, S.; Robertson, A.W.; Mankin, J.; Bauer-Gottwein, P.; Yakovlev, A. Will climate change exacerbate water stress in Central Asia? Clim. Chang. 2012, 112, 881–899. [Google Scholar] [CrossRef]
- Yao, J.; Chen, Y. Trend analysis of temperature and precipitation in the Syr Darya Basin in Central Asia. Theor. Appl. Climatol. 2015, 120, 521–531. [Google Scholar] [CrossRef]
- Micklin, P.P. Desiccation of the Aral Sea: a water management disaster in the Soviet Union. Science 1988, 241, 1170–1176. [Google Scholar] [CrossRef]
- Lioubimtseva, E.; Cole, R. Uncertainties of climate change in arid environments of Central Asia. Rev. Fish. Sci. 2006, 14, 29–49. [Google Scholar] [CrossRef]
- Reyer, C.P.; Otto, I.M.; Adams, S.; Albrecht, T.; Baarsch, F.; Cartsburg, M.; Coumou, D.; Eden, A.; Ludi, E.; Marcus, R. Climate change impacts in Central Asia and their implications for development. Reg. Environ. Chang. 2015, 17, 1639–1650. [Google Scholar] [CrossRef]
- Jones, P.; Briffa, K.; Osborn, T.; Lough, J.; van Ommen, T.; Vinther, B.; Luterbacher, J.; Wahl, E.; Zwiers, F.; Mann, M. High-resolution palaeoclimatology of the last millennium: a review of current status and future prospects. Holocene 2009, 19, 3–49. [Google Scholar] [CrossRef]
- Esper, J.; Treydte, K.; Gärtner, H.; Neuwirth, B. A tree ring reconstruction of climatic extreme years since 1427 AD for Western Central Asia. Palaeobotanist 2001, 50, 141–152. [Google Scholar]
- Esper, J.; Schweingruber, F.H.; Winiger, M. 1300 years of climatic history for Western Central Asia inferred from tree-rings. Holocene 2002, 12, 267–277. [Google Scholar] [CrossRef]
- Esper, J.; Shiyatov, S.; Mazepa, V.; Wilson, R.; Graybill, D.; Funkhouser, G. Temperature-sensitive Tien Shan tree ring chronologies show multi-centennial growth trends. Clim. Dyn. 2003, 21, 699–706. [Google Scholar]
- Yuan, Y.; Jin, L.; Shao, X.; He, Q.; Li, Z.; Li, J. Variations of the spring precipitation day numbers reconstructed from tree rings in the Urumqi River drainage, Tianshan Mts. over the last 370 years. Chin. Sci. Bull. 2003, 48, 1507–1510. [Google Scholar] [CrossRef]
- Chen, F.; Yuan, Y.; Wei, W.; Yu, S.; Li, Y.; Zhang, R.; Zhang, T.; Shang, H. Chronology development and climate response analysis of Schrenk spruce (Picea Schrenkiana) tree-ring parameters in the Urumqi river basin, China. Geochronometria 2010, 36, 17–22. [Google Scholar] [CrossRef]
- Chen, F.; Yuan, Y.J.; Wei, W.S.; Zhang, T.W.; Shang, H.M.; Zhang, R. Precipitation reconstruction for the southern Altay Mountains (China) from tree rings of Siberian spruce, reveals recent wetting trend. Dendrochronologia 2014, 32, 266–272. [Google Scholar] [CrossRef]
- Zhang, T.W.; Yuan, Y.J.; Liu, Y.; Wei, W.S.; Yu, S.L.; Chen, F.; Fan, Z.A.; Shang, H.M.; Zhang, R.B.; Qin, L. A tree-ring based precipitation reconstruction for the Baluntai region on the southern slope of the central Tien Shan Mountains, China, since AD 1464. Quat. Int. 2013, 283, 55–62. [Google Scholar] [CrossRef]
- Solomina, O.; Maximova, O.; Cook, E. Picea schrenkiana ring width and density at the upper and lower tree limits in the Tien Shan mts Kyrgyz republic as a source of paleoclimatic information. Geogr. Environ. Sustain. 2014, 1, 66–79. [Google Scholar] [CrossRef]
- Opała-Owczarek, M.; Niedźwiedź, T. Last 1100 yr of precipitation variability in western central Asia as revealed by tree-ring data from the Pamir-Alay. Quat. Res. 2019, 91, 81–95. [Google Scholar] [CrossRef]
- Fritts, H.C. Tree-Rings and Climate; Academic Press: London, UK, 1976. [Google Scholar]
- Tian, Q.; Gou, X.; Zhang, Y.; Peng, J.; Wang, J.; Chen, T. Tree-ring based drought reconstruction (AD 1855–2001) for the Qilian Mountains, northwestern China. Tree-ring Res. 2007, 63, 27–36. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A multiscalar drought index sensitive to global warming: the standardized precipitation evapotranspiration index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Palmer, W.C. Meteorological Drought; US Department of Commerce, Weather Bureau: Washington, DC, USA, 1965.
- Cook, E.R.; Meko, D.M.; Stahle, D.W.; Cleaveland, M.K. Drought reconstructions for the continental United States. J. Clim. 1999, 12, 1145–1162. [Google Scholar] [CrossRef]
- Cook, E.R.; Seager, R.; Kushnir, Y.; Briffa, K.R.; Büntgen, U.; Frank, D.; Krusic, P.J.; Tegel, W.; van der Schrier, G.; Andreu-Hayles, L.; et al. Old World megadroughts and pluvials during the Common Era. Sci. Adv. 2015, 1, e1500561. [Google Scholar] [CrossRef] [PubMed]
- Davi, N.; Jacoby, G.; Fang, K.; Li, J.; D’Arrigo, R.; Baatarbileg, N.; Robinson, D. Reconstructed drought across Mongolia based on a large-scale tree-ring network: 1520–1993. J. Geophys. Res. 2010, 115, D22103. [Google Scholar] [CrossRef]
- Fang, K.; Davi, N.; Gou, X.; Chen, F.; Cook, E.; Li, J.; D’Arrigo, R. Spatial drought reconstructions for central High Asia based on tree rings. Clim. Dyn. 2010, 35, 941–951. [Google Scholar] [CrossRef]
- Seftigen, K.; Björklund, J.; Cook, E.R.; Linderholm, H.W. A tree-ring field reconstruction of Fennoscandian summer hydroclimate variability for the last millennium. Clim. Dyn. 2015, 44, 3141–3154. [Google Scholar] [CrossRef]
- Touchan, R.; Anchukaitis, K.J.; Meko, D.M.; Sabir, M.; Attalah, S.; Aloui, A. Spatiotemporal drought variability in northwestern Africa over the last nine centuries. Clim. Dyn. 2011, 37, 237–252. [Google Scholar] [CrossRef]
- Chen, F.; Yuan, Y.J.; Chen, F.H.; Wei, W.S.; Yu, S.L.; Chen, X.J.; Fan, Z.A.; Zhang, R.B.; Zhang, T.W.; Shang, H.M. A 426-year drought history for Western Tian Shan, Central Asia, inferred from tree rings and linkages to the North Atlantic and Indo-Pacific Oceans. Holocene 2013, 23, 1095–1104. [Google Scholar] [CrossRef]
- Chen, F.; Yuan, Y.J.; Yu, S.L.; Zhang, T.W.; Shang, H.M.; Zhang, R.B.; Qin, L.; Fan, Z.A. A 225-year long drought reconstruction for east Xinjiang based on Siberia larch (Larix sibirica) tree-ring widths: Reveals the recent dry trend of the eastern end of Tien Shan. Quat. Int. 2015, 358, 42–47. [Google Scholar] [CrossRef]
- Chen, F.; Yuan, Y.J.; Wei, W.S.; Yu, S.L.; Zhang, T.W.; Shang, H.M.; Zhang, R.B.; Qin, L.; Fan, Z.A. Tree-ring recorded hydroclimatic change in Tienshan mountains during the past 500 years. Quat. Int. 2015, 358, 35–41. [Google Scholar] [CrossRef]
- Chen, F.; Yu, S.L.; He, Q.; Zhang, R.B.; Kobuliev, Z.V.; Mamadjonov, Y.M. Comparison of drought signals in tree-ring width records of juniper trees from Central and West Asia during the last four centuries. Arab. J. Geosci. 2016, 9, 255. [Google Scholar] [CrossRef]
- Seim, A.; Tulyaganov, T.; Omurova, G.; Nikolyai, L.; Botman, E.; Linderholm, H.W. Dendroclimatological potential of three juniper species from the Turkestan range, northwestern Pamir-Alay Mountains, Uzbekistan. Trees 2016, 30, 733–748. [Google Scholar] [CrossRef]
- Seim, A.; Omurova, G.; Azisov, E.; Musuraliev, K.; Aliev, K.; Tulyaganov, T.; Nikolyai, L.; Botman, E.; Helle, G.; Dorado Liñan, I.; et al. Climate change increases drought sensitivity of mountain juniper trees in Central Asia. PloS ONE 2016, 11, e0153888. [Google Scholar] [CrossRef]
- Holmes, R.L. Computer-assisted quality control in tree-ring dating and measurement. Tree-Ring Bull. 1983, 43, 69–95. [Google Scholar]
- Cook, E.R.; Kairiukstis, L.A. Methods of Dendrochronology: Applications in the Environmental Sciences; Kluwer Academic Publishers: Boston, MA, USA, 1990. [Google Scholar]
- Wigley, T.; Briffa, K.R.; Jones, P.D. On the average value of correlated time series, with applications in dendroclimatology and hydrometeorology. J. Appl. Meteorol. Climatol. 1984, 23, 201–213. [Google Scholar] [CrossRef]
- Jolliffe, I. Principal component analysis; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Torrence, C.; Compo, G.P. A practical guide to wavelet analysis. Bull. Amer. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Mann, M.E.; Lees, J.M. Robust estimation of background noise and signal detection in climatic time series. Clim. Chang. 1996, 33, 409–445. [Google Scholar] [CrossRef]
- Rayner, N.; Parker, D.E.; Horton, E.; Folland, C.; Alexander, L.; Rowell, D.; Kent, E.; Kaplan, A. Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century. J. Geophy. Res. Atmos. 2003, 108, D14. [Google Scholar] [CrossRef]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J. The NCEP/NCAR 40-year reanalysis project. Bull. Amer. Meteorol. Soc. 1996, 77, 437–471. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, Q.B.; Ma, K.; Xiao, S. A tree-ring record of 500-year dry-wet changes in northern Tibet. China. Holocene 2008, 18, 579–588. [Google Scholar] [CrossRef]
- Gou, X.; Gao, L.; Deng, Y.; Chen, F.; Yang, M.; Still, C. An 850-year tree-ring-based reconstruction of drought history in the western Qilian Mountains of northwestern China. Int. J. Climatol. 2015, 35, 3308–3319. [Google Scholar] [CrossRef]
- Zhang, Q.-B.; Evans, M.N.; Lyu, L. Moisture dipole over the Tibetan Plateau during the past five and a half centuries. Nat. Commun. 2015, 6, 8062. [Google Scholar] [CrossRef]
- Anfodillo, T.; Carrer, M.; Rento, S.; Urbinati, C. Long and short term growth dynamics of Picea abies (L.) Karst, Larix decidua Mill., Pinus cembra (L.) and climatic factors: First results of an integrated study at the timberline in eastern Italian Alps. Ecology 1998, 29, 253–259. [Google Scholar]
- Gou, X.; Zhou, F.; Zhang, Y.; Chen, Q.; Zhang, J. Forward modeling analysis of regional scale tree-ring patterns around the northeastern tibetan plateau, northwest China. Biogeosci. Discuss. 2013, 10, 9969–9988. [Google Scholar] [CrossRef]
- Adams, H.D.; Guardiolaclaramonte, M.; Barrongafford, G.A.; Villegas, J.C.; Breshears, D.D.; Zou, C.B.; Troch, P.A.; Huxman, T.E. Temperature sensitivity of drought-induced tree mortality portends increased regional die-off under global-change-type drought. Proc. Natl. Acad. Sci. USA 2009, 106, 7063–7066. [Google Scholar] [CrossRef] [PubMed]
- Williams, A.P.; Allen, C.D.; Macalady, A.K.; Griffin, D.; Woodhouse, C.A.; Meko, D.M.; Swetnam, T.W.; Rauscher, S.A.; Seager, R.; Grissino-Mayer, H.D. Temperature as a potent driver of regional forest drought stress and tree mortality. Nature Clim. Chang. 2013, 3, 292–297. [Google Scholar] [CrossRef]
- Li, J.; Cook, E.; Chen, F.; Gou, X.; D’Arrigo, R.; Yuan, Y. An extreme drought event in the central Tien Shan area in the year 1945. J. Arid Environ. 2010, 74, 1225–1231. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, M.; Huang, A.; Li, H.; Huo, W.; Yang, Q. Relationships between the West Asian subtropical westerly jet and summer precipitation in northern Xinjiang. Theor. Appl. Climatol. 2014, 116, 403–411. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, T.; Krinner, G.; Wang, X.; Gasser, T.; Peng, S.; Piao, S.L.; Yao, T. The weakening relationship between Eurasian spring snow cover and Indian summer monsoon rainfall. Sci. Adv. 2019, 5, eaau8932. [Google Scholar] [CrossRef] [PubMed]
- Vecchi, G.A.; Xie, S.P.; Fischer, A. Ocean-atmosphere covariability in the western Arabian Sea. J. Clim. 2004, 17, 1213–1224. [Google Scholar] [CrossRef]
- Li, J.; Xie, S.P.; Cook, E.R.; Morales, M.S.; Christie, D.A.; Johnson, N.C.; Chen, F.H.; D’Arrigo, R.; Fowler, A.M.; Gou, X. El Niño modulations over the past seven centuries. Nature Clim. Chang. 2013, 3, 822–826. [Google Scholar] [CrossRef]
- Gong, D.Y.; Luterbacher, J. Variability of the low-level cross-equatorial jet of the western Indian Ocean since 1660 as derived from coral proxies. Geophys. Res. Lett. 2008, 35, L01705. [Google Scholar] [CrossRef]
- Mariotti, A. How ENSO impacts precipitation in southwest central Asia. Geophy. Res. Lett. 2007, 34, 16. [Google Scholar] [CrossRef]
- Barlow, M.; Cullen, H.; Lyon, B. Drought in central and southwest Asia: La Niña, the Warm Pool, and Indian Ocean precipitation. J. Clim. 2002, 15, 697–700. [Google Scholar] [CrossRef]
- Hale, G.E. The law of sun-spot polarity. Proc. Natl. Acad. Sci. USA 1924, 10, 53. [Google Scholar] [CrossRef]
- Hodell, D.A.; Brenner, M.; Curtis, J.H.; Guilderson, T. Solar forcing of drought frequency in the Maya lowlands. Science 2001, 292, 1367–1370. [Google Scholar] [CrossRef]
- Li, J.; Gou, X.; Cook, E.R.; Chen, F. Tree-ring based drought reconstruction for the central Tien Shan area in northwest China. Geophy. Res. Lett. 2006, 33, L07715. [Google Scholar] [CrossRef]
- Beer, J.; Mende, W.; Stellmacher, R. The role of the sun in climate forcing. Quat. Sci. Rev. 2000, 19, 403–415. [Google Scholar] [CrossRef]
- Reid, G.C. Influence of solar variability on global sea surface temperatures. Nature 1987, 329, 142–143. [Google Scholar] [CrossRef]
- Friis-Christensen, E.; Lassen, K. Length of the solar cycle: an indicator of solar activity closely associated with climate. Science 1991, 254, 698–700. [Google Scholar] [CrossRef] [PubMed]
- Mitchell, J.M.; Stockton, C.W.; Meko, D.M. Evidence of a 22-year rhythm of drought in the western United States related to the Hale solar cycle since the 17th century. In Solar-Terrestrial Influences on Weather and Climate; Springer: Berlin/Heidelberg, Germany, 1979; pp. 125–143. [Google Scholar]
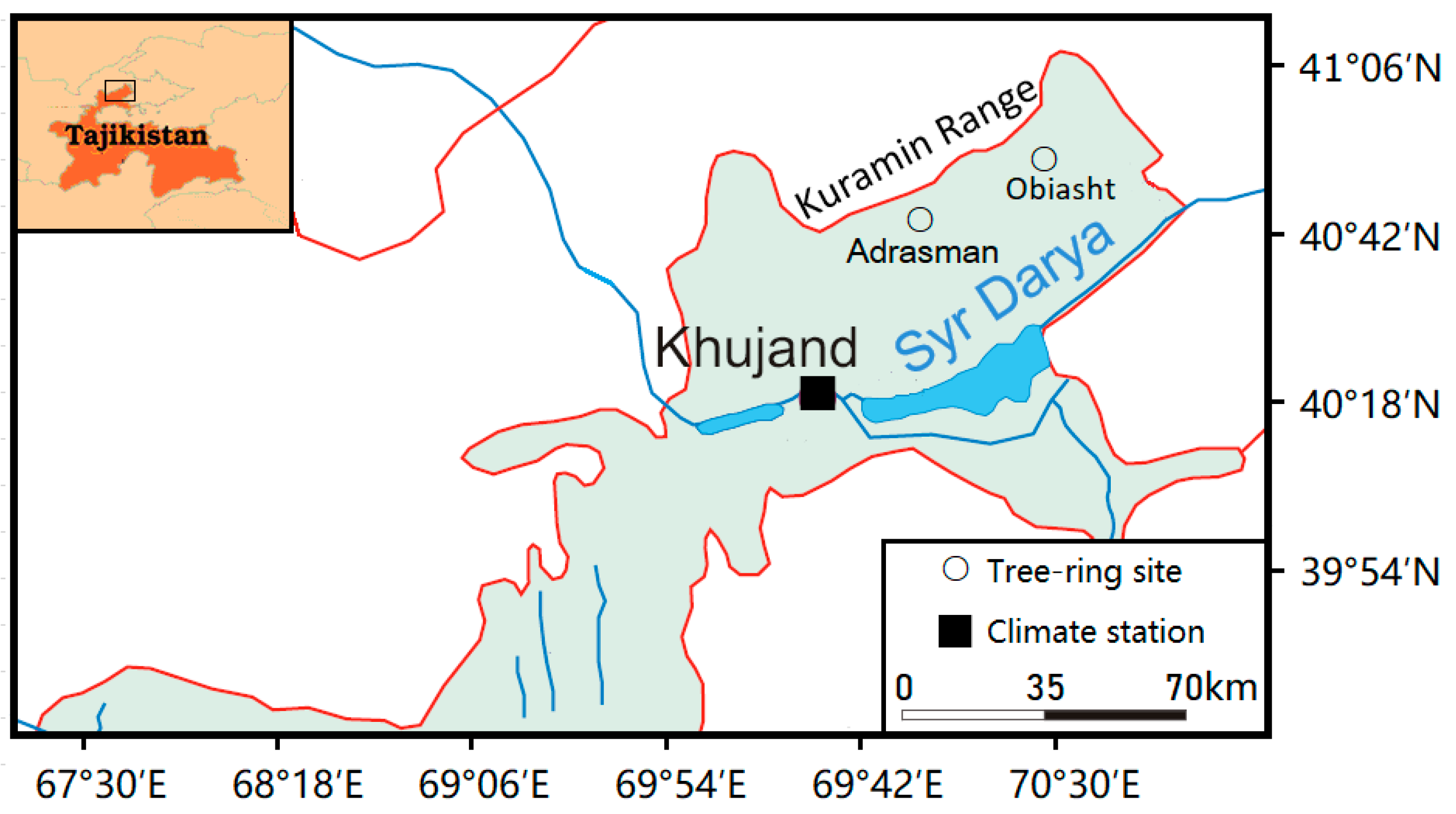

| Site Code | Latitude (N) | Longitude (E) | Tree Number | Elevation (m) | Aspect | Slope | Species |
|---|---|---|---|---|---|---|---|
| Obiasht | 40°52’ | 70°27’ | 24 | 1663 | E | 30° | Zeravshan juniper (Juniperus seravschanica) |
| Adrasman | 40°42’ | 70°04’ | 27 | 2035 | SE | 20° | Zeravshan juniper (Juniperus seravschanica) |
| Correlation | Chronology Code | Obiasht | Adrasman | Regional Chronology |
|---|---|---|---|---|
| Chronology | Obiasht | 1.00 | ||
| correlations | Adrasman | 0.52 | 1.00 | |
| Regional Chronology | 0.63 | 0.95 | 1.00 | |
| Mean tree to tree correlation | 0.56 | 0.49 | 0.41 | |
| Statistics | Calibration (1957–2012) | Verification (1901–1956) | Calibration (1901–1956) | Verification (1957–2012) | Full Calibration (1901–2012) |
|---|---|---|---|---|---|
| r | 0.705 | 0.637 | 0.637 | 0.705 | 0.637 |
| r2 | 0.497 | 0.406 | 0.406 | 0.497 | 0.406 |
| RE | 0.351 | 0.360 | |||
| CE | 0.282 | 0.329 | |||
| Sign test | 41+/15−* | 41+/15−* | |||
| First-order sign test | 45+/10−* | 46+/9−* |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, F.; Zhang, T.; Seim, A.; Yu, S.; Zhang, R.; Linderholm, H.W.; Kobuliev, Z.V.; Ahmadov, A.; Kodirov, A. Juniper Tree-Ring Data from the Kuramin Range (Northern Tajikistan) Reveals Changing Summer Drought Signals in Western Central Asia. Forests 2019, 10, 505. https://doi.org/10.3390/f10060505
Chen F, Zhang T, Seim A, Yu S, Zhang R, Linderholm HW, Kobuliev ZV, Ahmadov A, Kodirov A. Juniper Tree-Ring Data from the Kuramin Range (Northern Tajikistan) Reveals Changing Summer Drought Signals in Western Central Asia. Forests. 2019; 10(6):505. https://doi.org/10.3390/f10060505
Chicago/Turabian StyleChen, Feng, Tongwen Zhang, Andrea Seim, Shulong Yu, Ruibo Zhang, Hans W. Linderholm, Zainalobudin V. Kobuliev, Ahsan Ahmadov, and Anvar Kodirov. 2019. "Juniper Tree-Ring Data from the Kuramin Range (Northern Tajikistan) Reveals Changing Summer Drought Signals in Western Central Asia" Forests 10, no. 6: 505. https://doi.org/10.3390/f10060505
APA StyleChen, F., Zhang, T., Seim, A., Yu, S., Zhang, R., Linderholm, H. W., Kobuliev, Z. V., Ahmadov, A., & Kodirov, A. (2019). Juniper Tree-Ring Data from the Kuramin Range (Northern Tajikistan) Reveals Changing Summer Drought Signals in Western Central Asia. Forests, 10(6), 505. https://doi.org/10.3390/f10060505






