Coarse Woody Debris Management with Ambiguous Chance Constrained Robust Optimization
Abstract
1. Introduction
1.1. Deadwood
1.2. Aspects to Consider for Deadwood Management Decision Making
2. Materials and Methods
2.1. Deadwood
2.2. Dealing with Uncertainties
- Stochastic optimization: For this purpose, the essential requirement is a randomly distributed uncertainty. Then the uncertainty can be defined in a probabilistic way and described using distribution functions. Typically, the main focus of these models is the expected value of the objective. However, there are also expansions like chance constrained programming, which deal with questions on the actual form of the solution space.
- Robust optimization: In contrast to the stochastic approach any assumptions on the distribution of uncertainty are disclaimed. Only the borders of the uncertainty region are defined. The focus lies on finding solutions that cope with all possible values of the uncertain data in an optimal way. The main interest is not on the expected value of the objective but on the feasibility of a solution that incorporates most of the possible values of the uncertain parameters [47]. Consequently, the solution is also feasible for the edge of the uncertainty space [48]. The objective is typically expressed as a min-max- or (,)-condition.
2.3. Data Demanding Stochastic Model
2.3.1. Data Uncertainty
2.3.2. Expected Return Uncertainty
2.4. Robust Model for Situations without Information about the Probability Distribution of the Uncertainty
- : The constraint can be reformulated as with . Then, we transform the “greater than” constraint of the robust problem of Equation (14) into a “less than” constraint to be able to linearise it in the end:Now the uncertain a can be expressed as using the nominal value and the uncertainty d. Therefore, the constraint of Equation (17) can be reformulated:As the box constraint must hold for all d, it holds also for the worst-case:Therefore, the constraint of Equation (19) can be replaced with a worst-case guess:Reduced to a 1-norm maximization problem, the constraint of Equation (16) can finally be reformulated as a linear program, setting or :
- : The constraint is approximated by a cone (or ellipsoid, ball), using the Euclidean norm. This is the most effective way to count for uncertainties as the “ball shape” of the uncertainty region emphasizes the more likely values of the uncertain data by cutting off the unlikely “corners”. Using the definition of d from above, the constraint can be reformulated as . As the ball constraint must hold for all d, it holds also for the worst-case, so the term in the constraint of Equation (18) can be reformulated (Cauchy-Schwarz inequality):So, the constraint of Equation (18) can be written as:Therefore, the optimization problem of the constraint of Equation (16) results in a conic quadratic program (SOCP):
2.5. Model Implementation
2.6. Model Application
3. Results
3.1. Analysing the Two Forest Enterprises Shows the General Tendencies
- All scenarios
- (a)
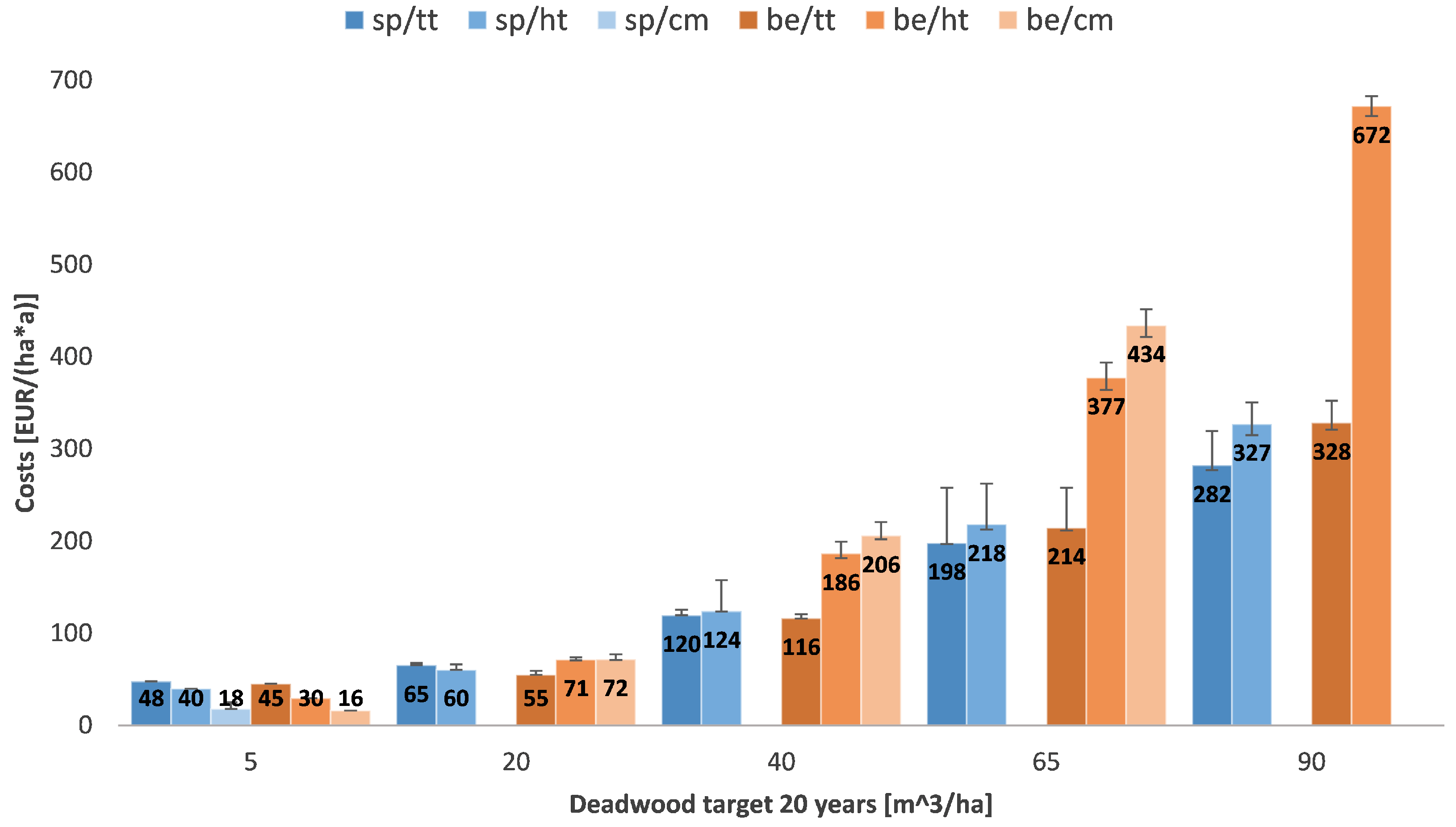
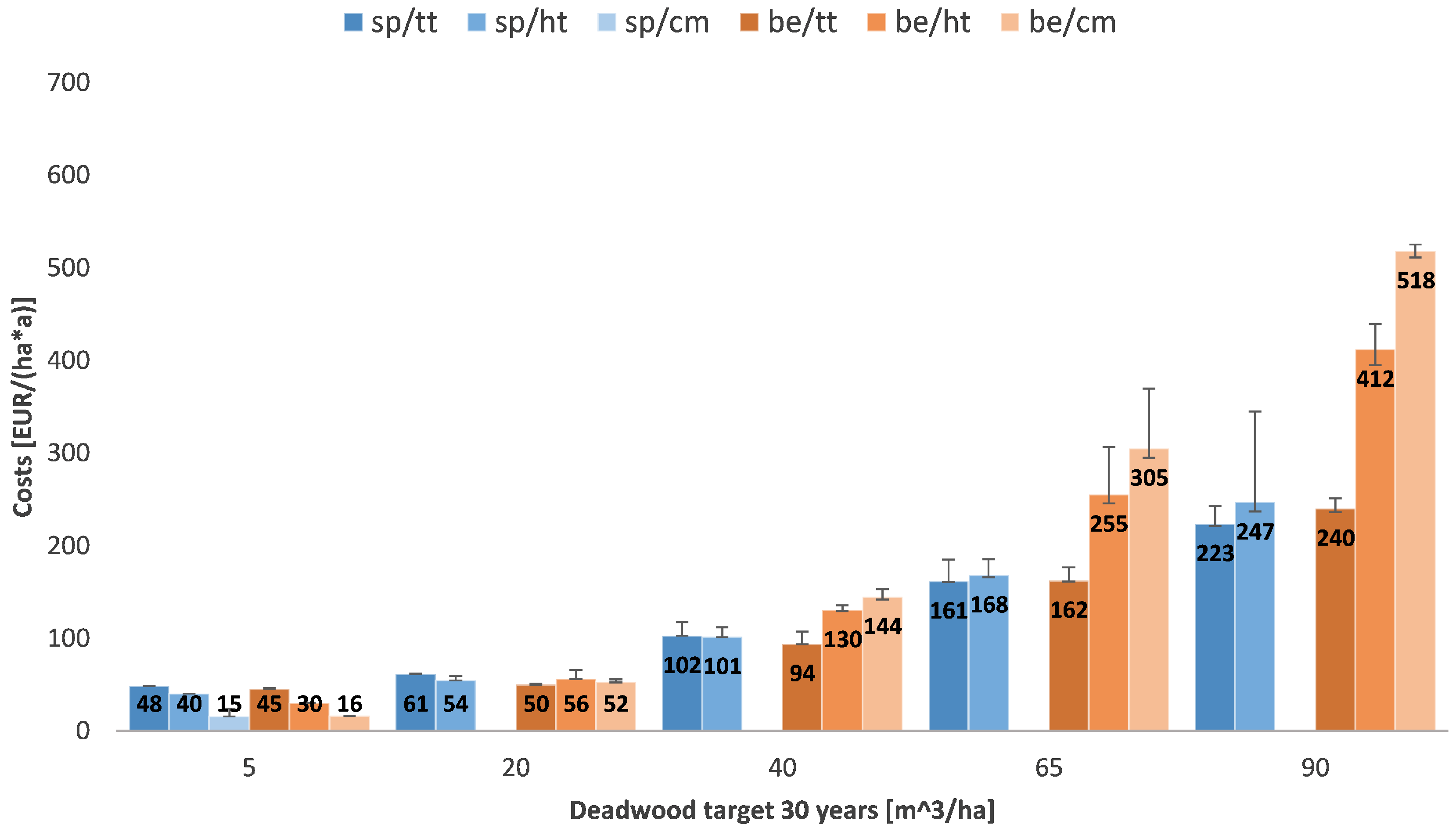
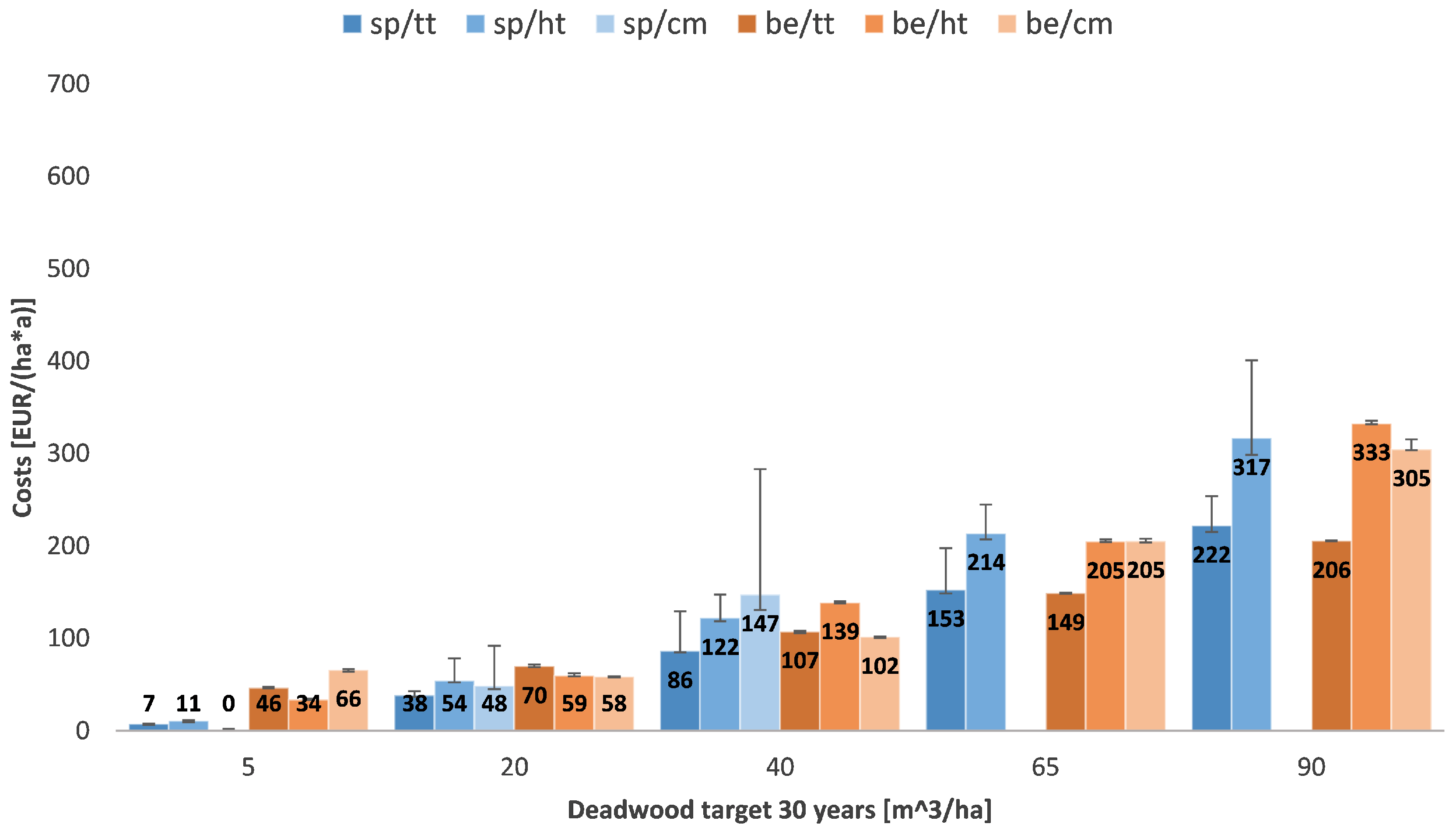
- The higher the desired deadwood amount is set, the higher are the linked costs.
- (b)
- The longer the time horizon to reach the desired deadwood amount is chosen, the more cost-effective the target that can be reached.
- (c)
- The actual costs depend on the stand structure of the forest enterprise.
- (d)
- There is no clear ranking between the spruce and the beech scenarios.
- (e)
- A segregative approach leads to lower costs than the integrative patterns.
- Spruce scenarios
- (a)
- Starting from deadwood amounts of 20 and more, the crown material option is more expensive than the heavy timber strategy. The total tree approach is the most cost-effective. For low deadwood targets (5 ) the crown material option is the cheapest.
- (b)
- Within a larger forest enterprise more deadwood objectives can be reached with crown material.
- Beech scenarios
- (a)
- In most scenarios the total tree strategy has the biggest cost advantage.
- (b)
- From deadwood amounts of 40 and more, the heavy timber strategy is more cost-intensive than the use of total trees. (In the case of “Eichelberg” this is already true for a deadwood target of 20 .)
- (c)
- The ranking between the crown material and the heavy timber strategy depends on the enterprise.
3.2. Comparison of the Robust Model with the Stochastic Approach Reveals Its Stability
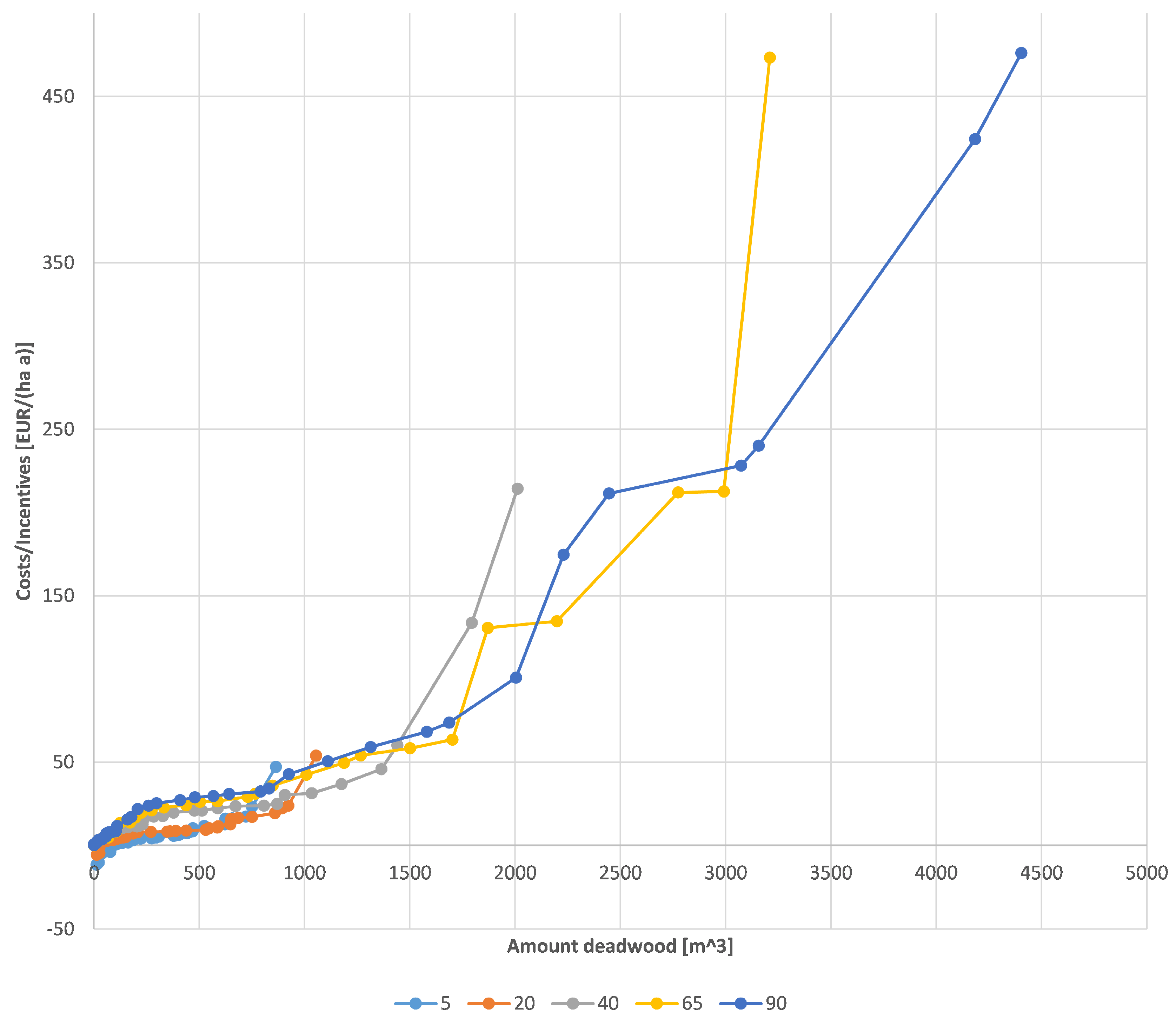
3.3. Analysis of Deadwood Supply Derives Effective Strategy Combinations
4. Discussion
4.1. Robust and Stochastic Approach Lead to Similar Results
4.2. Some Results Are Comparable to Other Studies
4.3. Other Results Reveal Additional Important Aspects of Deadwood Management
4.4. Supply Analysis as A Management Approach to React on Market Prices
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Harmon, M.E.; Franklin, J.F.; Swanson, F.J.; Sollins, P.; Gregory, S.V.; Lattin, J.D.; Anderson, N.H.; Cline, S.P.; Aumen, N.G.; Sedell, J.R.; et al. Ecology of Coarse Woody Debris in Temperate Ecosystems. In Advances in Ecological Research; Caswell, H., Ed.; Elsevier Academic Press: Amsterdam, The Netherlands; London, UK, 2004; Volume 34, pp. 59–234. [Google Scholar] [CrossRef]
- Jonsson, B.G.; Kruys, N. Ecology of Coarse Woody Debris in Boreal Forests: Future Research Directions. Ecol. Bull. 2001, 49, 279–281. [Google Scholar]
- Bütler, R.; Angelstam, P.; Ekelund, P.; Schlaepfer, R. Dead wood threshold values for the three-toed woodpecker presence in boreal and sub-Alpine forest. Biol. Conserv. 2004, 119, 305–318. [Google Scholar] [CrossRef]
- Müller, J. Waldstrukturen als Steuergröße für Artengemeinschaften in kollinen bis submontanen Buchenwäldern; Technische Universität München: Munich, Germany, 2005. [Google Scholar]
- Müller, J.; Bußler, H.; Utschick, H. Wie viel Totholz braucht der Wald?—Ein wissenschaftsbasiertes Konzept gegen den Artenschwund der Totholzzönosen. Nat. Landsch. 2007, 39, 165–170. [Google Scholar]
- Meyer, P. Dead wood research in forest reserves of Northwest-Germany: Methodology and results. Forstwiss. Cent. 1999, 118, 167–180. [Google Scholar] [CrossRef]
- Bobiec, A. Living stands and dead wood in the Białowieża forest: Suggestions for restoration management. For. Ecol. Manag. 2002, 165, 125–140. [Google Scholar] [CrossRef]
- Butler, J.; Alexander, K.; Green, T. Decaying Wood: An Overview of Its Status and Ecology in the United Kingdom and Continental Europe; USDA Forest Service Gen. Tech. Rep; USDA Forest Service: Washington, DC, USA, 2002; pp. 11–19.
- Mountford, E.P. Fallen dead wood levels in the nearnatural beech forest at La Tillaie reserve, Fontainebleau, France. Forestry 2002, 75, 203–208. [Google Scholar] [CrossRef]
- Christensen, M.; Hahn, K.; Mountford, E.P.; Ódor, P.; Standovár, T.; Rozenbergar, D.; Diaci, J.; Wijdeven, S.; Meyer, P.; Winter, S.; et al. Dead wood in European beech (Fagus sylvatica) forest reserves. For. Ecol. Manag. 2005, 210, 267–282. [Google Scholar] [CrossRef]
- Boncina, A. Comparison of structure and biodiversity in the Rajhenav virgin forest remnant and managed forest in the Dinaric region of Slovenia. Glob. Ecol. Biogeogr. 2000, 9, 201–211. [Google Scholar] [CrossRef]
- Bretz Guby, N.A.; Dobbertin, M. Quantitative Estimates of Coarse Woody Debris and Standing Dead Trees in Selected Swiss Forests. Glob. Ecol. Biogeogr. Lett. 1996, 5, 327–341. [Google Scholar] [CrossRef]
- Bultman, J.D.; Southwell, C.R. Natural Resistance of Tropical American Woods to Terrestrial Wood-Destroying Organisms. Biotropica 1976, 8, 71. [Google Scholar] [CrossRef]
- Lieberman, D.; Lieberman, M.; Peralta, R.; Hartshorn, G.S. Mortality Patterns and Stand Turnover Rates in a Wet Tropical Forest in Costa Rica. J. Ecol. 1985, 73, 915. [Google Scholar] [CrossRef]
- Brown, P.M.; Shepperd, W.D.; Mata, S.A.; McClain, D.L. Longevity of windthrown logs in a subalpine forest of central Colorado. Can. J. For. Res. 1998, 28, 932–936. [Google Scholar] [CrossRef]
- Minderman, G. Addition, Decomposition and Accumulation of Organic Matter in Forests. J. Ecol. 1968, 56, 355–362. [Google Scholar] [CrossRef]
- Foster, J.R.; Lang, G.E. Decomposition of red spruce and balsam fir boles in the White Mountains of New Hampshire. Can. J. For. Res. 1982, 12, 617–626. [Google Scholar] [CrossRef]
- Berg, B. Decomposition of root litter and some factors regulating the process: Long-term root litter decomposition in a scots pine forest. Soil Biol. Biochem. 1984, 16, 609–617. [Google Scholar] [CrossRef]
- Boddy, L.; Swift, M.J. Wood Decomposition in an Abandoned Beech and Oak Coppiced Woodland in SE England: III. Decomposition and Turnover of Twigs and Branches. Holarct. Ecol. 1984, 7, 229–238. [Google Scholar] [CrossRef]
- Scheu, S.; Schauermann, J. Decomposition of roots and twigs: Effects of wood type (beech and ash), diameter, site of exposure and macrofauna exclusion. Plant Soil 1994, 163, 13–24. [Google Scholar] [CrossRef]
- Sturtevant, B.R.; Bissonette, J.A.; Long, J.N.; Roberts, D.W. Coarse Woody Debris as a Function of Age, Stand Structure, and Disturbance in Boreal Newfoundland. Ecol. Appl. 1997, 7, 702. [Google Scholar] [CrossRef]
- Mackensen, J.; Bauhus, J. The Decay of Coarse Woody Debris; National Carbon Accounting System Technical Report; Australian Greenhouse Office: Canberra, Australia, 1999. [Google Scholar]
- Alban, D.H.; Pastor, J. Decomposition of aspen, spruce, and pine boles on two sites in Minnesota. Can. J. For. Res. 1993, 23, 1744–1749. [Google Scholar] [CrossRef]
- Næsset, E. Decomposition rate constants of Picea abies logs in southeastern Norway. Can. J. For. Res. 1999, 29, 372–381. [Google Scholar] [CrossRef]
- Müller-Using, S.; Bartsch, N. Totholzdynamik eines Buchenbestandes (Fagus sylvatica L.) im Solling: Nachlieferung, Ursache und Zersetzung von totholz. Allg. Forst Jagdztg. 2003, 174, 122–130. [Google Scholar]
- Müller-Using, S.; Bartsch, N. Decay dynamic of coarse and fine woody debris of a beech (Fagus sylvatica L.) forest in Central Germany. Eur. J. For. Res. 2009, 128, 287–296. [Google Scholar] [CrossRef]
- Jenny, H.; Gessel, S.P.; Bingham, F.T. Comparative study of decomposition rates of organic matter in temperate and tropical regions. Soil Sci. 1949, 68, 419–432. [Google Scholar] [CrossRef]
- Olson, J.S. Energy Storage and the Balance of Producers and Decomposers in Ecological Systems. Ecology 1963, 44, 322–331. [Google Scholar] [CrossRef]
- Harmon, M.E.; Krankina, O.N.; Sexton, J. Decomposition vectors: A new approach to estimating woody detritus decomposition dynamics. Can. J. For. Res. 2000, 30, 76–84. [Google Scholar] [CrossRef]
- Rock, J.; Badeck, F.W.; Harmon, M.E. Estimating decomposition rate constants for European tree species from literature sources. Eur. J. For. Res. 2008, 127, 301–313. [Google Scholar] [CrossRef]
- Meyer, P.; Menke, N.; Nagel, J.; Hansen, J.; Kawaletz, H.; Paar, U.; Evers, J. Entwicklung eines Managementmoduls für Totholz im Forstbetrieb: Abschlussbericht des von der Deutschen Bundesstiftung Umwelt geförderten Projekts. Available online: https://www.nw-fva.de/fileadmin/user_upload/Sachgebiet/Waldnaturschutz_Naturwald/dbu_totholz_abschlussbericht.pdf (accessed on 11 June 2019).
- Zell, J.; Kändler, G.; Hanewinkel, M. Predicting constant decay rates of coarse woody debris—A meta-analysis approach with a mixed model. Ecol. Model. 2009, 220, 904–912. [Google Scholar] [CrossRef]
- Penman, J. Good Practice Guidance for Land Use, Land-Use Change and Forestry; The Institute for Global Environmental Strategies for the IPCC: Kanagawa, Japan, 2003. [Google Scholar]
- Carpenter, S.R. Decay of heterogenous detritus: A general model. J. Theor. Biol. 1981, 89, 539–547. [Google Scholar] [CrossRef]
- Mäkinen, H.; Hynynen, J.; Sievänen, R.; Siitonen, J. Predicting the decomposition of Scots pine, Norway spruce, and birch stems in Finland. Ecol. Appl. 2006, 16, 1865–1879. [Google Scholar] [CrossRef]
- Kruys, N.; Jonsson, B.G.; Ståhl, G. A stage-based matrix model for decay-class dynamics of woody debris. Ecol. Appl. 2002, 12, 773–781. [Google Scholar] [CrossRef]
- Jonsson, M.; Ranius, T.; Ekvall, H.; Bostedt, G.; Dahlberg, A.; Ehnström, B.; Nordén, B.; Stokland, J.N. Cost-effectiveness of silvicultural measures to increase substrate availability for red-listed wood-living organisms in Norway spruce forests. Biol. Conserv. 2006, 127, 443–462. [Google Scholar] [CrossRef]
- Wikström, P.; Eriksson, L.O. Solving the stand management problem under biodiversity-related considerations. For. Ecol. Manag. 2000, 126, 361–376. [Google Scholar] [CrossRef]
- Ranius, T.; Ekvall, H.; Jonsson, M.; Bostedt, G. Cost-efficiency of measures to increase the amount of coarse woody debris in managed Norway spruce forests. For. Ecol. Manag. 2005, 206, 119–133. [Google Scholar] [CrossRef]
- Jonsson, M.; Ranius, T.; Ekvall, H.; Bostedt, G. Cost-effectiveness of silvicultural measures to increase substrate availability for wood-dwelling species: A comparison among boreal tree species. Scand. J. For. Res. 2010, 25, 46–60. [Google Scholar] [CrossRef]
- Tikkanen, O.P.; Matero, J.; Mönkkönen, M.; Juutinen, A.; Kouki, J. To thin or not to thin: Bio-economic analysis of two alternative practices to increase amount of coarse woody debris in managed forests. Eur. J. For. Res. 2012, 131, 1411–1422. [Google Scholar] [CrossRef]
- Jacobsen, J.B.; Vedel, S.E.; Thorsen, B.J. Assessing costs of multifunctional NATURA 2000 management restrictions in continuous cover beech forest management. Forestry 2013, 86, 575–582. [Google Scholar] [CrossRef]
- Santaniello, F.; Line, D.B.; Ranius, T.; Rudolphi, J.; Widenfalk, O.; Weslien, J. Effects of partial cutting on logging productivity, economic returns and dead wood in boreal pine forest. For. Ecol. Manag. 2016, 365, 152–158. [Google Scholar] [CrossRef]
- Ekvall, H.; Bostedt, G.; Jonsson, M. Least-cost allocation of measures to increase the amount of coarse woody debris in forest estates. J. For. Econ. 2013, 19, 267–285. [Google Scholar] [CrossRef]
- Härtl, F.; Hahn, A.; Knoke, T. Risk-sensitive planning support for forest enterprises: The YAFO model. Comput. Electr. Agric. 2013, 58–70. [Google Scholar] [CrossRef]
- Härtl, F.H. Der Einfluss des Holzpreises auf die Konkurrenz zwischen stofflicher und thermischer Holzverwertung. Ein forstbetrieblicher Planungsansatz unter Berücksichtigung von Risikoaspekten; Holz- und Forstwirtschaft, Shaker Verlag: Aachen, Germany, 2015. [Google Scholar]
- Ben-Tal, A.; El Ghaoui, L.; Nemirovski, A. Robust Optimization; Princeton Series in Applied Mathematics; Princeton University Press: Princeton, NJ, USA, 2009. [Google Scholar]
- Scholl, A. Robuste Planung und Optimierung: Grundlagen—Konzepte und Methoden—Experimentelle Untersuchungen; Physica-Verl.: Heidelberg, Germany, 2001. [Google Scholar]
- Goldfarb, D.; Iyengar, G. Robust Portfolio Selection Problems. Math. Oper. Res. 2003, 28, 1–38. [Google Scholar] [CrossRef]
- Mulvey, J.M.; Ruszczynski, A. A new scenario decomposition method for large-scale stochastic optimization. Oper. Res. 1995, 43, 477–490. [Google Scholar] [CrossRef]
- Kouvelis, P.; Yu, G. Robust Discrete Optimization and Its Applications; Nonconvex Optimization and Its Applications; Kluwer Academic Publishers: Dordrecht, The Netherlands; Boston, MA, USA, 1997; Volume 14. [Google Scholar]
- Ben-Tal, A.; Nemirovski, A. Robust solutions of uncertain linear programs. Oper. Res. Lett. 1999, 25, 1–13. [Google Scholar] [CrossRef]
- Knight, F.H. Risk, Uncertainty and Profit; Hart, Schaffner and Marx prize Essays; Houghton Mifflin: Boston, MA, USA, 1921; Volume 31. [Google Scholar]
- Ellsberg, D. Risk, Ambiguity, and the Savage Axioms. Q. J. Econ. 1961, 75, 643–669. [Google Scholar] [CrossRef]
- Garlappi, L.; Uppal, R.; Wang, T. Portfolio Selection with Parameter and Model Uncertainty: A Multi-Prior Approach. Rev. Financ. Stud. 2006, 20, 41–81. [Google Scholar] [CrossRef]
- Gorissen, B.L.; Yanıkoğlu, İ.; den Hertog, D. A practical guide to robust optimization. Omega 2015, 53, 124–137. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W. Chance-constrained programming. Manag. Sci. 1959, 6, 73–79. [Google Scholar] [CrossRef]
- Zymler, S.; Kuhn, D.; Rustem, B. Distributionally robust joint chance constraints with second-order moment information. Math. Program. 2013, 137, 167–198. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Convex Optimization, 7th ed.; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Delage, E.; Ye, Y. Distributionally Robust Optimization Under Moment Uncertainty with Application to Data-Driven Problems. Oper. Res. 2010, 58, 595–612. [Google Scholar] [CrossRef]
- Wiesemann, W.; Kuhn, D.; Sim, M. Distributionally Robust Convex Optimization. Oper. Res. 2014, 62, 1358–1376. [Google Scholar] [CrossRef]
- Yanıkoğlu, İ.; den Hertog, D. Safe Approximations of Ambiguous Chance Constraints Using Historical Data. INFORMS J. Comput. 2013, 25, 666–681. [Google Scholar] [CrossRef]
- Stambaugh, R.F. Analyzing investments whose histories differ in length. J. Financ. Econ. 1997, 45, 285–331. [Google Scholar] [CrossRef]
- Yanıkoğlu, İ.; den Hertog, D.; Kleijnen, J.P.C. Robust dual-response optimization. IIE Trans. 2015, 48, 298–312. [Google Scholar] [CrossRef]
- Zhu, L.; Coleman, T.F.; Li, Y. Min-max robust and CVaR robust mean-variance portfolios. J. Risk 2009, 11, 55–85. [Google Scholar] [CrossRef]
- Erdogan, E. Ambiguous Chance Constrained Programs: Algorithms and Applications. Ph.D. Thesis, Columbia University, New York, NY, USA, 2006. [Google Scholar]
- Paragon Decision Technology B.V. AIMMS: Advanced Interactive Multidimensional Modeling System; AIMMS B.V. (Former Paragon Decision Technology B.V.): Haarlem, The Netherlands, 2011. [Google Scholar]
- Wächter, A.; Biegler, L.T. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math. Program. 2006, 106, 25–57. [Google Scholar] [CrossRef]
- IBM Corp. ILOG CPLEX. 2011. Available online: https://www.ibm.com/analytics/cplex-optimizer (accessed on 11 June 2019).
- Drud, A. CONOPT– A Large-Scale GRG Code. ORSA J. Comput. 1994, 6, 207. [Google Scholar] [CrossRef]
- ARKI Consulting; Development A/S. CONOPT 3. Available online: http://www.conopt.com (accessed on 11 June 2019).
- Roelofs, M.; Bisschop, J. AIMMS The Language Reference: AIMMS 3.12; AIMMS B.V. (Former Paragon Decision Technology B.V.): Haarlem, The Netherlands, 2011. [Google Scholar]
- Pretzsch, H.; Biber, P.; Ďurský, J. The single tree-based stand simulator SILVA: Construction, application and evaluation: National and Regional Climate Change Impact Assessments in the Forestry Sector. For. Ecol. Manag. 2002, 162, 3–21. [Google Scholar] [CrossRef]
- BaySF/StaFoV. Holzpreisstatistik für das Kalenderjahr... für die Jahre 1975–2014; Bayerisches Staatsministerium für Ernährung, Landwirtschaft und Forsten: Munich, Germany, 2015. [Google Scholar]
- Möhring, B.; Rüping, U. A concept for the calculation of financial losses when changing the forest management strategy. For. Policy Econ. 2008, 10, 98–107. [Google Scholar] [CrossRef]
- Bay, S.F. Naturschutzkonzept der Bayerischen Staatsforsten. 2009. Available online: https://www.baysf.de/fileadmin/user_upload/03-wald_schuetzen/pdf/Naturschutzkonzept_Bayerische_Staatsforsten.pdf (accessed on 11 June 2019).
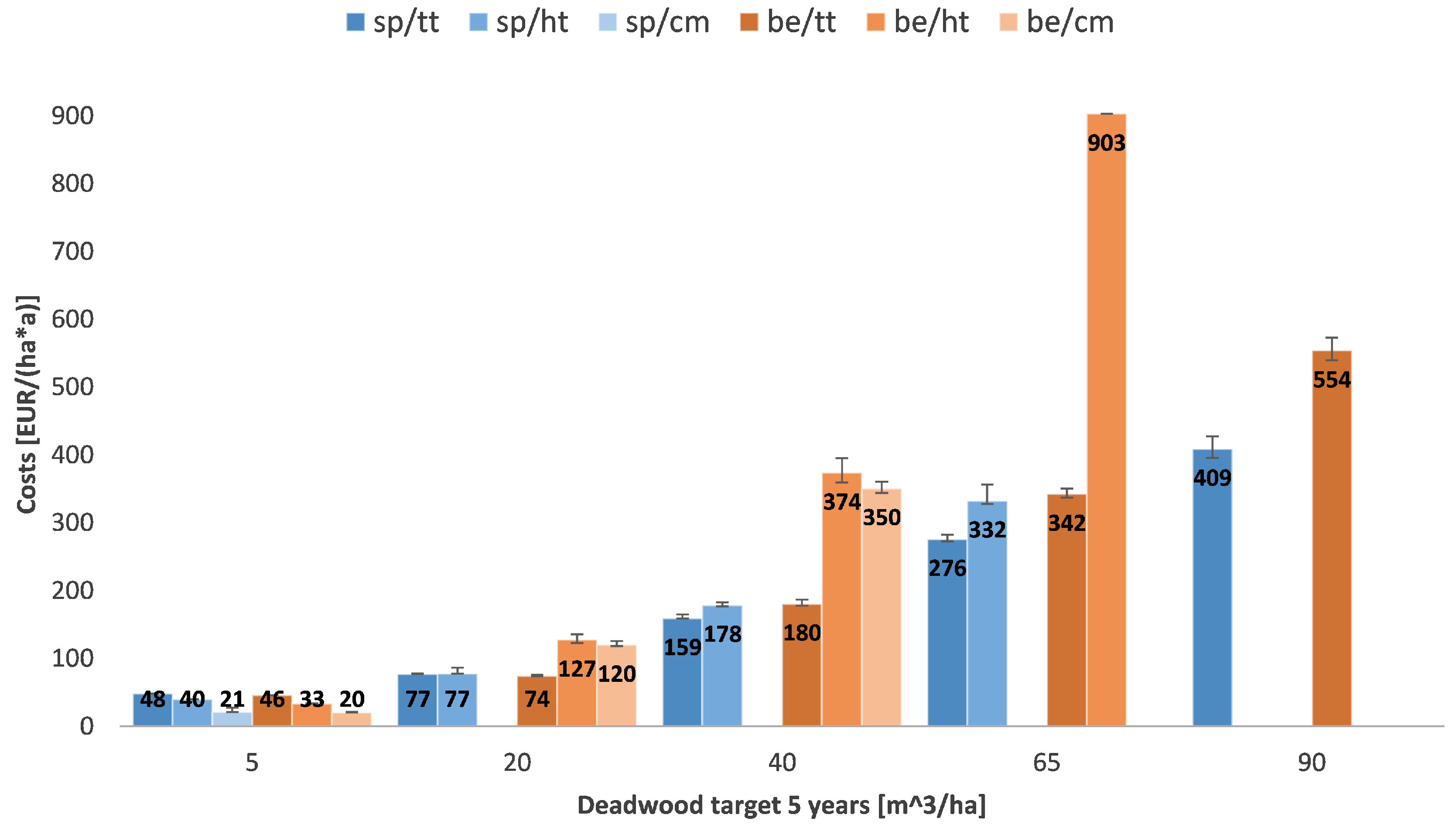
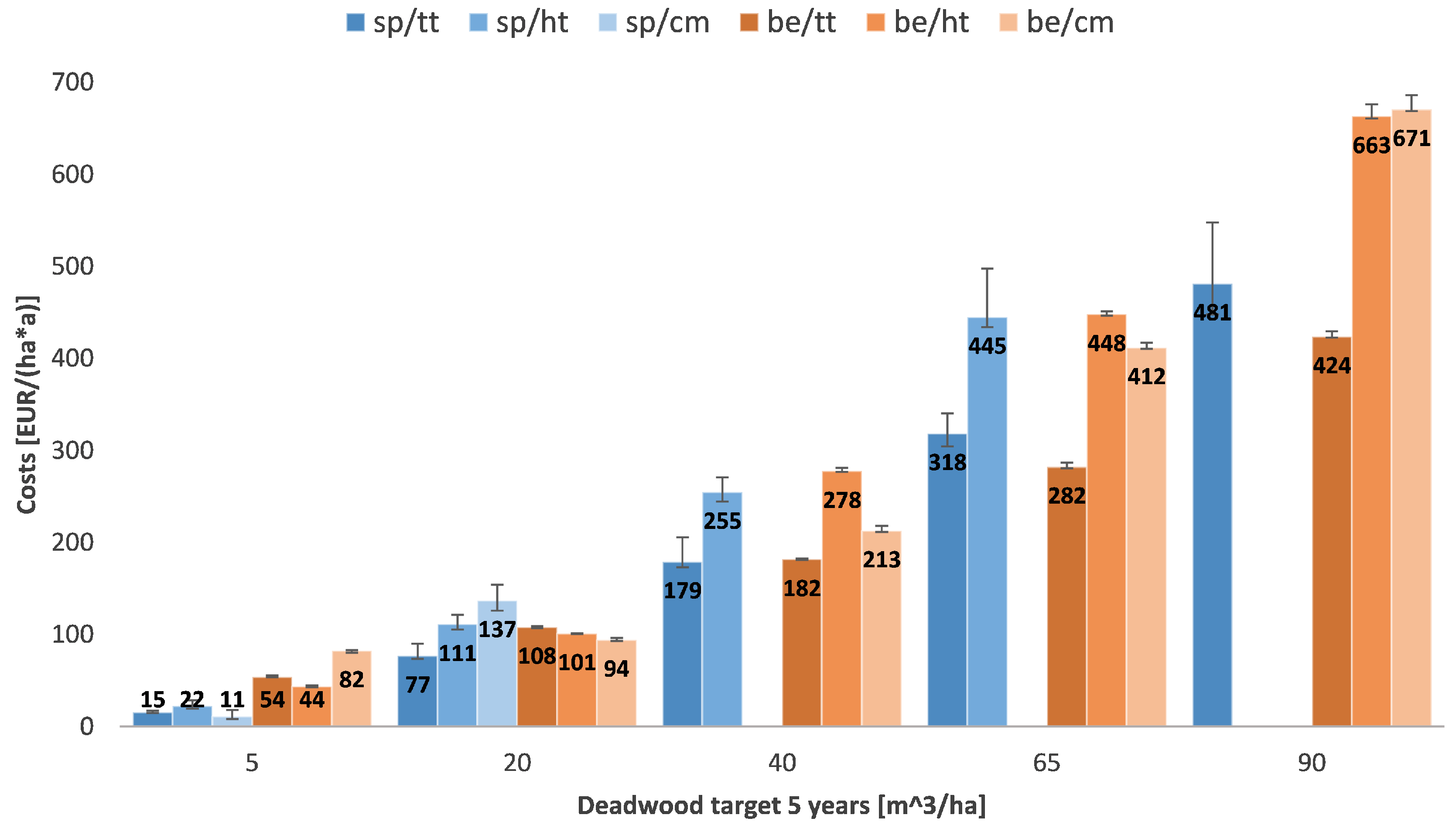
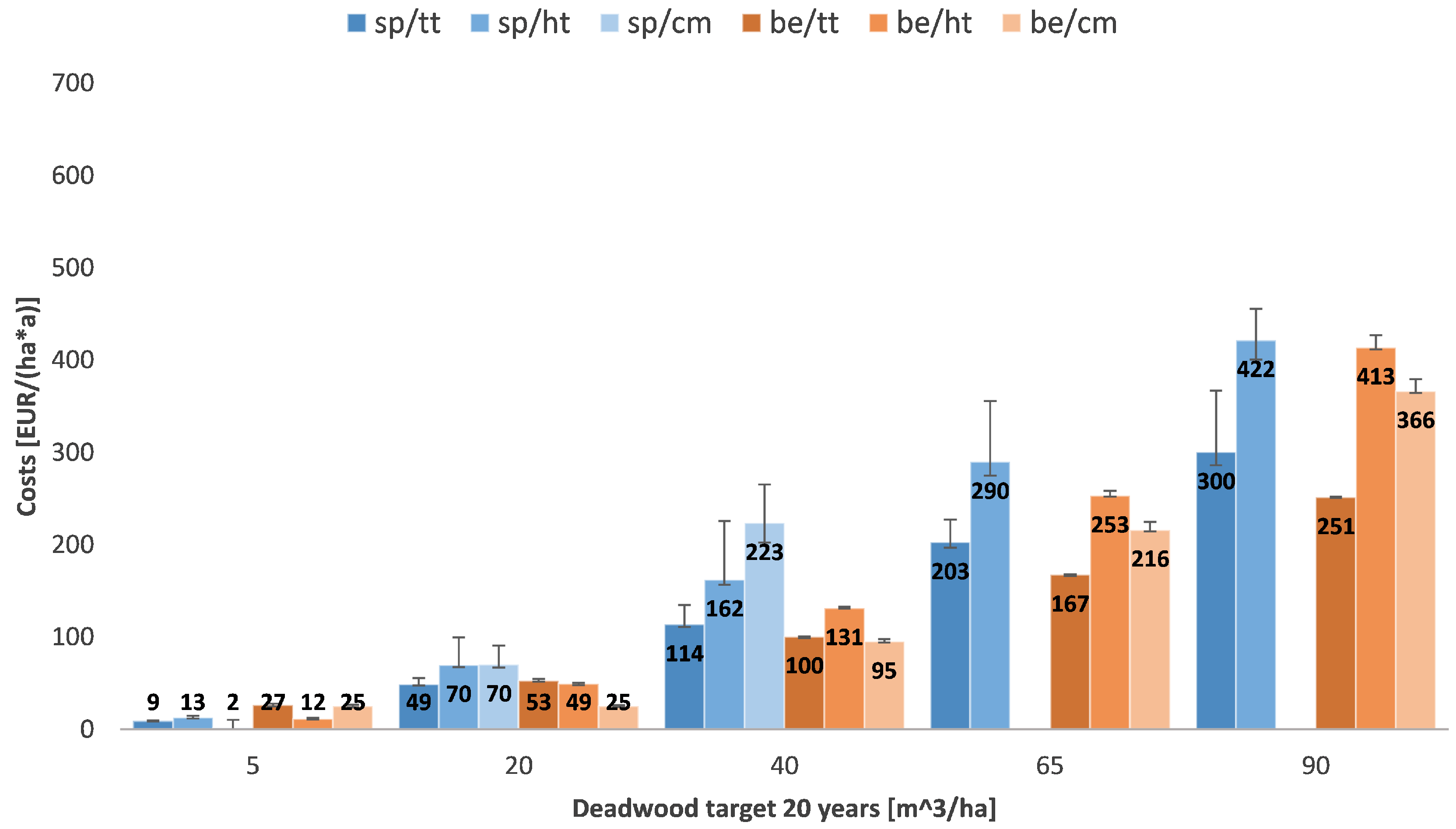


| Stand | A | B |
|---|---|---|
| Species | beech | spruce/beech |
| Age [years] | 100 | 80 |
| Spruce trees [N] | - | 500 |
| Beech trees [N] | 300 | 350 |
| Volume of beech [] | 450 | 250 |
| Avg. DBH of beech [cm] | 35 | 30 |
| Timber value [] | 65 | 40 |
| Risk of disturbance | low | medium |
| Enterprise | Eichelberg | Neureichenau |
|---|---|---|
| Ownership | private | public |
| Political location | rural district of Passau | rural districts of Passau |
| and Freyung-Grafenau | ||
| Geographical location | river Danube | river Danube and Bavarian Forest |
| Altitude [] | 400 | 300–1360 |
| Area [] | 220 | 17,300 |
| Main tree species | spruce, fir, beech, oak | spruce, beech, fir |
| Volume [] | 450 | 313 |
| Increment [] | 10.7 | 8.6 |
| Avg. temperature [] | 8.3 | 5.5–8.3 |
| Precipitation [mm] | 850–950 | 806–1309 |
| Initial deadwood [] | 4.7 | 0 |
| Target [m3 ha−1] | Tree Species | Time Horizon [years] | Sorting Strategy | Segregation [%] |
|---|---|---|---|---|
| 5, 20, 40, 65, 90 | beech (be), | 5, 20, 30 | total tree (tt), | 100, 50, 25, 20, |
| spruce (sp) | heavy timber (ht), | 10, 5, 2, 1 | ||
| crown material (cm) |
| Time Horizon | Strategy | Target | Costs 1 | Costs 2 | Min. | Max. |
|---|---|---|---|---|---|---|
| [years] | [mha] | [€haa] | [€/ha/a] | [€haa] | [€haa] | |
| 5 | sp/ht | 5 | 22.6 | 39.6 | 39.6 | 39.7 |
| 20 | 44.0 | 77.3 | 77.3 | 86.3 | ||
| 40 | 101.7 | 178.4 | 176.5 | 182.5 | ||
| 65 | 189.3 | 332.2 | 327.6 | 356.4 | ||
| sp/tt | 5 | 27.4 | 48.0 | 48.0 | 48.0 | |
| 20 | 43.8 | 76.9 | 76.8 | 77.9 | ||
| 40 | 90.6 | 159.0 | 158.6 | 164.8 | ||
| 65 | 157.1 | 275.7 | 272.4 | 282.7 | ||
| 90 | 232.8 | 408.7 | 395.5 | 427.2 | ||
| sp/cm | 5 | 11.8 | 20.7 | 20.6 | 27.2 | |
| be/ht | 5 | 7.2 | 33.3 | 33.3 | 33.9 | |
| 20 | 27.7 | 127.4 | 122.8 | 135.5 | ||
| 40 | 81.3 | 373.7 | 359.5 | 395.1 | ||
| 65 | 196.4 | 902.9 | 902.9 | 902.9 | ||
| be/tt | 5 | 9.9 | 45.5 | 45.5 | 45.5 | |
| 20 | 16.1 | 74.0 | 73.5 | 76.0 | ||
| 40 | 39.2 | 180.3 | 177.8 | 186.6 | ||
| 65 | 74.5 | 342.5 | 336.9 | 350.4 | ||
| 90 | 120.5 | 553.9 | 539.8 | 572.7 | ||
| be/cm | 5 | 4.4 | 20.5 | 20.4 | 21.4 | |
| 20 | 26.1 | 120.0 | 118.3 | 125.8 | ||
| 40 | 76.2 | 350.5 | 344.2 | 360.5 | ||
| 20 | sp/ht | 5 | 22.6 | 39.6 | 39.6 | 39.7 |
| 20 | 34.4 | 60.3 | 60.3 | 66.3 | ||
| 40 | 70.6 | 123.9 | 123.4 | 157.6 | ||
| 65 | 124.3 | 218.2 | 212.3 | 262.4 | ||
| 90 | 186.3 | 327.0 | 315.0 | 350.5 | ||
| sp/tt | 5 | 27.4 | 48.0 | 48.0 | 48.0 | |
| 20 | 37.2 | 65.4 | 65.3 | 67.7 | ||
| 40 | 68.2 | 119.7 | 119.7 | 125.5 | ||
| 65 | 112.7 | 197.9 | 196.6 | 257.8 | ||
| 90 | 160.9 | 282.3 | 276.9 | 319.2 | ||
| sp/cm | 5 | 10.2 | 17.8 | 17.8 | 25.2 | |
| be/ht | 5 | 6.5 | 29.7 | 29.7 | 29.7 | |
| 20 | 15.5 | 71.4 | 70.6 | 73.9 | ||
| 40 | 40.5 | 186.4 | 181.5 | 199.2 | ||
| 65 | 82.0 | 377.2 | 363.9 | 393.6 | ||
| 90 | 146.1 | 671.8 | 660.9 | 682.7 | ||
| be/tt | 5 | 9.9 | 45.4 | 45.4 | 45.4 | |
| 20 | 11.9 | 54.9 | 54.8 | 59.1 | ||
| 40 | 25.3 | 116.4 | 115.8 | 120.8 | ||
| 65 | 46.6 | 214.5 | 211.4 | 258.0 | ||
| 90 | 71.4 | 328.5 | 320.6 | 352.2 | ||
| be/cm | 5 | 3.5 | 15.9 | 15.9 | 16.1 | |
| 20 | 15.6 | 71.8 | 70.8 | 77.1 | ||
| 40 | 44.8 | 205.8 | 201.8 | 220.7 | ||
| 30 | sp/ht | 5 | 22.6 | 39.6 | 39.5 | 39.6 |
| 20 | 30.7 | 53.9 | 53.9 | 59.1 | ||
| 40 | 57.7 | 101.2 | 101.0 | 111.6 | ||
| 65 | 95.6 | 167.8 | 165.6 | 185.1 | ||
| 90 | 140.5 | 246.6 | 236.6 | 344.4 | ||
| sp/tt | 5 | 27.4 | 48.0 | 48.0 | 48.0 | |
| 20 | 34.7 | 61.0 | 60.9 | 61.3 | ||
| 40 | 58.3 | 102.4 | 102.4 | 117.4 | ||
| 65 | 91.9 | 161.3 | 160.6 | 184.8 | ||
| 90 | 127.2 | 223.2 | 220.9 | 242.3 | ||
| sp/cm | 5 | 8.6 | 15.2 | 15.1 | 23.5 | |
| be/ht | 5 | 6.5 | 29.7 | 29.7 | 29.7 | |
| 20 | 12.2 | 55.9 | 55.6 | 65.5 | ||
| 40 | 28.4 | 130.5 | 129.0 | 135.2 | ||
| 65 | 55.5 | 255.0 | 245.5 | 306.1 | ||
| 90 | 89.5 | 411.7 | 394.8 | 438.9 | ||
| be/tt | 5 | 9.9 | 45.4 | 45.4 | 45.4 | |
| 20 | 10.8 | 49.7 | 49.7 | 50.3 | ||
| 40 | 20.4 | 93.7 | 93.3 | 106.7 | ||
| 65 | 35.2 | 162.0 | 161.0 | 176.2 | ||
| 90 | 52.2 | 239.8 | 235.9 | 250.8 | ||
| be/cm | 5 | 3.5 | 15.9 | 15.9 | 16.1 | |
| 20 | 11.4 | 52.5 | 51.8 | 55.3 | ||
| 40 | 31.4 | 144.4 | 141.5 | 153.0 | ||
| 65 | 66.3 | 304.6 | 294.4 | 369.4 | ||
| 90 | 112.6 | 517.8 | 510.9 | 524.7 |
| Time Horizon | Strategy | Target | Costs 1 | Costs 2 | Min. | Max. |
|---|---|---|---|---|---|---|
| [years] | [mha] | [€haa] | [€haa] | [€haa] | [€haa] | |
| 5 | sp/ht | 5 | 18.9 | 22.4 | 19.6 | 28.8 |
| 20 | 93.9 | 111.1 | 105.5 | 121.3 | ||
| 40 | 215.4 | 254.8 | 244.3 | 270.7 | ||
| 65 | 376.2 | 445.1 | 434.1 | 497.7 | ||
| sp/tt | 5 | 13.0 | 15.4 | 14.6 | 17.3 | |
| 20 | 65.0 | 76.9 | 73.6 | 90.0 | ||
| 40 | 151.3 | 179.1 | 173.1 | 205.8 | ||
| 65 | 269.1 | 318.4 | 304.5 | 340.5 | ||
| 90 | 406.7 | 481.2 | 447.8 | 547.7 | ||
| sp/cm | 5 | 9.4 | 11.2 | 8.2 | 17.9 | |
| 20 | 115.8 | 137.0 | 125.8 | 154.2 | ||
| be/ht | 5 | 1.0 | 43.7 | 42.9 | 44.7 | |
| 20 | 2.4 | 101.1 | 100.6 | 101.6 | ||
| 40 | 6.6 | 277.7 | 276.5 | 281.0 | ||
| 65 | 10.7 | 448.1 | 446.3 | 451.3 | ||
| 90 | 15.9 | 663.2 | 660.9 | 676.0 | ||
| be/tt | 5 | 1.3 | 53.9 | 53.5 | 55.8 | |
| 20 | 2.6 | 108.1 | 106.8 | 109.1 | ||
| 40 | 4.3 | 181.8 | 181.0 | 182.6 | ||
| 65 | 6.7 | 282.2 | 280.8 | 286.9 | ||
| 90 | 10.1 | 423.9 | 422.6 | 429.5 | ||
| be/cm | 5 | 2.0 | 82.4 | 80.3 | 83.2 | |
| 20 | 2.3 | 94.2 | 92.9 | 96.2 | ||
| 40 | 5.1 | 212.6 | 211.7 | 218.0 | ||
| 65 | 9.8 | 411.7 | 410.5 | 417.1 | ||
| 90 | 16.0 | 670.8 | 668.9 | 686.0 | ||
| 20 | sp/ht | 5 | 11.0 | 13.0 | 11.8 | 14.7 |
| 20 | 58.9 | 69.6 | 67.5 | 99.5 | ||
| 40 | 137.1 | 162.3 | 156.7 | 225.8 | ||
| 65 | 244.9 | 289.8 | 274.7 | 355.5 | ||
| 90 | 356.3 | 421.5 | 400.6 | 455.5 | ||
| sp/tt | 5 | 7.8 | 9.2 | 8.6 | 9.6 | |
| 20 | 41.1 | 48.7 | 47.6 | 55.6 | ||
| 40 | 96.2 | 113.8 | 110.8 | 134.8 | ||
| 65 | 171.2 | 202.6 | 196.7 | 227.1 | ||
| 90 | 253.9 | 300.4 | 286.0 | 366.8 | ||
| sp/cm | 5 | 1.4 | 1.7 | −2.0 | 10.2 | |
| 20 | 59.4 | 70.2 | 67.1 | 90.7 | ||
| 40 | 188.9 | 223.5 | 202.5 | 265.2 | ||
| be/ht | 5 | 0.3 | 11.5 | 10.6 | 12.4 | |
| 20 | 1.2 | 49.3 | 48.2 | 50.4 | ||
| 40 | 3.1 | 131.4 | 130.6 | 132.8 | ||
| 65 | 6.1 | 253.2 | 252.2 | 258.2 | ||
| 90 | 9.9 | 413.5 | 411.5 | 427.0 | ||
| be/tt | 5 | 0.6 | 26.5 | 25.0 | 27.9 | |
| 20 | 1.3 | 52.7 | 51.5 | 54.4 | ||
| 40 | 2.4 | 100.3 | 98.9 | 100.6 | ||
| 65 | 4.0 | 167.5 | 166.2 | 167.9 | ||
| 90 | 6.0 | 251.2 | 250.7 | 252.2 | ||
| be/cm | 5 | 0.6 | 25.2 | 23.7 | 26.6 | |
| 20 | 0.6 | 25.3 | 24.4 | 26.5 | ||
| 40 | 2.3 | 95.0 | 94.2 | 97.6 | ||
| 65 | 5.2 | 215.9 | 214.5 | 224.5 | ||
| 90 | 8.8 | 366.3 | 364.6 | 379.6 | ||
| 30 | sp/ht | 5 | 9.0 | 10.6 | 9.0 | 11.2 |
| 20 | 45.6 | 54.0 | 52.4 | 78.3 | ||
| 40 | 103.2 | 122.0 | 118.4 | 147.4 | ||
| 65 | 180.6 | 213.7 | 207.0 | 244.7 | ||
| 90 | 267.6 | 316.6 | 298.4 | 401.0 | ||
| sp/tt | 5 | 6.2 | 7.3 | 6.2 | 7.8 | |
| 20 | 32.5 | 38.4 | 36.4 | 42.8 | ||
| 40 | 72.9 | 86.2 | 84.7 | 129.3 | ||
| 65 | 129.0 | 152.6 | 148.5 | 197.5 | ||
| 90 | 187.6 | 222.0 | 215.2 | 253.8 | ||
| sp/cm | 5 | 0.2 | 0.2 | -2.0 | 1.7 | |
| 20 | 41.0 | 48.5 | 44.9 | 91.9 | ||
| 40 | 124.5 | 147.3 | 130.4 | 283.3 | ||
| be/ht | 5 | 0.8 | 33.6 | 33.1 | 34.6 | |
| 20 | 1.4 | 59.5 | 58.7 | 62.1 | ||
| 40 | 3.3 | 138.7 | 137.9 | 140.0 | ||
| 65 | 4.9 | 204.8 | 204.0 | 206.9 | ||
| 90 | 8.0 | 332.6 | 331.6 | 335.6 | ||
| be/tt | 5 | 1.1 | 46.3 | 45.8 | 47.4 | |
| 20 | 1.7 | 69.8 | 68.6 | 71.8 | ||
| 40 | 2.6 | 107.2 | 105.8 | 107.8 | ||
| 65 | 3.6 | 148.8 | 148.1 | 149.2 | ||
| 90 | 4.9 | 205.5 | 205.1 | 206.1 | ||
| be/cm | 5 | 1.6 | 65.9 | 63.9 | 66.7 | |
| 20 | 1.4 | 58.5 | 57.8 | 58.8 | ||
| 40 | 2.4 | 101.5 | 100.3 | 101.9 | ||
| 65 | 4.9 | 205.2 | 203.8 | 207.6 | ||
| 90 | 7.3 | 304.7 | 303.5 | 315.5 |
| Time Horizon | Strategy | Target | Stochastic | Robust | Diff. | |||
|---|---|---|---|---|---|---|---|---|
| Mean | Std.dev. | Mean | Std.dev. | Mean | Std.dev. | |||
| [years] | [mha] | [€haa] | [€haa] | [€haa] | [€haa] | [%] | [%] | |
| baseline | 0 | 598.0 | 67.4 | 583.1 | 54.1 | −2.5 | −19.7 | |
| 5 | sp/tt | 20 | 561.8 | 70.6 | 547.7 | 60.5 | −2.5 | −14.4 |
| 65 | 420.6 | 43.4 | 413.4 | 39.1 | −1.7 | −9.8 | ||
| be/tt | 20 | 579.8 | 64.8 | 568.5 | 53.3 | −1.9 | −17.7 | |
| 65 | 515.7 | 49.1 | 503.9 | 36.2 | −2.3 | −26.3 | ||
| 20 | sp/tt | 20 | 551.5 | 60.2 | 542.1 | 54.5 | −1.7 | −9.5 |
| 65 | 469.9 | 49.7 | 460.8 | 40.8 | −1.9 | −17.9 | ||
| be/tt | 20 | 581.9 | 65.2 | 569.2 | 55.7 | −2.2 | −14.6 | |
| 65 | 552.0 | 53.5 | 538.0 | 38.6 | −2.5 | −27.8 | ||
| 30 | sp/tt | 20 | 562.7 | 64.1 | 546.8 | 52.4 | −2.8 | −18.2 |
| 65 | 496.1 | 62.2 | 480.2 | 45.5 | −3.2 | −26.8 | ||
| be/tt | 20 | 586.3 | 59.7 | 573.7 | 53.7 | −2.2 | −10.1 | |
| 65 | 551.5 | 64.5 | 537.9 | 49.3 | −2.5 | −23.7 | ||
| Mean | −2.3 | −18.2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Härtl, F.; Knoke, T. Coarse Woody Debris Management with Ambiguous Chance Constrained Robust Optimization. Forests 2019, 10, 504. https://doi.org/10.3390/f10060504
Härtl F, Knoke T. Coarse Woody Debris Management with Ambiguous Chance Constrained Robust Optimization. Forests. 2019; 10(6):504. https://doi.org/10.3390/f10060504
Chicago/Turabian StyleHärtl, Fabian, and Thomas Knoke. 2019. "Coarse Woody Debris Management with Ambiguous Chance Constrained Robust Optimization" Forests 10, no. 6: 504. https://doi.org/10.3390/f10060504
APA StyleHärtl, F., & Knoke, T. (2019). Coarse Woody Debris Management with Ambiguous Chance Constrained Robust Optimization. Forests, 10(6), 504. https://doi.org/10.3390/f10060504






