Abstract
Remotely-sensed data are commonly used to evaluate forest metrics, such as canopy cover, to assess change detection, and to inform land management planning. Often, canopy cover is measured only at the scale of the spatial data product used in the analysis, and there is a mismatch between the management question and the scale of the data. We compared four readily available remotely sensed landscape data products— Light detection and ranging (LiDAR), Landsat-8, Sentinel-2, and National Agriculture Imagery Program (NAIP) imagery —at different spatial grains and multiple extents to assess their consistency and efficacy for quantifying key landscape characteristics of forest canopy patches and sensitivity to change. We examined landscape-scale patterns of forest canopy cover across three landscapes in northern Arizona and assessed their performance using six landscape metrics. Changes in grain and extent affect canopy cover patch metrics and the inferences that can be made from each data product. Overall data products performed differently across landscape metrics. When performing analyses and choosing data layers, it is essential to match the scale of the data product to the management question and understand the limitations inherent in using canopy cover as a stand-alone metric.
1. Introduction
United States federal land management agencies are directed to manage national forests to promote resilient landscapes, defined as within their natural range of variability [1]. Public lands in the western US require restoration to address the uncharacteristic current conditions, such as high tree densities, high fuel loads, bark beetle infestations, and subsequent high fire hazard [1,2,3]. Currently, forests are subject to a variety of disturbances, including large wildfires, insects, pathogens, and post-fire flooding. While these disturbances were always components of the historical ecosystem, they are now strongly influenced by human activities and climate change and uncharacteristic disturbances have become more frequent, higher in intensity, and cover larger areas than historically [4,5]. USDA Forest Service restoration goals need to be accomplished at an accelerated pace to maintain resiliency [6,7,8]. In addition, public lands have seen both leadership direction and political pressure to include increased participation in planning and decision making from multiple agencies and stakeholders [9]. As a result, both land managers and stakeholders are interested in understanding landscape-level processes at scales appropriate to planning and implementation and quantifying metrics that are indicative of resilient and restored ecosystems that capture the natural range of variability.
Understanding spatial and temporal patterns in forested landscapes is an important component of ecosystem complexity and forest ecology. However, these are difficult concepts to quantify and capture for land management practitioners and non-technical stakeholders [10,11,12]. Forests are composed of a mosaic of patches, differing in their structure, shape, and spatial arrangement, and these patterns affect overall ecological processes [10,13,14]. Adjacent patches interact with one another to compose the larger landscape and influence landscape patterns and processes at larger scales, yet forest management historically has been done on traditional, stand-level scales. Recent work examining the distribution and proportion of forest attributes across the landscape informs questions concerning forest restoration and resilience, wildfire, hydrology, and wildlife habitat management [10,13], but is not fully incorporated into land management planning and active management.
Quantifying spatial heterogeneity of forest structure can be used as a tool to measure the ecological integrity of a system and forest structural and compositional complexity. Scale is an important component of our ecological view of the landscape. Metrics used to describe forest structure, and spatial heterogeneity of a landscape will vary dependent on the scale at which they are examined [10,15]. Scale within a landscape context can be defined in terms of both grain and extent [15,16,17]. The spatial grain of the landscape is the smallest resolution of the data. Extent is the overall size of the landscape or area encompassed by the observation. Extent and grain determine the upper and lower limits of the observation, and changes in both grain and extent affect the patterns detected and the inferences we make. Canopy cover is a metric that is widely used in modeling species habitat relationships, spatial patterns, fragmentation, forest resilience, stand density and many other areas of interest [13,18,19]. It has also been used in land management direction as a surrogate for wildlife habitat quality. However, canopy cover is measured or extracted in multiple ways at multiple spatial scales and extents that can vary by the user-defined parameters. Often this metric is used without explicitly defining how canopy cover was measured or classified.
Remote sensing is an effective tool for understanding current landscape conditions, monitoring forest change, and understanding how forest ecosystems respond to disturbances. The advancement in technology and available data sources provide a means to assess a range of spatial information and real-time data, conduct surveys, and provide continuous data sources across large landscapes [20]. There is often a lack of spatially explicit data that characterize forest heterogeneity at multiple scales. In many cases, field or ground data are not readily available, they are time-consuming and costly to collect, and are often not spatially replicated across large areas or available at the scale of the analysis. Therefore, using readily available and spatially explicit remotely sensed data products can aid in elucidating landscape patterns of canopy cover and other forest structure metrics when field data are not available or not feasible. Remotely sensed data products can provide spatially continuous information with higher efficiency and lower cost.
Light detection and ranging (LiDAR) has become increasingly useful in the three-dimensional characterization of forest canopy and other forest attributes such as stand structure, biomass, and tree density [21,22]. Airborne LiDAR data can be used to characterize tree-level forest structure and over large areas [23,24], and individual-tree detection methods can be used to characterize forest structure, tree spatial patterns, and canopy metrics [25,26]. Additionally, LiDAR can provide accurate, high-resolution descriptions of overstory structure and patterns with high accuracy at multiple scales [27].
Remotely sensed data, coupled with field observations, can be an important data source to support the monitoring of forest restoration via mechanical thinning and burning treatments and provide baseline forest inventory data where there is none. This study examines readily available remotely sensed landscape data products to assess their consistency and efficacy for quantifying key landscape characteristics of forest canopy patches and sensitivity to change due to forest management actions or diversity. In this analysis, we compared four remotely sensed data products at different spatial grains and multiple spatial extents to examine landscape-scale patterns of forest canopy cover across three landscapes in northern Arizona, USA. Our objectives were to observe how changes in grain and extent affect canopy cover patch characteristics. We specifically asked: 1) How do readily available and repeatable remotely sensed products—Landsat-8, Sentinel-2, the National Agriculture Imagery Program, and LiDAR—that are at different spatial grains compare in their ability to accurately predict canopy cover, and 2) how do forest canopy patch metrics vary across remotely sensed data products and spatial extents?
2. Materials and Methods
2.1. Study Area
We examined landscape patterns of canopy cover across three ponderosa pine/gambel oak (Pinus ponderosa var. scopulorum Engelm./Quercus gambelii Nutt.) forests spanning a gradient of intact, un-managed ponderosa pine forest to a highly managed forest in northern Arizona, USA. Our three landscapes were Powell Plateau and Tepeats Creek near the North Rim of the Grand Canyon, and Windmill Draw/Jacks Canyon located on the Mogollon Rim (Figure 1). Powell Plateau (~1800 ha in size) represents a relict landscape of ponderosa pine and oak on limestone soils that has remained a relatively intact, functional landscape with a natural fire disturbance history into the 20th century [28]. Tepeats Creek (~2100 ha) represents a ponderosa pine and oak forest on limestone soils with fire exclusion and timber management since the late 19th century, and Windmill Draw/Jacks Canyon (~2400 ha, hereafter referred to as “Windmill Draw”) represents a ponderosa pine and oak forest on basalt soils with fire exclusion and timber management since the late 19th century, both typical of current southwestern forest conditions [29].
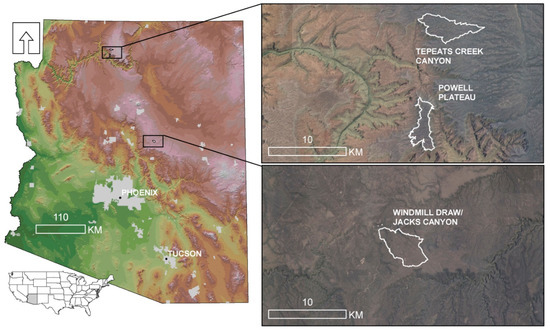
Figure 1.
Map of study landscapes in northern Arizona, USA. Powell Plateau and Tepeats Creek on the North Rim of the Grand Canyon, and Windmill Draw/Jacks Canyon on the Mogollon Rim.
2.2. Remotely Sensed Data
We used remotely sensed data from four sources to examine patterns of canopy cover across our three study landscapes. We used Landsat-8 data (30 m cell resolution), Sentinel-2 data (10 m cell resolution), orthographic aerial imagery from the National Agriculture Imagery Program (NAIP) (1 m cell resolution), and aerial LiDAR data (1 m cell resolution) across our three landscapes. In this analysis, we compared landscape metrics calculated from these four spatial products (i.e., different grains—Landsat-8, Sentinel-2, NAIP, and LiDAR) and then make comparisons across landscapes. The Landsat and Sentinel data are easily available to land management agencies and are released relatively often, while NAIP imagery is released every two to four years depending on location. LiDAR, although more accurate, is currently at a higher cost and flown by individual agencies or coalitions of natural resource management stakeholders. Currently, it is not consistently collected across the nation, but the USGS 3D Elevation Program (3DEP) has set a goal to complete nationwide LiDAR data coverage by 2023 [30]. Our objective was to address how remotely sensed canopy cover patch metrics vary over multiple spatial extents and how the grain (cell resolution) of normally used products affects landscape metrics commonly used to assess restoration success, and thus, patterns detected.
Airborne LiDAR data were used to create a digital elevation model (DEM), digital surface model (DSM), and a canopy height model (CHM) for each site at 1 m spatial resolution. The Airborne LiDAR data were collected over two acquisition periods, August–Sept 2012 for Powell and Tepeats Creek and August–Sept 2013 for Windmill Draw. The data were requisitioned by the USDA Forest Service and acquired by Quantum Spatial using Leica ALS50 Phase II and ALS60 systems either dual mounted or separately in a Cessna Caravan and a Partenavia fixed-wing aircraft, respectively. The sensor was flown at an altitude of 900 m aboveground with ≥50% side-lap (≥100% overlap), resulting in an average volumetric point-density of ≥8 pulses per m2. These data were then classified as ground or non-ground by the vendor using TerraScan v.12.004 and v.13.008, which uses the Axelsson algorithm to classify the DTM points [31]. The horizontal and vertical positioning errors in the point cloud data were ≤15 cm. Resulting CHM pixels above 2 m were classified as either canopy or not canopy, with no effort undertaken to differentiate between deciduous and coniferous vegetation.
Additionally, we utilized National Agriculture Imagery Program (NAIP) imagery collected for Arizona in 2015. This imagery is available free via Google Earth Engine (GEE) [32] and includes four bands (red, green, blue, and infrared) with a 1 m ground sample distance. At a minimum, the horizontal accuracy of the imagery must be within 6 m and cloud cover must be less than 10% per quarter USGS topographic quadrangle tile. NAIP Imagery was loaded into R (https://www.r-project.org/) using the raster package (https://cran.r-project.org/web/packages/raster) and a ratio band was calculated by dividing the near-infrared and red (bands 4 and 1, respectively) [33]. The ratio band was merged with the red, green, blue, and near-infrared bands. Test classifications indicated that 25 classes limited confusion between tree canopy and forest openings and a 25-class unsupervised classification was run using the RStoolbox package (https://cran.r-project.org/web/packages/RStoolbox) and then each class was evaluated by overlaying with LiDAR CHM to verify canopy and not canopy classes. We then classified the resulting layer into a binary map of canopy and not canopy cover at 1 m spatial resolution and georeferenced this layer to the LiDAR CHM. We then generated 1000 random points within each landscape and performed an accuracy assessment using the LiDAR classified canopy and not canopy image as truth. Resulting overall classification accuracies were 63.3%, 61.8%, and 76.3% for Powell, Tepeats Creek, and Windmill Draw areas, respectively.
Sentinel-2 is part of the Copernicus Earth Observation Program of the European Union. We utilized cloud-free (<10%) fall imagery (October 2015 for Windmill Draw and August 2016 for Powell plateau and Tepeats Creek) from Sentinel-2 were used to characterize canopy cover across the study area. The satellite is equipped with a wide swath multi spectral instrument (MSI) which collects near-nadir imagery in 13 spectral bands (coastal aerosol, red, green, blue, three red edge, two near-infrared, water vapor and three shortwave infrared) ranging from 10 to 60 m resolution [34]. For this study, we used the 10 m resolution visible, and near-infrared bands and each Sentinel-2 image was atmospherically corrected to bottom of atmosphere reflectance using the Sen2Cor algorithm provided by the European Space Agency Sentinel Application Platform [35]. Using the same approach as we used with the NAIP imagery, we performed a 25-class unsupervised classification, with the resulting image being reclassified into a binary map of canopy and not canopy cover at 10 m spatial resolution. To perform an accuracy assessment with this product, we aggregated the LiDAR canopy and not canopy image to 10 m using the raster package and reclassified pixels to canopy where ≥50% (an approximate non-linear interpolation based on the FAO classification using 10% cover at 0.5 ha [36], Hansen et al.’s classification of cover using 25% at 30 m [37], and an assumed 90% cover at 1 m for LiDAR) of the LiDAR canopy image pixels were classified as canopy. This layer was then compared to the classified Sentinel-2 canopy image using 1000 randomly generated points and resulting overall classification accuracies were 72.4%, 56.8%, and 63.1% for Powell, Tepeats Creek and Windmill Draw, respectively.
Lastly, Landsat-8 imagery was used to assess canopy cover at the coarsest grain, 30 m spatial resolution. We obtained Landsat-8 operational land imagery from the fall (October–November) 2015. These images contain seven bands (five visible and near-infrared bands and two short-wave infrared) processed to orthorectified surface reflectance by GEE using the Landsat surface reflectance code (LaSRC), which makes use of the coastal aerosol band to perform aerosol inversion tests, uses auxiliary climate data from MODIS, and uses a unique radiative transfer model. We used a cloud, cloud-shadow, and cirrus cloud mask included in the SR data using CFMASK [38]. As with the other products, we performed a 25-class unsupervised classification, with the resulting image being reclassified into a binary map of canopy and not canopy cover at 30 m spatial resolution. To perform an accuracy assessment with this product, we aggregated the LiDAR canopy and not canopy image to 30 m using the raster package and reclassified pixels to canopy where ≥25% [37] of the LiDAR canopy image pixels were classified as canopy. This layer was then compared to the classified Landsat-8 canopy image using 1000 randomly generate points and resulting overall classification accuracies were 74.6%, 69.3%, and 85.3% for Powell, Tepeats Creek, and Windmill Draw, respectively.
2.3. Use of LiDAR as Reference Data
Airborne LiDAR is a widely accepted method of collecting and generating precise, georeferenced spatial information about features of the earth’s surface, shape, and physical characteristics [39]. Recent advances have produced mapping technologies that allow scientists to examine environmental features such as forests, watersheds, and ecosystem attributes with accuracy and precision [39]. LiDAR technology provides horizontal and vertical information at high spatial resolution and vertical accuracies. It has been used to accurately assess forest canopy metrics and other forest attributes such as stand structure, biomass, and tree density [21,22]. LiDAR provides very detailed, wall-to-wall maps of forest canopy cover (via reclassification of the CHM to cover/not cover binary maps) that are problematic and laborious to produce with traditional field and photointerpretation methods. Furthermore, validating the accuracy of LiDAR-derived canopy cover using highly uncertain field observations should be avoided, as the results of ocular and vertical sighting methods are prone to sampling problems and are difficult to confirm [40]. As a result of these uncertainties, LiDAR-derived canopy cover maps are increasingly being used as reference data for assessing accuracies of alternative methods, which typically show agreement with LiDAR-derived canopy cover estimates but are subject to high levels of bias (underestimate low and to overestimate high canopy cover) and imprecision [41,42,43]. Given that LiDAR-derived estimates are continuous and high resolution, making them useful in forest monitoring and management, we chose to use LiDAR-derived metrics as reference data and compare the performance of the three other spatially derived products to LiDAR.
For each landscape, the four data products that vary in grain (Landsat-8 30 m, Sentinel-2 10 m, NAIP 1 m, and LiDAR 1 m) were compared over multiple spatial extents (Figure 2). For all four data products, each patch was delineated by contiguous pixels of canopy cover, and we used the eight neighbor rule for cell-based indices- meaning contiguous cells were defined as those that were either directly or adjacently contiguous. After classification of each data layer into canopy/not canopy, we used landscape metrics to quantify key characteristics of forest canopy patches and to quantify forest cover patterns and make comparisons among different landscapes. A total of six patch metrics were examined to explain the variability of patches across landscapes of different extent (Table 1). With our simple binary classification, the proportion of landscape (PLand), patch density (PD), and mean patch area (MPA) are basic descriptors of the canopy distribution. These characteristics inform the descriptors of spatial connectedness and distribution, including the aggregation index (AI), patch cohesion index (PCI), and landscape division index (LDI).
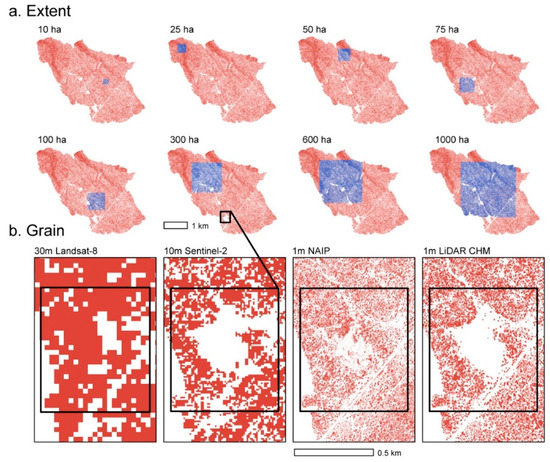
Figure 2.
Remotely sensed data products and associated grain of each data source: Landsat-8 (30 m), Sentinel-2 (10 m), NAIP (1 m), and LiDAR (1 m). The top panel (a) shows the canopy cover of Windmill Draw landscape, with the blue areas representing the relative size of each extent (10–1000 ha) analyzed. The lower panel (b) shows size of the spatial grain (resolution) and level of information available for each data product within an example extent.

Table 1.
Description of landscape metrics evaluated across grain and extent on three landscapes in northern Arizona, USA. Metrics derived from FRAGSTATS (www.umass.edu/landeco/research/fragstats/fragstats.html).
For each landscape and each remote sensing product, we performed a landscape pattern analysis of canopy cover using the SDM Tool package (https://CRAN.R-project.org/package=SDMTools) in R (R Studio https://www.r-project.org/). SDM Tools calculates landscape metrics (similar to FRAGSTATS [44]) and outputs values for each metric. We sampled each landscape metric across five to seven different spatial extents: 10, 25, 50, 75, 100, 300, 600, 1000 ha. We performed 100 Markov Chain Monte Carlo (MCMC) simulations to sample each landscape at these multiple extents. Our three landscapes varied in size, therefore, all three landscapes did not get sampled at the largest extents. Powell Plateau was sampled 10 ha–300 ha, Tepeats Creek was sampled 10 ha–600 ha, and Windmill Draw was sampled 10 ha–1000 ha (Figure 2).
3. Results
General patterns of patch characteristics were observed across spatial extents and between the four data products (Landsat-8 30 m, Sentinel-2 10 m, NAIP 1 m, LiDAR 1 m) that match our understanding of expected changes of patches with scale and grain. This study more specifically tested readily available remotely sensed data products to assess their consistency and efficacy for quantifying key characteristics of forest canopy and sensitivity to change due to forest management or diversity. Here we report the differences in data products (grain) and how the patterns change across spatial extents.
3.1. Ability of the Four Spatial Products (Landsat-8, Sentinel-2, NAIP, and LiDAR) to Predict Metrics of Canopy Cover
The proportion of landscape (PLand) comprised of canopy cover was underpredicted by NAIP and overpredicted by Landsat-8 and Sentinel-2 across our three landscapes. PLand was best predicted by the Sentinel-2 data (10 m), which produced means most similar to the LiDAR data (1 m) on Powell Plateau, our remnant functional landscape with an intact natural disturbance regime (Table 2, Figure 3). NAIP (1 m), while still underestimated, effective1y best characterized PLand on Windmill Draw, a highly managed forest landscape experiencing both fire exclusion and extensive timber management. Landsat-8 (30 m) overestimated PLand on all three landscapes.

Table 2.
Proportion of landscape (PLand) comprised of canopy cover across each landscape and data product (Landsat-8 30 m, Sentinel-2 10 m, NAIP 1 m, LiDAR 1 m), and across multiple spatial extents. Mean values and standard error (SE) are shown.
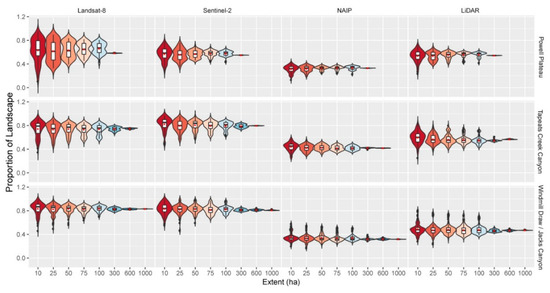
Figure 3.
Violin plots (colored by extent and depicting probability density of the data at different values smoothed by a kernel density estimator), box-and-whisker plots (black and white), and mean (red dot) for the proportion of landscape (ha) under forested canopy cover for each landscape and data product (Landsat-8 30 m, Sentinel-2 10 m, NAIP 1 m, LiDAR 1 m), and across multiple spatial extents. Insets with rescaled y-axis provided for clarity.
The number of patches of canopy cover, or patch density (PD), was not accurately predicted by any of our spatial products across landscapes or spatial extents. NAIP at 1 m resolution highly over-predicted the patch density by 2.5 to 3 times across all three landscapes (Table 3, Figure 4). The small pixel size can fragment patches that the LiDAR point cloud keeps aggregated, thus resulting in many more patches across the landscape, at all extents. Landsat (30 m) and Sentinel-2 (10 m) highly underestimated PD at their native cell resolutions. Mean Patch Area (MPA), the average area composed of patches of canopy cover, was highly overestimated (one to two orders of magnitude) by Landsat and Sentinel-2 as compared to LiDAR (Table 4, Figure 5). NAIP underestimated mean patch area by three to four times on all landscapes across all spatial extents.

Table 3.
Patch density (PD), the average number of patches of canopy cover on each landscape, delineated by each data product (Landsat-8 30 m, Sentinel-2 10 m, NAIP 1 m, LiDAR 1 m) and across multiple spatial extents. Mean values and standard error (SE) are shown.
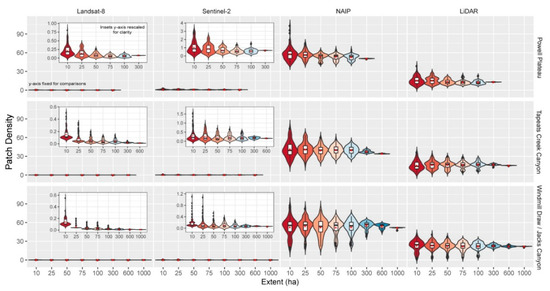
Figure 4.
Violin plots (colored by extent and depicting probability density of the data at different values smoothed by a kernel density estimator), box-and-whisker plots (black and white) and mean (red dot) for patch density (patches per ha). Patch density is the number of patches per landscape area under forested canopy cover for each landscape and data product (Landsat-8 30 m, Sentinel-2 10 m, NAIP 1 m, LiDAR 1 m), and across multiple spatial extents. Insets with rescaled y-axis provided for clarity.

Table 4.
Mean Patch Area (MPA) (ha), the average area composed of patches of canopy cover, across each landscape and data product (Landsat-8 30 m, Sentinel-2 10 m, NAIP 1 m, LiDAR 1 m), and across multiple spatial extents. Mean values and standard error (SE) are shown.
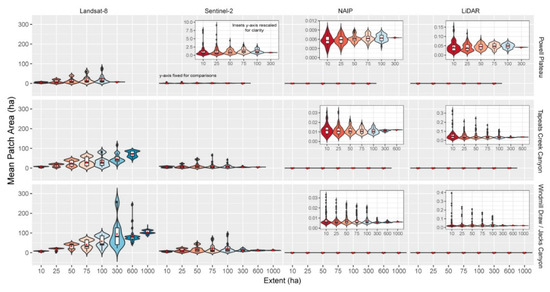
Figure 5.
Violin plots (colored by extent and depicting probability density of the data at different values smoothed by a kernel density estimator), box-and-whisker plots (black and white), and mean (red dot) for mean patch area (ha) (average size of patches) for each landscape and data product (Landsat-8 30 m, Sentinel-2 10 m, NAIP 1 m, LiDAR 1 m), and across multiple spatial extents. Insets with rescaled y-axis provided for clarity.
Canopy cover was highly aggregated, an attribute that was detected by all four data products across all spatial extents sampled (Figure 6). Sentinel-2 was able to detect aggregation more accurately on Tepeats Creek and Windmill Draw, but under-predicted aggregation on Powell Plateau. Landsat-8 best predicted aggregation on Windmill Draw, and under-predicted aggregation on Tepeats Creek and Powell Plateau (Table 5, Figure 6). NAIP under-estimated aggregation on all three landscapes and across all extents, especially on Powell Plateau.
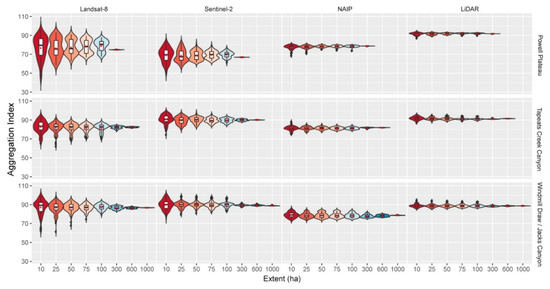
Figure 6.
Violin plots (colored by extent and depicting probability density of the data at different values smoothed by a kernel density estimator), box-and-whisker plots (black and white) and mean (red dot) for aggregation index (0–100). Aggregation index indicates how adjacent patches of canopy cover are to each other for each landscape and data product (Landsat-8 30 m, Sentinel-2 10 m, NAIP 1 m, LiDAR 1 m), and across multiple spatial extents. Insets with rescaled y-axis provided for clarity.

Table 5.
Aggregation index (AI) (%) of canopy cover across each landscape and data product (Landsat-8 30 m, Sentinel-2 10 m, NAIP 1 m, LiDAR 1 m), and across multiple spatial extents. Mean values and standard error (SE) are shown.
All three landscapes had a high patch cohesion index and high physical patch connectivity of canopy cover across all four data grains and across all spatial extents (Figure 7, Table 6). Patch cohesion is sensitive to aggregation of canopy cover and increases as canopy cover becomes more clumped or aggregated in its distribution. NAIP and Sentinel-2 most accurately predicted patch cohesion on all three landscapes across all extents, while Landsat-8 consistently and increasingly under-predicted patch cohesion at extents 50 ha and smaller (Table 6).
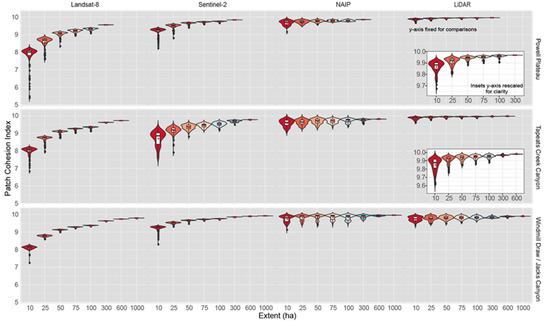
Figure 7.
Violin plots (colored by extent and depicting probability density of the data at different values smoothed by a kernel density estimator), box-and-whisker plots (black and white) and mean (red dot) for patch cohesion index (%). Patch cohesion index describes the physical connectedness of patches of canopy cover for each landscape and data product (Landsat-8 30 m, Sentinel-2 10 m, NAIP 1 m, LiDAR 1 m), and across multiple spatial extents. Insets with rescaled y-axis provided for clarity.

Table 6.
Patch cohesion (PC) index measuring the physical connectedness of patches of canopy cover for each landscape and data product (Landsat-8 30 m, Sentinel-2 10 m, NAIP 1 m, LiDAR 1 m), and across spatial extents. Mean values and standard error (SE) are shown.
Landscape division index was best predicted by NAIP, especially on Powell Plateau and Windmill Draw, but poorly captured within-extent variability (Figure 8, Table 7). Landsat-8 and Sentinel-2 highly under-predicted LDI by two to four times across all landscapes and extents. NAIP over-estimated LDI on Powell Plateau, but performed well at larger spatial extents 300 ha and 600, and 1000 ha on Tepeats Creek and Windmill Draw (Table 7).
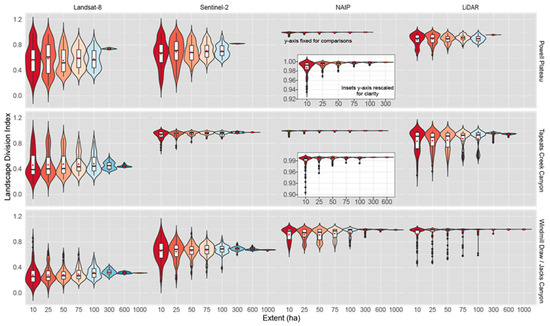
Figure 8.
Violin plots (colored by extent and depicting probability density of the data at different values smoothed by a kernel density estimator), box-and-whisker plots (black and white) and mean (red dot) for landscape division index (%). Landscape division index is presented for each landscape and data product (Landsat-8 30 m, Sentinel-2 10 m, NAIP 1 m, LiDAR 1 m), and across multiple spatial extents and is defined as the probability that two animals placed in different areas somewhere in the extent might find one another. Insets with rescaled y-axis provided for clarity.

Table 7.
Landscape division index (LDI) of canopy cover across all three landscapes across for each data product (Landsat-8 30 m, Sentinel-2 10 m, NAIP 1 m, LiDAR 1 m), and across multiple spatial extents. Mean values and standard error (SE) are shown.
3.2. Forest Canopy Patch Metrics across Remotely-Sensed Data Product, Landscape, and Extent
We examined how patch metrics varied across the landscapes and extents for each data product. PLand varied across landscapes and extent for all four spatial products. In addition to the median and mean values, the ability to capture the variability on the landscape is important to both land managers and stakeholders. For this metric, there was little observed variability at extents larger than 300 ha and was best observed using extents smaller than 75 ha or 100 ha (Table 2, Figure 3). The values of the PLand varied across landscapes. However, not consistently across remotely sensed products and spatial grain. The LiDAR data product showed similar canopy cover across Tepeats Creek and Powell Plateau, with lower values at Windmill Draw. Conversely, the Landsat-8 and Sentinel-2 data products both had the highest canopy cover at Windmill Draw. NAIP at 1 m resolution underestimated PLand at Powell Plateau across all spatial extents.
We standardized patch density (PD) by area in hectares (Figure 4). There were consistent patterns of high overestimation of PD by NAIP, and high underestimation of PD by Sentinel-2 and Landsat-8 compared to LiDAR. On Powell Plateau at 100 ha extent, LiDAR predicted 12.4 patches, while NAIP predicted 52.7 patches, Landsat-8 predicted 0.06 patches, and Sentinel-2 predicted 0.59 patches (Table 3). Patch density of both single trees or groups of trees are categorized as a patch, and in these forests canopy patches on the landscape were dominated by many small patches. This trend was steady across all spatial extents. The metric was amplified by a higher number of small trees and density decreased by the area sampled. For both LiDAR and NAIP, patch density was not sensitive to the extent measured. However, using Landsat-8 data (30 m grain) and Sentinel-2 data (10 m grain), patch density decreased with spatial extent by nearly an order of magnitude from smallest (10 ha) to largest (300 ha). This correlates with the inability of these spatial products at those spatial grains to detect small patches. Landsat-8-derived patch density at a 10-ha extent was limited by this extent and showed higher patch density.
Patch density (PD) and mean patch area (MPA) are closely related, and remotely sensed products with high PD will have lower MPA. For example, On Tepeats Creek at 50 ha extent, LiDAR predicted the mean patch area to be 0.046 ha in size, NAIP predicted it to be 0.006 ha in size, Sentinel-2 predicted 1.096 and Landsat-8 predicted 13.9 ha in size (Table 4, Figure 5). The effect of extent was similar to the patterns in PD: Landsat-8 and Sentinel-2 data had an increasing MPA with an increased spatial extent on all three landscapes, which was expected due to the larger cell resolution that samples the data. NAIP and LiDAR showed little sensitivity to spatial extents (Table 4).
Aggregation (AI) was high on all three landscapes (Figure 6, Table 5), and varied little across all landscapes as estimated using LiDAR (i.e., reported standard errors ranged from 0.001 to 0.192). The NAIP had consistently lower AI values than the other products on Tepeats and Windmill Draw areas. This was directly related to the native cell resolution of NAIP at 1 m, the high PD and low MPA. Landscape Aggregation was well estimated using the Landsat-8 data. This was due to the larger cell resolution (30 m), which tended to form more contiguous patches. NAIP at 1 m cell resolution detected more discrete single patches that are not aggregated. At the landscape-scale, NAIP at 1 m cell resolution under-predicted aggregation. All products were consistent across extents, showing little sensitivity to extent.
Patch Cohesion (PC) increased as canopy cover became more clumped or aggregated in its distribution, and therefore more physically connected. All three landscapes had a high patch cohesion, consistent with the aggregation index and supporting the observation that canopy cover was highly connected. This pattern was found across all products and landscapes (Figure 7, Table 6). Although NAIP had much different values than LiDAR on patch description metrics (PLand, PD, MPA), for patch cohesion, it was more similar to LiDAR on all three landscapes and across all extents. Sentinel-2 performed well at estimating patch cohesion across all spatial extents (Table 6). Landsat-8 consistently under-predicted patch cohesion at smaller extents (10–25 ha) and was more accurate at predicting patch cohesion at ≥100 ha (Table 6). Patch cohesion was sensitive to the aggregation of canopy cover and increased as canopy cover becomes more clustered or aggregated in its distribution.
Landscape division index (LDI) is the probability that two randomly chosen pixels in the landscape are not in the same patch and is based on the cumulative patch area distribution. NAIP had a high probability of landscape division across all spatial extents as it tended to break up large patches into many smaller patches, yet it was accurate on Windmill Draw (Table 7). Landsat-8 had a lower probability of LDI because it measured canopy cover across the landscape as a smaller number of larger sized patches. The four data products displayed variability of patterns across spatial extents due to their native cell resolutions. NAIP showed consistent unimodal distributions of LDI at smaller extents. LiDAR only showed this at the Windmill Draw landscape.
4. Discussion
This analysis provided insights into remotely sensed data products, their native cell resolutions (grain), and how metrics can describe patch and landscape characteristics of canopy cover. We examined six forest canopy patch metrics and described their differences across data products (Landsat-8 30 m, Sentinel-2 10 m, NAIP 1 m, and LiDAR 1 m), spatial extent, and among study landscapes. LiDAR was used as a reference for evaluating landscapes, as well as for assessing the accuracy of the other products. In the United States, little resources are available for ground-based assessment, and remote sensing techniques are increasingly explored for usability with minimal ground-truthing. Our accuracy assessment on each remotely sensed data product put us within the acceptable range of accuracy for spatial products [45].
Spatial heterogeneity directly affects ecosystem patterns and processes but can be difficult to measure in a consistent way to inform federal land management priorities. Heterogeneity is characterized by a focal patch type interacting with the mosaic of surrounding patches or patch types across an area of interest [46] and can influence a variety of ecological responses, including animal movement, species interactions, fire spread and behavior, and overall ecosystem function [47]. For land managers, landscape heterogeneity is important to support multiple seral stages as habitat for wildlife species, biodiversity, ecosystem function, and can aid in characterizing fuels and wildfire spread [48,49,50,51]. We chose a variety of metrics to quantify landscape pattern attributes and assess sensitivity to management practices found in western, frequent-fire forests.
Patch attributes such as mean patch density (PD) that depend on discriminating smaller patches are highly underestimated by coarser grained products (Landsat-8 and Sentinel-2). The grain of both Landsat-8 and Sentinel-2 is too large to detect individual small patches. Small patches are lumped together, resulting in fewer, but larger patches. The proportion of landscape of canopy cover (PLand) can be a highly variable metric, especially at smaller extents (10–25 ha) but is more stable at larger extents (≥300 ha). On all three landscapes, fine-scale heterogeneity becomes harder to detect by each data product at scales 300 ha and larger. On our highly managed landscape, Windmill Draw, there is less fine-scale landscape variability of canopy cover. Landsat-8 (30 m grain) and Sentinel-2 (10 m grain) over-predicted proportion of canopy cover because each pixel size is larger, so when the pixel moves across the landscape at various spatial extents, it often finds canopy cover in the pixel and classifies it as cover (See Figure 2). On the other hand, NAIP under-predicted PLand across all landscapes and spatial extents because the 1 m data product cell resolution was too small to accurately estimate the true pattern of PLand across the landscapes.
Canopy cover is a difficult metric to use solely to assess forest conditions and forest restoration and fuels reduction projects [52,53,54]. However, canopy cover has been incorporated into southwestern US forest service directives (USDA FS Region 3), including forest planning, as a surrogate for wildlife habitat. Canopy patterns measured at smaller scales do not necessarily scale up appropriately, and the processes identified at small scales are not always the drivers at larger spatial scales. When this happens, incorrect inferences can be made for the phenomena or species of interest and incorrect management actions may be chosen. Canopy cover should be selected at the appropriate scale for the analysis or phenomena of interest, including appropriate grain (cell resolution) and spatial extent. Canopy cover-informed spatial metrics, combined with additional forest structural information, including tree size (height and diameter), age, species composition, and tree densities are all important factors in determining if management actions have restored forest structure to within the natural range of variability [55,56,57]. Used together, these variables are more informative for quantifying wildlife habitat, potential fire behavior, landscape connectivity, and forest restoration success and resilience to disturbances [51,57,58,59].
Heterogeneity in frequent-fire ponderosa pine forests has been captured at fine scales [60]. To capture this remotely, LiDAR is a very robust data source that can accurately produce models of canopy cover and openings due to the inherent quality of the data. NAIP has a very small (≤1 m) cell resolution and the user has to classify shadows, bare ground, shrubs and more, therefore there are inherent classification errors at the 1 m. Re-scaling NAIP data to a minimum cell resolution of 2.5 m could help reduce some classification error and increase the accuracy of a binary canopy/not canopy classification. From a management perspective and in a landscape ecology context, forest heterogeneity is often characterized on large landscapes (1000′s–10,000′s of hectares in size) where patterns of large-scale heterogeneity are often detected. Southwestern US forests that evolved with frequent fire have fine-scale heterogeneity [60], which is often harder to describe in a binary landscape. As the USDA Forest Service is tasked to meet urgent goals of managing for forest resiliency to future disturbances, metrics of fine-scale heterogeneity and the methods to summarize these metrics across large scales will be useful to assess treatment success. Using other information in tandem with canopy cover, such as tree size and age classes, structural composition, and species composition will be more informative and helpful in elucidating landscape patterns and processes than using canopy cover alone. Although analyses should include structural and compositional variables, remotely sensed data acquisitions may be faster, and better assessed to quickly inform adaptive management.
Limitations of This Study
In this study we calculated landscape metrics on a single class (canopy cover), and therefore can only make inferences on canopy cover and canopy cover-related landscape metrics. We did not describe spatial patterns of patches and openings nor make comparisons among classes. Additionally, our three landscapes varied in size, and therefore landscape metrics were calculated on different maximum extents. Differences in data product and grain (cell resolution) caused differences in how landscape patterns of canopy cover were calculated and were more evident than differences due to spatial extent. Accuracy of unsupervised classification of our data products ranged from 56% to 85%, and while acceptable by most classification standards this is still an important source of uncertainty. The LiDAR data used in this analysis is the best estimate of canopy cover in our study area, and interpretations of results should be made accordingly.
5. Conclusions
Spatial products at different resolutions performed differently across patch metrics and across our three landscapes. Overall, Sentinel-2 data at 10 m and NAIP at 1 m resolution most often successfully characterized patch metrics in our analysis compared to LiDAR. Landsat-8 varied in its ability to accurately characterize patch metrics due to its coarse cell resolution of 30 m, while NAIP at 1 m resolution often underestimated canopy cover patterns. Metrics that describe spatial connectedness and distribution of patches, such as aggregation index and patch cohesion index, were well described by all three spatial data products. LiDAR data provide the most accurate and high-resolution data that can be used to characterize forest structure, tree spatial patterns, and canopy metrics on our three landscapes in northern Arizona, USA. Analyses may benefit from using more than one spatial data product at different grains and at multiple spatial extents to describe forest heterogeneity and structural characteristics within a landscape.
Author Contributions
Conceptualization, T.N.W., A.J.S.M., A.E.M.W.; methodology, T.N.W., A.J.S.M., A.E.M.W.; software, A.J.S.M.; validation, T.N.W. and A.J.S.M.; formal analysis, T.N.W. and A.J.S.M.; investigation, T.N.W. and A.J.S.M.; data curation, A.J.S.M.; writing—original draft preparation, T.N.W., A.J.S.M. and A.E.M.W.; writing—review & editing, T.N.W. and A.J.S.M.; visualization, A.J.S.M.
Funding
This report was funded by a grant from the US Forest Service. NAU is an equal opportunity provider. The APC was funded by the Ecological Restoration Institute.
Acknowledgments
We would like to thank the Ecological Restoration Institute for funding, the Kaibab and Coconino National Forests and the Southwestern Regional Office for access to the LiDAR data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- USDA Forest Service. National Forest System Land Management Planning. Available online: https://www.fs.usda.gov/planningrule (accessed on 4 February 2019).
- USDA Forest Service. Forest Service Handbook; USDA Forest Service: Washington, DC, USA, 2015.
- Calkin, D.E.; Thompson, M.P.; Finney, M.A. Negative consequences of positive feedbacks in US wildfire management. For. Ecosyst. 2015, 2, 1418. [Google Scholar] [CrossRef]
- Westerling, A.L.; Hidalgo, H.G.; Cayan, D.R.; Swetnam, T.W. Warming and Earlier Spring Increase Western U.S. Forest Wildfire Activity. Science 2006, 313, 940–943. [Google Scholar] [CrossRef]
- Westerling, A.L. Increasing western US forest wildfire activity: Sensitivity to changes in the timing of spring. Philos. Trans. Soc. B Boil. Sci. 2016, 371, 20150178. [Google Scholar] [CrossRef] [PubMed]
- GAO. Forest Restoration: Adjusting Agencies’ Information-Sharing Strategies Could Benefit Landscape-Scale Projects; GAO-15-398; United States Government Accountability Office: Washington, DC, USA, 2015.
- USDA Forest Service. Increasing the Pace of Restoration and Job Creation on Our National Forests; USFS Report; United States Department of Agriculture, Forest Service: Washington, DC, USA, 2012.
- United States Department of Agriculture Forest Service (USDA FS). From Accelerating Restoration to Creating and Maintaining Resilient Landscapes and Communities across the Nation: Update on Progress from 2012; FS-1069; United States Department of Agriculture, Forest Service: Washington, DC, USA, 2015.
- Collaborative Forest Landscape Restoration Program. Available online: https://www.fs.fed.us/restoration/documents/cflrp/titleIV.pdf (accessed on 4 February 2019).
- Turner, M.G.; Gardner, R.H.; O’Neill, R.V. Landscape Ecology in Theory and Practice: Pattern and Process; Springer: New York, NY, USA, 2001. [Google Scholar]
- Abella, S.R.; Denton, C.W. Spatial variation in reference conditions: Historical tree density and pattern on a Pinus ponderosa landscape. Can. J. 2009, 39, 2391–2403. [Google Scholar] [CrossRef]
- Dickinson, Y.; Pelz, K.; Giles, E.; Howie, J. Have we been successful? Monitoring horizontal forest complexity for forest restoration projects. Restor. Ecol. 2015, 24, 8–17. [Google Scholar] [CrossRef]
- Chapin, F.S.; Matson, P.A.; Vitousek, P.M.; Iii, F.S.C. Landscape Heterogeneity and Ecosystem Dynamics. In Principles of Terrestrial Ecosystem Ecology; Springer Nature: Basingstoke, UK, 2011; pp. 369–397. [Google Scholar]
- Farina, A. Principles and Methods in Landscape Ecology: Toward a Science of Landscape; Springer: Dordrecht, The Netherlands, 2006. [Google Scholar]
- Wiens, J.A. Spatial Scaling in Ecology. Funct. Eco. 1989, 3, 385–397. [Google Scholar] [CrossRef]
- Forman, R.T.T.; Godron, M. Landscape Ecology; John Wiley & Sons: New York, NY, USA, 1986; p. 620. [Google Scholar]
- Turner, M.G.; Dale, V.H.; Gardner, R.H. Predicting across scales: Theory development and testing. Landsc. Ecol. 1989, 3, 245–252. [Google Scholar] [CrossRef]
- Gustafson, E.J.; Lytle, D.E.; Swaty, R.; Loehl, C. Simulating the cumulative effects of multiple forest management strategies on landscape measures of forest sustainability. Landsc. Eco. 2007, 22, 141–156. [Google Scholar] [CrossRef]
- Spies, T.A.; Ripple, W.J.; Bradshaw, G.A. Dynamics and Pattern of a Managed Coniferous Forest Landscape in Oregon. Ecol. Appl. 1994, 4, 555–568. [Google Scholar] [CrossRef]
- Wu, H.; Li, Z.-L. Scale Issues in Remote Sensing: A Review on Analysis, Processing and Modeling. Sensors 2009, 9, 1768–1793. [Google Scholar] [CrossRef] [PubMed]
- Means, J.E.; Acker, S.A.; Fitt, B.J.; Renslow, M.; Emerson, L.; Hendrix, C.J. Predicting forest stand characteristics with airborne scanning lidar. Photogram. Eng. Remote Sens. 2000, 66, 1367–1371. [Google Scholar]
- Lefsky, M.A.; Hudak, A.T.; Cohen, W.B.; Acker, S. Geographic variability in lidar predictions of forest stand structure in the Pacific Northwest. Remote. Sens. Environ. 2005, 95, 532–548. [Google Scholar] [CrossRef]
- Kane, V.R.; Lutz, J.A.; Roberts, S.L.; Smith, D.F.; McGaughey, R.J.; Povak, N.A.; Brooks, M.L. Landscape-scale effects of fire severity on mixed-conifer and red fir forest structure in Yosemite National Park. Ecol. Manag. 2013, 287, 17–31. [Google Scholar] [CrossRef]
- Stephens, S.L.; Lydersen, J.M.; Collins, B.M.; Fry, D.L.; Meyer, M.D. Historical and current landscape-scale ponderosa pine and mixed conifer forest structure in the Southern Sierra Nevada. Ecosphere 2015, 6, 1–63. [Google Scholar] [CrossRef]
- A Jeronimo, S.M.; Kane, V.R.; Churchill, D.J.; McGaughey, R.J.; Franklin, J.F. Applying LiDAR Individual Tree Detection to Management of Structurally Diverse Forest Landscapes. J. For. 2018, 116, 336–346. [Google Scholar] [CrossRef]
- Churchill, D.J.; Larson, A.J.; Dahlgreen, M.C.; Franklin, J.F.; Hessburg, P.F.; Lutz, J.A. Restoring forest resilience: From reference spatial patterns to silvicultural prescriptions and monitoring. Ecol. Manag. 2013, 291, 442–457. [Google Scholar] [CrossRef]
- Wiggins, H.L.; Nelson, C.R.; Larson, A.J.; Safford, H.D. Using LiDAR to develop high-resolution reference models of forest structure and spatial pattern. Ecol. Manag. 2019, 434, 318–330. [Google Scholar] [CrossRef]
- Fulé, P.Z.; Heinlein, T.A.; Covington, W.W.; Moore, M.M. Assessing fire regimes on Grand Canyon landscapes with fire-scar and fire-record data. Int. J. Wildland Fire 2004, 12, 129–145. [Google Scholar] [CrossRef]
- Covington, W.W.; Moore, M.M.; Moore, M.M. Southwestern ponderosa pine forest structure: Changes since Euro-American settlement. J. For. 1994, 92, 39–47. [Google Scholar]
- Sugarbaker, L.J.; Constance, E.W.; Heidemann, H.K.; Jason, A.L.; Lukas, V.; Saghy, D.L.; Stoker, J.M. The 3D Elevation Program Initiative: A Call for Action; U.S. Geological Survey Circular: Reston, VA, USA, 2014; p. 35.
- Axelsson, P. DEM Generation from Laser Scanner Data Using TIN Models; The International Archives of the Photogrammetry and Remote Sensing: Amsterdam, The Netherlands, 2000; pp. 110–117. [Google Scholar]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote. Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Pelz, K.A.; Dickinson, Y.L. Monitoring Forest Cover Spatial Patterns with Aerial Imagery: A Tutorial; Colorado Forest Restoration Institute, Colorado State University: Fort Collins, CO, USA, 2014; p. 43. [Google Scholar]
- European Space Agency (ESA). Available online: www.esa.int/ESA (accessed on 4 February 2019).
- Müller-Wilm, U. Sen2Cor 2.5.5—Software Release Note. Available online: https://step.esa.int/main/new-release-of-sen2cor-2-5-5-is-available/ (accessed on 4 February 2019).
- FAO. FRA2000 on Definitions of Forest and Forest Change: FRA Working Paper 33. Available online: http://www.fao.org/3/ad665e/ad665e00.htm (accessed on 4 February 2019).
- Hansen, M.C.; Stehman, S.V.; Potapov, P.V. Quantification of global gross forest cover loss. Proc. Natl. Acad. Sci. USA 2010, 107, 8650–8655. [Google Scholar] [CrossRef]
- Foga, S.; Scaramuzza, P.L.; Guo, S.; Zhu, Z.; Dilley, R.D.; Beckmann, T.; Schmidt, G.L.; Dwyer, J.L.; Hughes, M.J.; Laue, B. Cloud detection algorithm comparison and validation for operational Landsat data products. Remote Sens. Environ. 2017, 194, 379–390. [Google Scholar] [CrossRef]
- National Oceanic and Atmospheric Administration (NOAA) Coastal Services Center. Lidar 101: An Introduction to Lidar Technology, Data, and Applications; NOAA Coastal Services Center: Charleston, SC, USA, 2012. [Google Scholar]
- Maltamo, M.; Naesset, E. Forestry applications of airborne laser scanning concepts and case studies. In Managing Forest Ecosystems; Managing Forest Ecosystems; Springer: Dordrecht, The Netherland, 2014. [Google Scholar]
- Gatziolis, D. Comparison of lidar- and photointerpretation-based estimates of canopy cover. In Monitoring across Borders: 2010 Joint Meeting of the Forest Inventory and Analysis (FIA) Symposium and the Southern Mensurationists; McWilliams, W., Roesch, F.A., Eds.; e-Gen. Technical report SRS-157; U.S. Department of Agriculture, Forest Service, Southern Research Station: Asheville, NC, USA, 2012; pp. 231–235. [Google Scholar]
- Korhonen, L.; Ali-Sisto, D.; Tokola, T. Tropical forest canopy cover estimation using satellite imagery and airborne lidar reference data. Silva Fenn. 2015, 49, 18. [Google Scholar] [CrossRef]
- Ma, Q.; Su, Y.; Guo, Q. Comparison of Canopy Cover Estimations From Airborne LiDAR, Aerial Imagery, and Satellite Imagery. IEEE J. Sel. Top. Appl. Earth Obs. Sens. 2017, 10, 4225–4236. [Google Scholar] [CrossRef]
- McGarigal, K.; Cushman, S.A.; Neel, M.C.; Ene, E. FRAGSTATS: Spatial Pattern Analysis Program for Categorical Maps. Available online: www.umass.edu/landeco/research/fragstats/fragstats.html (accessed on 4 February 2019).
- Homer, C.; Dewitz, J.; Yang, L.; Jin, S.; Danielson, P.; Xian, G.; Coulston, J.; Herold, N.; Wickham, J.; Megown, K. Completion of the 2011 National Land Cover Database for the conterminous United States–representing a decade of land cover change information. Photogram. Eng. Remote Sens. 2015, 81, 345–354. [Google Scholar]
- Forman, T.T. Some general principles of landscape and regional ecology. Landsc. Eco. 1995, 10, 133–142. [Google Scholar] [CrossRef]
- Fahrig, L. Non-optimal animal movement in human-altered landscapes. Funct. Ecol. 2007, 21, 1003–1015. [Google Scholar] [CrossRef]
- Wiens, J.A. Central Concepts and Issues of Landscape Ecology. In Applying Landscape Ecology in Biological Conservation; Springer Nature: Basingstoke, UK, 2002; pp. 3–21. [Google Scholar]
- Lovett, G.M.; Jones, C.G.; Turner, M.G.; Weathers, K.C. Ecosystem Function in Heterogeneous Landscapes; Springer: New York, NY, USA, 2005. [Google Scholar]
- Fahrig, L.; Baudry, J.; Brotons, L.; Burel, F.G.; Crist, T.O.; Fuller, R.J.; Sirami, C.; Siriwardena, G.M.; Martin, J. Functional landscape heterogeneity and animal biodiversity in agricultural landscapes. Eco. Lett. 2011, 14, 101–112. [Google Scholar] [CrossRef]
- Reynolds, R.T.; Meador, A.J.S.M.; Youtz, J.A.; Nicolet, T.; Matonis, M.S.; Jackson, P.L.; DeLorenzo, D.G.; Graves, A.D. Restoring Composition and Structure in Southwestern Frequent-Fire Forests: A Science-Based Framework for Improving Ecosystem Resiliency; Gen. Tech. Rep. RMRSGTR-310; Department of Agriculture, Forest Service, Rocky Mountain Research Station: Fort Collins, CO, USA, 2013; p. 2013.
- Huffman, D.W.; Sánchez-Meador, A.J.; Greco, B. Canopy Cover and How it Relates to Other Forest Attributes as an Indicator of Forest Conditions. Available online: https://cdm17192.contentdm.oclc.org/digital/collection/p17192coll1/id/861/rec/25 (accessed on 4 February 2019).
- Roccaforte, J.P.; Fulé, P.Z.; Covington, W.W. Landscape-scale changes in canopy fuels and potential fire behaviour following ponderosa pine restoration treatments. Int. J. Wildland Fire 2008, 17, 293–303. [Google Scholar] [CrossRef]
- Agee, J.K.; Skinner, C.N. Basic principles of forest fuel reduction treatments. Ecol. Manag. 2005, 211, 83–96. [Google Scholar] [CrossRef]
- Fulé, P.Z.; Covington, W.W.; Moore, M.M. Determining reference conditions for forest ecosystem management pf southwestern Ponderosa pine forests. Ecol. Appl. 1997, 7, 895–908. [Google Scholar] [CrossRef]
- Sánchez-Meador, A.J.; Parysow, P.F.; Moore, M.M. A new method for delineating tree patches and assessing spatial reference conditions of Ponderosa pine forests in northern Arizona. Restor. Eco. 2011, 19, 490–499. [Google Scholar] [CrossRef]
- Battaglia, M.A.; Gannon, B.; Brown, P.M.; Fornwalt, P.J.; Cheng, A.S.; Huckaby, L.S. Changes in forest structure since 1860 in ponderosa pine dominated forests in the Colorado and Wyoming Front Range, USA. Ecol. Manag. 2018, 422, 147–160. [Google Scholar] [CrossRef]
- Covington, W.W.; Moore, M.M.; Heinlein, T.A.; Waltz, A.E.M.; Fulé, P.Z. Natural variability in forests of the Grand Canyon, USA. J. Biogeogr. 2002, 29, 31–47. [Google Scholar]
- Dickson, B.G.; Sisk, T.D.; Sesnie, S.E.; Reynolds, R.T.; Rosenstock, S.S.; Vojta, C.D.; Ingraldi, M.F.; Rundall, J.M. Integrating single-species management and landscape conservation using regional habitat occurrence models: The northern goshawk in the Southwest, USA. Landsc. Ecol. 2014, 29, 803–815. [Google Scholar] [CrossRef]
- Sánchez-Meador, A.J.; Moore, M.M.; Bakker, J.D.; Parysow, P.F. 108 years of change in spatial pattern following selective harvest of a ponderosa pine stand in northern Arizona, USA. J. Veg. Sci. 2009, 20, 79–90. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).