Abstract
Eucalyptus cladocalyx F. Muell is a tree species suitable for low-rainfall sites, even with annual average precipitation as low as 150 mm per year. Its wood is classified as highly durable and its permanence in soil is longer than 25 years, so it can be used for multiple applications. Given that about 41% of the world’s land area is classified as drylands, added to the impact of climate change on the availability of water resources, it becomes necessary to use plant species that can tolerate environments with low water availability. In this study, a Bayesian analysis of genetic parameters showed that wood density (WD) was moderately heritable, with a posterior mean of h2 = 0.29 and a Bayesian credibility region (90%) of 0.06–0.74, while the slenderness coefficient (SC) was highly heritable, with a posterior mean of h2 = 0.48 and a Bayesian credibility region (90%) of 0.11–0.87. Through Bayesian regression analysis, we identified four and three significant associations for WD and SC, respectively. Another important finding of the bi-trait Bayesian analysis was the detection of three large-effect pleiotropic QTLs located on LG4 at 52 cM, on LG2 at 125 cM, and on LG6 at 81 cM. Bayesian bi-trait regression and the posterior probability of association indicated that three QTLs presented strong evidence of association with WD and SC. This provides convincing evidence that the loci qtlWD130/qtlSC130, qtlWD195/qtlSC195, and qtlWD196/qtlSC196 have a significant pleiotropic effect. The association mapping based on multivariate Bayesian regression was useful for the identification of genomic regions with pleiotropic effects. These loci can be used in molecular marker-assisted breeding to select trees with better wood density.
1. Introduction
The endemic species Eucalyptus cladocalyx F. Muell from southern Australia is naturally distributed in three geographical regions: Kangaroo Island, the Eyre Peninsula, and the Flinders Range [1]. An interesting feature is its natural evolution to tolerate environments where the annual rainfall is lower than 200 mm [2,3]. The trees of E. cladocalyx have tremendous potential for the production of wood with multiple applications, due to its straight and poorly branched stems [4]. Lundqvist et al. [5] compared the physical properties of the wood of three genotypes of eucalyptus tolerant to drought: E. grandis × E. camaldulensis hybrid, E. gomphocephala and E. cladocalyx, and concluded that E. cladocalyx is one of the most suitable species to produce structural wood, given the high density of wood and rigidity of its microfibrils.
According to the Australian classification of natural durability of wood, E. cladocalyx is one of the most resistant to biodegradation [6], with a useful life of 25 years or more, in contact with the soil [7]. Natural durability has been described as the resistance of wood to biological decomposition by fungi, bacteria, insects, or marine organisms without copper/chromium/arsenate treatment to preserve it [8]. Therefore, considering the health problems and environmental pollution associated with the use of chemical preservatives, E. cladocalyx has been used to produce high natural durability wood with potential uses in the agricultural and industrial sectors [6,9].
The density of the wood is considered one of the most informative properties in terms of the physical and mechanical behavior of a tree, followed by the production of sawn wood [10]. It has been observed that a higher density of wood also implies greater natural durability [11]. Wood density is related to the structure of the cells of the vessels and the parenchyma [12], in which species resistant to cavitation have a greater density in the wood [13]. In this sense, density is positively correlated with tolerance to drought, so arid environments tend to be dominated by species with high wood density [13].
According to several authors, wood density is moderately to highly heritable in most forest species [10,14,15]. However, other studies have indicated that wood density can vary depending on local environmental conditions [13,16,17]. Bush et al. [6] determined that the wood density of E. cladocalyx varies considerably based on the different regions of origin of the species, presenting moderate heritability (h2 = 0.41).
Association studies based on DNA markers provide a comprehensive approach to identify genetic loci associated with the phenotypic response of complex traits. Association studies have identified many quantitative trait loci (QTL) associated with wood density in E. urophylla, E. grandis [18], and E. globulus [19], along with microfibrils angle and total lignin content in E. nitens [19]. Wood density and other mechanical properties are highly variable among species and sites, and even between and within the trees themselves [20]. Due to the relevance of this type of trait for the wood industry, several studies have been developed to estimate genetic parameters and identify genes, or regions in the genome, related to the production of structural components of wood (for example, cellulose and lignin) and the spatial arrangement of the microfibrils [21,22,23,24,25,26]. In general, these studies have been explored with molecular markers and transcriptomic analyzes in the principal forest species. For example, Nakahama et al. [24] showed that genes related to the biosynthesis of lignocellulosic compounds (for example, cellulose synthase, invertase, l-cinnamate-4-hydroxylase and cinnamoyl-CoA reductase) and genes related to the modification of the cell wall (for example, expansins and xyloglucan endo-transglycosylase/hydrolase) are mostly expressed in Eucalyptus hybrids that have a high wood density.
On the other hand, a factor that is also relevant in the production of sawn wood is the tree growth stress, which is the product of the stresses of the same growth of the tree when forming a new layer of the trunk during the differentiation of the fibers [27]. One of the best indicators of this type of stress is the slenderness coefficient [28]. This variable reveals the capacity of a tree to sustain itself against these tensions and the tensions of the environment, e.g., wind [29]. Although the slenderness of a tree depends on environmental factors such as the availability of light, wind, and plant density [30,31,32], it has been concluded that this trait is also controlled by genetic components [33,34]. Moreover, the slenderness of a tree is also influenced by the density of its wood [35].
Due to the potential of E. cladocalyx for the production of high-quality wood at low-rainfall sites, and that wood density and the slenderness of trees are traits closely related to the quality of the wood, the following objectives were proposed: (i) to determine Bayesian genetic parameters of wood density, measured indirectly by means of Pilodyn, and the slenderness of E. cladocalyx trees grown under arid environmental conditions, (ii) to identify genomic regions associated with density of wood and slenderness, using a key set of 130 microsatellite markers, and (iii) corroborate the pleiotropy of the loci associated with both traits, using a multivariate Bayesian regression approach.
2. Materials and Methods
2.1. DNA Extraction and Genotyping
The association analysis was focused on a sample of 245 E. cladocalyx trees, corresponding to 5 blocks × 49 half-sib families, from a provenance-progeny trial established in 2001 [2]. Forty-seven families come from five natural provenances: Flinders Chase (35°57’ S, 136°42’ E), Marble Range (34°30’ S, 135°30’ E), Mount Remarkable (32°43’ S, 138°06’ E), Cowell (33°38’ S, 136°40’ E) and Wirrabara (33°06’ S, 138°14’ E), distributed geographical in three regions of southern Australia (Eyre Peninsula, Flinders Ranges and Kangaroo Island), and two families from a local seed resource (31°40’ S, 71°14’ W). The trial was situated in a dryland area within the region of Coquimbo, Choapa Province (31°38′ S Latitude; 71°19′ W Longitude; and altitude of 297 m) in the south of the Atacama Desert, Chile. Total genomic DNA was isolated from juvenile leaves using the method CTAB according to da Silva [36] with some modifications. A total of 130 SSR polymorphic markers distributed across the genome of E. cladocalyx were used for genotyping the association population [37]. Polymerase chain reaction (PCR) was performed as follows: 0.3 uM of each primer, 40 ng of genomic DNA, 1 U of Taq DNA polymerase, 0.2 mM of each dNTP, 10 mM of Tris-HCl pH 8.3, 50 mM of KCl and 1.5 mM of MgCl2. The amplification was run as follows: initial heat at 95 °C for 5 min followed by 40 cycles of 95 °C for 1 min, annealing temperature of each primer for 1 min, 72 °C for 1 min, and a final extension of 72 °C for 5 min. Finally, the PCR products were separated and visualized according to the methods described by Mora et al. [37].
2.2. Traits Assessment
Wood density (WD) of 17-year-old trees was indirectly estimated after removal of the bark based on Pilodyn penetration using a Pilodyn 6J Forest (PROCEQ, Zurich, Switzerland). Penetration depth (in millimeters) was measured two to three times per tree at breast height, until two identical measurements (at a precision of 2.0 mm) were obtained. The slenderness coefficient (SC) was calculated as follows: SC = height (m)/DBH (m) according to Benomar et al. [38], where DBH corresponds to the diameter at breast height. The measurements of height and DBH were taken from Arriagada et al. [2]. The Tukey‒Kramer multiple comparison test was performed to determine significant differences between the means of each provenance for the traits evaluated.
2.3. Genetic Parameters
The subsequent marginal distributions for the parameters, narrow-sense heritability and variance components, were estimated using a Bayesian approach, via Gibbs sampling algorithm, in MTGSAM [39] using the following base model:
where y is the vector of observed values of WD and SC; b and p are vectors of fixed effect of block and provenance, respectively; f is the vector of random effects of family, and is the residual error. X, Z, and W are known incidence matrices. Posterior estimates for the narrow-sense heritability of traits, were calculated from posterior samples of variance components obtained by the model (1) detailed above, using the expression:
where and are the additive genetic and residual variances. This Bayesian analysis was contrasted with the restricted maximum likelihood (REML) method in ASReml 3.4 [40]. Coefficients of additive genetic variation (CVa) were calculated from posterior samples of additive genetic variance as follows:
where is the additive genetic variance and is the overall mean. Additive genetic correlations between WD and SC was estimated by:
where correspond to posterior distribution samples of genotypic covariance between the traits, and , correspond to posterior mean distribution samples of genotypic variance for WD and SC. Variance and covariance components were assumed to have an Inverted Wishart prior distribution. A uniform prior distribution (Flat) was considered for known environmental effects (blocks), whereas a normal distribution was used for the vector of traits of interest and additive genetic effects. The convergence and autocorrelation of the Gibbs chains were assessed using the tests available in the CODA library of the R program, Coventry, England [41].
2.4. Population Structure and Kinship Analysis
The software STRUCTURE, Stanford [CA], United States 2.3.2 [42] was used to cluster the individuals into a number (K) of genetically homogeneous subpopulations based on an admixture model with correlated allele frequencies between provenances. For each K value (previously K = 1–6), 10 runs were conducted separately each with 100,000 Monte Carlo Markov Chain (MCMC) replicates and a burn-in period of 10,000 iterations. The optimal K value was determined with the highest ΔK method [43]. The membership coefficient (Q) of each individual was used to form the population structure Q matrix. Only markers with allele frequencies of 5% or higher were included in data analyses. The software TASSEL, Ithaca [NY], United States 3.0 [44] was used to calculate the genetic relatedness among all pairs of individuals (kinship matrix).
2.5. Bayesian Association Mapping and Pleiotropy
The residuals from a general linear model for each trait were used as the adjusted phenotypes for the Bayesian association analysis (taking into account the effects of block and genetic structure). This approach is used to reduce the sources of unexplained variability, e.g., the effects of block and genetic structure, which implies a reduction in the error rate and increase the statistical power of association study. The probability that a locus is associated with a given trait was evaluated by the Bayes Factor (BF) and the Posterior Probability of Association (PPA) [45]. The BF is the ratio of marginal likelihoods between the probabilities of the model of association (M1) and a null model of no association (M0) [46]:
where the marginal likelihoods for M1 and M0 are defined by:
in which θ denotes the regression parameters, Gi denotes the genotype of the ith individual at the jth marker, Φ denotes the phenotype of the ith individual in a study of N samples, and pijk = P(Gij = k) is the probability that the genotype at the jth marker of the ith individual is k [46]. The Laplace approximation was used to estimate the marginal likelihoods of M1 and M0 [46].
The PPA combines the evidence in the observed association data (BF) with the prior probability (π) that a marker is associated. The π and BF are used to compute the posterior odds (PO):
where π is the prior probability that a given marker is associated with a trait. BF was calculated using a Bayesian regression analysis in the SNPTEST software [46]. The PPA was calculated from this PO, as follows:
The possible pleiotropic effect of one loci associated with more of one trait was corroborated by a multivariate Bayesian regression in SNPTEST [46]. Additionally, the association mapping was performed in TASSEL 3.0 software [44], employing the unified mixed linear model (Q + kinship) [47].
3. Results
3.1. Genetic Parameters
The trees from Wirrabara had the highest average depth of penetration of pilodyn at 16.8 mm, in contrast to the individuals from Cowell (13.0 mm), indicating that the latter has a denser wood. In contrast, the mean slenderness coefficient varied between 83.4 and 109.3 for the trees from Wirrabara and Cowell, respectively. Regarding regions, the trees from the Flinders Mountain Range had the highest slenderness coefficient and the lowest wood density, while the individuals of the Kangaroo Island and the Eyre Peninsula presented the highest wood density and the lowest coefficient of slenderness (Table 1).

Table 1.
Population means for wood density and slenderness coefficient in the populations of E. cladocalyx.
Based on subsequent marginal distributions, the density of the wood in E. cladocalyx showed a moderate heritability (mean of = 0.29), with a credibility range (90%) of 0.06 to 0.74; while the heritability for the slenderness coefficient was high = 0.48 (credibility region from 0.11 to 0.87). The posterior mean of the genetic correlation between wood density and the slenderness coefficient was negative with a value of 0.3 and a credibility range of −0.49 to −0.11. The estimates of heritability via REML were similar to those obtained by the Bayesian method, with values of 0.30 and 0.45, for wood density and slenderness coefficient, respectively. The genetic correlation between both traits was moderate and negative (−0.34). The estimations of variance components, the heritability values and their genetic correlation, based on the point estimates (mean, mode, and median) of the posterior marginal distributions (and from the REML method), are shown in Table 2.

Table 2.
Variance components, heritability for wood density (WD) and slenderness coefficient (SC), and the genetic correlation between the traits in the population of E. cladocalyx.
3.2. Genetic Structure
The trees from the five Australian locations evaluated in this study were grouped into three genetically differentiated groups, which coincide with the three geographical regions from which each population originates. Additionally, individuals from Illapel (local population) were grouped mainly with individuals from the Flinders Mountain Range (Figure 1). Consistent with the above, the mean Fst value of a given cluster is not contained within the credibility regions of the other groups, which confirms the significant genetic differentiation (Table 3).
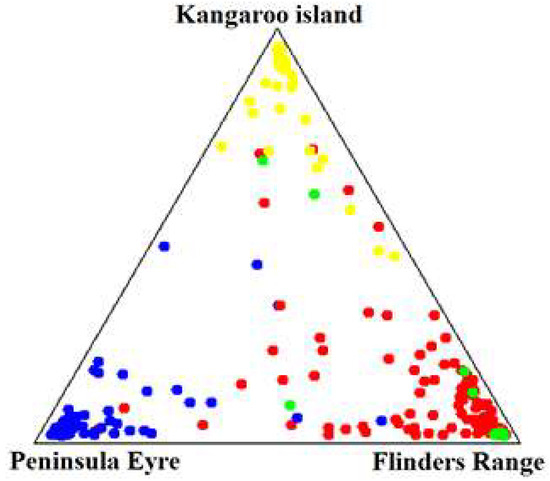
Figure 1.
Bayesian clustering approach showing three groups genetically differentiated, according to the geographical origin of E. cladocalyx in Australia. The blue dots correspond to the populations from Marble Range and Cowell, the yellow dots correspond to the population from Flinders Chase, the red dots correspond to the populations from Wirrabara and Remarkable, and the green dots correspond to the local population taken from Illapel, Chile.

Table 3.
Bayesian point estimation (mode, median, and mean) and 90% credible regions of Fst calculated in each group genetically differentiated of E. cladocalyx.
3.3. Bayesian Association Mapping and Pleiotropy
A total of 13 putative associations, comprising 9 SSR markers, were identified for wood density and slenderness coefficient by the association mapping based on a unified mixed model (frequentist) (Table 4) [47]. Six loci were associated with WD, where the loci qtlWD130 located on chromosome 4 at 52.1 cM, explained the highest proportion of the phenotypic variance (17%). Similarly, seven markers were associated with SC, and the greater proportion of the phenotypic variance was explained by the loci qtlSR56 (21%). Four of these loci showed significant associations with WD and SC concomitantly. This suggests a common genetic control between the traits, which could result in possible pleiotropic effects for these loci. On the other hand, less loci were identified in the Bayesian association mapping (four and three loci associated with WD and SC, respectively), which presented a moderate (3 < BF <10) to extremely strong (100 < BF) evidence of association (model M1) (Figure 2, Table 4), according to the scale presented by Andraszewicz et al. [48]. The posterior likelihood of association (PPA) indicated that loci with moderate evidence of association (3 < BF <10) have a PPA of less than 0.35, while loci with strong evidence of association (10 < BF < 30) showed a PPA between 0.35 and 0.61. Furthermore, loci with extremely strong evidence (100 > BF) have PPA values greater than 0.84 (Table 4).

Table 4.
Summary of loci associated with wood density (WD) and slenderness coefficient (SC) using a unified mixed linear model and Bayesian regression analysis, measured in 17-year-old trees of E. cladocalyx in arid conditions.
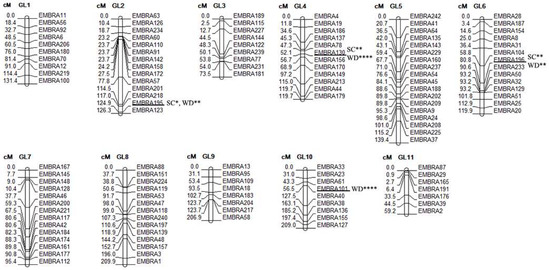
Figure 2.
Loci associated with wood density (WD) and slenderness coefficient (SC) across the genome of E. cladocalyx (Bayesian multivariate mapping). To the left the distance in centiMorgan (cM) and to the right the name of the molecular markers (SSR, n = 130). LG: Linkage Group. * moderate evidence of association (3 < BF < 10); ** strong evidence of association (10 < BF < 30); ** very strong evidence of association (30 < BF < 100). **** extreme evidence of association (100 < BF). BF: Bayes Factor.
Three QTL associated with both traits were detected through a multivariate Bayesian analysis [46] on LG2 at 125 cM, on LG4 at 52 cM, and on LG6 at 81 cM. The bi-trait QTL analysis indicated that these loci presented a BF > 15, indicating that the evidence of association is between the categories of strong and extremely strong association. Furthermore, these loci have a PPA of 0.45 to 0.99, indicating a high probability of association (Table 4).
4. Discussion
4.1. Phenotypic Variability and Genetic Parameters
According to the results, wood density (WD) and the slenderness coefficient (SC) varied significantly among the provenances of E. cladocalyx evaluated in this study. The morphological variability of E. cladocalyx (such as stem straightness, flowering intensity, diameter and tree height) has been previously reported in other studies [49,50,51]. For example, Mora et al. [49] and Vargas-Reeve et al. [51] determined that trees from the Flinders Range have a diameter of the stem larger than trees from other natural regions of the species. In general, a larger diameter correlates negatively with SC in trees, in which it has been observed that trees with a greater diameter have a lower SC [28,52,53]. Consistently, the trees from Wirrabara and Mount Remarkable showed the lowest SC values, while the trees from Cowell were the slenderest. A high SC value indicates that trees are more susceptible to damage by mechanical pressures [29]. According to Navratil [54], trees with a SC greater than 100 have a high probability of suffering from wind damage. In this sense, the individuals of the Flinders Mountain Range would present a greater mechanical resistance than the trees from the Eyre Peninsula. Interestingly, the Flinders Chase, Cowell and Marble Range populations had the lowest penetration values of pilodyn (WD), which indicates that these trees have a higher wood density than those from the Flinders Range. It should be noted that Bush et al. [6] reported that trees from the Eyre peninsula have a lower wood density (based on the water displacement method, TAPPI [55]) than trees that come from the Flinders Mountain Range and Kangaroo Island. Moreover, these authors also demonstrated that there is a negative correlation between wood density and tree diameter in E. cladocalyx. The variability observed among the populations for WD and SC, had similarities with the natural distribution of the same. Mora et al. [49] indicate that in genetically differentiated groups a reduction of genetic variability is observed. This presents evidence that the location of origin of an individual influenced the expression of their traits. Moreover, in WD the populations belonging to Eyre Peninsula and Kangaroo Island regions did not present significant differences between them (Table 1), indicating a possible genetic flow between these regions that is not shared with the Flinders Range region.
According to REML and Bayesian estimates, the heritability for WD and SC was moderate and high, respectively, indicating that the phenotypic variability observed between provenances for these traits is explained by an important additive genetic component. Bush et al. [6] determined that wood density in E. cladocalyx presents a narrow-sense heritability of 0.39, which could be considered moderate to high, while in E. globulus, Stackpole et al. [25] determined that wood density is a highly heritable trait, with a value of h2 = 0.51. Our results are subtly lower than in previous studies in E. cladocalyx and in other Eucalyptus species. In general, the values of heritability, both broad and narrow, are comparatively lower in environments with low water availability [56,57,58], which would confirm the differences between our results and previous studies.
The SC is not a trait usually evaluated in the genetic studies of Eucalyptus. However, it has been determined that this trait has moderate to high heritability in other species. For example, Pastorino et al. [33] determined that the heritability of SC in cypress is 0.15, while Chaendaekattu and Mydin [34] reported a heritability for SC between 0.25 and 0.43 in trees of Hevea brasiliensis. It should be noted that the heritability for stem diameter and the height in trees of E. cladocalyx, variables related to SC, is low to moderate [49,59], however, the results of the present study suggest that SC is a more inheritable trait than height and diameter in E. cladocalyx.
The WD and SC presented a negative genetic correlation. Slender shafts tend to be denser [60], therefore, the degree of penetration of Pilodyn in the stem is expected to be lower in slender trees. A greater Pilodyn penetration implies that the tree is less dense, therefore, the correlation between the density and slenderness of a tree is expected to be negative.
4.2. Genetic Structure
The population of E. cladocalyx evaluated in this study is composed of three genetically differentiated groups, which is consistent with the findings of McDonald et al. [61], Mora et al. [37], and Arriagada et al. [2]. The individuals were grouped according to the three geographical regions from which the evaluated populations were taken (Flinders Range, Eyre Peninsula, and Kangaroo Island). In addition, between the determined genetic groups, there is a significant and moderate differentiation according to the values of Fst, which is consistent with previous studies in E. cladocalyx [61,62,63].
The effect of the genetic structure of the population on the analysis of association and detection of QTLs has been widely discussed [64,65]. Particularly, the presence of a significant genetic structure, and inadequate information on kinship among individuals can generate false marker-trait associations [66]. For all QTLs analyses, a full model considering the genetic structure effects was contrasted with a null model not including these effects. The genetic structure effect was significant for all association analyses; therefore, it was used for the detection of QTLs in this study [47]. In several plant species, the effect of the structure and the degree of kinship in the association studies has been evaluated [65,67].
4.3. Bayesian Association Mapping and Pleiotropy
Wood density is one of the most important indicators of sawn wood quality and pulp yield [24]. Several studies have shown that density has a moderate to high genetic control in different species of Eucalyptus [25,26], which suggests that this trait could be subject to genetic improvement through selection assisted by molecular markers. In this context, a significant number of studies have been conducted to identify markers associated with wood density in Eucalyptus. For example, Bundock et al. [68] detected QTLs associated with wood density in E. globulus, on chromosomes 6 and 11, which explained between 8% and 12% of the phenotypic variation, respectively. Thumma et al. [19] identified QTLs that explained between 3.6% and 5.6% of the variation in wood density of E. nitens, using RFLP and SSR markers. These findings are concordant with our results. Some of the QTLs detected in this study explained about 16% of the phenotypic variation of wood density in E. cladocalyx (qtlWD130 and qtlWD101), which can be used as selection criteria for higher trees for this phenotype.
In the present study, QTL qtlWD195, located on chromosome 2 at a distance of 124.9 cM, explained 7% of the wood density variation of E. cladocalyx. Similarly, in the same chromosome, Gion et al. [18] reported two QTLs, at 123 cM and 124 cM, associated with wood density in hybrids of E. urophylla and E. grandis, explaining up to 10% of the phenotypic variation. Similarly, the QTL qtlWD101, identified on chromosome 10 at 56.5 cM, is consistent with a region indicated on the same chromosome by Freeman et al. [69] in E. globulus, which was also stable in several populations and sites. Furthermore, in this same chromosomal region, Hamilton et al. [70] identified QTLs associated with acoustic wave velocity, an indirect measure of wood density in E. globulus. According to our results and previous studies, chromosome 10 could be strongly involved in the genetic control of wood density in E. cladocalyx and other Eucalyptus species.
The SC has been widely used to measure the stability and resistance of the tree to the mechanical pressures of the environment. Moreover, like wood density, the slenderness coefficient is used to evaluate the potential of a tree for the production of paper and sawn wood [28,71]. Another important finding of the bi-trait Bayesian analysis was the existence of three large-effect pleiotropic QTLs located on LG4 at 52 cM, on LG2 at 125 cM, and on LG6 at 81 cM, indicating that both traits are genetically related.
The detection of QTL for the SC has been poorly addressed. However, the results of the present study can be contrasted with the mapping of previously reported QTLs for tree diameter and height variables, since both traits determine the slenderness of a tree. Freeman et al. [69] detected a QTL on chromosome 4 associated with the diameter at breast height (DBH) in E. globulus, whose position is close to qtlSC130, reported in the present study.
According to Stephens and Balding [45], the BF is comparable to the likelihood ratio, but compares two different models instead of two parameter values in a model. BF is often used as an indicator of the evidence of association of a locus to a trait, in which the moderate or strong categories are considered as definitive evidence against the null model (M0). According to this principle, PPA has been used as a probabilistic measure of posterior evidence, which combines the previous probability of association (π) and the evidence of association in the observed data (BF). Because π is small, the BF must be large to provide convincing evidence of an association.
We determined that a locus with a BF > 8 delivers a moderate evidence to determine that the hypothesis of association with the given trait is more likely than the null hypothesis of non-association. The unified mixed model indicated that 13 loci showed a significant association with traits. However, only six of these loci presented strong evidence of association (BF>15 and PPA>0.44) through the Bayesian regression analysis. Additionally, the Bayesian bi-trait regression (pleiotropy analysis) indicated that three of the four loci identified through the unified mixed model presented strong evidence of association with WD and SC. This provides convincing evidence that the loci qtlWD130/qtlSC130, qtlWD195/qtlSC195 and qtlWD196/qtlSC196, have a significant pleiotropic effect, being associated with both traits under study.
5. Conclusions
E. cladocalyx has a recognized potential to produce structural timber under arid environmental conditions. According to our results, wood density and the slenderness of the trees of E. cladocalyx presented a moderate and high genetic control, respectively. Several of the associations found for wood density were located in chromosomal regions previously reported for this trait in other Eucalyptus species, revealing collinearity of QTLs. In the context of marker-assisted selection, the QTLs associated with WD (4) and SC (2) can be used as selection criteria in breeding programs for the species under arid conditions. The QTLs identified in this study explained 48% and 20% of the observed genetic variance in WD and SC, respectively. This may be an indication that the coverage of markers in insufficient. Thus, it would be appropriate to include a greater amount of markers in future studies.
Author Contributions
Conceptualization, F.M., O.A., C.E.V., R.B. and C.M.; Data curation, P.B. and C.E.V.; Formal analysis, G.S.M. and C.M.; Funding acquisition, F.M.; Methodology, O.A., C.M., and F.M.; Project administration, F.M.; Resources, O.A. and F.M.; Supervision, C.M., P.B., R.B. and F.M.; Writing—original draft, O.A. and C.E.V.; Writing—review & editing, P.B., C.M. and F.M.
Funding
The study was supported by FONDECYT (Grant Number 1170695).
Acknowledgments
The authors thank Mr. Augusto Gomes for providing the samples of E. cladocalyx. Paulina Ballesta thanks CONICYT for a doctoral fellowship (CONICYT-PCHA/Doctorado Nacional/año 2016-folio 21160624). Carlos Maldonado thanks CONICYT for a doctoral fellowship (CONICYT-PCHA/Doctorado Nacional/año 2017-folio 21171466).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bush, D.; Kain, D.; Kanowski, P.; Matheson, C. Genetic parameter estimates informed by a marker-based pedigree: A case study with Eucalyptus cladocalyx in southern Australia. Tree Genet. Genomes 2015, 11, 798. [Google Scholar] [CrossRef]
- Arriagada, O.; Amaral Junior, A.T.; Mora, F. Thirteen years under arid conditions: Exploring marker-trait associations in Eucalyptus cladocalyx for complex traits related to flowering, stem form and growth. Breed. Sci. 2018, 68, 367–374. [Google Scholar] [CrossRef] [PubMed]
- McMahon, L.; Brendan, G.; Hean, R. Eucalyptus cladocalyx. Primefact 2010, 1077, 1–5. [Google Scholar]
- Clarke, B.; Mcleod, I.; Vercoe, T. Trees for farm Forestry: 22 Promising Species; RIRDC Press: Canberra, Australia, 2009. [Google Scholar]
- Lundqvist, S.O.; Grahn, T.; Olsson, L.; Seifert, T. Comparison of wood, fibre and vessel properties of drought-tolerant eucalypts in South Africa. Southern For. 2017, 79, 215–225. [Google Scholar] [CrossRef]
- Bush, D.; McCarthy, K.; Meder, R. Genetic variation of natural durability traits in Eucalyptus cladocalyx (sugar gum). Ann. For. Sci. 2011, 68, 1057–1066. [Google Scholar] [CrossRef]
- Wessels, C.B.; Crafford, P.L.; Du Toit, B.; Grahn, T.; Johansson, M.; Lundqvist, S.O.; Säll, H.; Seifert, T. Variation in physical and mechanical properties from three drought tolerant Eucalyptus species grown on the dry west coast of Southern Africa. Eur. J. Wood Wood Prod. 2016, 74, 563–575. [Google Scholar] [CrossRef]
- Li, Y.; Apiolaza, L.A.; Altaner, C. Genetic variation in heartwood properties and growth traits of Eucalyptus bosistoana. Eur. J. For. Res. 2018, 137, 565–572. [Google Scholar] [CrossRef]
- Khan, B.I.; Solo-Gabriele, H.M.; Townsend, T.G.; Cai, Y. Release of arsenic to the environment from CCA-treated wood. 1. Leaching and speciation during service. Environ. Sci. Technol. 2006, 40, 988–993. [Google Scholar] [CrossRef]
- Thistlethwaite, F.R.; Ratcliffe, B.; Klápště, J.; Porth, I.; Chen, C.; Stoehr, M.U.; El-Kassaby, Y.A. Genomic prediction accuracies in space and time for height and wood density of Douglas-fir using exome capture as the genotyping platform. BMC Genomics 2017, 18, 930. [Google Scholar] [CrossRef]
- Sundararaj, R.; Shanbhag, R.R.; Nagaveni, H.C.; Vijayalakshmi, G. Natural durability of timbers under Indian environmental conditions—An overview. Int. Biodeterior. Biodegrad. 2015, 103, 196–214. [Google Scholar] [CrossRef]
- Naidoo, S.; Zbonák, A.; Ahmed, F. The effect of moisture availability on wood density and vessel characteristics of Eucalyptus grandis in the warm temperate region of South Africa. In Proceedings of the 5th International Symposium on Wood Structure and Properties, Sielnica, Slovakia, 3–6 September 2006; pp. 117–122. [Google Scholar]
- Nabais, C.; Hansen, J.K.; David-Schwartz, R.; Klisz, M.; López, R.; Rozenberg, P. The effect of climate on wood density: What provenance trials tell us? For. Ecol. Manag. 2018, 408, 148–156. [Google Scholar] [CrossRef]
- Isik, F.; Mora, C.R.; Schimleck, L.R. Genetic variation in Pinus taeda wood properties predicted using non-destructive techniques. Ann. For. Sci. 2011, 68, 283–293. [Google Scholar] [CrossRef]
- Fundova, I.; Funda, T.; Wu, H.X. Non-destructive wood density assessment of Scots pine (Pinus sylvestris L.) using Resistograph and Pilodyn. PLoS ONE 2018, 13, e0204518. [Google Scholar] [CrossRef] [PubMed]
- Woodcock, D.W.; Shier, A.D. Does canopy position affect wood specific gravity in temperate forest trees. Ann. Bot. 2003, 91, 529–537. [Google Scholar] [CrossRef] [PubMed]
- Chave, J.; Muller-Landau, H.C.; Baker, T.R.; Easdale, T.A.; ter Steege, H.; Webb, C.O. Regional and phylogenetic variation of wood density across 2456 neotropical tree species. Ecol. Appl. 2006, 16, 2356–2367. [Google Scholar] [CrossRef]
- Gion, J.M.; Carouché, A.; Deweer, S.; Bedon, F.; Pichavant, F.; Charpentier, J.P.; Baillères, H.; Rozenberg, P.; Carocha, V.; Ognouabi, N.; et al. Comprehensive genetic dissection of wood properties in a widely-grown tropical tree: Eucalyptus. BMC Genomics 2011, 12, 301. [Google Scholar] [CrossRef] [PubMed]
- Thumma, B.R.; Baltunis, B.S.; Bell, J.C.; Emebiri, L.C.; Moran, G.F.; Southerton, S.G. Quantitative trait locus (QTL) analysis of growth and vegetative propagation traits in Eucalyptus nitens full-sib families. Tree Genet. Genomes 2010, 6, 877–889. [Google Scholar] [CrossRef]
- Louzada, J.L. Genetic correlations between wood density components in Pinus pinaster Ait. Ann. For. Sci. 2003, 60, 285–294. [Google Scholar] [CrossRef]
- Li, X.; Wu, H.X.; Southerton, S.G. Transcriptome profiling of Pinus radiata juvenile wood with contrasting stiffness identifies putative candidate genes involved in microfibril orientation and cell wall mechanics. BMC Genomics 2011, 12, 1–16. [Google Scholar] [CrossRef]
- Southerton, S.G.; MacMillan, C.P.; Bell, J.C.; Bhuiyan, N.; Dowries, G.; Ravenwood, I.C.; Joyce, K.R.; Williams, D.; Thumma, B.R. Association of allelic variation in xylem genes with wood properties in Eucalyptus nitens. Aust. For. 2010, 73, 259–264. [Google Scholar] [CrossRef]
- Kanberga-Silina, K.; Jansons, A.; Rungis, D. Expression of three phenylpropanoid pathway genes in Scots pine (Pinus sylvestris L.) in open-pollinated families with differing relative wood densities during early and late wood formation. Silvae Genet. 2015, 64, 148–159. [Google Scholar] [CrossRef]
- Nakahama, K.; Urata, N.; Shinya, T.; Hayashi, K.; Nanto, K.; Rosa, A.C.; Kawaoka, A. RNA-seq analysis of lignocellulose-related genes in hybrid Eucalyptus with contrasting wood basic density. BMC Plant Biol. 2018, 18, 156. [Google Scholar] [CrossRef] [PubMed]
- Stackpole, D.J.; Vaillancourt, R.E.; Alves, A.; Rodrigues, J.; Potts, B.M. Genetic variation in the chemical components of Eucalyptus globulus wood. G3-Genes Genome Genet. 2011, 1, 151–159. [Google Scholar] [CrossRef] [PubMed]
- Stackpole, D.J.; Vaillancourt, R.E.; de Aguigar, M.; Potts, B.M. Age trends in genetic parameters for growth and wood density in Eucalyptus globulus. Tree Genet. Genomes 2010, 6, 179–193. [Google Scholar] [CrossRef]
- Fournier, M.; Baillères, H.; Chanson, B. Tree biomechanics: Growth, cumulative prestresses and re-orientations. Biomimetics 1994, 2, 229–251. [Google Scholar]
- Jullien, D.; Widmann, R.; Loup, C.; Thibaut, B. Relationship between tree morphology and growth stress in mature European beech stands. Ann. For. Sci. 2013, 70, 133–142. [Google Scholar] [CrossRef]
- Eguakun, F.S.; Oyebade, B.A. Linear and nonlinear slenderness coefficient models for Pinus caribaea (Morelet) stands in Southwestern Nigeria. J. Agri. Vet. Sci. 2015, 8, 26–30. [Google Scholar]
- Rust, S. Analysis of regional variation of height growth and slenderness in populations of six urban tree species using a quantile regression approach. Urban For. Urban Green. 2014, 13, 336–343. [Google Scholar] [CrossRef]
- Harja, D.; Vincent, G.; Mulia, R.; van Noordwijk, M. Tree shape plasticity in relation to crown exposure. Trees-Struct. Funct. 2012, 26, 1275–1285. [Google Scholar] [CrossRef]
- Watt, M.S.; Kirschbaum, U. Moving beyond simple linear allometric relationships between tree height and diameter. Ecol. Model. 2011, 222, 3910–3916. [Google Scholar] [CrossRef]
- Pastorino, M.J.; Ghirardi, S.; Grosfeld, J.; Gallo, L.A.; Puntieri, J.G. Genetic variation in architectural seedling traits of Patagonian cypress natural populations from the extremes of a precipitation range. Ann. For. Sci. 2010, 67, 508. [Google Scholar] [CrossRef]
- Chaendaekattu, N.; Mydin, K.K. Inheritance pattern and genetic correlations among growth and wood quality traits in Para rubber tree (Hevea brasiliensis) and implications for breeding. Tree Genet. Genomes 2018, 14, 63. [Google Scholar] [CrossRef]
- Ducey, M.J. Evergreenness and wood density predict height–diameter scaling in trees of the northeastern United States. For. Eecol. Manag. 2012, 279, 21–26. [Google Scholar] [CrossRef]
- Silva, M.N.D. Extraction of genomic DNA from leaf tissues of mature native species of the cerrado. Rev. Árvore 2010, 34, 973–978. [Google Scholar] [CrossRef]
- Mora, F.; Arriagada, O.; Ballesta, P.; Ruiz, E. Genetic diversity and population structure of a drought-tolerant species of Eucalyptus, using microsatellite markers. J. Plant Biochem. Biotechnol. 2017, 26, 274–281. [Google Scholar] [CrossRef]
- Benomar, L.; DesRochers, A.; Larocque, G.R. The effects of spacing on growth, morphology and biomass production and allocation in two hybrid poplar clones growing in the boreal region of Canada. Trees 2012, 26, 939–949. [Google Scholar] [CrossRef]
- Van Tassell, C.P.; Van Vleck, L.D. Multiple-trait Gibbs sampler for animal models: Flexible programs for Bayesian and likelihood-based (co) variance component inference. J. Anim. Sci. 1996, 74, 2586–2597. [Google Scholar] [CrossRef]
- Gilmour, A.R.; Thompson, R.; Cullis, B.R.; Welham, S.J. ASReml estimates variance matrices from multivariate data using the animal model. In Proceedings of the 7th World Congress on Genetics Applied to Livestock Production, Montpellier, France, 19–23 August 2002; Volume 28, pp. 1–2. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2014; Available online: http://www.R-project.org/ (accessed on 10 December 2018).
- Pritchard, J.K.; Stephens, M.; Donnelly, P. Inference of population structure using multilocus genotype data. Genetics 2000, 155, 945–959. [Google Scholar]
- Evanno, G.; Regnaut, S.; Goudet, J. Detecting the number of clusters of individuals using the software structure: A simulation study. Mol. Ecol. 2005, 14, 2611–2620. [Google Scholar] [CrossRef]
- Bradbury, P.J.; Zhang, Z.; Kroon, D.E.; Casstevens, T.M.; Ramdoss, Y.; Buckler, E.S. TASSEL: Software for association mapping of complex traits in diverse samples. Bioinformatics 2007, 23, 2633–2635. [Google Scholar] [CrossRef]
- Stephens, M.; Balding, D.J. Bayesian statistical methods for genetic association studies. Nat. Rev. Genet. 2009, 10, 681–690. [Google Scholar] [CrossRef] [PubMed]
- Marchini, J.; Band, G. SNPTEST. 2016. Available online: https://mathgen.stats.ox.ac.uk/genetics_software/snptest/snptest.html (accessed on 15 December 2018).
- Yu, J.; Pressoir, G.; Briggs, W.H.; Bi, I.V.; Yamasaki, M.; Doebley, J.F.; McMullen, M.D.; Gaut, B.S.; Nielsen, D.M.; Holland, J.B.; et al. A unified mixed-model method for association mapping that accounts for multiple levels of relatedness. Nat. Genet. 2006, 38, 203–208. [Google Scholar] [CrossRef] [PubMed]
- Andraszewicz, S.; Scheibehenne, B.; Rieskamp, J.; Grasman, R.; Verhagen, J.; Wagenmakers, E.J. An introduction to Bayesian hypothesis testing for management research. J. Manag. 2015, 41, 521–543. [Google Scholar] [CrossRef]
- Mora, F.; Gleadow, R.; Perret, S.; Scapim, C.A. Genetic variation for early flowering, survival and growth in sugar gum (Eucalyptus cladocalyx F. Muell) in southern Atacama Desert. Euphytica 2009, 169, 335–344. [Google Scholar] [CrossRef]
- Cané-Retamales, C.; Mora, F.; Vargas-Reeve, F.; Perret, S.; Contreras-Soto, R. Bayesian threshold analysis of breeding values, genetic correlation and heritability of flowering intensity in Eucalyptus cladocalyx under arid conditions. Euphytica 2011, 178, 177–183. [Google Scholar] [CrossRef]
- Vargas-Reeve, F.; Mora, F.; Perret, S.; Scapim, C.A. Heritability of stem straightness and genetic correlations in Eucalyptus cladocalyx in the semi-arid region of Chile. Crop Breed Appl. Biotechnol. 2013, 13, 107–112. [Google Scholar] [CrossRef]
- Díaz-Bravo, S.; Espinosa, M.; Valenzuela, L.; Cancino, J.; Lasserre, J.P. Efecto del raleo en el crecimiento y algunas propiedades de la madera de Eucalyptus nitens en una plantación de 15 años. Maderas-Cienc. Tecnol. 2012, 14, 373–388. [Google Scholar] [CrossRef]
- Hallinger, M.; Johansson, V.; Schmalholz, M.; Sjöberg, S.; Ranius, T. Factors driving tree mortality in retained forest fragments. For. Ecol. Manag. 2016, 368, 163–172. [Google Scholar] [CrossRef]
- Navratil, S. Silvicultural systems for managing deciduous and mixedwood stands with white spruce understory. In Silvicultural of Temperate and Boreal Broadleaf-Conifer Mixture; Comeau, P.G., Thomas, K.D., Eds.; Ministry of Forests: Victoria, BC, USA, 1996; pp. 35–46. [Google Scholar]
- TAPPI. Basic density and moisture content of pulpwood. TAPPI 1989, 258, 98. [Google Scholar]
- Hung, T.D.; Brawner, J.T.; Meder, R.; Lee, D.J.; Southerton, S.; Thinh, H.H.; Dieters, M.J. Estimates of genetic parameters for growth and wood properties in Eucalyptus pellita F. Muell. to support tree breeding in Vietnam. Ann. For. Sci. 2015, 72, 205–217. [Google Scholar] [CrossRef]
- Mohammadi, R.; Sadeghzadeh, D.; Armion, M.; Amri, A. Evaluation of durum wheat experimental lines under different climate and water regime conditions of Iran. Crop Pasture Sci. 2011, 62, 137–151. [Google Scholar] [CrossRef]
- Ramírez-Valiente, J.A.; Valladares, F.; Huertas, A.D.; Granados, S.; Aranda, I. Factors affecting cork oak growth under dry conditions: Local adaptation and contrasting additive genetic variance within populations. Tree Genet. Genomes 2011, 7, 285–295. [Google Scholar] [CrossRef]
- Bush, D.; Kain, D.; Matheson, C.; Kanowski, P. Marker-based adjustment of the additive relationship matrix for estimation of genetic parameters—An example using Eucalyptus cladocalyx. Tree Genet. Genomes 2011, 7, 23–35. [Google Scholar] [CrossRef]
- Lenz, P.; Auty, D.; Achim, A.; Beaulieu, J.; Mackay, J. Genetic improvement of white spruce mechanical wood traits-early screening by means of acoustic velocity. Forests 2013, 4, 575–594. [Google Scholar] [CrossRef]
- McDonald, M.W.; Rawlins, M.; Butchet, P.A.; Bell, J.C. Regional divergence and inbreeding in Eucalyptus cladocalyx (Myrtaceae). Aust. J. Bot. 2003, 51, 393–403. [Google Scholar] [CrossRef]
- Ballesta, P.; Mora, F.; Contreras-Soto, R.I.; Ruiz, E.; Perret, S. Analysis of the genetic diversity of Eucalyptus cladocalyx (sugar gum) using ISSR markers. Acta Sci-Agron. 2015, 37, 133–140. [Google Scholar] [CrossRef]
- Bush, D.; Thumma, B. Characterising a Eucalyptus cladocalyx breeding population using SNP markers. Tree Genet. Genomes 2013, 9, 741–752. [Google Scholar] [CrossRef]
- Korte, A.; Farlow, A. The advantages and limitations of trait analysis with GWAS: A review. Plant Methods 2013, 9, 29. [Google Scholar] [CrossRef]
- Cappa, E.P.; El-Kassaby, Y.A.; Garcia, M.N.; Acuña, C.; Borralho, N.M.; Grattapaglia, D.; Poltri, S.N.M. Impacts of population structure and analytical models in genome-wide association studies of complex traits in forest trees: A case study in Eucalyptus globulus. PLoS ONE 2013, 8, e81267. [Google Scholar] [CrossRef]
- Li, M.; Liu, X.; Bradbury, P.; Yu, J.; Zhang, Y.M.; Todhunter, R.J.; Buckler, E.S.; Zhang, Z. Enrichment of statistical power for genome-wide association studies. BMC Biol. 2014, 12, 73. [Google Scholar] [CrossRef]
- Uchiyama, K.; Iwata, H.; Moriguchi, Y.; Ujino-Ihara, T.; Ueno, S.; Taguchi, Y.; Tsubomura, M.; Mishima, K.; Iki, T.; Watanabe, A.; et al. Demonstration of genome-wide association studies for identifying markers for wood property and male strobili traits in Cryptomeria japonica. PLoS ONE 2013, 8, e79866. [Google Scholar] [CrossRef] [PubMed]
- Bundock, P.C.; Potts, B.M.; Vaillancourt, R.E. Detection and stability of quantitative trait loci (QTL) in Eucalyptus globulus. Tree Genet. Genomes 2008, 4, 85–95. [Google Scholar] [CrossRef]
- Freeman, J.S.; Potts, B.M.; Downes, G.M.; Pilbeam, D.; Thavamanikumar, S.; Vaillancourt, R.E. Stability of quantitative trait loci for growth and wood properties across multiple pedigrees and environments in Eucalyptus globulus. New Phytol. 2013, 198, 1121–1134. [Google Scholar] [CrossRef] [PubMed]
- Hamilton, M.G.; Freeman, J.S.; Blackburn, D.P.; Downes, G.M.; Pilbeam, D.J.; Potts, B.M. Independent lines of evidence of a genetic relationship between acoustic wave velocity and kraft pulp yield in Eucalyptus globulus. Ann. For. Sci. 2017, 74, 17. [Google Scholar] [CrossRef]
- Pirralho, M.; Flores, D.; Sousa, V.B.; Quilhó, T.; Knapic, S.; Pereira, H. Evaluation on paper making potential of nine Eucalyptus species based on wood anatomical features. Ind. Crop Prod. 2014, 54, 327–334. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).