Aboveground Biomass Allocation and Additive Allometric Models for Natural Larix gmelinii in the Western Daxing’anling Mountains, Northeastern China
Abstract
:1. Introduction
2. Materials and Methods
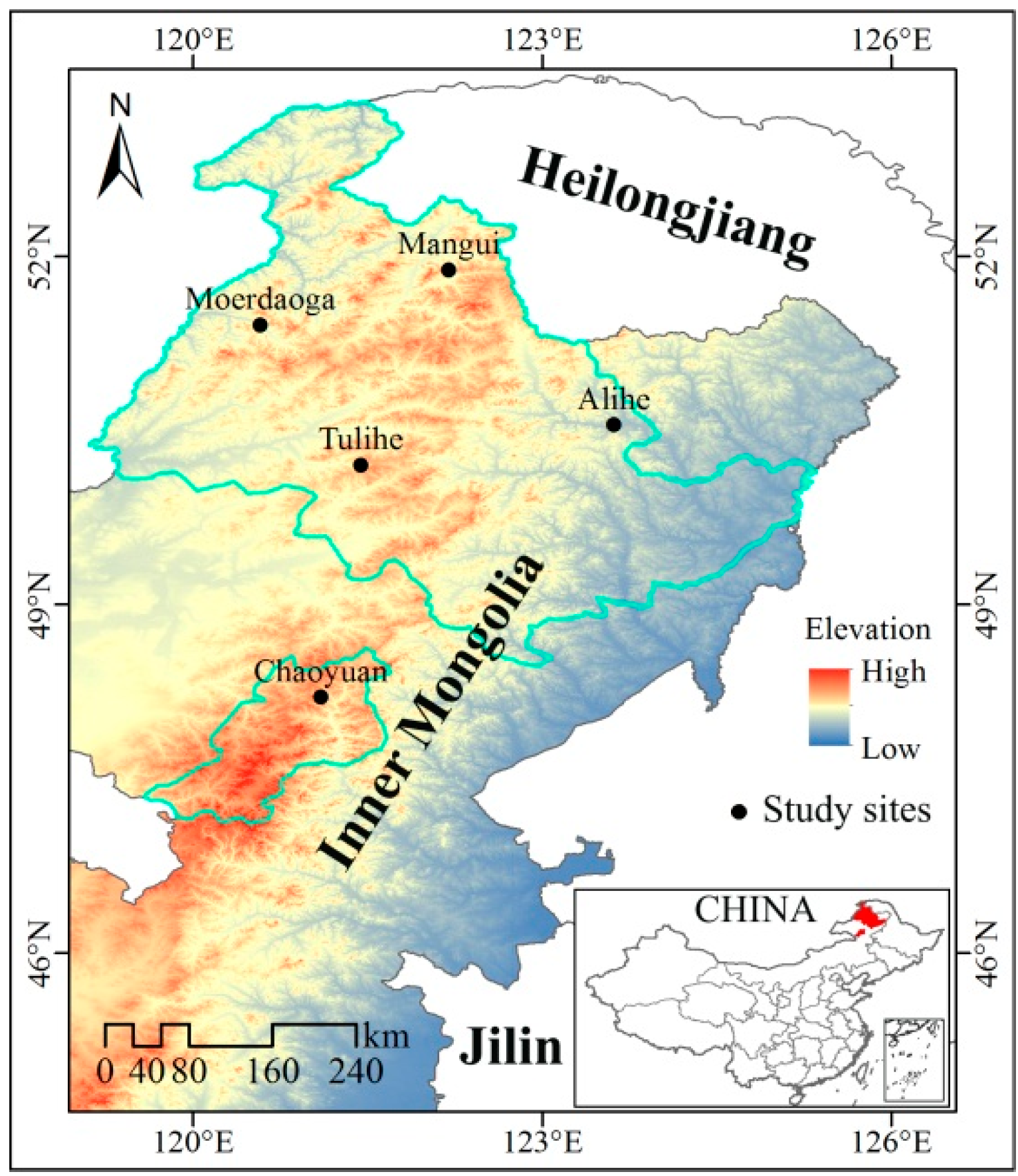
2.1. Study Area
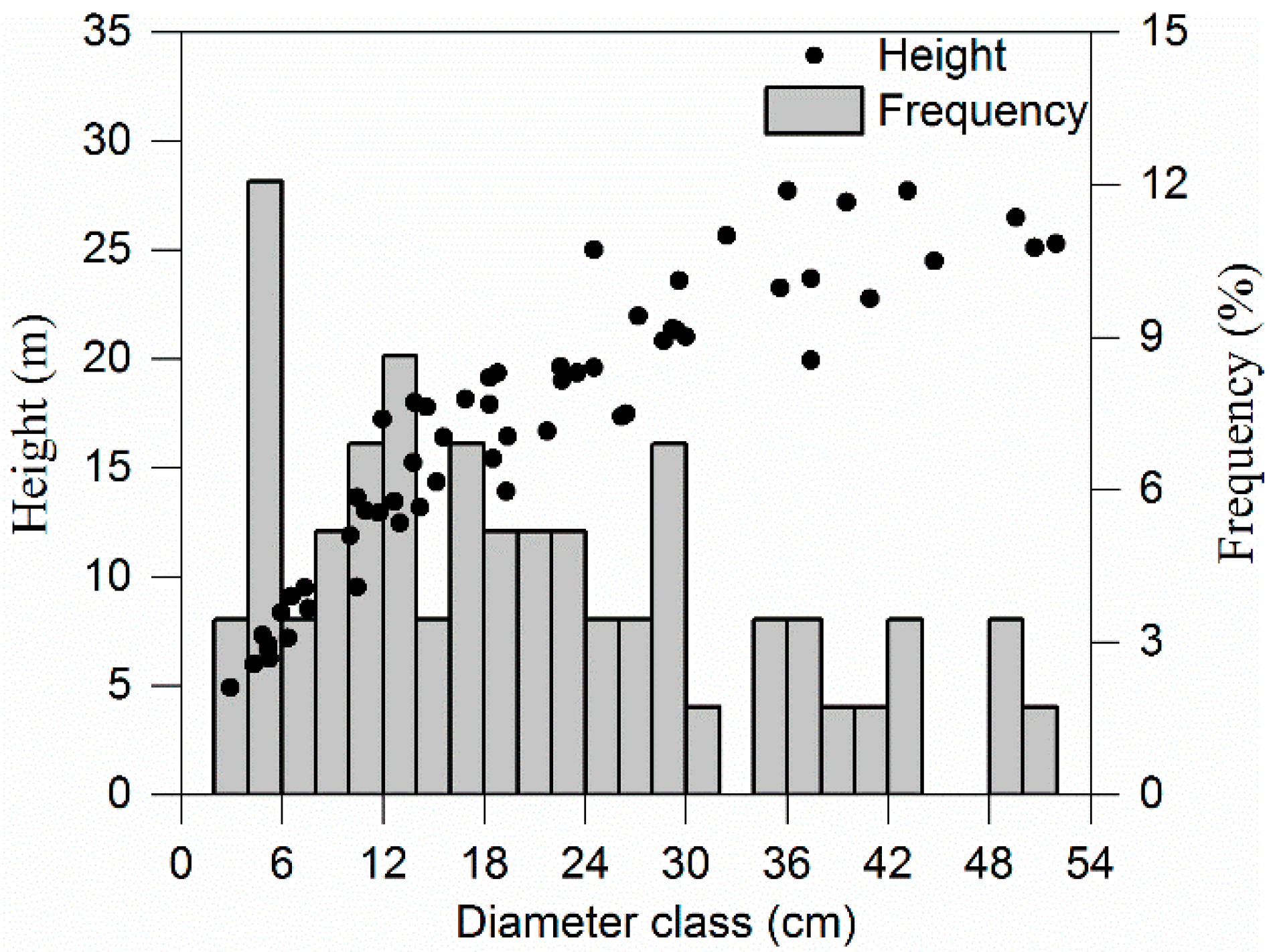
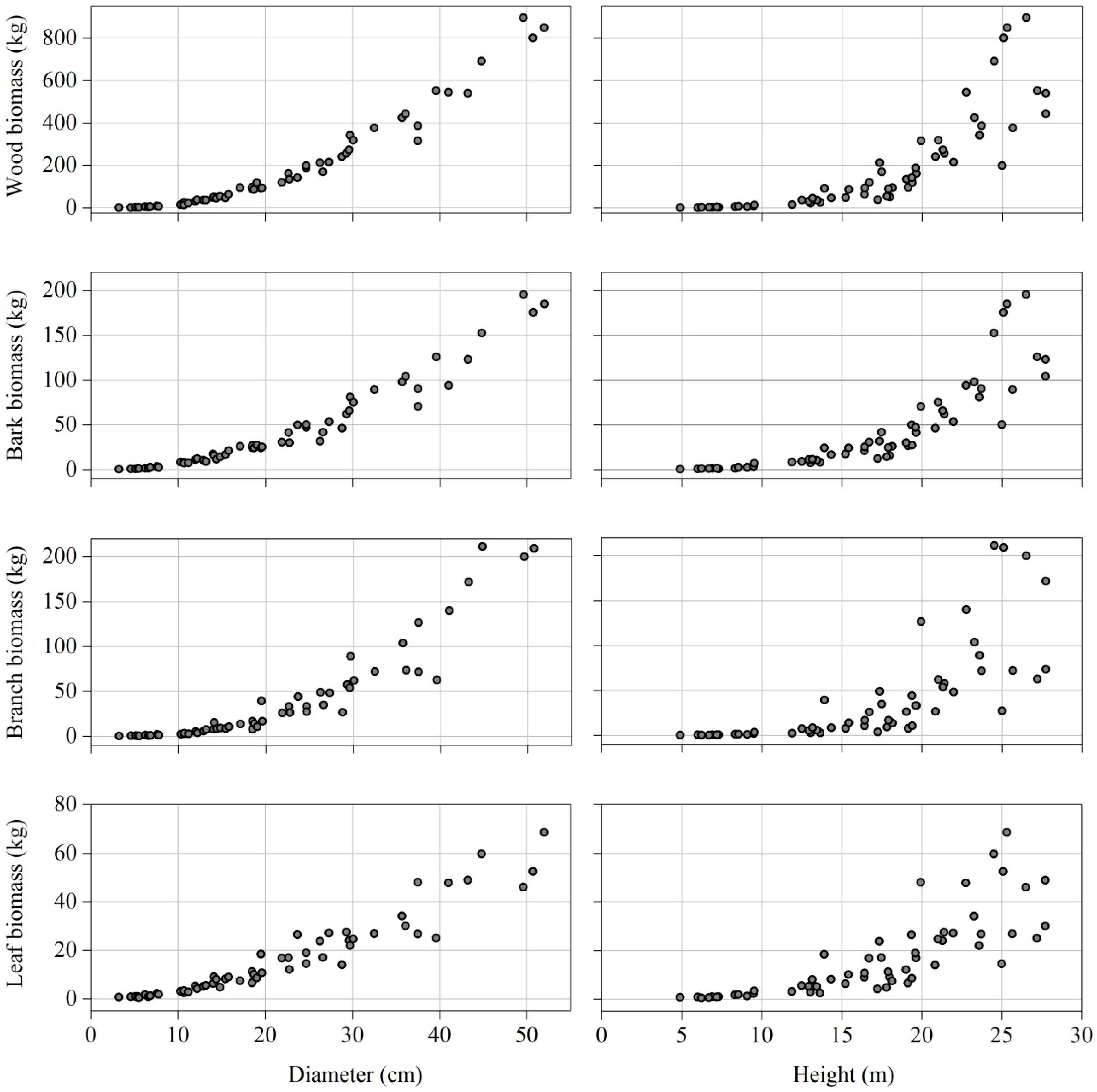
2.2. Tree Biomass Data
2.3. Data Analysis
2.4. Model Evaluation and Reconstruction
2.5. Model Validation
2.6. Antilogarithm Transformation Correction
2.7. Evaluation of Existing Biomass Equations
3. Results
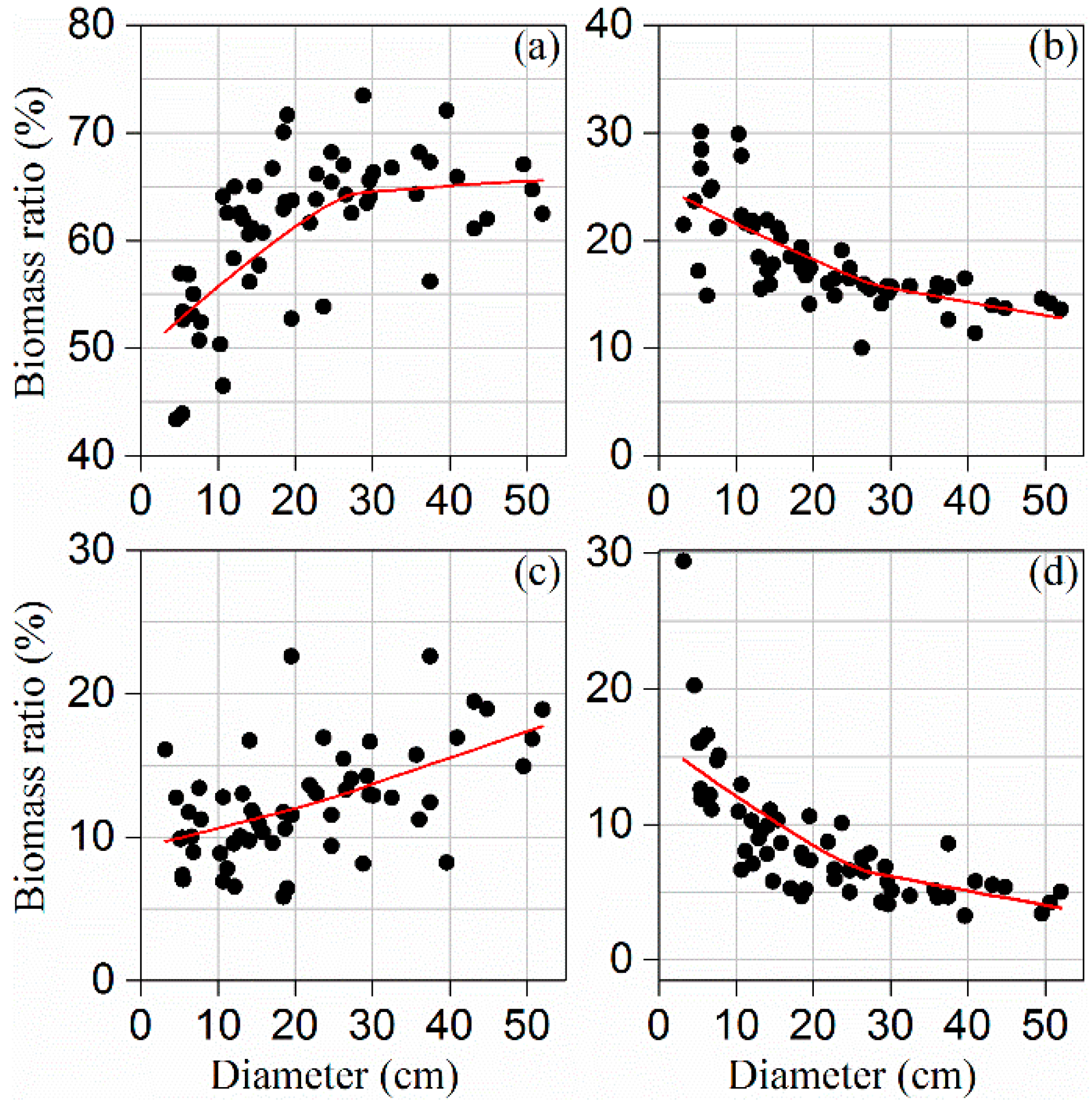
3.1. Biomass Allocation
3.2. Allometric Models
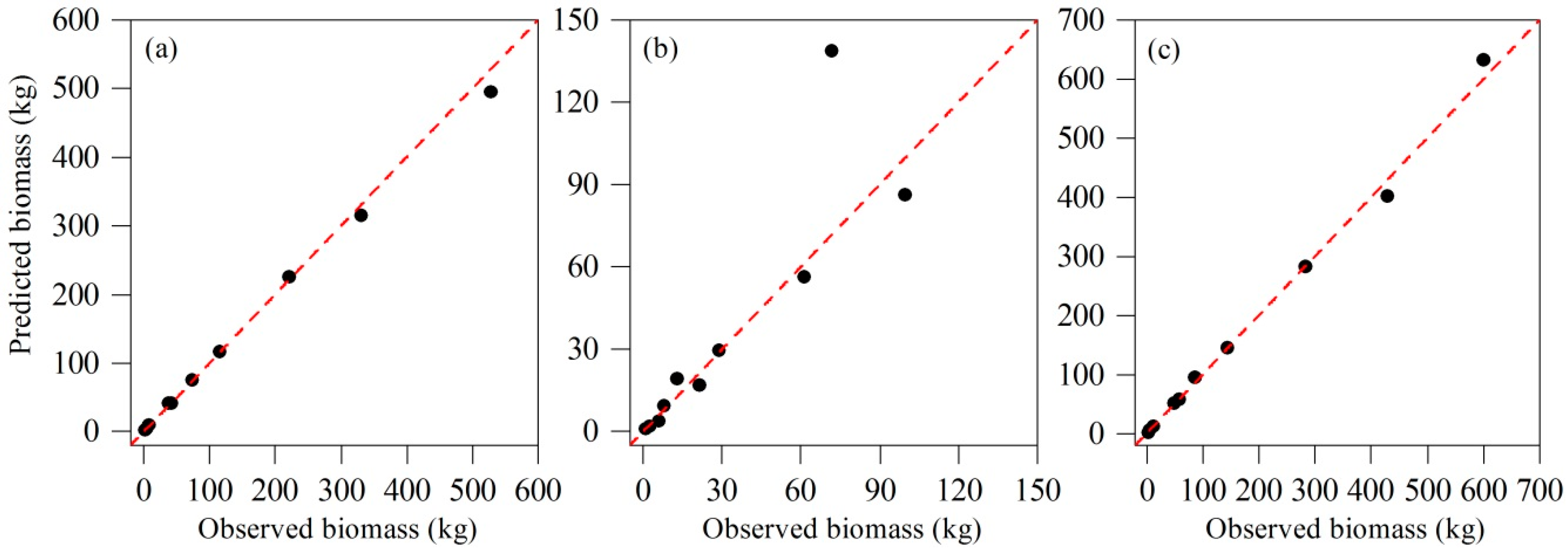
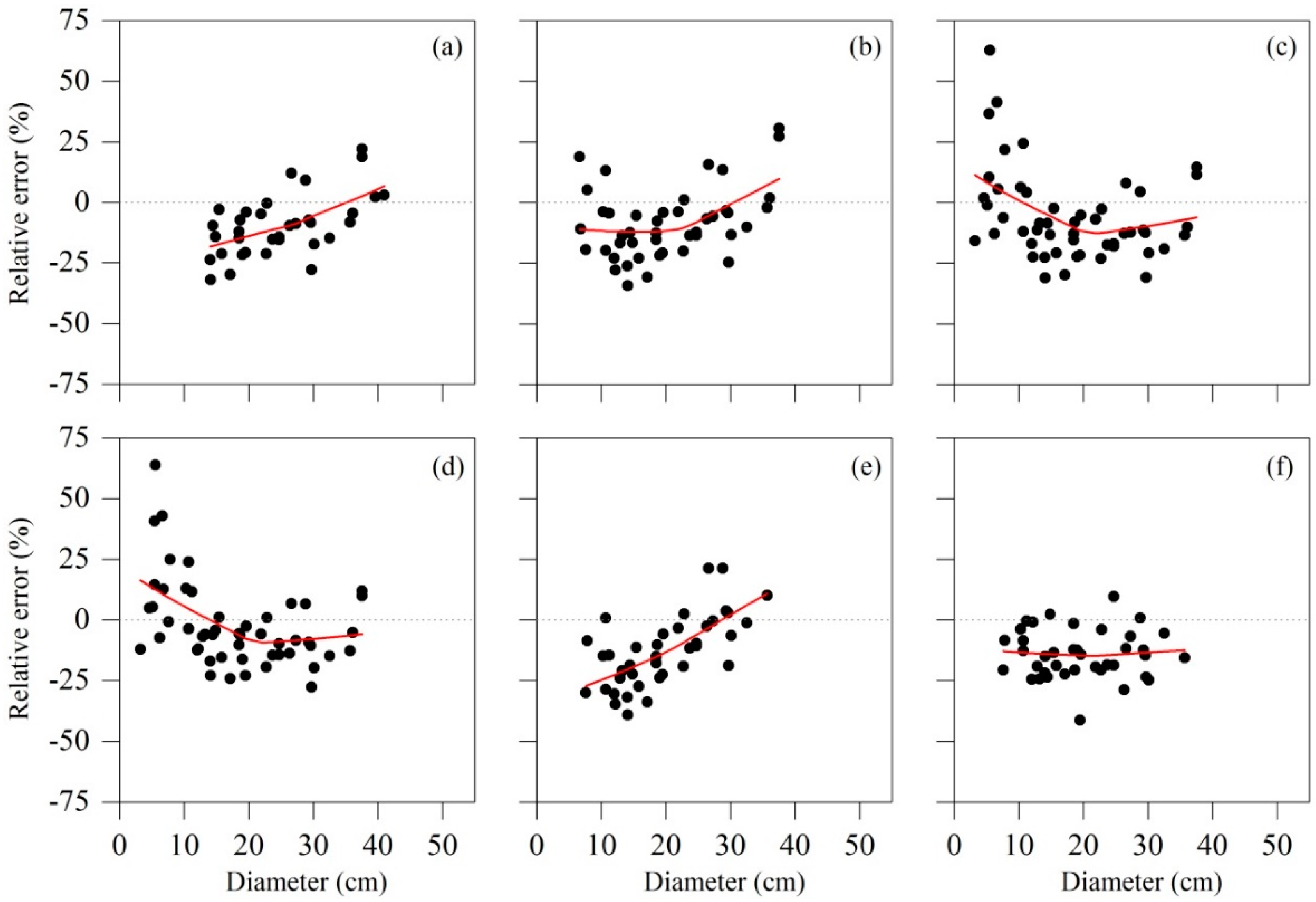
3.3. Model Validation for the Best Model System
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, C.; Gower, S.T.; Wang, Y.; Zhao, H.; Yan, P.; Bond-Lamberty, B.P. The influence of fire on carbon distribution and net primary production of boreal Larix gmelinii forests in north-eastern China. Glob. Chang. Biol. 2001, 7, 719–730. [Google Scholar] [CrossRef]
- Gower, S.T.; Krankina, O.; Olson, R.J.; Apps, M.; Linder, S.; Wang, C. Net primary production and carbon allocation patterns of boreal forest ecosystems. Ecol. Appl. 2001, 11, 1395–1411. [Google Scholar] [CrossRef]
- Martin, J.L.; Gower, S.T.; Plaut, J.; Holmes, B. Carbon pools in a boreal mixedwood logging chronosequence. Glob. Chang. Biol. 2005, 11, 1883–1894. [Google Scholar] [CrossRef]
- Fang, J.; Chen, A.; Peng, C.; Zhao, S.; Ci, L. Changes in forest biomass carbon storage in China between 1949 and 1998. Science 2001, 292, 2320–2322. [Google Scholar] [CrossRef] [PubMed]
- Pacala, S.W.; Hurtt, G.C.; Baker, D.; Peylin, P.; Houghton, R.A.; Birdsey, R.A.; Heath, L.; Sundquist, E.T.; Stallard, R.F.; Ciais, P.; et al. Consistent land- and atmosphere-based U.S. carbon sink estimates. Science 2001, 292, 2316–2320. [Google Scholar] [CrossRef] [PubMed]
- Pan, Y.; Birdsey, R.A.; Fang, J.; Houghton, R.; Kauppi, P.E.; Kurz, W.A.; Phillips, O.L.; Shvidenko, A.; Lewis, S.L.; Canadell, J.G.; et al. A large and persistent carbon sink in the world’s forests. Science 2011, 333, 988–993. [Google Scholar] [CrossRef] [PubMed]
- Mugasha, W.A.; Eid, T.; Bollandsas, O.M.; Malimbwi, R.E.; Chamshama, S.A.O.; Zahabu, E.; Katani, J.Z. Allometric models for prediction of above- and belowground biomass of trees in the miombo woodlands of Tanzania. For. Ecol. Manag. 2013, 310, 87–101. [Google Scholar] [CrossRef]
- He, J.S. Carbon cycling of Chinese forests: From carbon storage, dynamics to models. Sci. China Life Sci. 2012, 55, 188–190. [Google Scholar] [CrossRef]
- Brown, S.L.; Schroeder, P.; Kern, J.S. Spatial distribution of biomass in forests of the eastern USA. For. Ecol. Manag. 1999, 123, 81–90. [Google Scholar] [CrossRef]
- Bayen, P.; Bognounou, F.; Lykke, A.M.; Ouedraogo, M.; Thiombiano, A. The use of biomass production and allometric models to estimate carbon sequestration of Jatropha curcas L. plantations in western Burkina Faso. Environ. Dev. Sustain. 2016, 18, 143–156. [Google Scholar] [CrossRef]
- Maccracken, J.G.; Ballenberghe, V.V. Mass-diameter regressions for moose browse on the Copper River Delta, Alaska. J. Range Manag. 1993, 46, 302–308. [Google Scholar] [CrossRef]
- Truax, B.; Gagnon, D.; Fortier, J.; Lambert, F. Biomass and volume yield in mature hybrid poplar plantations on temperate abandoned farmland. Forests 2014, 5, 3107–3130. [Google Scholar] [CrossRef]
- Kauppi, P.E.; Tomppo, E.; Ferm, A. C and N storage in living trees within Finland since 1950s. Plant Soil 1995, 168, 633–638. [Google Scholar] [CrossRef]
- Alongi, D.M.; Clough, B.F.; Dixon, P.; Tirendi, F. Nutrient partitioning and storage in arid-zone forests of the mangroves Rhizophora stylosa and Avicennia marina. Trees 2003, 17, 51–60. [Google Scholar] [CrossRef]
- Alvarez, E.; Duque, A.; Saldarriaga, J.; Cabrera, K.; Salas, G.D.; del Valle, I.; Lema, A.; Moreno, F.; Orrego, S.; Rodriguez, L. Tree above-ground biomass allometries for carbon stocks estimation in the natural forests of Colombia. For. Ecol. Manag. 2012, 267, 297–308. [Google Scholar] [CrossRef]
- Dong, L.; Zhang, L.; Li, F. Developing additive systems of biomass equations for nine hardwood species in Northeast China. Trees 2015, 29, 1149–1163. [Google Scholar] [CrossRef]
- Dimobe, K.; Mensah, S.; Goetze, D.; Ouédraogo, A.; Kuyah, S.; Porembski, S.; Thiombiano, A. Aboveground biomass partitioning and additive models for Combretum glutinosum and Terminalia laxiflora in West Africa. Biomass Bioenergy 2018, 115, 151–159. [Google Scholar] [CrossRef]
- Wang, C.K. Biomass allometric equations for 10 co-occurring tree species in Chinese temperate forests. For. Ecol. Manag. 2006, 222, 9–16. [Google Scholar] [CrossRef]
- Canga, E.; Dieguez-Aranda, I.; Afif-Khouri, E.; Camara-Obregon, A. Above-ground biomass equations for Pinus radiata D. Don in Asturias. For. Syst. 2013, 22, 408–415. [Google Scholar] [CrossRef]
- Mbow, C.; Verstraete, M.M.; Sambou, B.; Diaw, A.T.; Neufeldt, H. Allometric models for aboveground biomass in dry savanna trees of the Sudan and Sudan-Guinean ecosystems of Southern Senegal. J. For. Res. 2014, 19, 340–347. [Google Scholar] [CrossRef]
- Youkhana, A.H.; Ogoshi, R.M.; Kiniry, J.R.; Meki, M.N.; Nakahata, M.H.; Crow, S.E. Allometric models for predicting aboveground biomass and carbon stock of tropical perennial C4 grasses in Hawaii. Front. Plant Sci. 2017, 8. [Google Scholar] [CrossRef] [PubMed]
- Bi, H.Q.; Long, Y.; Turner, J.; Lei, Y.; Snowdon, P.; Li, Y.; Harper, R.; Zerihun, A.; Ximenes, F. Additive prediction of aboveground biomass for Pinus radiata (D. Don) plantations. For. Ecol. Manag. 2010, 259, 2301–2314. [Google Scholar] [CrossRef]
- MacFarlane, D.W. A generalized tree component biomass model derived from principles of variable allometry. For. Ecol. Manag. 2015, 354, 43–55. [Google Scholar] [CrossRef]
- Lima, A.J.N.; Suwa, R.; Ribeiro, G.H.P.M.; Kajimoto, T.; dos Santos, J.; da Silva, R.P.; de Souza, C.A.S.; de Barros, P.C.; Noguchi, H.; Ishizuka, M.; et al. Allometric models for estimating above- and below-ground biomass in Amazonian forests at Sao Gabriel da Cachoeira in the upper Rio Negro, Brazil. For. Ecol. Manag. 2012, 277, 163–172. [Google Scholar] [CrossRef]
- Muukkonen, P.; Makipaa, R. Biomass equations for European trees: Addendum. Silv. Fenn. 2006, 40, 763–773. [Google Scholar] [CrossRef]
- Ter-Mikaelian, M.T.; Korzukhin, M.D. Biomass equations for sixty-five North American tree species. For. Ecol. Manag. 1997, 97, 1–24. [Google Scholar] [CrossRef]
- Estrada, G.C.D.; Soares, M.L.G.; Santos, D.M.C.; Fernandez, V.; de Almeida, P.M.M.; Estevam, M.R.M.; Machado, M.R.O. Allometric models for aboveground biomass estimation of the mangrove Avicennia schaueriana. Hydrobiologia 2014, 734, 171–185. [Google Scholar] [CrossRef]
- Dickinson, Y.L.; Zenner, E.K. Allometric equations for the aboveground biomass of selected common eastern hardwood understory species. North J. Appl. For. 2010, 27, 160–165. [Google Scholar]
- Xiao, X.; White, E.P.; Hooten, M.B.; Durham, S.L. On the use of log-transformation vs. nonlinear regression for analyzing biological power laws. Ecology 2011, 92, 1887–1894. [Google Scholar] [CrossRef]
- Djomo, A.N.; Chimi, C.D. Tree allometric equations for estimation of above, below and total biomass in a tropical moist forest: Case study with application to remote sensing. For. Ecol. Manag. 2017, 391, 184–193. [Google Scholar] [CrossRef]
- Chave, J.; Andalo, C.; Brown, S.; Cairns, M.A.; Chambers, J.Q.; Eamus, D.; Folster, H.; Fromard, F.; Higuchi, N.; Kira, T.; et al. Tree allometry and improved estimation of carbon stocks and balance in tropical forests. Oecologia 2005, 145, 87–99. [Google Scholar] [CrossRef] [PubMed]
- Zianis, D.; Xanthopoulos, G.; Kalabokidis, K.; Kazakis, G.; Ghosn, D.; Roussou, O. Allometric equations for aboveground biomass estimation by size class for Pinus brutia Ten. trees growing in North and South Aegean Islands, Greece. Eur. J. For. Res. 2011, 130, 145–160. [Google Scholar] [CrossRef]
- Sprugel, D.G. Correcting for bias in log-transformed allometric equations. Ecology 1983, 64, 209–210. [Google Scholar] [CrossRef]
- Beauchamp, J.J.; Olson, J.S. Corrections for bias in regression estimates after logarithmic transformation. Ecology 1973, 54, 1403–1407. [Google Scholar] [CrossRef]
- Yandle, D.O.; Wiant, H.V., Jr. Estimation of plant biomass based on the allometric equation. Can. J. For. Res. 2011, 11, 833–834. [Google Scholar] [CrossRef]
- Clifford, D.; Cressie, N.; England, J.R.; Roxburgh, S.H.; Paul, K.I. Correction factors for unbiased, efficient estimation and prediction of biomass from log-log allometric models. For. Ecol. Manag. 2013, 310, 375–381. [Google Scholar] [CrossRef]
- Komiyama, A.; Poungparn, S.; Kato, S. Common allometric equations for estimating the tree weight of mangroves. J. Trop. Ecol. 2005, 21, 471–477. [Google Scholar] [CrossRef]
- Lambert, M.C.; Ung, C.H.; Raulier, F. Canadian national tree aboveground biomass equations. Can. J. For. Res. 2005, 35, 1996–2018. [Google Scholar] [CrossRef]
- Kuyah, S.; Sileshi, G.W.; Rosenstock, T.S. Allometric models based on bayesian frameworks give better estimates of aboveground biomass in the miombo woodlands. Forests 2016, 7, 13. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, J.; Franklin, S.B.; Liang, J.; Ding, P.; Luo, Y.; Lu, Z.; Bao, D.; Jiang, M. Improving allometry models to estimate the above- and belowground biomass of subtropical forest, China. Ecosphere 2015, 6. [Google Scholar] [CrossRef]
- Parresol, B.R. Assessing tree and stand biomass: A review with examples and critical comparisons. For. Sci. 1999, 45, 573–593. [Google Scholar]
- Kozak, A. Methods for ensuring additivity of biomass components by regression analysis. For. Chron. 1970, 46, 402–405. [Google Scholar] [CrossRef]
- Parresol, B.R. Additivity of nonlinear biomass equations. Can. J. For. Res. 2001, 31, 865–878. [Google Scholar] [CrossRef]
- Bi, H.Q.; Turner, J.; Lambert, M.J. Additive biomass equations for native eucalypt forest trees of temperate Australia. Trees 2004, 18, 467–479. [Google Scholar] [CrossRef]
- Tang, S.; Zhang, H.; Xu, H. Study on establish and estimate method of compatible biomass model. Sci. Silvae. Sin. 1999, 36, 19–27. [Google Scholar]
- Riofrio, J.; Herrero, C.; Grijalva, J.; Bravo, F. Aboveground tree additive biomass models in Ecuadorian highland agroforestry systems. Biomass Bioenergy 2015, 80, 252–259. [Google Scholar] [CrossRef]
- Carvalho, J.P.; Parresol, B.R. Additivity in tree biomass components of Pyrenean oak (Quercus pyrenaica Willd.). For. Ecol. Manag. 2003, 179, 269–276. [Google Scholar] [CrossRef]
- Menendez-Miguelez, M.; Canga, E.; Barrio-Anta, M.; Majada, J.; AlvarezAlvarez, P. A three level system for estimating the biomass of Castanea sativa Mill. coppice stands in north-west Spain. For. Ecol. Manag. 2013, 291, 417–426. [Google Scholar] [CrossRef]
- Dong, L.; Zhang, L.; Li, F. A compatible system of biomass equations for three conifer species in Northeast, China. For. Ecol. Manag. 2014, 329, 306–317. [Google Scholar] [CrossRef]
- Dong, L.; Zhang, L.; Li, F. Developing two additive biomass equations for three coniferous plantation species in northeast China. Forests 2016, 7, 136. [Google Scholar] [CrossRef]
- Zeng, W.S. Integrated individual tree biomass simultaneous equations for two larch species in northeastern and northern China. Scand. J. For. Res. 2015, 30, 594–604. [Google Scholar] [CrossRef]
- Liu, Q.J. Nested regression for establishing tree biomass equations. Chin. J. Plant Ecol. 2009, 33, 331–337. [Google Scholar]
- Jia, Q.Q.; Liu, Q.J.; Li, J.Q. Individual-based fine root biomass and its functional relationship with leaf for Pinus tabuliformis in northern China. Eur. J. For. Res. 2015, 134, 705–714. [Google Scholar] [CrossRef]
- Chen, A.F.; Li, R.Y.; Wang, H.L.; He, B. Quantitative assessment of human appropriation of aboveground net primary production in China. Ecol. Model. 2015, 312, 54–60. [Google Scholar] [CrossRef]
- Kajimoto, T. Aboveground net production and dry matter allocation of Pinus pumila forests in the Kiso mountain range, central Japan. Ecol. Res. 1994, 9, 193–204. [Google Scholar] [CrossRef]
- Mensah, S.; Veldtman, R.; Seifert, T. Allometric models for height and aboveground biomass of dominant tree species in South African Mistbelt forests. South. For. 2016, 79, 19–30. [Google Scholar] [CrossRef]
- Dong, L.; Zhang, L.; Li, F. Additive biomass equations based on different dendrometric variables for two dominant species (Larix gmelini Rupr. and Betula platyphylla Suk.) in natural forests in the eastern Daxing’an Mountains, Northeast China. Forests 2018, 9, 261. [Google Scholar] [CrossRef]
- Liu, J.G.; Liu, R.P. The primary research for the biomass of Larix gmelinii in Daxing’anling forest region. Inn. Mong. For. Investig. Des. 2015, 38, 17–18. [Google Scholar]
- Moore, J.R. Allometric equations to predict the total above-ground biomass of radiata pine trees. Ann. For. Sci. 2010, 67, 806. [Google Scholar] [CrossRef]
- Risio, L.; Herrero, C.; Bogino, S.M.; Bravo, F. Aboveground and belowground biomass allocation in native Prosopis caldenia Burkart secondaries woodlands in the semi-arid Argentinean pampas. Biomass Bioenergy 2014, 66, 249–260. [Google Scholar] [CrossRef]
- Blujdea, V.N.B.; Pilli, R.; Dutca, I.; Ciuvat, L.; Abrudan, I.V. Allometric biomass equations for young broadleaved trees in plantations in Romania. For. Ecol. Manag. 2012, 264, 172–184. [Google Scholar] [CrossRef]
- Mensah, S.; Kakaï, R.G.; Seifert, T. Patterns of biomass allocation between foliage and woody structure: The effects of tree size and specific functional traits. Ann. For. Res. 2016, 59, 1–12. [Google Scholar] [CrossRef]
- Jomura, M.; Wang, W.J.; Masyagina, O.V.; Homma, S.; Kanazawa, Y.; Zu, Y.G.; Koike, T. Permafrost Ecosystems; Springer: Dordrecht, The Netherlands, 2009; pp. 385–411. [Google Scholar]
- Pajtik, J.; Konopka, B.; Lukac, M. Individual biomass factors for beech, oak and pine in Slovakia: A comparative study in young naturally regenerated stands. Trees 2011, 25, 277–288. [Google Scholar] [CrossRef]
- Huff, S.; Ritchie, M.; Temesgen, H. Allometric equations for estimating aboveground biomass for common shrubs in northeastern California. For. Ecol. Manag. 2017, 398, 48–63. [Google Scholar] [CrossRef]
- Kalita, R.M.; Das, A.K.; Nath, A.J. Allometric equations for estimating above-and belowground biomass in Tea (Camellia sinensis (L.) O. Kuntze) agroforestry system of Barak Valley, Assam, northeast India. Biomass Bioenergy 2015, 83, 42–49. [Google Scholar] [CrossRef]
- Antonio, N.; Tome, M.; Tome, J.; Soares, P.; Fontes, L. Effect of tree, stand, and site variables on the allometry of Eucalyptus globulus tree biomass. Can. J. For. Res. 2007, 37, 895–906. [Google Scholar] [CrossRef]
- Wagner, R.G.; Ter-Mikaelian, M.T. Comparison of biomass component equations for four species of northern coniferous tree seedlings. Ann. For. Sci. 1999, 56, 193–199. [Google Scholar] [CrossRef]
- Xiang, W.; Zhou, J.; Ouyang, S.; Zhang, S.; Lei, P.; Li, J.; Deng, X.; Fang, X.; Forrester, D.I. Species-specific and general allometric equations for estimating tree biomass components of subtropical forests in southern China. Eur. J. For. Res. 2016, 135, 963–979. [Google Scholar] [CrossRef]
- Madgwick, H.A.I.; Satoo, T. On estimating the aboveground weights of tree stands. Ecology 1975, 56, 1446–1450. [Google Scholar] [CrossRef]
- Gonzalez-Garcia, M.; Hevia, A.; Majada, J.; Barrio-Anta, M. Above-ground biomass estimation at tree and stand level for short rotation plantations of Eucalyptus nitens (Deane & Maiden) Maiden in Northwest Spain. Biomass Bioenergy 2013, 54, 147–157. [Google Scholar]
- Kozak, A.; Kozak, R. Does cross validation provide additional information in the evaluation of regression models? Can. J. For. Res. 2003, 33, 976–987. [Google Scholar] [CrossRef]
- Quint, T.C.; Dech, J.P. Allometric models for predicting the aboveground biomass of Canada yew (Taxus canadensis Marsh.) from visual and digital cover estimates. Can. J. For. Res. 2010, 40, 2003–2014. [Google Scholar] [CrossRef]
| Statistics | Mean | Min | Max | SD |
|---|---|---|---|---|
| dbh (cm) | 21.5 | 3.2 | 52.0 | 12.98 |
| h (m) | 16.96 | 4.91 | 27.72 | 6.35 |
| Basic density of branch (g/cm3) | 0.456 | 0.395 | 0.515 | 0.049 |
| Basic density of wood (g/cm3) | 0.498 | 0.393 | 0.513 | 0.033 |
| Basic density of stem bark (g/cm3) | 0.372 | 0.346 | 0.389 | 0.012 |
| average mass per leaf fascicle (g) | 0.0210 | 0.0163 | 0.0241 | 0.0027 |
| average area per needle (cm2) | 0.134 | 0.066 | 0.184 | 0.032 |
| average mass per short shoot (g) | 0.0060 | 0.0035 | 0.0075 | 0.0021 |
| Stem biomass (kg) | 189.95 | 0.73 | 896.66 | 228.98 |
| Bark biomass (kg) | 44.47 | 0.47 | 195.40 | 49.33 |
| Branch biomass (kg) | 40.43 | 0.15 | 317.71 | 63.11 |
| Leaf biomass (kg) | 21.78 | 0.63 | 108.47 | 23.02 |
| Aboveground biomass (kg) | 296.63 | 2.21 | 1360.47 | 357.44 |
| Biomass (kg) | ||||
|---|---|---|---|---|
| dbh (cm) | h (m) | Stem | Crown | Aboveground |
| 4.0 | 4.50 | 1.41 | 1.06 | 2.47 |
| 6.0 | 6.23 | 3.34 | 2.47 | 5.81 |
| 8.0 | 7.00 | 7.16 | 5.96 | 13.12 |
| 12.0 | 15.75 | 41.66 | 8.07 | 49.73 |
| 15.6 | 9.00 | 36.98 | 21.54 | 58.52 |
| 16.4 | 15.30 | 73.54 | 13.17 | 86.71 |
| 19.8 | 16.45 | 115.68 | 28.93 | 144.61 |
| 26.0 | 19.00 | 221.49 | 61.42 | 282.91 |
| 31.2 | 18.70 | 330.49 | 99.74 | 430.23 |
| 38.0 | 20.00 | 527.73 | 71.57 | 599.30 |
| Source | Site | Origin | dbh Range (cm) | Sample Size | Predictor | RE (%) |
|---|---|---|---|---|---|---|
| This study | IM | Natural | 3.2–52.0 | 58 | ||
| Wang [18] | HLJ | Plantation | 13.7–41.4 | 10 | dbh | −9.46 |
| Dong et al. [49] | HLJ, JL | Natural | 6.5–38.1 | 122 | dbh | −8.56 |
| Zeng [51] | HLJ, LN, IM | Natural, plantation | 2.0–38.8 | 50 | dbh | −5.84 |
| dbh, h | −2.07 | |||||
| Dong et al. [50] | HLJ | Plantation | 7.6–35.7 | 90 | dbh | −13.04 |
| dbh, h | −14.19 |
| Model | Predictor | Component | Regression Coefficients | Fitting Statistics | |||
|---|---|---|---|---|---|---|---|
| lnα(SE) | β(SE) | RMSE | MAE | Adj.R2 | |||
| 4 | dbh | Wood | −3.374 *** (0.099) | 2.644 *** (0.034) | 0.208 | 0.167 | 0.987 |
| 5 | dbh2 × h | Wood | −4.262 *** (0.075) | 1.000 *** (0.009) | 0.130 | 0.104 | 0.995 |
| 4 | dbh | Bark | −3.302 *** (0.105) | 2.188 *** (0.036) | 0.197 | 0.164 | 0.984 |
| 5 | dbh2 × h | Bark | −4.031 *** (0.086) | 0.827 *** (0.010) | 0.147 | 0.117 | 0.991 |
| 4 | dbh | Branch | −4.770 *** (0.156) | 2.585 *** (0.053) | 0.334 | 0.244 | 0.968 |
| 5 | dbh2 × h | Branch | −5.623 *** (0.186) | 0.975 *** (0.022) | 0.373 | 0.287 | 0.960 |
| 4 | dbh | Leaf | −3.025 *** (0.141) | 1.819 *** (0.048) | 0.273 | 0.212 | 0.958 |
| 5 | dbh2 × h | Leaf | −3.611 *** (0.163) | 0.683 *** (0.019) | 0.296 | 0.235 | 0.950 |
| Component | Biomass Equations | RMSE | MAE | Adj.R2 | CF |
|---|---|---|---|---|---|
| Wood | lnWwd = −4.270 + 1.001ln(dbh2 × h) | 0.130 | 0.104 | 0.995 | 1.008 |
| Bark | lnWbk = −4.016 + 0.825ln(dbh2 × h) | 0.147 | 0.117 | 0.991 | 1.011 |
| Branch | lnWbr = −4.832 + 2.601ln(dbh) | 0.331 | 0.243 | 0.969 | 1.056 |
| Leaf | lnWlf = −3.080 + 1.833ln(dbh) | 0.272 | 0.211 | 0.958 | 1.038 |
| Crown | lnWcw = ln(e−4.832dbh2.601 + e−3.080dbh1.833) | 0.297 | 0.221 | 0.968 | 1.045 |
| Aboveground | lnWag = ln(e−4.270(dbh2 × h)1.001 + e–4.016(dbh2 × h)0.825 + e−4.832dbh2.601 + e−3.080dbh1.833) | 0.129 | 0.101 | 0.995 | 1.008 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, S.; Jia, Q.; Liu, Q.; Zhou, G.; Wang, H.; Yu, J. Aboveground Biomass Allocation and Additive Allometric Models for Natural Larix gmelinii in the Western Daxing’anling Mountains, Northeastern China. Forests 2019, 10, 150. https://doi.org/10.3390/f10020150
Meng S, Jia Q, Liu Q, Zhou G, Wang H, Yu J. Aboveground Biomass Allocation and Additive Allometric Models for Natural Larix gmelinii in the Western Daxing’anling Mountains, Northeastern China. Forests. 2019; 10(2):150. https://doi.org/10.3390/f10020150
Chicago/Turabian StyleMeng, Shengwang, Quanquan Jia, Qijing Liu, Guang Zhou, Huimin Wang, and Jian Yu. 2019. "Aboveground Biomass Allocation and Additive Allometric Models for Natural Larix gmelinii in the Western Daxing’anling Mountains, Northeastern China" Forests 10, no. 2: 150. https://doi.org/10.3390/f10020150
APA StyleMeng, S., Jia, Q., Liu, Q., Zhou, G., Wang, H., & Yu, J. (2019). Aboveground Biomass Allocation and Additive Allometric Models for Natural Larix gmelinii in the Western Daxing’anling Mountains, Northeastern China. Forests, 10(2), 150. https://doi.org/10.3390/f10020150





