Mapping Forest Canopy Height in Mountainous Areas Using ZiYuan-3 Stereo Images and Landsat Data
Abstract
1. Introduction
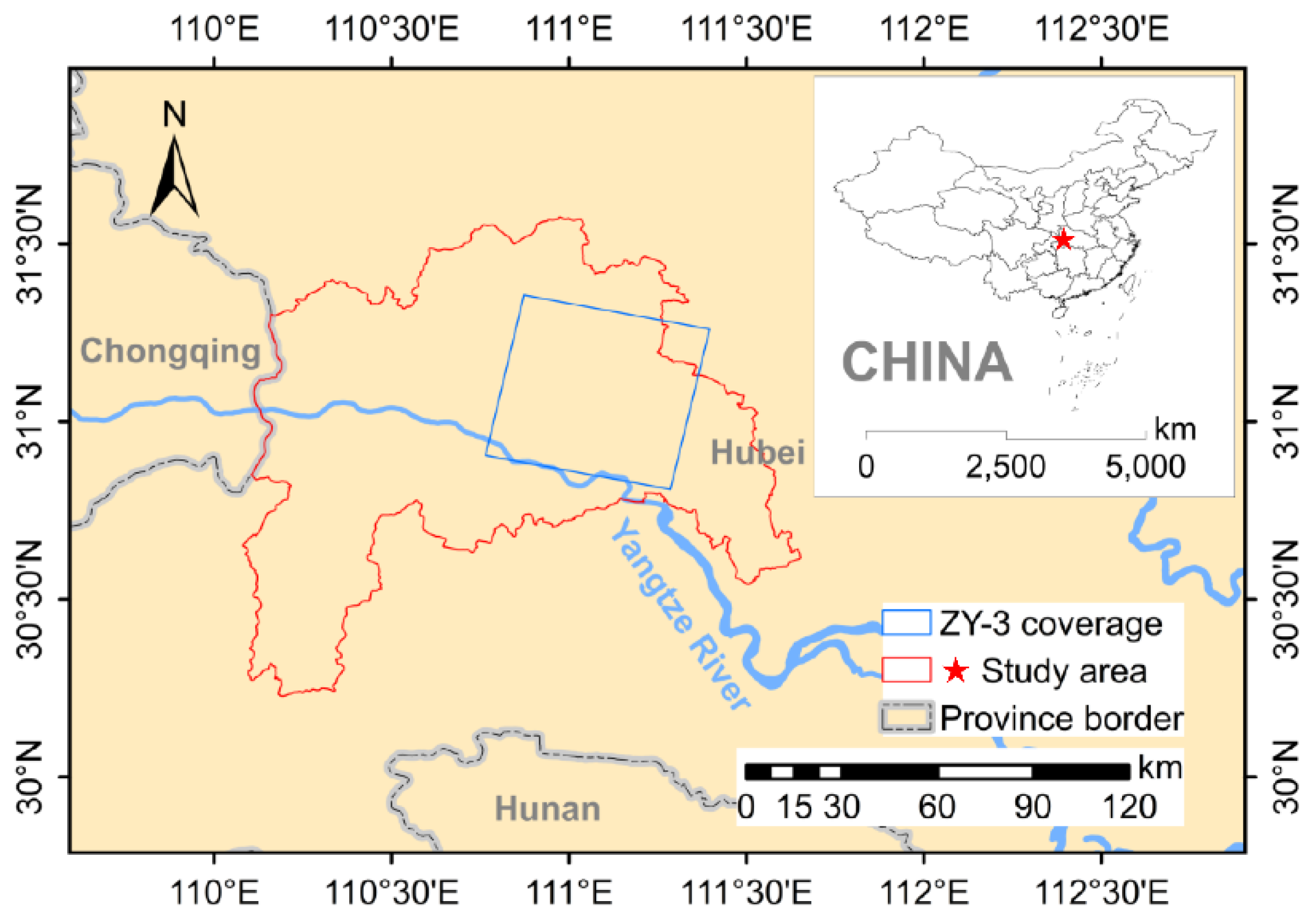
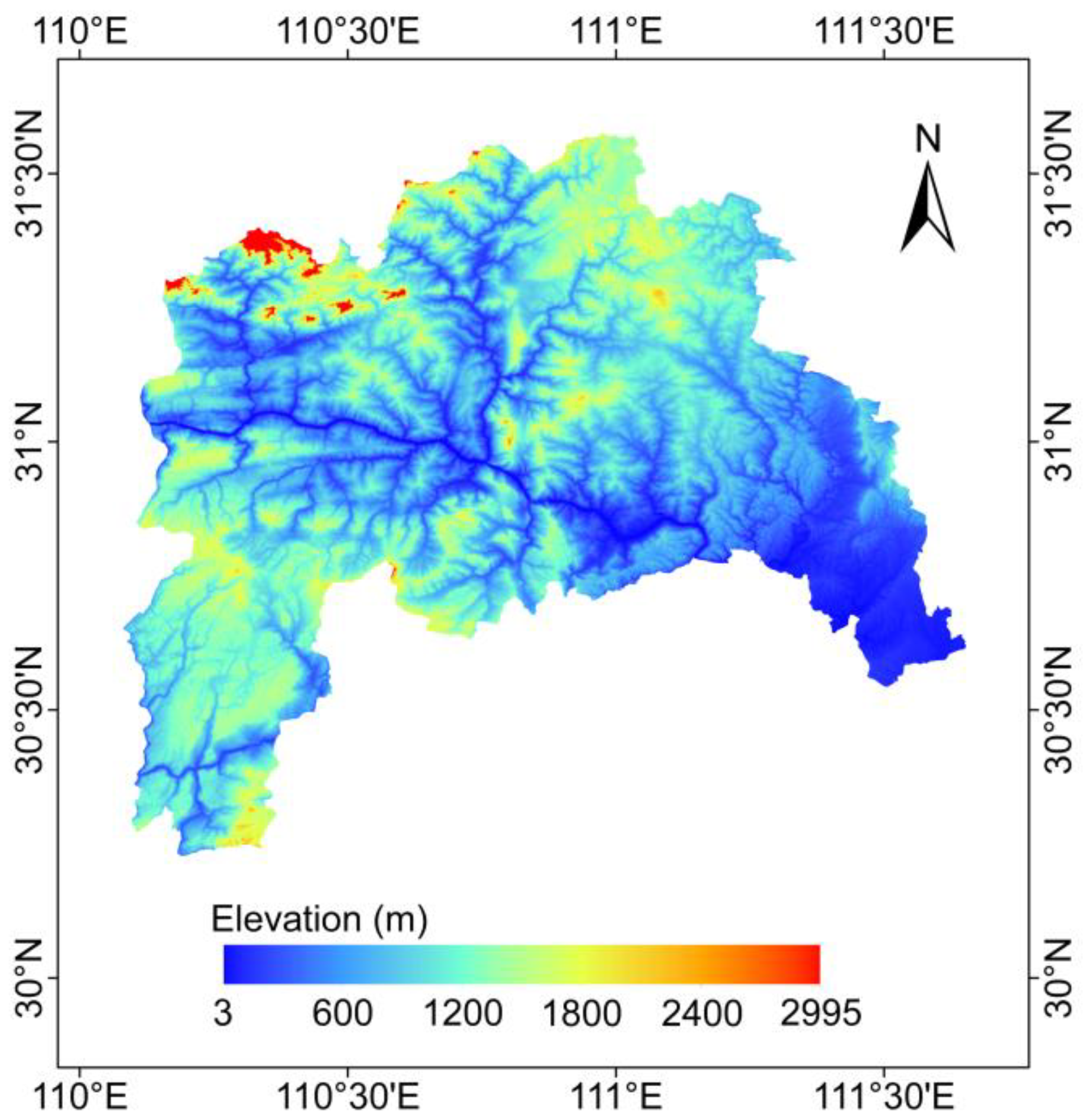
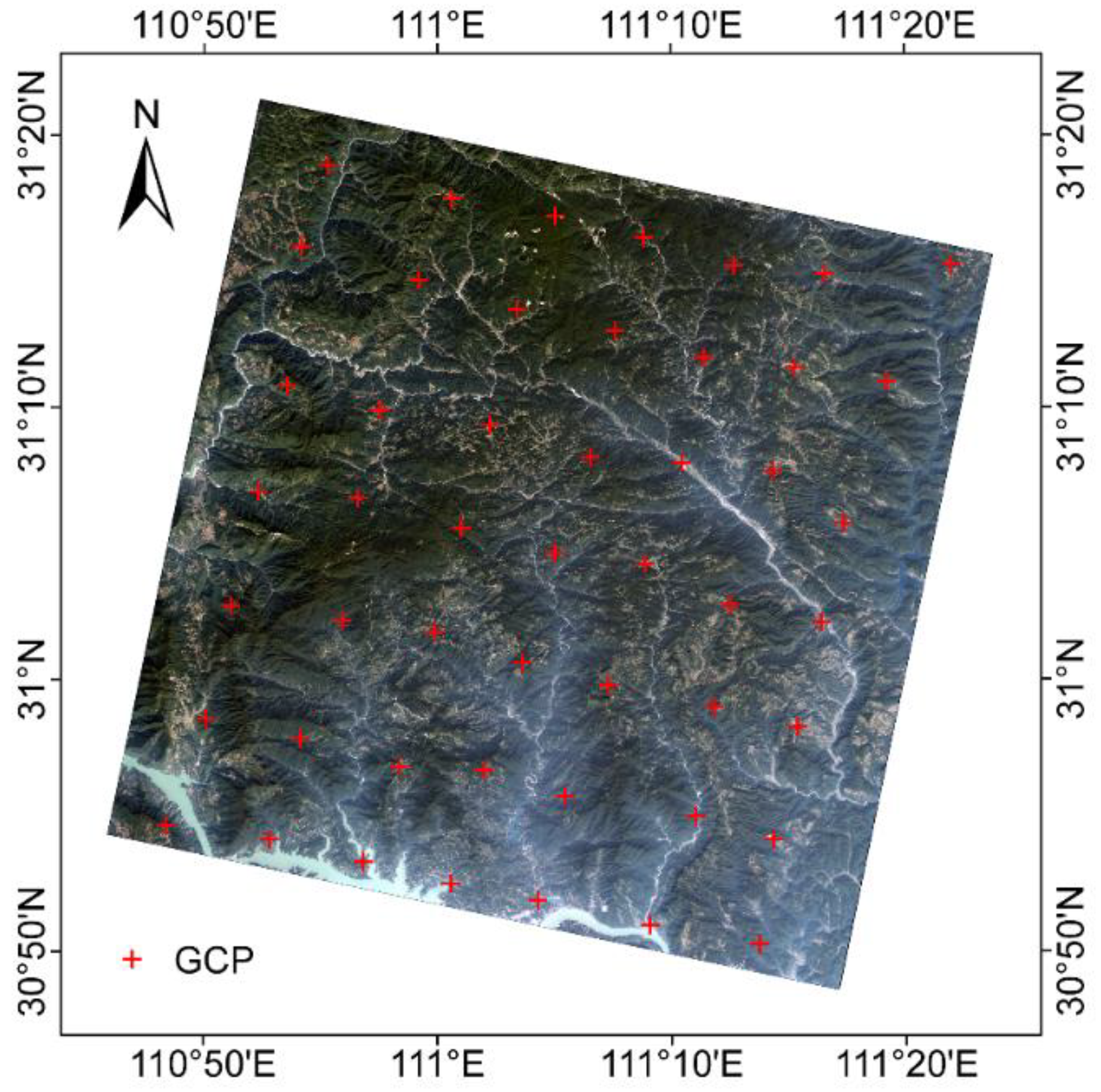
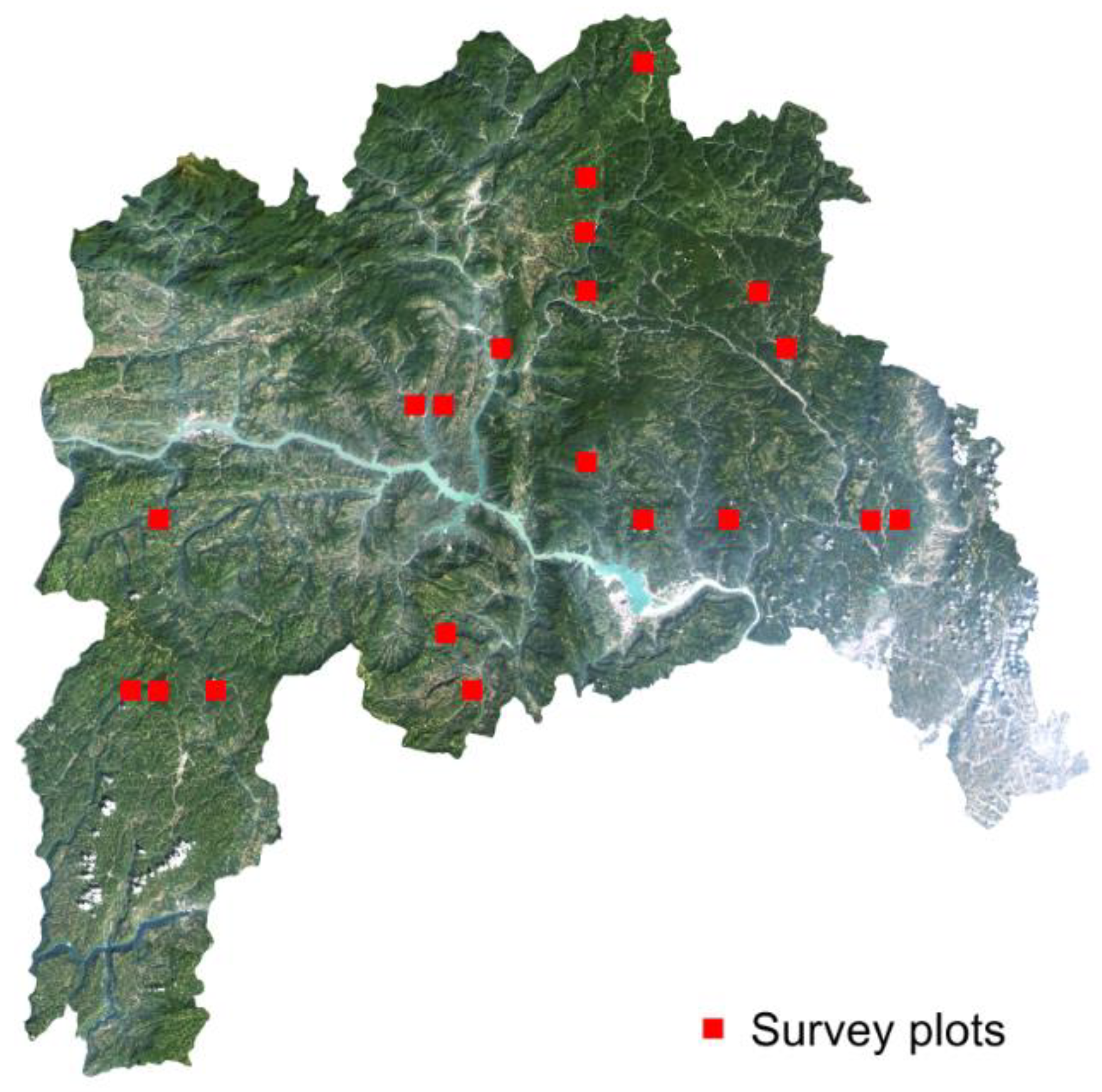
2. Study Area
3. Data
3.1. ZY-3 Data
3.2. SRTMGL1 Data
3.3. Landsat 8 OLI Surface Reflectance Data
3.4. Field Data
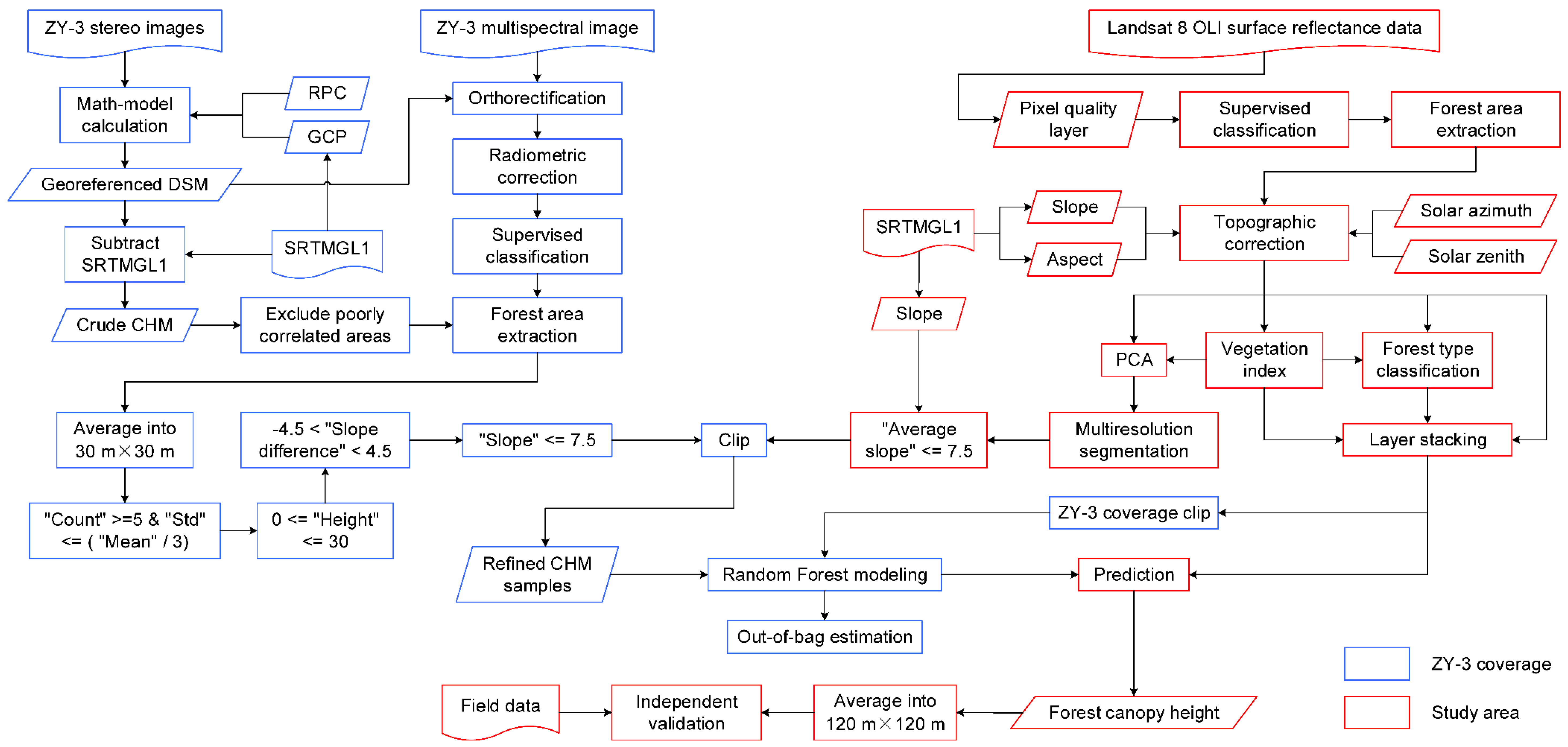
4. Methods
4.1. Extraction and Refinement of Crude CHM
4.2. Preparation of Landsat Data
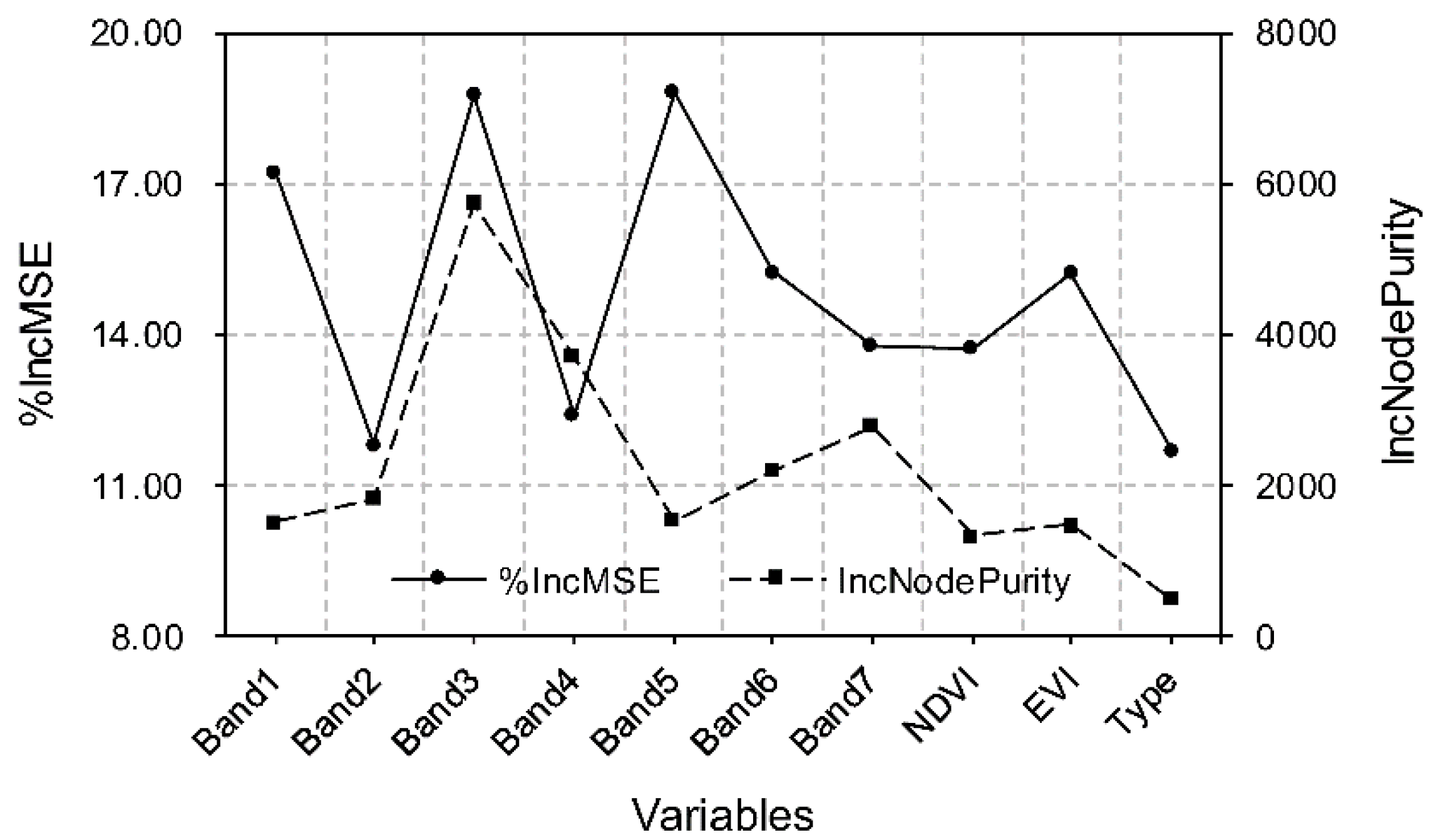
4.3. Random Forest Modeling and Extrapolation
5. Results and Discussion
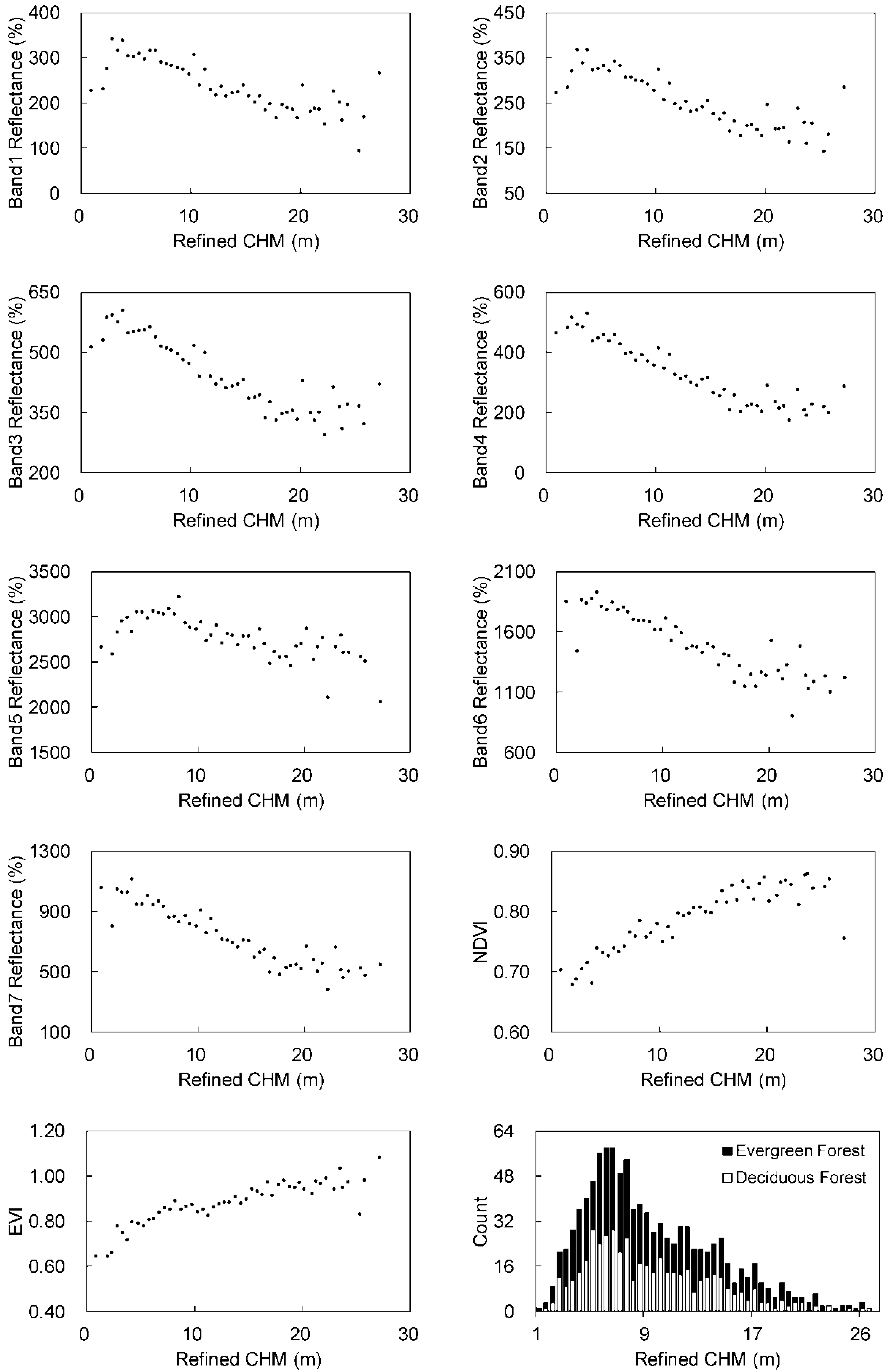
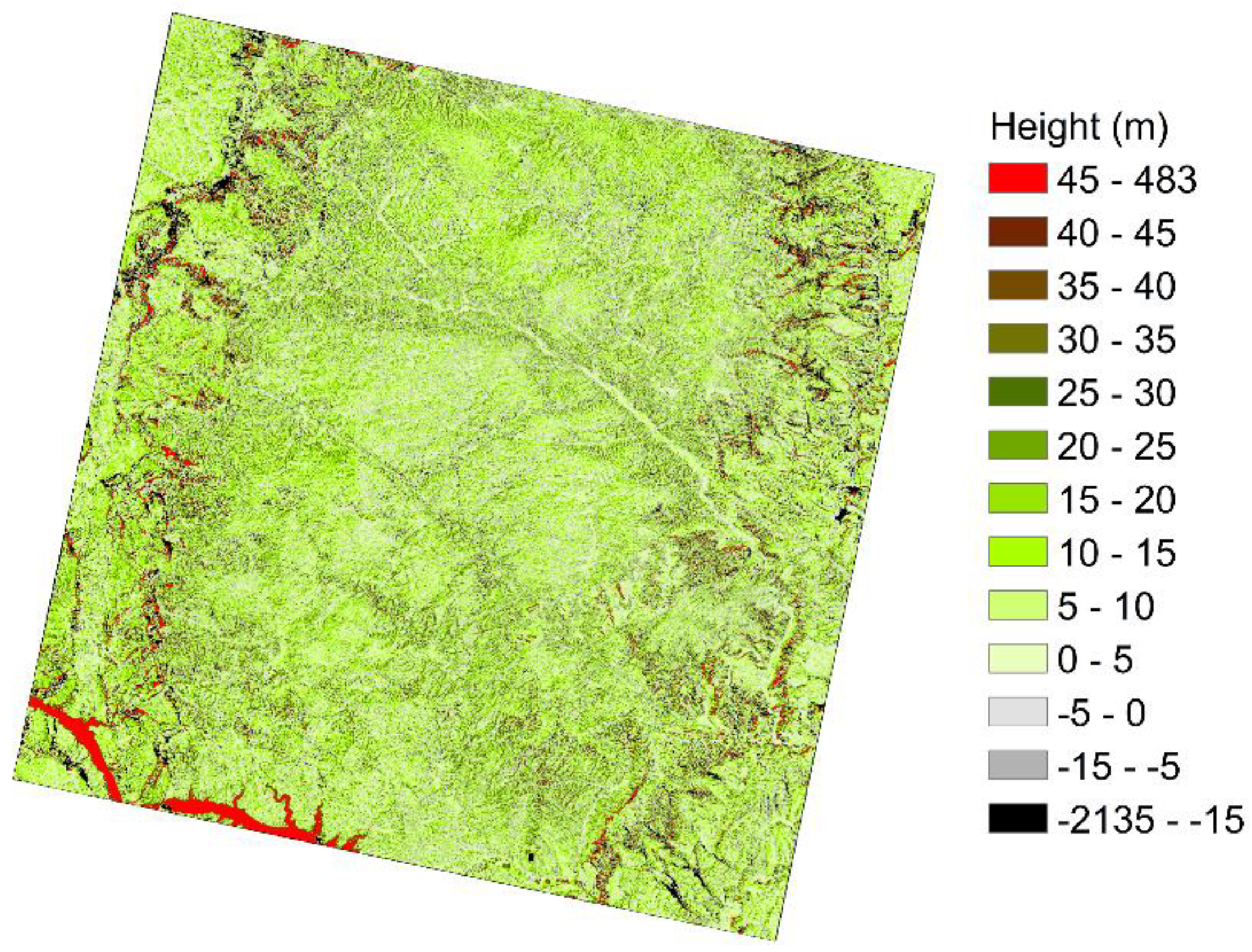
5.1. Refined CHM Samples
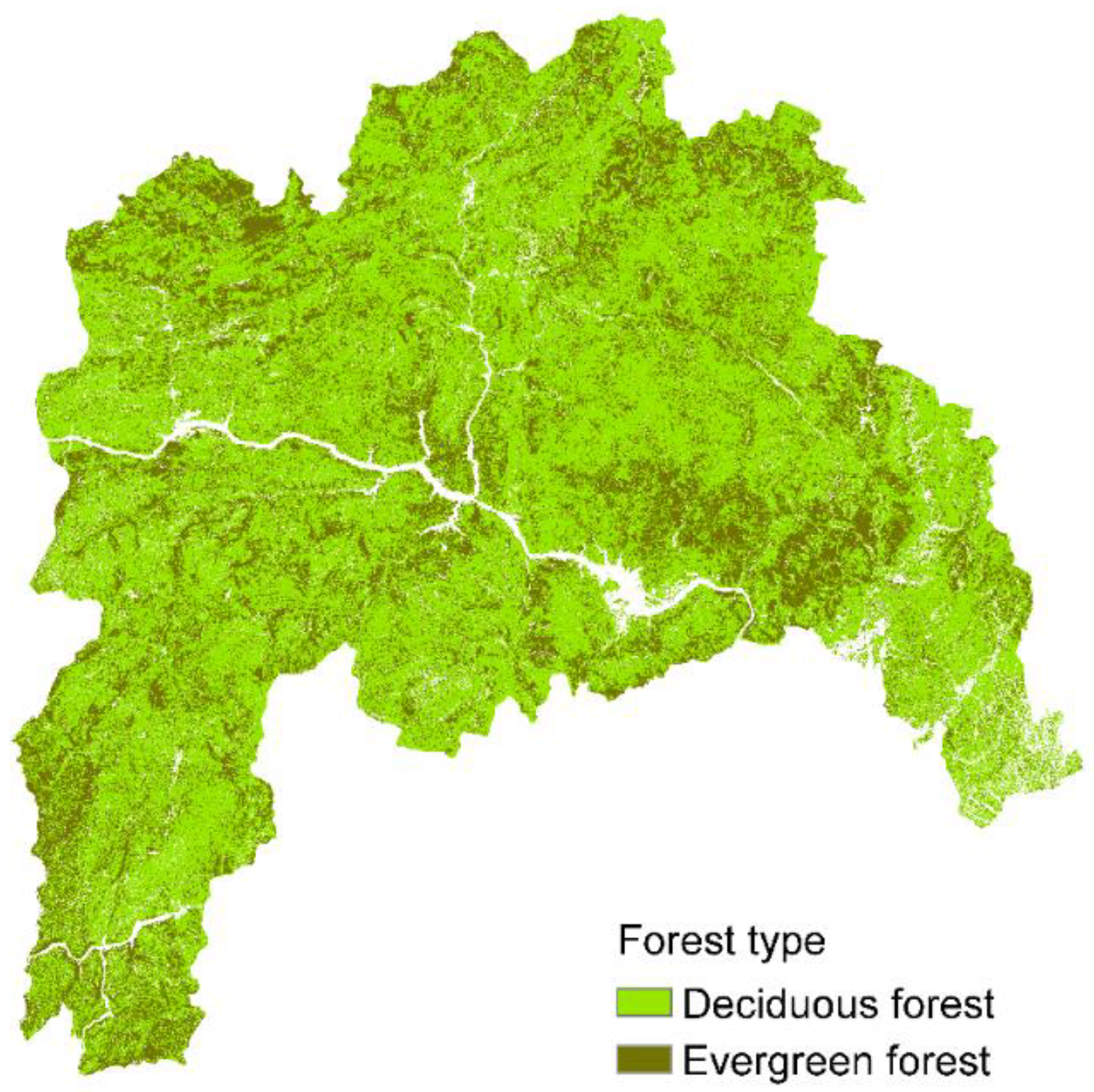
5.2. Forest Type Classification
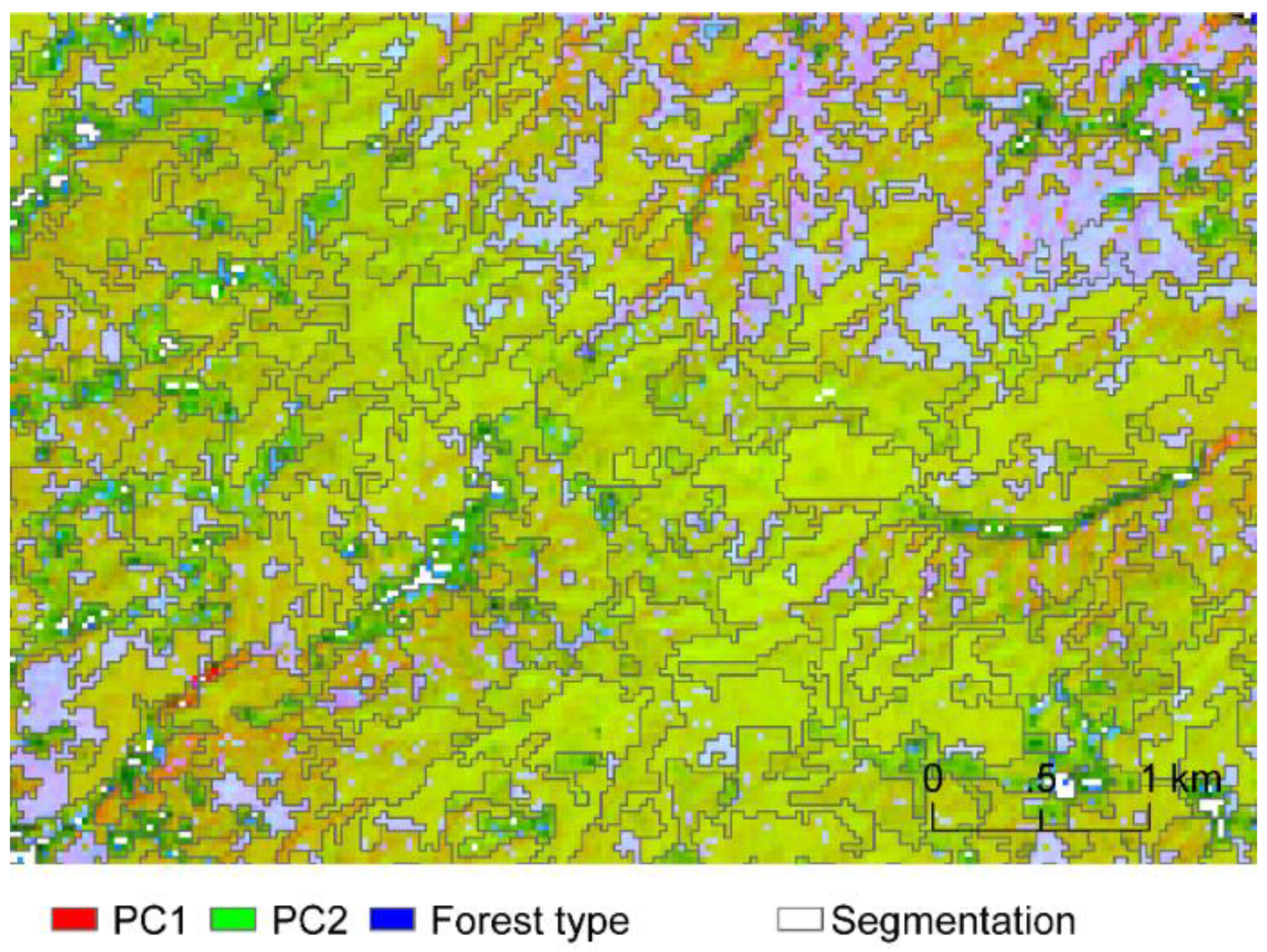
5.3. PCA and Multi-resolution Segmentation
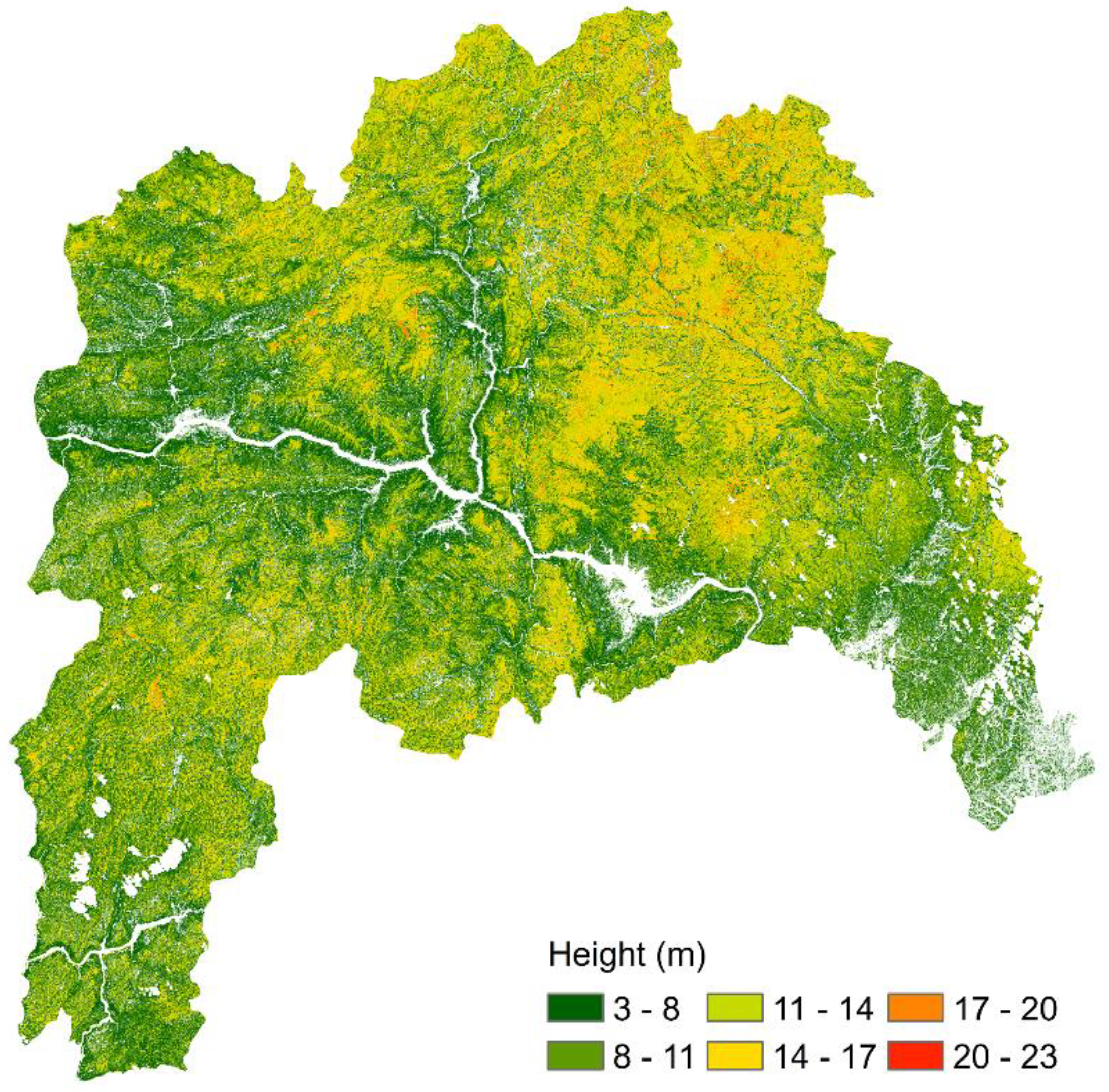
5.4. 30 m × 30 m Resolution Forest Canopy Height Mapping
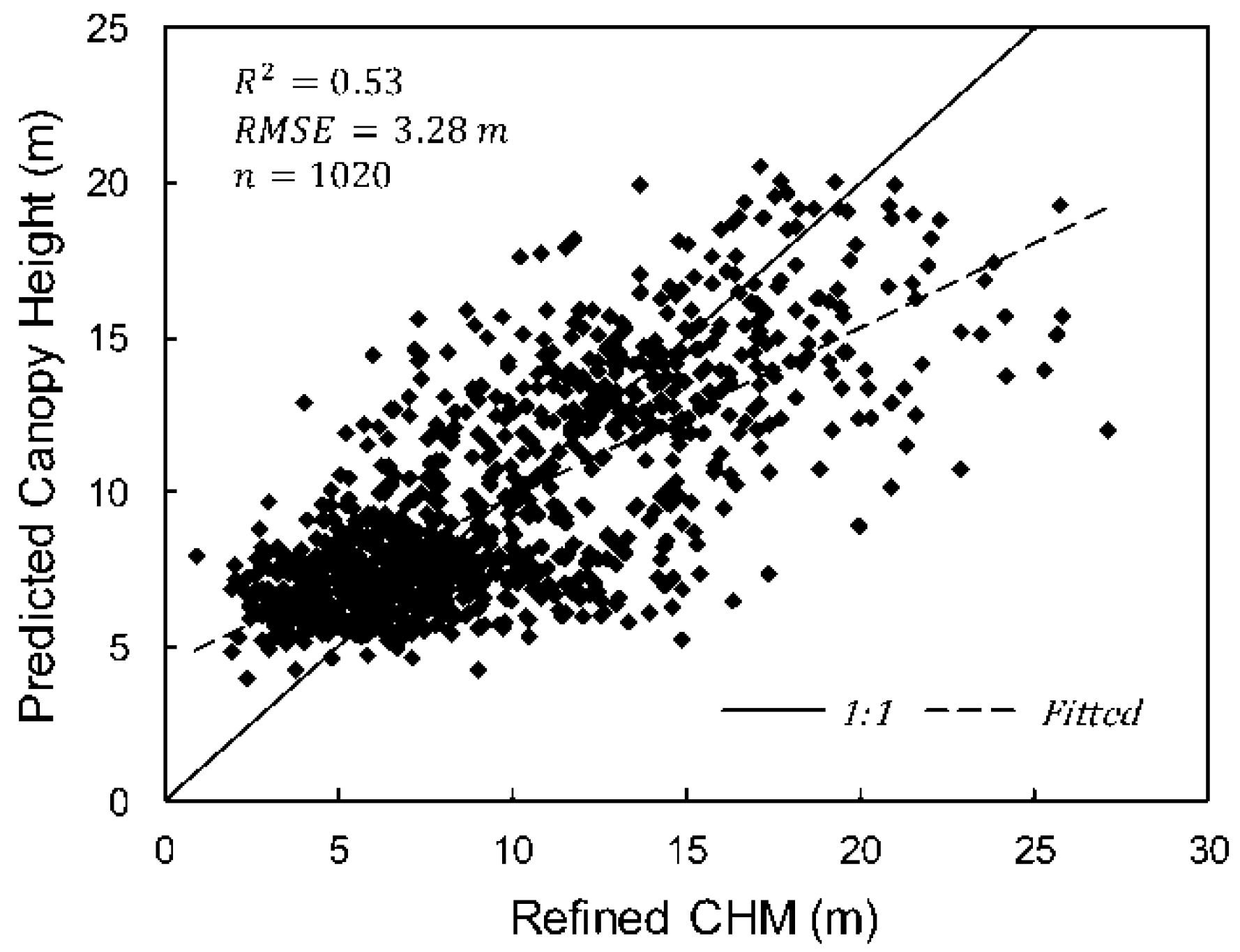
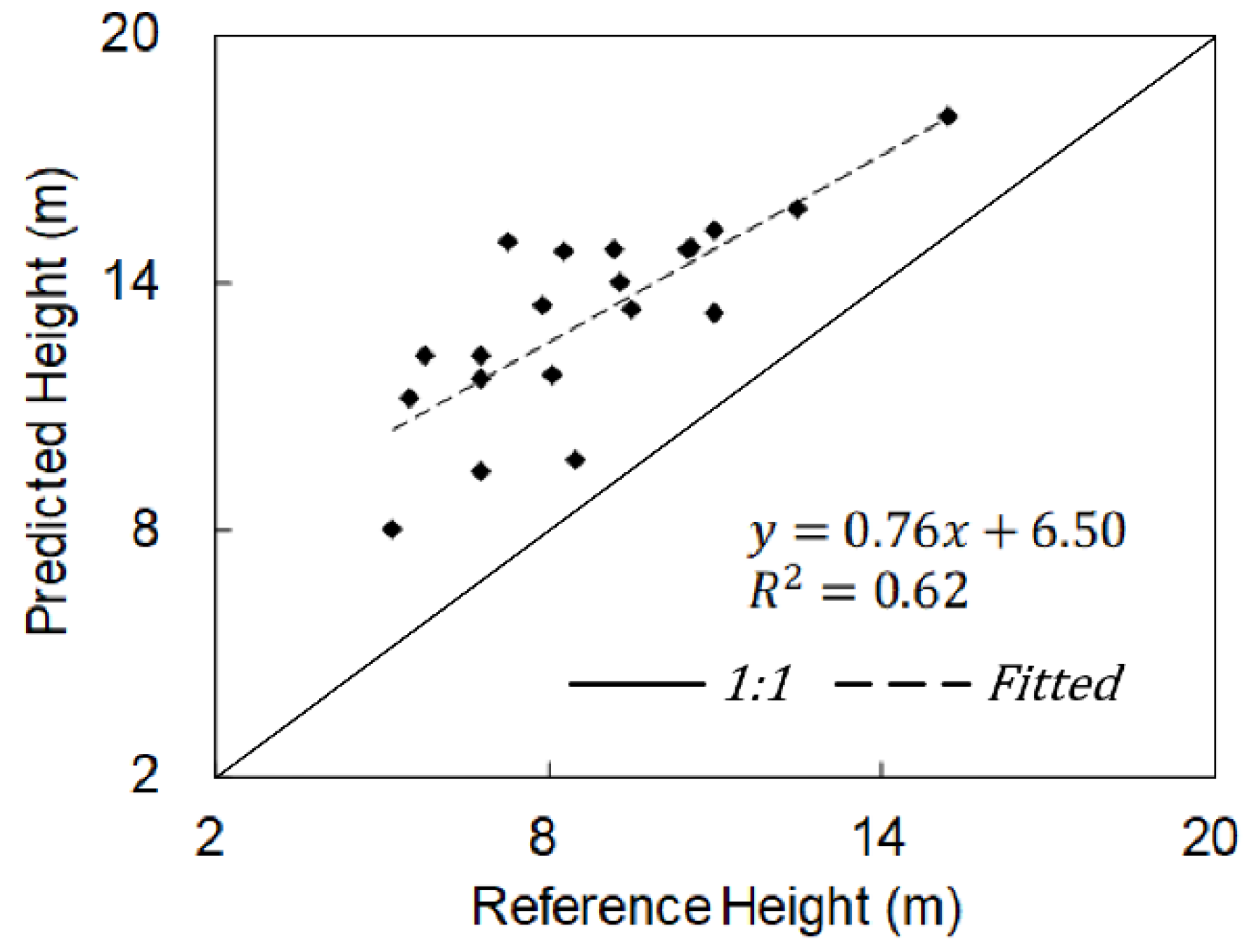
5.5. Independent Validation of the Predicted Forest Canopy Height
5.6. Limitations and Future Outlook
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Lefsky, M.A.; Keller, M.; Pang, Y.; de Camargo, P.B.; Hunter, M.O. Revised method for forest canopy height estimation from Geoscience Laser Altimeter System waveforms. J. Appl. Remote Sens. 2007, 1, 1–18. [Google Scholar]
- Lefsky, M.A. A global forest canopy height map from the Moderate Resolution Imaging Spectroradiometer and the Geoscience Laser Altimeter System. Geophys. Res. Lett. 2010, 37, 1–5. [Google Scholar] [CrossRef]
- Simard, M.; Pinto, N.; Fisher, J.B.; Baccini, A. Mapping forest canopy height globally with spaceborne lidar. J. Geophys. Res. Biogeosci. 2011, 116, 1–12. [Google Scholar] [CrossRef]
- Roussel, J.R.; Caspersen, J.; Béland, M.; Thomas, S.; Achim, A. Removing bias from LiDAR-based estimates of canopy height: Accounting for the effects of pulse density and footprint size. Remote Sens. Environ. 2017, 198, 1–16. [Google Scholar] [CrossRef]
- Vastaranta, M.; Holopainen, M.; Karjalainen, M.; Kankare, V.; Hyyppa, J.; Kaasalainen, S.; Hyyppa, H. SAR radargrammetry and scanning LiDAR in predicting forest canopy height. IEEE Int. Geosci. Remote Sens. Symp. 2012, 53, 6515–6518. [Google Scholar]
- Balzter, H.; Rowland, C.S.; Saich, P. Forest canopy height and carbon estimation at Monks Wood National Nature Reserve, UK, using dual-wavelength SAR interferometry. Remote Sens. Environ. 2007, 108, 224–239. [Google Scholar] [CrossRef]
- Ghasemi, N.; Tolpekin, V.; Stein, A. A modified model for estimating tree height from PolInSAR with compensation for temporal decorrelation. Int. J. Appl. Earth Obs. 2018, 73, 313–322. [Google Scholar] [CrossRef]
- Balenovic, I.; Seletkovic, A.; Pernar, R.; Jazbec, A. Estimation of the mean tree height of forest stands by photogrammetric measurement using digital aerial images of high spatial resolution. Ann. For. Res. 2015, 58, 125–143. [Google Scholar] [CrossRef]
- Herrero, H.M.; Felipe, G.B.; Belmar, L.S.; Hernandez, L.D.; Rodriguez, G.P.; Gonzalez, A.D. Dense Canopy Height Model from a low-cost photogrammetric platform and LiDAR data. Trees-Struct. Funct. 2016, 30, 1287–1301. [Google Scholar] [CrossRef]
- Zhou, T.; Popescu, S.C.; Krause, K.; Sheridan, R.D.; Putman, E. Gold—A novel deconvolution algorithm with optimization for waveform LiDAR processing. ISPRS-J. Photogramm. Remote Sens. 2017, 129, 131–150. [Google Scholar] [CrossRef]
- Anderson, J.; Martin, M.E.; Smith, M.L.; Dubayah, R.O.; Hofton, M.A.; Hyde, P.; Peterson, B.E.; Blair, J.B.; Knox, R.G. The use of waveform lidar to measure northern temperate mixed conifer and deciduous forest structure in New Hampshire. Remote Sens. Environ. 2006, 105, 248–261. [Google Scholar] [CrossRef]
- Boudreau, J.; Nelson, R.F.; Margolis, H.A.; Beaudoin, A.; Guindon, L.; Kimes, D.S. Regional aboveground forest biomass using airborne and spaceborne LiDAR in Québec. Remote Sens. Environ. 2008, 112, 3876–3890. [Google Scholar] [CrossRef]
- Huang, H.; Liu, C.; Wang, X.; Biging, G.S.; Chen, Y.; Yang, J.; Gong, P. Mapping vegetation heights in China using slope correction ICESat data, SRTM, MODIS-derived and climate data. ISPRS-J. Photogramm. Remote Sens. 2017, 129, 189–199. [Google Scholar] [CrossRef]
- Bolton, D.K.; Coops, N.C.; Wulder, M.A. Investigating the agreement between global canopy height maps and airborne LiDAR derived height estimates over Canada. Can. J. Remote Sens. 2013, 39, S139–S151. [Google Scholar] [CrossRef]
- Hilker, T.; Wulder, M.A.; Coops, N.C. Update of forest inventory data with LiDAR and high spatial resolution satellite imagery. Can. J. Remote Sens. 2008, 34, 5–12. [Google Scholar] [CrossRef]
- Hansen, M.C.; Potapov, P.V.; Goetz, S.J.; Turubanova, S.; Tyukavina, A.; Krylov, A.; Kommareddy, A.; Egorov, A. Mapping tree height distributions in Sub-Saharan Africa using Landsat 7 and 8 data. Remote Sens. Environ. 2016, 185, 221–232. [Google Scholar] [CrossRef]
- Garestier, F.; Dubois-Fernandez, P.C.; Guyon, D.; Le Toan, T. Forest biophysical parameter estimation using L- and P-band polarimetric SAR data. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3379–3388. [Google Scholar] [CrossRef]
- Karjalainen, M.; Kankare, V.; Vastaranta, M.; Holopainen, M.; Hyyppä, J. Prediction of plot-level forest variables using TerraSAR-X stereo SAR data. Remote Sens. Environ. 2012, 117, 338–347. [Google Scholar] [CrossRef]
- Capaldo, P.; Nascetti, A.; Porfiri, M.; Pieralice, F.; Fratarcangeli, F.; Crespi, M.; Toutin, T. Evaluation and comparison of different radargrammetric approaches for Digital Surface Models generation from COSMO-SkyMed, TerraSAR-X, RADARSAT-2 imagery: Analysis of Beauport (Canada) test site. ISPRS-J. Photogramm. Remote Sens. 2015, 100, 60–70. [Google Scholar] [CrossRef]
- Solberg, S.; Astrup, R.; Breidenbach, J.; Nilsen, B.; Weydahl, D. Monitoring spruce volume and biomass with InSAR data from TanDEM-X. Remote Sens. Environ. 2013, 139, 60–67. [Google Scholar] [CrossRef]
- Zhang, Y.; He, C.; Xu, X.; Chen, D. Forest vertical parameter estimation using PolInSAR imagery based on radiometric correction. ISPRS Int. J. Geo-Inf. 2016, 5, 186. [Google Scholar] [CrossRef]
- Neuenschwander, A.; Pitts, K. The ATL08 land and vegetation product for the ICESat-2 Mission. Remote Sens. Environ. 2019, 221, 247–259. [Google Scholar] [CrossRef]
- Qi, W.; Dubayah, R.O. Combining Tandem-X InSAR and simulated GEDI lidar observations for forest structure mapping. Remote Sens. Environ. 2016, 187, 253–266. [Google Scholar] [CrossRef]
- Le Toan, T.; Quegan, S.; Davidson, M.W.J.; Balzter, H.; Paillou, P.; Papathanassiou, K.; Plummer, S.; Rocca, F.; Saatchi, S.; Shugart, H.; et al. The BIOMASS mission: Mapping global forest biomass to better understand the terrestrial carbon cycle. Remote Sens. Environ. 2011, 115, 2850–2860. [Google Scholar] [CrossRef]
- Moreira, A.; Krieger, G.; Hajnsek, I.; Papathanassiou, K.; Younis, M.; Lopez-Dekker, P.; Huber, S.; Villano, M.; Pardini, M.; Eineder, M.; et al. Tandem-L: A Highly Innovative Bistatic SAR Mission for Global Observation of Dynamic Processes on the Earth’s Surface. IEEE Geosci. Remote Sens. Mag. 2015, 3, 8–23. [Google Scholar] [CrossRef]
- White, J.C.; Wulder, M.A.; Vastaranta, M.; Coops, N.C.; Pitt, D.; Woods, M. The utility of image-based point clouds for forest inventory: A comparison with airborne laser scanning. Forests 2013, 4, 518–536. [Google Scholar] [CrossRef]
- Aguilar, M.A.; Del Mar Saldaña, M.; Aguilar, F.J. Generation and quality assessment of stereo-extracted DSM from GeoEye-1 and WorldView-2 imagery. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1259–1271. [Google Scholar] [CrossRef]
- Immitzer, M.; Stepper, C.; Böck, S.; Straub, C.; Atzberger, C. Use of WorldView-2 stereo imagery and National Forest Inventory data for wall-to-wall mapping of growing stock. For. Ecol. Manag. 2016, 359, 232–246. [Google Scholar] [CrossRef]
- Jayathunga, S.; Owari, T.; Tsuyuki, S. Evaluating the Performance of Photogrammetric Products Using Fixed-Wing UAV Imagery over a Mixed Conifer-Broadleaf Forest: Comparison with Airborne Laser Scanning. Remote Sens. 2018, 10, 187. [Google Scholar] [CrossRef]
- Véga, C.; St-Onge, B. Height growth reconstruction of a boreal forest canopy over a period of 58 years using a combination of photogrammetric and lidar models. Remote Sens. Environ. 2008, 112, 1784–1794. [Google Scholar] [CrossRef]
- Järnstedt, J.; Pekkarinen, A.; Tuominen, S.; Ginzler, C.; Holopainen, M.; Viitala, R. Forest variable estimation using a high-resolution digital surface model. ISPRS-J. Photogramm. Remote Sens. 2012, 74, 78–84. [Google Scholar] [CrossRef]
- Pearse, G.D.; Dash, J.P.; Persson, H.J.; Watt, M.S. Comparison of high-density LiDAR and satellite photogrammetry for forest inventory. ISPRS-J. Photogramm. Remote Sens. 2018, 142, 257–267. [Google Scholar] [CrossRef]
- Gan, J.; Ge, J.; Liu, Y.; Wang, Z.; Wu, X.; Ding, S. Forest ecosystem quality change over ten years (2000–2010) in the Three Gorges Dalaoling Nature Reserve. Plant Sci. J. 2015, 33, 766–774. [Google Scholar]
- Wang, T.; Zhang, G.; Li, D.; Tang, X.; Jiang, Y.; Pan, H.; Zhu, X.; Fang, C. Geometric accuracy validation for ZY-3 satellite imagery. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1168–1171. [Google Scholar] [CrossRef]
- Li, D. China’s first civilian three-line-array stereo mapping satellite ZY-3. Acta Geodaetica et Cartographica Sinica 2012, 41, 317–322. [Google Scholar]
- Pan, H.; Zhang, G.; Tang, X.; Wang, X.; Zhou, P.; Xu, M.; Li, D. Accuracy analysis and verification of ZY-3 products. Acta Geodaetica et Cartographica Sinica 2013, 42, 738–744. [Google Scholar]
- Ni, W.; Sun, G.; Ranson, K.J.; Pang, Y.; Zhang, Z.; Yao, W. Extraction of ground surface elevation from ZY-3 winter stereo imagery over deciduous forested areas. Remote Sens. Environ. 2015, 159, 194–202. [Google Scholar] [CrossRef]
- Farr, T.G.; Kobrick, M. Shuttle radar topography mission produces a wealth of data. Eos 2000, 81, 583–585. [Google Scholar] [CrossRef]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The Shuttle Radar Topography Mission. Rev. Geophys. 2007, 45, 1–43. [Google Scholar] [CrossRef]
- Kobrick, M. On the toes of giants-How SRTM was born. Photogramm. Eng. Remote Sens. 2006, 72, 206–210. [Google Scholar]
- Nikolakopoulos, K.G.; Kamaratakis, E.K.; Chrysoulakis, N. SRTM vs ASTER elevation products. Comparison for two regions in Crete, Greece. Int. J. Remote Sens. 2006, 27, 4819–4838. [Google Scholar] [CrossRef]
- Rosen, P.A.; Hensley, S.; Joughin, I.R.; Li, F.K.; Madsen, S.N.; Rodríguez, E.; Goldstein, R.M. Synthetic aperture radar interferometry. Proc. IEEE 2000, 88, 333–380. [Google Scholar] [CrossRef]
- Hu, Z.; Peng, J.; Hou, Y.; Shan, J. Evaluation of recently released open global digital elevation models of Hubei, China. Remote Sens. 2017, 9, 262. [Google Scholar] [CrossRef]
- Krieger, G.; Moreira, A.; Fiedler, H.; Hajnsek, I.; Werner, M.; Younis, M.; Zink, M. TanDEM-X: A satellite formation for high-resolution SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3317–3341. [Google Scholar] [CrossRef]
- De Oliveira, C.G.; Paradella, W.R.; da Silva, A.D.Q. Assessment of radargrammetric DSMs from TerraSAR-X Stripmap images in a mountainous relief area of the Amazon region. ISPRS-J. Photogramm. Remote Sens. 2011, 66, 67–72. [Google Scholar] [CrossRef]
- Su, Y.; Guo, Q. A practical method for SRTM DEM correction over vegetated mountain areas. ISPRS-J. Photogramm. Remote Sens. 2014, 87, 216–228. [Google Scholar] [CrossRef]
- Vermote, E.; Justice, C.; Claverie, M.; Franch, B. Preliminary analysis of the performance of the Landsat 8/OLI land surface reflectance product. Remote Sens. Environ. 2016, 185, 46–56. [Google Scholar] [CrossRef]
- Zhu, Z.; Woodcock, C.E. Object-based cloud and cloud shadow detection in Landsat imagery. Remote Sens. Environ. 2012, 118, 83–94. [Google Scholar] [CrossRef]
- Wang, Y.; Li, G.; Ding, J.; Guo, Z.; Tang, S.; Wang, C.; Huang, Q.; Liu, R.; Chen, J.M. A combined GLAS and MODIS estimation of the global distribution of mean forest canopy height. Remote Sens. Environ. 2016, 174, 24–43. [Google Scholar] [CrossRef]
- Teillet, P.M.; Guindon, B.; Goodenough, D.G. On the slope-aspect correction of multispectral scanner data. Can. J. Remote Sens. 1982, 8, 84–106. [Google Scholar] [CrossRef]
- Breiman, L. Random forest. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Congalton, R.G. A review of assessing the accuracy of classifications of remotely sensed data. Remote Sens. Environ. 1991, 37, 35–46. [Google Scholar] [CrossRef]



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, M.; Cao, C.; Dang, Y.; Ni, X. Mapping Forest Canopy Height in Mountainous Areas Using ZiYuan-3 Stereo Images and Landsat Data. Forests 2019, 10, 105. https://doi.org/10.3390/f10020105
Liu M, Cao C, Dang Y, Ni X. Mapping Forest Canopy Height in Mountainous Areas Using ZiYuan-3 Stereo Images and Landsat Data. Forests. 2019; 10(2):105. https://doi.org/10.3390/f10020105
Chicago/Turabian StyleLiu, Mingbo, Chunxiang Cao, Yongfeng Dang, and Xiliang Ni. 2019. "Mapping Forest Canopy Height in Mountainous Areas Using ZiYuan-3 Stereo Images and Landsat Data" Forests 10, no. 2: 105. https://doi.org/10.3390/f10020105
APA StyleLiu, M., Cao, C., Dang, Y., & Ni, X. (2019). Mapping Forest Canopy Height in Mountainous Areas Using ZiYuan-3 Stereo Images and Landsat Data. Forests, 10(2), 105. https://doi.org/10.3390/f10020105





