Management Strategies for Conservation of Tanoak in California Forests Threatened by Sudden Oak Death: A Disease-Community Feedback Modelling Approach
Abstract
1. Introduction
- (a)
- How does forest composition affect pathogen spread without management?
- (b)
- Can forest composition be modified to prevent or ameliorate disease outbreaks?
- (c)
- How does forest composition affect the effectiveness of management strategies?
- (a)
- no management?
- (b)
- removal of bay laurel to reduce pathogen spread, with and without herbicide application to prevent stump resprouting, and with and without follow-up removals?
- (c)
- preventive chemical protection of tanoak?
- (d)
- a combination of treatments b (pathogen-centred) and c (host-centred)?
2. Materials and Methods
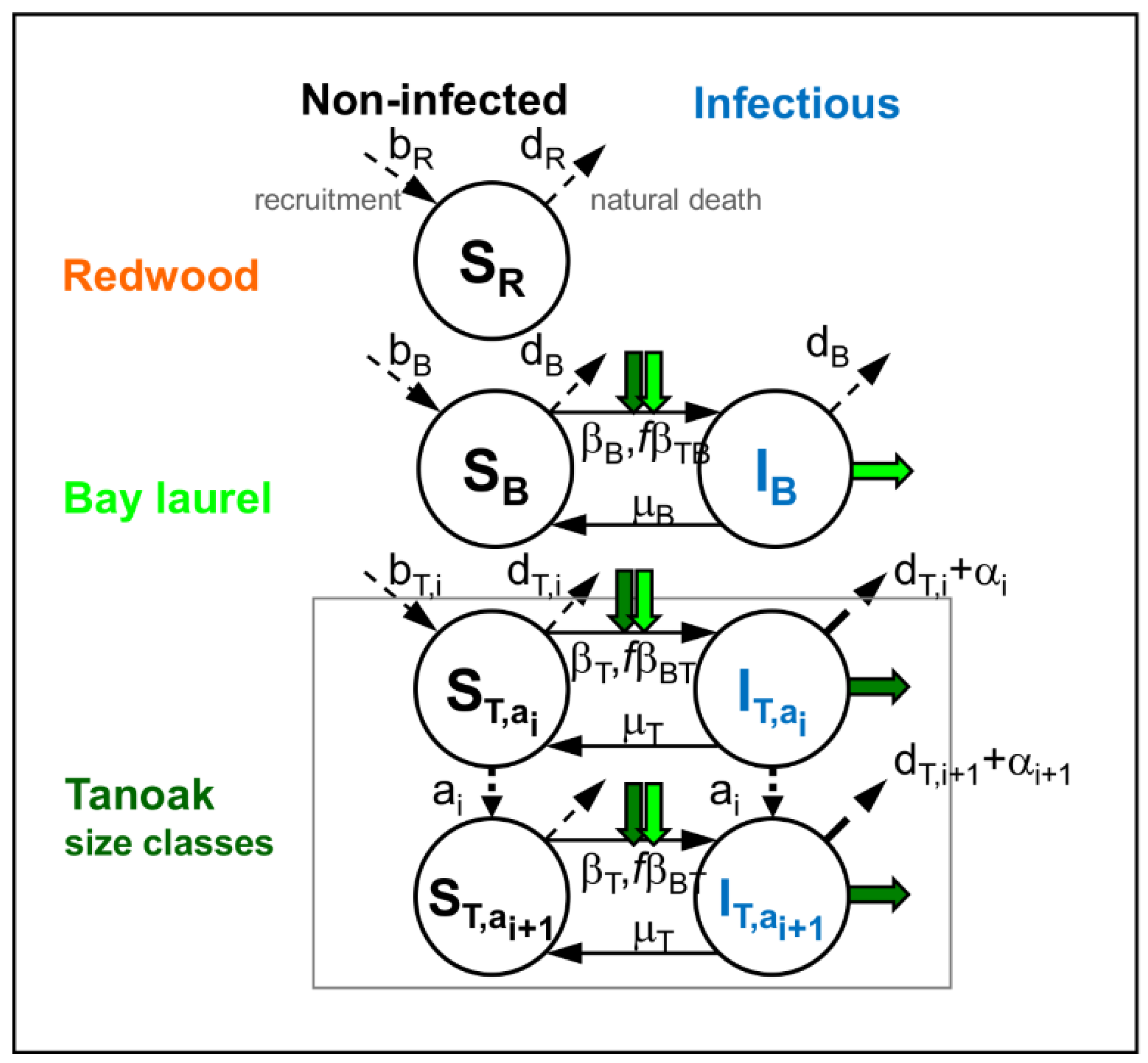
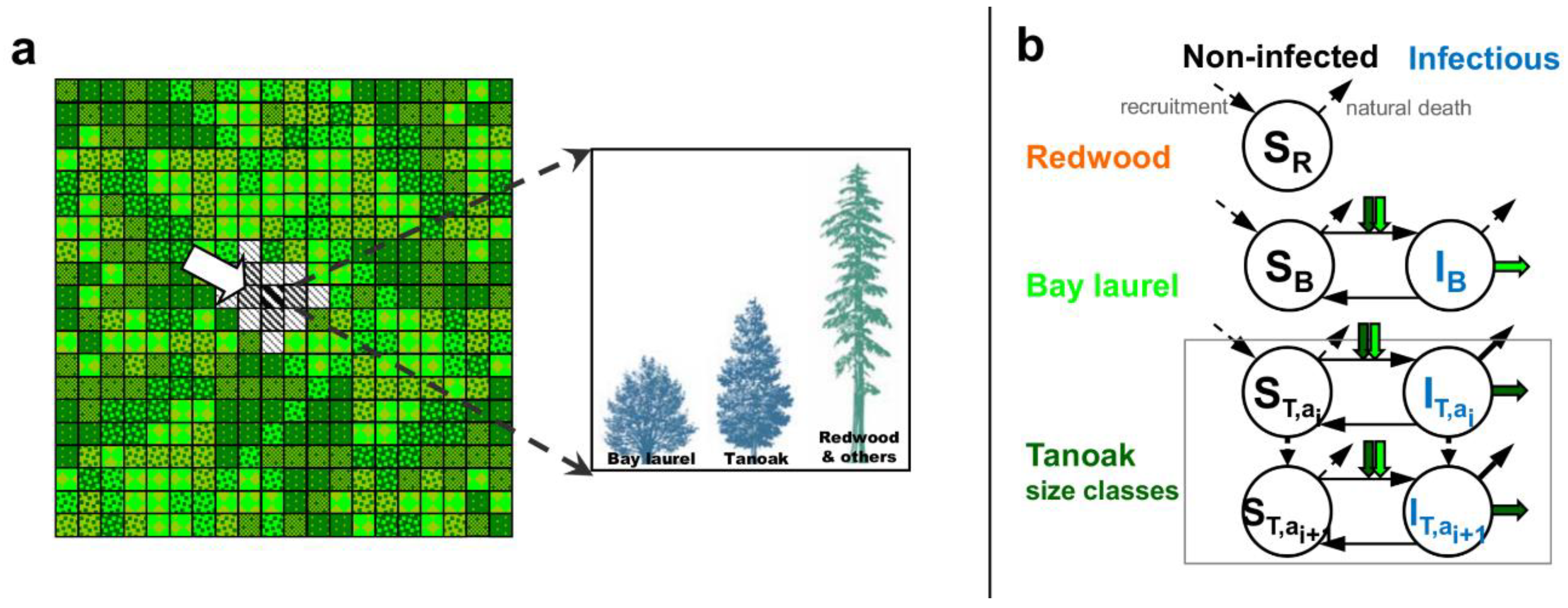
2.1. Model of Disease Impacts on the Community Dynamics with no Management (Q1a, Q2a)
2.2. Stand Spatial Composition before and after Disease
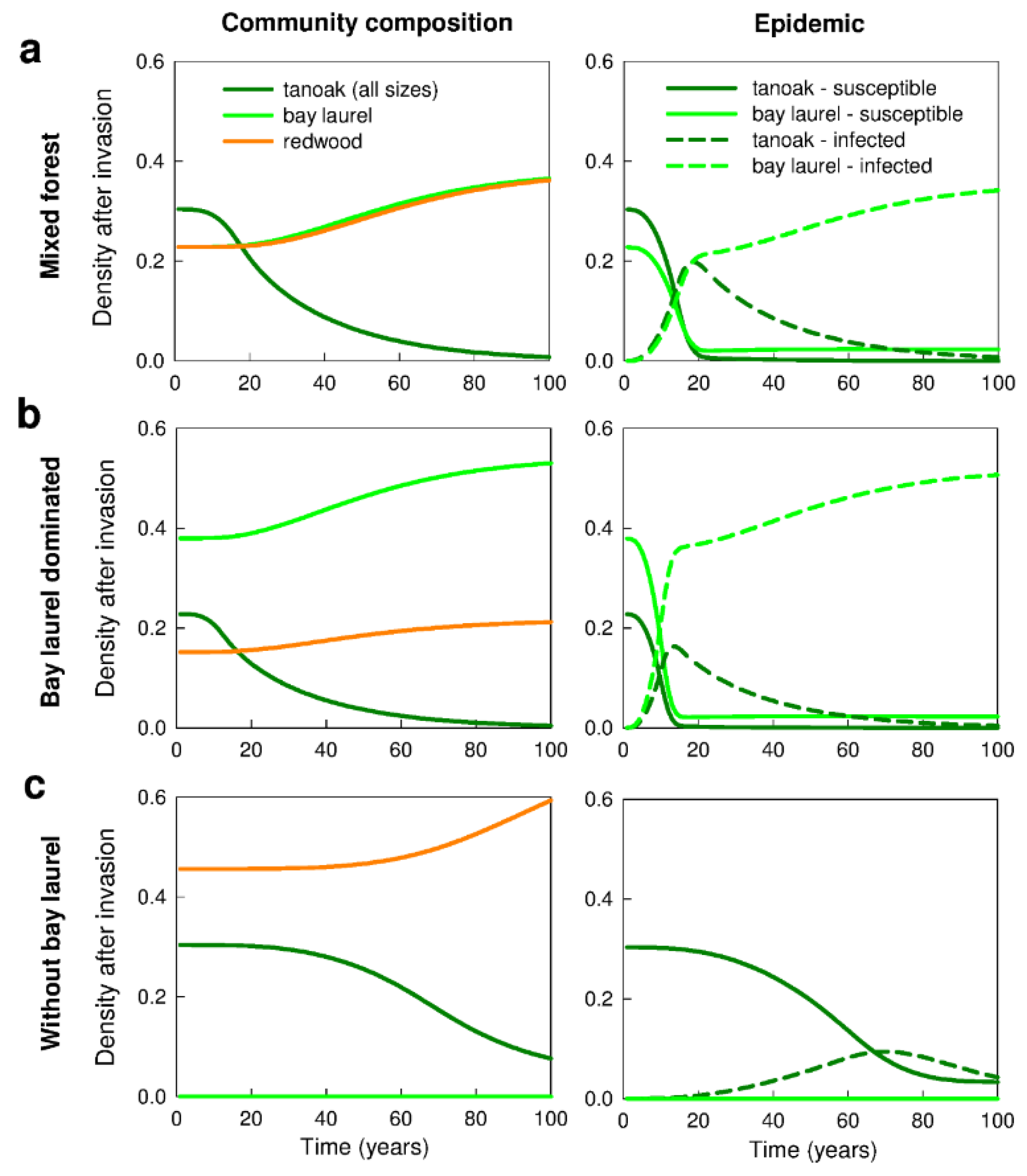
Forest Composition Scenarios (Q1)
2.3. Model of Disease Impacts on the Community Dynamics with Management Strategies (Q1b,c, Q2b–d)
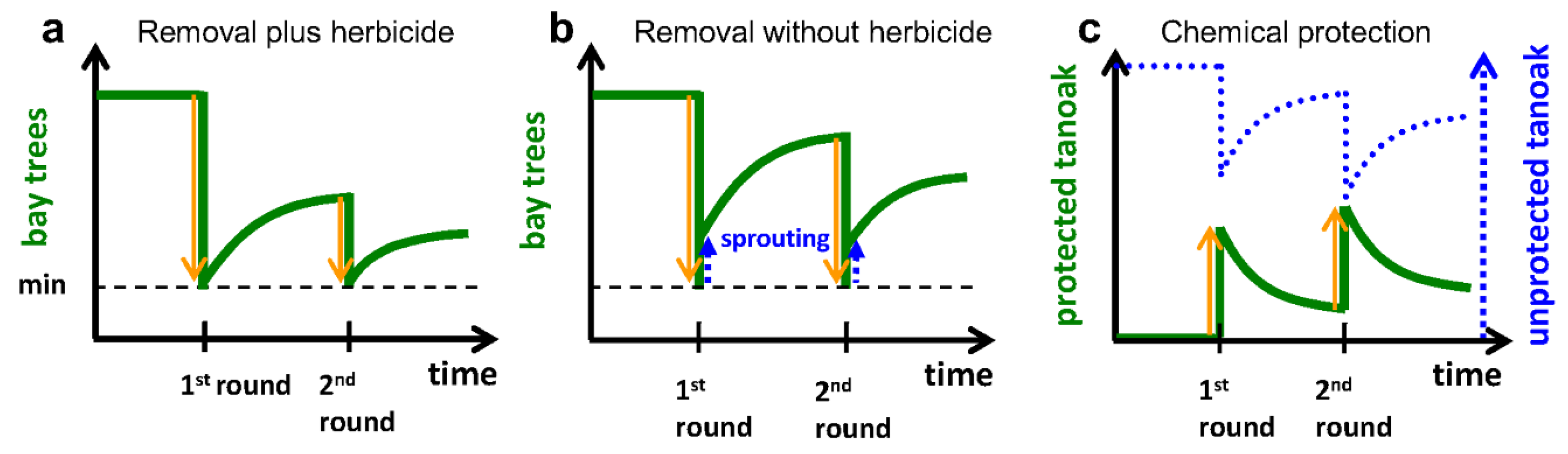
2.3.1. Removal of Bay Laurel (Q2b)
2.3.2. Chemical Protection of Tanoak (Q2c)
2.3.3. Combination of Treatments (Q2d)
2.3.4. Management Parameters (Q2b–d)
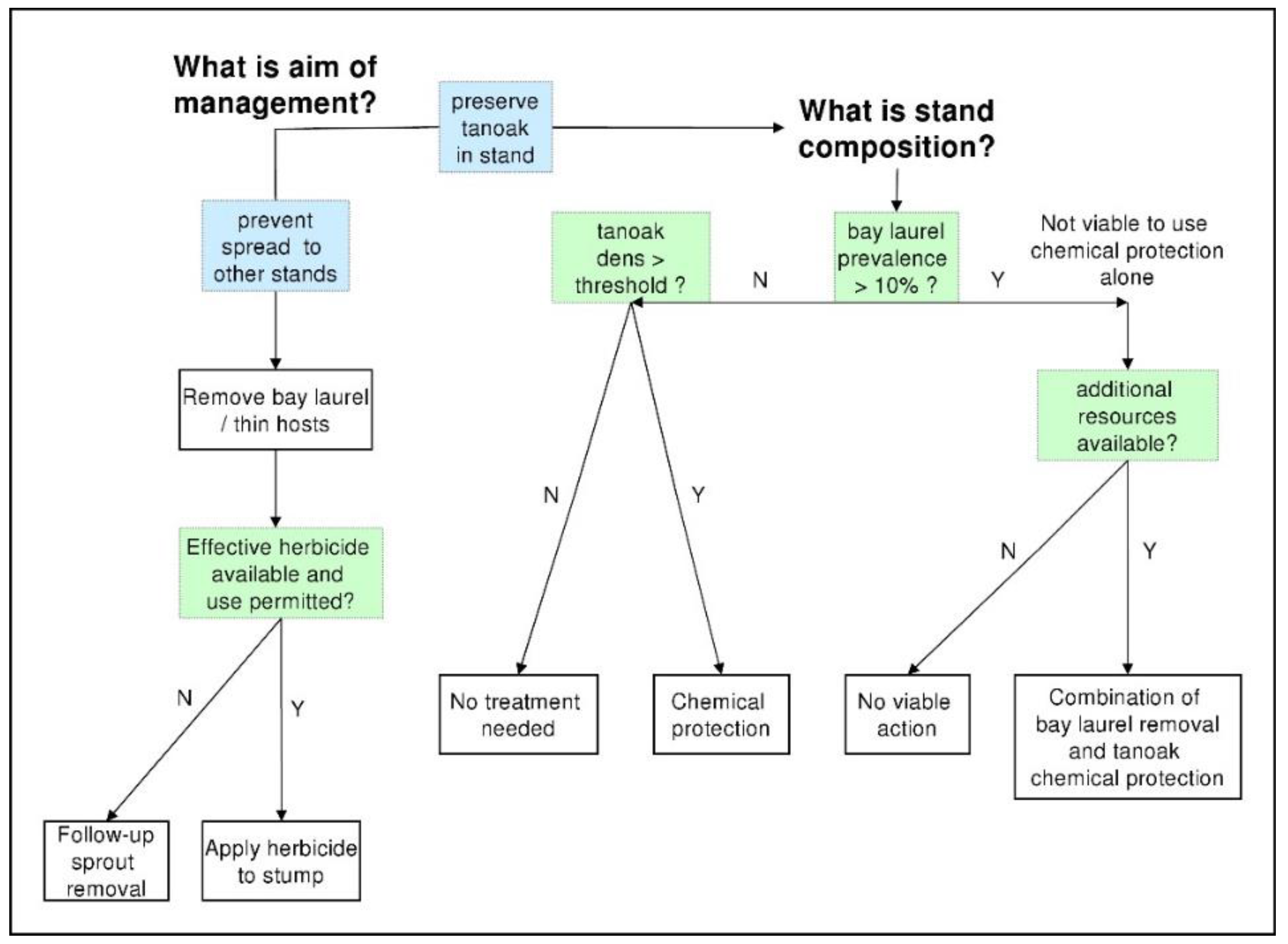
2.4. Management Evaluation
3. Results
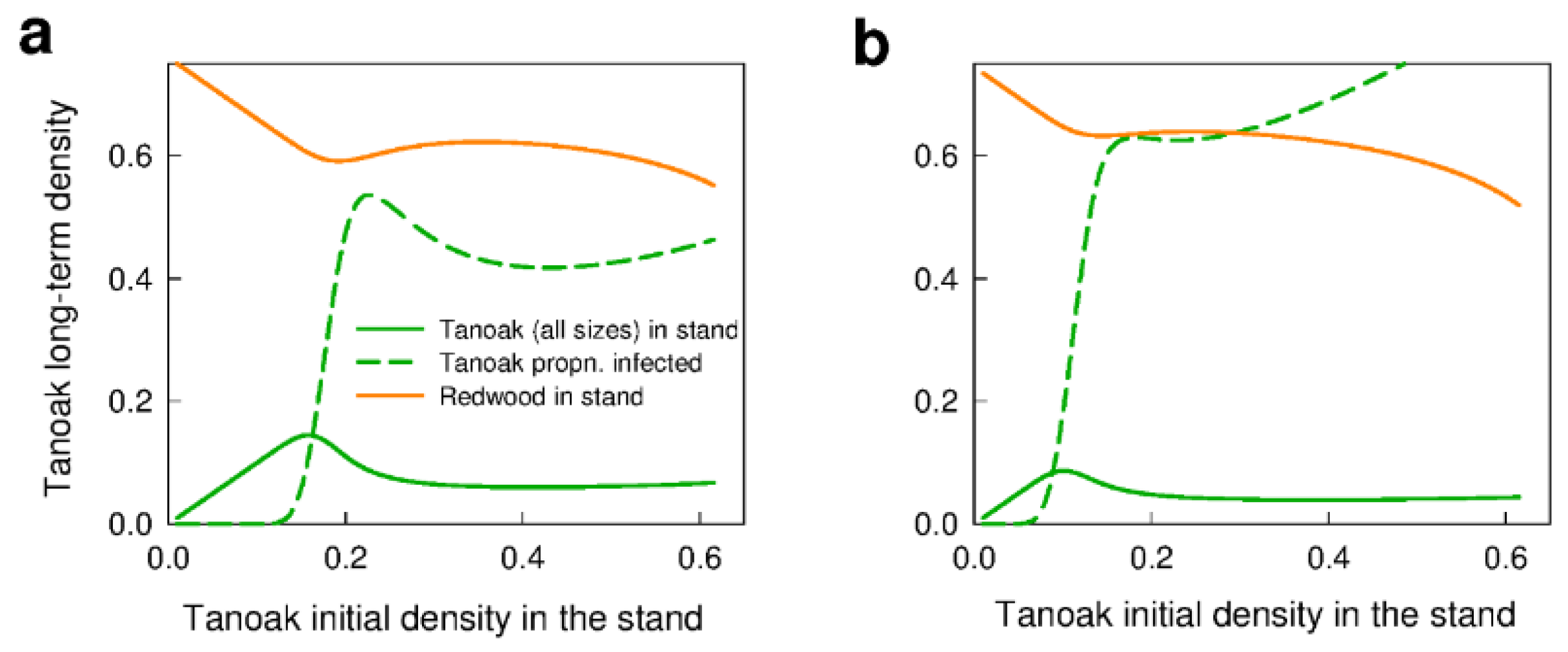
3.1. No Management—Disease Impacts and the Effect of Forest Composition (Q1a,b, Q2a)
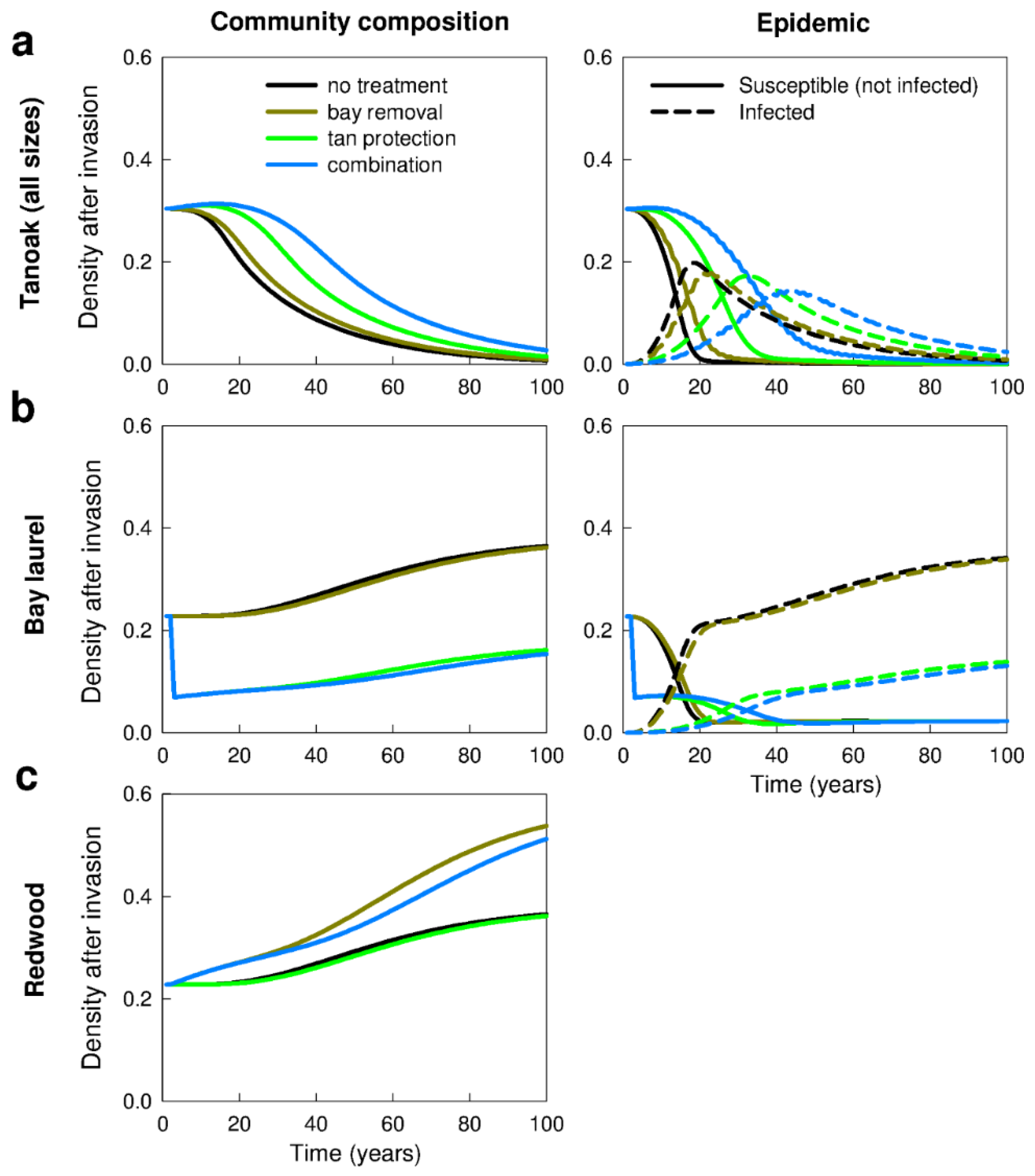
3.2. Management Strategies—Effects on Disease Impacts (Q2b–d)
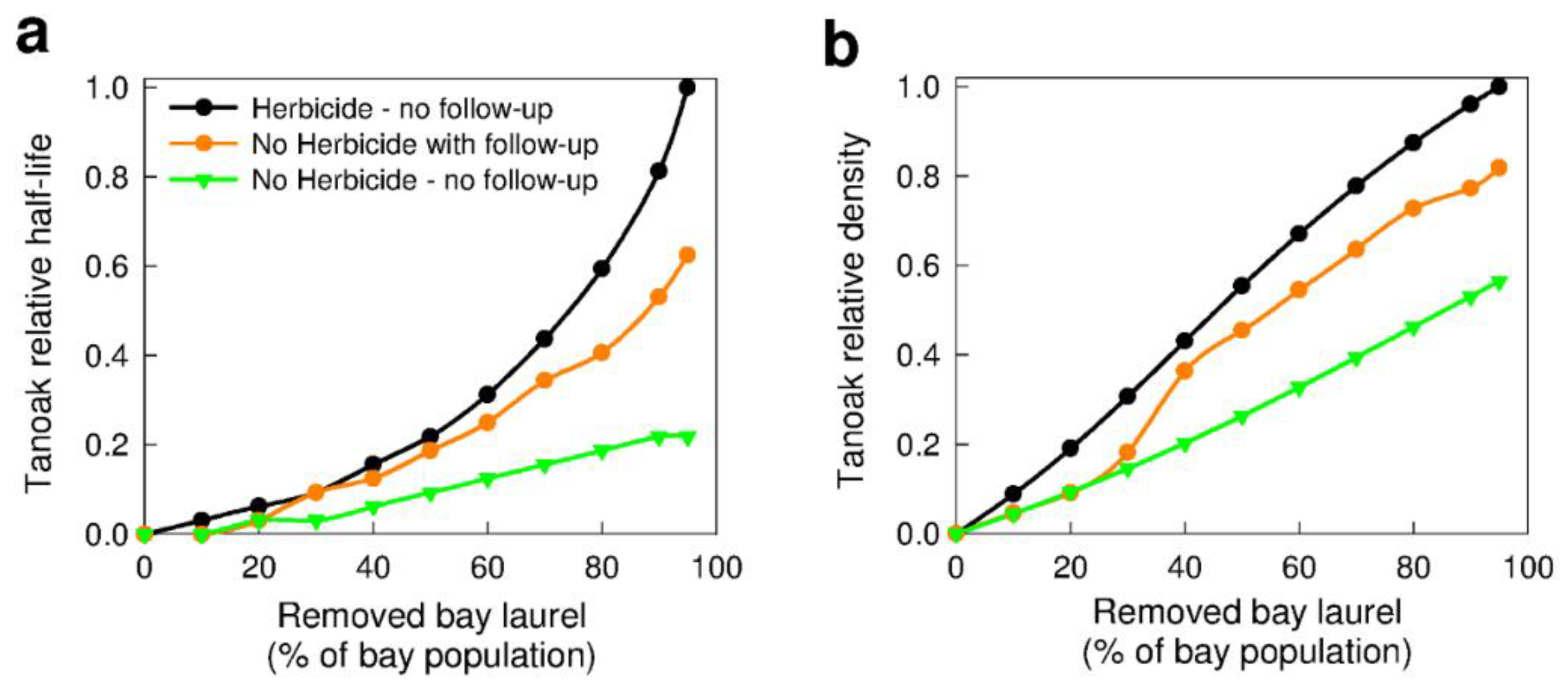
3.2.1. Removal of Bay Laurel (Q2b)
3.2.2. Forest Composition—Effects on Removal of Bay Laurel (Q1c)
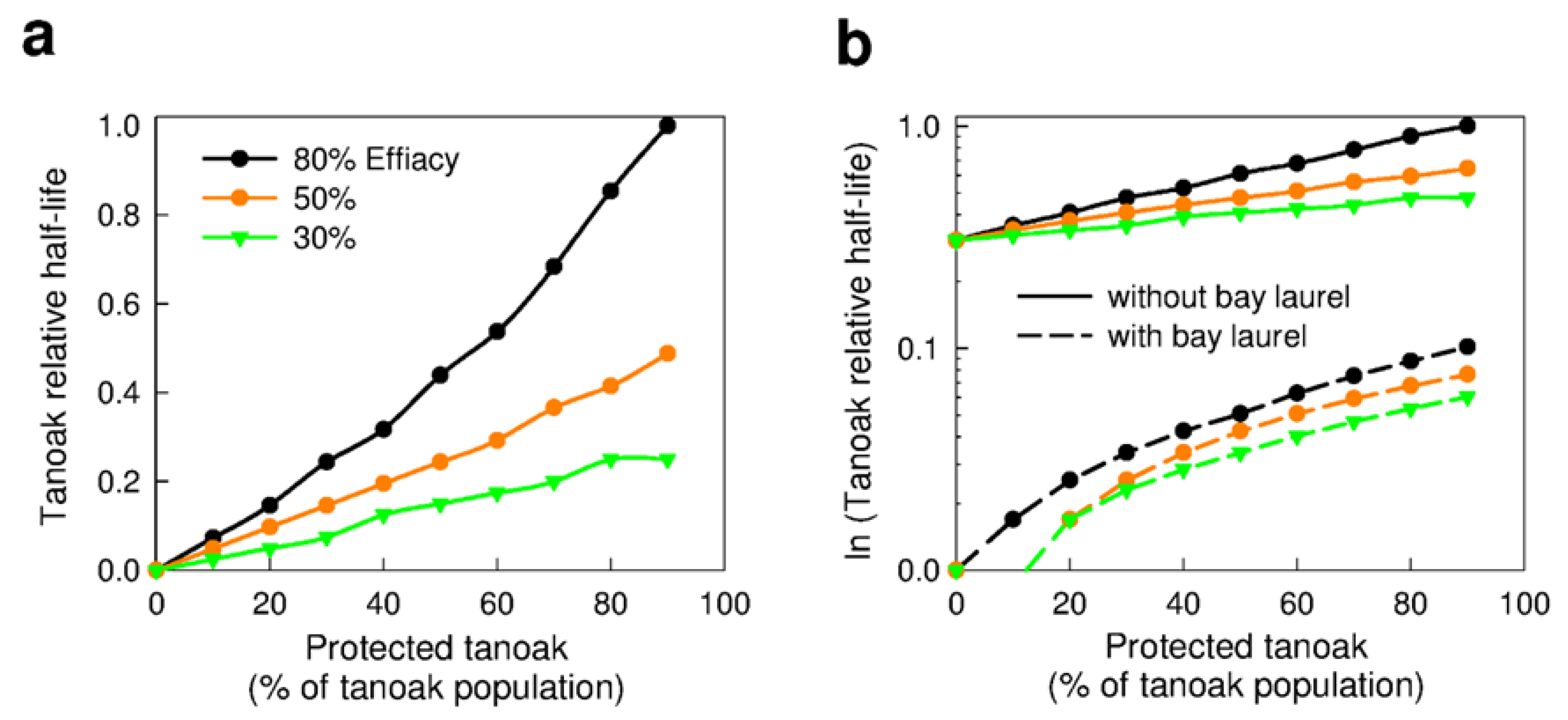
3.2.3. Chemical Protection of Tanoak (Q1b, Q2c)
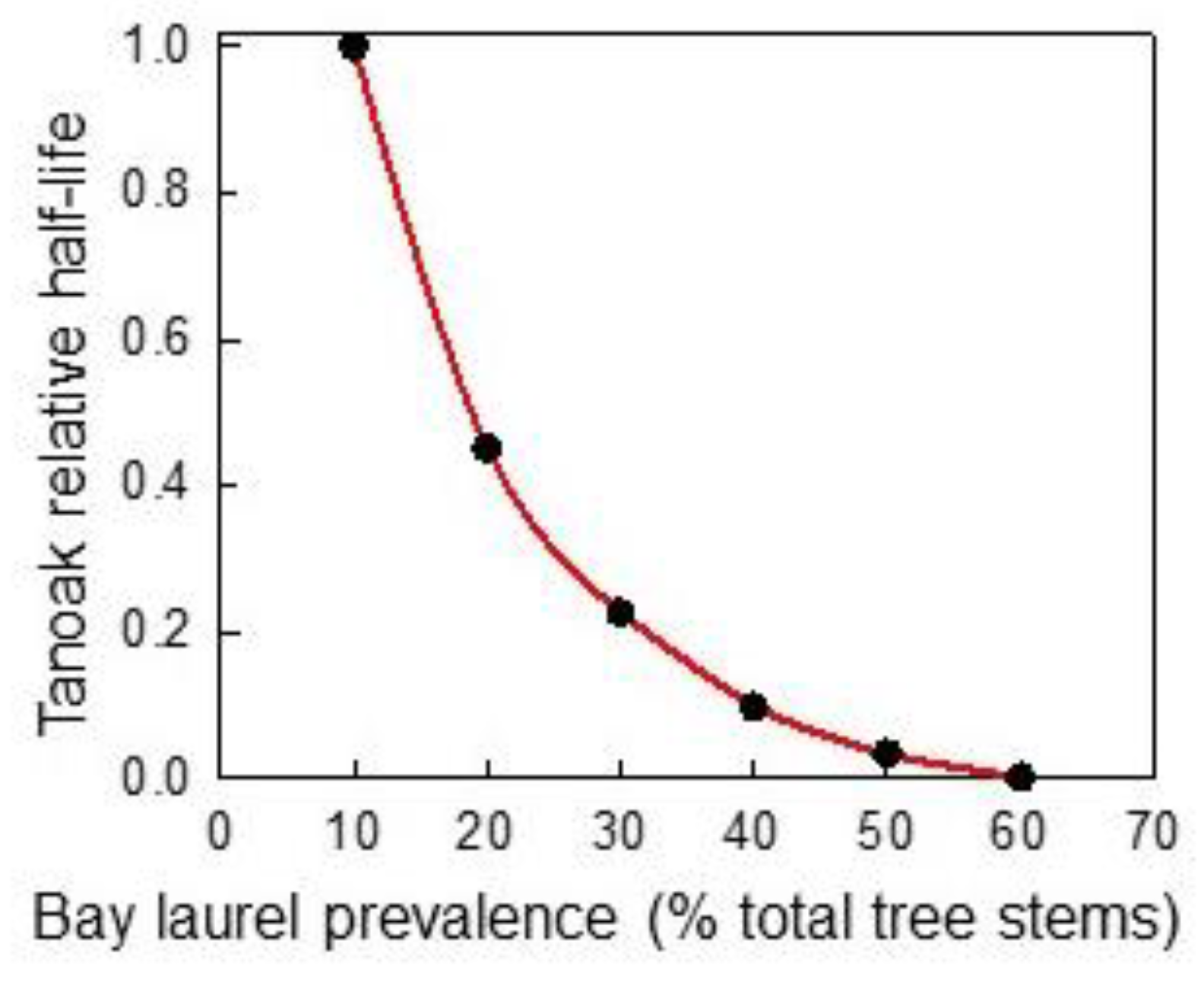
3.2.4. Forest Composition—Effects on Chemical Protection of Tanoak (Q1c)
3.2.5. Combination of Treatments (Q2d)
4. Discussion
4.1. Forest Composition—Influence on Disease Impacts and Selection of Management Strategies (Q1a–c)
4.2. Management Strategies—Effects on Disease Impacts (Q2a,d)
Factors Limiting the Effectiveness of Management
4.3. Model Assumptions and Extension
4.4. Experimental Testing and Extension to Other Systems
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Model of the Unmanaged Community Dynamics
| Parameter | Meaning | Unit | Values |
|---|---|---|---|
| Birth Rates | |||
| bT | Tanoak birth rate | Year−1 | 0.0164 |
| bB | Bay laurel birth rate | Year−1 | 0.0833 |
| bR | Redwood birth rate | Year−1 | 0.0833 |
| Death Rates | |||
| dT,i | Tanoak death rate in size class i = 1, 2, 3, 4 | Year−1 | 0.0059, 0.0028, 0.001, 0.0315 |
| dB | Bay laurel death rate | Year−1 | 0.020 |
| dR | Redwood death rate | Year−1 | 0.020 |
| Tanoak Size-Transition Rates | |||
| ai | From size class i to size class i + 1, i = 1, 2, 3 | Year−1 | 0.0504, 0.0167, 0.0134 |
| Rates of Infection within a Plot | |||
| βT,i | From tanoak to other tanoak in class i = 1, 2, 3, 4 | Year−1 | 0.38, 0.31, 0.34, 0.23 |
| βB | Within bay laurel | Year−1 | 1.33 |
| βBT | From bay laurel to tanoak | Year−1 | 1.46 |
| βTB | From tanoak to bay laurel | Year−1 | 0.3 |
| f | Proportion of spores produced that are deposited within a plot | – | 0.5 |
| Recovery Rates | |||
| μT | Tanoak | Year−1 | 0.01 |
| μB | Bay laurel | Year−1 | 0.1 |
| Rates of Diseased-Induced Death of Tanoak | |||
| αi | Tanoak in size class i | Year−1 | 0.069, 0.076, 0.134, 0.468 |
Appendix B. Model of the Implementation of Management Strategies
Appendix B.1. Removal of Bay Laurel
Appendix B.2. Protection of Tanoak
| Parameter | Unit | Values |
|---|---|---|
| Removal of Bay Laurel | ||
| Coverage: proportion of initial average density 1 that can be cut in each cell, c | – | 0–1 |
| Minimum density: trees that remain in each cell even when the coverage of the strategy allows further removal | – | 0–1 |
| Time of first round of treatment | Year | 1 |
| Time of optional second round of treatment | Year | 6 |
| Probability of stump resprouting (without herbicide application), r | Year−1 | 0.5 |
| Chemical Protection of Tanoak | ||
| Coverage: proportion of initial average density to be protected in each cell, c | – | 0–1 |
| Efficacy of protection, e, maximum value | – | 0.7–0.9 |
| Rate of decay of protection, γ | Year−1 | 0.7 |
| Frequency of treatment | Year−1 | 0.5 |
References
- Brasier, C.M. The biosecurity threat to the UK and global environment from international trade in plants. Plant Pathol. 2008, 57, 792–808. [Google Scholar] [CrossRef]
- Loo, J.A. Ecological impacts of non-indigenous invasive fungi as forest pathogens. Biol. Invasions 2009, 11, 81–96. [Google Scholar] [CrossRef]
- Santini, A.; Ghelardini, L.; De Pace, C.; Desprez-Loustau, M.L.; Capretti, P.; Chandelier, A.; Cech, T.; Chira, D.; Diamandis, S.; Gaitniekis, T.; et al. Biogeographical patterns and determinants of invasion by forest pathogens in Europe. New Phytol. 2013, 197, 238–250. [Google Scholar] [CrossRef] [PubMed]
- Lovett, G.M.; Weiss, M.; Liebhold, A.M.; Holmes, T.P.; Leung, B.; Lambert, K.F.; Orwig, D.A.; Campbell, F.T.; Rosenthal, J.; McCullough, D.G.; et al. Nonnative forest insects and pathogens in the United States: Impacts and policy options. Ecol. Appl. 2016, 26, 1437–1455. [Google Scholar] [CrossRef] [PubMed]
- Liebhold, A.M. Forest pest management in a changing world. Int. J. Pest Manag. 2012, 58, 289–295. [Google Scholar] [CrossRef]
- Liebhold, A.M.; Brockerhoff, E.G.; Garrett, L.J.; Parke, J.L.; Britton, K.O. Live plant imports: The major pathway for forest insect and pathogen invasions of the US. Front. Ecol. Environ. 2012, 10, 135–143. [Google Scholar] [CrossRef]
- Thakur, M.P.; van der Putten, W.H.; Cobben, M.M.P.; van Kleunen, M.; Geisen, S. Microbial invasions in terrestrial ecosystems. Nat. Rev. Microbiol. 2019, 17, 621–631. [Google Scholar] [CrossRef]
- Boyd, I.L.; Freer-Smith, P.H.; Gilligan, C.A.; Godfray, H.C.J. The consequence of tree pests and diseases for ecosystem services. Science 2013, 342, 1235773. [Google Scholar] [CrossRef]
- Kinloch, B.B. White pine blister rust in North America: Past and prognosis. Phytopathology 2003, 93, 1044–1047. [Google Scholar] [CrossRef]
- Paillet, F.L. Chestnut: History and ecology of a transformed species. J. Biogeogr. 2002, 29, 1517–1530. [Google Scholar] [CrossRef]
- Grunwald, N.J.; Goss, E.M.; Press, C.M. Phytophthora ramorum: A pathogen with a remarkably wide host range causing sudden oak death on oaks and ramorum blight on woody ornamentals. Mol. Plant Pathol. 2008, 9, 729–740. [Google Scholar] [CrossRef] [PubMed]
- Frankel, S.J. Sudden oak death and Phytophthora ramorum in the USA: A management challenge. Australas. Plant Pathol. 2008, 37, 19–25. [Google Scholar] [CrossRef]
- Hansen, E.M.; Kanaskie, A.; Prospero, S.; McWilliams, M.; Goheen, E.M.; Osterbauer, N.; Reeser, P.; Sutton, W. Epidemiology of Phytophthora ramorum in Oregon tanoak forests. Can. J. For. Res. Rev. Can. Rech. For. 2008, 38, 1133–1143. [Google Scholar] [CrossRef]
- Metz, M.R.; Frangioso, K.M.; Wickland, A.C.; Meentemeyer, R.K.; Rizzo, D.M. An emergent disease causes directional changes in forest species composition in coastal California. Ecosphere 2012, 3, 23. [Google Scholar] [CrossRef]
- Grunwald, N.J.; LeBoldus, J.M.; Hamelin, R.C. Ecology and evolution of the sudden Oak death pathogen Phytophthora ramorum. Annu. Rev. Phytopathol. 2019, 57, 301–321. [Google Scholar] [CrossRef]
- Meentemeyer, R.K.; Rank, N.E.; Shoemaker, D.A.; Oneal, C.B.; Wickland, A.C.; Frangioso, K.M.; Rizzo, D.M. Impact of sudden oak death on tree mortality in the Big Sur ecoregion of California. Biol. Invasions 2008, 10, 1243–1255. [Google Scholar] [CrossRef]
- Brasier, C.; Webber, J. Plant pathology: Sudden larch death. Nature 2010, 466, 824–825. [Google Scholar] [CrossRef]
- Harris, A.R.; Webber, J.F. Sporulation potential, symptom expression and detection of Phytophthora ramorum on larch needles and other foliar hosts. Plant Pathol. 2016, 65, 1441–1451. [Google Scholar] [CrossRef]
- Jung, T.; Perez-Sierra, A.; Duran, A.; Jung, M.H.; Balci, Y.; Scanu, B. Canker and decline diseases caused by soil- and airborne Phytophthora species in forests and woodlands. Persoonia 2018, 40, 182–220. [Google Scholar] [CrossRef]
- O’Hanlon, R.; Choiseul, J.; Brennan, J.M.; Grogan, H. Assessment of the eradication measures applied to Phytophthora ramorum in Irish Larix kaempferi forests. For. Pathol. 2018, 48, e12389. [Google Scholar] [CrossRef]
- Xie, B.; Cao, C.; Chen, W.; Yu, B. Prediction and analysis of the potential risk of sudden oak death in China. J. For. Res. 2019, 30, 2357–2366. [Google Scholar] [CrossRef]
- Davidson, J.M.; Patterson, H.A.; Rizzo, D.M. Sources of inoculum for Phytophthora ramorum in a redwood forest. Phytopathology 2008, 98, 860–866. [Google Scholar] [CrossRef] [PubMed]
- Davidson, J.M.; Patterson, H.A.; Wickland, A.C.; Fichtner, E.J.; Rizzo, D.M. Forest type influences transmission of Phytophthora ramorum in California Oak Woodlands. Phytopathology 2011, 101, 492–501. [Google Scholar] [CrossRef] [PubMed]
- Rizzo, D.M.; Garbelotto, M.; Hansen, E.A. Phytophthora ramorum: Integrative research and management of an emerging pathogen in California and Oregon forests. Annu. Rev. Phytopathol. 2005, 43, 309–335. [Google Scholar] [CrossRef] [PubMed]
- Hayden, K.J.; Nettel, A.; Dodd, R.S.; Garbelotto, M. Will all the trees fall? Variable resistance to an introduced forest disease in a highly susceptible host. For. Ecol. Manag. 2011, 261, 1781–1791. [Google Scholar] [CrossRef]
- Cobb, R.C.; Meentemeyer, R.K.; Rizzo, D.M. Apparent competition in canopy trees determined by pathogen transmission rather than susceptibility. Ecology 2010, 91, 327–333. [Google Scholar] [CrossRef]
- Varner, J.M.; Kuljian, H.G.; Kreye, J.K. Fires without tanoak: The effects of a non-native disease on future community flammability. Biol. Invasions 2017, 19, 2307–2317. [Google Scholar] [CrossRef]
- Monahan, W.B.; Koenig, W.D. Estimating the potential effects of sudden oak death on oak-dependent birds. Biol. Conserv. 2006, 127, 146–157. [Google Scholar] [CrossRef]
- Bergemann, S.E.; Garbelotto, M. High diversity of fungi recovered from the roots of mature tanoak (Lithocarpus densiflorus) in northern California. Can. J. Bot. 2006, 84, 1380–1394. [Google Scholar] [CrossRef]
- Cobb, R.C.; Rizzo, D.M.; Hayden, K.J.; Garbelotto, M.; Filipe, J.A.N.; Gilligan, C.A.; Dillon, W.; Meentemeyer, R.K.; Valachovic, Y.S.; Goheen, E.; et al. Biodiversity conservation in the face of dramatic forest disease: An integrated conservation strategy for tanoak (Notholithocarpus densiflorus) threatened by sudden oak death. Madrono 2013, 60, 151–165. [Google Scholar] [CrossRef]
- Bowcutt, F. Tanoak target: The rise and fall of herbicide use on a common native tree. Environ. Hist. 2011, 16, 197–225. [Google Scholar] [CrossRef]
- Grunwald, N.J.; Garbelotto, M.; Goss, E.M.; Heungens, K.; Prospero, S. Emergence of the sudden oak death pathogen Phytophthora ramorum. Trends Microbiol. 2012, 20, 131–138. [Google Scholar] [CrossRef] [PubMed]
- Garbelotto, M.; Schmidt, D.; Swain, S.; Hayden, K.; Lione, G. The ecology of infection between a transmissive and a dead-end host provides clues for the treatment of a plant disease. Ecosphere 2017, 8, e01815. [Google Scholar] [CrossRef]
- Kanaskie, A.; Goheen, E.M.; Hansen, E.M.; Sutton, W.; Reeser, P.; Osterbauer, N. Monitoring the effectiveness of Phytophthora ramorum eradication treatments in southwest Oregon tanoak forests. In Proceedings of the Annual Meeting of the American-Phytopathology-Society, Portland, OR, USA, 1–5 August 2009; p. S61. [Google Scholar]
- Kanaskie, A.; Hansen, E.M.; Goheen, E.M.; Osterbauer, N.; McWilliams, M.; Laine, J.; Thompson, M.; Savona, S.; Timeus, H.; Wiese, R.; et al. Detection and eradication of Phytophthora ramorum from Oregon forests, 2001–2011. In Proceedings of the Sudden Oak Death Fifth Science Symposium, Petaluma, CA, USA, 19–22 June 2012; PSW-GTR-243. pp. 3–13. [Google Scholar]
- Peterson, E.; Hansen, E.M.; Kanaskie, A. Spatial relationship between Phytophthora ramorum and roads or streams in Oregon tanoak forests. For. Ecol. Manag. 2014, 312, 216–224. [Google Scholar] [CrossRef]
- Hansen, E.M.; Reeser, P.; Sutton, W.; Kanaskie, A.; Navarro, S.; Goheen, E.M. Efficacy of local eradication treatments against the sudden oak death epidemic in Oregon tanoak forests. For. Pathol. 2019, 49, e12530. [Google Scholar] [CrossRef]
- Alexander, J.; Lee, C. Lessons learned from a decade of sudden Oak death in California: Evaluating local management. Environ. Manag. 2010, 46, 315–328. [Google Scholar] [CrossRef]
- Valachovic, Y.; Lee, C.; Marshall, J.; Scanlon, H. Forest treatment strategies for Phytophthora ramorum. In Proceedings of the Sudden Oak Death Fourth Science Symposium, Santa Cruz, CA, USA, 15–18 June 2009; PSW-GTR-222. pp. 239–248. [Google Scholar]
- Kanaskie, A.; Hansen, E.M.; Sutton, W.; Reeser, P.; Choquette, C. Application of phosphonate to prevent sudden oak death in south-western Oregon tanoak (Notholithocarpus densiflorus) forests. N. Z. J. For. Sci. 2011, 41S, S177–S187. [Google Scholar]
- Garbelotto, M.; Schmidt, D. Phosphonate controls sudden oak death pathogen for up to 2 years. Calif. Agric. 2009, 63, 10–17. [Google Scholar] [CrossRef]
- Elliott, M.; Shamoun, S.F.; Sumampong, G.; James, D.; Masri, S.; Varga, A. Evaluation of several commercial biocontrol products on European and North American populations of Phytophthora ramorum. Biocontrol Sci. Technol. 2009, 19, 1007–1021. [Google Scholar] [CrossRef]
- Swiecki, T.J.; Bernhardt, E. Assessing methods to protect susceptible oak and tanoak stands from sudden oak death. In Proceedings of the Sudden Oak Death Fourth Science Composium, Santa Cruz, CA, USA, 2010; Available online: https://www.fs.usda.gov/treesearch/pubs/35024 (accessed on 3 December 2019).
- Filipe, J.A.N.; Cobb, R.C.; Meentemeyer, R.K.; Lee, C.A.; Valachovic, Y.S.; Cook, A.R.; Rizzo, D.M.; Gilligan, C.A. Landscape epidemiology and control of pathogens with cryptic and long-distance dispersal: Sudden oak death in northern Californian forests. PLoS Comput. Biol. 2012, 8, e1002328. [Google Scholar] [CrossRef]
- Cobb, R.C.; Filipe, J.A.N.; Meentemeyer, R.K.; Gilligan, C.A.; Rizzo, D.M. Ecosystem transformation by emerging infectious disease: Loss of large tan oak from California forests. J. Ecol. 2012, 100, 712–722. [Google Scholar] [CrossRef]
- Filipe, J.A.N.; Gibson, G.J. Comparing approximations to spatio-temporal models for epidemics with local spread. Bull. Math. Biol. 2001, 63, 603–624. [Google Scholar] [CrossRef] [PubMed]
- Harrington, T.B.; Tappeiner, J.C. Long-term effects of tanoak competition on Douglas-fir stand development. Can. J. For. Res. Rev. Can. Rech. For. 2009, 39, 765–776. [Google Scholar] [CrossRef]
- Maloney, P.E.; Lynch, S.C.; Kane, S.F.; Jensen, C.E.; Rizzo, D.M. Establishment of an emerging generalist pathogen in redwood forest communities. J. Ecol. 2005, 93, 899–905. [Google Scholar] [CrossRef]
- Lorimer, C.G.; Porter, D.J.; Madej, M.A.; Stuart, J.D.; Veirs, S.D.; Norman, S.P.; O’Hara, K.L.; Libby, W.J. Presettlement and modern disturbance regimes in coast redwood forests: Implications for the conservation of old-growth stands. For. Ecol. Manag. 2009, 258, 1038–1054. [Google Scholar] [CrossRef]
- Valachovic, Y.; Cobb, R.C.; Rizzo, D.M.; Twieg, B.; Lee, C.; Glebocki, R. Is stump sprout treatment necessary to effectively control Phytophthora ramorum in California’s wildlands? In Sudden Oak Death Fourth Science Composium; Us Dept Agr, Forest Serv Pacific Sw Forest & Range Exptl Stn: Petaluma, CA, USA, 2013; Volume 243, pp. 114–117. [Google Scholar]
- Ballard, B.D.; Nowak, C.A. Timing of cut-stump herbicide applications for killing hardwood trees on power line rights-of-way. Arboric. Urban For. 2006, 32, 118–125. [Google Scholar]
- Anderson, R.M.; May, R.M. Vaccination and herd-immunity to infectious-diseases. Nature 1985, 318, 323–329. [Google Scholar] [CrossRef]
- Brown, L.B.; Allen-Diaz, B. Forest stand dynamics and sudden oak death: Mortality in mixed-evergreen forests dominated by coast live oak. For. Ecol. Manag. 2009, 257, 1271–1280. [Google Scholar] [CrossRef]
- Horner, I.J.; Hough, E.G.; Horner, M.B. Forest efficacy trials on phosphite for control of kauri dieback. N. Z. Plant Prot. 2015, 68, 7–12. [Google Scholar] [CrossRef]
- Garbelotto, M.; Schmidt, D.J.; Harnik, T.Y. Phosphite injections and bark application of phosphite + Pentrabark™ control sudden oak death in coast live oak. Arboric. Urban For. 2007, 33, 309–317. [Google Scholar] [CrossRef]
- Gilligan, C.A. Sustainable agriculture and plant diseases: An epidemiological perspective. Philos. Trans. R. Soc. B Biol. Sci. 2008, 363, 741–759. [Google Scholar] [CrossRef] [PubMed]
- Peterson, E.K.; Hansen, E.M.; Kanaskie, A. Temporal epidemiology of sudden Oak death in Oregon. Phytopathology 2015, 105, 937–946. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Cunniffe, N.J.; Cobb, R.C.; Meentemeyer, R.K.; Rizzo, D.M.; Gilligan, C.A. Modeling when, where, and how to manage a forest epidemic, motivated by sudden oak death in California. Proc. Natl. Acad. Sci. USA 2016, 113, 5640–5645. [Google Scholar] [CrossRef] [PubMed]
- Mascheretti, S.; Croucher, P.J.P.; Vettraino, A.; Prospero, S.; Garbelotto, M. Reconstruction of the sudden Oak death epidemic in California through microsatellite analysis of the pathogen Phytophthora ramorum. Mol. Ecol. 2008, 17, 2755–2768. [Google Scholar] [CrossRef]
- Meentemeyer, R.K.; Cunniffe, N.J.; Cook, A.R.; Filipe, J.A.N.; Hunter, R.D.; Rizzo, D.M.; Gilligan, C.A. Epidemiological modeling of invasion in heterogeneous landscapes: Spread of sudden Oak death in California (1990–2030). Ecosphere 2011, 2, art17. [Google Scholar] [CrossRef]
- Maloy, O.C. White pine blister rust control in North America: A case history. Annu. Rev. Phytopathol. 1997, 35, 87–109. [Google Scholar] [CrossRef]
- Hunter, S.; Williams, N.; McDougal, R.; Scott, P.; Garbelotto, M. Evidence for rapid adaptive evolution of tolerance to chemical treatments in Phytophthora species and its practical implications. PLoS ONE 2018, 13, e0208961. [Google Scholar] [CrossRef]
- Swiecki, T.J.; Quinn, M.; Sims, L.; Bernhardt, E.; Oliver, L.; Popenuck, T.; Garbelotto, M.M. Three new Phytophthora detection methods, including training dogs to sniff out the pathogen, prove reliable. Calif. Agric. 2018, 72, 217–225. [Google Scholar] [CrossRef]
- Kalantarzadeh, M.; Mulholland, D.A.; De Leij, F.A.A.M.; Webber, J.F. Induced antimicrobial activity in heat-treated woodchips inhibits the activity of the invasive plant pathogen Phytophthora ramorum. Plant Pathol. 2019, 68, 889–900. [Google Scholar] [CrossRef]
- Woodcock, P.; Cottrell, J.E.; Buggs, R.J.A.; Quine, C.P. Mitigating pest and pathogen impacts using resistant trees: A framework and overview to inform development and deployment in Europe and North America. Forestry 2018, 91, 1–16. [Google Scholar] [CrossRef]
- Cobb, R.C.; Ross, N.; Hayden, K.J.; Eyre, C.A.; Dodd, R.S.; Frankel, S.J.; Garbelotto, M.; Rizzo, D.M. Promise and pitfalls of endemic resistance for cultural resources threatened by Phytophthora ramorum. Phytopathology 2019, 109, 760–769. [Google Scholar] [CrossRef] [PubMed]
- Conrad, A.O.; McPherson, B.A.; Lopez-Nicora, H.D.; D’Amico, K.M.; Wood, D.L.; Bonello, P. Disease incidence and spatial distribution of host resistance in a coast live oak/sudden oak death pathosystem. For. Ecol. Manag. 2019, 433, 618–624. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Filipe, J.A.N.; Cobb, R.C.; Salmon, M.; Gilligan, C.A. Management Strategies for Conservation of Tanoak in California Forests Threatened by Sudden Oak Death: A Disease-Community Feedback Modelling Approach. Forests 2019, 10, 1103. https://doi.org/10.3390/f10121103
Filipe JAN, Cobb RC, Salmon M, Gilligan CA. Management Strategies for Conservation of Tanoak in California Forests Threatened by Sudden Oak Death: A Disease-Community Feedback Modelling Approach. Forests. 2019; 10(12):1103. https://doi.org/10.3390/f10121103
Chicago/Turabian StyleFilipe, João A. N., Richard C. Cobb, Maëlle Salmon, and Christopher A. Gilligan. 2019. "Management Strategies for Conservation of Tanoak in California Forests Threatened by Sudden Oak Death: A Disease-Community Feedback Modelling Approach" Forests 10, no. 12: 1103. https://doi.org/10.3390/f10121103
APA StyleFilipe, J. A. N., Cobb, R. C., Salmon, M., & Gilligan, C. A. (2019). Management Strategies for Conservation of Tanoak in California Forests Threatened by Sudden Oak Death: A Disease-Community Feedback Modelling Approach. Forests, 10(12), 1103. https://doi.org/10.3390/f10121103





