1. Introduction
Wood remains a widely used material. Among its primary uses, wood is the principal resource used in the manufacture of paper and pulp. Wood possesses a strength performance index and structural stiffness per weight similar or superior to that for the best engineering composites when considered in bending, which makes it a favorable structural material [
1]. Furthermore, wood is often regarded for inspiration in the development of new bio-inspired structures and biomimetic materials [
2]. Because wood is a complex hierarchical material, researchers continue striving to evaluate and understand the moisture-related properties of wood to develop improved wood products and biomimetic materials. Specifically, fundamental understanding of the wood moisture-induced swelling, especially at the smallest length scales, is still lacking largely due to the difficulties associated with the experimental techniques capable of accessing these scales.
The interaction of wood with water is a major concern when it comes to wood and wood-based materials. The absorption of moisture causes dimensional instabilities and swelling forces in the wood that may cause splits [
3,
4]. Additionally, moisture accumulation in wood is required for the growth and proliferation of fungi, which leads to wood degradation by wood-decay fungi [
5]. Excessive moisture accumulation can even lead to corrosion of fasteners in wood–metal connections used in constructions, especially in wood treated with copper-based preservatives [
6,
7]. Both wood decay and fastener corrosion can be prevented if wood is kept at moisture contents below about 15% [
8]. However, despite these negative effects, the interactions between wood and moisture can give inspiring ideas. For example, moisture changes in a bundle of wood cells cause a moisture-activated torsional behavior. Wood cell bundles are capable of generating a specific torque higher than that of commercial motors [
9] and carbon nanotubes yarns [
10]. Moreover, wood cell bundles possess moisture-activated shape memory twist capabilities [
11,
12]. Thermally-induced shape memory effects are also observed in wood veneers; for example, a cooled wood veneer in a loaded position is capable of recovering its original form when heated [
13]. A better understanding of wood moisture-induced swelling will provide insights into solving issues related to influences that cause susceptibility to degradation of wood products as well as inspiration for the development of advanced wood-based materials and bioinspired materials. For instance, the moisture-induced torsional actuation has inspired the development of actuating fibers made from helically assembled aligned carbon nanotubes that can produce a torque upon exposure to solvent or vapor [
14].
The effect of moisture on the swelling and shrinking properties of wood at the bulk level has been documented for well over a century [
15,
16,
17]. At the bulk level, swelling is anisotropic. From dry to wet, wood generally swells about 10% in the tangential direction, 5% in the radial direction, and 0.1% in the longitudinal direction. The smaller shrinkage in the longitudinal direction results from the stiff cellulose microfibrils orientation, which is more or less parallel to the longitudinal axis in the thick S
2 cell wall layer. While the cellulose microfibrils are mostly unaffected by the moisture absorption process [
18,
19,
20], the encrusting matrix swells during moisture absorption. Since the microfibril angle in the thick S
2 layer is relatively low, it follows that when wood absorbs moisture, the cellulose microfibrils restrain the swelling causing minimal deformation along their longitudinal direction.
Different wood species exhibit different levels of anisotropy and swell different amounts (for example, see tables in Chapter 4 of the
Wood Handbook [
21]). It has been observed that within a tree species, the amount of moisture-induced swelling is roughly proportional to the wood density [
22,
23]. Wood with a higher density swells more than wood with a lower density. This behavior contradicts what would be expected for a cellular solid composed of a homogeneous material and pores filled with air. In this cellular solid, the amount of swelling is independent of the distribution, orientation, and quantity of pores; it swells the same as a non-porous solid composed of the same material [
24,
25]. This density dependence shows that wood behaves differently from a homogenous porous material. The differences must be caused by intra cell wall structures with smaller length scales [
24,
25].
Despite the well-established observations of swelling and shrinkage at the bulk level, many of the proposed explanations for the anisotropy in the transverse plane and density effects are not satisfactory. For example, a very simple explanation often provided for the density effect in wood swelling is that void space does not swell. Thus, low-density wood will swell less than high-density wood because it has more void volume [
17,
19,
26]. Nonetheless, as explained in the previous paragraph, this explanation is not valid even for the simpler case of a homogeneous porous material [
24,
25] and thus cannot explain the density effect observed in wood’s swelling behavior. The underlying causes for some aspects of the anisotropic swelling and density effects remain unclear.
Although the swelling of bulk wood originates in the smaller scale levels of structure, the understanding of the complex swelling in these smaller structures is still incomplete. This review aims to advance the understanding of moisture-induced swelling and contraction in wood and provide ideas for future research.
The discussion is organized as follows.
Section 2 describes the relevant levels of hierarchical structure in wood and the basics of wood–water relations.
Section 3 reviews the current state of understanding of the moisture-induced swelling and shrinkage at each structural level of wood. Finally,
Section 4 provides an overall summary and suggestions for future research directions.
2. Wood Structure
Wood is an anisotropic cellular material with a hierarchical structure spanning from molecular-scale up to tubular cells, which are cemented together to form the wood in a tree. To describe the wood structure is necessary to contemplate wood’s different components across different length scales.
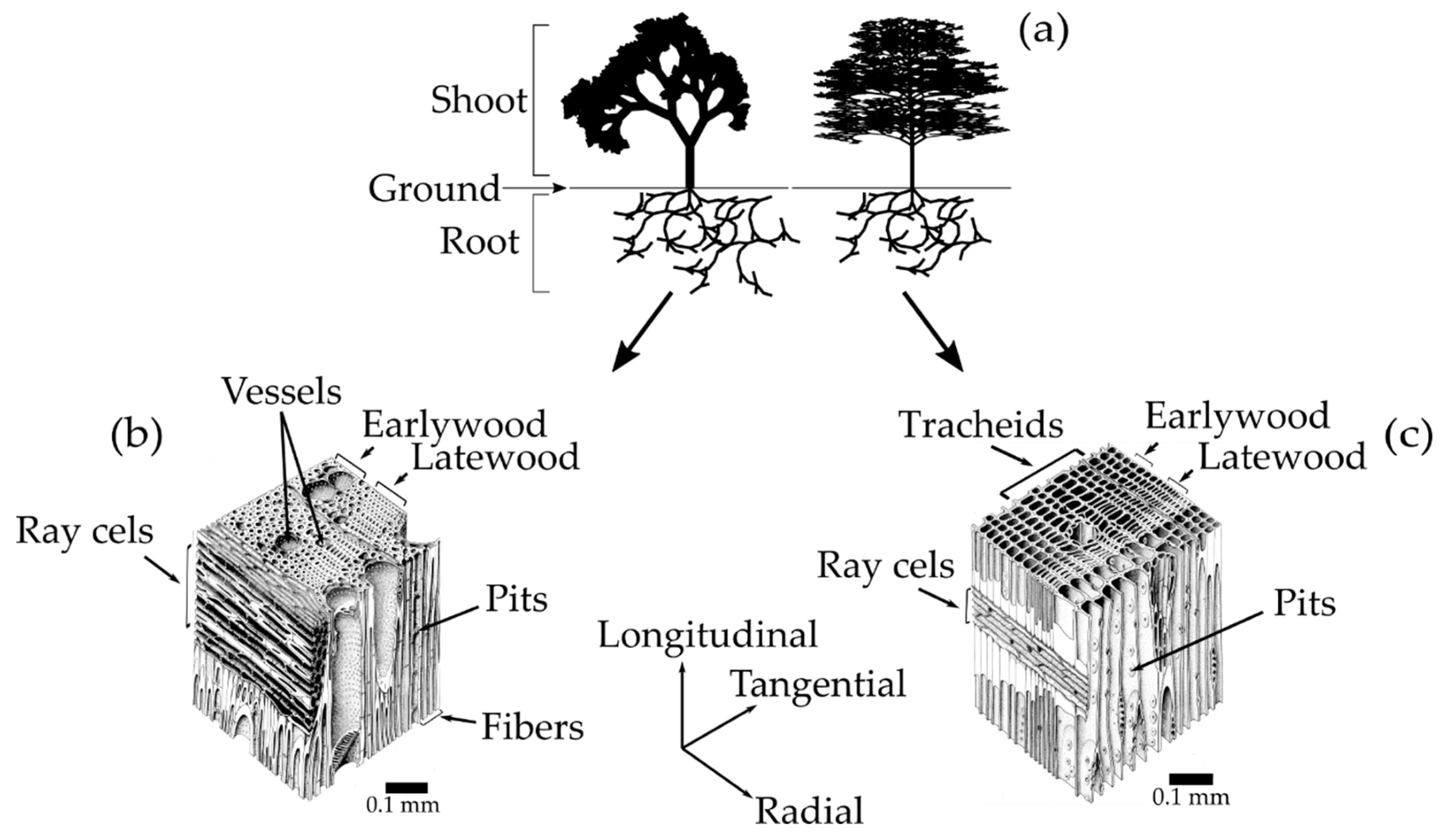
Trees are divided into two main sub-categories, softwoods and hardwoods [
22,
27]. Softwood is wood that comes from gymnosperm plants, which germinate from seeds that are not enclosed in an ovule, typically conifers with needle-type leaves (
Figure 1a-right). Hardwood is wood that comes from angiosperm plants, whose seed is surrounded by an ovule, mostly flowering and broadleaved trees (
Figure 1a-left) [
22]. Besides the seeds from which they are derived, the most important distinction between softwoods and hardwoods is found in their cellular structure (
Figure 1b,c).
2.1. Cellular Structure
The softwood cellular structure is composed mainly of axial tracheids and ray cells (
Figure 1c) [
21,
22]. In a cross-sectional view, the tracheids appear as rectangular cells with 3–10 μm thick walls that are thicker and thinner in the latewood and earlywood, respectively. The ray cells appear as rectangular prisms, typically 15 μm high by 10 μm wide and 120–250 μm long in the radial direction from the pith to the bark [
18,
25]. The tracheids are elongated tubular cells (1 mm to 10 mm long on average depending on wood species) aligned along the longitudinal direction of the tree trunk [
21]. Their hollow interiors are called lumina. The tracheids, which compose up to 90% of the volume of the wood, are the most important cells in terms of the mechanical support and water transport in softwoods [
22]. The water-transport system between tracheids consists of cavities in the cell walls known as pits. The tracheids end overlap with each other and are interconnected by pairs of pits that allow water to flow from cell to cell. The ray cells are aligned along the radial direction, and their primary function is the synthesis, storage, and lateral conduction of biochemical products [
21,
22].
In hardwoods, three important types of cells are found: vessels, fibers, and ray cells (
Figure 1b). The vessels are long hollow tubes composed of stacks of specialized cells called vessel elements. Vessel’s primary function is the conduction of water, which flows through end to end vessel connections called perforations. Vessels have 100–1200 μm of length and appear as large openings in the transverse plane of wood with the diameter ranging from 50–200 μm [
21,
27]. The fibers are 2–10 times longer than vessel elements [
22]. Hardwood fibers (composing around 24% of the volume of the wood) are similar to softwood tracheids, but because they only function as mechanical support, they have smaller lumina [
22]. The ray cells in hardwoods are much more diverse in terms of structure than in softwoods, but function in a similar manner.
2.2. Cell Wall Structure
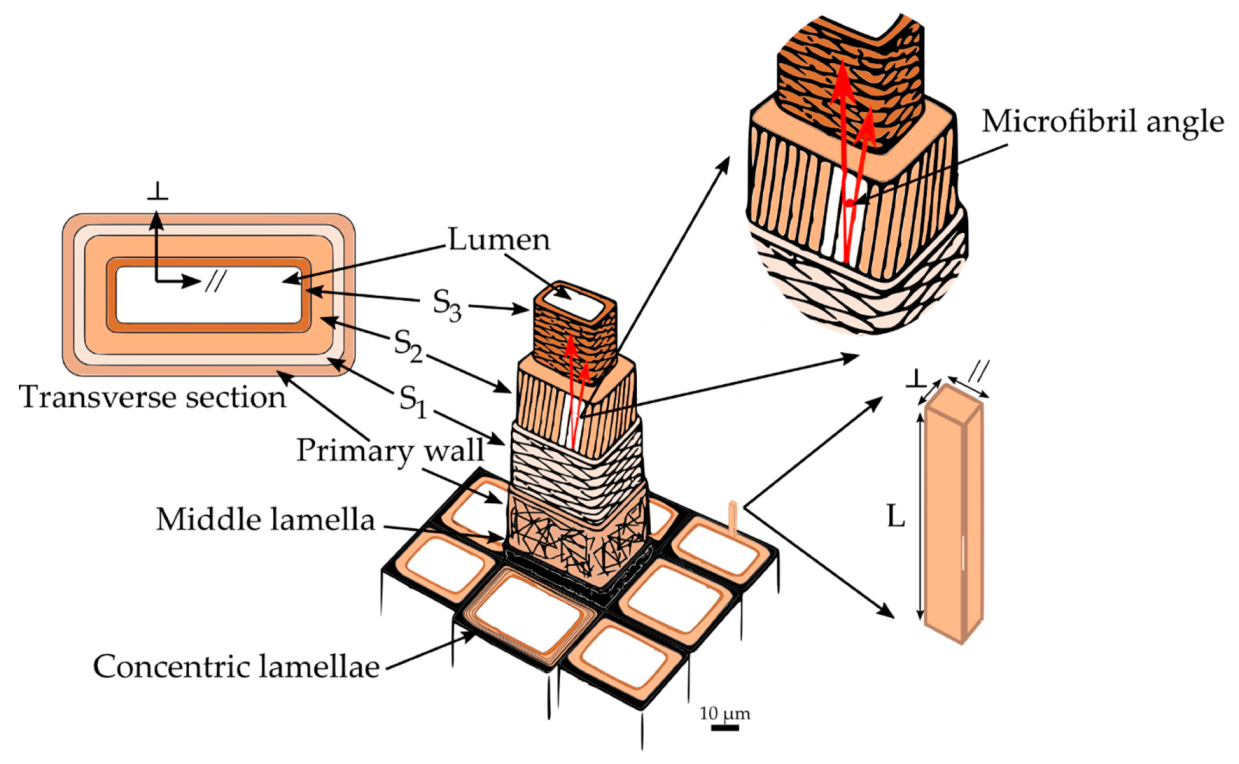
The cell wall structure of fibers in hardwoods and tracheids in softwoods is very similar. Hence, for the remaining discussion, fibers and tracheids will be referred to simply as wood cells. A single wood cell can be thought of as a hollow tube with a wall consisting of several layers appearing as concentric lamellae (
Figure 2). The adhesion between the cells is provided by the outermost layer, the middle lamella. It is a 0.5–1.5 μm thick layer made up principally of lignin with some hemicelluloses [
18,
22]. Attached to the middle lamella is the primary wall. The primary wall is a very thin, flexible layer (approximately 0.1 μm thick) [
22]. Generally, the primary wall is indistinguishable from the middle lamella, and both are grouped into a layer called the compound middle lamella. Next to the primary wall is the secondary wall, which consists of three different layers: S
1, S
2, and S
3 [
21,
22]. The S
1 layer is an intermediate between the primary wall and the other two secondary layers. It represents about 5%–10% of the total thickness of the cell wall, and is the thinnest layer of the secondary wall, being only 0.1–0.35 μm thick [
3,
18]. The S
2 layer is the thickest in the secondary wall and plays a dominant role in the mechanical properties of wood. Its thickness varies between 1–10 μm and accounts for 75%–85% of the total thickness of the cell wall [
21]. The last and innermost layer of the secondary wall is the S
3 layer, with 0.5–1.1 μm of thickness [
3,
21]. Finally, at the center of the wood cell is located a void space known as the lumen, usually filled with water or air.
2.3. Secondary Cell Wall Layer Nanostructure
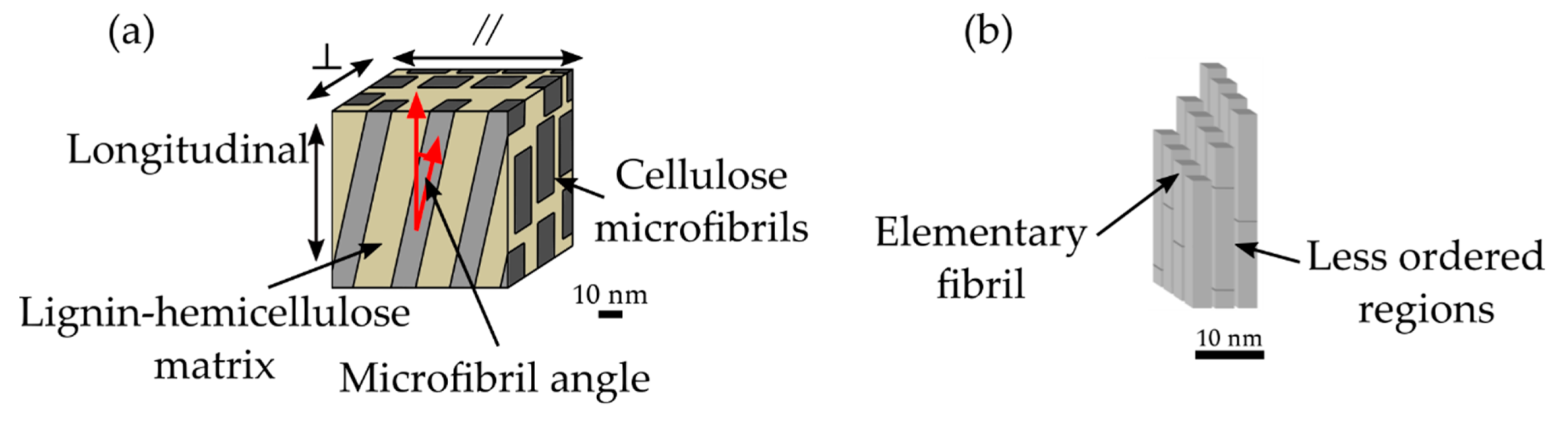
Each secondary cell wall layer can be considered as a nanofiber-reinforced composite material consisting of helically-wound cellulose microfibrils embedded in a matrix of amorphous cellulose, hemicelluloses, and lignin (
Figure 3a) [
18]. Cellulose and hemicelluloses are sugar-based polymers, rich in hydrophilic molecules that permit absorption of water, whereas lignin is a less hydrophilic complex aromatic polymer considered as an encrusting substance in the cell wall layers [
22]. During the biogenesis of the cell wall, the elementary fibrils are grouped into microfibrils (
Figure 3b), taking up around 44% volume of the secondary wall S
2 layer [
28]. Although the detailed structure of cellulose microfibrils is not completely known, microscopy-based studies have suggested that their size is between 15 nm to 25 nm [
29,
30,
31,
32]. These microfibrils are composed of elementary fibrils that are approximately 3 nm in diameter, with less ordered regions between them composed of amorphous cellulose and hemicelluloses [
33,
34,
35,
36]. The size of the elementary fibrils is still in debate, though scattering studies have suggested that an elementary fibril cross-section contains about 18–24 cellulose chains [
37,
38]. In general, in the secondary wall, the microfibrils are arranged in sheets or lamellae parallel to the lumen surface. The longitudinal organization of cellulose microfibrils in the S
2 cell wall layer is also debated, with proposals including parallel organization [
32], such as illustrated in
Figure 3a, and interconnections between microfibrils, such as by a liberated elementary fibrils that bridge between neighboring microfibrils [
28] or undulated structures [
39,
40,
41]. The orientation of the microfibrils with respect to the longitudinal cell axis is called the microfibril angle (MFA). The secondary cell wall layers can be differentiated by the orientations of cellulose microfibrils. The S
1 and S
3 layer contain lamellae in which the microfibrils have opposite helical directions (S–Z helices) and angles ranging from 50° to 70° for the S
1 and over 70° for the S
3 layer [
22]. In the thick S
2 layer, they have a Z helical direction with an MFA of 5° to 30° with little variation within a growth ring.
2.4. Wood–Water Relations
Wood, like many other biological materials, is a hygroscopic material. Wood is constantly exchanging moisture with the ambient air based upon the temperature and relative humidity (RH) of the surrounding environment. Mathematically, the moisture content (MC) in wood is defined as
MC = moisture content, m
water = mass of water in the wood, m
wet = mass of specimen at given MC, m
dry = mass of the oven-dry wood [
4,
42].
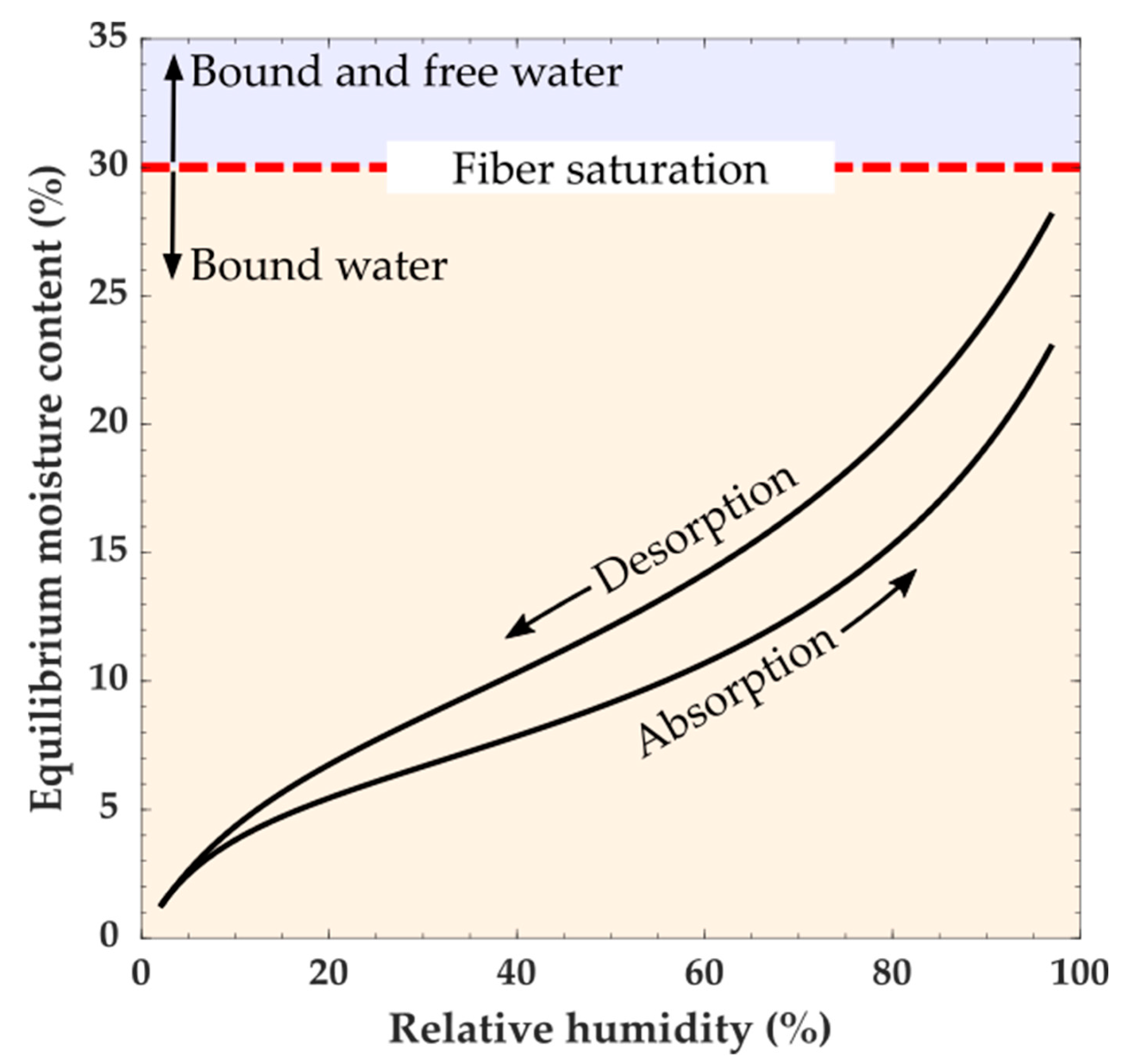
Moisture in wood can be categorized as being either free or bound water. Free water is defined as water present in the macroscopic voids of wood, such as lumina, and can be in a vapor, liquid, or solid state. Bound water is water absorbed into the wood polymers. Below fiber saturation (which depending on the definition is typically 30% MC) moisture exists as water vapor in the macroscopic void spaces in the wood cellular structure and bound water [
43,
44]. Changes in the amount of bound water cause wood dimensional instabilities (swelling and shrinking). The total amount of bound water depends on the ambient temperature and RH, and because of hysteresis whether the water is being absorbed or desorbed. It should also be noted that water sorption is a time-dependent process, and the amount of bound water will also depend on the conditioning time and size of the piece of wood being conditioned. At constant temperature and RH, wood will eventually reach a constant MC known as equilibrium moisture content (EMC). At a given temperature, the relationship between the EMC and RH is described by a moisture sorption isotherm (
Figure 4). For each RH value, a sorption isotherm indicates the corresponding EMC. The EMC, as a function of RH, has a hysteretic behavior [
4,
42]. Measurements of MC in equilibrium with a given RH and temperature are typically higher when reached by desorption than by absorption. In practice, wood likely does not reach a completely steady-state EMC value, and when EMC values are reported, they would depend on the criteria of the experimenter to define EMC [
45]. Because swelling and shrinkage in wood are caused by changes in the amount of bound water, changes in the amount of free water do not cause dimensional instabilities.
2.5. Swelling Pressures
The enormous swelling pressures that are generated in wood have long been known, and even utilized. The ancient Egyptians split boulders by wetting dry pieces of wood wedged into grooves cut into the boulders [
22]. By analyzing swelling stresses in wooden dowels with different densities, Tarkow and Turner estimated swelling pressures as high as 90 MPa forming in the cell wall during water absorption [
46]. This swelling pressure agrees well with an estimate that can be made using cellulose crystal lattice strains measured during moisture sorption. Zabler et al. measured a 0.6% transverse lattice strain decrease in crystalline cellulose as a 200 μm-thick spruce earlywood section was conditioned from dry to wet state [
47]. Using an estimated 20 GPa transverse elastic modulus for crystalline cellulose [
48], swelling stress of 120 MPa can be estimated. Collectively, these experiments suggest swelling pressures of around 100 MPa likely form in the swelling wood cell wall.
A hydrostatic swelling pressure forms in polymers when the swelling is constrained by mechanical constraints [
49,
50]. As the swelling increases, the forces needed to push against the mechanical constraints to increase the swelling become larger, and consequently, the swelling pressure increases. There is a molecular-scale mechanical constraint inherent in the wood polymer matrix, such as chemical or physical cross-linking and entanglements. However, considering that the compression yield stress is estimated to only be 60 MPa in the wood polymer matrix of a wet S
2 layer [
51], there must be additional sources of mechanical constraint to balance the estimated 100 MPa swelling pressure that likely forms in wet wood. The added mechanical constraint may come from structures at larger length scales, such as the cellulose microfibrils in the nanostructure, S
1 and S
3 layers in the cell wall structure, and neighboring wood cells in the cellular structure. Because wood polymers absorb less water under states of compression [
49,
52], the potential impacts of these multiscale constraints should be considered when studying moisture sorption and swelling in small wood specimens or extracted wood polymers because they may have fewer constraints, and therefore lower swelling pressures, than intact bulk wood.
3. Wood Moisture-Induced Swelling and Shrinking
3.1. Molecular Scale
As previously described, wood is a cellular structure with polymeric cell walls. Depending on conditions, free water can be present as ice, liquid water, or water vapor in the pores of the cellular structure. Water also exists as bound water, which is absorbed water held by inter-molecular attractions in the accessible wood polymers inside of the cell walls. All wood polymers are accessible except for the highly-ordered cellulose chains in the interior of the elementary fibrils [
35].
In amorphous polymers, absorbed water is proposed to exist in different states classified by its local molecular environment [
53,
54]. These states include molecular solution water randomly mixed in the polymer network, water hydrogen-bonded to hydrogen bonding polymer moieties like hydroxyl groups, and water absorbed in molecular ‘holes’. Here, molecular ‘holes’ refer to free volume elements in the polymer matrix capable of accommodating water molecules without causing swelling. At higher levels of moisture, clusters of water molecules may also form inside of the polymer matrix [
55,
56,
57]. Swelling and shrinking are mostly caused by changes in the amounts of all bound water except for the water absorbed in the holes. The other states of bound water require local polymer chains to be pushed apart in order to create the volume needed to accommodate the water molecule. These are the molecular-scale origins of moisture-induced swelling in polymeric materials like wood cell walls.
Water in the amorphous wood polymers is expected to exist in similar states as in other amorphous polymers. With the large number of hydroxyl groups on wood polymers, hydrogen-bonded water is expected to be especially prevalent [
44,
58]. Both experiments and computer simulations suggest the first water molecules at low MC are largely absorbed in molecular-scale holes, which results in minimal swelling at low MC [
59,
60,
61]. Between about 5% and 20% MC, the swelling increases approximately linearly with increases in MC [
44,
62]. As observed in simulations, this linear behavior is due to the fact that the absorbed water molecules increase the wood polymer chain-to-chain distance causing the breaking of hydrogen bonds and making space for more water molecules [
63]. Quasielastic neutron scattering studies provide experimental evidence suggesting water clusters form at higher MC [
64]. The suggested clusters have estimated radii of confinement that 3–6 Å as the RH increases from 20%–98% RH. Based on the approximate 30 Å
3 water molecule volume, these clusters contain approximately 4–30 water molecules.
The amount of bound water in wood, and therefore the extent of swelling is controlled by thermodynamics [
65]. A steady-state amount of bound water is reached when the bound water chemical potential is in equilibrium with the free water chemical potential. Consequentially, changes in free water chemical potential result in changes in the amount of bound water. For example, water vapor chemical potential increases with ambient RH, which causes increases in the amount of bound water in wood. The chemical potential of pure water is greater than the chemical potential of water in wood. Therefore, the absorption of water creates Gibbs energy of mixing, which has contributions from the heat of mixing and entropy of mixing [
66,
67]. The elastic energy needed to distort the wood polymers arises from the mixing energy released by the interaction between water and the wood polymers during absorption [
49,
50,
66,
67,
68]. Therefore, the extent of swelling is mainly controlled by the amount of mixing energy and elastic properties of the swelling polymer. Swelling is promoted by increases in mixing energy or decreases in elastic stiffness.
Much remains to be resolved about the molecular-scale sorption and swelling mechanism in wood. The molecular-scale processes have mostly been accessible by computation methods, such as molecular dynamics (MD) simulations [
35,
60,
69,
70,
71], that typically investigate idealized wood polymers. Although these studies have provided useful insights, they lack the structural complexity inherent in the wood polymers inside of cell walls. Traditional MD or Grand Canonical Monte Carlo (GCMC) simulations are unable to directly probe the effects of swelling; thus, hybrid MD/GCMC methods are more suitable for this research [
72]. Nevertheless, using hybrid methods is much more time consuming to investigate a typical system, comprised of 10
3 to 10
5 atoms, even for relatively short times (10 to 100 ns). Furthermore, experimental validation of many of the computational results is lacking. Experimental scattering and spectroscopy techniques—including nuclear magnetic resonance, Fourier-transform infrared spectroscopy, and neutron scattering—show promise and have also been used to probe the interactions between wood polymers and water [
73,
74,
75,
76,
77,
78,
79]. However, because most experiments have focused on extracted or derived polymers, it remains uncertain how much of the gained information is applicable to wood polymers inside of the cell wall, especially considering the high swelling pressures that likely form inside of the wood cell walls. Experiments that can probe intact unmodified wood, such as solid state nuclear magnetic resonance (NMR) [
73,
74,
75,
80] and quasielastic neutron scattering [
64], are needed in addition to computation methods to gain more information about the molecular-scale interactions between in situ wood polymers and water [
81]. Experiments that can determine the swelling in the polymer structures that occur with the addition of each water molecule from dry over the entire moisture range would be particularly helpful, but it is likely that new high-resolution techniques, analysis methods, or both will be needed. Specific information needed from future research include: identifying and quantifying the states of water (e.g., molecular solution water, hydrogen-bonded water, water absorbed in ‘holes’, and water in clusters) in wood as a function of water activity, MC, temperature, and pressure; better estimates of the changes in the energy of mixing and elastic energy stored in the wood polymers during moisture sorption; effects of external forces on the moisture sorption in wood polymers; temperature effects on the equilibrated structures; time-resolved studies that can offer insights on the transient changes occurring during moisture uptake; and comparisons between in situ wood polymers and extracted materials.
3.2. Elementary Fibril
As mentioned before, crystalline cellulose does not absorb water molecules within its inner structure. However, synchrotron X-ray diffraction measurements have shown that the cellulose crystalline lattice is deformed with changes in wood’s MC. Zabler et al. studied the deformation of the cellulose elementary fibrils with changes in MC [
47]. They performed synchrotron wide-angle X-ray diffraction experiments to monitor and measure in situ the cellulose structure of 0.2-mm-thick sections of spruce (
Picea sitchensis (Bong.)) earlywood. By measuring the cellulose crystalline lattice parameters, they found an anisotropic elastic deformation of the cellulose crystals in the elementary fibrils. MC changes from 0% over the entire moisture range caused a lateral compression to the cellulose crystals of about 0.6%, whereas longitudinally, they expanded by 0.2%. They hypothesized that the dimensional change of the elementary fibrils upon moisture changes is a result of compressive stresses created by the condensation or evaporation of molecular layers of water formed on the hydrophilic surface of the elementary fibrils. The shrinking in the transverse plane of the elementary fibrils is opposite to the swelling that has been observed in the macroscopic deformation of wood cells and bulk wood.
Abe and Yamamoto also used X-ray diffraction to measure the deformations in the cellulose crystals of the elementary fibrils and investigated the mechanical interactions between the cellulose elementary fibrils and the matrix substance in wood cell walls. A lateral lattice strain of 1.51% was measured in the elementary fibrils of a 2-mm-thick Sugi (
Cryptomeria japonica D. Don) earlywood section during dehydration from 25% to 5% MC [
82,
83]. Given that the crystalline cellulose barely interacts with water molecules, they suggested that the matrix substance filling in the gaps between the cellulose elementary fibrils causes the cellulose elementary fibril to expand transversely during water desorption. While the mechanism of this process is not completely known, they concluded from their results that the lateral expansion of the microfibrils is an elastic deformation caused by the swollen matrix substance, which develops swelling pressures that compress the cellulose elementary fibrils transversely when wetted and releases them when dry [
83].
Zabler et al. and Abe and Yamamoto suggest two different reasons for the mechanism of crystalline cellulose deformation. The cause of the moisture-induced strains in the crystalline cellulose still needs to be determined. As mentioned in
Section 2.5, swelling stress of 120 MPa within the S
2 layer can be estimated, which is similar to the 90 MPa swelling pressures estimated by Tarkow and Turner [
46]. Considering that swelling pressures inside of cell walls can be quite large, it seems a more plausible idea from our perspective that swelling pressures explain the cause of the moisture-induced strains in crystalline cellulose.
Studies at this scale typically rely on X-ray diffraction methods, which have been mostly used in forest products research to quantify changes in the cellulose crystallinity [
84,
85,
86]. However, experiments that focus on the moisture-induced changes experienced by the crystalline lattice have been limited. Studies would benefit from an improved model to interpret the measured strains; a model that can validate the role of swelling pressures in the measured strains. Currently, it is unclear whether the swelling pressures are responsible for all of the deformations experienced by the lattice, or if the observed behavior can be attributed to other external forces. For instance, if tensile forces are being generated along the S
2 during swelling, then some of the transverse deformation observed in the cellulose crystals could be attributed to a Poisson’s ratio effect. Likewise, we still need systematic studies that can help elucidate how the swelling pressures are affected by the constraints present in the cell wall across length scales ranging from microfibrils in the nanostructure to the effect of neighboring cells in the cellular structure. The constraint effect of neighboring cells may help explain why Abe and Yamamoto observed a higher 1.51% lateral lattice strain in their 2-mm-thick section as compared to the 0.6% measured by Zabler et al. in the thinner 0.2-mm-thick section that they used. Systematic studies measuring moisture-induced elementary fibril lattice strains in different size specimens from the same piece of wood would aid in elucidating these constraint effects on elementary fibril deformations. Consequentially, if the elementary fibril deformations are directly related to swelling pressures, then the systematic studies would also provide information about the relationships between multi-scale constraint effects and swelling pressures. Furthermore, systematic studies are needed that probe the combined effects of temperature, moisture, and even type of wood (i.e., latewood vs. earlywood, tension vs. compression wood, softwood vs. hardwood) on the crystalline lattice structure. For example, variations in the source of wood will have an impact on the overall cellulose crystallinity of the samples, and thus the total swelling strains and pressures observed will likely be affected, yet experiments that address this issue are lacking. Last but not least, microscopy studies that can also measure the elementary fibril diameter might provide valuable insights in terms of the effects of sample preparation and variability in these measurements, particularly if they are combined with diffraction.
3.3. Secondary Cell Wall Layer Nanostructure
Water is absorbed in the amorphous wood polymers composing the matrix of the S
2 nanostructure. Features of the S
2 nanostructure include the cellulose microfibrils, lamellae, and individual nanoscale domains of lignin, hemicelluloses, or cellulose. Of the S
2 nanostructure features, swelling in the microfibril has been the most extensively studied. Fernandes et al. used small-angle neutron scattering (SANS) to study the moisture-dependence of the swelling of the cellulose microfibrils in spruce wood and found that the elementary fibril spacing increased with moisture-content [
34]. These studies agreed with earlier small-angle X-ray scattering experiments from Jakob et al. [
33]. More recently, Plaza et al. used SANS to conduct a systematic study on the moisture-induced nanostructural changes in 500-μm-thick latewood sections obtained from the three primary planes of loblolly pine (
Pinus taeda L.) [
87]. Changes in the anisotropic scattering features arising from the S
2 lamellar structure were observed in this study, but the size of the lamellae was inaccessible due to highly convoluted scattering data. Nevertheless, by tracking the change in elementary fibril spacing as a function of RH, they were able to measure a swelling strain of about 16% between elementary fibrils in sections conditioned from 25% to 85% RH. Similar swelling strains were measured in each of the primary planes, indicating a transverse isotropic swelling behavior in the microfibrils. Taking this into account and assuming microfibril rectangular cross-section, the swelling at the elementary fibril level was compared with the transverse swelling of the S
2 [
88]. Based on this comparison, it was found that the increase in the microfibril cross-sectional area accounts for 55% of the increase in the S
2 transverse area due to moisture-uptake between 25% and 85% RH. Plaza et al. also performed experiments on 25-μm-thick sections from the tangential-longitudinal and radial-longitudinal orientations. In these thinner sections, the wood cells were cut longitudinally, which effectively released the mechanical hoop constraints from S
1 and S
3 layers. Interestingly, it was found that the elementary fibril spacing in the thin sections was greater than in the thicker sections at high RH. This indicates that swelling at the nanoscale can be affected by mechanical constraints from the S
1 and S
3 layers and neighboring cells.
Moisture-induced changes in the unmodified wood nanostructure are typically only accessible by scattering methods, mainly due to their minimal sample preparation requirements and flexible test environments. Conventional electron microscopy techniques are performed under vacuum and not conducive to experiments at high moisture conditions. Nevertheless, the measured scattering signal is quite convoluted because all nanostructural features, whose sizes lie in the range of 1 to 100 nm, contribute to the signal. Thus, experimental studies on unmodified wood could benefit from complementary studies on isolated polymers to help analyze the data and deconvolute the scattering signal. In particular, what is missing is experiments that can provide insights on the moisture-induced changes that occur beyond the microfibril, such as changes in the size of the lignin or hemicelluloses domains, and the S2 lamellar structure. Studies combining experimental techniques with computational approaches could also be useful in further deconvoluting the experimental data. The effects of mechanical constraints, such as the presence of stiff microfibrils, S1 and S3 layers, and even neighboring cells, must also be better understood. For example, it remains unclear whether the differences in the elementary fibril swelling observed by Plaza et al. in the 500-μm-thick and 25-μm-thick sections were related to differences in swelling pressures or some other effect.
3.4. Cell Wall
As expected, based on its anisotropic structure, swelling and shrinking at the cell wall level is anisotropic. In [
89], the hygroexpansion coefficient of a never dried single wood cell extracted from Norway spruce (
Picea abies (L.) Karst.) was measured using a combined numerical-experimental method. It was found that the wood cell experienced anisotropic deformation with hygroscopic coefficient values of 0.014%/% and 0.17%/% (hygroscopic coefficient is defined as Δε/ΔRH) along the microfibril length of the cell wall and the transverse direction, respectively. It is worth to notice that the hygroexpansion along the microfibrils length is about 12 times lower than in the transverse plane. This is because of the nature of the cell wall structure, where the deformation is restrained by the microfibrils along its longitudinal direction. Furthermore, in [
88], three micropillars of the S
2 cell wall layer of Norway spruce latewood were created using a focused ion beam, and the three-dimensional moisture-induced swelling was quantified using high-resolution X-ray nanotomography. They found that the volumetric strains at the cell wall level are significantly larger than those observed at the cellular level. Two micropillars (mainly composed of S
2 layer) revealed anisotropic moisture-induced swelling with larger strains in the perpendicular direction than in the parallel direction (see
Figure 2 for parallel and perpendicular definitions). The obtained values for one of the micropillars were 2.1% and −0.02%; for the second micropillar were 1.25% and 0.65% in the perpendicular and parallel directions, respectively. They explain this behavior based on the model presented by Boutelje [
90], where it is proposed that a larger part of the absorbed water may be contained between the concentric lamellae formed by the cellulose microfibrils. The concentric lamellae are then displaced more from each other in the perpendicular direction than in the parallel one. The increased swelling in the perpendicular direction as compared to the parallel direction was also observed by monitoring the movement of residual nanoindentations in the S
2 layer before and after swelling with ethylene glycol, which is expected to cause swelling similar to moisture-uptake [
91].
The third micropillar in [
88], which contained some portion of the S
1 layer, revealed smaller strains in the direction parallel to the cell wall thickness. The obtained values for the third micropillar were 0.6% and 0.8% in the perpendicular and parallel directions, respectively [
88]. The behavior of this third micropillar reveals some understanding of the reduction in the moisture-induced swelling at larger length scales of wood. Because the microfibril angle in the S
2 layer is low, in other words, the microfibrils are nearly parallel to the long axis of the cell, the S
2 expands transversely in proportion to the moisture change. In contrast, the microfibril angle in the thinner S
1 and S
3 layers is high, thus these layers do not swell much in the transverse plane and tend to provide a hoop constraint that restrains the dimensional changes in the transverse plane of the S
2 secondary wall. The overall arrangement of the cell wall layers reduces the swelling at higher length scales.
Tomography-based methods with sub-micron resolution have provided the most recent advances in our knowledge of the swelling of the cell wall, yet future experiments that focus on the role of neighboring cells in the measured swelling are still needed. Additionally, more systematic studies that can help discern the role of the individual cell wall layers in the dissipation and generation of swelling stresses are also needed. However, improved sample preparation techniques will likely be needed to ensure that surface damage does not affect the measured swelling of the cell wall layers. The combined effects of moisture, temperature, and even pressure on the swelling at this length scale can also be further explored, and experiments would benefit from improved models that can take into account the polymer distribution and heterogeneous hygroscopic nature of the wood cell walls. Detailed studies that can compare the changes in the mechanical properties of the individual cell wall layers with their MC and the swelling pressures are also needed. For instance, our knowledge of how the hygroscopic expansion coefficients of the cell wall change as a function of environmental conditions is still lacking, despite their value as a material property that could be used to model the moisture-induced swelling of wood cell walls.
3.5. Single Cell and Cells Bundles
A single wood cell or a bundle of wood cells composed of a small group of intact wood cells have been observed to twist when subjected to MC changes [
11,
12,
92,
93,
94]. The moisture-induced twisting is caused by swelling of the relatively hydrophilic S
2 cell wall matrix constrained by stiff cellulose microfibrils, which spiral around the cell [
89,
92]. The amount of twisting highly depends on the MFA in the S
2 cell wall layer, the cell wall thickness, and the number of cells present in the bundle [
12,
92]. In support, Plaza et al. investigated the moisture-induced torsional actuation of wood cells bundles consisting of a few cells. They observed that a cells bundle was capable of generating two revolutions per centimeter of length when conditioned from 0% to 100% RH; the bundle twist was proportional to the MC [
11].
The moisture-induced twisting generates a torque that can be measured using a torque sensor inspired by Coulomb and Cavendish torsional balance [
95,
96]. Using this design, it was found that a wood cells bundle with a thickness of 50 µm (thus, consisting of about a single cell) generates a specific torque of approximately 25 N·m/kg, which is much larger than the torques generated by carbon nanotube yarns and commercial motors [
12]. Though the effects of the bundle thickness or MFA on the specific torque have not been studied yet, it is expected that these factors will also play a role in the specific torque generated.
These cell-level twisting deformations are predicted from the analysis of chiral elasticity to be less pronounced on larger length scales [
97]. Chirality requires a generalized elasticity approach to be understood; classical anisotropic elasticity does not suffice. In intact bulk wood, the twisting phenomena with changes in moisture content will almost certainly occur. The phenomena are predicted to be larger for thin specimens than for thick ones. However, a holistic understanding of multiscale swelling and shrinking in wood requires an improved understanding of these twisting deformations and torques. In particular, experiments that can probe the volumetric swelling and twisting of free-standing single cells and wood cells bundles composed of different numbers of cells would be valuable. X-ray computed tomography (XCT) studies utilizing in situ humidity chambers are promising for making such measurements [
98]. Given that tensile experiments on single tracheids have already shown that the stiffness and strength measured depend on sample preparation [
99], it is necessary to verify that single cell extraction methods do not introduce artifacts in swelling measurements. Studies that can determine the role of the individual cell wall layers or even the middle lamella on the twisting of single cells would also be valuable. These studies could help determine if these components can constrain the twisting and swelling, similarly, to neighboring cells. The ability to also measure torque adds the possibility to estimate the internal swelling pressures generated due to moisture-sorption in single cells and wood cells bundles.
3.6. Cellular Structure
A majority of the early work on the swelling of the cellular structure has relied on microscopy techniques [
100,
101,
102] and measurements of the macroscopic dimensional changes [
103,
104]. However, why the swelling along the tangential direction is greater than swelling in the radial one is still a subject of investigation and debate. The presence of ray cells, specifically because of their orientation, have been considered to have an effect on the swelling in the radial direction. Supporting this idea, Patera et al. recently investigated the role of rays in the cellular structure in restraining the radial swelling of earlywood using phase-contrast XCT and three-dimensional image analysis [
105]. Given that ray cell walls are thicker than earlywood longitudinal cells, they concluded that the presence of ray cells could restrain radial swelling in the earlywood. The variation in the swelling along the tangential and radial directions has also been attributed to differences in the cell composition along the parallel and perpendicular directions of the S
2 cell wall layer, differences in the MFA, as well as the influence of the middle lamella [
21,
23,
65,
106]. Although there is no consensus, it is recognized that differences between tangential and radial swelling are related to the cell wall structure and the arrangement of the cells. Studies based on computational mechanical modeling have also shown that the geometry of the cell walls and the cell wall layered structure can play a role in the anisotropic swelling of a cellular solid. Honeycomb cellular solids with homogenous cell walls swell isotropically, while honeycombs with a layered cell wall structure displayed anisotropic swelling behavior [
107,
108].
Differences in the swelling between earlywood and latewood have also been explored using microscopy and, most recently, phase-contrast XCT. In general, studies have shown that latewood swells more than earlywood, but the latter is more transversely anisotropic [
26,
100]. The effects of hysteresis have also been investigated, and it has been shown that the swelling strains are not hysteretic as a function of MC [
105].
There is still a lack of knowledge about how the wood cell lumen is affected during swelling. It has been suggested that the linear proportionality of the moisture-induced swelling and the density implies that the lumen does not experience any size change, and lumen size is assumed to be constant in models dealing with the cell wall structure of wood [
22,
109]. However, some studies have revealed changes in the lumen area. Using light microscopy imaging on the surface of blocks of wood was found that the lumen area in low-density wood (African Whitewood (
Triplochiton scleroxylon)) increases from dry to wet, whereas, in higher density wood, it decreases (Poplar (
Populus x canadensis) and Beech (
Fagus sylvatica L.)). Nevertheless, these studies probed sections of wood that contained both latewood and earlywood and thus, the differences reported may have been due to an overall density difference in the bulk wood [
110]. Furthermore, in [
111], using optometric methods on cross-sectional surfaces, researchers found that for Douglas fir (
Pseudotsuga menziesii (Mirbel) Franco.), the lumen in earlywood expands while in latewood it contracts during drying. Conversely, another microscopy study carried on microtomed sections of spruce and beech earlywood and latewood, found a slight increase or no change at all in the diameter of the lumen from earlywood upon swelling, while in latewood the lumen size decreased [
112]. Although inconclusive, the current results suggest that as MC increases, the lumina shrink in higher density wood and expand in lower density wood.
A majority of the studies at this length scale have relied on two-dimensional imaging capabilities to map the changes occurring in the cellular structure and lumen areas. Studies that can probe the unmodified earlywood and latewood inside of the three-dimensional bulk wood without changing the native cellular structure are needed to determine whether or not the lumen area changes during swelling. Such measurements could be made by analyzing three-dimensional volumes of cellular structures obtained by XCT with in situ humidity chambers [
98,
113]. It would also be valuable to compare results from the same wood using the X-ray tomography experiments and the more conventional two-dimensional studies on sections to better understand constraint effects. Another valuable piece of information that is often lacking in the literature is a more quantitative analysis of the structural features present in the samples studied. For example, the role of ray cells could be further elucidated if their spatial distribution was quantitatively correlated to the dimensional changes observed during the swelling of the cellular structure. Likewise, experiments that can allow determining the role of neighboring cells on the overall hygroscopic swelling coefficient would be valuable, particularly if it is also correlated to the samples’ MC and swelling pressure.
4. Summary and Future Research Directions
Wood is a complex hierarchical material, whose moisture-induced swelling must be understood and investigated across different length scales. Studies focusing on the swelling of the cellular structure will inevitably be affected by the smaller length scale features and vice-versa. Furthermore, the behavior observed at larger length scales might not be representative of the smaller length scales. For instance, at the molecular level, 5%–20% MC swelling of the hydrophilic polymers is approximately linear with the increase in MC. However, crystalline cellulose in the elementary fibrils is mostly inaccessible to water, and as a result, it is transversely compressed upon moisture uptake. At the microfibril level, the spacing between the elementary fibrils increases with MC, leading to an overall increase in the microfibril cross-sectional area. This area increase accounts for a majority of the S2 transverse swelling. This swelling and, consequently, the swelling of the cell wall can be constrained by the presence of the cell wall concentric layers and even neighboring cells. Due to the complex structure of wood, swelling is anisotropic across all length scales. Longitudinal swelling is typically restrained by the microfibrils, and thus, deformations along this axis are minimal across all length scales. At the cell wall level, swelling in the transverse plane along the perpendicular direction to the cell wall is the largest. Whereas at the bulk scale, wood swells most in the tangential direction. Differences between the radial and tangential swelling have mostly been attributed to the arrangement of the cells, but it is likely that the cell wall ultrastructural features also play a role. Interestingly, the swelling of the helically embedded microfibrils leads to moisture-induced twisting in bundles of wood cells consisting of only a few wood cells. This behavior has inspired the development of new materials and could be used in the future in accelerated moisture-durability tests.
Future research aiming to improve our understanding of swelling in wood across length scales and its implications would benefit from a more holistic approach. Multi-scale studies and integration of the data across length scales will be necessary to develop predictive models that can conclusively explain the role of the cell wall ultrastructural features in the anisotropic swelling of the cellular structure. The use of XCT shows promise to further elucidate the cellular swelling, although future studies would benefit from improved models that can take into account the hygroscopic and complex polymer chemistry of the cell walls. Such models could help correlate changes in the dimensions of the lumina to the wood density and cell wall properties. The effects of sample preparation, as well as the role of mechanical constraints like the number of neighboring cells on the measured swelling, should also be addressed. Not taking into account these factors could lead to overlooking artifacts that could compromise the accuracy of the swelling measurements, particularly at the cell wall level and below. Moreover, future research should also provide insights into the generation and dissipation of moisture-induced swelling pressures and their implications on the swelling across length scales. For example, we need experiments that can determine the role of these pressures on the molecular-scale wood–water interactions such as the deformation of the crystalline cellulose structure, the formation of water clusters, and overall swelling of the hydrophilic polymers. Likewise, swelling pressures might also affect the hygromechanical properties of the cell wall, yet experiments and computational studies that can provide insights on this topic are needed. Finally, integrating our knowledge of the cellular swelling ab intra will be valuable in establishing models that can predict the behavior of the bulk wood as a function of environmental conditions, thus, unlocking the potential of wood beyond its role as a construction material.