Integrating TimeSync Disturbance Detection and Repeat Forest Inventory to Predict Carbon Flux
Abstract
1. Introduction
2. Methods
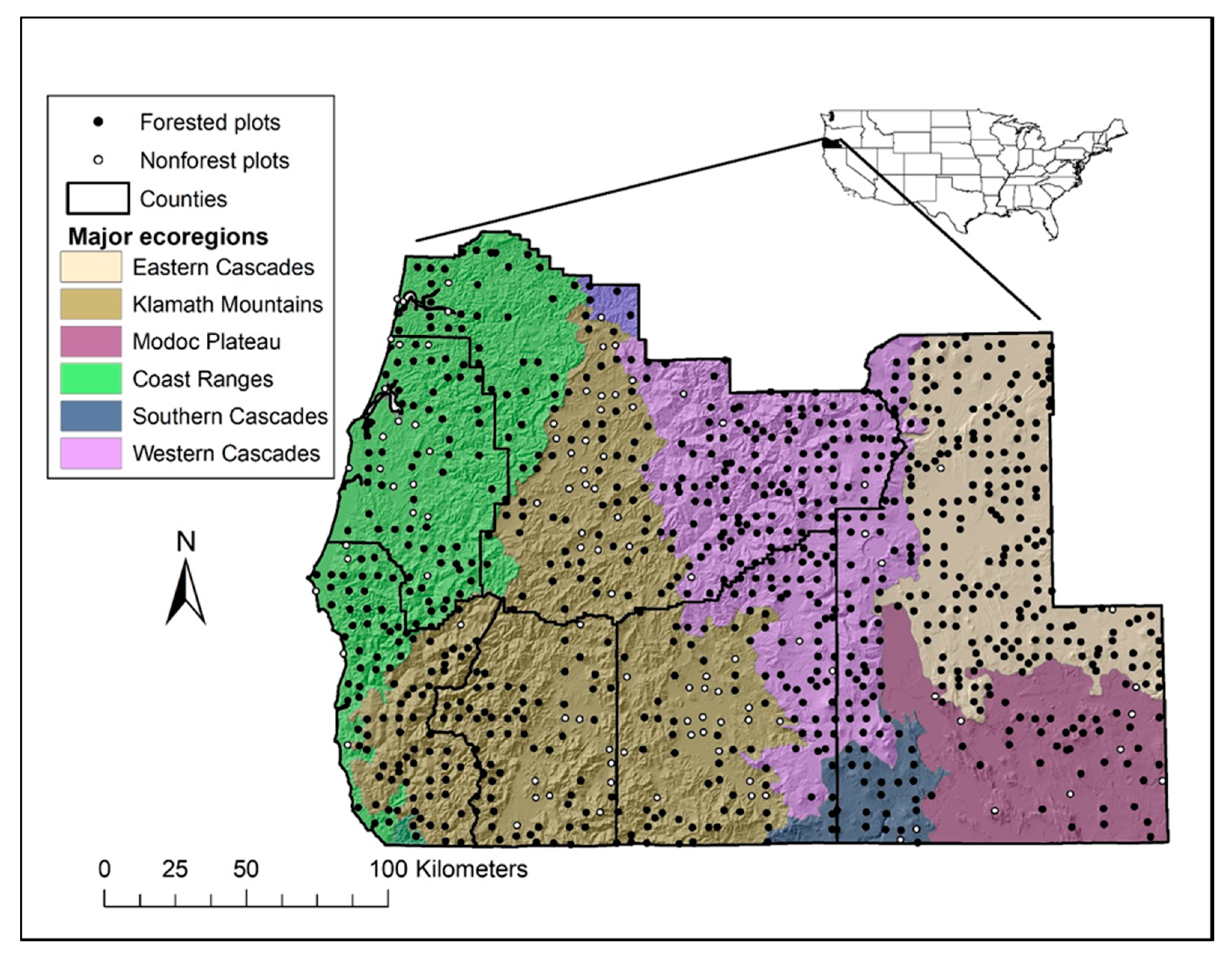
2.1. Study Area
2.2. Plot Data
2.3. Remote-Sensed Data
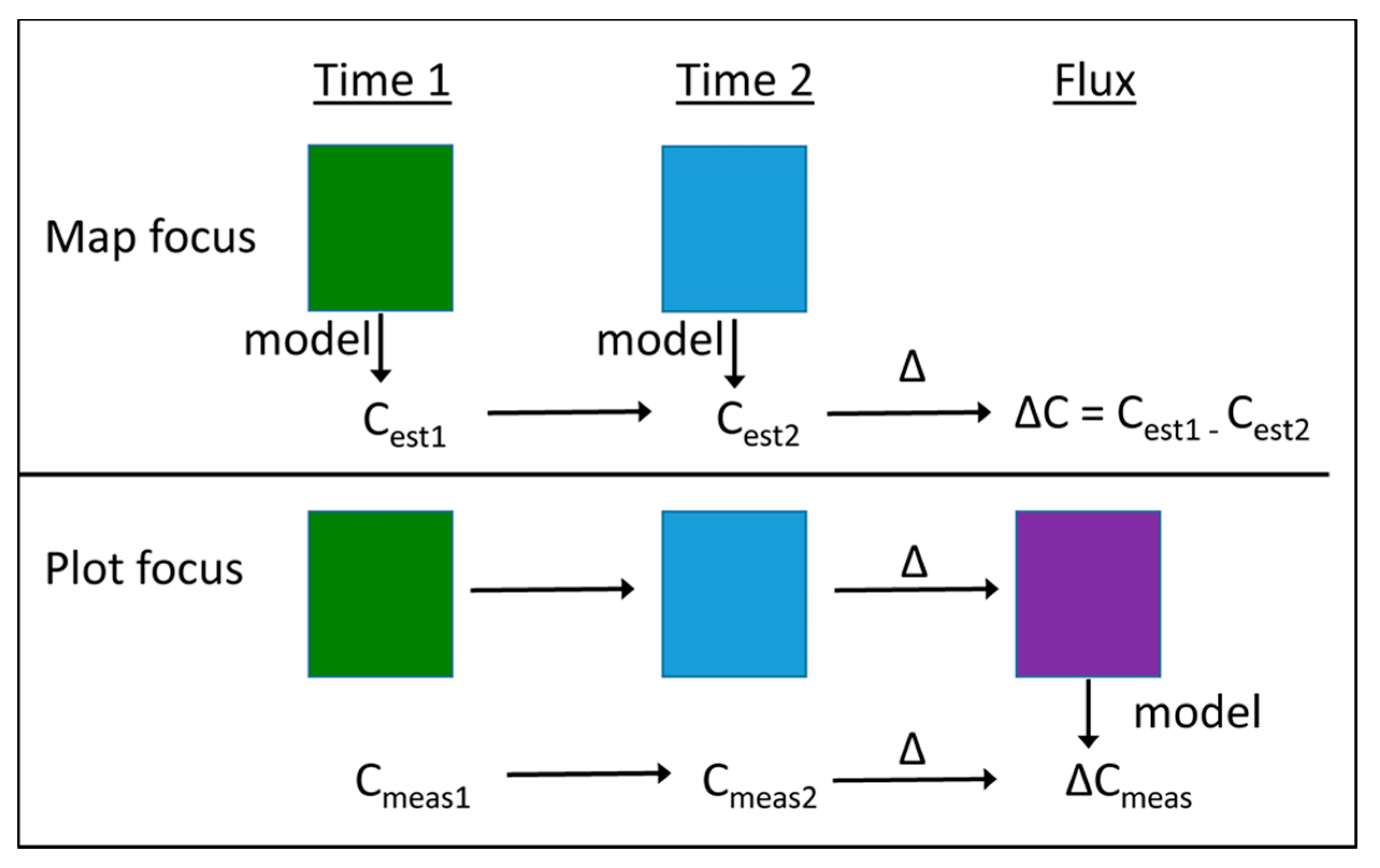
2.4. Statistical Analyses
3. Results
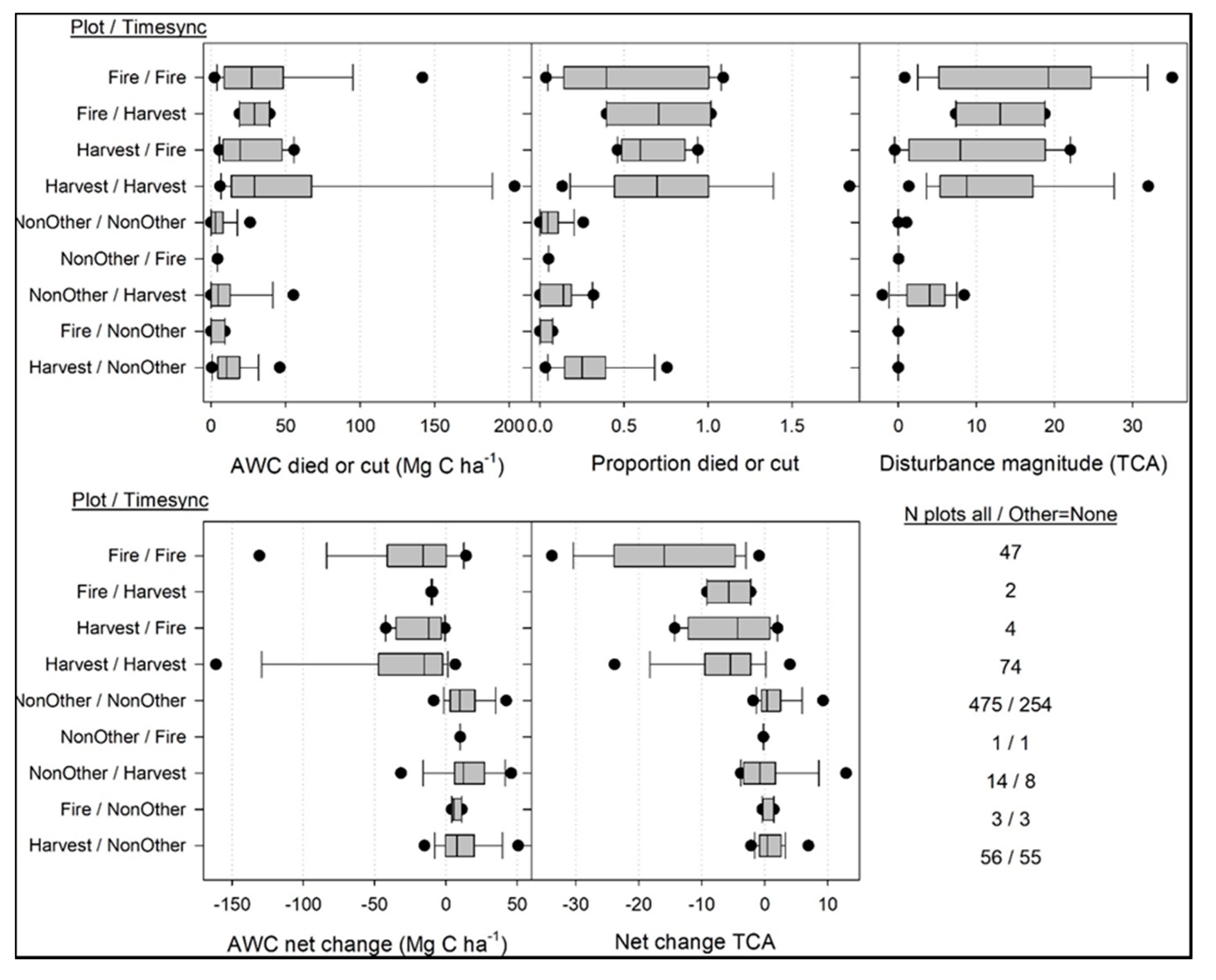
3.1. Comparison of Plot- and TimeSync-Detected Disturbances
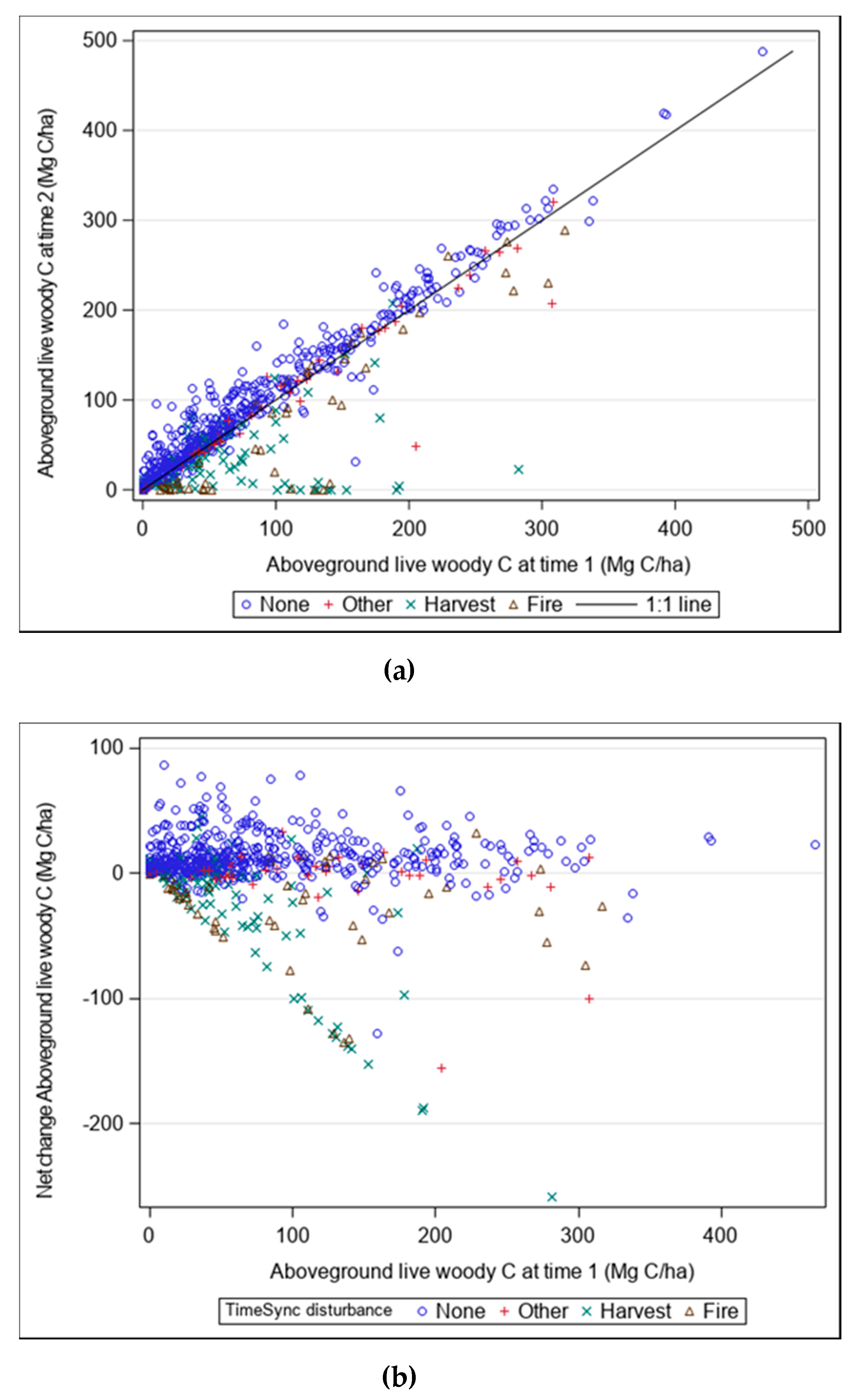
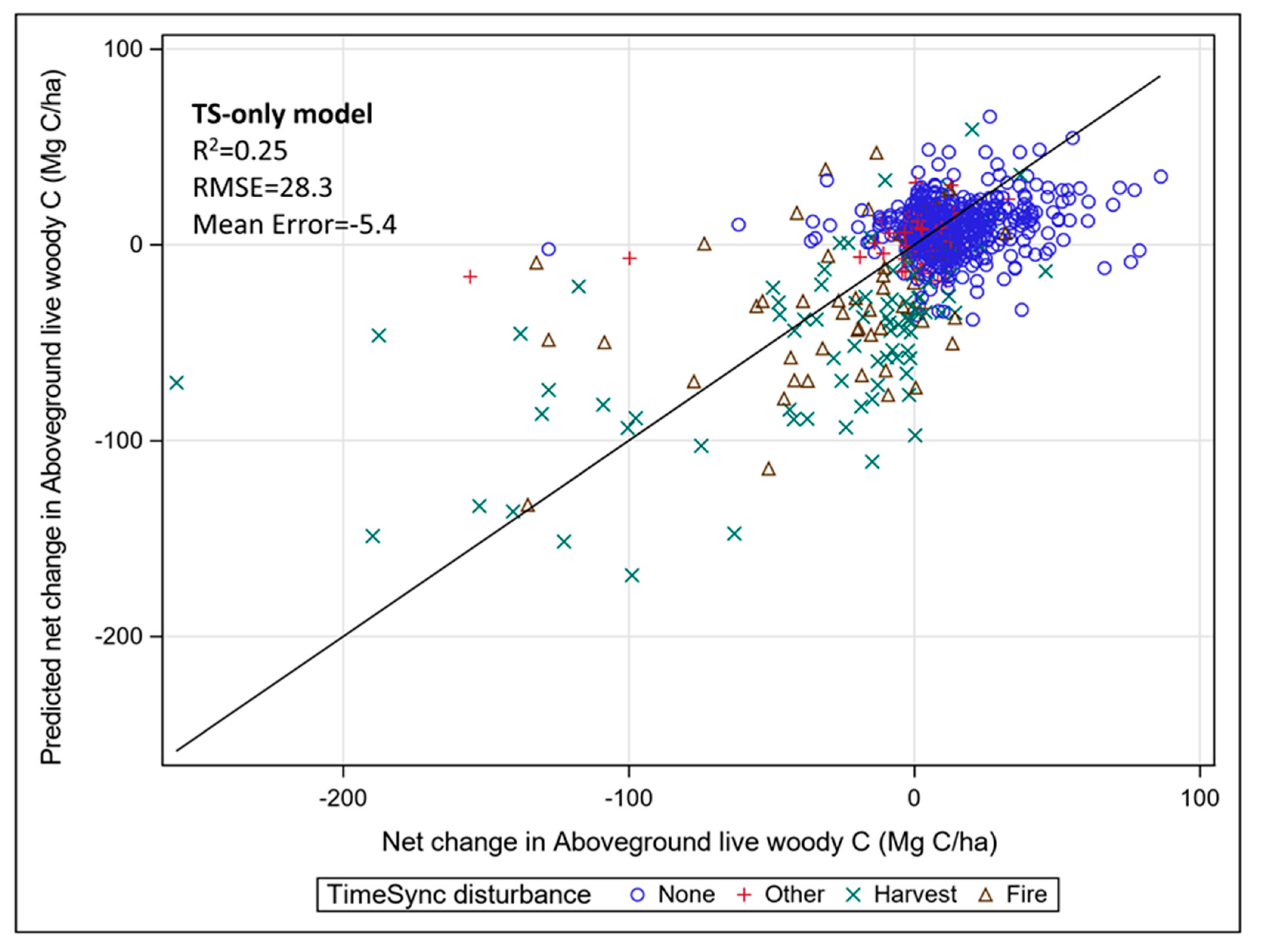
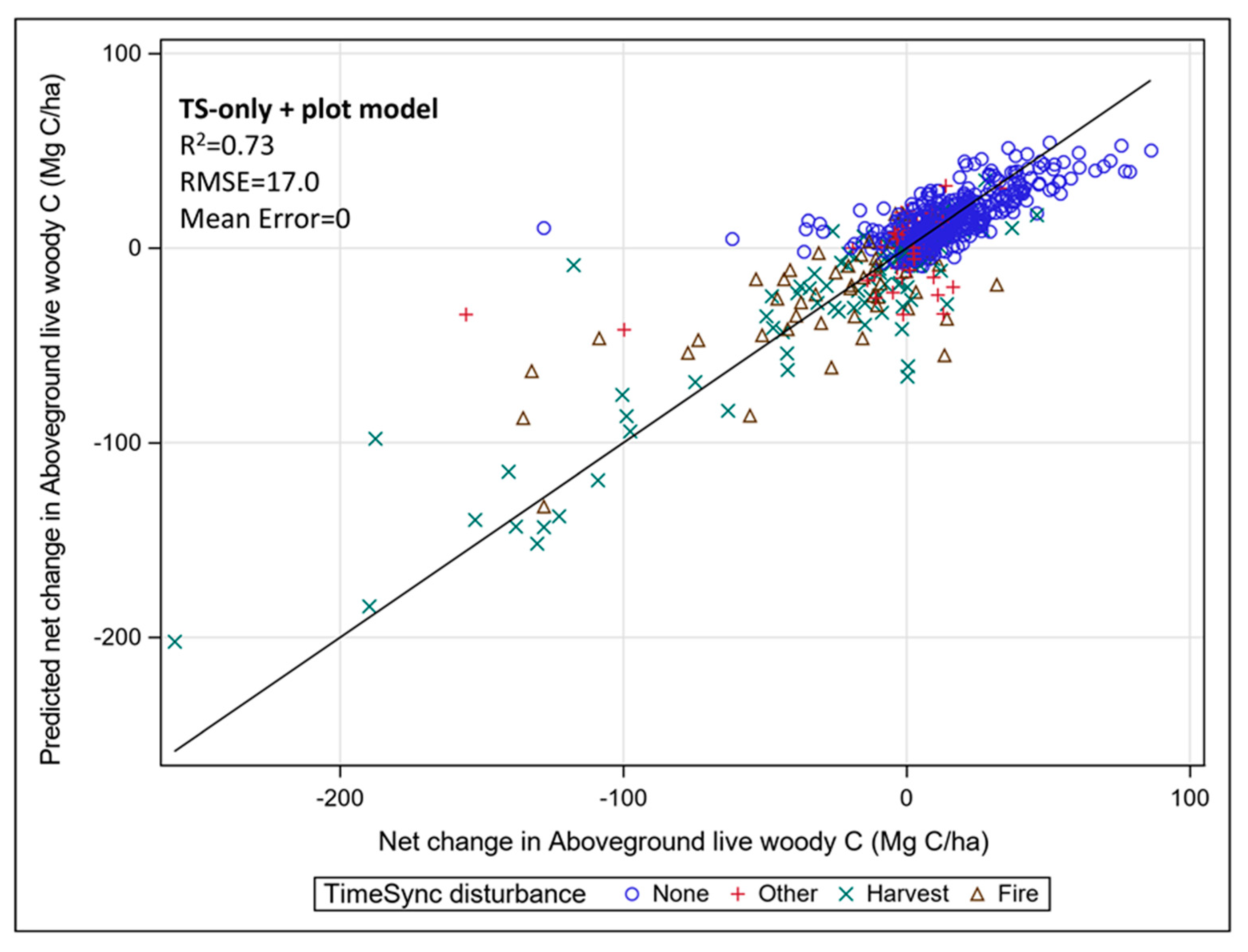
3.2. Modeling Change in Live-Tree Carbon
4. Discussion
4.1. Disturbance Detection
4.2. Modeling C Stocks and Stock Change with Only Spatial Predictors
4.3. Modeling C Flux with Plot and Spatial Predictors
4.4. Effect of Ecosystem Type
4.5. Implications for Improving Carbon Assessments
5. Conclusions
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Hoegh-Guldberg, O.; Jacob, D.; Taylor, M.; Bindi, M.; Brown, S.; Camilloni, I.; Diedhiou, A.; Djalante, R.; Ebi, K.L.; Engelbrecht, F.; et al. Impacts of 1.5 °C Global Warming on Natural and Human Systems. In Global Warming of 1.5 °C. An IPCC Special Report on the Impacts of Global Warming of 1.5 °C above Pre-Industrial Levels and Related Global Greenhouse Gas Emission Pathways, in the Context of Strengthening the Global Response to the Threat of Climate Change, Sustainable Development, and Efforts to Eradicate Poverty; Intergovernmental Panel on Climate Change: Geneva, Switzerland, 2018. [Google Scholar]
- McKinley, D.C.; Ryan, M.G.; Birdsey, R.A.; Giardina, C.P.; Harmon, M.E.; Heath, L.S.; Houghton, R.A.; Jackson, R.B.; Morrison, J.F.; Murray, B.C.; et al. A synthesis of current knowledge on forests and carbon storage in the United States. Ecol. Appl. 2011, 21, 1902–1924. [Google Scholar] [CrossRef] [PubMed]
- Hayes, D.J.; Turner, D.P.; Stinson, G.; McGuire, A.D.; Wei, Y.; West, T.O.; Heath, L.S.; de Jong, B.; McConkey, B.G.; Birdsey, R.A.; et al. Reconciling estimates of the contemporary North American carbon balance among terrestrial biosphere models, atmospheric inversions, and a new approach for estimating net ecosystem exchange from inventory-based data. Glob. Chang. Biol. 2012, 18, 1282–1299. [Google Scholar] [CrossRef]
- Pan, Y.D.; Birdsey, R.A.; Fang, J.Y.; Houghton, R.; Kauppi, P.E.; Kurz, W.A.; Phillips, O.L.; Shvidenko, A.; Lewis, S.L.; Canadell, J.G.; et al. A large and persistent carbon sink in the world’s forests. Science 2011, 333, 988–993. [Google Scholar] [CrossRef] [PubMed]
- IPCC. 2013 Revised Supplementary Methods and Good Practice Guidance Arising from the Kyoto Protocol; Hiraishi, T., Krug, T., Tanabe, K., Srivastava, N., Baasansuren, J., Fukuda, M., Troxler, T.G., Eds.; IPCC: Geneva, Switzerland, 2014. [Google Scholar]
- Bechtold, W.A.; Patterson, P.L. The Enhanced Forest Inventory and Analysis Program-National Sampling Design and Estimation Procedures; USDA Forest Service, Southern Research Station: Asheville, NC, USA, 2005; p. 85.
- Kangas, A.; Maltamo, M. Forest Inventory: Methodology and Applications; Springer: Dordrecht, The Netherlands, 2006; p. 362. [Google Scholar]
- Gillespie, A.J.R. Rationale for a national annual forest inventory program. J. For. 1999, 97, 16–20. [Google Scholar]
- Heath, L.S.; Smith, J.E.; Woodall, C.W.; Azuma, D.; Waddell, K.L. Carbon stocks on forestland of the United States, with emphasis on USDA Forest Service ownership. Ecosphere 2011, 2, 1–21. [Google Scholar] [CrossRef]
- U.S. Environmental Protection Agency. Inventory of U.S. Greenhouse Gas Emissions and Sinks: 1990–2016; Environmental Protection Agency, Office of Atmospheric Programs: Washington, DC, USA, 2018; p. 655.
- Woodall, C.W.; Coulston, J.W.; Domke, G.M.; Walters, B.F.; Wear, D.N.; Smith, J.E.; Andersen, H.-E.; Clough, B.J.; Cohen, W.B.; Griffith, D.M.; et al. The U.S. Forest Carbon Accounting Framework: Stocks and Stock Change, 1990–2016; U.S. Department of Agriculture, Forest Service, Northern Research Station: Newtown Square, PA, USA, 2015; p. 49.
- Cohen, W.B.; Yang, Z.G.; Kennedy, R. Detecting trends in forest disturbance and recovery using yearly Landsat time series: 2. TimeSync-Tools for calibration and validation. Remote Sens. Environ. 2010, 114, 2911–2924. [Google Scholar] [CrossRef]
- Cohen, W.B.; Healey, S.P.; Yang, Z.; Stehman, S.V.; Brewer, C.K.; Brooks, E.B.; Gorelick, N.; Huang, C.; Hughes, M.J.; Kennedy, R.E.; et al. How similar are forest disturbance maps derived from different landsat time series algorithms? Forests 2017, 8, 98. [Google Scholar] [CrossRef]
- Schroeder, T.A.; Healey, S.P.; Moisen, G.G.; Frescino, T.S.; Cohen, W.B.; Huang, C.; Kennedy, R.E.; Yang, Z. Improving estimates of forest disturbance by combining observations from Landsat time series with U.S. forest service forest inventory and analysis data. Remote Sens. Environ. 2014, 154, 61–73. [Google Scholar] [CrossRef]
- Turner, D.P.; Cohen, W.B.; Kennedy, R.E.; Fassnacht, K.S.; Briggs, J.M. Relationships between leaf area index and Landsat TM spectral vegetation indices across three temperate zone sites. Remote Sens. Environ. 1999, 70, 52–68. [Google Scholar] [CrossRef]
- Turner, D.P.; Ritts, W.D.; Kennedy, R.E.; Gray, A.N.; Yang, Z. Regional carbon cycle responses to 25 years of variation in climate and disturbance in the US Pacific Northwest. Reg. Environ. Chang. 2016, 16, 2345–2355. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Næsset, E.; Gobakken, T.; Bollandsås, O.M. Indirect and direct estimation of forest biomass change using forest inventory and airborne laser scanning data. Remote Sens. Environ. 2015, 164, 36–42. [Google Scholar] [CrossRef]
- Healey, S.P.; Yang, Z.; Cohen, W.B.; Pierce, D.J. Application of two regression-based methods to estimate the effects of partial harvest on forest structure using Landsat data. Remote Sens. Environ. 2006, 101, 115–126. [Google Scholar] [CrossRef]
- Massey, A.; Mandallaz, D. Design-based regression estimation of net change for forest inventories. Can. J. For. Res. 2015, 45, 1775–1784. [Google Scholar] [CrossRef]
- Bollandsås, O.M.; Ene, L.T.; Gobakken, T.; Næsset, E. Estimation of biomass change in montane forests in Norway along a 1200 km latitudinal gradient using airborne laser scanning: A comparison of direct and indirect prediction of change under a model-based inferential approach. Scand. J. For. Res. 2018, 33, 155–165. [Google Scholar] [CrossRef]
- Cleland, D.T.; Freeouf, J.A.; Keys, J.E., Jr.; Nowacki, G.J.; Carpenter, C.A.; McNab, W.H. Ecological Subregions: Sections and Subsections for the Conterminous United States; USDA Forest Service: Washington, DC, USA, 2007.
- Thornton, P.E.; Running, S.W.; White, M.A. Generating surfaces of daily meteorological variables over large regions of complex terrain. J. Hydrol. 1997, 190, 214–251. [Google Scholar] [CrossRef]
- Franklin, J.F.; Dyrness, C.T. Natural Vegetation of Oregon and Washington; USDA Forest Service Pacific Northwest Research Station: Portland, OR, USA, 1973; p. 417.
- Palmer, M.; Kuegler, O.; Christensen, G. Oregon’s Forest Resources, 2006–2015: Ten-Year Forest Inventory and Analysis Report; USDA Forest Service, Pacific Northwest Research Station: Portland, OR, USA, 2018; p. 54.
- Davis, R.J.; Ohmann, J.L.; Kennedy, R.E.; Cohen, W.B.; Gregory, M.J.; Yang, Z.; Roberts, H.M.; Gray, A.N.; Spies, T.A. Northwest Forest Plan-The First 20 Years (1994–2013): Status and Trends of Late-Successional and Old-Growth Forests; U.S. Department of Agriculture, Forest Service, Pacific Northwest Research Station: Portland, OR, USA, 2015; p. 112.
- Azuma, D.L.; Bednar, L.F.; Hiserote, B.A.; Veneklase, C.A. Timber Resource Statistics for Western Oregon, 1997; USDA Forest Service Pacific Northwest Research Station: Portland, OR, USA, 2004; p. 120.
- Azuma, D.L.; Dunham, P.A.; Hiserote, B.A.; Veneklase, C.A. Timber Resource Statistics for Eastern Oregon, 1999; USDA Forest Service Pacific Northwest Research Station: Portland, OR, USA, 2004; p. 42.
- Azuma, D.L.; Hiserote, B.A.; Dunham, P.A. The Western Juniper Resource of Eastern Oregon; USDA Forest Service Pacific Northwest Research Station: Portland, OR, USA, 2005; p. 18.
- Max, T.A.; Schreuder, H.T.; Hazard, J.W.; Oswald, D.D.; Teply, J.; Alegria, J. The Pacific Northwest Region Vegetation and Inventory Monitoring System; USDA Forest Service, Pacific Northwest Research Station: Portland, OR, USA, 1996; p. 22.
- USDA Forest Service. FIA Volume Equation Documentation Updated on 9-19-2014; USDA Forest Service: Portland, OR, USA, 2014; p. 57.
- Means, J.E.; Hansen, H.A.; Koerper, G.J.; Alaback, P.B.; Klopsch, M.W. Software for Computing Plant Biomass--BIOPAK Users Guide; USDA Forest Service Pacific Northwest Forest and Range Experiment Station: Portland, OR, USA, 1994; p. 184.
- USDA Forest Service. Regional Biomass Equations Used by FIA to Estimate Bole, Bark, and Branches; Updated 09-19-2014; USDA Forest Service: Portland, OR, USA, 2014; p. 23.
- Gray, A.N.; Whittier, T.R. Carbon stocks and changes on Pacific Northwest national forests and the role of disturbance, management, and growth. For. Ecol. Manag. 2014, 328, 167–178. [Google Scholar] [CrossRef]
- Gray, A.N.; Whittier, T.R.; Azuma, D.L. Estimation of above-ground forest carbon flux in oregon: Adding components of change to stock-difference assessments. For. Sci. 2014, 60, 317–326. [Google Scholar] [CrossRef]
- Waddell, K.L.; Hiserote, B. The PNW-FIA Integrated Database, Version 2.0; USDA Forest Service Pacific Northwest Research Station, Forest Inventory and Analysis Program: Portland, OR, USA, 2005.
- Hanson, E.J.; Azuma, D.L.; Hiserote, B.A. Site Index Equations and Mean Annual Increment Equations for Pacific Northwest Research Station Forest Inventory and Analysis Inventories, 1985–2001; USDA Forest Service, Pacific Northwest Research Station: Portland, OR, USA, 2002; p. 24.
- Atzet, T.; White, D.E.; McCrimmon, L.A.; Martinez, P.A.; Fong, P.R.; Randall, V.D. Field Guide to the Forested Plant Associations of Southwestern Oregon; USDA Forest Service Pacific Northwest Region: Portland, OR, USA, 1996; p. 372.
- McCain, C.; Diaz, N. Field Guide to the Forested Plant Associations of the Northern Oregon Coast Range; USDA Forest Service, Pacific Northwest Region: Portland, OR, USA, 2002; p. 250.
- Simpson, M. Forested Plant Associations of the Oregon East Cascades; USDA Forest Service Pacific Northwest Region: Portland, OR, USA, 2007; p. 602.
- Kennedy, R.E.; Yang, Z.G.; Cohen, W.B. Detecting trends in forest disturbance and recovery using yearly Landsat time series: 1. LandTrendr—Temporal segmentation algorithms. Remote Sens. Environ. 2010, 114, 2897–2910. [Google Scholar] [CrossRef]
- Powell, S.L.; Cohen, W.B.; Yang, Z.; Pierce, J.D.; Alberti, M. Quantification of impervious surface in the snohomish water resources inventory area of western Washington from 1972–2006. Remote Sens. Environ. 2008, 112, 1895–1908. [Google Scholar] [CrossRef]
- Duane, M.V.; Cohen, W.B.; Campbell, J.L.; Hudiburg, T.; Turner, D.P.; Weyermann, D.L. Implications of alternative field-sampling designs on landsat-based mapping of stand age and carbon stocks in Oregon forests. For. Sci. 2010, 56, 405–416. [Google Scholar]
- Pflugmacher, D.; Cohen, W.B.; Kennedy, R.E.; Yang, Z.Q. Using Landsat-derived disturbance and recovery history and lidar to map forest biomass dynamics. Remote Sens. Environ. 2014, 151, 124–137. [Google Scholar] [CrossRef]
- Pflugmacher, D.; Cohen, W.B.; Kennedy, R.E. Using Landsat-derived disturbance history (1972–2010) to predict current forest structure. Remote Sens. Environ. 2012, 122, 146–165. [Google Scholar] [CrossRef]
- Latta, G.; Temesgen, H.; Barrett, T.M. Mapping and imputing potential productivity of Pacific Northwest forests using climate variables. Can. J. For. Res. 2009, 39, 1197–1207. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Bell, D.M.; Cohen, W.B.; Reilly, M.; Yang, Z. Visual interpretation and time series modeling of Landsat imagery highlight drought’s role in forest canopy declines. Ecosphere 2018, 9, e02195. [Google Scholar] [CrossRef]
- Cohen, W.B.; Yang, Z.; Healey, S.P.; Kennedy, R.E.; Gorelick, N. A LandTrendr multispectral ensemble for forest disturbance detection. Remote Sens. Environ. 2018, 205, 131–140. [Google Scholar] [CrossRef]
- Kennedy, R.E.; Yang, Z.; Gorelick, N.; Braaten, J.; Cavalcante, L.; Cohen, W.B.; Healey, S. Implementation of the LandTrendr algorithm on google earth engine. Remote Sens. 2018, 10, 691. [Google Scholar] [CrossRef]
- Tao, X.; Huang, C.; Zhao, F.; Schleeweis, K.; Masek, J.; Liang, S. Mapping forest disturbance intensity in North and South Carolina using annual Landsat observations and field inventory data. Remote Sens. Environ. 2019, 221, 351–362. [Google Scholar] [CrossRef]
- Battles, J.J.; Bell, D.M.; Kennedy, R.E.; Saah, D.S.; Collins, B.M.; York, R.A.; Sanders, J.E.; Lopez-Ornelas, F. Innovations in Measuring and Managing Forest Carbon Stocks in California; A Report for: California’s Fourth Climate Change Assessment; California Natural Resources Agency: Sacramento, CA, USA, 2018; p. 99.
- Houghton, R.A. Aboveground forest biomass and the global carbon balance. Glob. Chang. Biol. 2005, 11, 945–958. [Google Scholar] [CrossRef]
- Poudel, K.P.; Flewelling, J.W.; Temesgen, H. Predicting volume and biomass change from multi-temporal lidar sampling and remeasured field inventory data in Panther Creek Watershed, Oregon, USA. Forests 2018, 9, 28. [Google Scholar] [CrossRef]
- Mauro, F.; Ritchie, M.; Wing, B.; Frank, B.; Monleon, V.; Temesgen, H.; Hudak, A. Estimation of changes of forest structural attributes at three different spatial aggregation levels in northern california using multitemporal LiDAR. Remote Sens. 2019, 11, 923. [Google Scholar] [CrossRef]
- Powell, S.L.; Cohen, W.B.; Healey, S.P.; Kennedy, R.E.; Moisen, G.G.; Pierce, K.B.; Ohmann, J.L. Quantification of live aboveground forest biomass dynamics with Landsat time-series and field inventory data: A comparison of empirical modeling approaches. Remote Sens. Environ. 2010, 114, 1053–1068. [Google Scholar] [CrossRef]
- Andersen, H.-E.; Reutebuch, S.E.; McGaughey, R.J.; d’Oliveira, M.V.N.; Keller, M. Monitoring selective logging in western Amazonia with repeat lidar flights. Remote Sens. Environ. 2014, 151, 157–165. [Google Scholar] [CrossRef]
- Cohen, W.B.; Yang, Z.Q.; Stehman, S.V.; Schroeder, T.A.; Bell, D.M.; Masek, J.G.; Huang, C.Q.; Meigs, G.W. Forest disturbance across the conterminous United States from 1985–2012: The emerging dominance of forest decline. For. Ecol. Manag. 2016, 360, 242–252. [Google Scholar] [CrossRef]
- Kane, V.R.; North, M.P.; Lutz, J.A.; Churchill, D.J.; Roberts, S.L.; Smith, D.F.; McGaughey, R.J.; Kane, J.T.; Brooks, M.L. Assessing fire effects on forest spatial structure using a fusion of Landsat and airborne LiDAR data in Yosemite National Park. Remote Sens. Environ. 2014, 151, 89–101. [Google Scholar] [CrossRef]
- Schroeder, T.A.; Gray, A.; Harmon, M.E.; Wallin, D.O.; Cohen, W.B. Estimating live forest carbon dynamics with a Landsat-based curve-fitting approach. J. Appl. Remote Sens. 2008, 2, 023519. [Google Scholar] [CrossRef]
- Condés, S.; McRoberts, R.E. Updating national forest inventory estimates of growing stock volume using hybrid inference. For. Ecol. Manag. 2017, 400, 48–57. [Google Scholar] [CrossRef]
- Henderson, J.A.; Lesher, R.D.; Peter, D.H.; Ringo, C.D. A Landscape Model for Predicting Potential Natural Vegetation of the Olympic Peninsula Usa Using Boundary Equations and Newly Developed Environmental Variables; USDA Forest Service, Pacific Northwest Research Station: Portland, OR, USA, 2011; p. 35.
- Healey, S.P.; Cohen, W.B.; Yang, Z.Q.; Brewer, C.K.; Brooks, E.B.; Gorelick, N.; Hernandez, A.J.; Huang, C.Q.; Hughes, M.J.; Kennedy, R.E.; et al. Mapping forest change using stacked generalization: An ensemble approach. Remote Sens. Environ. 2018, 204, 717–728. [Google Scholar] [CrossRef]
- Saxena, R.; Watson, L.T.; Wynne, R.H.; Brooks, E.B.; Thomas, V.A.; Zhiqiang, Y.; Kennedy, R.E. Towards a polyalgorithm for land use change detection. ISPRS J. Photogramm. Remote Sens. 2018, 144, 217–234. [Google Scholar] [CrossRef]
- Eskelson, B.N.I.; Monleon, V.J. Post-fire surface fuel dynamics in California forests across three burn severity classes. Int. J. Wildland Fire 2018, 27, 114–124. [Google Scholar] [CrossRef]
- Christensen, G.A.; Gray, A.N.; Kuegler, O.; Tase, N.A.; Rosenberg, M.; Loeffler, D.; Anderson, N.; Stockmann, K.; Morgan, T.A. AB 1504 California Forest Ecosystem and Harvested Wood Product Carbon Inventory: 2017 Reporting Period; California Department of Forestry and Fire Protection: Sacramento, CA, USA, 2019; p. 552.
- Mauro, F.; Monleon, V.J.; Temesgen, H.; Ford, K.R. Analysis of area level and unit level models for small area estimation in forest inventories assisted with LiDAR auxiliary information. PLoS ONE 2017, 12, e0189401. [Google Scholar] [CrossRef] [PubMed]
- Gray, A.N.; Whittier, T.R.; Harmon, M.E. Carbon stocks and accumulation rates in Pacific Northwest forests: Role of stand age, plant community, and productivity. Ecosphere 2016, 7, e01224. [Google Scholar] [CrossRef]
- Garcia, M.; Saatchi, S.; Casas, A.; Koltunov, A.; Ustin, S.; Ramirez, C.; Garcia-Gutierrez, J.; Balzter, H. Quantifying biomass consumption and carbon release from the California Rim fire by integrating airborne LiDAR and Landsat OLI data. J. Geophys. Res. Biogeosci. 2017, 122, 340–353. [Google Scholar] [CrossRef] [PubMed]
- Cohen, W.B.; Spies, T.A. Estimating structural attributes of douglas-fir western hemlock forest stands from landsat and spot imagery. Remote Sens. Environ. 1992, 41, 1–17. [Google Scholar] [CrossRef]
- Healey, S.P.; Urbanski, S.P.; Patterson, P.L.; Garrard, C. A framework for simulating map error in ecosystem models. Remote Sens. Environ. 2014, 150, 207–217. [Google Scholar] [CrossRef]
- Hudiburg, T.; Law, B.; Turner, D.P.; Campbell, J.; Duane, M. Carbon dynamics of Oregon and Northern California forests and potential land-based carbon storage. Ecol. Appl. 2009, 19, 163–180. [Google Scholar] [CrossRef]
- Wang, W.J.; He, H.S.; Fraser, J.S.; Thompson, F.R., III; Shifley, S.R.; Spetich, M.A. LANDIS PRO: A landscape model that predicts forest composition and structure changes at regional scales. Ecography 2014, 37, 225–229. [Google Scholar] [CrossRef]
- Huntzinger, D.N.; Michalak, A.M.; Schwalm, C.; Ciais, P.; King, A.W.; Fang, Y.; Schaefer, K.; Wei, Y.; Cook, R.B.; Fisher, J.B.; et al. Uncertainty in the response of terrestrial carbon sink to environmental drivers undermines carbon-climate feedback predictions. Sci. Rep. 2017, 7, 4765. [Google Scholar] [CrossRef]
| Predictor | TC Type | Description | |
|---|---|---|---|
| Stand attributes 1 | |||
| BM1 | Above-ground live tree C at first plot measurement (time 1) | ||
| REMPER | Number of years between plot measurements | ||
| MAI | Mean annual increment at culmination, estimate of site productivity (m3 ha−1 year−1) | ||
| STDAGE_T1 | Stand age at time 1 (first measurement) | ||
| GROWMODEL | Extrapolated increase in biomass of undisturbed plot between measurements (Mg ha−1) | ||
| After disturbance (AD) | |||
| ADDUR | Number of years in the segment after the biggest disturbance | ||
| ADMAG | TCA + TCD | Change over the segment after the biggest disturbance | |
| ADREC | TCA + TCD | Change between the end of the biggest disturbance and the second plot measurement | |
| ADROC | TCA + TCD | = ADMAG/ADDUR, annual rate of change | |
| ADVAL | TCA + TCD | Value at the end of the biggest disturbance | |
| Before disturbance (BD) | |||
| BDDUR | Number of years in the segment preceding the biggest disturbance | ||
| BDMAG | TCA + TCD | Change over the segment preceding the biggest disturbance | |
| BDROC | TCA + TCD | = BDMAG/BDDUR, annual rate of change | |
| BDVAL | TCA + TCD | Value at the beginning of the biggest disturbance | |
| Current condition (CC) | |||
| CCTC | TCA + TCD | Value at the time of the second plot measurement | |
| CCCHG | TCA + TCD | Change in value between first and second plot measurement | |
| Current trend (CT) | |||
| CTROC | TCA + TCD | Annual rate of change for the last segment | |
| Greatest disturbance (GD) | |||
| GDAGT_FIRE | Indicator variable for biggest disturbance = Fire | ||
| GDAGT_HARV | Indicator variable for biggest disturbance = Harvest | ||
| GDAGT_OTHR | Indicator variable for biggest disturbance = Mechanical or Other disturbance | ||
| GDDUR | Number of years for the biggest disturbance segment | ||
| GDMAG | TCA+TCD | Change over the biggest disturbance segment | |
| GDRCH | TCA+TCD | = GDMAG/BDVAL, proportional change for the biggest disturbance | |
| GDROC | TCA+TCD | = GDMAG/GDDUR, annual rate of change for the biggest disturbance | |
| GDTSE | Number of years from the end of the biggest disturbance to the second plot measurement | ||
| GDTSS | Number of years from the beginning of the biggest disturbance and the second plot measurement | ||
| Last monotonic trend (LM) | |||
| LMDUR | Number of years for segments before the second measurement with the same sign (+/−) of change | ||
| LMMAG | TCA + TCD | Change over the segments before the second measurement with the same sign (+/−) of change | |
| LMROC | TCA + TCD | = LMMAG/LMDUR, annual rate of change | |
| Total decline (TD) | |||
| TDDUR | TCA + TCD | Number of years segments between plot measurements declined in value | |
| TDMAG | TCA + TCD | Sum of decline segment values between plot measurements | |
| TDROC | TCA + TCD | = TDMAG/TDDUR, annual rate of change of decline | |
| Total recovery (TR) | |||
| TRDUR | TCA + TCD | Number of years segments between plot measurements increased in value | |
| TRMAG | TCA + TCD | Sum of increasing segment values between plot measurements | |
| TRROC | TCA + TCD | = TRMAG/TRDUR, annual rate of change of recovery | |
| Plot Events | ||||||||
|---|---|---|---|---|---|---|---|---|
| TimeSync Events | Fire | Fire & Cut | Harvest | Insect & Disease | Weather | Animal | None | Total |
| Fire | 47 | 3 | 1 | 1 | 52 | |||
| Harvest | 2 | 4 | 70 | 5 | 1 | 8 | 90 | |
| Mechanical | 2 | 2 | ||||||
| Stress | 1 | 20 | 1 | 2 | 24 | |||
| Other disturbance | 2 | 4 | 6 | |||||
| Other non-disturbance | 8 | 5 | 13 | |||||
| None | 3 | 55 | 163 | 7 | 7 | 254 | 489 | |
| Total | 52 | 7 | 127 | 198 | 8 | 8 | 276 | 676 |
| Plot | TimeSync | N Plots | Live Tree C Cut or Died | Net Change | TimeSync Change Variables | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mg ha−1 | Std | Percent | Std | Mg ha−1 | Std | CCCHG_a | Std | GDMAG_a | Std | |||
| Both disturbed 1 | ||||||||||||
| Fire | Fire | 47 | 37.5 | 38.3 | 52% | 40% | −26.2 | 38.9 | −16.0 | 10.9 | −17.0 | 11.6 |
| Fire | Harvest | 2 | 29.2 | 14.4 | 71% | 44% | −9.9 | 0.6 | −5.7 | 4.9 | −13.1 | 8.1 |
| Harvest | Fire | 4 | 25.1 | 21.7 | 65% | 21% | −16.8 | 17.8 | −5.2 | 6.8 | −9.4 | 9.4 |
| Harvest | Harvest | 74 | 57.7 | 65.9 | 76% | 46% | −38.6 | 55.9 | −6.7 | 7.7 | −11.6 | 9.0 |
| Sum | 127 | |||||||||||
| Both undisturbed | ||||||||||||
| NonOther | NonOther | 475 | 6.9 | 13.8 | 8% | 10% | 12.0 | 19.9 | 1.7 | 4.7 | −0.2 | 1.0 |
| One disturbed | ||||||||||||
| NonOther | Fire | 1 | 4.4 | 5% | 10.0 | −0.2 | −3.8 | |||||
| NonOther | Harvest | 14 | 9.9 | 15.3 | 12% | 12% | 14.1 | 18.5 | 0.1 | 4.5 | −3.4 | 3.0 |
| Fire | NonOther | 3 | 3.1 | 5.3 | 3% | 4% | 6.9 | 3.8 | 0.2 | 1.0 | 0 | 0 |
| Harvest | NonOther | 56 | 14.1 | 12.8 | 32% | 30% | 11.4 | 18.7 | 1.1 | 3.2 | 0.0 | 0.2 |
| Sum | 74 | |||||||||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gray, A.N.; Cohen, W.B.; Yang, Z.; Pfaff, E. Integrating TimeSync Disturbance Detection and Repeat Forest Inventory to Predict Carbon Flux. Forests 2019, 10, 984. https://doi.org/10.3390/f10110984
Gray AN, Cohen WB, Yang Z, Pfaff E. Integrating TimeSync Disturbance Detection and Repeat Forest Inventory to Predict Carbon Flux. Forests. 2019; 10(11):984. https://doi.org/10.3390/f10110984
Chicago/Turabian StyleGray, Andrew N., Warren B. Cohen, Zhiqiang Yang, and Eric Pfaff. 2019. "Integrating TimeSync Disturbance Detection and Repeat Forest Inventory to Predict Carbon Flux" Forests 10, no. 11: 984. https://doi.org/10.3390/f10110984
APA StyleGray, A. N., Cohen, W. B., Yang, Z., & Pfaff, E. (2019). Integrating TimeSync Disturbance Detection and Repeat Forest Inventory to Predict Carbon Flux. Forests, 10(11), 984. https://doi.org/10.3390/f10110984





