Semi-Automated Sample-Based Forest Degradation Monitoring with Photointerpretation of High-Resolution Imagery
Abstract
:1. Introduction
- Classification systems often more closely align with information needs than those associated with maps made with classified satellite imagery. The short reacquisition cycle of many high-resolution imagery sources (for example, NAIP is reacquired every 3–5 years) also allows for the consistent monitoring of individual points with the same classification system and protocols.
- The use of a survey sampling estimation paradigm leverages estimators and error metrics like confidence intervals with which decision-makers are accustomed to making decisions. Generally speaking, uncertainty metrics provided with most remote sensing maps cannot be viewed through the lens of survey sampling theory.
- PI plot networks can be interwoven with existing ground plot networks, creating opportunities for harmonization of ground- and PI-based reporting cycles, definitions, and estimation tools. For example, if a ground plot-based inventory cycle is 10 years, PI can be conducted over the same area every 5 years to provide mid-cycle updates of certain attributes that can be perceived on imagery.
- Efficient, low-cost protocols can be designed using less specialized knowledge and training than that which is typically needed for production mapping, something appealing to many REDD participants.
2. Materials and Methods
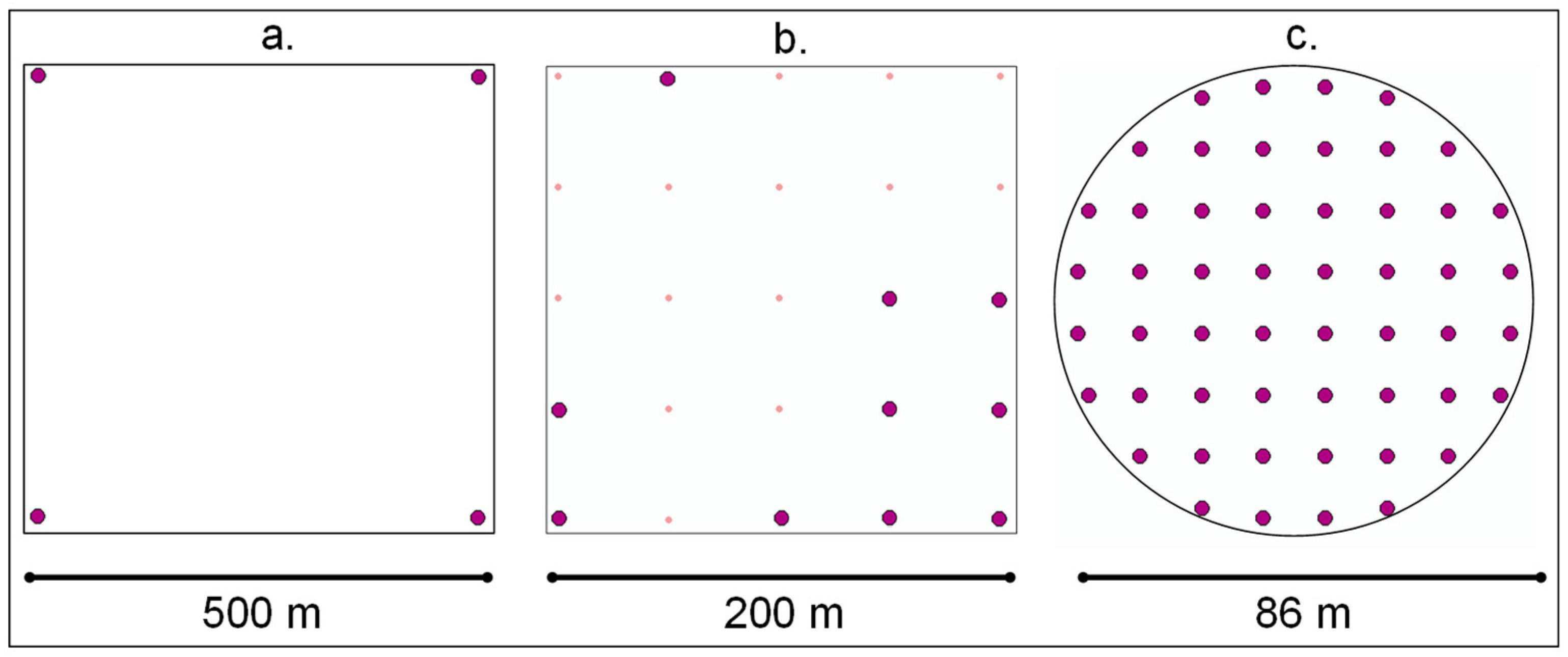
2.1. Study Sites and Sample Design
2.2. Plot Design
2.3. Fragmentation and Degradation Indicators
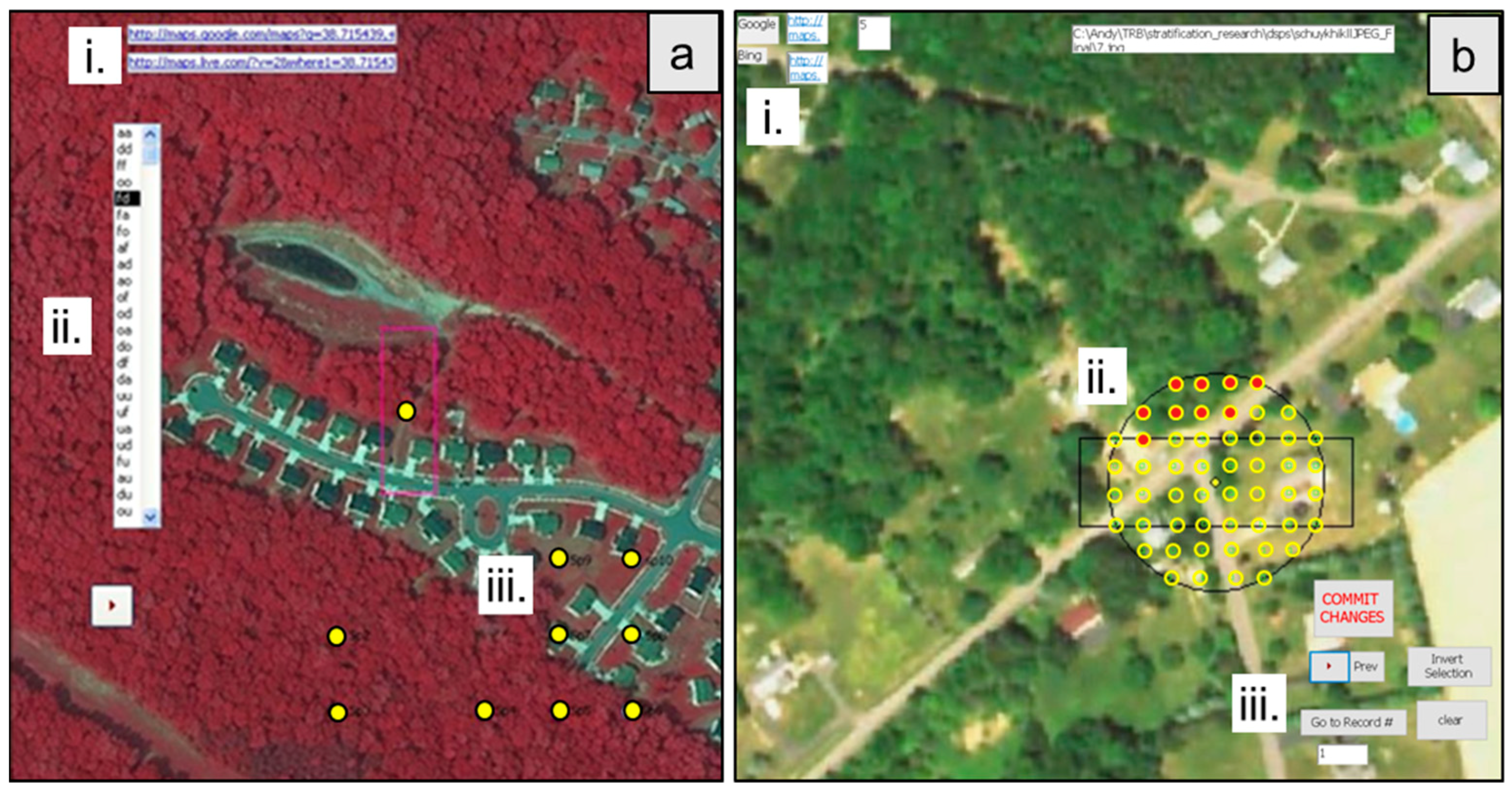
2.4. Data Collection Methods and Metric Calculation for the MD and PG Study Areas
2.4.1. PI and Subpopulation-Level Estimation Procedures
2.4.2. Variance Estimation for PAI for the MD and PG Study Areas
2.4.3. Comparison with Traditional Raster Data and Methods for the PG Study Area
2.5. Data Collection Methods, Metric Calculation, and Estimation Procedures for the SC Study Area
3. Results and Discussion
3.1. PG and MD Study Areas
3.1.1. PAI and NLCD Metrics in the PG Study Area
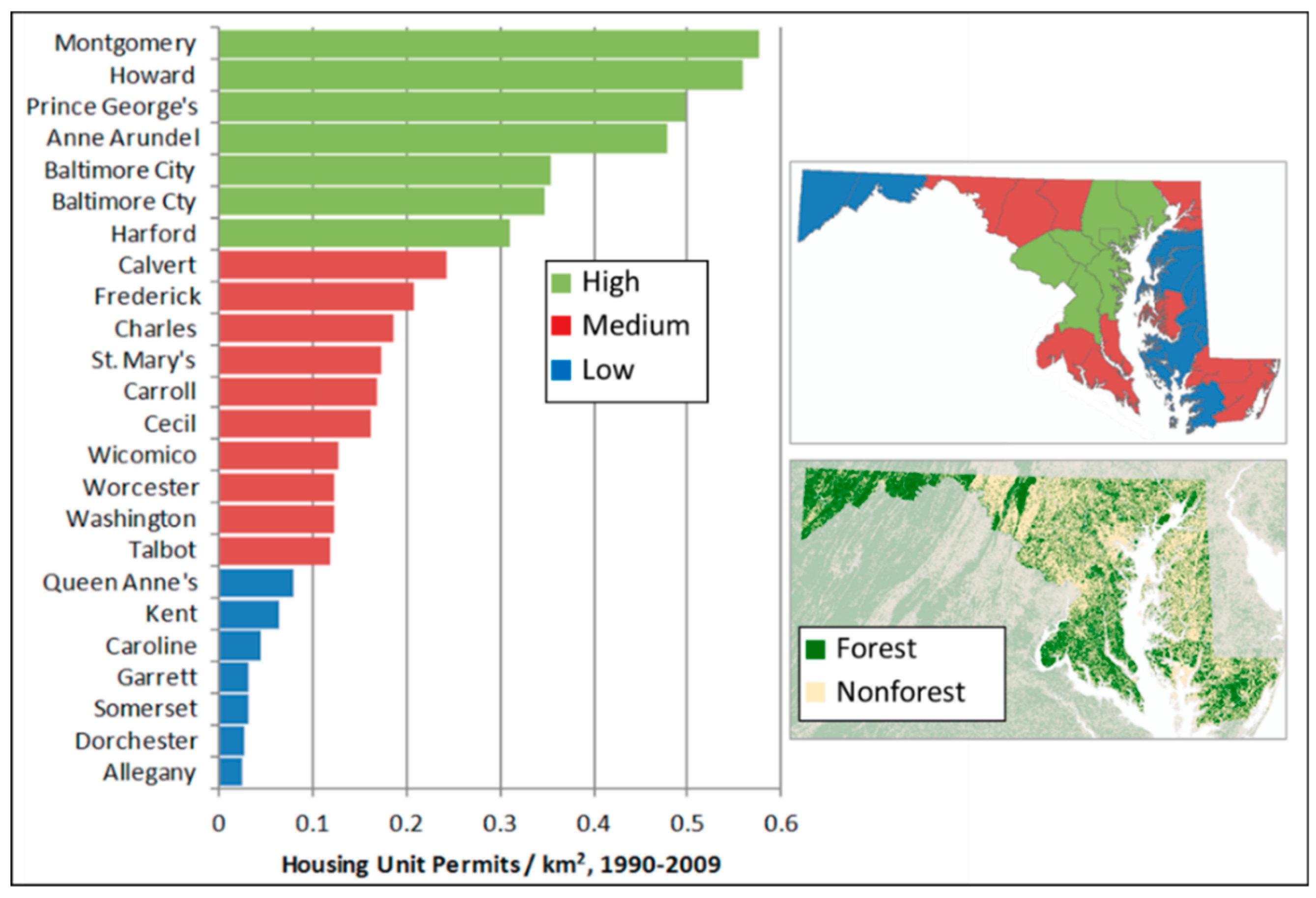
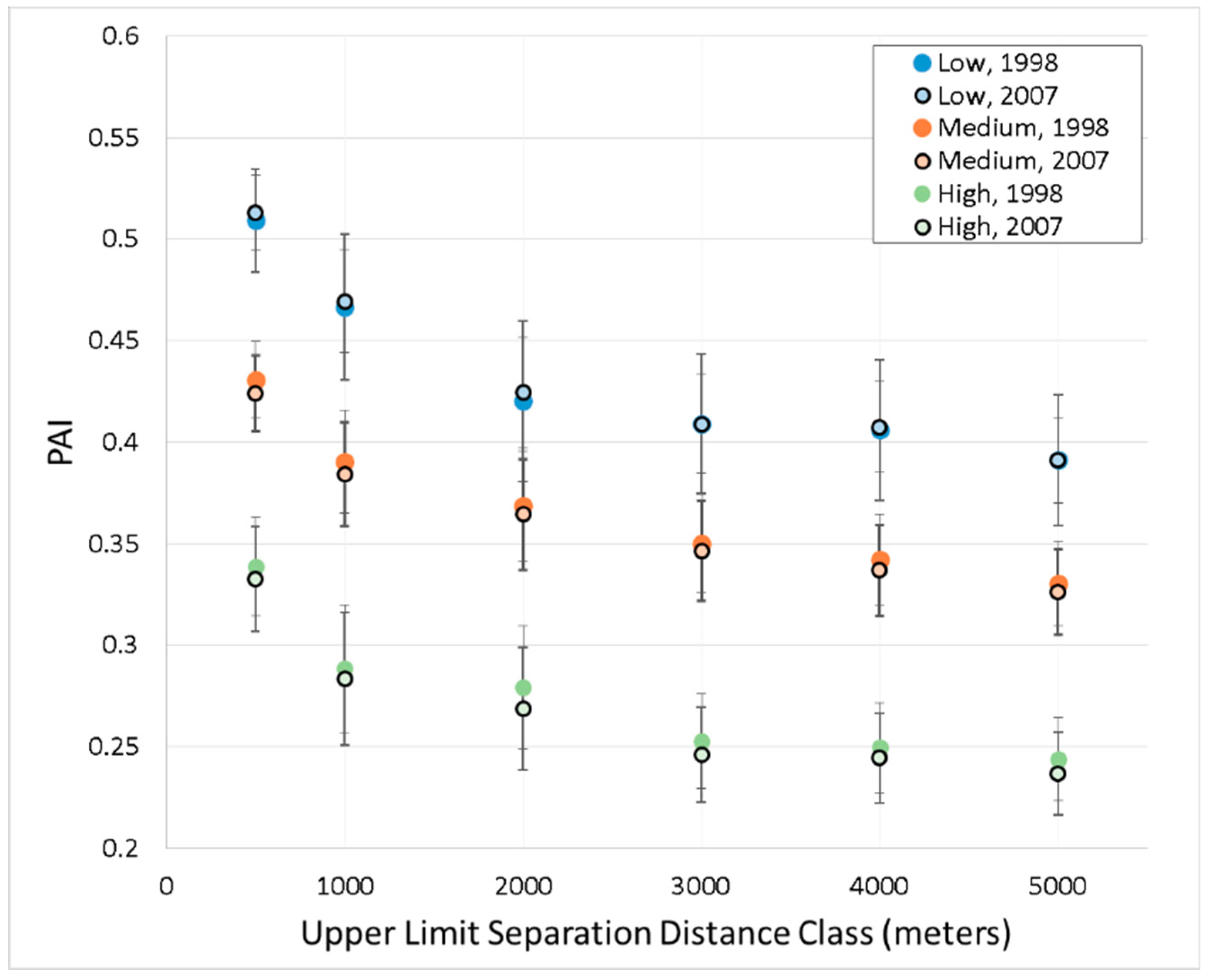
3.1.2. Temporal Differences in PAI across Different Scales and Historical Housing Permit Densities in the MD Study Area
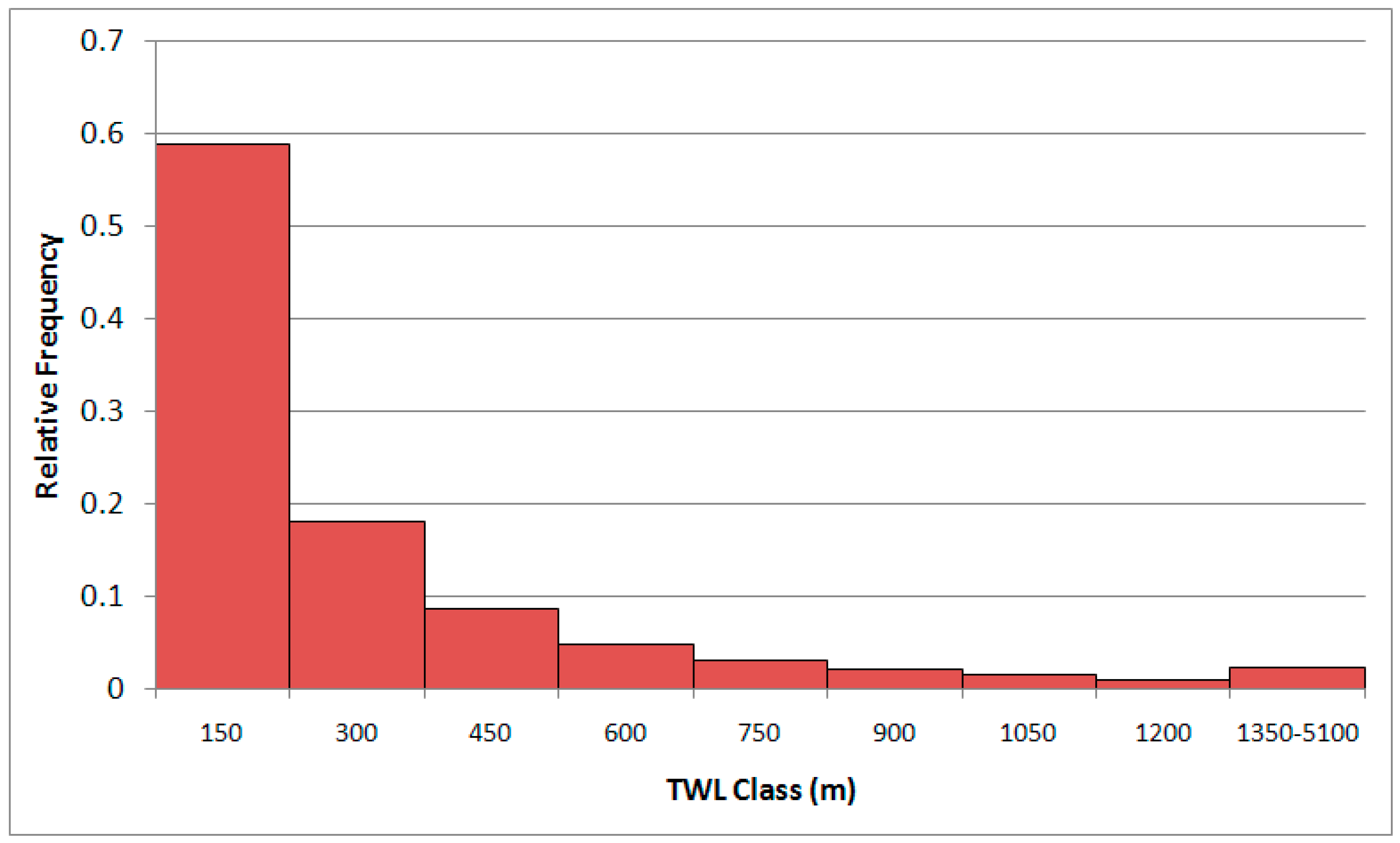
3.2. Sample-Based Estimates of Metrics and Change in the SC Study Area
3.3. Additional Considerations for Landscape Metrics and Sample-Based Estimation
3.3.1. The Validity of Fragmentation Metrics and Functional Significance
3.3.2. Costs
3.3.3. Applications
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- UNFCCC Secretariat. Key Decisions Relevant for Reducing Emissions from Deforestation and Forest Degradation in Developing Countries (REDD+); UNFCCC Secretariat: Bonn, Germany, 2016. [Google Scholar]
- Thompson, I.; Guariguata, M.; Okabe, K.; Bahamondez, C.; Nasi, R.; Heymell, V.; Sabogal, C. An operational framework for defining and monitoring forest degradation. Ecol. Soc. 2013, 18, 20. [Google Scholar] [CrossRef]
- FAO. Assessing Forest Degradation: Towards the Development of Globally Applicable Guidelines; Forest Resources Assessment Working Paper 177; Food and Agriculture Organization of the United Nations: Rome, Italy, 2011. [Google Scholar]
- Shapiro, A.C.; Aguilar-Amuchastegui, N.; Hostert, P.; Bastin, J.-F. Using fragmentation to assess degradation of forest edges in Democratic Republic of Congo. Carbon Balance Manag. 2016, 11, 11. [Google Scholar] [CrossRef] [PubMed]
- Riitters, K.; Wickham, J.; Costanza, J.; Vogt, P. A global evaluation of forest interior area dynamics using tree cover data from 2000 to 2012. Landsc. Ecol. 2016, 31, 137–148. [Google Scholar] [CrossRef]
- Riitters, K.; Wickham, J.; O’Neill, R.; Jones, B.; Smith, E. Global-scale patterns of forest fragmentation. Conserv. Ecol. 2000, 4, 3. [Google Scholar] [CrossRef]
- Wulder, M.; White, J.; Han, T.; Coops, N.; Cardille, J.; Holland, T.; Grills, D. Monitoring Canada’s forests. Part 2: National forest fragmentation and pattern. Can. J. Remote Sens. 2008, 34, 563–584. [Google Scholar] [CrossRef]
- US Department of Agriculture, Forest Service. Forest Inventory and Analysis National Core Field Guide, Volume 1: Field Data Collection Procedures for Phase 2 Plots, Version 8.0; U.S. Department of Agriculture, Forest Service, Forest Inventory and Analysis, Washington Office: Washington, DC, USA, 2019. Available online: https://www.fia.fs.fed.us/library/field-guides-methods-proc/docs/2018/core_ver8-0_10_2018_final.pdf (accessed on 3 September 2019).
- Homer, C.; Dewitz, J.; Fry, J.; Coan, M.; Hossain, N.; Larson, C.; Herold, N.; McKerrow, A.; Vandriel, J.N.; Wickham, J. Completion of the 2001 National Land Cover Database for the Conterminous United States. Photogramm. Eng. Remote Sens. 2007, 73, 337–341. [Google Scholar]
- Hansen, M.C.; Potapov, P.V.; Moore, R.; Hancher, M.; Turubanova, S.A.; Tyukavina, A.; Thau, D.; Stehman, S.V.; Goetz, S.J.; Loveland, T.R.; et al. High-resolution global maps of 21st-century forest cover change. Science 2013, 342, 850–853. [Google Scholar] [CrossRef]
- US Department of Agriculture, Forest Service. EVALIDator Web-Application. 2019. Available online: http://fsxopsx1056.fdc.fs.usda.gov:900/Evalidator/evalidator.jsp (accessed on 19 June 2019).
- Nowak, D.J.; Greenfield, E.J. Evaluating the national land cover database tree canopy and impervious cover estimates across the conterminous United States: A comparison with photo-interpreted estimates. Environ. Manag. 2010, 46, 378–390. [Google Scholar] [CrossRef]
- Fassnacht, K.S.; Cohen, W.B.; Spies, T.A. Key issues in making and using satellite-based maps in ecology: A primer. For. Ecol. Manag. 2006, 222, 167–181. [Google Scholar] [CrossRef]
- O’Neil-Dunne, J.P.M.; MacFaden, S.W.; Royar, A.R.; Pelletier, K.C. An object-based system for LiDAR data fusion and feature extraction. Geocarto Int. 2013, 28, 227–242. [Google Scholar] [CrossRef]
- APFO. National Aerial Imagery Program Imagery (NAIP) Information Sheet. 2018. Available online: https://www.fsa.usda.gov/Internet/FSA_File/naip_info_sheet_2015.pdf (accessed on 3 September 2019).
- Belward, A.S.; Skøien, J.O. Who launched what, when and why; trends in global land-cover observation capacity from civilian earth observation satellites. ISPRS J. Photogramm. Remote Sens. 2015, 103, 115–128. [Google Scholar] [CrossRef]
- Dash, J.; Ogutu, B.O. Recent advances in space-borne optical remote sensing systems for monitoring global terrestrial ecosystems. Prog. Phys. Geogr. 2016, 40, 322–351. [Google Scholar] [CrossRef]
- Bey, A.; Sánchez-Paus Díaz, A.; Maniatis, D.; Marchi, G.; Mollicone, D.; Ricci, S.; Bastin, J.-F.; Moore, R.; Federici, S.; Rezende, M.; et al. Collect Earth: Land use and land cover assessment through augmented visual interpretation. Remote Sens. 2016, 8, 807. [Google Scholar] [CrossRef]
- Lister, T.W.; Lister, A.J.; Alexander, E. Land use change monitoring in Maryland using a probabilistic sample and rapid photointerpretation. Appl. Geogr. 2014, 51, 1–7. [Google Scholar] [CrossRef]
- Megown, K.; Lister, A.; Patterson, P.; Frescino, T.; Jacobs, D.; Webb, J.; Daniels, N.; Finco, M. Image-based change estimation (ICE): Monitoring land use, land cover and agent of change information for all lands. In Proceedings of the Forest Inventory and Analysis (FIA) Symposium 2015, Gen. Tech. Rep. PNW-GTR-931, Portland, OR, USA, 8–10 December 2015; Stanton, S., Christensen, G.A., Eds.; USDA Forest Service, Pacific Northwest Research Station: Portland, OR, USA, 2015; p. 218. [Google Scholar]
- Nowak, D.J.; Greenfield, E.J. Declining urban and community tree cover in the United States. Urban For. Urban Green 2018, 32, 32–55. [Google Scholar] [CrossRef]
- Nowak, D.J.; Greenfield, E.J. Tree and impervious cover in the United States. Landsc. Urban Plan. 2012, 107, 21–30. [Google Scholar] [CrossRef] [Green Version]
- Westfall, J.A.; Lister, A.J.; Scott, C.T.; Weber, T.A. Double sampling for post-stratification in forest inventory. Eur. J. For. Res. 2019, 138, 375–382. [Google Scholar] [CrossRef]
- Schepaschenko, D.; See, L.; Lesiv, M.; Bastin, J.-F.; Mollicone, D.; Tsendbazar, N.-E.; Bastin, L.; McCallum, I.; Laso Bayas, J.C.; Baklanov, A.; et al. Recent advances in forest observation with visual interpretation of very high-resolution imagery. Surv. Geophys. 2019, 40, 839–862. [Google Scholar] [CrossRef]
- Kennedy, R.E.; Yang, Z.; Cohen, W.B. Detecting trends in forest disturbance and recovery using yearly Landsat time series: 1. LandTrendr—Temporal segmentation algorithms. Remote Sens. Environ. 2010, 114, 2897–2910. [Google Scholar] [CrossRef]
- Lister, A.J.; Leites, L.P. A Sentinel satellite-based forest ecosystem change detection system. In Doing More with the Core, Proceedings of the 2017 Forest Inventory and Analysis (FIA) Science Stakeholder Meeting, Vol. RMRS-P-75, Park City, UT, USA, 24–26 October 2017; USDA Forest Service, Rocky Mountain Research Station: Park City, UT, USA, 2017; pp. 45–48. [Google Scholar]
- Pflugmacher, D.; Cohen, W.B.; Kennedy, R.E. Using Landsat-derived disturbance history (1972–2010) to predict current forest structure. Remote Sens. Environ. 2012, 122, 146–165. [Google Scholar] [CrossRef]
- Saah, D.; Johnson, G.; Ashmall, B.; Tondapu, G.; Tenneson, K.; Patterson, M.; Poortinga, A.; Markert, K.; Quyen, N.H.; San Aung, K.; et al. Collect Earth: An online tool for systematic reference data collection in land cover and use applications. Environ. Model. Softw. 2019, 118, 166–171. [Google Scholar] [CrossRef]
- McGarigal, K.; Cushman, S.A.; Neel, M.C.; Ene, E. FRAGSTATS: Spatial Pattern Analysis Program for Categorical Maps; University of Massachusetts, Amherst: Amherst, MA, USA, 2002. [Google Scholar]
- Mladenoff, D.J.; DeZonia, B. APACK 2.17 User’s Guide; University of Wisconsin, Forest Landscape Ecology Lab: Madison, WI, USA, 2001. [Google Scholar]
- Kleinn, C.; Traub, B. Describing landscape pattern by sampling methods. In Advances in Forest Inventory for Sustainable Forest Management and Biodiversity Monitoring; Corona, P., Köhl, M., Marchetti, M., Eds.; Springer: Dordrecht, The Netherlands, 2003; pp. 175–189. [Google Scholar]
- Nelson, M.; Lister, A.; Hansen, M. Estimating number and size of forest patches from FIA plot data. In Proceedings of the Eighth Annual Forest Inventory and Analysis Symposium, Gen. Tech. Report WO-79, Monterey, CA, USA, 16–19 October 2006; U.S. Department of Agriculture, Forest Service: Washington, DC, USA, 2009; pp. 159–164. [Google Scholar]
- Meneguzzo, D.; Hansen, M. Quantifying forest fragmentation using Geographic Information Systems and Forest Inventory and Analysis plot data. In Proceedings of the Eighth Annual Forest Inventory and Analysis Symposium, Monterey, CA, USA, 16–19 October 2006; U.S. Department of Agriculture, Forest Service: Washington, DC, USA, 2009; pp. 143–147. [Google Scholar]
- Kleinn, C. Estimating metrics of forest spatial pattern from large area forest inventory cluster samples. For. Sci. 2000, 46, 548–557. [Google Scholar]
- Ramezani, H. Forest edge length estimation—A case study using the Swedish National Forest Inventory (NFI). Scand. J. For. Res. 2017, 32, 782–788. [Google Scholar] [CrossRef]
- Ramezani, H.; Holm, S.; Allard, A.; Stahl, G. Monitoring landscape metrics by point sampling: Accuracy in estimating Shannon’s diversity and edge density. Environ. Monit. Assess. 2010, 164, 403–421. [Google Scholar] [CrossRef] [PubMed]
- Ramezani, H.; Holm, S. Sample based estimation of landscape metrics; accuracy of line intersect sampling for estimating edge density and Shannon’s diversity index. Environ. Ecol. Stat. 2011, 18, 109–130. [Google Scholar] [CrossRef]
- Ramezani, H.; Ramezani, F. Potential for the wider application of national forest inventories to estimate the contagion metric for landscapes. Environ. Monit. Assess. 2015, 187, 116. [Google Scholar] [CrossRef] [PubMed]
- Lister, A.; Scott, C. Use of space-filling curves to select sample locations in natural resource monitoring studies. Environ. Monit. Assess. 2009, 149, 71–80. [Google Scholar] [CrossRef]
- Burrows, S.N.; Gower, S.T.; Clayton, M.K.; Mackay, D.S.; Ahl, D.E.; Norman, J.M.; Diak, G. Application of geostatistics to characterize leaf area index (LAI) from flux tower to landscape scales using a cyclic sampling design. Ecosystems 2002, 5, 667–679. [Google Scholar]
- Shannon, C.E.; Weaver, W. The Mathematical Theory of Communication; University of Illinois Press: Urbana, IL, USA, 1962. [Google Scholar]
- Turner, M.G. Landscape ecology: The effect of pattern on process. Annu. Rev. Ecol. Syst. 1989, 20, 171–197. [Google Scholar] [CrossRef]
- Miller, J.N.; Brooks, R.P.; Croonquist, M.J. Effects of landscape patterns on biotic communities. Landsc. Ecol. 1997, 12, 137–153. [Google Scholar] [CrossRef]
- He, H.S.; DeZonia, B.; Mladenoff, D.J. An aggregation index (AI) to quantify spatial patterns of landscapes. Landsc. Ecol. 2000, 15, 591–601. [Google Scholar] [CrossRef]
- Riitters, K.H.; Oneill, R.V.; Wickham, J.D.; Jones, K.B. A note on contagion indices for landscape analysis. Landsc. Ecol. 1996, 11, 197–202. [Google Scholar] [CrossRef]
- Li, X.; He, H.S.; Bu, R.; Wen, Q.; Chang, Y.; Hu, Y.; Li, Y. The adequacy of different landscape metrics for various landscape patterns. Pattern Recognit. 2005, 38, 2626–2638. [Google Scholar] [CrossRef]
- ESRI. ArcGIS Desktop; ESRI: Redlands, CA, USA, 2018. [Google Scholar]
- Rosenkrantz, D.J.; Stearns, R.E.; Lewis, P.M. An analysis of several heuristics for the traveling salesman problem. In Fundamental Problems in Computing: Essays in Honor of Professor Daniel J. Rosenkrantz; Ravi, S.S., Shukla, S.K., Eds.; Springer: Dordrecht, The Netherlands, 2009; pp. 45–69. [Google Scholar]
- Hasler, M.; Hornik, K. TSP: Traveling Salesperson Problem; R Package. 2018. Available online: https://CRAN.R-project.org/package=TSP (accessed on 3 September 2019).
- U.S. Department of Commerce. 2010 & 2009 Maryland Comparison of Total and Single Family Housing Units; Bureau of the Census, Manufacturing Mining and Construction Statistics Division: Washington, DC, USA, 2010. Available online: https://planning.maryland.gov/msdc/Pages/newhh/2010/annual2010.aspx (accessed on 3 September 2019).
- Jenks, G.F. The data model concept in statistical mapping. Int. Yearb. Cartogr. 1967, 7, 186–190. [Google Scholar]
- Thompson, S.K. Sampling, 3rd ed.; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 2012. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2017. [Google Scholar]
- Curran, P.J. The semivariogram in remote sensing: An introduction. Remote Sens. Environ. 1988, 24, 493–507. [Google Scholar] [CrossRef]
- Westfall, J.A.; Pugh, S.A.; Coulston, J.W. Conducting Tests for Statistically Significant Differences Using Forest Inventory Data; U.S. Department of Agriculture, Forest Service, Northern Research Station: Newtown Square, PA, USA, 2013; p. 10.
- Forman, R.T.T. Land Mosaics: The Ecology of Landscapes and Regions; Cambridge University Press: Cambridge, MA, USA, 1995. [Google Scholar]
- Turner, M.G.; Gardner, R.H.; O’Neill, R.V. Landscape Ecology in Theory and Practice: Pattern and Process; Springer: New York, NY, USA, 2001. [Google Scholar]
- Ramezani, H.; Holm, S.; Allard, A.; Ståhl, G. A review of sampling-based approaches for estimating landscape metrics. Nor. Geogr. Tidsskr. Nor. J. Geogr. 2013, 67, 61–71. [Google Scholar] [CrossRef]
- Riitters, K.H.; O’Neill, R.V.; Hunsacker, C.T.; Wickham, J.D.; Yankee, D.H.; Timmins, S.P.; Jones, K.B.; Jackson, B.L. A factor analysis of landscape pattern and structure metrics. Landsc. Ecol. 1995, 10, 23–39. [Google Scholar] [CrossRef]
- Tinkham, W.T.; Mahoney, P.R.; Hudak, A.T.; Domke, G.M.; Falkowski, M.J.; Woodall, C.W.; Smith, A.M.S. Applications of the United States Forest Inventory and Analysis dataset: A review and future directions. Can. J. For. Res. 2018, 48, 1–18. [Google Scholar] [CrossRef]
- Crow, T.R. Moving to the big picture: Applying knowledge from landscape ecology to managing U.S. National Forests. In Forest Landscape Ecology: Transferring Knowledge to Practice; Perera, A.H., Buse, L.J., Crow, T.R., Eds.; Springer: New York, NY, USA, 2006; pp. 157–180. [Google Scholar]
- Morin, R.S.; Lister, A.; Doyle, J. Use of FIA data and GIS to characterize the effects of fragmentation on the forests of New Hampshire. In Proceedings of the 2009 Society of American Foresters National Convention, Opportunities in a Forested World, Orlando, FL, USA, 30 September–4 October 2009; Society of American Foresters: Bethesda, MD, USA, 2009. [Google Scholar]
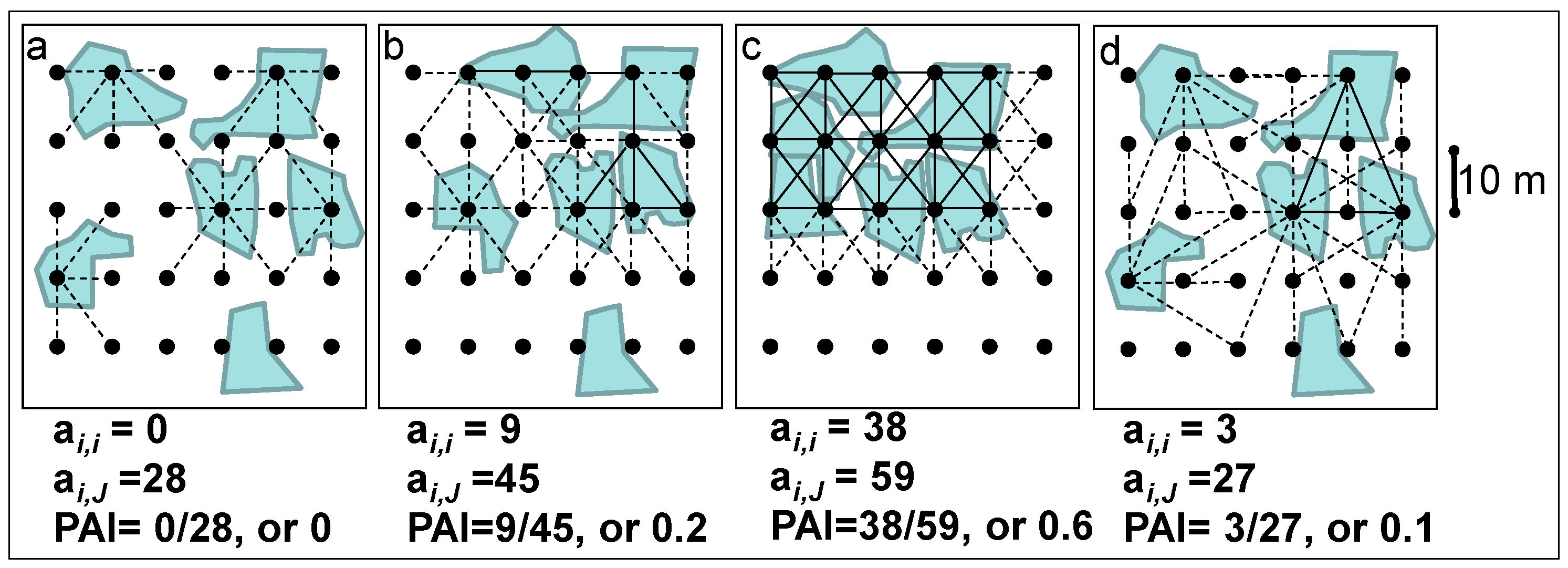


| Metric | Subset of Plots Used | Equation | Description |
|---|---|---|---|
| Point Aggregation Index (PAI) 1 | Plots with at least 1 forested point (n = 1602) | The number of forest-forest point adjacencies divided by the total number of adjacencies between forest and any other type (including forest) in the estimation area. Calculated with Aij, an i × j (i = j = 1…m points in the estimation area) adjacency matrix with binary elements (1= a forested point adjacent to another forested point, 0 otherwise) and Bij, an i × j adjacency matrix with binary elements (1 = a forested point adjacent to any point type, 0 otherwise). Values can range from 0 (the case where there are no adjacent forest points) to 1 (the case where all points are forest). | |
| TSP distance (TSPd) | Plots with at least 2 forested points (n = 1599) | The shortest path distance (meters) calculated using an algorithmic solution to what is known as the Traveling Salesperson Problem (TSP), farthest insertion method [48] found within the R package TSP [49]. di = the ith member of the set D of interpoint distances leading to the shortest overall distance between all forested points on the plot, returning to the first point. Values range from the minimum distance between two adjacent points (the case where there are 2 adjacent forested points on the plot; 12 m in the case of SC) to the sum of the shortest path roundtrip distance between all points on the plot (the case where all points on the plot are forest; approximately 675 m in the case of SC). | |
| Relative TSP distance (rTSPd) | Plots with at least 2 forested points (n = 1599) | Relative (average per point) distance along the shortest path between all forested points on the plot, returning to point 1. k = the number of forested points in the plot. Values range from ½ the distance between 2 adjacent points (the case where there are k = 2 adjacent forested points on the plot) to 1/kth of the sum of the shortest path roundtrip distance between all points on the plot (the case where all points on the plot are forest; in the case of SC, k = 52). | |
| Nearest Neighbour distance (NNd) | Plots with at least 2 forested points (n = 1599) | Nearest neighbor distance, calculated as the nonzero minimum of the i × j (i = j = 1…k forested points on the plot) distance matrix C with elements comprised of geographic distance between forested points i and j. Values range from the minimum distance between two adjacent points (the case where there are k = 2 adjacent forested points on the plot; 12 m in the case of SC) to the maximum distance between 2 points on the plot (the case where there are k = 2 forest points located at the extreme ends of the plot; approximately 82 m in the case of SC). | |
| Mean Interpoint Distance (MId) | Plots with at least 2 forested points (n = 1599) | The average distance between forested points on the plot, calculated as the mean of the i × j (i = j = 1…k forested points on the plot) distance matrix D with elements comprised of geographic distance between forested points i and j. Values range from ½ the distance between 2 adjacent points (the case where there are 2 adjacent forested points on the plot) to ½ the distance between the 2 points located at extreme ends of the plot (the case where there are 2 forested points located at the extreme ends of the plot). | |
| Number of f-f point adjacencies (NA) | Plots with at least 1 forested point (n = 1602) | The number of forest-forest point adjacencies on the plot, summarized from Aij, the i × j (i = j = 1…m points in the plot) adjacency matrix with binary elements (1= a forested point adjacent to another forested point, 0 otherwise). Values range from 0 (the case where there are no forest-forest adjacencies) to the total count of possible point to point adjacencies on the plot (the case where all points are forest; 170 m in the case of SC). | |
| Relative number of adjacencies (rNA) | Plots with at least 1 forested point (n = 1602) | The number of forest-forest point adjacencies divided by the total number of possible adjacencies of any type on the plot, calculated with NA and Dij, the i × j (i = j = 1…m points in the plot) adjacency matrix obtained when all points are a forest. Values range between 0 (the case where there are no forest-forest adjacencies) and 1 (the case where all points are forest). | |
| Mean Forest Proportion 18-m window (MFP18) | All plots (n = 2099) | Mean of the proportions of forested points surrounding each of the m points on the plot. pl = the proportion of forest points around point l. Values range from 0 (the case where there are no forested points on the plot) to 1 (the case where all points on the plot are forest). The radius of the buffer used will vary by plot design (for the SC area, 18 m was chosen). | |
| SD Forest Proportion 18-m window (SDFP18) | All plots (n = 2099) | The standard deviation of the proportions of forested points surrounding each of the m points on the plot. Values range from 0 (all points are either forest or nonforest) to a maximum value of approximately 0.5 (when half of the points on the plot are surrounded by forest). |
| Original | Degraded | Change (Degraded − Original) | |||||
|---|---|---|---|---|---|---|---|
| Metric | Mean | SE | Mean | SE | Mean | SE | CI Half-Width |
| PAI | 0.84 | 0.0055 (0.7%) | 0.82 | 0.0054 (0.7%) | −0.02 | 0.0006 (4%) | 0.001 |
| TSPd | 528.46 | 4.2896 (0.8%) | 525.25 | 4.2727 (0.8%) | −3.21 | 0.2075 (6.5%) | 0.407 |
| rTSPd | 12.83 | 0.0354 (0.3%) | 12.88 | 0.0356 (0.3%) | 0.05 | 0.0061 (11.6%) | 0.012 |
| NNd | 10.09 | 0.0156 (0.2%) | 10.09 | 0.0157 (0.2%) | 0.00 | 0.0013 (92.7%) | 0.002 |
| MID | 41.15 | 0.1724 (0.4%) | 41.13 | 0.173 (0.4%) | −0.01 | 0.0068 (46.1%) | 0.013 |
| NA | 130.60 | 1.3301 (1%) | 128.01 | 1.3086 (1%) | −2.59 | 0.1013 (3.9%) | 0.199 |
| rNA | 0.77 | 0.0078 (1%) | 0.75 | 0.0077 (1%) | −0.02 | 0.0006 (3.9%) | 0.001 |
| MFP18 | 0.62 | 0.0106 (1.7%) | 0.61 | 0.0105 (1.7%) | −0.01 | 0.0003 (4.6%) | 0.001 |
| SDFP18 | 0.09 | 0.0033 (3.6%) | 0.10 | 0.0032 (3.2%) | 0.01 | 0.0005 (6.3%) | 0.001 |
| PF | 0.62 | 0.0106 (1.7%) | 0.61 | 0.0105 (1.7%) | −0.01 | 0.0003 (4.5%) | 0.001 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lister, A.; Lister, T.; Weber, T. Semi-Automated Sample-Based Forest Degradation Monitoring with Photointerpretation of High-Resolution Imagery. Forests 2019, 10, 896. https://doi.org/10.3390/f10100896
Lister A, Lister T, Weber T. Semi-Automated Sample-Based Forest Degradation Monitoring with Photointerpretation of High-Resolution Imagery. Forests. 2019; 10(10):896. https://doi.org/10.3390/f10100896
Chicago/Turabian StyleLister, Andrew, Tonya Lister, and Thomas Weber. 2019. "Semi-Automated Sample-Based Forest Degradation Monitoring with Photointerpretation of High-Resolution Imagery" Forests 10, no. 10: 896. https://doi.org/10.3390/f10100896




