Effect of the Strain Rate and Fiber Direction on the Dynamic Mechanical Properties of Beech Wood
Abstract
1. Introduction
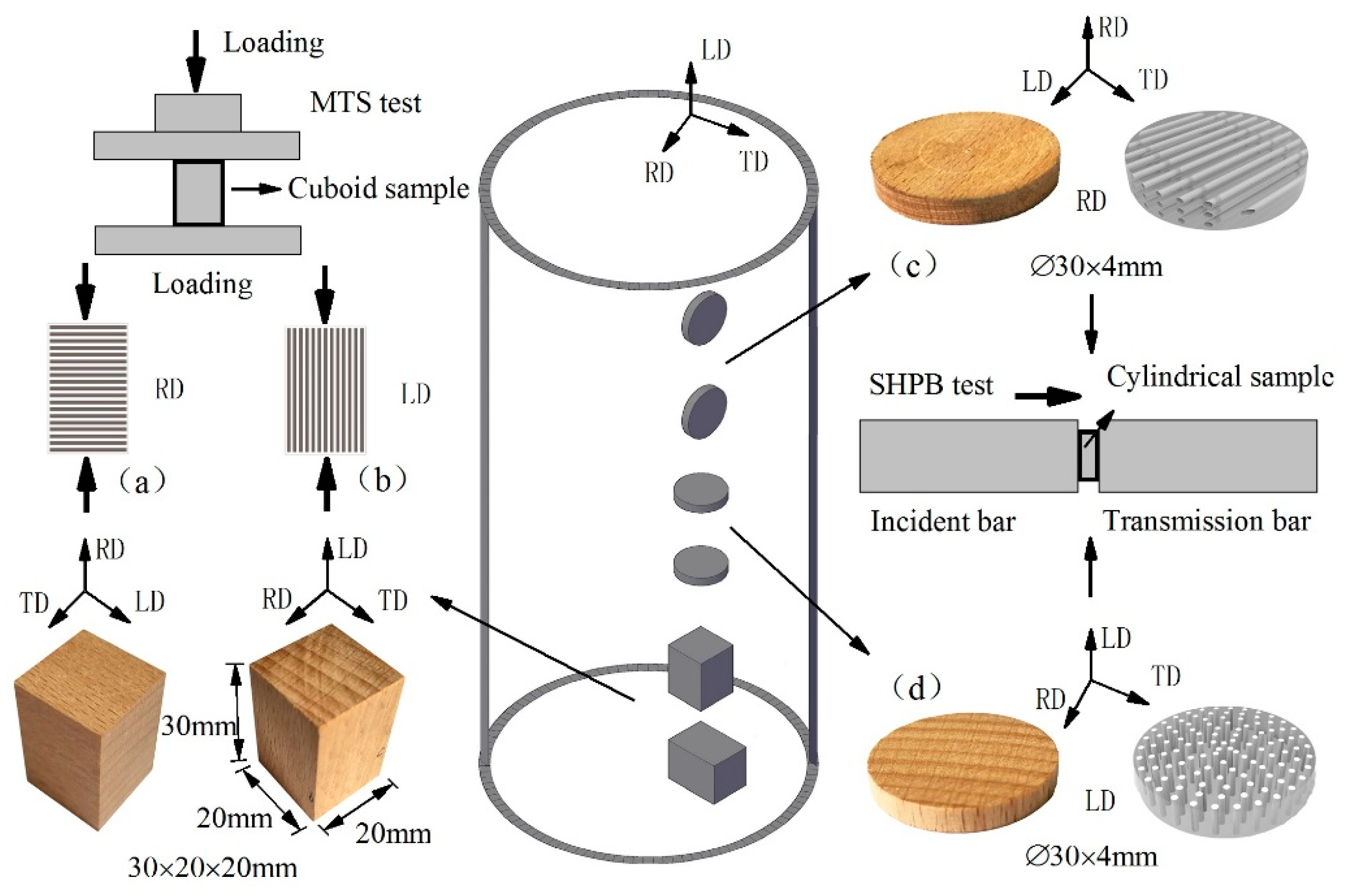
2. Materials and Methods
2.1. Quasi-Static Compression Tests
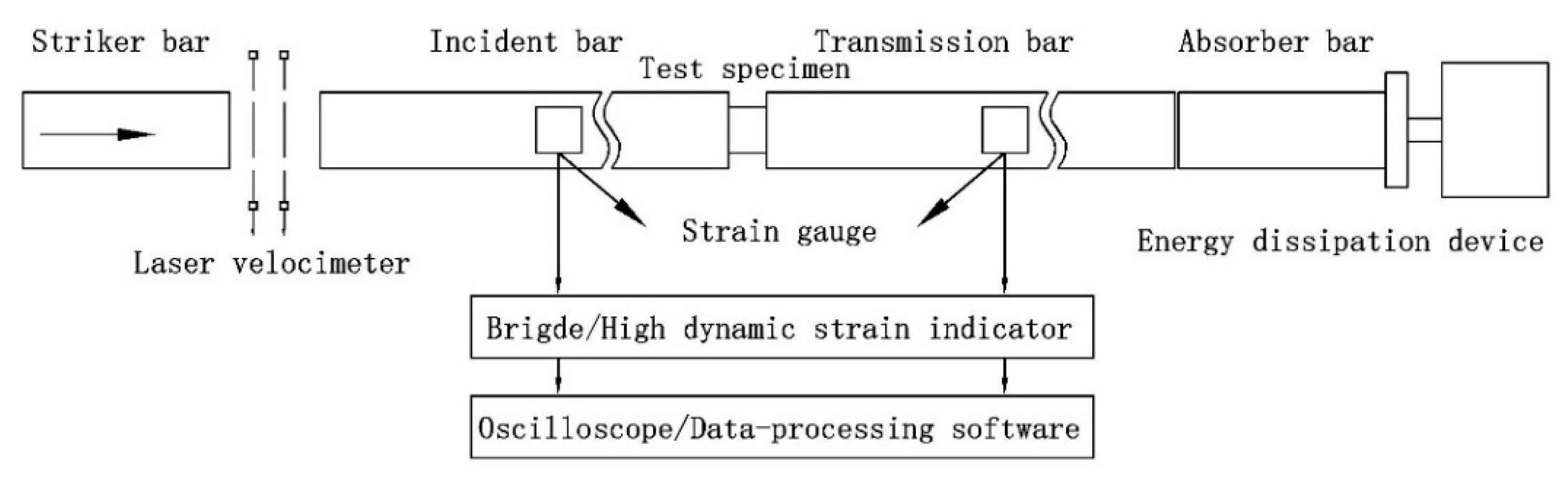
2.2. Dynamic Compression Tests
3. Results and Discussion
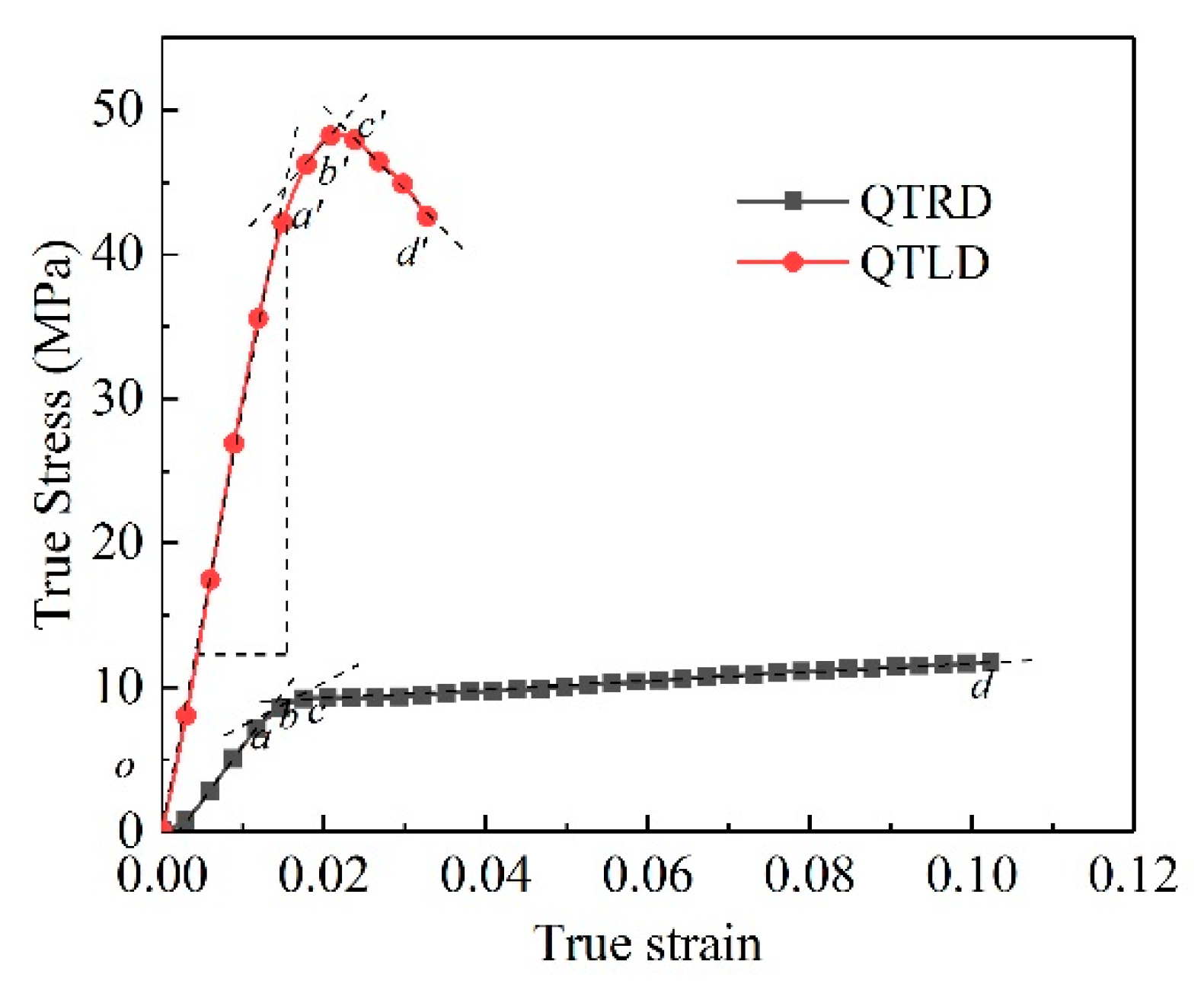
3.1. Quasi-Static Compression Test Results
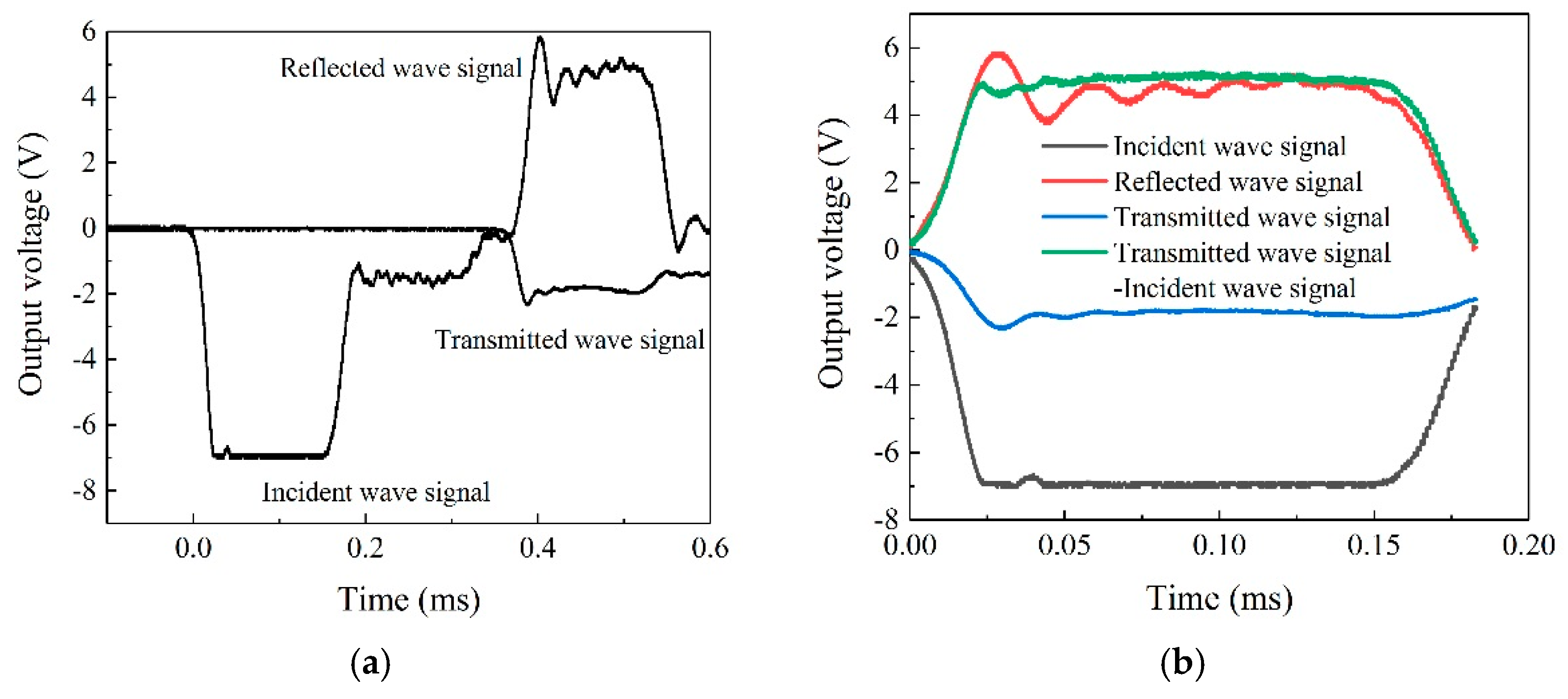
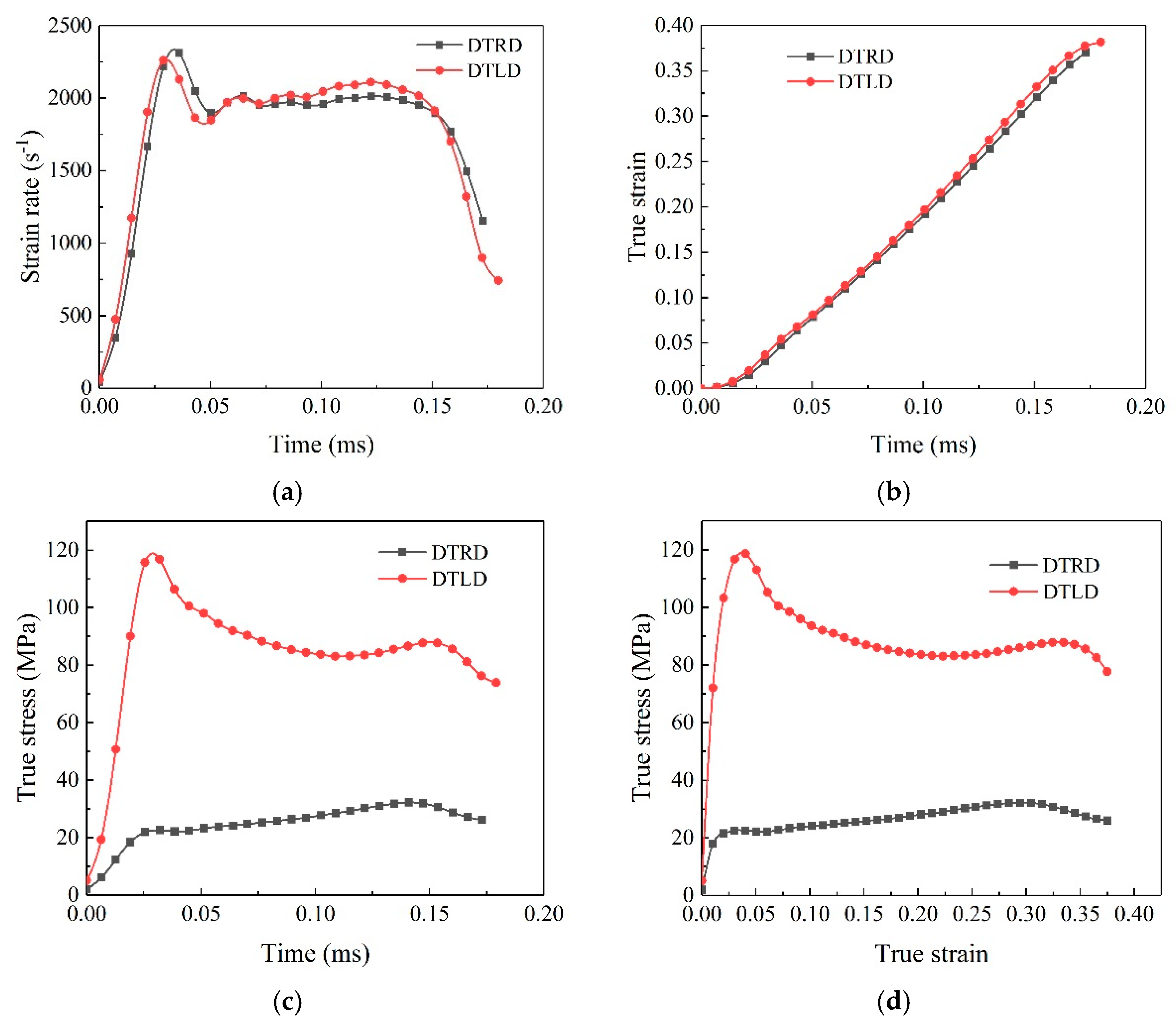
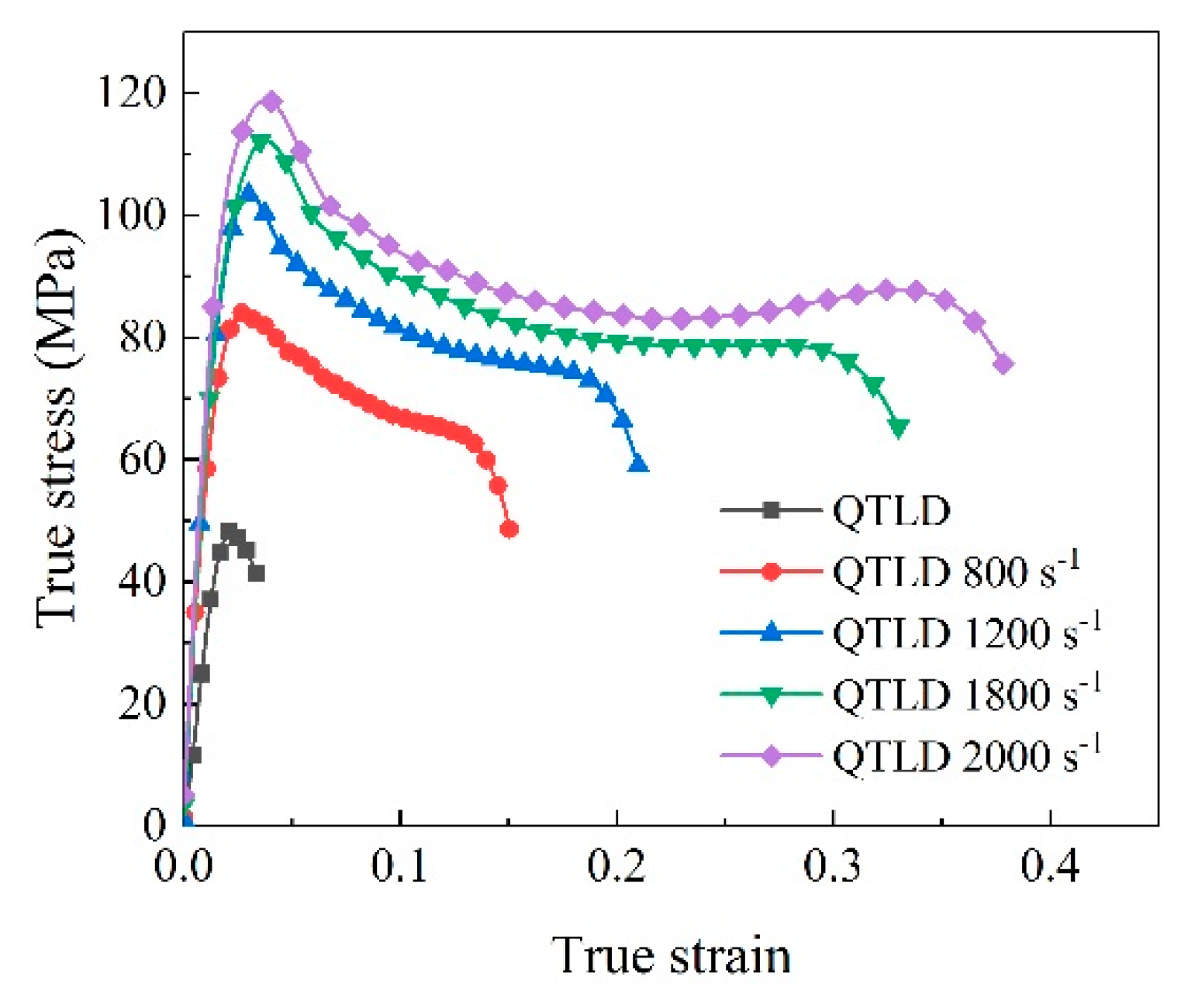
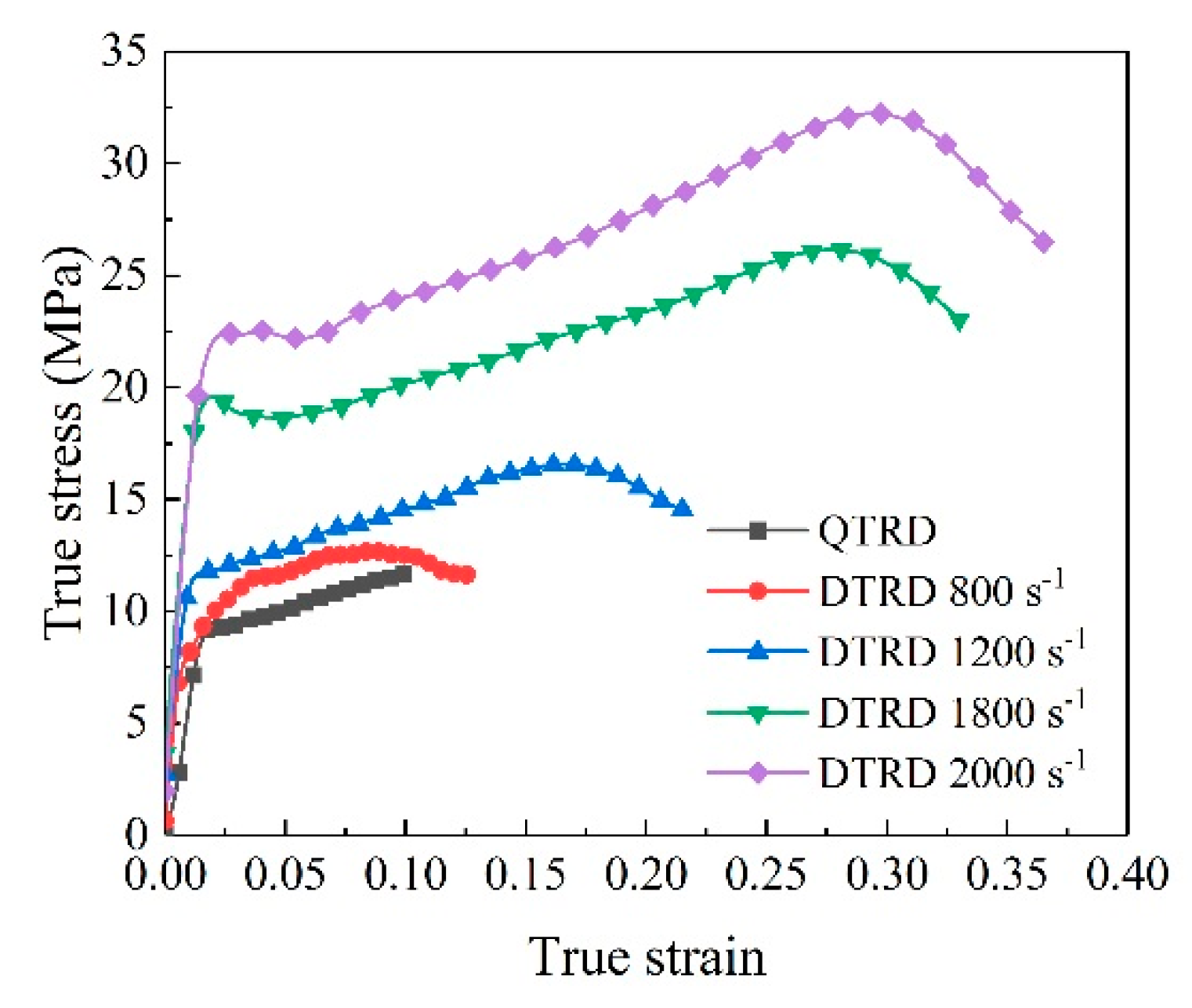
3.2. SHPB Compressive Test Results
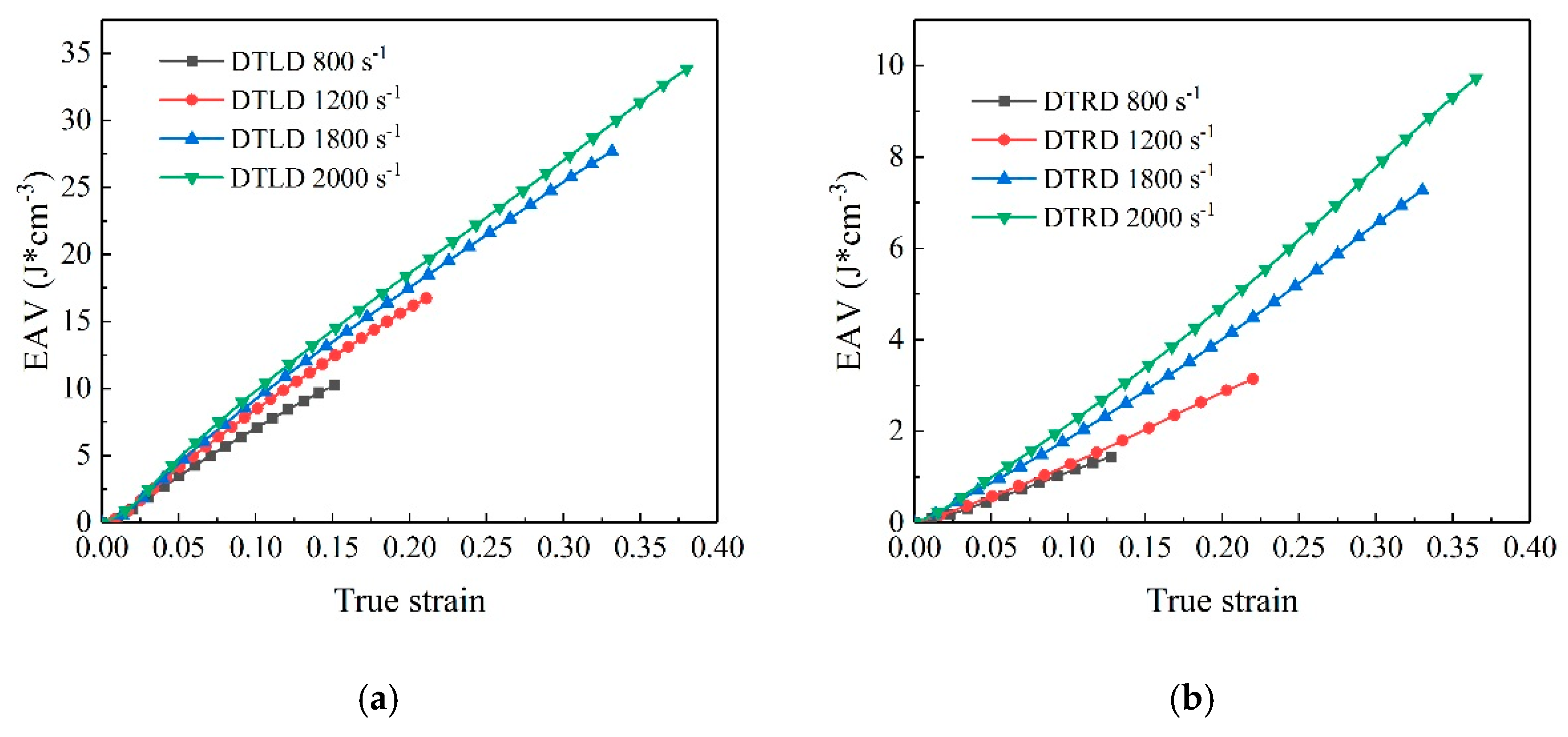
3.3. Strain Rate Sensitivity
3.4. Failure Mechanism
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- King, W.S.; Yen, J.Y.R.; Yen, Y.N.A. Joint characteristics of traditional Chinese wooden frames. Eng. Struct. 1996, 18, 635–644. [Google Scholar] [CrossRef]
- Bu, J. Studies on Growth Patterns and Wood Properties. Master’s Thesis, Central South University, Changsha, China, 2013. [Google Scholar]
- Detvaj, J.; Janovčíková, P. Efficient exploitation of beech wood by production of an atypical structural element—A hollow wooden post. Drvna Ind. 2017, 68, 261–266. [Google Scholar] [CrossRef]
- Gejdos, M.; Potkany, M. The potential of beech wood use in selected countries of the central Europe for valuable processing purposes. In Proceedings of the 10th Annual International Scientific Conference on More Wood, Better Management, Increasing Effectiveness: Setting Points and Perspectives, Prague, Czech Republic, 24–26 May 2017. [Google Scholar]
- Hu, L.L.; You, F.F.; Yu, T.X. Analyses on the dynamic strength of honeycombs under the y-directional crushing. Mater. Design 2014, 53, 293–301. [Google Scholar] [CrossRef]
- Duarte, I.; Teixeira-Dias, F.; Graca, A.; Ferreira, A.J.M. Failure modes and influence of the quasi-static deformation rate on the mechanical behavior of sandwich panels with aluminum foam cores. Mech. Adv. Mater. Struct. 2010, 17, 335–342. [Google Scholar] [CrossRef]
- Li, Z.Q.; Xi, C.Q.; Jing, L.; Wang, Z.H.; Zhao, L.M. Effect of loading rate on the compressive properties of open-cell metal foams. Mater. Sci. Eng. A 2014, 592, 221–229. [Google Scholar] [CrossRef]
- Xi, H.F.; Tang, L.Q.; Luo, S.H.; Liu, Y.P.Z.; Jiang, Y.; Liu, Z.J. A numerical study of temperature effect on the penetration of aluminum foam sandwich panels under impact. Compos. Part B-Eng. 2017, 130, 217–229. [Google Scholar] [CrossRef]
- Yu, K.; Hu, H.; Belouettar, S.; Potier-Ferry, M. Multi-scale techniques to analyze instabilities in sandwich structures. Compos. Struct. 2013, 96, 751–762. [Google Scholar] [CrossRef]
- Susainathan, J.; Eyma, F.; Luycker, E.D.; Cantarel, A.; Bouvet, C.; Castanie, B. Experimental investigation of compression and compression after impact of wood-based sandwich structures. Compos. Struct. 2019, 220, 236–249. [Google Scholar] [CrossRef]
- Yuan, L.; Batra, R.C. Optimum first failure load design of one/two-core sandwich plates under blast loads, and their ultimate loads. Compos. Struct. 2019, 224, 111. [Google Scholar] [CrossRef]
- Qi, Y.; Xie, L.; Bai, Y.; Liu, W.; Fang, H. Axial compression behaviours of pultruded GFRP—Wood composite columns. Sensors 2019, 19, 755. [Google Scholar] [CrossRef] [PubMed]
- Yamada, H.; Tateyama, K.; Sasaki, H.; Naruke, S.; Kishimoto, H.; Yoshimoto, M. Impact resistance to ballistic ejecta of wooden buildings and a simple reinforcement method using aramid fabric. J. Volcanol. Geotherm. Res. 2018, 359, 37–46. [Google Scholar] [CrossRef]
- Bachtiar, E.V.; Clerc, G.; Brunner, A.J.; Kaliske, M.; Niemz, P. Static and dynamic tensile shear test of glued lap wooden joint with four different types of adhesives. Holzforschung 2017, 71, 391–396. [Google Scholar] [CrossRef]
- Easterling, K.E.; Harrysson, R.; Gibson, L.J.; Ashby, M.F. On the mechanics of balsa and other woods. Proc. R. Soc. Lond. A 1982, 383, 31–41. [Google Scholar] [CrossRef]
- Kokta, B.V.; Chen, R.; Daneault, C.; Valade, J.L. Use of wood fibers in thermoplastic composite. Polym. Compos. 1983, 4, 229–232. [Google Scholar] [CrossRef]
- Woodhams, R.T.; Thomas, G.; Rodgers, D.K. Wood fibers as reinforcing fillers for polyolefins. Plym. Eng. Sci. 1984, 24, 1166–1171. [Google Scholar] [CrossRef]
- Borůvka, V.; Zeidler, A.; Holeček, T.; Dudík, R. Elastic and strength properties of heat-treated beech and birch wood. Forests 2018, 9, 197. [Google Scholar] [CrossRef]
- Derikvand, M.; Kotlarewski, N.; Lee, M.; Jiao, H.; Nolan, G. Characterisation of physical and mechanical properties of unthinned and unpruned plantation-grown eucalyptus nitens H. Deane & Maiden Lumber. Forests 2019, 10, 194. [Google Scholar]
- Okai, R.; Frimpong-Mensah, K.; Yeboah, D. Characterization of strength properties of branchwood and stemwood of some tropical hardwood species. Wood Sci. Technol. 2004, 38, 163–171. [Google Scholar] [CrossRef]
- Kolsky, H. An investigation of the mechanical properties of materials at very high rates of loading. Proc. Phys. Soc. B 1949, 62, 676–700. [Google Scholar] [CrossRef]
- Wu, Y.; Song, W.; Zhao, W.; Tan, X. An experimental study on dynamic mechanical properties of fiber-reinforced concrete under different strain rates. Appl. Sci. 2018, 8, 1904. [Google Scholar] [CrossRef]
- Xia, K.; Nasseri, M.H.B.; Mohanty, B.; Lu, F.; Chen, R.; Luo, S.N. Effects of microstructures on dynamic compression of Barre granite. Int. J. Rock Mech. Min. 2008, 45, 879–887. [Google Scholar] [CrossRef]
- Chen, W.; Song, B.; Frew, D.J.; Forrestal, M.J. Dynamic small strain measurements of a metal specimen with a split Hopkinson pressure bar. Exp. Mech. 2003, 43, 20–23. [Google Scholar] [CrossRef]
- Sankaye, S.S. Dynamic Testing to Determine Some Mechanical Properties of Aluminum, Copper, and Dry Eglin Sand Using Split Hopkinson Pressure Bar (SHPB), High Speed Photography and Digital Image Correlation (DIC). Master’s Thesis, Oklahoma State University, Stillwater Oklahoma, OK, USA, 2001. [Google Scholar]
- Hu, D.; Song, B.; Dang, L.; Zhang, Z. Effect of strain rate on mechanical properties of the bamboo material under quasi-static and dynamic loading condition. Compos. Struct. 2018, 200, 635–646. [Google Scholar] [CrossRef]
- Wouts, J.; Haugou, G.; Oudjene, M.; Coutellier, D.; Morvan, H. Strain rate effects on the compressive response of wood and energy absorption capabilities—Part A: Experimental investigations. Compos. Struct. 2016, 149, 315–328. [Google Scholar] [CrossRef]
- Reid, S.R.; Peng, C. Dynamic uniaxial crushing of wood. Int. J. Impact Eng. 1997, 19, 531–570. [Google Scholar] [CrossRef]
- Renaud, M.; Rueff, M.; Rocaboy, A.C. Mechanical behavior of saturated wood under compression. Wood Sci. Tehchnol. 1996, 30, 153–164. [Google Scholar]
- Widehammar, S. Stress-strain relationships for spruce wood: Influence of strain rate, moisture content and loading direction. Exp. Mech. 2004, 44, 44–48. [Google Scholar] [CrossRef]
- Tagarielli, V.L.; Deshpande, V.S.; Fleck, N.A. The high strain rate response of PVC foams and end-grain balsa wood. Compos. Part B Eng. 2008, 39, 83–91. [Google Scholar] [CrossRef]
- Moilanen, C.S.; Björkqvist, T.; Engberg, B.A.; Salminen, L.I.; Saarenrinne, P. High strain rate radial compression of Norway spruce earlywood and latewood. Cellulose 2016, 23, 873–889. [Google Scholar] [CrossRef]
- Wouts, J.; Haugou, G.; Oudjene, M.; Coutellier, D.; Morvan, H. Strain rate effects on the compressive response of wood and energy absorption capabilities—Part B: Experimental investigation under rigid lateral confinement. Compos. Struct. 2018, 204, 95–104. [Google Scholar] [CrossRef]






| Test Condition | Loading Strain Rate (s−1) | Yield Stress (MPa) | Ultimate Stress (MPa) |
|---|---|---|---|
| QTLD | 3.33 × 10−3 | 44.9 | - |
| DTLD | 800 | 78.4 | 83.94 |
| 1200 | 97.8 | 103.5 | |
| 1800 | 107.6 | 112.4 | |
| 2000 | 114.1 | 119 | |
| QTRD | 3.33 × 10−3 | 8.12 | - |
| DTRD | 800 | 8.52 | 12.7 |
| 1200 | 10.3 | 16.6 | |
| 1800 | 17.5 | 26.17 | |
| 2000 | 20.6 | 32.26 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pang, S.; Liang, Y.; Tao, W.; Liu, Y.; Huan, S.; Qin, H. Effect of the Strain Rate and Fiber Direction on the Dynamic Mechanical Properties of Beech Wood. Forests 2019, 10, 881. https://doi.org/10.3390/f10100881
Pang S, Liang Y, Tao W, Liu Y, Huan S, Qin H. Effect of the Strain Rate and Fiber Direction on the Dynamic Mechanical Properties of Beech Wood. Forests. 2019; 10(10):881. https://doi.org/10.3390/f10100881
Chicago/Turabian StylePang, Shumeng, Yingjing Liang, Weijun Tao, Yijie Liu, Shi Huan, and Hongfa Qin. 2019. "Effect of the Strain Rate and Fiber Direction on the Dynamic Mechanical Properties of Beech Wood" Forests 10, no. 10: 881. https://doi.org/10.3390/f10100881
APA StylePang, S., Liang, Y., Tao, W., Liu, Y., Huan, S., & Qin, H. (2019). Effect of the Strain Rate and Fiber Direction on the Dynamic Mechanical Properties of Beech Wood. Forests, 10(10), 881. https://doi.org/10.3390/f10100881




