Site-Specific Allometric Models for Prediction of Above-and Belowground Biomass of Subtropical Forests in Guangzhou, Southern China
Abstract
:1. Introduction
2. Materials and Methods
2.1. The Experimental Site
2.2. Sample Tree Selection
2.3. Tree Biomass Measurement
2.4. Allometric Model Development and Evaluation
3. Results
3.1. Biomass Allocation Patterns and Correlations with DBH
3.2. Wood Density and Correlation with DBH
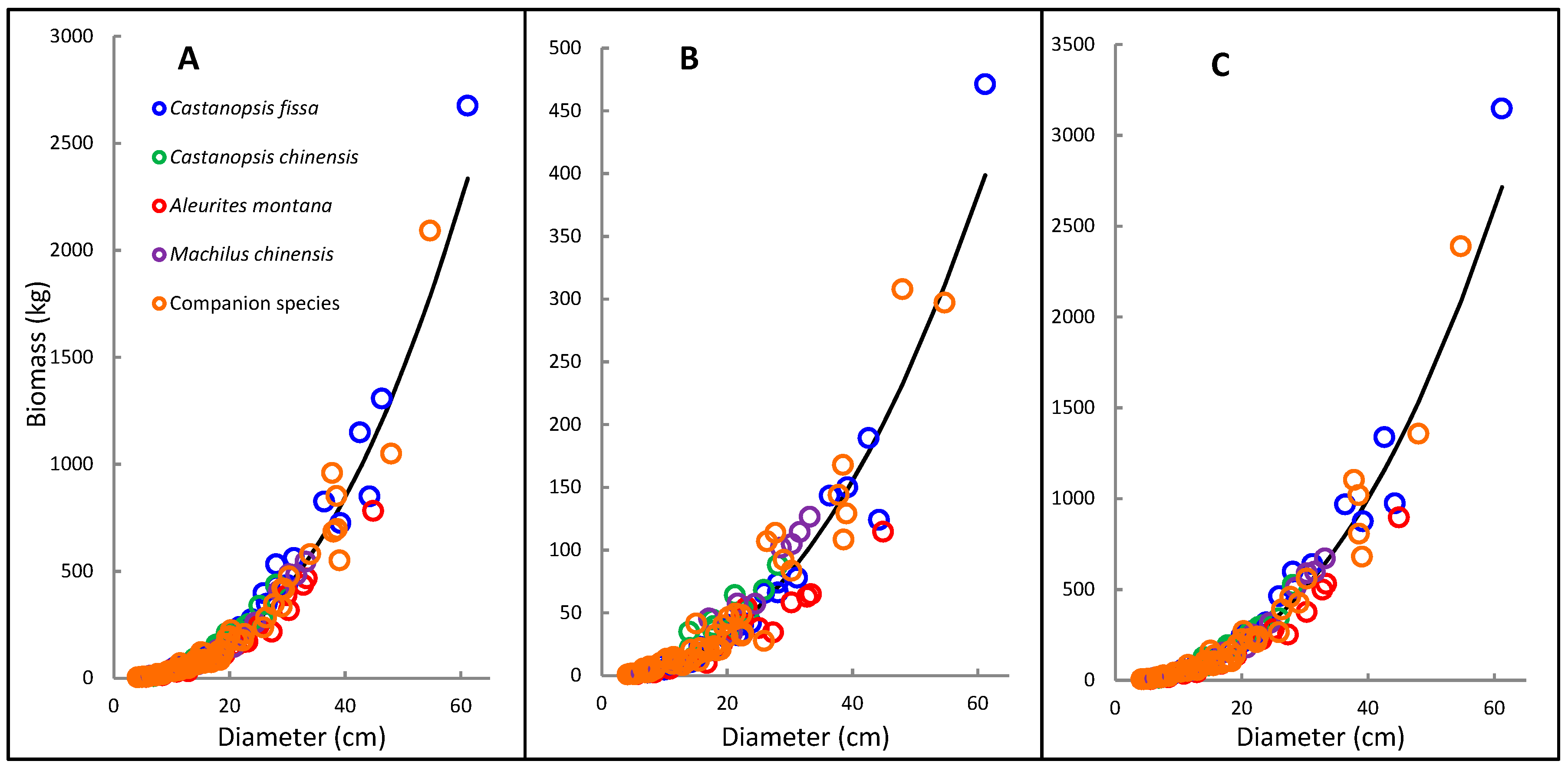
3.3. Allometric Models for Biomass Estimation with Different Variables
4. Discussion
4.1. Effect of Adding Tree Height on Biomass Estimation
4.2. Effect of Adding Wood Density on Biomass Estimation
4.3. Belowground Biomass
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Components | Regression Model | Coefficient Symbol | VIF | SEE | R2 | RMSE | CV (%) | Bias (%) | ||
|---|---|---|---|---|---|---|---|---|---|---|
| a | b | c | ||||||||
| Stem | (1) | −2.202 ± 0.1 | 1.138 ± 0.017 | 0.529 | 0.933 | 53.8 | 35.02 | −2.65 | ||
| (2) | −3.364 ± 0.1 | 0.927 ± 0.012 | 0.195 | 0.932 | 54.2 | 35.32 | −1.91 | |||
| (3) | −3.112 ± 0.147 | 0.979 ± 0.025 | 0.712 ± 0.094 | 3.114 | 0.501 | 0.940 | 51.0 | 33.22 | −1.85 | |
| (4) | −1.494 ± 0.094 | 1.155 ± 0.018 | 0.403 | 0.939 | 51.3 | 33.43 | −2.98 | |||
| (5) | −1.933 ± 0.119 | 1.15 ± 0.017 | 0.483 ± 0.127 | 1.036 | 0.240 | 0.948 | 47.1 | 30.67 | −2.40 | |
| Branch | (1) | −4.342 ± 0.187 | 1.352 ± 0.032 | 0.000 | 0.881 | 45.3 | 53.35 | −9.93 | ||
| (2) | −5.499 ± 0.268 | 1.075 ± 0.032 | 0.000 | 0.771 | 62.9 | 74.11 | −15.13 | |||
| (3) | −3.202 ± 0.305 | 1.551 ± 0.053 | −0.891 ± 0.195 | 3.114 | 0.000 | 0.898 | 41.9 | 49.41 | −8.74 | |
| (4) | −3.528 ± 0.162 | 1.378 ± 0.031 | 0.000 | 0.810 | 57.3 | 67.59 | −9.10 | |||
| (5) | −3.846 ± 0.223 | 1.374 ± 0.031 | 0.891 ± 0.238 | 1.036 | 0.000 | 0.854 | 50.3 | 59.25 | −8.92 | |
| Leaf | (1) | −4.156 ± 0.226 | 1.092 ± 0.039 | 0.491 | 0.689 | 17.1 | 89.84 | −15.92 | ||
| (2) | −5.075 ± 0.295 | 0.866 ± 0.035 | 0.417 | 0.574 | 20.0 | 105.10 | −19.48 | |||
| (3) | −3.078 ± 0.378 | 1.28 ± 0.066 | −0.843 ± 0.242 | 3.114 | 0.220 | 0.756 | 15.1 | 79.61 | −14.88 | |
| (4) | −3.54 ± 0.191 | 1.121 ± 0.037 | 0.492 | 0.781 | 14.3 | 75.30 | −14.16 | |||
| (5) | −3.493 ± 0.266 | 1.121 ± 0.037 | 1.192 ± 0.285 | 1.036 | 0.412 | 0.785 | 14.2 | 74.67 | −14.14 | |
References
- Houghton, R.A. Aboveground forest biomass and the global carbon balance. Glob. Chang. Biol. 2005, 11, 945–958. [Google Scholar] [CrossRef]
- Yu, G.; Chen, Z.; Piao, S.; Peng, C.; Ciais, P.; Wang, Q.; Li, X.; Zhu, X. High carbon dioxide uptake by subtropical forest ecosystems in the East Asian monsoon region. Proc. Natl. Acad. Sci. USA 2014, 111, 4910–4915. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brown, S. Measuring carbon in forests: Current status and future challenges. Environ. Pollut. 2002, 116, 363–372. [Google Scholar] [CrossRef]
- Xie, Y.; Sha, Z.; Yu, M. Remote sensing imagery in vegetation mapping: A review. J. Plant Ecol. 2008, 1, 9–23. [Google Scholar] [CrossRef]
- Molto, Q.; Rossi, V.; Blanc, L. Error propagation in biomass estimation in tropical forests. Methods Ecol. Evol. 2013, 4, 175–183. [Google Scholar] [CrossRef]
- Hossain, M.; Saha, C.; Abdullah, S.M.R.; Saha, S.; Siddique, M.R.H. Allometric biomass, nutrient and carbon stock models for Kandelia candel of the Sundarbans, Bangladesh. Trees 2016, 30, 709–717. [Google Scholar] [CrossRef]
- Henry, M.; Picard, N.; Trotta, C.; Manlay, R.J.; Valentini, R.; Bernoux, M.; Saintandré, L. Estimating tree biomass of sub-Saharan African forests: A review of available allometric equations. J. Physiol. 2011, 547, 963. [Google Scholar] [CrossRef]
- Ubuy, M.H.; Eid, T.; Bollandsås, O.M.; Birhane, E. Aboveground biomass models for trees and shrubs of exclosures in the drylands of Tigray, northern Ethiopia. J. Arid Environ. 2018, 156, 9–18. [Google Scholar] [CrossRef]
- Kuyah, S.; Sileshi, G.W.; Rosenstock, T.S. Allometric models based on bayesian frameworks give better estimates of aboveground biomass in the miombo woodlands. Forests 2016, 7, 13. [Google Scholar] [CrossRef]
- Picard, N.; Bosela, F.B.; Rossi, V. Reducing the error in biomass estimates strongly depends on model selection. Ann. For. Sci. 2015, 72, 811–823. [Google Scholar] [CrossRef]
- Roxburgh, S.H.; Paul, K.I.; Clifford, D.; England, J.R.; Raison, R.J. Guidelines for constructing allometric models for the prediction of woody biomass: How many individuals to harvest? Ecosphere 2016, 6, 1–27. [Google Scholar] [CrossRef]
- Basuki, T.M.; Laake, P.E.V.; Skidmore, A.K.; Hussin, Y.A. Allometric equations for estimating the above-ground biomass in tropical lowland Dipterocarp forests. For. Ecol. Manag. 2009, 257, 1684–1694. [Google Scholar] [CrossRef]
- Melson, S.L.; Harmon, M.E.; Fried, J.S.; Domingo, J.B. Estimates of live-tree carbon stores in the Pacific Northwest are sensitive to model selection. Carbon Balance Manag. 2011, 6, 2. [Google Scholar] [CrossRef] [PubMed]
- Chaturvedi, R.K.; Raghubanshi, A.S. Allometric models for accurate estimation of aboveground biomass of teak in tropical dry forests of India. For. Sci. 2015, 61, 938–949. [Google Scholar] [CrossRef]
- Mugasha, W.A.; Eid, T.; Bollandsås, O.M.; Malimbwi, R.E.; Chamshama, S.A.O.; Zahabu, E.; Katani, J.Z. Allometric models for prediction of above- and belowground biomass of trees in the miombo woodlands of Tanzania. For. Ecol. Manag. 2013, 310, 87–101. [Google Scholar] [CrossRef]
- Paul, K.I.; Roxburgh, S.H.; England, J.R.; Ritson, P.; Hobbs, T.; Brooksbank, K.; Raison, R.J.; Larmour, J.S.; Murphy, S.; Norris, J. Development and testing of allometric equations for estimating above-ground biomass of mixed-species environmental plantings. For. Ecol. Manag. 2013, 310, 483–494. [Google Scholar] [CrossRef]
- Huang, R.; Zhou, L.; Chen, W. The progresses of recent studies on the variabilities of the east Asian monsoon and their causes. Adv. Atmos. Sci. 2003, 20, 55–69. [Google Scholar] [CrossRef]
- Zhong, Z. The typical subtropical evergreen broadleaved forest of China. J. Southwest China Norm. Univ. 1987, 3, 109–121. [Google Scholar]
- Wang, X.H.; Kent, M.; Fang, X.F. Evergreen broad-leaved forest in Eastern China: Its ecology and conservation and the importance of resprouting in forest restoration. For. Ecol. Manag. 2007, 245, 76–87. [Google Scholar] [CrossRef]
- Fang, J.; Chen, A.; Peng, C.; Zhao, S.; Ci, L. Changes in forest biomass carbon storage in China between 1949 and 1998. Science 2001, 5525, 2320–2322. [Google Scholar] [CrossRef]
- Lin, D.; Lai, J.; Muller-Landau, H.C.; Mi, X.; Ma, K. Topographic variation in aboveground biomass in a subtropical evergreen broad-leaved forest in China. PLoS ONE 2012, 7, e48244. [Google Scholar] [CrossRef] [PubMed]
- Xiang, W.; Zhou, J.; Ouyang, S.; Zhang, S.; Lei, P.; Li, J.; Deng, X.; Fang, X.; Forrester, D.I. Species-specific and general allometric equations for estimating tree biomass components of subtropical forests in southern China. Eur. J. For. Res. 2016, 135, 1–17. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, J.; Franklin, S.B.; Liang, J.; Ding, P.; Luo, Y.; Lu, Z.; Bao, D.; Jiang, M. Improving allometry models to estimate the above- and belowground biomass of subtropical forest, China. Ecosphere 2015, 6, 1–15. [Google Scholar] [CrossRef]
- Chave, J.; Réjouméchain, M.; Búrquez, A.; Chidumayo, E.; Colgan, M.S.; Delitti, W.B.; Duque, A.; Eid, T.; Fearnside, P.M.; Goodman, R.C. Improved allometric models to estimate the aboveground biomass of tropical trees. Glob. Chang. Biol. 2014, 20, 3177–3190. [Google Scholar] [CrossRef] [PubMed]
- Zeng, W.; Fu, L.; Xu, M.; Wang, X.; Chen, Z.; Yao, S. Developing individual tree-based models for estimating aboveground biomass of five key coniferous species in China. J. For. Res. 2018, 29, 1251–1261. [Google Scholar] [CrossRef]
- Moussa, M.; Mahamane, L. Allometric models for estimating aboveground biomass and carbon in Faidherbia albida and Prosopis africana under agroforestry parklands in drylands of Niger. J. For. Res. 2018, 29, 1703–1717. [Google Scholar] [CrossRef]
- Gou, M.; Xiang, W.; Song, T.; Lei, P.; Zhang, S.; Ouyang, S.; Zeng, Y.; Deng, X.; Fang, X.; Wang, K. Allometric equations for applying plot inventory and remote sensing data to assess coarse root biomass energy in subtropical forests. Bioenergy Res. 2017, 10, 536–546. [Google Scholar] [CrossRef]
- Lin, K.; Lyu, M.; Jiang, M.; Chen, Y.; Li, Y.; Chen, G.; Xie, J.; Yang, Y. Improved allometric equations for estimating biomass of the three Castanopsis carlesii H. forest types in subtropical China. New For. 2017, 48, 1–21. [Google Scholar] [CrossRef]
- Brassard, B.W.; Chen, H.Y.H.; Bergeron, Y.; Paré, D. Coarse root biomass allometric equations for Abies balsamea, Picea mariana, Pinus banksiana, and Populus tremuloides in the boreal forest of Ontario, Canada. Biomass Bioenergy 2011, 35, 4189–4196. [Google Scholar] [CrossRef]
- Addo-Danso, S.D.; Prescott, C.E.; Smith, A.R. Methods for estimating root biomass and production in forest and woodland ecosystem carbon studies: A review. For. Ecol. Manag. 2016, 359, 332–351. [Google Scholar] [CrossRef]
- Carl, C.; Biber, P.; Landgraf, D.; Buras, A.; Pretzsch, H. Allometric models to predict aboveground woody biomass of black locust (Robinia pseudoacacia L.) in short rotation coppice in previous mining and agricultural areas in Germany. Forests 2017, 8, 328. [Google Scholar] [CrossRef]
- Peng, S.; He, N.; Yu, G.; Wang, Q. Aboveground biomass estimation at different scales for subtropical forests in China. Bot. Stud. 2017, 58, 45. [Google Scholar] [CrossRef] [PubMed]
- Zuur, A.F.; Ieno, E.N.; Elphick, C.S. A protocol for data exploration to avoid common statistical problems. Methods Ecol. Evol. 2010, 1, 3–14. [Google Scholar] [CrossRef]
- Ifo, A.S.; Gomat, H.Y.; Wenina, Y.E.M.; Lokegna, D.L.; Nzonzi, O.R.M.; Ngala, G.C.A.; Henry, M.; Boundzanga, G.C.; Jourdain, C.; Picard, N. Carbon stocks and tree allometries in the savannahs of the Plateau Batéké, central Africa. For. Ecol. Manag. 2018, 427, 86–95. [Google Scholar] [CrossRef]
- Zanne, A.E.; Lopez-Gonzalez, G.; Coomes, D.A.; Ilic, J.; Jansen, S.; Lewis, S.L.; Miller, R.B.; Swenson, N.G.; Wiemann, M.C.; Chave, J. Data from: Global wood density database. Dry. Digit. Repos. 2009. [Google Scholar] [CrossRef]
- Mcnicol, I.M.; Berry, N.J.; Bruun, T.B.; Hergoualc’h, K.; Mertz, O.; Neergaard, A.D.; Ryan, C.M. Development of allometric models for above and belowground biomass in swidden cultivation fallows of Northern Laos. For. Ecol. Manag. 2015, 357, 104–116. [Google Scholar] [CrossRef]
- Chave, J.; Andalo, C.; Brown, S.; Cairns, M.A.; Chambers, J.Q.; Eamus, D.; Fölster, H.; Fromard, F.; Higuchi, N.; Kira, T.; et al. Tree allometry and improved estimation of carbon stocks and balance in tropical forests. Oecologia 2005, 145, 87–99. [Google Scholar] [CrossRef]
- Feldpausch, T.R.; Lloyd, J.; Lewis, S.L.; Brienen, R.J.W.; Gloor, M.; Monteagudo Mendoza, A.; Lopez-Gonzalez, G.; Banin, L.; Abu Salim, K.; Affum-Baffoe, K.; et al. Tree height integrated into pantropical forest biomass estimates. Biogeosciences 2012, 9, 3381–3403. [Google Scholar] [CrossRef] [Green Version]
- Dutcă, I.; Mather, R.; Blujdea, V.N.B.; Ioraș, F.; Olari, M.; Abrudan, I.V. Site-effects on biomass allometric models for early growth plantations of Norway spruce (Picea abies (L.) Karst.). Biomass Bioenergy 2018, 116, 8–17. [Google Scholar] [CrossRef]
- Kuyah, S.; Dietz, J.; Muthuri, C.; Jamnadass, R.; Mwangi, P.; Coe, R.; Neufeldt, H. Allometric equations for estimating biomass in agricultural landscapes: I. Aboveground biomass. Agric. Ecosyst. Environ. 2012, 158, 216–224. [Google Scholar] [CrossRef]
- Bi, H.; Murphy, S.; Volkova, L.; Weston, C.; Fairman, T.; Li, Y.; Law, R.; Norris, J.; Lei, X.; Caccamo, G. Additive biomass equations based on complete weighing of sample trees for open eucalypt forest species in south-eastern Australia. For. Ecol. Manag. 2015, 349, 106–121. [Google Scholar] [CrossRef]
- Dormann, C.F.; Elith, J.; Bacher, S.; Buchmann, C.; Carl, G.; Carré, G.; Marquéz, J.R.G.; Gruber, B.; Lafourcade, B.; Leitão, P.J.; et al. Collinearity: A review of methods to deal with it and a simulation study evaluating their performance. Ecography 2013, 36, 27–46. [Google Scholar] [CrossRef]
- Ubuy, M.H.; Eid, T.; Bollandsas, O.M. Variation in wood basic density within and between tree species and site conditions of exclosures in Tigray, northern Ethiopia. Trees 2018, 32, 967–983. [Google Scholar] [CrossRef]
- Aalde, H.; Gonzalez, P.; Gytarsky, M.; Krug, T. 2006 IPCC Guidelines for National Greenhouse Gas Inventories, Volume 4: Agriculture, Forestry and Other Land Use; IPCC: Geneva, Switzerland, 2006. [Google Scholar]
- Koala, J.; Sawadogo, L.; Savadogo, P.; Aynekulu, E.; Heiskanen, J.; Saïd, M. Allometric equations for below-ground biomass of four key woody species in West African savanna-woodlands. Silva Fenn. 2017, 51, 1631. [Google Scholar] [CrossRef]
- Kachamba, J.D.; Eid, T.; Gobakken, T. Above- and belowground biomass models for trees in the miombo woodlands of Malawi. Forests 2016, 7, 38. [Google Scholar] [CrossRef]
- Vennetier, M.; Zanetti, C.; Meriaux, P.; Mary, B. Tree root architecture: New insights from a comprehensive study on dikes. Plant Soil 2015, 387, 81–101. [Google Scholar] [CrossRef]
- Kuyah, S.; Dietz, J.; Muthuri, C.; Jamnadass, R.; Mwangi, P.; Coe, R.; Neufeldt, H. Allometric equations for estimating biomass in agricultural landscapes: II. Belowground biomass. Agric. Ecosyst. Environ. 2012, 158, 225–234. [Google Scholar] [CrossRef]



| Species | Min DBH (cm) | Max DBH (cm) | <10 cm | 10–15 cm | 15–20 cm | 20–25 cm | 25–30 cm | >30 cm | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | B | A | B | A | B | A | B | A | B | A | B | |||
| Castanopsis fissa | 7.4 | 61.2 | 3 | 3 | 4 | 3 | 5 | 5 | 6 | 6 | 4 | 3 | 8 | 6 |
| Aleurites montana | 5.6 | 44.9 | 3 | 2 | 2 | 2 | 2 | 2 | 4 | 2 | 3 | 2 | 4 | 4 |
| Castanopsis chinensis | 6.9 | 28.1 | 1 | 1 | 4 | 3 | 4 | 3 | 5 | 4 | 3 | 2 | 0 | 0 |
| Machilus chinensis | 6.3 | 33.2 | 2 | 2 | 3 | 1 | 2 | 1 | 3 | 3 | 1 | 1 | 3 | 3 |
| Ormosia semicastrata | 5.9 | 27.7 | 2 | 0 | 2 | 0 | 4 | 1 | 1 | 1 | 2 | 2 | 0 | 0 |
| Canarium pimela | 7.2 | 48.0 | 1 | 1 | 1 | 1 | 2 | 1 | 0 | 0 | 1 | 1 | 4 | 4 |
| Sapium discolor | 7.2 | 29.2 | 2 | 2 | 2 | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 |
| Euodia meliaefolia | 19.4 | 38.5 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 2 | 2 |
| Cratoxylum cochinchinense | 7.6 | 20.3 | 2 | 2 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| Sterculia lanceolata | 4.2 | 11.3 | 3 | 3 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Erythrina variegata | 12.4 | 15.6 | 0 | 0 | 2 | 2 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| Schefflera octophylla | 16.9 | 22.4 | 0 | 0 | 0 | 0 | 2 | 2 | 1 | 1 | 0 | 0 | 0 | 0 |
| Archidendron lucidum | 8.5 | 37.8 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| Cinnamomum camphora | 11.5 | 18.5 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Cinnamomum porrectum | 11.4 | 29.1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| Schima superba | 8.4 | 18.0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| Altingia chinensis | 34.0 | 34.0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| Cyclobalanopsis myrsinifolia | 22.6 | 22.6 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| Diospyros morrisiana | 4.5 | 4.5 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Elaeocarpus japonicus | 15.8 | 15.8 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| Engelhardtia roxburghiana | 38.0 | 38.0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| Eurya Thunb | 4.9 | 4.9 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Evodia lepta | 5.3 | 5.3 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Machilus breviflora | 14.3 | 14.3 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Sinosideroxylon pedunculatum | 54.7 | 54.7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| Wikstroemia nutans | 7.7 | 7.7 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Total | 4.2 | 61.2 | 25 | 22 | 24 | 18 | 29 | 22 | 24 | 21 | 17 | 12 | 25 | 21 |
| Species | Leaves Proportion | Branches Proportion | Stem Proportion | Roots Proportion |
|---|---|---|---|---|
| Castanopsis fissa | 0.177 | 0.460 * | −0.464 * | −0.017 |
| Castanopsis chinensis | 0.587 * | 0.823 ** | −0.657 * | −0.406 |
| Aleurites montana | −0.795 ** | 0.764 ** | −0.383 | −0.371 |
| Machilus chinensis | −0.743 ** | 0.502 | −0.267 | 0.059 |
| Companion species | −0.124 | 0.539 ** | −0.389 ** | −0.278 * |
| All species | −0.091 | 0.501 ** | −0.314 ** | −0.303 ** |
| Components | Regression Model | Coefficient Symbol | VIF | SEE | R2 | RMSE | CV (%) | Bias (%) | ||
|---|---|---|---|---|---|---|---|---|---|---|
| a | b | c | ||||||||
| Aboveground | (1) | −2.081 ± 0.086 | 1.195 ± 0.015 | 0.197 | 0.955 | 76.7 | 29.81 | −1.96 | ||
| (2) | −3.225 ± 0.122 | 0.965 ± 0.015 | 0.242 | 0.902 | 112.5 | 43.72 | −2.82 | |||
| (3) | −2.275 ± 0.148 | 1.161 ± 0.026 | 0.152 ± 0.095 | 3.114 | 0.196 | 0.952 | 78.7 | 30.58 | −1.91 | |
| (4) | −1.350 ± 0.074 | 1.216 ± 0.014 | 0.190 | 0.942 | 86.5 | 33.59 | −1.83 | |||
| (5) | −1.712 ± 0.093 | 1.212 ± 0.013 | 0.662 ± 0.100 | 1.036 | 0.173 | 0.964 | 68.7 | 26.68 | −1.48 | |
| Belowground | (1) | −3.151 ± 0.159 | 1.111 ± 0.027 | 0.341 | 0.914 | 19.5 | 38.49 | −5.84 | ||
| (2) | −4.248 ± 0.197 | 0.900 ± 0.023 | 0.359 | 0.892 | 21.9 | 43.24 | −6.43 | |||
| (3) | −3.440 ± 0.284 | 1.062 ± 0.048 | 0.223 ± 0.181 | 3.145 | 0.340 | 0.917 | 19.2 | 37.89 | −5.74 | |
| (4) | −2.514 ± 0.130 | 1.137 ± 0.025 | 0.310 | 0.920 | 18.8 | 37.10 | −4.72 | |||
| (5) | −2.644 ± 0.178 | 1.136 ± 0.025 | 0.936 ± 0.189 | 1.041 | 0.310 | 0.928 | 17.8 | 35.21 | −4.67 | |
| Total | (1) | −1.768 ± 0.099 | 1.176 ± 0.017 | 0.211 | 0.954 | 94.9 | 30.42 | −2.26 | ||
| (2) | −2.928 ± 0.134 | 0.953 ± 0.016 | 0.245 | 0.905 | 136.6 | 43.79 | −2.89 | |||
| (3) | −2.052 ± 0.174 | 1.128 ± 0.030 | 0.218 ± 0.111 | 3.145 | 0.208 | 0.951 | 98.4 | 31.56 | −2.15 | |
| (4) | −1.073 ± 0.080 | 1.200 ± 0.016 | 0.190 | 0.947 | 101.7 | 32.62 | −1.84 | |||
| (5) | −1.365 ± 0.102 | 1.196 ± 0.015 | 0.746 ± 0.108 | 1.041 | 0.178 | 0.966 | 82.1 | 26.32 | −1.57 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, H.; Li, Z.; Zhou, G.; Qiu, Z.; Wu, Z. Site-Specific Allometric Models for Prediction of Above-and Belowground Biomass of Subtropical Forests in Guangzhou, Southern China. Forests 2019, 10, 862. https://doi.org/10.3390/f10100862
Zhao H, Li Z, Zhou G, Qiu Z, Wu Z. Site-Specific Allometric Models for Prediction of Above-and Belowground Biomass of Subtropical Forests in Guangzhou, Southern China. Forests. 2019; 10(10):862. https://doi.org/10.3390/f10100862
Chicago/Turabian StyleZhao, Houben, Zhaojia Li, Guangyi Zhou, Zhijun Qiu, and Zhongmin Wu. 2019. "Site-Specific Allometric Models for Prediction of Above-and Belowground Biomass of Subtropical Forests in Guangzhou, Southern China" Forests 10, no. 10: 862. https://doi.org/10.3390/f10100862
APA StyleZhao, H., Li, Z., Zhou, G., Qiu, Z., & Wu, Z. (2019). Site-Specific Allometric Models for Prediction of Above-and Belowground Biomass of Subtropical Forests in Guangzhou, Southern China. Forests, 10(10), 862. https://doi.org/10.3390/f10100862




