Effects of Stand Age on Biomass Allocation and Allometry of Quercus Acutissima in the Central Loess Plateau of China
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Destructive Tree Sampling
2.3. Data Analysis
3. Results
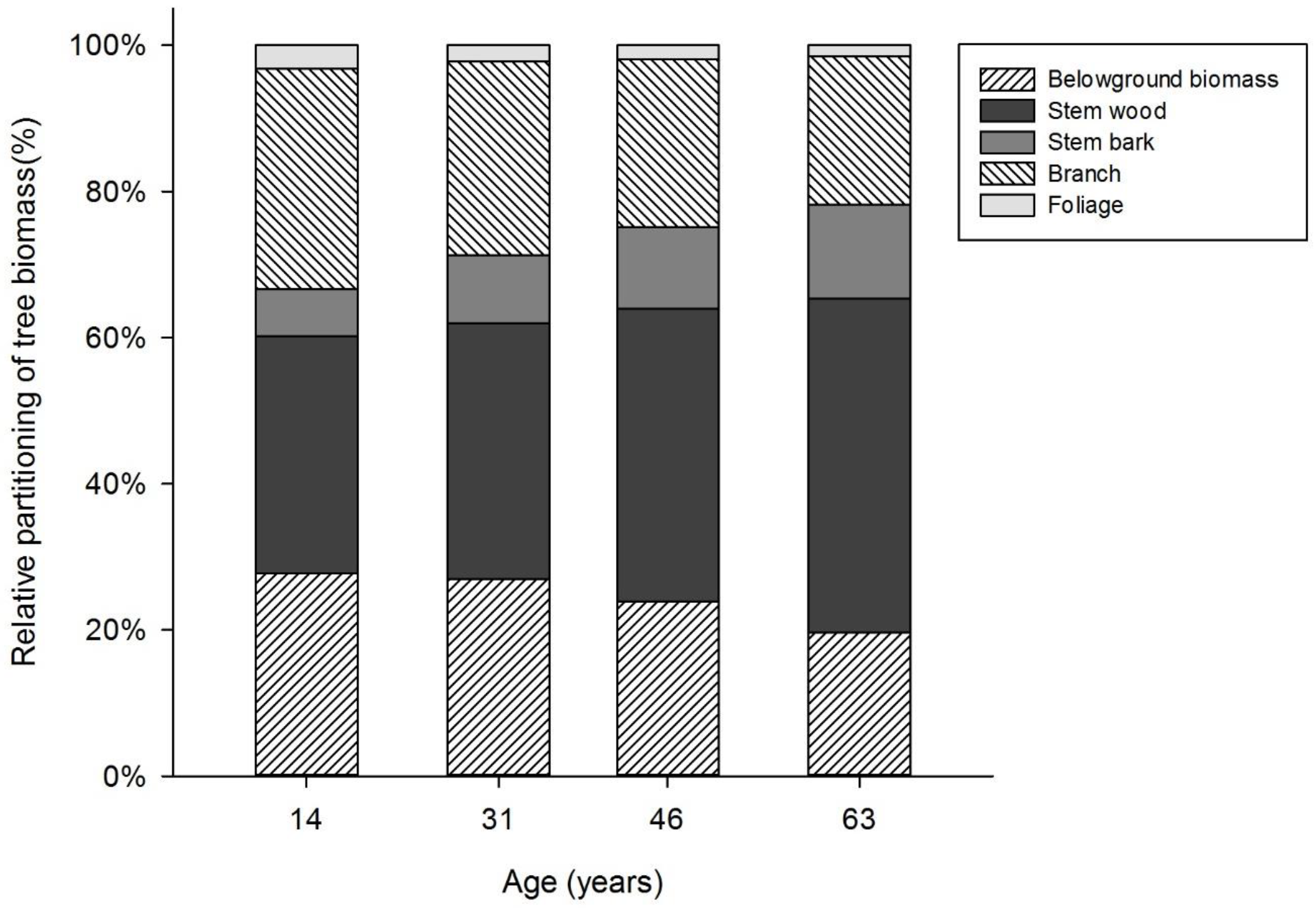
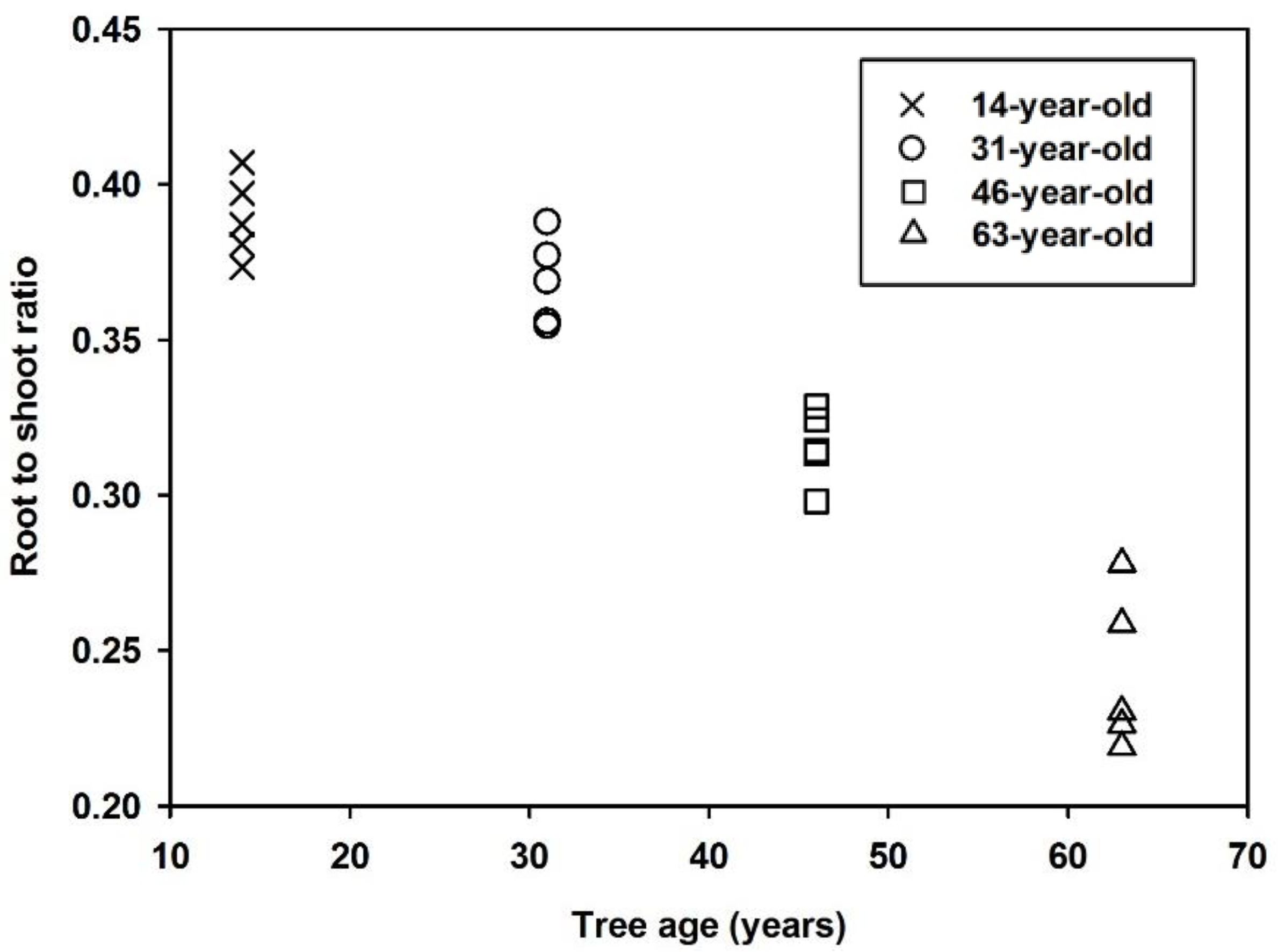
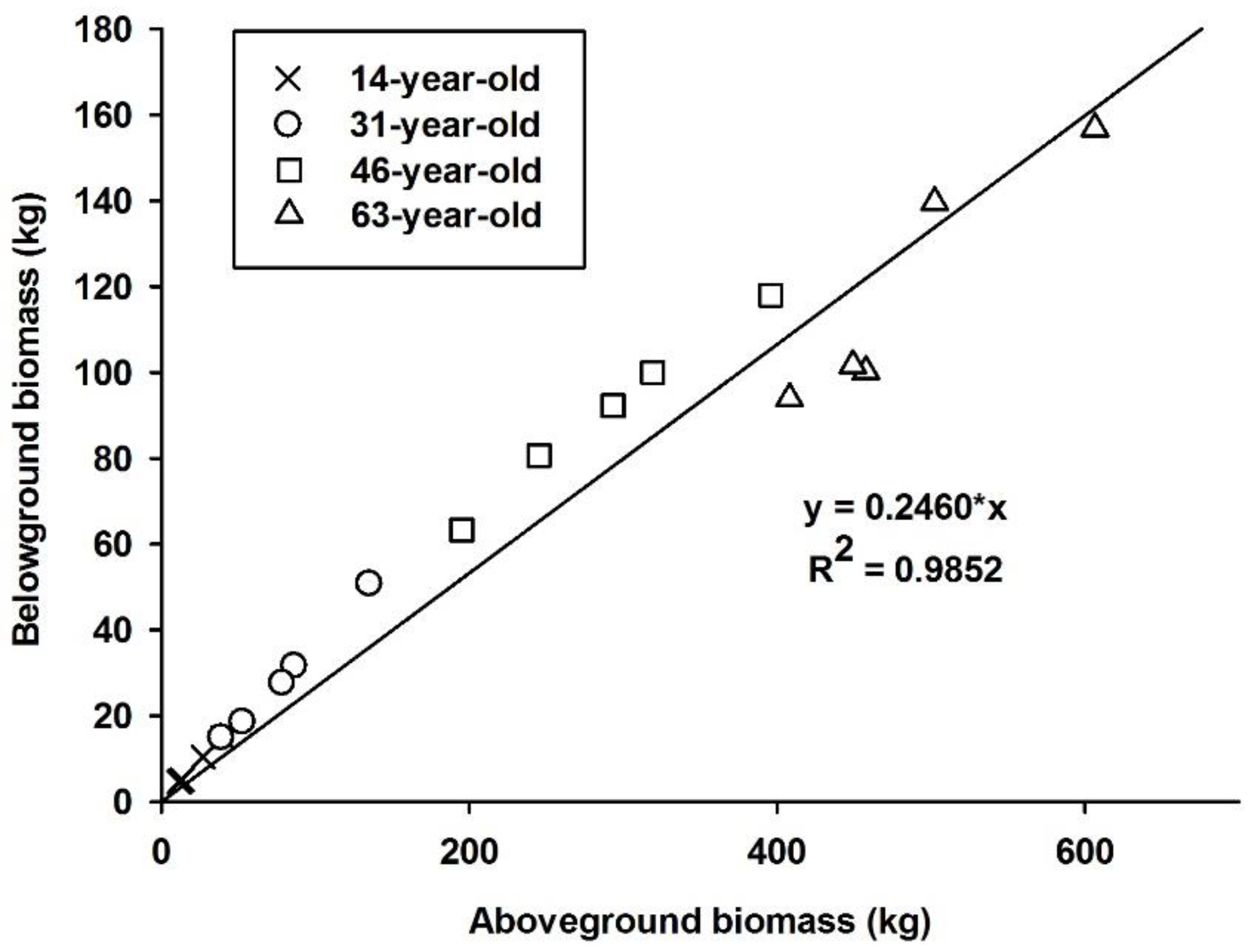
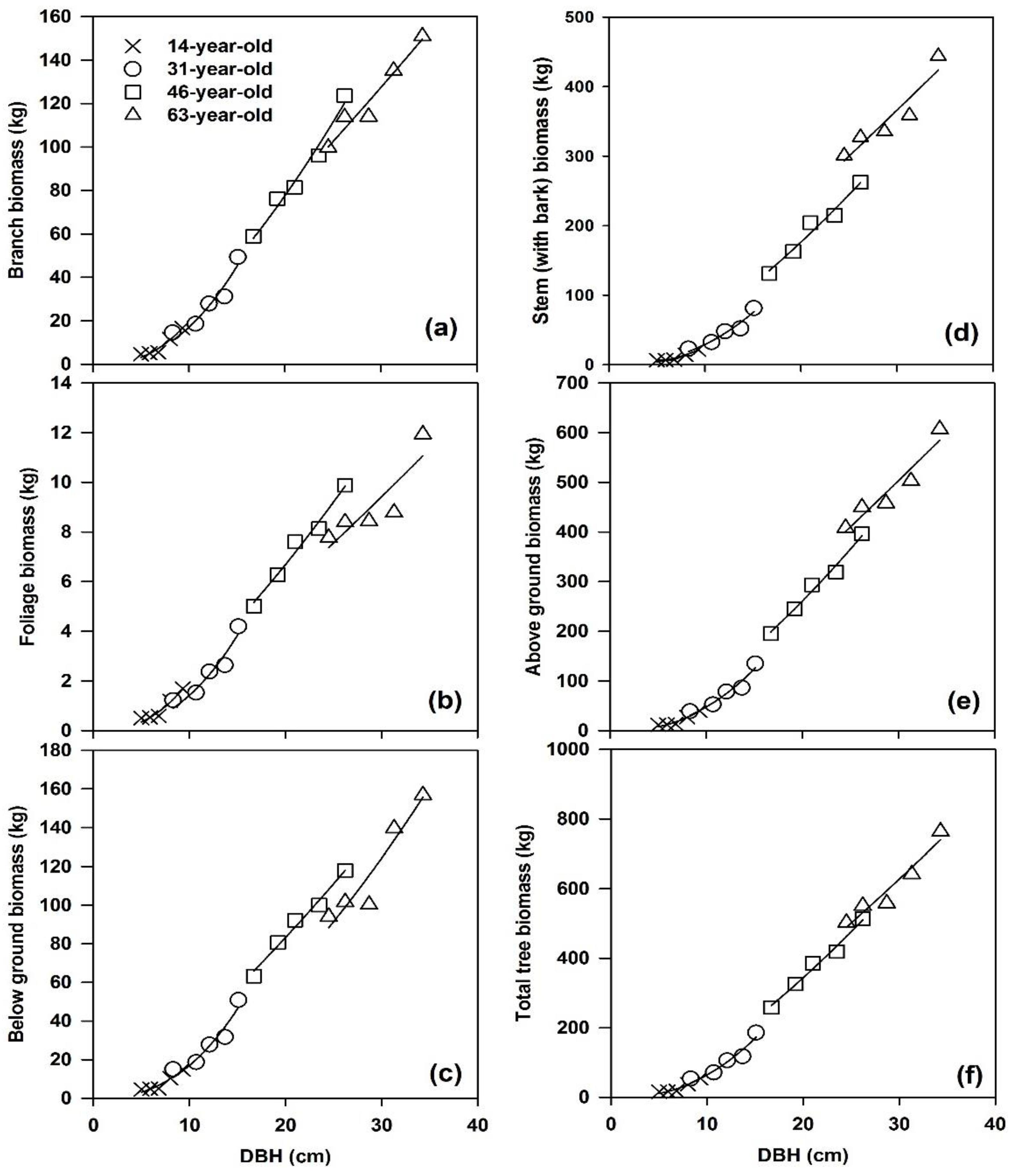
3.1. Biomass Allocation
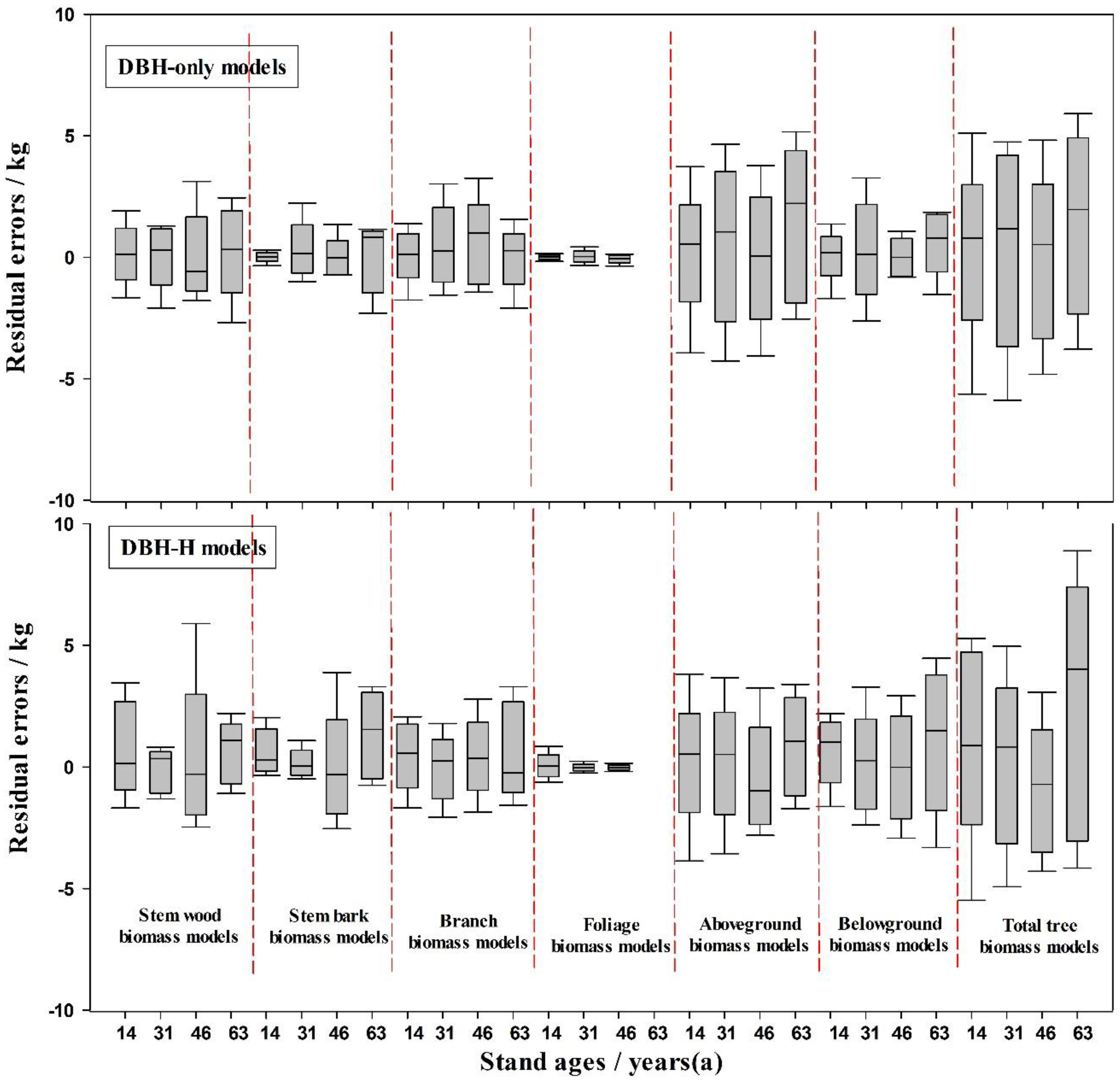
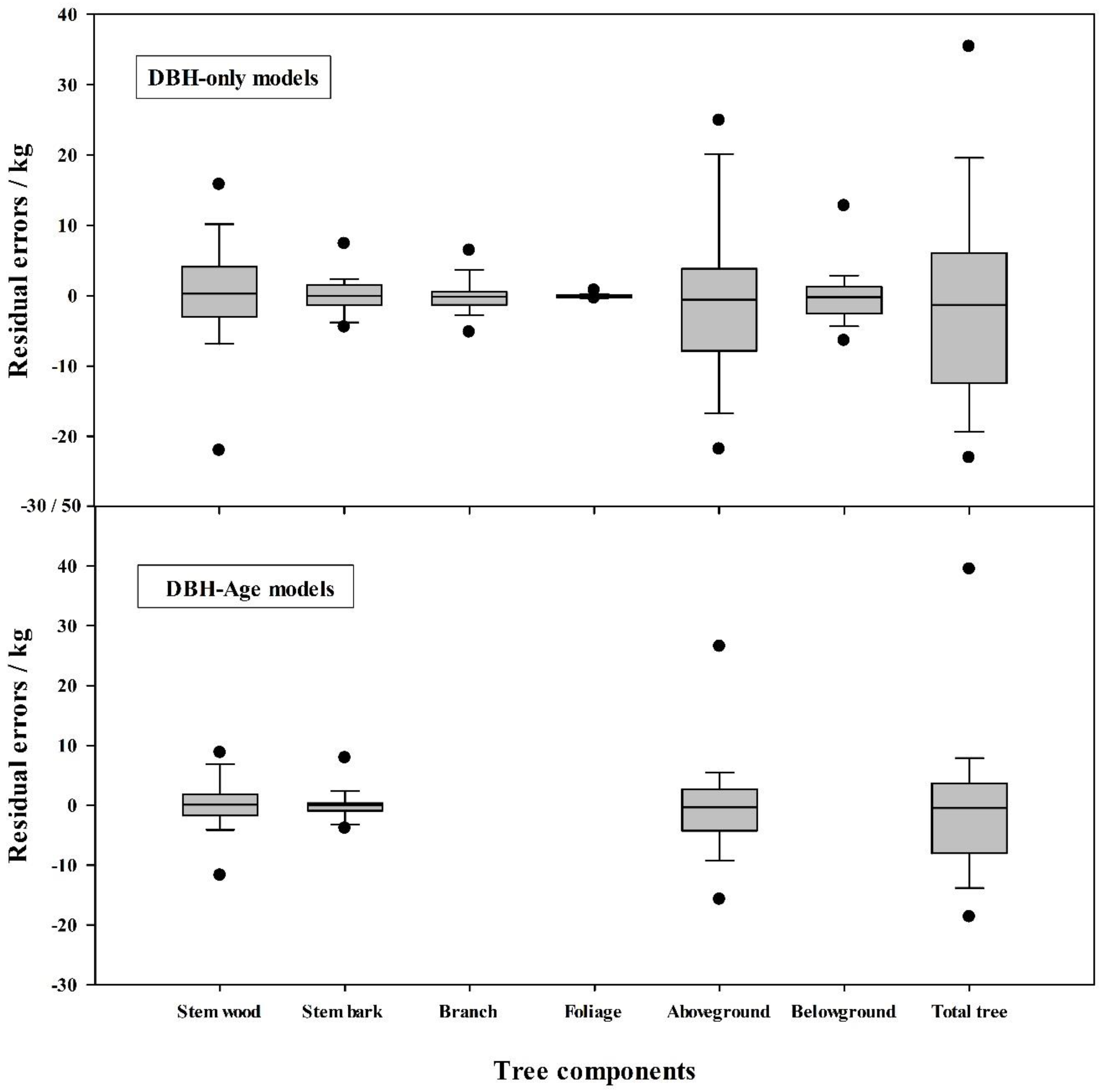
3.2. Effects of Stand Age on Biomass Equations
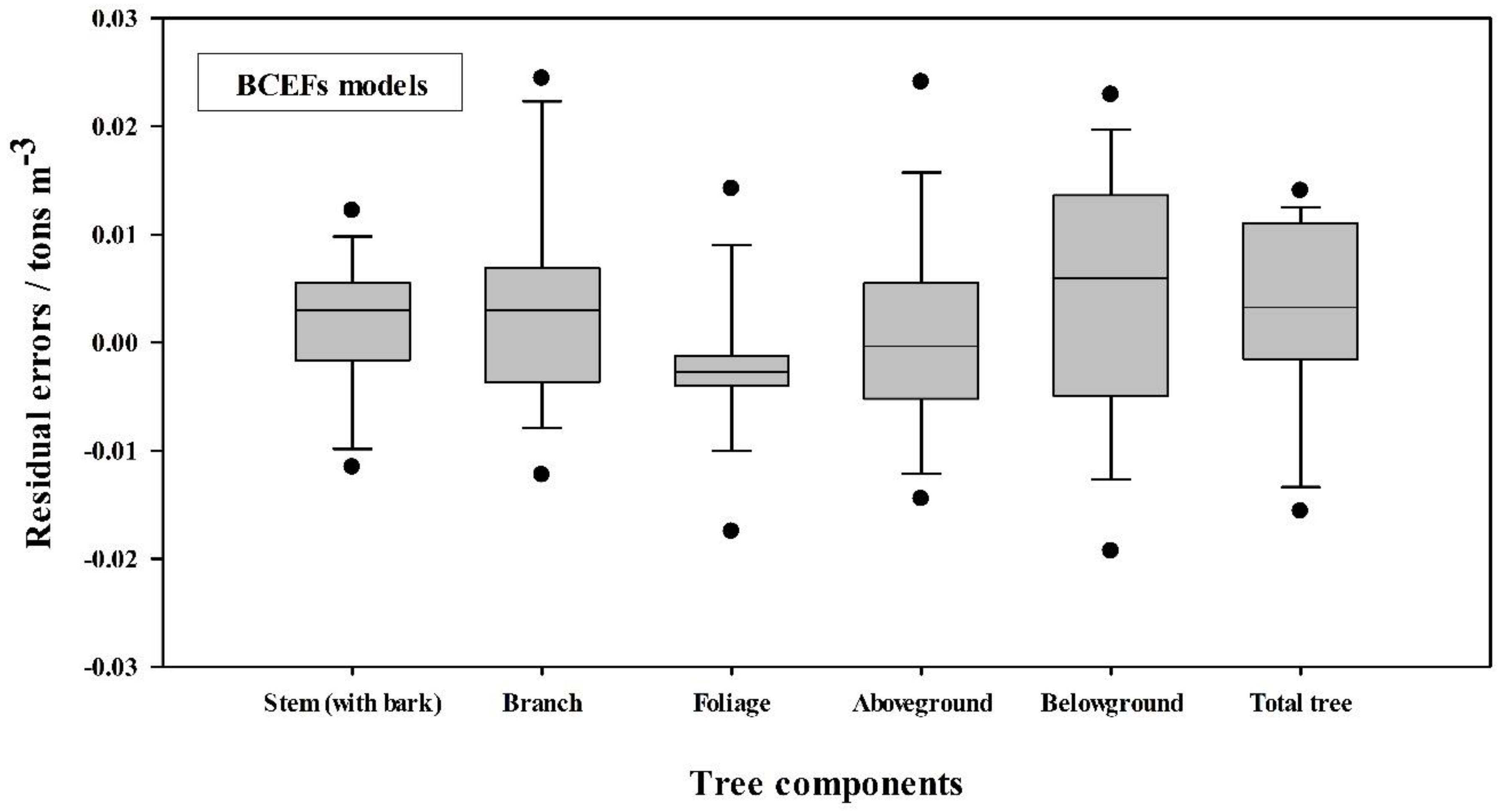
3.3. Effects of Stand Age on Biomass Conversion and Expansion Factors (BCEFs)
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Justine, M.F.; Yang, W.Q.; Wu, F.Z.; Tan, B.; Khan, M.N.; Zhao, Y.Y. Biomass stock and carbon sequestration in a chronosequence of Pinus massoniana plantations in the upper reaches of the Yangtze River. Forests 2015, 6, 3665–3682. [Google Scholar] [CrossRef]
- Yan, Y. Integrate carbon dynamic models in analyzing carbon sequestration impact of forest biomass harvest. Sci. Total Environ. 2018, 615, 581–587. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Song, T.Q.; Wang, K.L.; Du, H.; Yue, Y.M.; Wang, G.X.; Zeng, F.P. Biomass and carbon storage in an age-sequence of Cyclobalanopsis glauca plantations in southwest China. Ecol. Eng. 2014, 73, 184–191. [Google Scholar] [CrossRef]
- Peichl, M.; Arain, M.A. Allometry and partitioning of above- and belowground tree biomass in an age-sequence of white pine forests. For. Ecol. Manag. 2007, 253, 68–80. [Google Scholar] [CrossRef]
- Zhou, X.H.; Fu, Y.L.; Zhou, L.Y.; Li, B.; Luo, Y.Q. An imperative need for global change research in tropical forests. Tree Physiol. 2013, 33, 903–912. [Google Scholar] [CrossRef] [Green Version]
- Penman, J.; Gytarsky, M.; Hiraishi, T.; Krug, T.; Kruger, D.; Pipatti, R.; Buendia, L.; Miwa, K.; Ngara, T.; Tanabe, K. Good Practice Guidance for Land Use, Land-Use Change and Forestry; IPCC: Vienna, Austria, 2003; Volume 35, pp. 103–105. [Google Scholar]
- He, H.J.; Zhang, C.Y.; Zhao, X.H.; Fousseni, F.; Wang, J.S.; Dai, H.J.; Yang, S.; Zuo, Q. Allometric biomass equations for 12 tree species in coniferous and broadleaved mixed forests, Northeastern China. PLoS ONE 2018, 13, e0186226. [Google Scholar] [CrossRef]
- Dang, Y.; Wang, X.; Zeng, W. Using Segmented Modeling Approach to construct tree volume and biomass equations for larch in Northeastern China. For. Res. 2012, 25, 558–563. [Google Scholar]
- Zeng, M.; Nie, X.; Zeng, W. Compatible tree volume and aboveground biomass equations of Chinese Fir in China. Scientia Silvae Sinicae 2013, 49, 74–79. (In Chinese) [Google Scholar]
- Dong, L.H.; Zhang, L.J.; Li, F.R. Developing additive systems of biomass equations for nine hardwood species in Northeast China. Trees 2015, 29, 1149–1163. [Google Scholar] [CrossRef]
- Zou, W.T.; Zeng, W.S.; Zhang, L.J.; Zeng, M. Modeling crown biomass for four pine species in China. Forests 2015, 6, 433–449. [Google Scholar] [CrossRef]
- Zeng, W.S. Integrated individual tree biomass simultaneous equations for two larch species in northeastern and northern China. Scand. J. For. Res. 2015, 30, 594–604. [Google Scholar] [CrossRef]
- Zeng, W.S.; Fu, L.Y.; Xu, M.; Wang, X.J.; Chen, Z.X.; Yao, S.B. Developing individual tree-based models for estimating aboveground biomass of five key coniferous species in China. J. For. Res. 2018, 29, 1251–1261. [Google Scholar] [CrossRef]
- Meng, S.W.; Liu, Q.J.; Zhou, G.; Jia, Q.Q.; Zhuang, H.X.; Zhou, H. Aboveground tree additive biomass equations for two dominant deciduous tree species in Daxing’anling, northernmost China. J. For. Res. 2017, 22, 233–240. [Google Scholar] [CrossRef]
- Xue, Y.; Yang, Z.Y.; Wang, X.Y.; Lin, Z.P.; Li, D.X.; Su, S.F. Tree Biomass allocation and its model additivity for Casuarina equisetifolia in a tropical forest of Hainan Island, China. PLoS ONE 2016, 11, e0151858. [Google Scholar] [CrossRef] [PubMed]
- Dong, L.H.; Zhang, L.J.; Li, F.R. A three-step proportional weighting system of nonlinear biomass equations. For. Sci. 2015, 61, 35–45. [Google Scholar] [CrossRef]
- Tanhuanpaa, T.; Kankare, V.; Setlala, H.; Yli-Pelkonen, V.; Vastaranta, M.; Niemi, M.T.; Raisio, J.; Holopainen, M. Assessing above-ground biomass of open-grown urban trees: A comparison between existing models and a volume-based approach. Urban For. Urban Green. 2017, 21, 239–246. [Google Scholar] [CrossRef]
- Zeng, W.S. Using nonlinear mixed model and dummy variable model approaches to develop origin-based individual tree biomass equations. Trees 2015, 29, 275–283. [Google Scholar] [CrossRef]
- Wang, F.M.; Xu, X.; Zou, B.; Guo, Z.H.; Li, Z.A.; Zhu, W.X. Biomass accumulation and carbon sequestration in four different aged Casuarina equisetifolia coastal shelterbelt plantations in South China. PLoS ONE 2013, 8, e77449. [Google Scholar] [CrossRef]
- Lie, G.W.; Xue, L. Biomass allocation patterns in forests growing different climatic zones of China. Trees 2016, 30, 639–646. [Google Scholar] [CrossRef]
- Lehtonen, A.; Makipaa, R.; Heikkinen, J.; Sievanen, R.; Liski, J. Biomass expansion factors (BEFs) for Scots pine, Norway spruce and birch according to stand age for boreal forests. For. Ecol. Manag. 2004, 188, 211–224. [Google Scholar] [CrossRef] [Green Version]
- Konopka, B.; Patik, J.; Moravcik, M.; Lukac, M. Biomass partitioning and growth efficiency in four naturally regenerated forest tree species. Basic Appl. Ecol. 2010, 11, 234–243. [Google Scholar] [CrossRef]
- Mensah, S.; Veldtman, R.; du Toit, B.; Kakai, R.G.; Seifert, T. Aboveground biomass and carbon in a South African mistbelt forest and the relationships with tree species diversity and forest structures. Forests 2016, 7, 79. [Google Scholar] [CrossRef]
- Diedhiou, I.; Diallo, D.; Mbengue, A.A.; Hernandez, R.R.; Bayala, R.; Dieme, R.; Diedhiou, P.M.; Sene, A. Allometric equations and carbon stocks in tree biomass of Jatropha curcas L. in Senegal’s Peanut Basin. Glob. Ecol. Conserv. 2017, 9, 61–69. [Google Scholar] [CrossRef]
- Moore, J.R. Allometric equations to predict the total above-ground biomass of radiata pine trees. Ann. For. Sci. 2010, 67, 806. [Google Scholar] [CrossRef]
- Keller, M.; Palace, M.; Hurtt, G. Biomass estimation in the Tapajos National Forest, Brazil—Examination of sampling and allometric uncertainties. For. Ecol. Manag. 2001, 154, 371–382. [Google Scholar] [CrossRef]
- Xiang, W.H.; Liu, S.H.; Deng, X.W.; Shen, A.H.; Lei, X.D.; Tian, D.L.; Zhao, M.F.; Peng, C.H. General allometric equations and biomass allocation of Pinus massoniana trees on a regional scale in southern China. Ecol. Res. 2011, 26, 697–711. [Google Scholar] [CrossRef]
- Zianis, D.; Mencuccini, M. On simplifying allometric analyses of forest biomass. For. Ecol. Manag. 2004, 187, 311–332. [Google Scholar] [CrossRef] [Green Version]
- Morote, F.A.G.; Serrano, F.R.L.; Andres, M.; Rubio, E.; Jimenez, J.L.G.; de las Heras, J. Allometries, biomass stocks and biomass allocation in the thermophilic Spanish juniper woodlands of Southern Spain. For. Ecol. Manag. 2012, 270, 85–93. [Google Scholar] [CrossRef]
- Picard, N.; Rutishauser, E.; Ploton, P.; Ngomanda, A.; Henry, M. Should tree biomass allometry be restricted to power models? For. Ecol. Manag. 2015, 353, 156–163. [Google Scholar] [CrossRef]
- Gayon, J. History of the concept of allometry. Am. Zool. 2000, 40, 748–758. [Google Scholar] [CrossRef]
- Marquet, P.A.; Quinones, R.A.; Abades, S.; Labra, F.; Tognelli, M.; Arim, M.; Rivadeneira, M. Scaling and power-laws in ecological systems. J. Exp. Biol. 2005, 208, 1749–1769. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sileshi, G.W. A critical review of forest biomass estimation models, common mistakes and corrective measures. For. Ecol. Manag. 2014, 329, 237–254. [Google Scholar] [CrossRef]
- Jara, M.C.; Henry, M.; Rejou-Mechain, M.; Wayson, C.; Zapata-Cuartas, M.; Piotto, D.; Guier, F.A.; Lombis, H.C.; Lopez, E.C.; Lara, R.C.; et al. Guidelines for documenting and reporting tree allometric equations. Ann. For. Sci. 2015, 72, 763–768. [Google Scholar] [CrossRef]
- Winjum, J.K.; Brown, S.; Schlamadinger, B. Forest harvests and wood products: Sources and sinks of atmospheric carbon dioxide. For. Sci. 1998, 44, 272–284. [Google Scholar]
- Fang, J.Y.; Wang, Z.M. Forest biomass estimation at regional and global levels, with special reference to China’s forest biomass. Ecol. Res. 2001, 16, 587–592. [Google Scholar] [CrossRef]
- Tobin, B.; Nieuwenhuis, M. Biomass expansion factors for Sitka spruce (Picea sitchensis (Bong.) Carr.) in Ireland. Eur. J. For. Res. 2007, 126, 189–196. [Google Scholar] [CrossRef]
- Zhang, X.; Yao, L.I.; Fang, Y. Geographical distribution and prediction of potential ranges of Quercus acutissima in China. Acta Botanica Boreali-Occidentalia Sinica 2014, 34, 1685–1692. (In Chinese) [Google Scholar]
- Son, Y.; Park, I.H.; Yi, M.J.; Jin, H.O.; Kim, D.Y.; Kim, R.H.; Hwang, J.O. Biomass, production and nutrient distribution of a natural oak forest in central Korea. Ecol. Res. 2004, 19, 21–28. [Google Scholar] [CrossRef]
- Noh, N.J.; Son, Y.; Kim, R.H.; Seo, K.W.; Koo, J.W.; Park, I.H.; Lee, Y.J.; Lee, K.H.; Son, Y.M. Biomass accumulations and the distribution of nitrogen and phosphorus within three Quercus acutissima stands in Central Korea. J. Plant Biol. 2007, 50, 461–466. [Google Scholar] [CrossRef]
- Yuan, Y.F.; Guo, W.H.; Ding, W.J.; Du, N.; Luo, Y.J.; Liu, J.; Xu, F.; Wang, R.Q. Competitive interaction between the exotic plant Rhus typhina L. and the native tree Quercus acutissima Carr. in Northern China under different soil N:P ratios. Plant Soil 2013, 372, 389–400. [Google Scholar] [CrossRef]
- Chung, M.Y.; Nason, J.; Chung, M.G.; Kim, K.J.; Park, C.W.; Sun, B.Y.; Pak, J.H. Landscape-level spatial genetic structure in Quercus acutissima (Fagaceae). Am. J. Bot. 2002, 89, 1229–1236. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.Y.Y.; Fang, Y.M.M.; Yu, M.K.K.; Li, X.X.X.; Xia, T. Molecular characterization and genetic structure of Quercus acutissima germplasm in China using microsatellites. Mol. Biol. Rep. 2013, 40, 4083–4090. [Google Scholar] [CrossRef] [PubMed]
- Fang, S.Z.; Liu, Z.L.; Cao, Y.D.; Liu, D.; Yu, M.K.; Tang, L.Z. Sprout development, biomass accumulation and fuelwood characteristics from coppiced plantations of Quercus acutissima. Biomass Bioenergy 2011, 35, 3104–3114. [Google Scholar] [CrossRef]
- Wang, B.; Mu-Kui, Y.U.; Sun, H.J.; Cheng, X.R.; Shan, Q.H.; Fang, Y.M. Photosynthetic characters of Quercus acutissima from different provenances under effects of salt stress. Ying Yong Sheng Tai Xue Bao 2009, 20, 1817–1824. (In Chinese) [Google Scholar] [PubMed]
- Liao, J.; Fang, Y.M.; Mu-Kui, Y.U. Somatic embryogenesis and plant regeneration from mature embryo explants in Quercus acutissima Carr. Acta Botanica Boreali-Occidentalia Sinica 2012, 32, 398–402. (In Chinese) [Google Scholar]
- Cheng, Y.X.; Huo, A.D.; Zhang, J.; Lu, Y.D. Early warning of meteorological geohazard in the Loess Plateau: A study in Huangling County of Shaanxi Province in China. Environ. Earth Sci. 2015, 73, 1057–1065. [Google Scholar] [CrossRef]
- Chinese Standard GB/T 33027-2016. In Methodology for Field Long-Term Observation of Forest Ecosystem; Standards Press of China: Beijing, China, 2016.
- Ma, C.; Zhang, W.H.; Wu, M.; Xue, Y.Q.; Ma, L.W.; Zhou, J.Y. Effect of aboveground intervention on fine root mass, production, and turnover rate in a Chinese cork oak (Quercus variabilis Blume) forest. Plant Soil 2013, 368, 201–214. [Google Scholar] [CrossRef]
- Brassard, B.W.; Chen, H.Y.H.; Bergeron, Y.; Pare, D. Coarse root biomass allometric equations for Abies balsamea, Picea mariana, Pinus banksiana, and Populus tremuloides in the boreal forest of Ontario, Canada. Biomass Bioenergy 2011, 35, 4189–4196. [Google Scholar] [CrossRef]
- Zeng, W.; Tang, S. Goodness Evaluation and Precision Analysis of Tree Biomass Equations. Scientia Silvae Sinicae 2011, 47, 106–113. [Google Scholar]
- Dahlhausen, J.; Uhl, E.; Heym, M.; Biber, P.; Ventura, M.; Panzacchi, P.; Tonon, G.; Horvath, T.; Pretzsch, H. Stand density sensitive biomass functions for young oak trees at four different European sites. Trees 2017, 31, 1811–1826. [Google Scholar] [CrossRef]
- Huang, X.; Chonghua, X.U.; Jun, X.U.; Tao, X.; Xiaoniu, X.U. Structural equation model analysis of the relationship between environmental and stand factors and net primary productivity in Cunninghamia lanceolata forests. Acta Ecol. Sin. 2017, 37. (In Chinese) [Google Scholar]
- Helmisaari, H.S.; Makkonen, K.; Kellomaki, S.; Valtonen, E.; Malkonen, E. Below- and above-ground biomass, production and nitrogen use in Scots pine stands in eastern Finland. For. Ecol. Manag. 2002, 165, 317–326. [Google Scholar] [CrossRef]
- Mokany, K.; Raison, R.J.; Prokushkin, A.S. Critical analysis of root: Shoot ratios in terrestrial biomes. Glob. Chang. Biol. 2006, 12, 84–96. [Google Scholar] [CrossRef]
- Zhang, X.W.; Li, Y.; Liu, C.Y.; Xia, T.; Zhang, Q.; Fang, Y.M. Phylogeography of the temperate tree species Quercus acutissima in China: Inferences from chloroplast DNA variations. Biochem. Syst. Ecol. 2015, 63, 190–197. [Google Scholar] [CrossRef]
- Hu, T.; Sorensen, P.; Wahlstrom, E.M.; Chirinda, N.; Sharif, B.; Li, X.X.; Olesen, J.E. Root biomass in cereals, catch crops and weeds can be reliably estimated without considering aboveground biomass. Agric. Ecosyst. Environ. 2018, 251, 141–148. [Google Scholar] [CrossRef] [Green Version]
- Kalita, R.M.; Das, A.K.; Nath, A.J. Allometric equations for estimating above- and belowground biomass in Tea (Camellia sinensis (L.) O. Kuntze) agroforestry system of Barak Valley, Assam, northeast India. Biomass Bioenergy 2015, 83, 42–49. [Google Scholar] [CrossRef]
- Le Goff, N.; Ottorini, J.M. Root biomass and biomass increment in a beech (Fagus sylvatica L.) stand in North-East France. Ann. For. Sci. 2001, 58, 1–13. [Google Scholar] [CrossRef]
- Niklas, K.J.; Enquist, B.J. Canonical rules for plant organ biomass partitioning and annual allocation. Am. J. Bot. 2002, 89, 812–819. [Google Scholar] [CrossRef] [Green Version]
- Suchomel, C.; Pyttel, P.; Becker, G.; Bauhus, J. Biomass equations for sessile oak (Quercus petraea (Matt.) Liebl.) and hornbeam (Carpinus betulus L.) in aged coppiced forests in southwest Germany. Biomass Bioenergy 2012, 46, 722–730. [Google Scholar] [CrossRef]
- Jenkins, J.C.; Chojnacky, D.C.; Heath, L.S.; Birdsey, R.A. National-scale biomass estimators for United States tree species. For. Sci. 2003, 49, 12–35. [Google Scholar]
- Cienciala, E.; Cerny, M.; Tatarinov, F.; Apltauer, J.; Exnerova, Z. Biomass functions applicable to Scots pine. Trees 2006, 20, 483–495. [Google Scholar] [CrossRef]
- Kauppi, P.E.; Tomppo, E.; Ferm, A. C and N storage in living trees within Finland since 1950s. Plant Soil 1995, 168, 633–638. [Google Scholar] [CrossRef] [Green Version]
- Wang, B.; Gao, P.; Niu, X.; Sun, J.N. Policy-driven China’s Grain to Green Program: Implications for ecosystem services. Ecosyst. Serv. 2017, 27, 38–47. [Google Scholar] [CrossRef]
| Tree Component | Biomass (kg/tree) | |||
|---|---|---|---|---|
| 14 Years Old | 31 Years Old | 46 Years Old | 63 Years Old | |
| Stem wood | 9.33 ± 5.55 | 37.42 ± 17.96 | 152.71 ± 38.06 | 275.86 ± 41.85 |
| Stem bark | 1.85 ± 1.09 | 9.92 ± 4.48 | 42.48 ± 12.35 | 77.32 ± 13.32 |
| Branches | 8.70 ± 5.32 | 28.30 ± 13.54 | 87.23 ± 24.31 | 122.68 ± 20.25 |
| Foliage | 0.90 ± 0.52 | 2.39 ± 1.16 | 7.38 ± 1.85 | 9.06 ± 1.65 |
| Aboveground | 20.78 ± 12.48 | 78.02 ± 37.05 | 289.80 ± 76.02 | 484.91 ± 75.85 |
| Taproot | 2.49 ± 1.41 | 11.00 ± 5.79 | 41.49 ± 11.26 | 62.24 ± 17.40 |
| Large roots (≥2 cm) | 1.79 ± 1.04 | 6.06 ± 2.87 | 17.39 ± 3.82 | 21.59 ± 5.60 |
| Coarse roots (0.5–2 cm) | 2.34 ± 1.33 | 7.63 ± 3.47 | 21.43 ± 3.94 | 22.83 ± 2.92 |
| Small roots (0.2–0.5 cm) | 0.82 ± 0.47 | 2.52 ± 1.14 | 6.09 ± 1.00 | 7.02 ± 1.44 |
| Fine roots (<0.2 cm) | 0.55 ± 0.32 | 1.58 ± 0.76 | 4.43 ± 0.68 | 4.77 ± 0.88 |
| Belowground | 7.99 ± 4.57 | 28.79 ± 14.04 | 90.83 ± 20.54 | 118.46 ± 28.00 |
| Total tree | 28.76 ± 17.05 | 106.81 ± 51.07 | 380.63 ± 96.50 | 603.38 ± 102.68 |
| Tree Component | Variable (s) | Adj. R2 | S.E.E | c | a | S.E. (a) | b | S.E. (b) | Significance (p) | MPE (%) | TRE (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 14 years | |||||||||||
| Stem wood | DBH | 0.9277 | 1.4931 | 0.0504 | 2.6259 | 0.4148 | 0.0055 | 3.15 | 2.46 | ||
| DBH + H | 0.8915 | 1.8286 | 0.0494 | 2.5645 | 3.7563 | 0.0822 | 5.0362 | 0.0042 | 3.54 | 2.63 | |
| Stem bark | DBH | 0.9404 | 0.2668 | 0.0113 | 2.5682 | 0.3698 | 0.0041 | 2.97 | 2.73 | ||
| DBH + H | 0.9106 | 0.3268 | 0.0114 | 2.5956 | 3.3196 | −0.0367 | 4.4445 | 0.0447 | 3.48 | 3.78 | |
| Branch | DBH | 0.9372 | 1.3333 | 0.0445 | 2.6555 | 0.3970 | 0.0044 | 4.45 | 1.91 | ||
| DBH + H | 0.9064 | 1.6275 | 0.0514 | 3.0779 | 3.5687 | −0.5658 | 4.7543 | 0.0468 | 4.80 | 2.89 | |
| Foliage | DBH | 0.9350 | 0.1338 | 0.0060 | 2.5266 | 0.3782 | 0.0046 | 2.52 | 1.66 | ||
| DBH + H | 0.9025 | 0.1638 | 0.0059 | 2.4725 | 3.3818 | 0.0726 | 4.5323 | 0.0487 | 3.96 | 2.47 | |
| Aboveground | DBH | 0.9355 | 3.1684 | 0.1119 | 2.6289 | 0.3944 | 0.0046 | 3.54 | 3.16 | ||
| DBH + H | 0.9034 | 3.8788 | 0.1179 | 2.7828 | 3.5590 | −0.2060 | 4.7580 | 0.0483 | 4.80 | 4.15 | |
| Belowground | DBH | 0.9211 | 1.2842 | 0.0589 | 2.4759 | 0.4065 | 0.0062 | 1.20 | 2.9 | ||
| DBH + H | 0.8825 | 1.5671 | 0.0685 | 2.9255 | 3.5716 | −0.6014 | 4.7530 | 0.0087 | 2.04 | 2.98 | |
| Total tree | DBH | 0.9319 | 4.4500 | 0.1691 | 2.5862 | 0.3976 | 0.0050 | 1.94 | 3.1 | ||
| DBH + H | 0.8980 | 5.4444 | 0.1834 | 2.8255 | 3.5615 | −0.3204 | 4.7550 | 0.0051 | 4.88 | 3.12 | |
| 31 years | |||||||||||
| Stem wood | DBH | 0.9167 | 5.1817 | 0.0915 | 2.3940 | 0.4229 | 0.0068 | 1.88 | 3.64 | ||
| DBH + H | 0.9855 | 2.1653 | 0.0675 | 1.0405 | 0.4039 | 1.7623 | 0.4776 | 0.0073 | 1.52 | 2.23 | |
| Stem bark | DBH | 0.8842 | 1.5230 | 0.0475 | 2.1315 | 0.4483 | 0.0112 | 4.38 | 2.25 | ||
| DBH + H | 0.9283 | 1.1982 | 0.0337 | 0.9209 | 0.8297 | 1.6090 | 1.0015 | 0.0358 | 3.12 | −2.12 | |
| Branch | DBH | 0.8999 | 4.2822 | 0.0686 | 2.3967 | 0.4631 | 0.0089 | 2.83 | 3.82 | ||
| DBH + H | 0.9621 | 2.6360 | 0.0508 | 1.0287 | 0.6517 | 1.7777 | 0.7708 | 0.0190 | 2.40 | 2.43 | |
| Foliage | DBH | 0.8973 | 0.3732 | 0.0050 | 2.4539 | 0.4832 | 0.0093 | 2.80 | 3.79 | ||
| DBH + H | 0.9580 | 0.2388 | 0.0038 | 1.0548 | 0.7023 | 1.8083 | 0.8271 | 0.0210 | 2.48 | −3.78 | |
| Aboveground | DBH | 0.9107 | 11.0731 | 0.2076 | 2.3607 | 0.4312 | 0.0075 | 1.80 | 4.68 | ||
| DBH + H | 0.9767 | 5.6591 | 0.1523 | 1.0190 | 0.5057 | 1.7507 | 0.5996 | 0.0117 | 1.64 | 4.28 | |
| Belowground | DBH | 0.8936 | 4.5796 | 0.0581 | 2.4680 | 0.4930 | 0.0098 | 3.66 | 2.95 | ||
| DBH + H | 0.9541 | 3.0081 | 0.0438 | 1.0560 | 0.7349 | 1.8223 | 0.8647 | 0.0230 | 2.64 | 2.5 | |
| Total tree | DBH | 0.9067 | 15.6004 | 0.2644 | 2.3887 | 0.4461 | 0.0080 | 2.58 | 3.77 | ||
| DBH + H | 0.9716 | 8.5994 | 0.1952 | 1.0281 | 0.5626 | 1.7703 | 0.6657 | 0.0142 | 2.08 | 3.38 | |
| 46 years | |||||||||||
| Stem wood | DBH | 0.9633 | 7.2882 | 1.9630 | 1.4208 | 0.1438 | 0.0020 | 1.44 | −1.11 | ||
| DBH + H | 0.9621 | 7.4066 | 1.8512 | 1.1997 | 0.2772 | 0.2884 | 0.3067 | 0.0189 | 1.88 | −2.34 | |
| Stem bark | DBH | 0.9317 | 3.2261 | 0.2909 | 1.6252 | 0.2314 | 0.0050 | 2.32 | −3.79 | ||
| DBH + H | 0.9236 | 3.4121 | 0.2726 | 1.3057 | 0.4636 | 0.4092 | 0.5041 | 0.0382 | 2.88 | −3.95 | |
| Branch | DBH | 0.9694 | 4.2522 | 0.6056 | 1.6203 | 0.1487 | 0.0015 | 1.52 | 2.35 | ||
| DBH + H | 0.9801 | 3.4254 | 0.5663 | 1.3149 | 0.2267 | 0.3930 | 0.2466 | 0.0099 | 1.04 | −1.39 | |
| Foliage | DBH | 0.9711 | 0.3145 | 0.0916 | 1.4321 | 0.1284 | 0.0014 | 1.28 | 3.79 | ||
| DBH + H | 0.9740 | 0.2985 | 0.0864 | 1.2085 | 0.2312 | 0.2914 | 0.2556 | 0.0130 | 1.04 | −2.84 | |
| Aboveground | DBH | 0.9787 | 11.1010 | 2.8270 | 1.5103 | 0.1160 | 0.0009 | 1.20 | −3.53 | ||
| DBH + H | 0.9895 | 7.7734 | 2.6533 | 1.2491 | 0.1540 | 0.3384 | 0.1691 | 0.0052 | 0.72 | −2.35 | |
| Belowground | DBH | 0.9772 | 3.1031 | 1.7444 | 1.2904 | 0.1022 | 0.0010 | 1.04 | −2.34 | ||
| DBH + H | 0.9759 | 3.1906 | 1.6656 | 1.1368 | 0.1994 | 0.2025 | 0.2231 | 0.0121 | 1.88 | −3.7 | |
| Total tree | DBH | 0.9794 | 13.8416 | 4.3724 | 1.4573 | 0.1098 | 0.0008 | 1.12 | −3.4 | ||
| DBH + H | 0.9880 | 10.5871 | 4.1153 | 1.2215 | 0.1592 | 0.3068 | 0.1756 | 0.0060 | 0.72 | 2.15 | |
| 63 years | |||||||||||
| Stem wood | DBH | 0.8290 | 17.3042 | 7.7115 | 1.0621 | 0.2330 | 0.0203 | 1.92 | 4.23 | ||
| DBH + H | 0.9377 | 10.4483 | 6.5665 | 0.8865 | 0.1585 | 0.2719 | 0.1118 | 0.0312 | 0.96 | 3.93 | |
| Stem bark | DBH | 0.8169 | 5.6984 | 1.3325 | 1.2053 | 0.2744 | 0.0226 | 2.24 | 2.66 | ||
| DBH + H | 0.7381 | 6.8157 | 1.2739 | 1.1557 | 0.3668 | 0.0768 | 0.2485 | 0.0309 | 2.24 | 2.75 | |
| Branch | DBH | 0.9360 | 5.1241 | 2.1827 | 1.1960 | 0.1555 | 0.0045 | 1.28 | 2.47 | ||
| DBH + H | 0.9076 | 6.1552 | 2.2338 | 1.2212 | 0.2076 | −0.0391 | 0.1388 | 0.0462 | 1.28 | 2.49 | |
| Foliage | DBH | Not significant | |||||||||
| DBH + H | Not significant | ||||||||||
| Aboveground | DBH | 0.8898 | 25.1766 | 11.0850 | 1.1217 | 0.1930 | 0.0103 | 1.60 | 3.66 | ||
| DBH + H | 0.9017 | 23.7846 | 10.0729 | 1.0169 | 0.2043 | 0.1623 | 0.1413 | 0.0492 | 1.28 | 2.14 | |
| Belowground | DBH | 0.8700 | 10.0946 | 0.4063 | 1.6827 | 0.3208 | 0.0133 | 2.64 | 2.9 | ||
| DBH + H | 0.8412 | 11.1574 | 0.4337 | 1.8014 | 0.3974 | −0.1685 | 0.2463 | 0.0794 | 2.94 | 3.21 | |
| Total tree | DBH | 0.9119 | 30.4701 | 9.5113 | 1.2318 | 0.1881 | 0.0074 | 1.52 | 2.66 | ||
| DBH + H | 0.8876 | 34.4213 | 9.0247 | 1.1698 | 0.2378 | 0.0945 | 0.161 | 0.0062 | 1.84 | 3.22 | |
| Tree Component | Variable (s) | Adj. R2 | S.E.E. | c | a | S.E. (a) | b | S.E. (b) | Significance (p) | MPE (%) | TRE (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Stem wood | DBH | 0.9699 | 19.3445 | 0.4887 | 1.8672 | 0.1182 | <0.0001 | 3.15 | 1.86 | ||
| DBH + A | 0.9865 | 12.9381 | 0.1118 | 1.2795 | 0.1397 | 0.8464 | 0.1766 | <0.0001 | 2.9 | −0.62 | |
| Stem bark | DBH | 0.9720 | 5.3196 | 0.1081 | 1.9390 | 0.1195 | <0.0001 | 4.11 | −2.8 | ||
| DBH + A | 0.9838 | 4.0430 | 0.0297 | 1.4252 | 0.1575 | 0.7405 | 0.1984 | <0.0001 | 2.52 | −1.24 | |
| Branch | DBH | 0.9749 | 7.8268 | 0.7452 | 1.5208 | 0.0830 | <0.0001 | 2.6 | −2.44 | ||
| Foliage | DBH | 0.9424 | 0.8879 | 0.0965 | 1.3637 | 0.1115 | <0.0001 | 2.55 | −2.41 | ||
| Aboveground | DBH | 0.9781 | 28.9640 | 1.2282 | 1.7669 | 0.0937 | <0.0001 | 3.65 | 2.34 | ||
| DBH + A | 0.9856 | 23.4959 | 0.4908 | 1.3714 | 0.1399 | 0.5511 | 0.1717 | <0.0001 | 1.95 | −1.86 | |
| Belowground | DBH | 0.9600 | 9.8274 | 0.7773 | 1.5059 | 0.1041 | <0.0001 | 2.45 | 1.24 | ||
| Total tree | DBH | 0.9809 | 33.7310 | 1.8827 | 1.7094 | 0.0838 | <0.0001 | 3.05 | −2.48 | ||
| DBH + A | 0.9841 | 30.7497 | 1.0349 | 1.4361 | 0.1440 | 0.3722 | 0.1734 | <0.0001 | 2.1 | −1.24 |
| Tree Component | BCEFs (tons m−3) | |||
|---|---|---|---|---|
| 14 Years Old | 31 Years Old | 46 Years Old | 63 Years Old | |
| Stem (with bark) | 0.5182 ± 0.0151 | 0.4371 ± 0.0290 | 0.4048 ± 0.0158 | 0.4000 ± 0.0193 |
| Branch | 0.3988 ± 0.0190 | 0.2624 ± 0.0269 | 0.1807 ± 0.0139 | 0.1386 ± 0.0038 |
| Foliage | 0.0418 ± 0.0014 | 0.0220 ± 0.0024 | 0.0153 ± 0.0006 | 0.0102 ± 0.0007 |
| Aboveground | 0.9589 ± 0.0273 | 0.7216 ± 0.0576 | 0.6008 ± 0.0267 | 0.5488 ± 0.0212 |
| Belowground | 0.3733 ± 0.0223 | 0.2667 ± 0.0305 | 0.1896 ± 0.0077 | 0.1326 ± 0.0092 |
| Total tree | 1.3322 ± 0.0489 | 0.9882 ± 0.0877 | 0.7904 ± 0.0318 | 0.6815 ± 0.0159 |
| Tree Component | Equation Form | c | S.E. (c) | a | S.E. (a) | Adj. R2 | S.E.E. | Significance (p) | MPE (%) | TRE (%) |
|---|---|---|---|---|---|---|---|---|---|---|
| Stem (with bark) | Power | 0.8377 | 0.0523 | −0.1849 | 0.0181 | 0.8375 | 0.0210 | <0.01 | 0.32 | −0.12 |
| Branch | Power | 2.2627 | 0.2386 | −0.6525 | 0.0338 | 0.9548 | 0.0219 | <0.01 | 0.28 | 0.33 |
| Foliage | Power | 0.4119 | 0.0348 | −0.8649 | 0.0282 | 0.9835 | 0.0016 | <0.01 | 0.43 | 0.25 |
| Aboveground | Power | 2.6006 | 0.1591 | −0.3774 | 0.0185 | 0.9548 | 0.0352 | <0.01 | 0.18 | −0.11 |
| Belowground | Power | 1.8266 | 0.2460 | −0.5931 | 0.0426 | 0.9157 | 0.0274 | <0.01 | 0.11 | 0.15 |
| Total tree | Power | 4.2301 | 0.2993 | −0.4346 | 0.0216 | 0.9543 | 0.0553 | <0.01 | 0.15 | −0.35 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, B.; Xue, W.; Yu, S.; Zhou, J.; Zhang, W. Effects of Stand Age on Biomass Allocation and Allometry of Quercus Acutissima in the Central Loess Plateau of China. Forests 2019, 10, 41. https://doi.org/10.3390/f10010041
Yang B, Xue W, Yu S, Zhou J, Zhang W. Effects of Stand Age on Biomass Allocation and Allometry of Quercus Acutissima in the Central Loess Plateau of China. Forests. 2019; 10(1):41. https://doi.org/10.3390/f10010041
Chicago/Turabian StyleYang, Bin, Wenyan Xue, Shichuan Yu, Jianyun Zhou, and Wenhui Zhang. 2019. "Effects of Stand Age on Biomass Allocation and Allometry of Quercus Acutissima in the Central Loess Plateau of China" Forests 10, no. 1: 41. https://doi.org/10.3390/f10010041
APA StyleYang, B., Xue, W., Yu, S., Zhou, J., & Zhang, W. (2019). Effects of Stand Age on Biomass Allocation and Allometry of Quercus Acutissima in the Central Loess Plateau of China. Forests, 10(1), 41. https://doi.org/10.3390/f10010041





