Comparison of Different Algorithms to Orthorectify WorldView-2 Satellite Imagery

Abstract

Due to their level of spatial detail (pixel dimensions equal to or less than 1 m), very high-resolution satellite images (VHRSIs) need particular georeferencing and geometric corrections which require careful orthorectification. Although there are several dedicated algorithms, mainly commercial and free software for geographic information system (GIS) and remote sensing applications, the quality of the results may be inadequate in terms of the representation scale for which these images are intended. This paper compares the most common orthorectification algorithms in order to define the best approach for VHRSIs. Both empirical models (such as 2D polynomial functions, PFs; or 3D rational polynomial functions, RPFs) and rigorous physical and deterministic models (such as Toutin) are considered. Ground control points (GCPs) and check points (CPs)—whose positions in the image as, well as in the real world, are known—support algorithm applications. Tests were executed on a WorldView-2 (WV-2) panchromatic image of an area near the Gulf of Naples in Campania (Italy) to establish the best-performing algorithm. Combining 3D RPFs with 2D PFs produced the best results.

1. Introduction

Very high-resolution satellite images (VHRSIs) are widely used in several application fields, at both scientific and commercial levels, because of their detailed information (pixel dimensions equal to or less than 1 m in panchromatic band).

The geometric use of these images requires careful orientation and orthorectification in order to georeference the images and correct the geometric deformations introduced during acquisition [1].

Remotely sensed images contain such significant geometric distortions that they cannot be used directly with map-based products in a geographic information system (GIS) [2]. This characteristic is particularly pertinent to VHRSIs for several reasons (e.g., the reduced dimensions of the pixels and the off-nadir viewing).

Well-corrected and georeferenced VHRSIs such as IKONOS, WorldView-2 (WV-2), Quickbird, GeoEye, and Komposat are used for many purposes, i.e., map creation and updating, emergency mapping [3,4,5,6], vegetation mapping [7], coastline identification [8,9], etc. Production of high-resolution colored orthophotos can be achieved [10] by introducing pan-sharpening algorithms [11,12]. In the case of WV-2, the presence of eight multispectral bands instead of the traditional four provide a more powerful source of information, thus increasing thematic accuracy. Jawak et al. [13] demonstrate how WV-2 imagery, compared to previous sensors, improves the identification of land-cover targets, and consequently improves the land-cover classification.

To correct imagery geometric distortions, models and mathematical functions are necessary: either 2D/3D empirical models (such as 2D/3D polynomial or 3D rational polynomial functions, RPFs) or rigorous 2D/3D physical and deterministic models [2]. A physical model should model the platform (attitude, velocity, and altitude), sensor (field of view, panoramic effect), world (ellipsoid and 3D relief), and cartographic projection distortions [14].

Such 2D/3D empirical models can be used when the parameters of the acquisition systems or a rigorous 3D physical model are not available. In addition, they are based on different mathematical functions (2D or 3D polynomial functions, 3D rational functions) [15].

Physical models (also called rigorous models) are based on a standard photogrammetric approach, where the collinearity equations link the image and the ground coordinates, and the parameters involved have a physical meaning. In addition, knowledge regarding the sensor on the specific satellite and orbit characteristics is required [16].

These 2D/3D empirical models do not reflect the real physical condition of imaging, but they define it approximately. Three different sensor replacement models are defined in ISO 19130 “Geographic Information—Imagery Sensor Models for Geopositioning”: (1) simple polynomial fitting; (2) rational function model—RFM; and (3) universal sensor model—USM [14]. Simple polynomial fitting is useful only for low- and medium-resolution satellite images [17] and can be adopted for VHRSIs in small area mapping. In fact, we can also assume that the sensor moves linearly in space and that the attitude is almost unchanged [18]. The relationship between the position of a point on the image and the corresponding point on the object is represented by polynomial functions. The coefficients of each polynomial are computed using an appropriate number of ground control points (GCPs) with known locations (X, Y) on the map and easy detections (X’, Y’) in the image [19].

An RFM matches the image and object spaces through a ratio of two polynomial functions to compute the image row, and a similar ratio to compute the image column [20]. Also, in this case an appropriate number of GCPs is necessary to calculate the coefficients of each polynomial, named RPCs (rational polynomial coefficients). RPCs are widely adopted by image vendors and government agencies, who do not want to provide any satellite/sensor information with the image, and by commercial workstation suppliers; consequently, the various image vendors around the world provide third-order RF parameters [21]. RFMs have been used to approximate physical sensor models for many years due to their capability to maintain the full accuracy of different physical sensor models, their unique characteristic of sensor independence, and real-time calculation [22].

With USMs, an image scene is divided into multiple subdivisions or sections and RFM is applied to each section; the modified polynomials are of a variable order (up to the fifth power of the two horizontal coordinates and up to the third power for elevation); the denominator polynomials are usually omitted; image positional correction tables can be incorporated; and the ground coordinates can be expressed in any ground coordinate system [23].

Several applications about the use of 2D/3D empirical models as well as 2D/3D physical and deterministic models to orthorectify VHRSIs are available in literature. Chmiel et al. [24] compared rigorous approach and RFM to achieve the best geometric accuracy in orthorectified imagery products obtained from IKONOS (Geo Ortho-kit), QuickBird (Standard OrthoReady), and EROS 1A level data. Wolniewicz [25] analyzed the influence of the number and distribution of GCPs on the planimetric accuracy reached in the final QuickBird- and IKONOS-corrected panchromatic image using different orthorectification methods. Afify and Zhang [26] assessed the attainable geometric accuracies of RFMs applied to IKONOS and Quickbird images when user adjustments are introduced. Aguilar et al. [27] compared results recorded for IKONOS (Geo Ortho-kit) and QuickBird basic imagery, applying two different sensor models: (1) a 3D rational function refined by the user with zero- or first-order polynomial adjustment and (2) the 3D Toutin physical model. The influence of the number of GCPs on the geometric accuracy reached with RFM applied to GeoEye-1 images was analyzed by Maglione et al. [28].

This paper describes orthorectification that was conducted on WorldView-2 (WV-2) imagery using several algorithms which are available in common commercial and free software. Both rigorous and empirical approaches are considered and positional accuracies of the results are compared and discussed in order to define the best algorithm or the best combination. To our knowledge this, is the first work that compares several methods (including polynomial functions and rational functions, with variable number of GCPs) on WV-2 imagery. The paper is organized as follows. Section 2 describes the data and methods; various algorithms are applied to WV-2 imagery regarding the area around Vesuvius. Section 3 presents and discusses the results. Finally, Section 4 draws some conclusions.

2. Materials and Methods

2.1. WorldView2 Imagery

Launched in October 2009 by DigitalGlobe, the WV-2 satellite is positioned at an altitude of 770 km, with an orbit inclination of 97.2° and a period of 100 min. The revisited frequency is 1.1 days at nadir and 3.7 days at 20° off-nadir. The swath width, at nadir, is 16.4 km [29]. This satellite is part of DigitalGlobe’s constellation, which now also includes WorldView-3 [30,31,32]. The WV-2 satellite has two push-broom scanners which acquire panchromatic and multispectral images, respectively. The panchromatic images have a spatial resolution of 0.46 m, resampled to 0.50 m for commercial purposes, and the spectral interval is 0.450–0.800 μm. The multispectral images have a spatial resolution of 1.85 m, resampled to 2 m for commercial purposes; they are acquired in eight bands: Coastal (0.400–0.450 μm); Blue (0.450–0.510 μm); Green (0.510–0.580 μm); Yellow (0.585–0.625 μm); Red (0.630–0.690 μm); Red Edge (0.705–0.745 μm); Near-IR1 (0.770–0.895 μm); Near-IR2 (0.860–1.040 μm). The radiometric resolution for both panchromatic and multispectral images is 11 bits [29].

2.2. The Area Considered

In this study, WV-2 imagery concerning the area around Vesuvius (Campania, Italy) was considered (Figure 1). The dataset was acquired on 22 April 2015 and supplied by the provider as Ortho Ready Standard product (ORS2A), which means it had already been rectified using the average terrain elevation of the scene (low accuracy) [33]. The scene is georeferenced in the UTM/WGS84 33 N zone T coordinates system and extends from 40°46′22.06′′ north to 40°51′46.53′′ north in latitude and 14°20′2.74′′ east to 14°24′40.70′′ east in longitude.

This area is particularly interesting due to both its anthropological and natural features. In fact, most of the area is within the Vesuvius National Park, founded in 5 June 1995, which houses 610 vegetable species and 229 vertebrates and invertebrates [34]. The area also has one of the highest urban densities in Europe and includes the archeological remains of Pompeii, the ancient town that was destroyed by the eruption of Vesuvius in 79 AD. Thus, a high-performance VHRSI such as WV-2 would clearly support research activities in many fields, if corrected and georeferenced.

2.3. Algorithms for Orthorectification

In this section, several algorithms that are present in the software most commonly used for image orthorectification are described.

According to Toutin [2], whatever the mathematical functions used, the geometric correction method and processing steps are: acquisition of image; acquisition of the GCPs and check points (CPs) with image coordinates and map coordinates X, Y, Z; computation of the unknown parameters of the mathematical functions used for the geometric correction model; and image rectification with or without digital elevation model (DEM).

The two-dimensional (2D) polynomial model has been adopted for image rectification since the 1970s [35]. It relates images coordinates (X’, Y’) to cartographic coordinates (X, Y) by the following equations:

$$x\prime ={\displaystyle \sum _{i=0}^{m_1}{\displaystyle \sum _{j=0}^{m_2}{a}_{ij}}}{x}^i{y}^j,y\prime ={\displaystyle \sum _{i=0}^{m_1}{\displaystyle \sum _{j=0}^{m_2}{b}_{ij}}}{x}^i{y}^j$$

(1)

If n is the order of the equation, the following relations are valid:

$$0\le m_1\le n;0\le m_2\le n;m_1+m_2\le n.$$

(2)

The 2D polynomial function model of the first order (6 parameters) corrects the image by a rotation, a translation in x and y, scaling along both axes and an obliquitous transformation. The 2D first-order polynomial function is also called affine transformation. The 2D polynomial function model of second order (12 parameters) adds to the previous transformation’s correction of the torsion and convexity along both axes. A cubic polynomial function (20 parameters) further increases the correction flexibility, in a way that does not necessarily correspond to any physical reality of the image acquisition system [36].

By substituting the coordinate values of GCPs in Equation (1), polynomial coefficients (a_lij and b_lij) can be calculated. Consequently, the new location of each pixel in the cartographic plane can be defined. The minimum number of GCPs needed is established by the order n of the polynomial functions according to the formula [37]:

$$N_{{\min }_{GCPs}}=\frac{(n+1)\cdot (n+2)}{2}$$

(3)

To increase the positional accuracy of the resulting image, a greater number of GCPs is chosen, which are distributed regularly. Thus differences between map coordinates and corrected image coordinates for the same features tend to be reduced. To evaluate the quality of the results, errors not only for GCPs but also for other points, named check points (CPs), are considered [2,38].

Using polynomial functions is a very uncomplicated method to orthorectify VHRSI: often considered outdated, they correct for basic planimetric distortion at the GCPs; because they do not take ground elevation into consideration, they are limited to small and flat areas [39].

3D rational polynomial functions (RPFs) may be more useful. They define a relationship between the image coordinates (x’, y’) and the 3D object coordinates (X, Y, Z) [23,40].

Specifically:

$$x^{\prime }=\frac{P_1^n\left(X,Y,Z\right)}{P_2^n\left(X,Y,Z\right)}{y}^{\prime }=\frac{P_3^n\left(X,Y,Z\right)}{P_4^n\left(X,Y,Z\right)}$$

(4)

where $P_1^n,P_2^n,P_3^n,P_4^n$ are usually cubic polynomials. Each of these includes 20 coefficients and can be expressed as:

$$P_l^n\left(X,Y,Z\right)={\displaystyle \sum _{i=0}^{m_1}{\displaystyle \sum _{j=0}^{m_2}{\displaystyle \sum _{k=0}^{m_3}{a}_l{}_{{}_{ijk}}}}}{X}^i{Y}^j{Z}^k$$

(5)

where:

$$\begin{array}{l}n=3\\ l=1,2,3,4\\ 0\le m_1\le 3;\\ 0\le m_2\le 3;\\ 0\le m_3\le 3;\\ m_1+m_2+m_3\le 3\end{array}$$

(6)

Equations in (4) are known in the literature as Upward RFM, as they enable the image coordinates to be obtained starting from the 3D coordinates of a ground point [41].

Substituting P in (4) with the polynomials in (5) and eliminating the first coefficient in the denominator, there are 39 RPF coefficients in each equation: 20 coefficients in the numerator and 19 (and the constant 1) in the denominator [42]. In order to solve the 78 coefficients, at least 39 GCPs are required [43].

The 78 coefficients are calculated by the data provider considering the position of the satellite at the time of image acquisition. They are then included in the RPC (rational polynomial coefficient) file.

However, they can also be calculated using GCPs [43], as in the case above for polynomial functions (PFs). At least 39 of them are needed. In fact, if the camera model is not available, the ground control points need to be selected in a conventional way; that is, through collimation of the homologous points on the cartography or DEM (digital elevation model) or through specific GPS (Global Positioning System) survey campaigns [44]. Usually the Equations in (4) are resolved using a least squares iterative process, on the basis of the measurement of a large number of GCPs.

The accuracy of the results depends on the number and the distribution of GCPs. Several GCPs (more than 39) with a regular planimetric and altimetric distribution contribute to the high quality of the results [17,45,46]. A DEM of the whole area is also required for RPFs.

By applying PFs as well as RPFs to the primary image, a matrix of “empty” cells is computed. To calculate the radiometric value to be assigned to each pixel, a resampling method, such as nearest neighbor, bilinear interpolation, or cubic convolution, is used [47,48]. The nearest-neighbor algorithm is used for this application because it preserves the original radiometric values, which is fundamental for further image processes (calculation of vegetation indexes, classifications, etc.).

Several algorithms are described in the literature for VHRSI orthorectification using rigorous physical models. Based on the collinearity equations, they reconstruct the geometry of the scene during the image acquisition through the knowledge of parameters concerning both the platform and the sensor.

The traditional photogrammetric method of transforming from object space to image space using collinearity equations is highly suited to frame cameras, but not to pushbroom sensor products [23]. In fact, unlike the traditional frame-based aerial photos, each line of the linear array image is collected in a pushbroom fashion at a different instant of time; therefore, the perspective geometry is only valid for each line whereas it is close to a parallel projection in along-track direction; in addition, for each line, there is a different set of (time-dependent) values for the exterior orientation elements [49]. For 1-meter GSD pushbroom sensors such as IKONOS, fully parametrized camera models are extremely complex and difficult to implement; this is highlighted in the IKONOS System Geometric and Mathematical Model document that consists of 183 pages [50].

OrthoEngine—PCI geomatics software (PCI, 2016) supplies Toutin’s rigorous model [51,52]. Originally developed for SPOT, the model was also later extended for Landsat and satellites with synchronous imaging acquisition i.e., IKONOS II, QuickBird [53], WV-2, Komposat-2, and OrbView [54].

Other examples of rigorous models are mentioned in the literature, i.e., the model implemented in SISAR, which is a software for high-resolution satellite images at the Area di Geodesia e Geomatica—Sapienza Università di Roma. The approximate values of the physical parameters can be computed thanks to the information contained in the metadata file provided with each image and corrected by a least squares estimation process based on an appropriate number of GCPs [55].

In this work orthorectification processes were carried out on the WV-2 panchromatic image using PCI Geomatica OrthoEngine Version 2015. The following algorithms were applied:

• 2D PFs;
• 3D RPFs with original RPCs;
• 3D RPFs without original RPCs;
• Toutin’s rigorous model;
• A combination of 3D RPFs and 2D PFs.

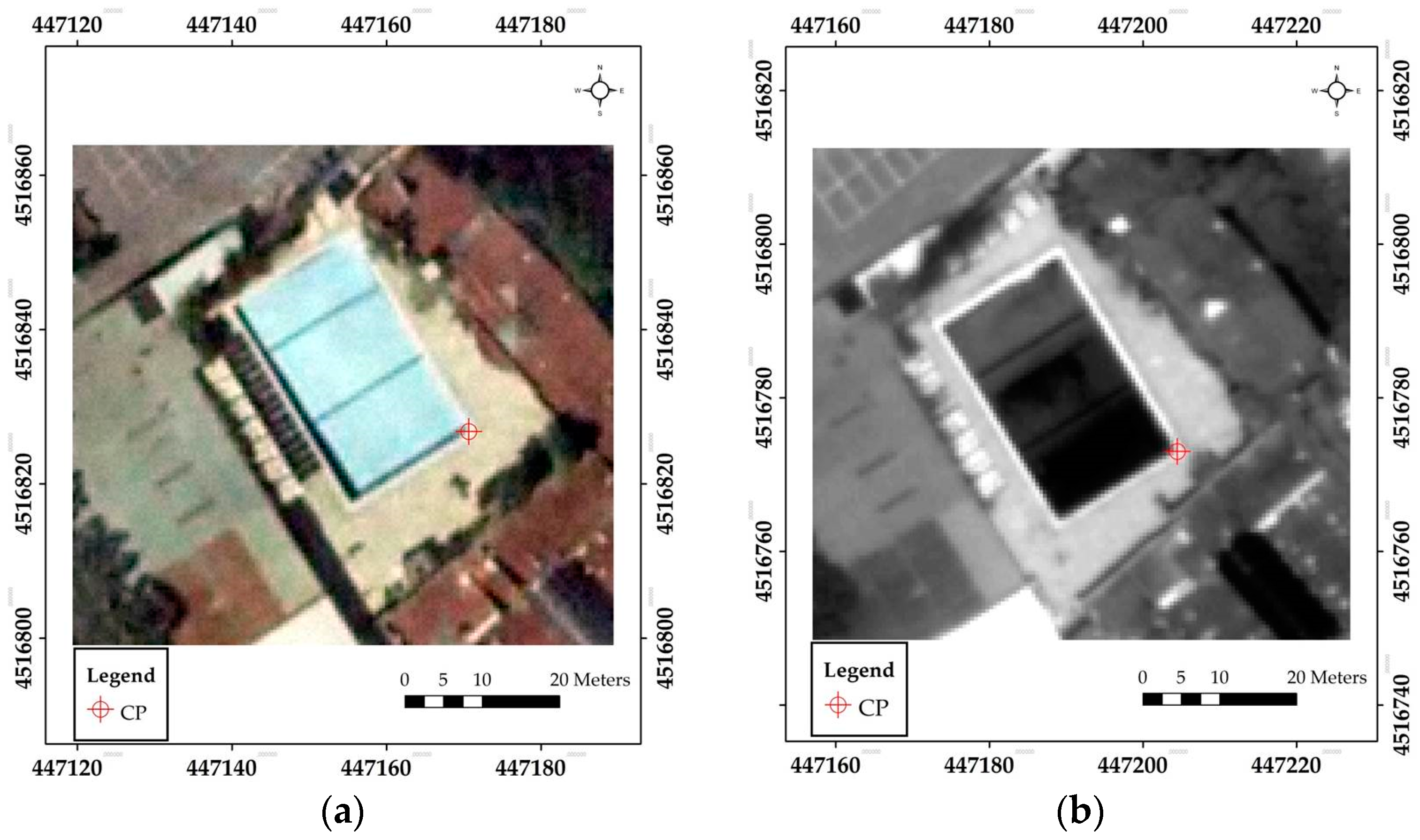
Both GCPs and CPs were homogeneously distributed over the study area and located on well-defined features. Clearly, the source, accuracy, distribution and number of GCPs and CPs are very important for a correct orthorectification [2]. To obtain a reliable measurement of GCPs and CPs with adequate planimetric accuracy, their (x, y) coordinates in UTM-WGS84 were derived from orthophotos of Campania with 0.20 m resolution (nominal scale: 1:5000). It should be noted that errors may occur when manually selecting corresponding points. Thus, specific GCPs and CPs were detected in well-defined locations such as road junctions and corners of buildings or swimming pools. For any ambiguous points, Canny edge detection algorithm [56] was used to support the identification of the corresponding points. In accordance with the literature [25], this helps in ensuring that the accuracy of the GCP and CP identification on the imagery was definitely below one pixel. Figure 2 reports an example of CP identification.

GCP and CP elevations were obtained by DEMs of the study area with a different horizontal resolution (cell size: 1 m, 20 m, 75 m). The DEM with a cell size of 1 m derived from laser-scanning data was supplied by the local administration (Provincia di Napoli) which indicates residuals of 0.16 m between the heights from the grid and those of the 3D points acquired with the RTK (real-time kinematic) survey. The DEM with a cell size of 20 m was provided by IGM (Istituto Geografico Militare), which indicates residuals of 7–10 m between the heights from the grid and those of the 3D points in plane and hilly zones. The DEM with a cell size of 75 m was provided by ISPRA (Istituto Superiore per la Protezione e la Ricerca Ambientale) and presents a vertical accuracy of 16–22 m in the considered area.

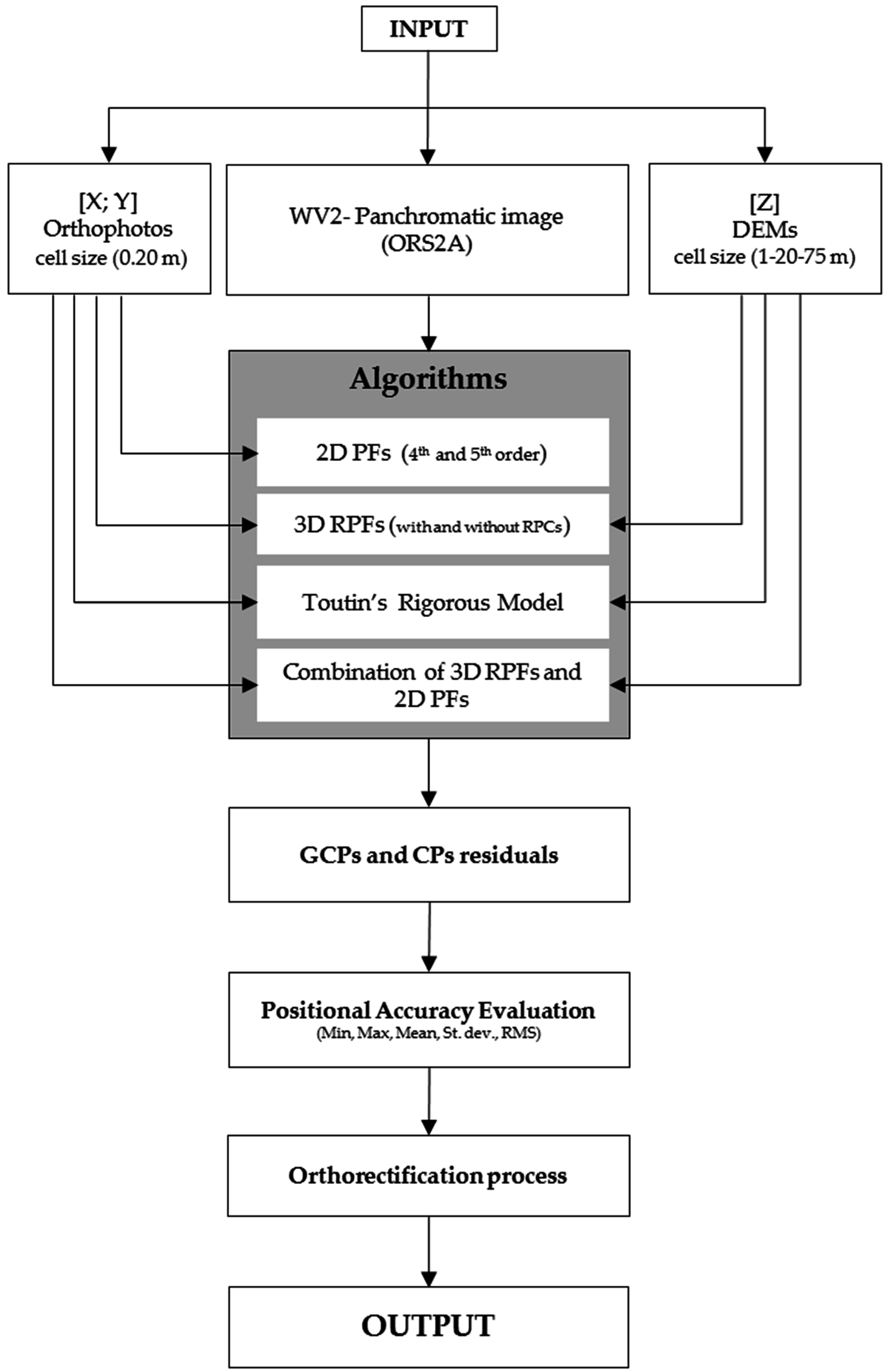
The flowchart in Figure 3 shows the inputs (orthophotos, WV-2 panchromatic image, DEMs), the algorithms used (2D PFs—fourth- and fifth-order; 3D RPFs with and without RPCs; Toutin’s rigorous model; and a combination of 3D RPFs and 2D PFs), and the most important steps (GCP and CP residuals calculation, positional accuracy evaluation based on minimum, maximum, mean, standard deviation, RMS calculation, orthorectification process, and output).

The orthorectification in two steps was introduced to increase the geopositional accuracy of the final WV-2 panchromatic image. In the first step, the best resulting 3D RPFs model (75 GCPs–15 CPs, DEM = 1 m) was applied. For the second step, first-order PFs using 15 GCPs was performed on the orthoimage resulting from the first step.

3. Results and Discussion

The positional accuracy of the primary panchromatic image was tested using 15 CPs. Figure 4 reports the CP distribution in the WV-2 primary panchromatic image.

Table 1. Residuals (in meters) obtained for CPs in the primary WV-2 panchromatic image.

Primary Panchromatic Image	Min	Max	Mean	St. dev.	RMS
CPs: 15	9.843	129.180	75.324	38.491	84.589

shows the statistical values (minimum, maximum, mean, standard deviation, RMS) of errors in these CPs. The low level of positional accuracy of the primary image (RMS = 84.589 m) is evident compared with the pixel dimensions.

The performance of each rectification was evaluated by the residuals obtained for GCPs and CPs in XY direction. Figure 5 illustrates the distribution of all GCPs datasets (5-10-15-45-60-75) in WV-2 primary panchromatic image. A homogenous distribution was attempted for each group of GCPs.

For all the tests performed, 15 CPs (the same as the previous test on the primary image) were introduced. Statistical values of these errors are reported in the following tables.

Table 2. Residuals (in meters) obtained for ground control points (GCPs) and CPs using polynomial functions.

2D PFs		Min	Max	Mean	St. dev.	RMS
4th order	GCPs: 45	0.460	46.009	11.080	9.826	14.810
	CPs: 15	0.538	74.462	15.799	18.063	23.997
	GCPs: 60	0.318	62.633	12.176	10.280	15.935
	CPs: 15	0.424	22.891	10.930	7.051	13.007
	GCPs: 75	0.672	65.419	11.076	9.836	14.813
	CPs: 15	0.831	26.640	10.669	8.023	13.349
5th order	GCPs: 45	0.320	34.806	7.515	7.459	10.589
	CPs: 15	1.717	43.673	16.866	13.993	21.915
	GCPs: 60	0.252	49.394	9.533	8.484	12.761
	CPs: 15	1.584	27.137	9.342	7.164	11.773
	GCPs: 75	0.358	52.241	8.622	8.264	11.943
	CPs: 15	1.010	20.907	8.250	5.691	10.022

shows how for both fourth- and fifth-order PFs, 60 GCPs produce better results than 45 GCPs while the introduction of another 15 GCPs leads to small increases in accuracy. However, the results are not suitable (RMS for CPs = 10–25 m) in terms of the image geometric resolution (0.5 m).

Table 3. Residuals (in meters) obtained for GCPs (0-5-10-15) and CPs using rational polynomial functions (RPFs) with rational polynomial coefficient (RPC) file.

3D RPFs with RPCs		Min	Max	Mean	St. dev.	RMS
DEM 1 m	GCPs: 0	-	-	-	-	-
	CPs: 15	1.420	4.612	3.096	1.057	3.272
	GCPs: 5	0.344	1.496	0.902	0.492	1.027
	CPs: 15	0.366	4.989	2.710	1.438	3.068
	GCPs: 10	0.129	3.538	1.397	0.945	1.687
	CPs: 15	0.077	4.592	2.059	1.347	2.461
	GCPs: 15	0.536	4.132	1.685	1.026	1.973
	CPs: 15	0.234	3.036	1.450	0.864	1.688
DEM 20 m	GCPs: 0	-	-	-	-	-
	CPs: 15	2.016	5.930	3.798	1.191	3.980
	GCPs: 5	0.728	3.882	2.475	1.109	2.712
	CPs: 15	0.573	7.175	2.190	1.653	2.744
	GCPs: 10	1.259	10.378	3.492	2.640	4.378
	CPs: 15	0.245	4.172	2.021	1.063	2.283
	GCPs: 15	0.334	10.395	2.594	2.558	3.643
	CPs: 15	0.380	4.036	2.027	1.082	2.298
DEM 75 m	GCPs: 0	-	-	-	-	-
	CPs: 15	1.139	7.366	4.255	1.844	4.638
	GCPs: 5	0.795	5.510	2.832	1.818	3.366
	CPs: 15	0.336	9.639	2.960	2.750	4.041
	GCPs: 10	0.537	8.658	3.537	2.577	4.376
	CPs: 15	0.577	7.217	3.202	1.897	3.722
	GCPs: 15	0.427	8.342	2.946	2.316	3.747
	CPs: 15	0.623	6.817	3.171	1.975	3.735

and

Table 4. Residuals (in meters) obtained for GCPs (45-60-75) and CPs using RPFs with RPC file.

3D RPFs with RPCs		Min	Max	Mean	St. dev.	RMS
DEM 1 m	GCPs: 45	0.103	5.499	1.513	1.076	1.857
	CPs: 15	0.231	2.121	1.237	0.604	1.377
	GCPs: 60	0.080	5.413	1.576	1.124	1.935
	CPs: 15	0.407	1.769	1.109	0.444	1.195
	GCPs: 75	0.047	5.509	1.481	1.097	1.843
	CPs: 15	0.318	1.844	1.072	0.454	1.164
DEM 20 m	GCPs: 45	0.285	19.997	2.889	3.406	4.466
	CPs: 15	0.522	3.233	1.863	1.030	2.129
	GCPs: 60	0.076	20.031	2.657	2.994	4.003
	CPs: 15	0.425	3.853	1.744	1.040	2.030
	GCPs: 75	0.099	20.846	2.286	2.655	3.504
	CPs: 15	0.157	4.292	1.644	1.105	1.981
DEM 75 m	GCPs: 45	0.011	22.695	3.374	3.668	4.984
	CPs: 15	0.636	5.965	3.238	1.561	3.595
	GCPs: 60	0.190	24.263	3.537	4.225	5.510
	CPs: 15	0.812	5.581	3.401	1.580	3.750
	GCPs: 75	0.041	23.955	3.414	3.905	5.187
	CPs: 15	1.004	5.678	3.254	1.569	3.613

show how the original RPC file supplied by image provider limits CP residuals using a low number of GCPs (i.e., when a DEM with a cell size of 1 m is used, only 5 GCPs mean that the RMS on CPs can be limited to 3.272 m). Although height accuracy is less important than planimetric accuracy, the influence of DEM resolution on elevation extraction is also evident (e.g., with 15 GCPs, the RMS residuals for CPs was 3.747 m using DEM with a 75 m cell size and 1.688 m using DEM with a 1 m cell size.

Table 5. Residuals (in meters) obtained for GCPs (45-60-75) and CPs using RPFs without RPC file.

3D RPFs without RPCs		Min	Max	Mean	St. dev.	RMS
DEM 1 m	GCPs: 45	0.050	3.695	0.886	0.728	1.147
	CPs: 15	0.130	7.632	2.093	1.903	2.828
	GCPs: 60	0.030	3.406	0.970	0.722	1.209
	CPs: 15	0.079	7.668	1.948	1.972	2.771
	GCPs: 75	0.078	3.742	1.027	0.807	1.306
	CPs: 15	0.266	3.527	1.354	1.078	1.731
DEM 20 m	GCPs: 45	0.064	8.989	1.670	1.553	2.280
	CPs: 15	0.840	23.205	3.778	5.362	6.559
	GCPs: 60	0.117	10.034	1.870	1.596	2.458
	CPs: 15	1.008	6.866	2.845	1.822	3.378
	GCPs: 75	0.076	9.790	1.913	1.515	2.441
	CPs: 15	0.513	6.221	2.867	1.808	3.389
DEM 75 m	GCPs: 45	0.094	6.054	1.693	1.482	2.250
	CPs: 15	0.917	53.431	7.725	12.634	14.809
	GCPs: 60	0.442	8.542	2.745	1.848	3.310
	CPs: 15	1.578	5.397	3.813	1.268	4.018
	GCPs: 75	0.090	10.415	2.482	2.107	3.255
	CPs: 15	0.622	13.869	4.262	3.204	5.331

shows that to achieve good results a great number of GCPs as well as a high-resolution DEM are required to calculate RPCs.

Table 6. Residuals (in meters) obtained for GCPs (5-10-15) and CPs using Toutin’s rigorous model.

Toutin’s Rigorous Model		Min	Max	Mean	St. dev.	RMS
DEM 1 m	GCPs: 5	0.553	1.996	1.227	0.469	1.313
	CPs: 15	1.435	6.444	3.786	1.604	4.112
	GCPs: 10	0.319	3.328	1.397	0.832	1.626
	CPs: 15	0.505	5.097	2.250	1.355	2.627
	GCPs: 15	0.203	3.864	1.680	1.005	1.958
	CPs: 15	0.370	3.108	1.517	0.846	1.737
DEM 20 m	GCPs: 5	0.508	2.102	1.317	0.538	1.423
	CPs: 15	1.617	9.244	4.448	2.434	5.071
	GCPs: 10	0.544	8.836	3.413	2.249	4.088
	CPs: 15	0.920	5.508	3.165	1.541	3.521
	GCPs: 15	0.674	9.438	2.774	2.185	3.532
	CPs: 15	0.927	5.190	2.854	1.360	3.162
DEM 75 m	GCPs: 5	0.621	3.040	1.938	0.871	2.125
	CPs: 15	1.298	10.945	5.203	2.836	5.926
	GCPs: 10	0.689	7.822	3.282	1.934	3.809
	CPs: 15	0.937	8.409	3.458	2.340	4.175
	GCPs: 15	0.549	8.030	2.769	1.895	3.355
	CPs: 15	0.830	7.829	3.495	2.199	4.129

and

Table 7. Residuals (in meters) obtained for GCPs (45-60-75) and CPs using Toutin’s rigorous model.

Toutin’s Rigorous Model		Min	Max	Mean	St. dev.	RMS
DEM 1 m	GCPs: 45	0.090	4.766	1.610	1.129	1.967
	CPs: 15	0.176	2.132	1.196	0.604	1.340
	GCPs: 60	0.029	4.985	1.615	1.070	1.937
	CPs: 15	0.270	1.813	1.083	0.494	1.190
	GCPs: 75	0.110	5.256	1.511	1.065	1.848
	CPs: 15	0.306	1.872	1.074	0.490	1.181
DEM 20 m	GCPs: 45	0.379	16.654	3.124	2.952	4.298
	CPs: 15	0.535	4.535	1.733	1.116	2.061
	GCPs: 60	0.098	17.002	2.919	2.724	3.993
	CPs: 15	0.603	4.600	1.724	1.072	2.030
	GCPs: 75	0.095	17.746	2.594	2.596	3.670
	CPs: 15	0.106	4.173	1.585	1.056	1.905
DEM 75 m	GCPs: 45	0.414	15.820	3.007	2.764	4.084
	CPs: 15	0.755	8.795	3.241	2.460	4.068
	GCPs: 60	0.264	20.095	3.256	3.454	4.747
	CPs: 15	0.450	8.138	3.435	2.399	4.190
	GCPs: 75	0.104	20.111	3.089	3.267	4.496
	CPs: 15	0.507	7.992	3.343	2.358	4.091

show how Toutin’s rigorous model obtains a good performance using a low number of GCPs and a high-resolution DEM (e.g., with 15 GCPs, RMS residuals for CPs was 4.129 m using DEM with a 75 m cell size and 1.737 m using DEM with a 1 m cell size).

Table 8. Residuals (in meters) obtained with a combination of RPFs (75GCPs–15CPs) and PFs first order (15 GCPs–15 CPs).

3D RPFs + 2D PFs		Min	Max	Mean	St. dev.	RMS
	GCPs: 15	0.211	1.727	0.849	0.516	0.993
	CPs: 15	0.460	2.586	1.197	0.605	1.341

reports the results obtained using the combination of RPF and PF algorithms. The GCPs used in this case are illustrated in Figure 6. This approach achieves low residuals, comparable with the WV-2 cell size as well as avoiding other geometrical distortions associated with higher-order PFs (i.e., twist with second-order). A combination of RPF and PF algorithms gave the best results.

4. Conclusions

The tests presented in this paper for WV-2 data show that RPFs are suitable for VHRSI orthorectification. Using the RPC file supplied by the provider, they can also be applied without GCPs, however the results present considerable positional errors, and few GCPs are sufficient to achieve good results. If RPCs are calculated by the user, several GCPs are necessary to limit residual values for Ground and Check Points.

RPFs need 3D information: Planimetric coordinates are not sufficient for GCPs, and a DEM of the entire scene is indispensable to complete the orthorectification. However, Z accuracy can be lower than that of the X and Y coordinates. As a consequence, height values can also be extracted from the DEM if they are not available from topographic and GPS surveys. Detailed maps (scale 1:5000 or greater) as well as remotely sensed images with the same resolution (or better) of the panchromatic image—but already orthorectified—are suitable for extracting planimetric coordinates of GCPs and CPs.

A low number of GCPs is sufficient to achieve a good performance with Toutin’s rigorous model.

The results obtained with WV-2 showed the analogous impact of DEM by increasing the geometric resolution for Z extraction for both RPFs as well as Toutin’s rigorous model.

Although PFs are inadequate for high-resolution satellite images, also when a large number of GCPs are used, they improve the results of RPFs if applied as a second step in the orthorectification process based on the combination of these algorithms.

Future research will be aimed at a comparison of similar algorithms extended to other VHRSIs such as WorldView-3, and GeoEye-2.