4.1. ESP Revisit
We review the edit sensitive parsing algorithm for building SLPs [
10]. This algorithm, referred to as ESP-comp, computes an SLP from an input sting
S. The tasks of ESP-comp are to (i) partition
S into
such that
for each
, (ii) if
, generate the production rule
and replace
by
X (this subtree is referred to as a 2-tree), and if
, generate the production rule
and
for
, and replace
by
Y (referred to as a 2-2-tree), (iii) iterate this process until
S becomes a symbol. Finally, the ESP-comp builds an SLP representing the string
S.
We focus on how to determine the partition . A string of the form with and is called a repetition. First, S is uniquely partitioned into the form by its maximal repetitions, where each is a maximal repetition of a symbol in , and each contains no repetition. Then, each is called type1, each of length at least is type2, and any remaining is type3. If , this symbol is attached to or with preference when both cases are possible. Thus, if , each and is longer than or equal to two. One of the substrings is referred to as .
Next, ESP-comp parses each
depending on the type. For type1 and type3 substrings, the algorithm performs the
left aligned parsing as follows. If
is even, the algorithm builds 2-tree from
for each
; otherwise, the algorithm builds a 2-tree from
for each
and builds a 2-2-tree from the last trigram
. For type2
, the algorithm further partitions it into short substrings of length two or three by
alphabet reduction [
8].
Alphabet reduction: Given a type2 string S, consider and as binary integers. Let p be the position of the least significant bit, in which , and let be the bit of at the p-th position. Then, is defined for any . Because S is repetition-free (i.e., type2), the label string is also type2. If the number of different symbols in S is n (denoted by ), then . For the , the next label string is iteratively computed until the final satisfying is obtained. is called the landmark if .
The alphabet reduction transforms S into such that any substring of of length at least contains at least one landmark because is also type2. Using this characteristic, the algorithm ESP-comp determines the bigrams to be replaced for any landmark , where any two landmarks are not adjacent, and then the replacement is deterministic. After replacing all landmarks, any remaining maximal substring s is replaced by the left aligned parsing, where if = 1, it is attached to its left or right block.
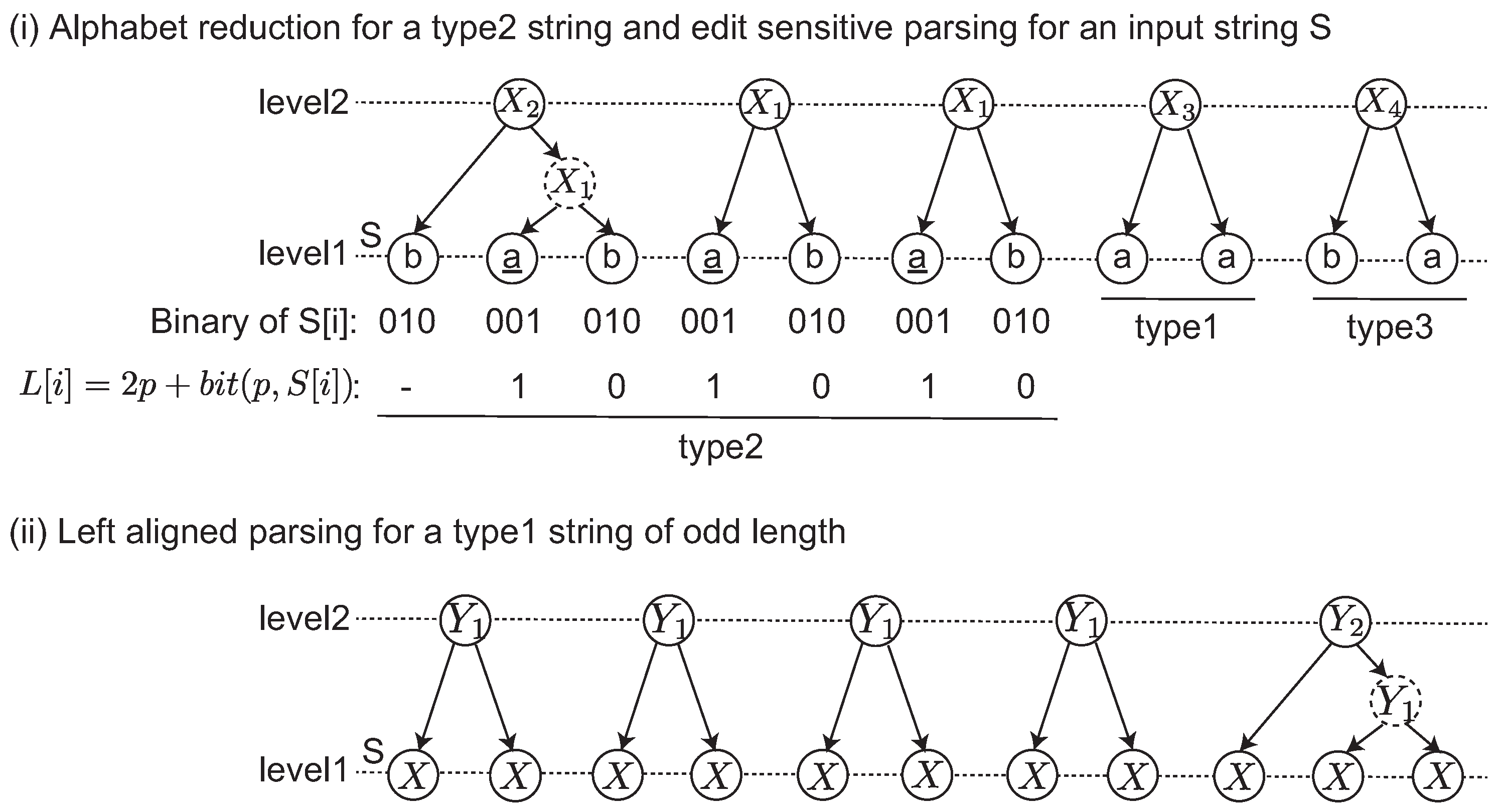
We give an example of the edit sensitive parsing of an input string in
Figure 1-(i) and (ii). The input string
S is divided into three maximal substrings depending on the types. The label string
L is computed for the type2 string. Originally,
L is iteratively computed until
. This case shows that a single iteration satisfies this condition. After the alphabet reduction, three landmarks
are found, and then each
is parsed. Any other remaining substrings including type1 and type3 are parsed by the left aligned parsing shown in
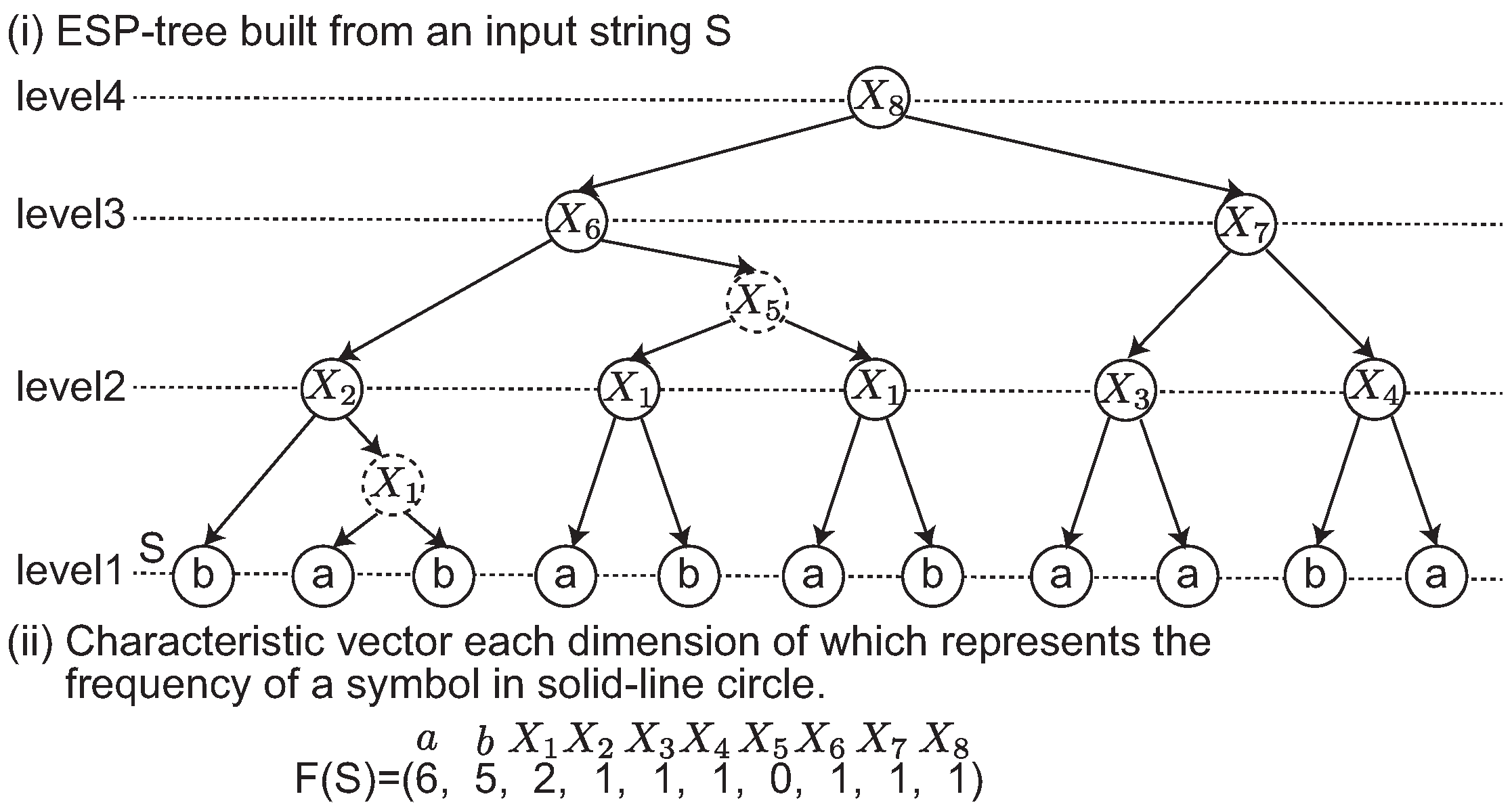
Figure 1-(ii). In this example, a dashed node denotes that it is an intermediate node in a 2-2-tree. Originally, an ESP tree is a ternary tree in which each node has at most three children. The intermediate node is introduced to represent ESP tree as a binary tree.
As shown in [
8], the alphabet reduction approximates the minimum CFG as follows. Let
S be a type2 string containing a substring
α at least twice. When
α is sufficiently long (e.g.,
), there is a partition
such that
and each landmark of
within
α is decided by only
. This means the long prefix
of
α is replaced by the same variables, independent of the occurrence of
α.
ESP-comp generates a new shorter string
of length from
to
, and it parses
iteratively. Given a string
S, ESP builds the ESP-tree of height
in
time and in
space. The approximation ratio of the smallest grammar by ESP is
[
10].