Structural Damage Localization by the Principal Eigenvector of Modal Flexibility Change
Abstract
:1. Introduction
2. Theory
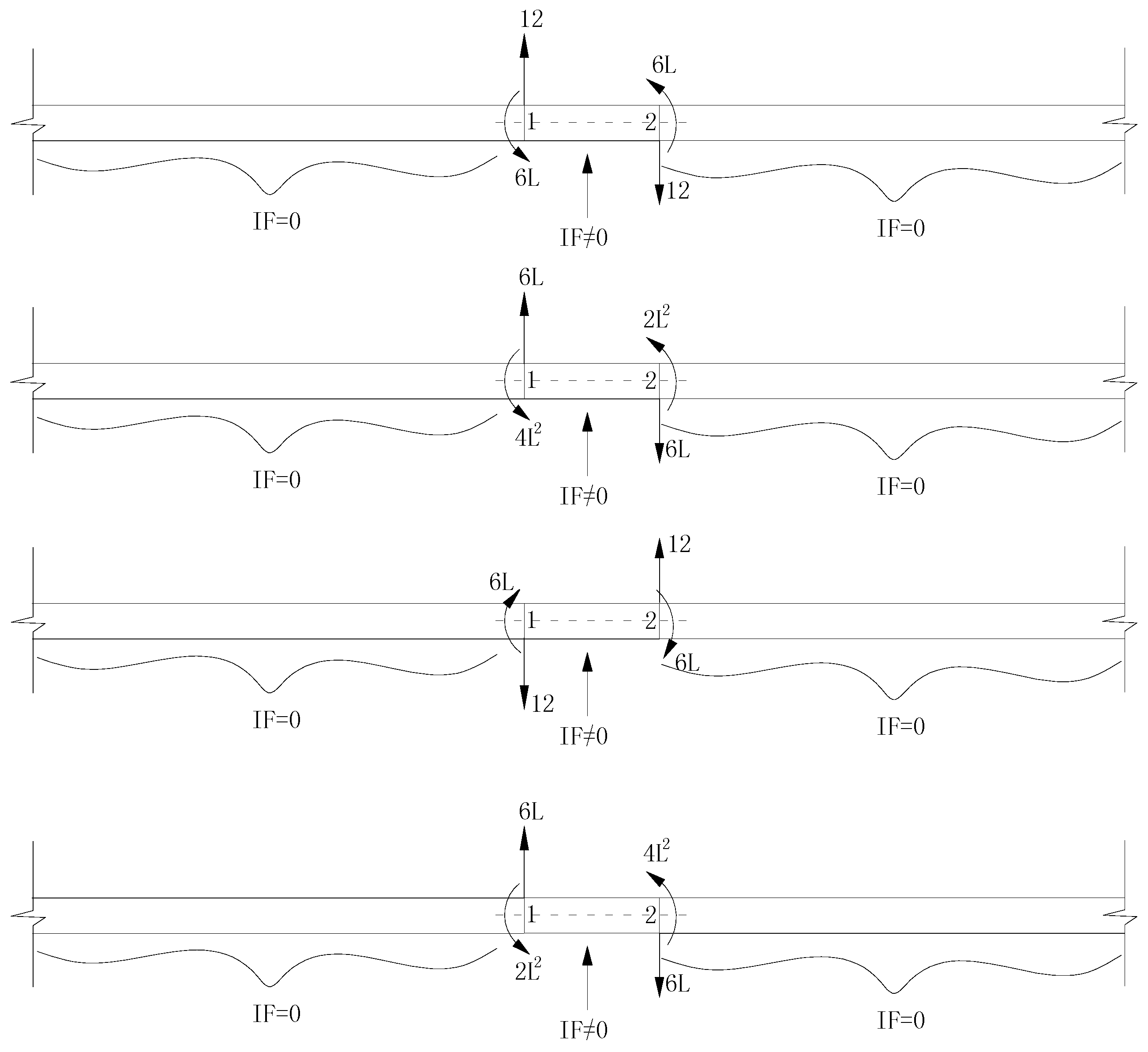
2.1. The Principle of Deflection-Based Damage Localization
2.2. Deflection Estimated by Modal Flexibility Change and PE Method for Damage Localization
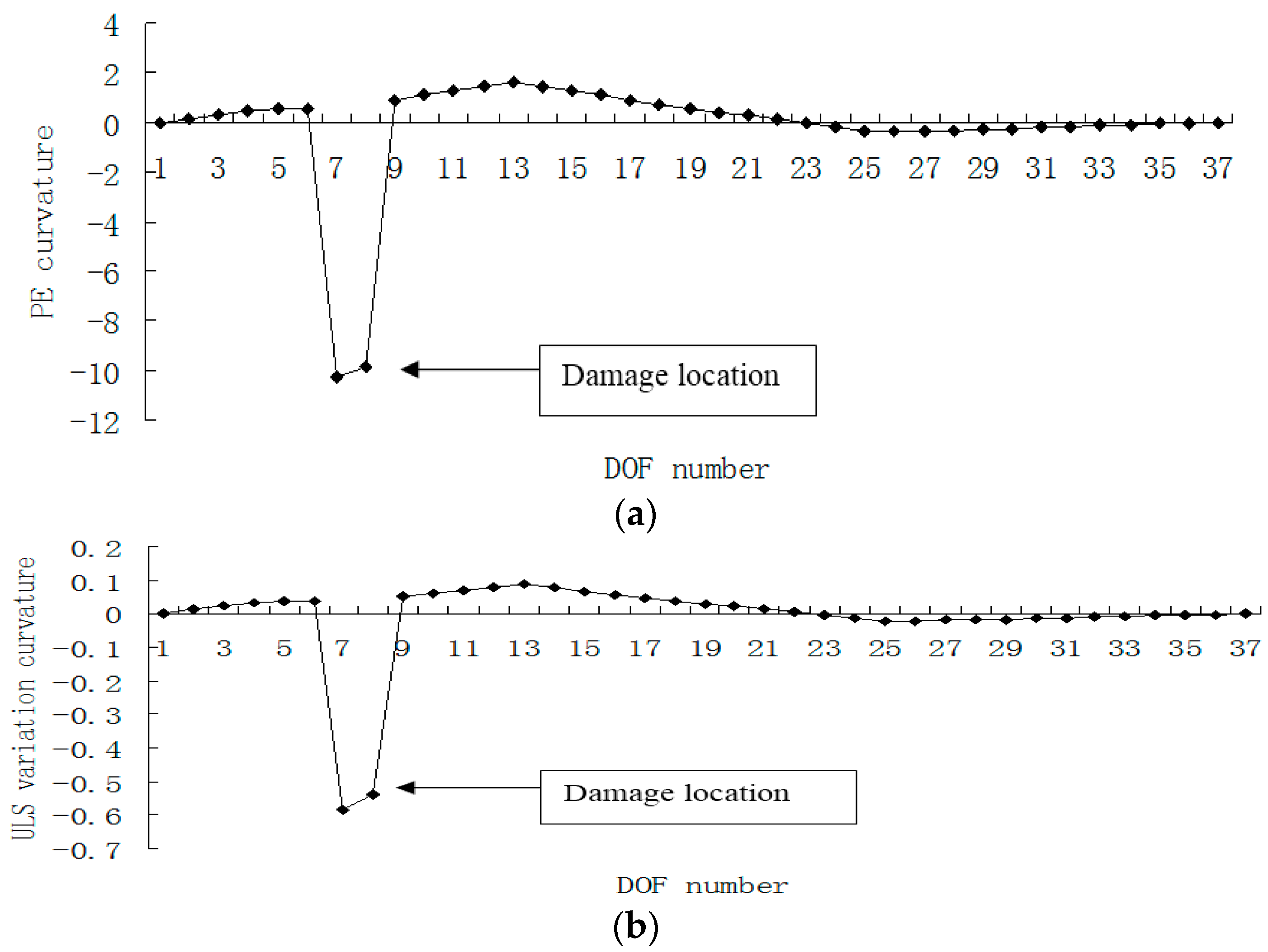
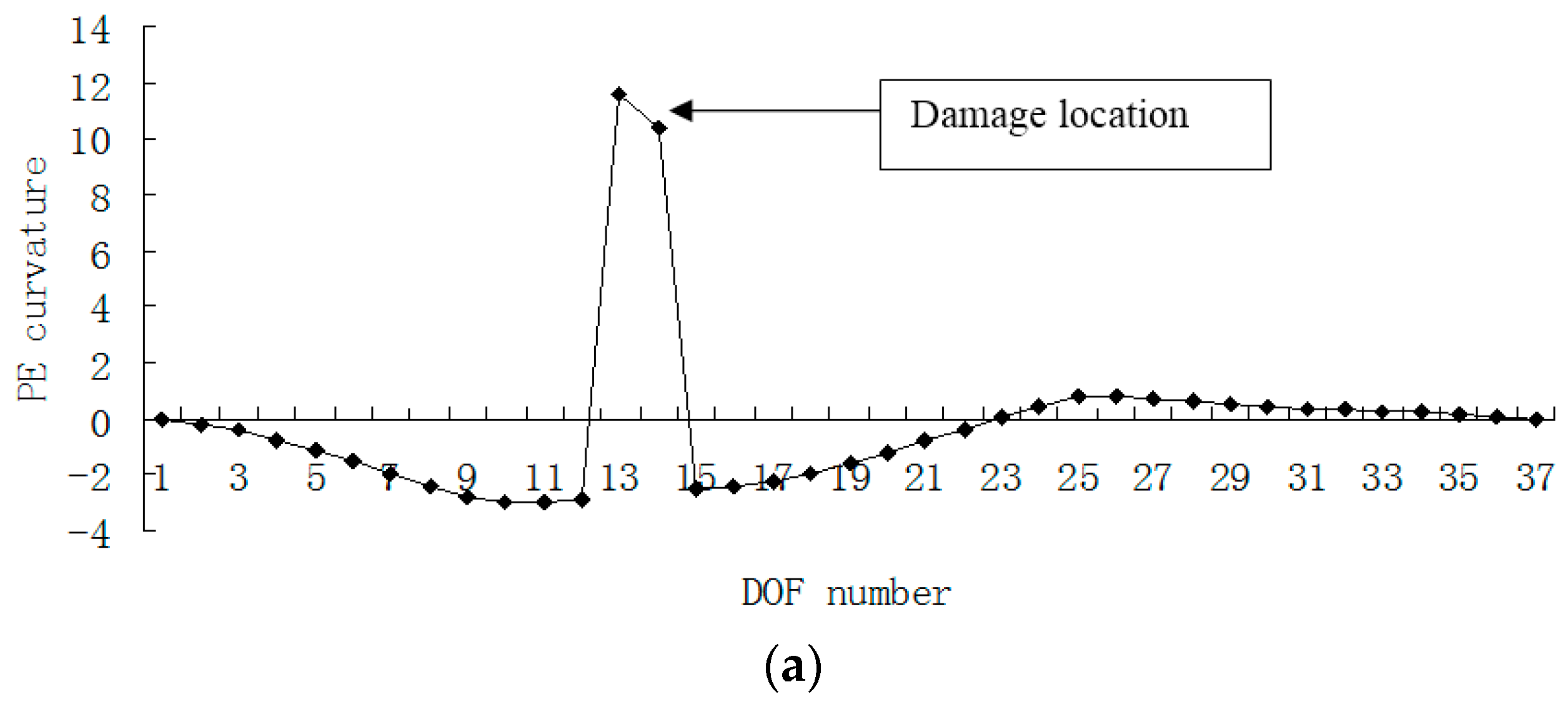
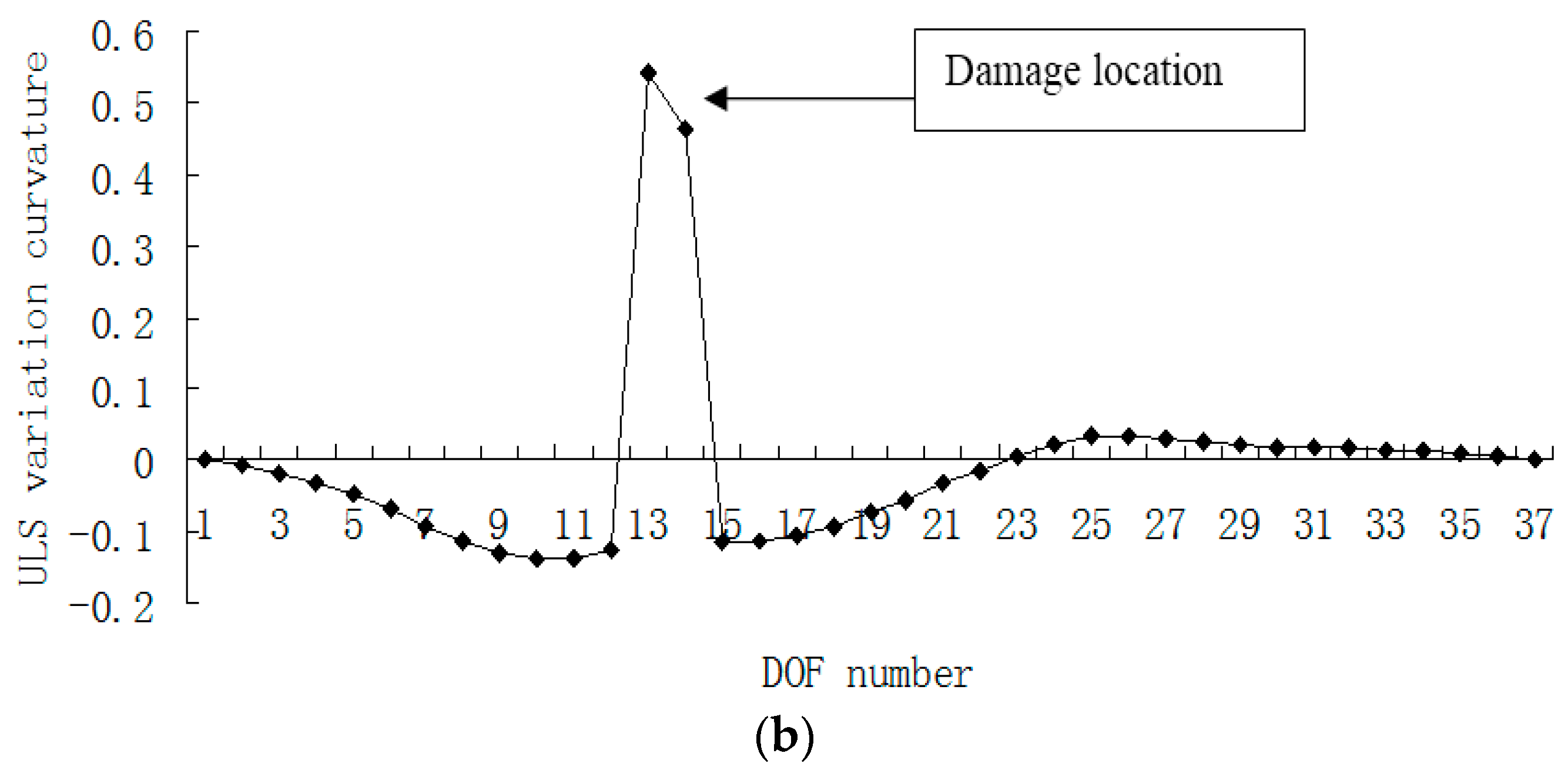
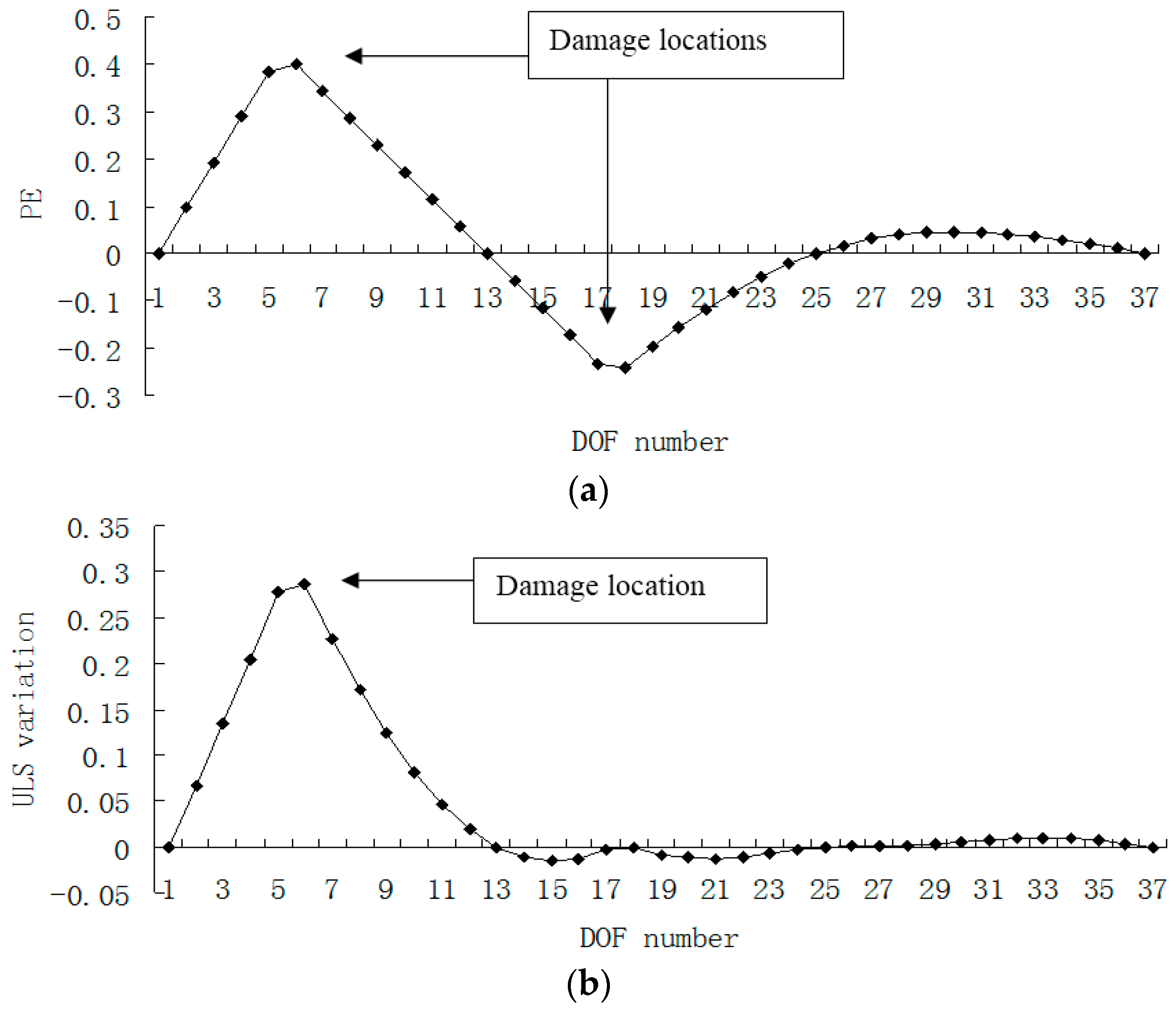
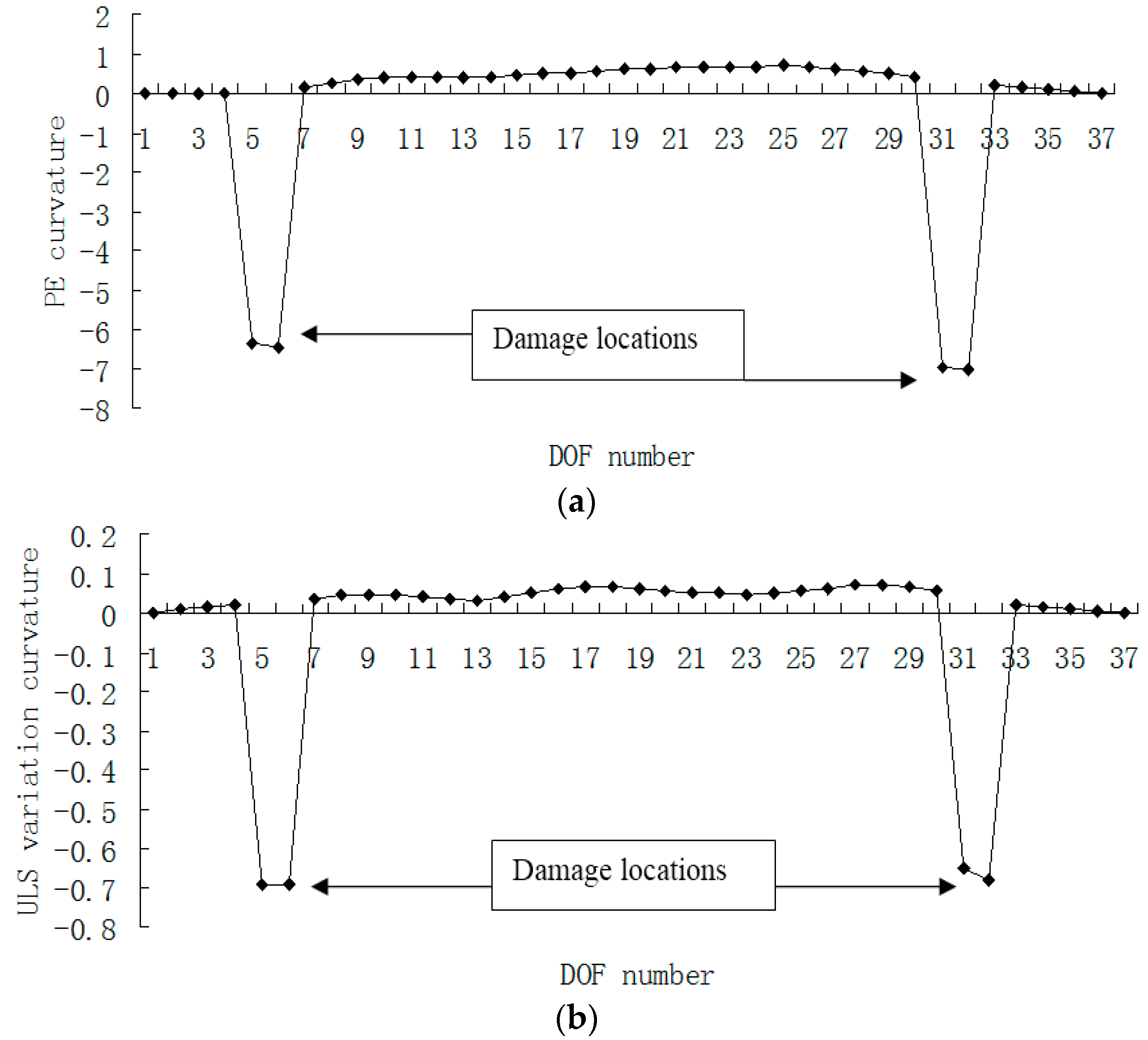
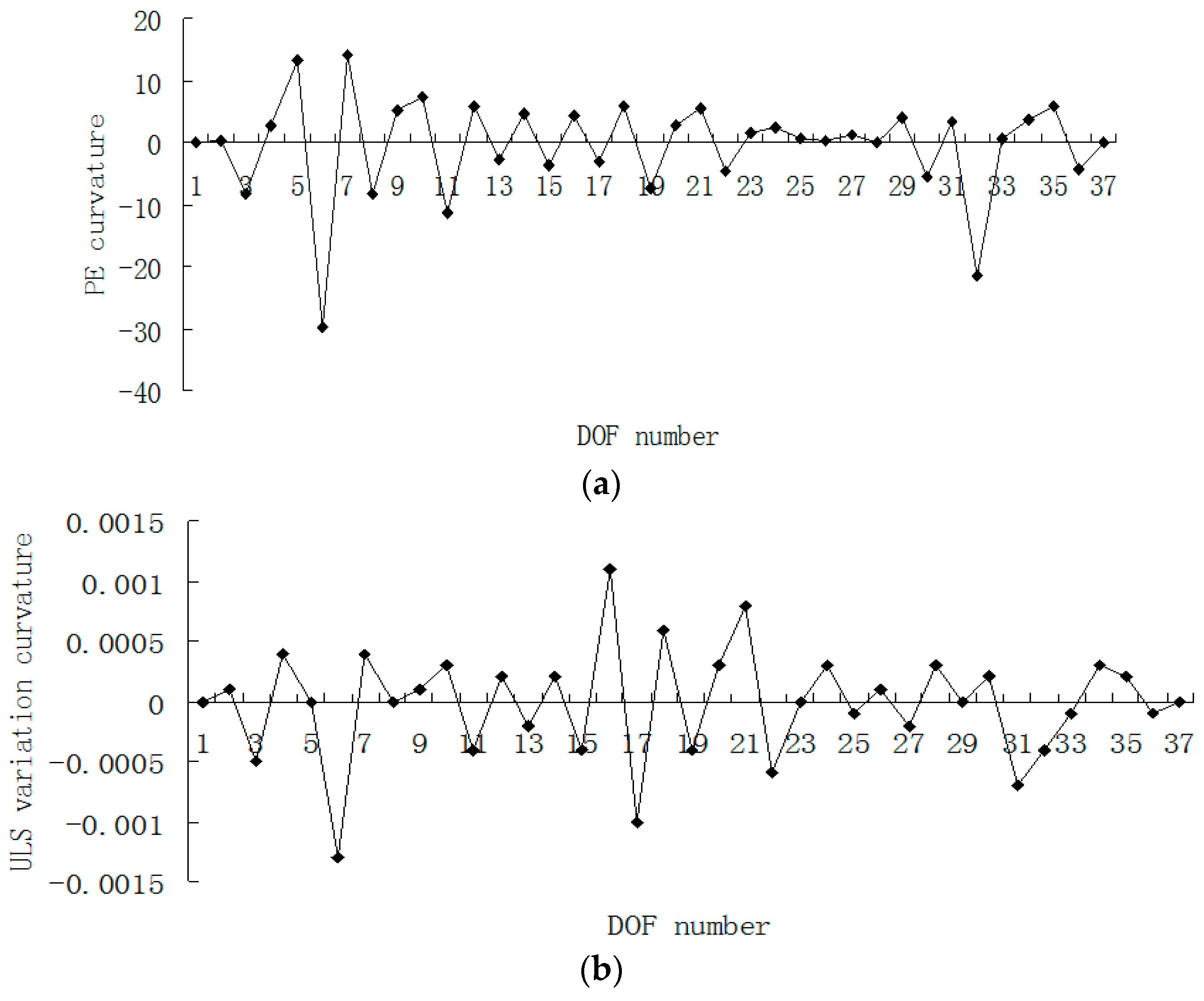
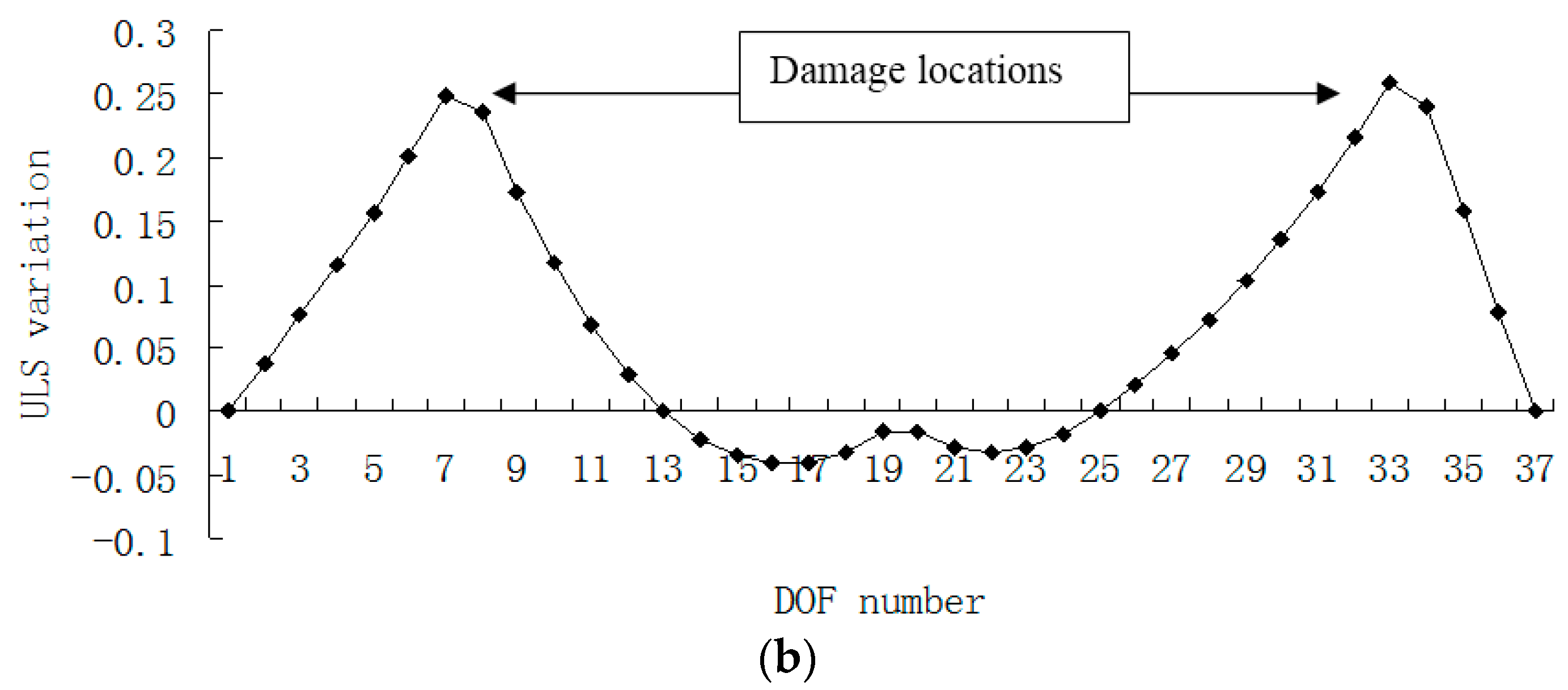
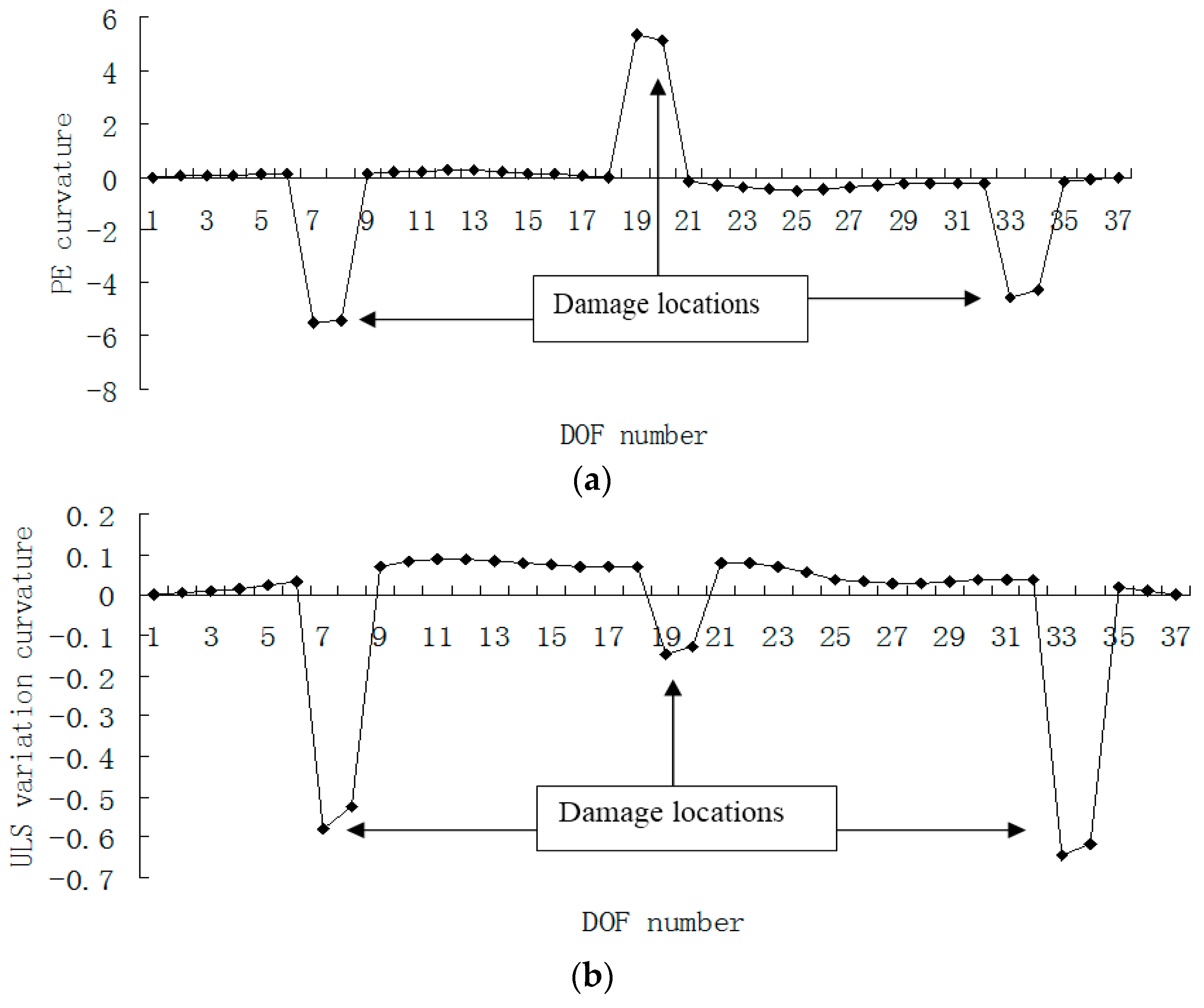
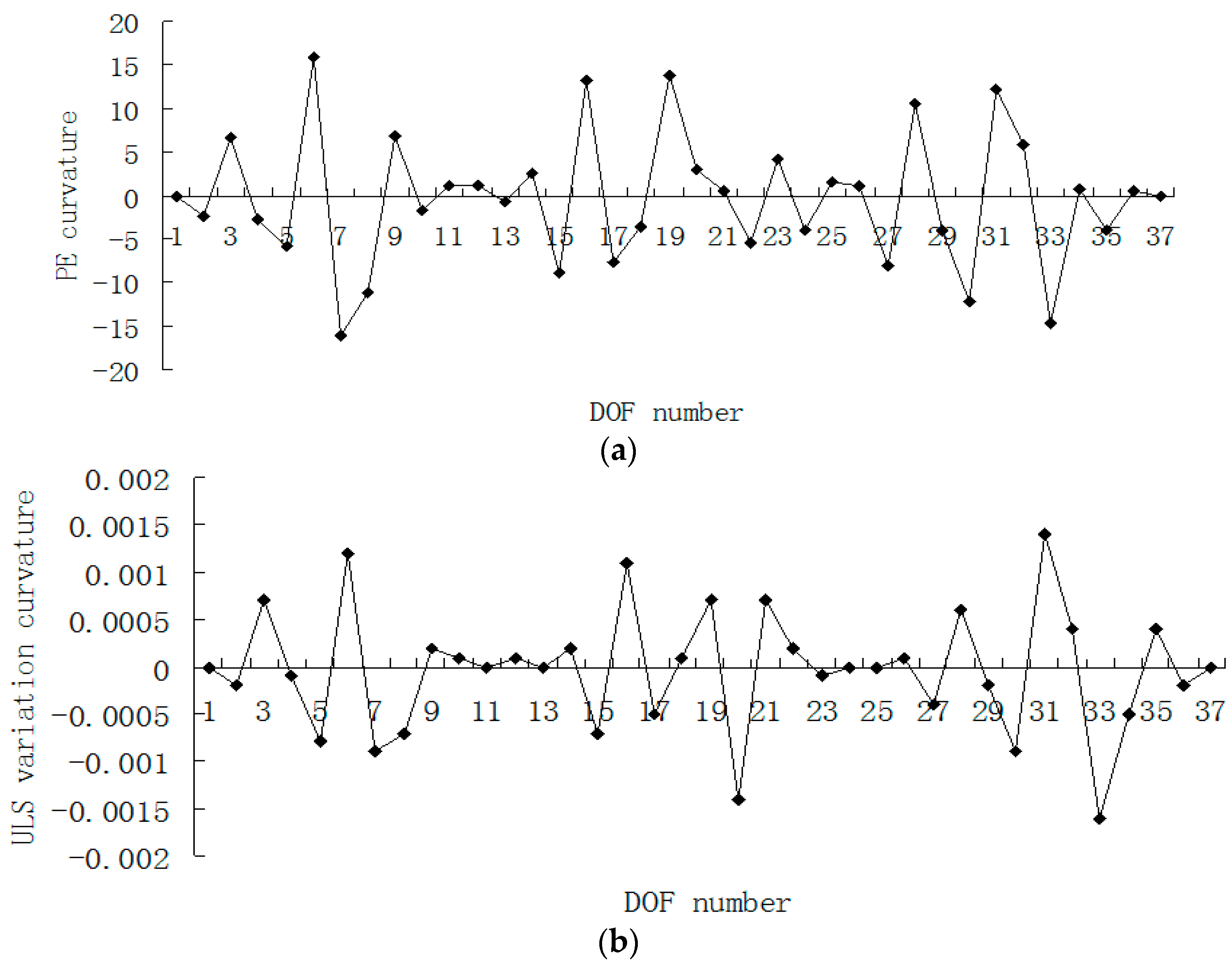
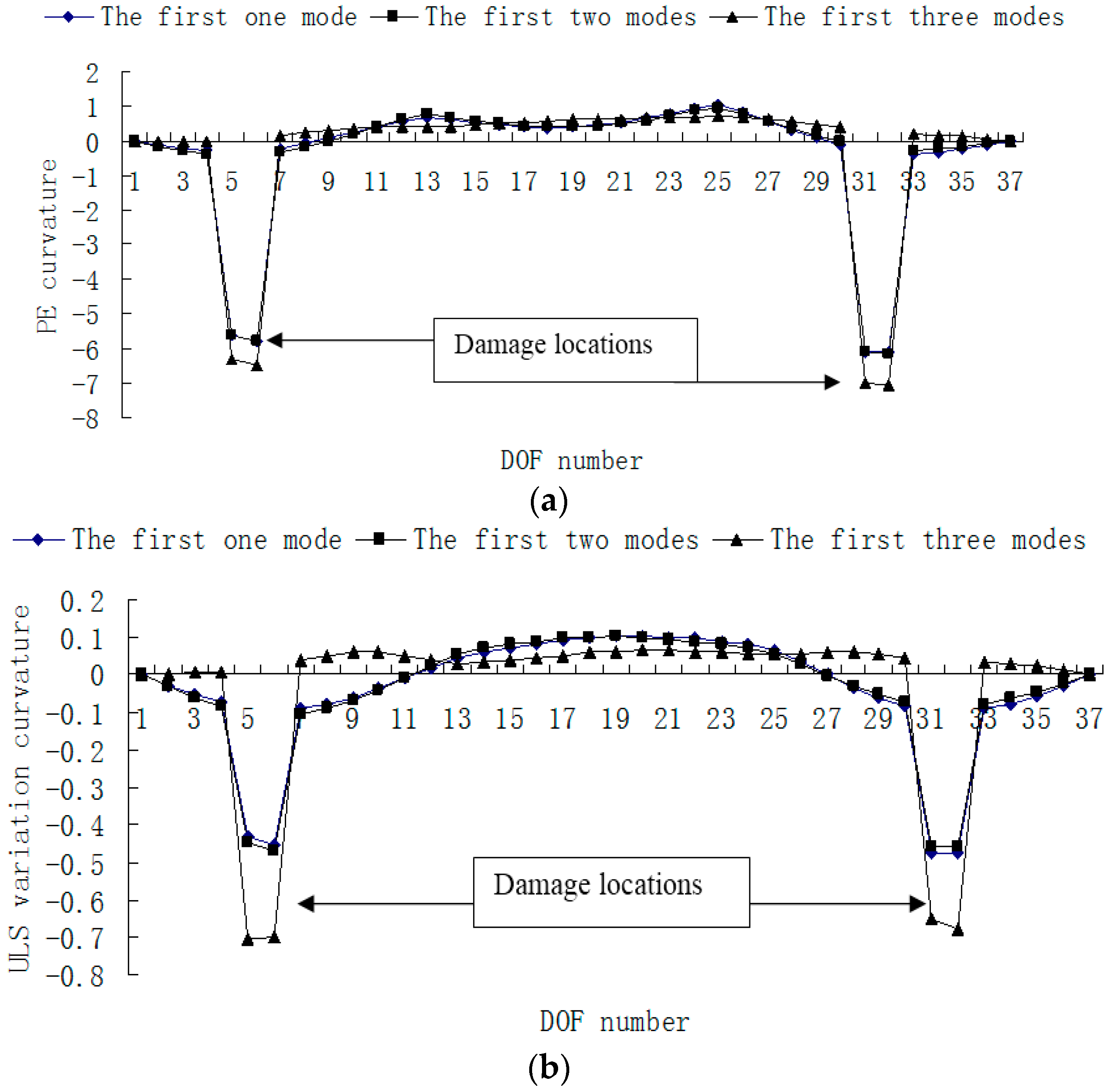
3. Numerical Example
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Doebling, S.W.; Farrar, C.R.; Prime, M.B. A summary review of vibration-based damage identification methods. Shock Vib. Dig. 1998, 30, 91–105. [Google Scholar] [CrossRef]
- Carden, E.P.; Fanning, P. Vibration based condition monitoring: A review. Struct. Health Monit. 2004, 3, 355–377. [Google Scholar] [CrossRef]
- Prinaris, A.; Alampalli, S.; Ettouney, M. Review of remote sensing for condition assessment and damage identification after extreme loading conditions. In Proceedings of the 2008 Structures Congress, Vancouver, BC, Canada, 24–26 April 2008.
- Ashokkumar, C.R.; Lyengar, N.G.R. Partial eigenvalue assignment for structural damage mitigation. J. Sound Vib. 2011, 330, 9–16. [Google Scholar] [CrossRef]
- Yang, Z.C.; Wang, L. Structural damage detection by changes in natural frequencies. J. Intell. Mater. Syst. Struct. 2010, 21, 309–319. [Google Scholar] [CrossRef]
- Zhu, H.P.; Li, L.; He, X.Q. Damage detection method for shear buildings using the changes in the first mode shape slopes. Comput. Struct. 2011, 89, 733–743. [Google Scholar] [CrossRef]
- Weber, B.; Paultre, P. Damage identification in a truss tower by regularized model updating. J. Struct. Eng. 2010, 136, 1943–1953. [Google Scholar] [CrossRef]
- Adewuyi, A.P.; Wu, Z.S. Modal macro-strain flexibility methods for damage localization in flexural structures using long-gage FBG sensors. Struct. Control Health Monit. 2011, 18, 341–360. [Google Scholar] [CrossRef]
- Limongelli, M.P. Frequency response function interpolation for damage detection under changing environment. Mech. Syst. Signal Process. 2010, 24, 2898–2913. [Google Scholar] [CrossRef]
- Lima, A.M.G.; Faria, A.W.; Rade, D.A. Sensitivity analysis of frequency response functions of composite sandwich plates containing viscoelastic layers. Compos. Struct. 2010, 92, 364–376. [Google Scholar] [CrossRef]
- Lu, Z.R.; Law, S.S. Differentiating different types of damage with response sensitivity in time domain. Mech. Syst. Signal Process. 2010, 24, 2914–2928. [Google Scholar] [CrossRef]
- Lu, Z.R.; Huang, M.; Liu, J.K. State-space formulation for simultaneous identification of both damage and input force from response sensitivity. Smart Struct. Syst. 2011, 8, 157–172. [Google Scholar] [CrossRef]
- Wong, C.N.; Huang, H.Z.; Xiong, J.Q.; Lan, H.L. Generalized-order perturbation with explicit coefficient for damage detection of modular beam. Arch. Appl. Mech. 2011, 81, 451–472. [Google Scholar] [CrossRef]
- Yang, Q.W. A new damage identification method based on structural flexibility disassembly. J. Vib. Control 2011, 17, 1000–1008. [Google Scholar] [CrossRef]
- Yang, Q.W.; Sun, B.X. Structural damage localization and quantification using static test data. Struct. Health Monit. 2011, 10, 381–389. [Google Scholar] [CrossRef]
- Yang, Q.W.; Liu, J.K.; Li, C.H.; Liang, C.F. A Universal fast algorithm for sensitivity-based structural damage detection. Sci. World J. 2013, 2013. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Aktan, A.E. Application of modal flexibility and its derivatives in structural identification. Res. Nondestruct. Eval. 1998, 10, 43–61. [Google Scholar] [CrossRef]
- Wu, D.; Law, S.S. Damage localization in plate structures from uniform load surface curvature. J. Sound Vib. 2004, 276, 227–244. [Google Scholar] [CrossRef]
- Wu, D.; Law, S.S. Sensitivity of uniform load surface curvature for damage identification in plate structures. J. Vib. Acoust. 2005, 127, 84–92. [Google Scholar] [CrossRef]
- Wang, J.; Qiao, P.Z. Improved damage detection for beam-type structures using a uniform load surface. Struct. Health Monit. 2007, 6, 99–110. [Google Scholar] [CrossRef]
- Choi, I.Y.; Lee, J.S.; Choi, E.; Cho, H.N. Development of elastic damage load theorem for damage detection in a statically determinate beam. Comput. Struct. 2004, 82, 2483–2492. [Google Scholar] [CrossRef]
- Sung, S.H.; Jung, H.J.; Jung, H.Y. Damage detection of beam-like structures using the normalized curvature of a uniform load surface. J. Sound Vib. 2013, 332, 1501–1519. [Google Scholar] [CrossRef]
- Tomaszewska, A. Influence of statistical errors on damage detection based on structural flexibility and mode shape curvature. Comput. Struct. 2010, 88, 154–164. [Google Scholar] [CrossRef]
- Koo, K.Y.; Lee, J.J.; Yun, C.B.; Kim, J.T. Damage detection in beam-like structures using deflections obtained by modal flexibility matrices. Smart Struct. Syst. 2008, 4, 605–628. [Google Scholar] [CrossRef]
- Qiao, P.; Lu, K.; Lestari, W.; Wang, J. Curvature mode shape-based damage detection in composite laminated plates. Compos. Struct. 2007, 80, 409–428. [Google Scholar] [CrossRef]
- Fan, W.; Qiao, P. Vibration-based damage identification methods: A review and comparative study. Struct. Health Monit. 2011, 10, 83–111. [Google Scholar] [CrossRef]
- Hamze, A.; Gueguen, P.; Roux, P.; Baillet, L. Comparative study of damage identification algorithms applied to a Plexiglas beam. In Proceedings of the 15th International Conference on Experimental Mechanics, Porto, Portuga, 22–27 July 2012; pp. 22–27.
- Domaneschi, M.; Limongelli, M.P.; Martinelli, L. Vibration based damage localization using MEMS on a suspension bridge model. Smart Struct. Syst. 2013, 12, 679–694. [Google Scholar] [CrossRef]
- Domaneschi, M.; Limongelli, M.P.; Martinelli, L. Damage detection and localization on a benchmark cable-stayed bridge. Earthq. Struct. 2015, 8, 1113–1126. [Google Scholar] [CrossRef]
- Manoach, E.; Samborski, S.; Mitura, A.; Warminski, J. Vibration based damage detection in composite beams under temperature variations using Poincare maps. Int. J. Mech. Sci. 2012, 62, 120–132. [Google Scholar] [CrossRef]
- Manoach, E.; Trendafilova, I. Large amplitude vibrations and damage detection of rectangular plates. J. Sound Vib. 2008, 315, 591–606. [Google Scholar] [CrossRef]
- Herstein, I.N.; Winter, D.J. Matrix Theory and Linear Algebra; Macmillan Publishing Company: Indianapolis, IN, USA, 1988. [Google Scholar]
- Datta, B.N. Numerical Linear Algebra and Applications; Brooks/Cole Publishing Company: Pacific Grove, CA, USA, 1995. [Google Scholar]
- Pandey, A.K.; Biswas, M. Damage detection in structures using changes in flexibility. J. Sound Vib. 1994, 169, 3–17. [Google Scholar] [CrossRef]
- Pandey, K.; Biswas, M. Experimental verification of flexibility difference method for locating damage in structures. J. Sound Vib. 1995, 184, 311–328. [Google Scholar] [CrossRef]












© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.-H.; Yang, Q.-W.; Sun, B.-X. Structural Damage Localization by the Principal Eigenvector of Modal Flexibility Change. Algorithms 2016, 9, 24. https://doi.org/10.3390/a9020024
Li C-H, Yang Q-W, Sun B-X. Structural Damage Localization by the Principal Eigenvector of Modal Flexibility Change. Algorithms. 2016; 9(2):24. https://doi.org/10.3390/a9020024
Chicago/Turabian StyleLi, Cui-Hong, Qiu-Wei Yang, and Bing-Xiang Sun. 2016. "Structural Damage Localization by the Principal Eigenvector of Modal Flexibility Change" Algorithms 9, no. 2: 24. https://doi.org/10.3390/a9020024
APA StyleLi, C.-H., Yang, Q.-W., & Sun, B.-X. (2016). Structural Damage Localization by the Principal Eigenvector of Modal Flexibility Change. Algorithms, 9(2), 24. https://doi.org/10.3390/a9020024




