A New Swarm Intelligence Approach for Clustering Based on Krill Herd with Elitism Strategy
Abstract
:1. Introduction
2. Fuzzy C-Means (FCM) Clustering Algorithm
3. KHE Method for Clustering Problem
3.1. KH Method
- (i)
- movement induced by other krill individuals;
- (ii)
- foraging action; and
- (iii)
- random diffusion
3.1.1. Motion Induced by Other Krill Individuals
3.1.2. Foraging Motion
3.1.3. Random Diffusion
3.2. KH Method with Elitism Strategy (KHE)
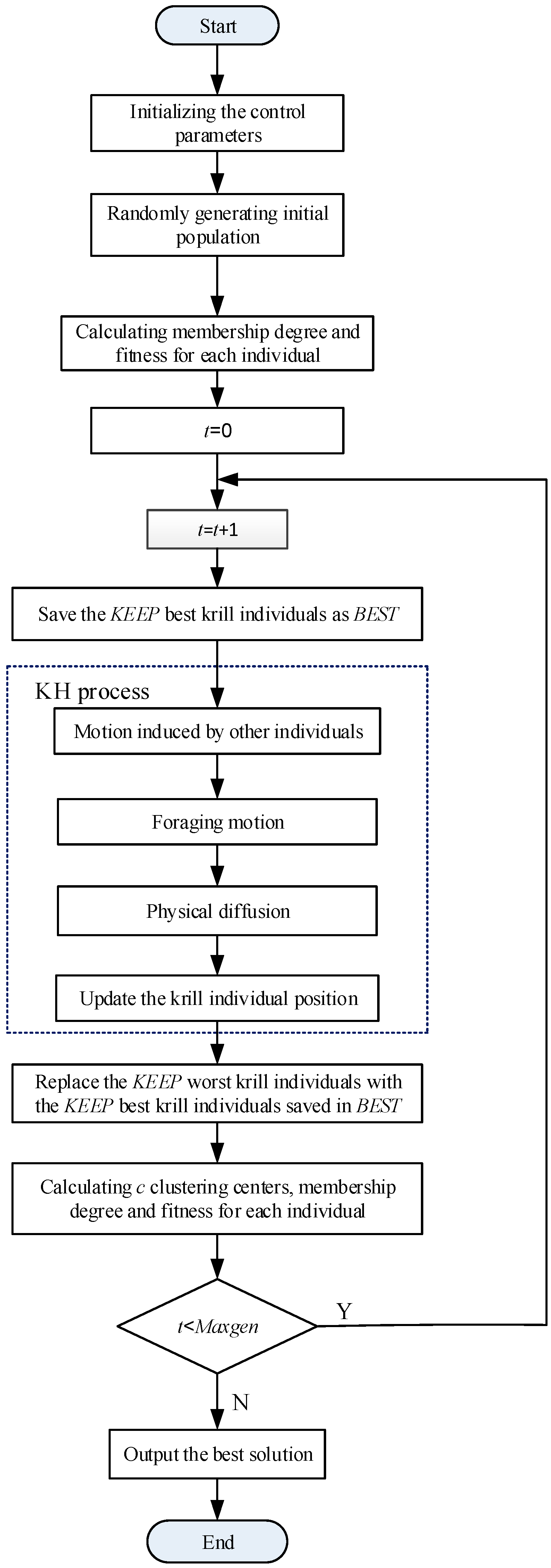
3.3. KHE Method for Clustering Problem
- (1)
- Initialize the control parameters. All the parameters used in KHE are firstly initialized.
- (2)
- Randomly initialize c cluster centers, and generate the initial population, calculate membership degree of each cluster center for all samples by Equation (4), and the fitness of each krill individual value fi, where i = 1, 2, …, NP. Here, NP is the number of population size.
- (3)
- Set t = 0.
- (4)
- Save the KEEP best krill individuals as BEST.
- (5)
- Implement three motions and update the positions of krill individuals in population.
- (6)
- Replace the KEEP worst krill individuals with the KEEP best krill individuals saved in BEST.
- (7)
- Calculate c clustering centers, membership degree and fitness for each individual.
- (8)
- If the t < Maxgen, t = t + 1, go to Equation (4); Otherwise, the algorithm is over and finds the final global optimal solution.
4. Simulation Results
| No. | Name | Definition |
|---|---|---|
| F01 | Dixon & Price | |
| F02 | Griewank | |
| F03 | Holzman 2 function | |
| F04 | Powell | |
| F05 | Quartic with noise | |
| F06 | Rosenbrock | |
| F07 | Sphere |
4.1. Convergent Performance Compared KHE with Six Other Methods
| Function | ACO | GA | HS | KH | KHE | PSO | SGA | |
|---|---|---|---|---|---|---|---|---|
| MEAN | F01 | 3.36E5 | 1.25E5 | 8.26E5 | 1.55E5 | 18.90 | 2.77E5 | 8.64E3 |
| F02 | 32.55 | 106.40 | 403.60 | 67.46 | 1.13 | 172.70 | 29.50 | |
| F03 | 8.72E4 | 3.51E4 | 2.07E5 | 3.74E4 | 1.86 | 8.36E4 | 2.29E3 | |
| F04 | 5.92E3 | 1.88E3 | 6.06E3 | 3.70E3 | 36.01 | 2.47E3 | 182.80 | |
| F05 | 17.75 | 7.92 | 54.68 | 10.14 | 4.44E−4 | 13.77 | 0.66 | |
| F06 | 5.47E3 | 1.86E3 | 3.99E3 | 1.22E3 | 31.60 | 1.38E3 | 313.10 | |
| F07 | 85.19 | 21.57 | 119.50 | 20.03 | 0.04 | 50.05 | 11.02 | |
| BEST | F01 | 1.14E5 | 1.71E4 | 3.13E5 | 5.31E4 | 3.37 | 2.44E4 | 1.41E3 |
| F02 | 14.90 | 33.08 | 266.10 | 35.84 | 1.02 | 91.07 | 9.64 | |
| F03 | 2.36E4 | 6.30E3 | 9.39E4 | 1.76E4 | 0.03 | 1.16E4 | 300.60 | |
| F04 | 2.43E3 | 388.10 | 2.26E3 | 1.00E3 | 2.41 | 1.01E3 | 52.56 | |
| F05 | 6.12 | 1.28 | 25.52 | 5.10 | 5.13E−6 | 4.22 | 0.08 | |
| F06 | 3.73E3 | 513.10 | 2.20E3 | 697.30 | 28.19 | 508.00 | 137.50 | |
| F07 | 55.53 | 5.80 | 70.20 | 10.44 | 3.84E−3 | 29.45 | 4.16 | |
| WORST | F01 | 8.46E5 | 3.63E5 | 1.26E6 | 2.85E5 | 167.60 | 2.39E6 | 4.90E4 |
| F02 | 69.45 | 235.90 | 498.70 | 101.70 | 1.63 | 568.30 | 68.65 | |
| F03 | 1.76E5 | 1.35E5 | 3.29E5 | 6.26E4 | 20.86 | 6.00E5 | 8.98E3 | |
| F04 | 8.89E3 | 4.42E3 | 1.07E4 | 6.35E3 | 218.40 | 4.72E3 | 558.50 | |
| F05 | 37.48 | 28.87 | 81.76 | 17.74 | 7.82E−3 | 32.10 | 5.08 | |
| F06 | 8.08E3 | 4.14E3 | 5.70E3 | 1.90E3 | 46.15 | 2.88E3 | 688.00 | |
| F07 | 126.40 | 42.72 | 143.40 | 33.13 | 0.31 | 65.62 | 21.11 |
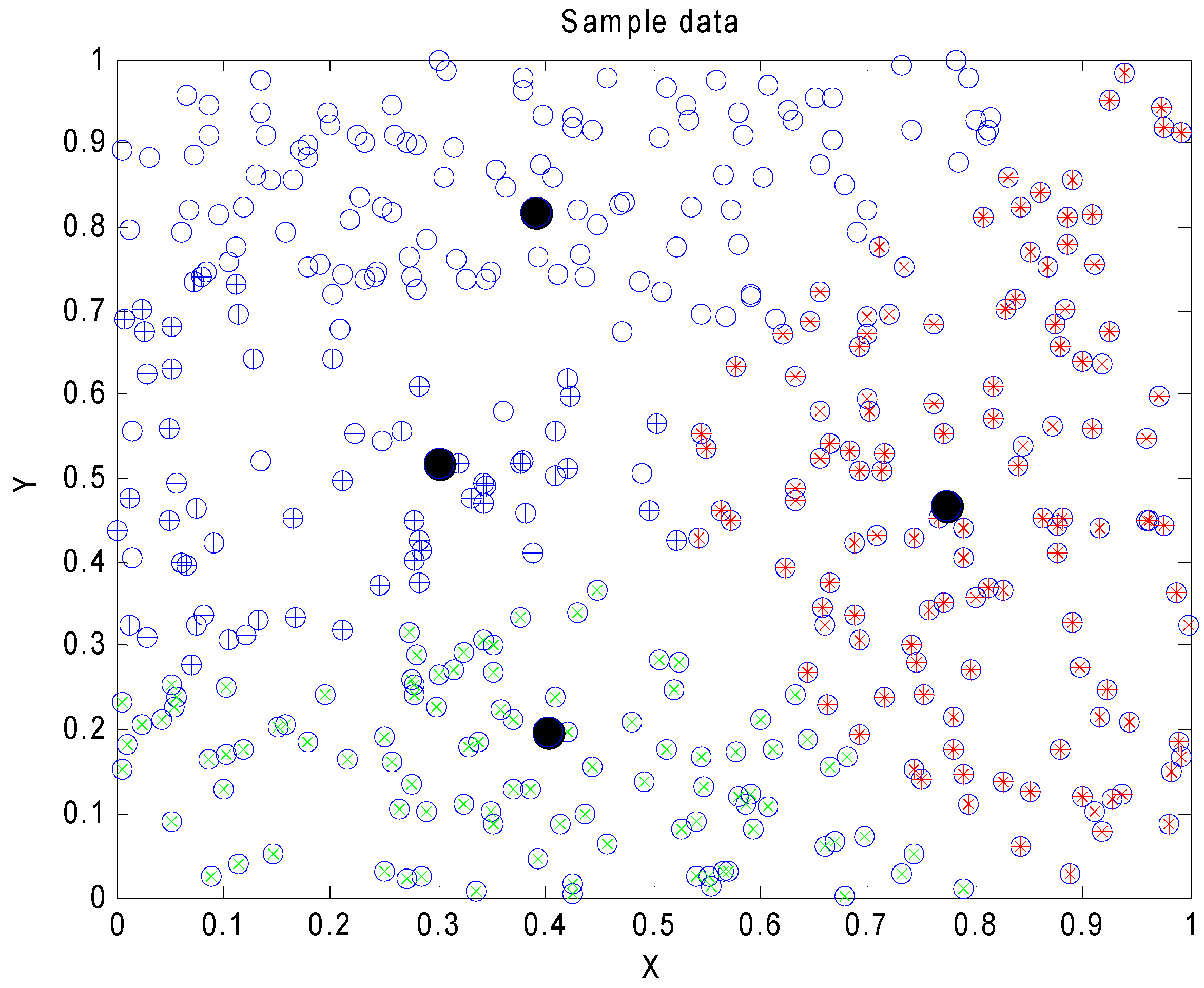
4.2. Clustering Problem Compared KHE with Seven Other Methods
| ACO | FCM | GA | HS | KH | KHE | PSO | SGA | |
|---|---|---|---|---|---|---|---|---|
| Mean | 3.303556 | 3.368558 | 3.303527 | 3.303536 | 3.303624 | 3.303510 | 3.303542 | 3.303523 |
| Best | 3.303474 | 3.303478 | 3.303466 | 3.303468 | 3.303471 | 3.303462 | 3.303463 | 3.303462 |
| Worst | 3.303766 | 3.728121 | 3.303766 | 3.303766 | 3.303766 | 3.303766 | 3.303766 | 3.303766 |
| Std | 5.6032E−5 | 0.09555 | 5.9076E−5 | 4.0144E−5 | 1.1470E−4 | 4.6495E−5 | 5.0819E−5 | 5.1780E−5 |
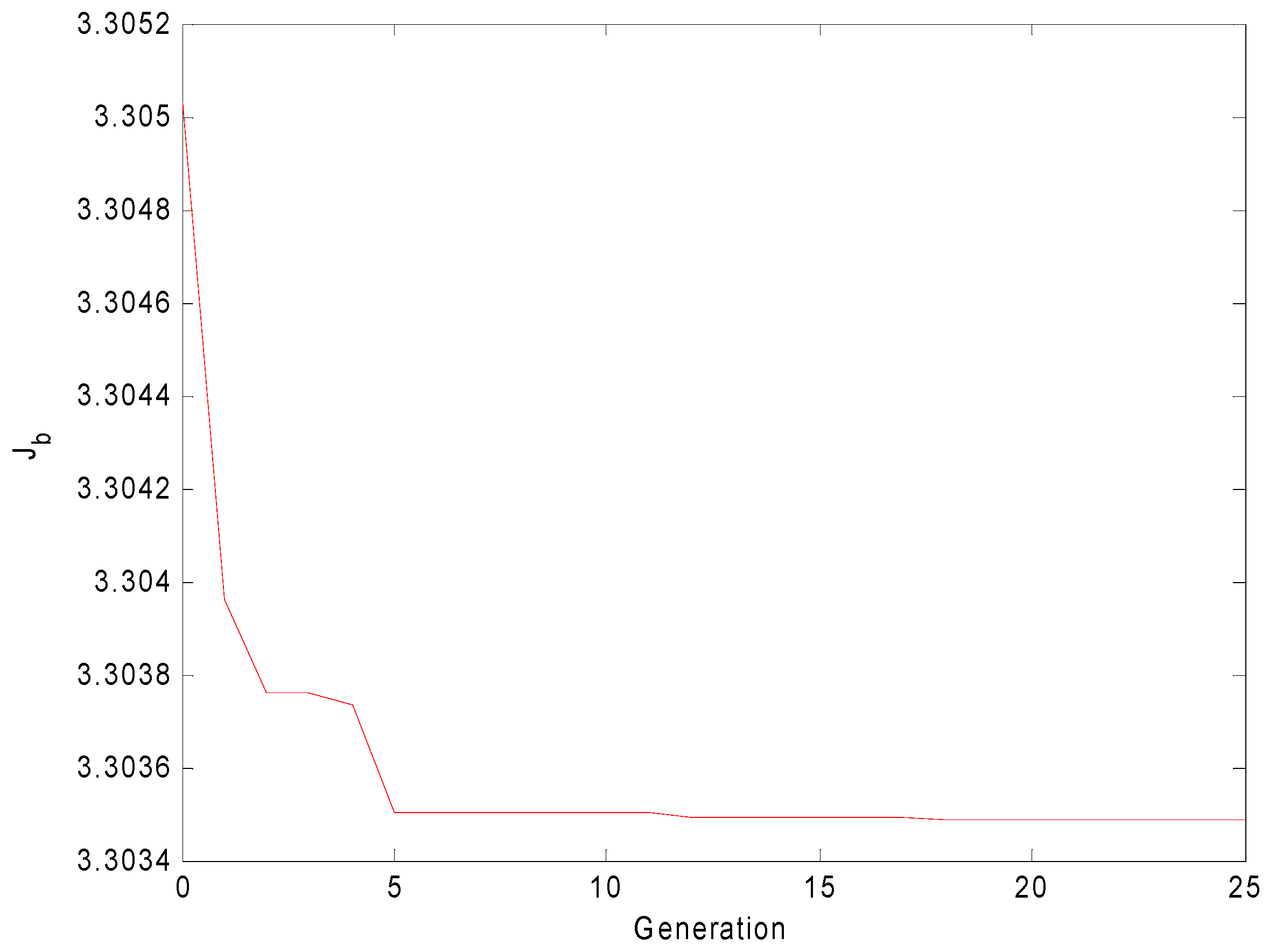

5. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar]
- Saremi, S.; Mirjalili, S.Z.; Mirjalili, S.M. Evolutionary population dynamics and grey wolf optimizer. Neural. Comput. Appl. 2014, 26, 1257–1263. [Google Scholar] [CrossRef]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization and Machine Learning; Addison-Wesley: New York, NY, USA, 1998. [Google Scholar]
- Simon, D. Biogeography-based optimization. IEEE Trans. Evol. Comput. 2008, 12, 702–713. [Google Scholar] [CrossRef]
- Saremi, S.; Mirjalili, S.; Lewis, A. Biogeography-based optimisation with chaos. Neural. Comput. Appl. 2014, 25, 1077–1097. [Google Scholar] [CrossRef]
- Wang, G.G.; Gandomi, A.H.; Alavi, A.H. An effective krill herd algorithm with migration operator in biogeography-based optimization. Appl. Math. Model. 2014, 38, 2454–2462. [Google Scholar] [CrossRef]
- Li, X.; Zhang, J.; Yin, M. Animal migration optimization: An optimization algorithm inspired by animal migration behavior. Neural. Comput. Appl. 2014, 24, 1867–1877. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. Gsa: A gravitational search algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Mirjalili, S.; Wang, G.G.; Coelho, L.D.S. Binary optimization using hybrid particle swarm optimization and gravitational search algorithm. Neural. Comput. Appl. 2014, 25, 1423–1435. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. Adaptive gbest-guided gravitational search algorithm. Neural. Comput. Appl. 2014, 25, 1569–1584. [Google Scholar] [CrossRef]
- Yang, X.S.; Deb, S. Cuckoo search via lévy flights. In Proceeding of the World Congress on Nature & Biologically Inspired Computing (NaBIC 2009), Coimbatore, India, 9–11 December 2009; Abraham, A., Carvalho, A., Herrera, F., Pai, V., Eds.; IEEE Publications: Coimbatore, India, 2009; pp. 210–214. [Google Scholar]
- Li, X.; Wang, J.; Yin, M. Enhancing the performance of cuckoo search algorithm using orthogonal learning method. Neural. Comput. Appl. 2013, 24, 1233–1247. [Google Scholar] [CrossRef]
- Wang, G.G.; Deb, S.; Gandomi, A.H.; Zhang, Z.; Alavi, A.H. Chaotic cuckoo search. Soft Comput. 2015. [Google Scholar] [CrossRef]
- Wang, G.G.; Gandomi, A.H.; Zhao, X.; Chu, H.E. Hybridizing harmony search algorithm with cuckoo search for global numerical optimization. Soft Comput. 2014, 25, 1423–1435. [Google Scholar] [CrossRef]
- Wang, G.G.; Gandomi, A.H.; Yang, X.S.; Alavi, A.H. A new hybrid method based on krill herd and cuckoo search for global optimization tasks. Int. J. Bio-Inspir. Comput. 2012. Available online: http://www.inderscience.com/info/ingeneral/forthcoming.php?jcode=ijbic (accessed on 21 October 2015).
- Khatib, W.; Fleming, P. The stud ga: A mini revolution? In Proceedings of the 5th International Conference on Parallel Problem Solving from Nature, New York, NY, USA, 4–9 May 1998; Eiben, A., Back, T., Schoenauer, M., Schwefel, H., Eds.; Springer-Verlag: New York, NY, USA, 1998; pp. 683–691. [Google Scholar]
- Fong, S.; Deb, S.; Yang, X.S. A heuristic optimization method inspired by wolf preying behavior. Neural. Comput. Appl. 2015, 26, 1725–1738. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Hatamlou, A. Multi-verse optimizer: A nature-inspired algorithm for global optimization. Neural. Comput. Appl. 2015. [Google Scholar] [CrossRef]
- Mirjalili, S. Dragonfly algorithm: A new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems. Neural. Comput. Appl. 2015. [Google Scholar] [CrossRef]
- Mirjalili, S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl-Based Syst. 2015. [Google Scholar] [CrossRef]
- Wang, G.G.; Deb, S.; Coelho, L.D.S. Earthworm optimization algorithm: A bio-inspired metaheuristic algorithm for global optimization problems. Int. J. Bio-Inspir. Comput. 2015. Available online: http://www.inderscience.com/info/ingeneral/forthcoming.php?jcode=ijbic_ (accessed on 21 October 2015).
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. A new heuristic optimization algorithm: Harmony search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Wang, G.; Guo, L.; Duan, H.; Wang, H.; Liu, L.; Shao, M. Hybridizing harmony search with biogeography based optimization for global numerical optimization. J. Comput. Theor. Nanosci. 2013, 10, 2318–2328. [Google Scholar] [CrossRef]
- Yang, X.S. Firefly algorithm, stochastic test functions and design optimisation. Int. J. Bio-Inspir. Comput. 2010, 2, 78–84. [Google Scholar] [CrossRef]
- Wang, G.G.; Guo, L.; Duan, H.; Wang, H. A new improved firefly algorithm for global numerical optimization. J. Comput. Theor. Nanosci. 2014, 11, 477–485. [Google Scholar] [CrossRef]
- Wang, G.; Guo, L.; Duan, H.; Liu, L.; Wang, H. A modified firefly algorithm for ucav path planning. Int. J. Hybrid Inf. Technol. 2012, 5, 123–144. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceeding of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948.
- Mirjalili, S.; Lewis, A. S-shaped versus v-shaped transfer functions for binary particle swarm optimization. Swarm. Evol. Comput. 2013, 9, 1–14. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A.; Sadiq, A.S. Autonomous particles groups for particle swarm optimization. Arab. J. Sci. Eng. 2014, 39, 4683–4697. [Google Scholar] [CrossRef]
- Wang, G.G.; Deb, S.; Cui, Z. Monarch butterfly optimization. Neural. Comput. Appl. 2015. [Google Scholar] [CrossRef]
- Dorigo, M.; Maniezzo, V.; Colorni, A. Ant system: Optimization by a colony of cooperating agents. IEEE Trans. Syst. Man Cybern. B Cybern. 1996, 26, 29–41. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.S. Nature-Inspired Metaheuristic Algorithms, 2nd ed.; Luniver Press: Frome, UK, 2010. [Google Scholar]
- Yang, X.S.; Gandomi, A.H. Bat algorithm: A novel approach for global engineering optimization. Eng. Comput. 2012, 29, 464–483. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Yang, X.S. Binary bat algorithm. Neural. Comput. Appl. 2013, 25, 663–681. [Google Scholar] [CrossRef]
- Zhang, J.W.; Wang, G.G. Image matching using a bat algorithm with mutation. Appl. Mech. Mater. 2012, 203, 88–93. [Google Scholar] [CrossRef]
- Yang, X.S.; He, X. Bat algorithm: Literature review and applications. Int. J. Bio-Inspir. Comput. 2013, 5, 141–149. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution-A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Zou, D.; Wu, J.; Gao, L.; Li, S. A modified differential evolution algorithm for unconstrained optimization problems. Neurocomputing 2013, 120, 469–481. [Google Scholar] [CrossRef]
- Zou, D.; Liu, H.; Gao, L.; Li, S. An improved differential evolution algorithm for the task assignment problem. Eng. Appl. Artif. Intell. 2011, 24, 616–624. [Google Scholar] [CrossRef]
- Wang, G.G.; Gandomi, A.H.; Yang, X.S.; Alavi, A.H. A novel improved accelerated particle swarm optimization algorithm for global numerical optimization. Eng. Comput. 2014, 31, 1198–1220. [Google Scholar] [CrossRef]
- Gandomi, A.H. Interior search algorithm (isa): A novel approach for global optimization. ISA Trans. 2014, 53, 1168–1183. [Google Scholar] [CrossRef] [PubMed]
- Zou, D.; Gao, L.; Wu, J.; Li, S.; Li, Y. A novel global harmony search algorithm for reliability problems. Comput. Ind. Eng. 2010, 58, 307–316. [Google Scholar] [CrossRef]
- Zou, D.; Gao, L.; Li, S.; Wu, J. An effective global harmony search algorithm for reliability problems. Expert Syst. Appl. 2011, 38, 4642–4648. [Google Scholar] [CrossRef]
- Zou, D.; Gao, L.; Li, S.; Wu, J. Solving 0–1 knapsack problem by a novel global harmony search algorithm. Appl. Soft. Compt. 2011, 11, 1556–1564. [Google Scholar] [CrossRef]
- Li, X.; Yin, M. Application of differential evolution algorithm on self-potential data. PLoS ONE 2012, 7, e51199. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Yin, M. An opposition-based differential evolution algorithm for permutation flow shop scheduling based on diversity measure. Adv. Eng. Softw. 2013, 55, 10–31. [Google Scholar] [CrossRef]
- Wang, G.; Guo, L.; Duan, H.; Liu, L.; Wang, H.; Shao, M. Path planning for uninhabited combat aerial vehicle using hybrid meta-heuristic de/bbo algorithm. Adv. Sci. Eng. Med. 2012, 4, 550–564. [Google Scholar] [CrossRef]
- Li, X.; Yin, M. Parameter estimation for chaotic systems by hybrid differential evolution algorithm and artificial bee colony algorithm. Nonlinear Dyn. 2014, 77, 61–71. [Google Scholar] [CrossRef]
- Li, X.; Wang, J.; Zhou, J.; Yin, M. A perturb biogeography based optimization with mutation for global numerical optimization. Appl. Math. Comput. 2011, 218, 598–609. [Google Scholar] [CrossRef]
- Li, X.; Yin, M. Multi-operator based biogeography based optimization with mutation for global numerical optimization. Comput. Math. Appl. 2012, 64, 2833–2844. [Google Scholar] [CrossRef]
- Li, X.; Yin, M. Self-adaptive constrained artificial bee colony for constrained numerical optimization. Neural. Comput. Appl. 2012, 24, 723–734. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mohd Hashim, S.Z.; Moradian Sardroudi, H. Training feedforward neural networks using hybrid particle swarm optimization and gravitational search algorithm. Appl. Math. Comput. 2012, 218, 11125–11137. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Let a biogeography-based optimizer train your multi-layer perceptron. Inf. Sci. 2014, 269, 188–209. [Google Scholar] [CrossRef]
- Li, X.; Yin, M. Multiobjective binary biogeography based optimization for feature selection using gene expression data. IEEE Trans. Nanobiosci. 2013, 12, 343–353. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Alavi, A.H. Krill herd: A new bio-inspired optimization algorithm. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 4831–4845. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Talatahari, S.; Tadbiri, F.; Alavi, A.H. Krill herd algorithm for optimum design of truss structures. Int. J. Bio-Inspir. Comput. 2013, 5, 281–288. [Google Scholar] [CrossRef]
- Wang, G.G.; Gandomi, A.H.; Alavi, A.H.; Hao, G.S. Hybrid krill herd algorithm with differential evolution for global numerical optimization. Neural. Comput. Appl. 2014, 25, 297–308. [Google Scholar] [CrossRef]
- Wang, G.G.; Gandomi, A.H.; Alavi, A.H. Stud krill herd algorithm. Neurocomputing 2014, 128, 363–370. [Google Scholar] [CrossRef]
- Wang, G.; Guo, L.; Wang, H.; Duan, H.; Liu, L.; Li, J. Incorporating mutation scheme into krill herd algorithm for global numerical optimization. Neural. Comput. Appl. 2014, 24, 853–871. [Google Scholar] [CrossRef]
- Guo, L.; Wang, G.G.; Gandomi, A.H.; Alavi, A.H.; Duan, H. A new improved krill herd algorithm for global numerical optimization. Neurocomputing 2014, 138, 392–402. [Google Scholar] [CrossRef]
- Wang, G.G.; Gandomi, A.H.; Alavi, A.H. Study of lagrangian and evolutionary parameters in krill herd algorithm. In Adaptation and Hybridization in Computational Intelligence; Fister, I., Fister, I., Jr., Eds.; Springer International Publishing: Cham, Switzerland, 2015; Volume 18, pp. 111–128. [Google Scholar]
- Wang, G.G.; Gandomi, A.H.; Alavi, A.H.; Deb, S. A hybrid method based on krill herd and quantum-behaved particle swarm optimization. Neural. Comput. Appl. 2015. [Google Scholar] [CrossRef]
- Wang, G.G.; Guo, L.; Gandomi, A.H.; Hao, G.S.; Wang, H. Chaotic krill herd algorithm. Inf. Sci. 2014, 274, 17–34. [Google Scholar] [CrossRef]
- Yang, X.S.; Cui, Z.; Xiao, R.; Gandomi, A.H.; Karamanoglu, M. Swarm Intelligence and Bio-Inspired Computation; Elsevier: Waltham, MA, USA, 2013. [Google Scholar]
- Jamil, M.; Yang, X.S. A literature survey of benchmark functions for global optimisation problems. Int. J. Math. Model. Numer. Optim. 2013, 4, 150–194. [Google Scholar] [CrossRef]
- Wang, G.G.; Gandomi, A.H.; Alavi, A.H. A chaotic particle-swarm krill herd algorithm for global numerical optimization. Kybernetes 2013, 42, 962–978. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, Z.; Liu, S. A optimization clustering algorithm based on simulated annealing and genetic algorithm. Microcomput. Inf. 2006, 22, 270–272. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.-Y.; Yi, J.-H.; Wang, G.-G. A New Swarm Intelligence Approach for Clustering Based on Krill Herd with Elitism Strategy. Algorithms 2015, 8, 951-964. https://doi.org/10.3390/a8040951
Li Z-Y, Yi J-H, Wang G-G. A New Swarm Intelligence Approach for Clustering Based on Krill Herd with Elitism Strategy. Algorithms. 2015; 8(4):951-964. https://doi.org/10.3390/a8040951
Chicago/Turabian StyleLi, Zhi-Yong, Jiao-Hong Yi, and Gai-Ge Wang. 2015. "A New Swarm Intelligence Approach for Clustering Based on Krill Herd with Elitism Strategy" Algorithms 8, no. 4: 951-964. https://doi.org/10.3390/a8040951
APA StyleLi, Z.-Y., Yi, J.-H., & Wang, G.-G. (2015). A New Swarm Intelligence Approach for Clustering Based on Krill Herd with Elitism Strategy. Algorithms, 8(4), 951-964. https://doi.org/10.3390/a8040951







