1. Introduction
We can find the origins of continuous Newton’s method in the seminal paper of Neuberger [
1]. Actually, it appears in the study of the basins of attraction related with the relaxed Newton’s method for solving a complex equation
It is well known, since the works of Cayley and Schröder at the end of the 19th century, and Fatou and Julia in the early 20th century, that the basins of attraction of Newton’s method (obtained for
in Equation (
1)) have an intricate fractal structure. Neuberger, as well other authors ([
2,
3]), has realized that this fractal structure shrinks away when
, as we can appreciate in
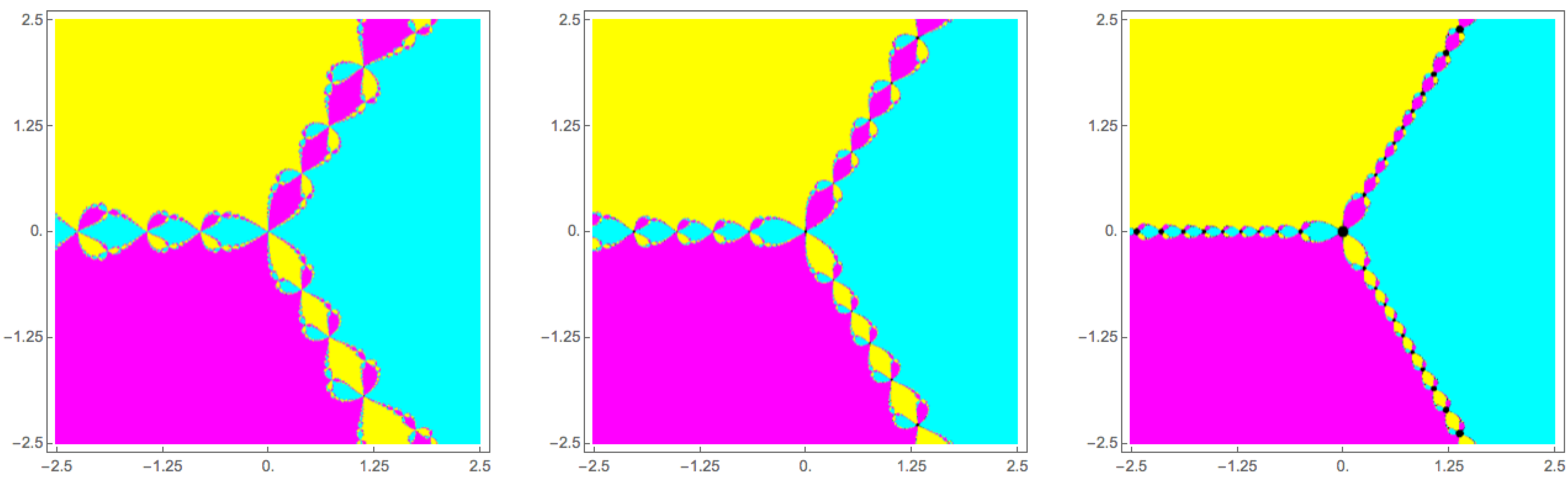
Figure 1.
Figure 1.
Basins of attraction of the relaxed Newton’s method given in Equation (
1) applied to the polynomial
for
,
and
, respectively.
Figure 1.
Basins of attraction of the relaxed Newton’s method given in Equation (
1) applied to the polynomial
for
,
and
, respectively.
We can identify iterative method Equation (
1) as an Euler approximation of the differential equation
with step size
h.
Initial value problem Equation (
2), or its improved version of finding a function
such that
for a given
z0 ∈
, where
p is a non-constant complex polynomial is known as continuous Newton’s method. We refer to [
1] for the theoretical basis of continuous Newton’s method. In particular, it is shown that solutions
of Equation (
2) (or Equation (3)) flow to a zero of
p while keeping the argument of
constant at
.
For instance, as it was pointed out by Jacobsen
et al. [
3], if
in Equation (
2), the explicit solution is
The choice of the appropriate branch of the cube root, defined by the rays
,
and
, determines the ternary division of the complex plane that can be seen in the three graphics of
Figure 1. According to these authors, the fractal boundaries in the basins of attraction of the roots can be originated by numerical errors inherent to the discretization of initial value problem Equation (
2).
This work is two fold. In
Section 2, we consider other different strategies (not only Euler’s method) for solving initial value problem Equation (
2). The efficiency of the iterative processes obtained in this way is analyzed.
2. Numerical Algorithms Applied to Continuous Newton’s Method
In [
3] the dynamical properties of six numerical methods for solving differential equations are considered when they are applied to continuous Newton’s method Equation (
2). In particular, they compare the basins of attraction of these methods applied to Equation (
2) for
. They estimate the corresponding fractal dimension using a box-counting algorithm. The main conclusion is that higher-order algorithms are not necessarily related with basin boundaries with smaller fractal dimension.
In this section we are concerned with some numerical properties of root-finding methods derived from the application of numerical methods for solving differential equations
as continuous Newton’s method Equation (
2). So, as it has been done in [
3], we use
for the approximations of
, where
and
h for the step size. The six methods considered by Jacobsen
et al. in [
3] are:
Runge-Kutta method of order 2:
Runge-Kutta method of order 4:
Adams-Bashforth method of order 2:
Note that, in the case of continuous Newton’s method, the function
that appears in differential equation Equation (4) is
So, the application of Euler’s method Equation (5) gives rise to the root-finding algorithm
that is the wel-known relaxed Newton’s method. Note that the role of the step size
h in the methods for solving differential equations is moved to a relaxing parameter in Equation (12). As it was stated in [
3] and we have previously mentioned,
h has a clear influence in the dynamical properties of an iterative method. We analyze now the influence of
h in the numerical properties of an iterative method. Let
be the iteration map related to the relaxed Newton’s method Equation (12) and let
be a simple root of
. It is a straightforward calculation to show that
So, we have that method Equation (12) is consistent (the roots of p are attracting fixed points of the iteration map ) only for . In addition, we obtain iterative methods with just linear convergence, except for the case , that is the classical Newton’s method with quadratic convergence.
Now, we see what happens with the refined Euler’s method defined in Equation (6). The corresponding root-finding algorithm can be written as
If
is a simple root of
, we have
, where
Therefore,
,
and then
As a consequence, iterative method Equation (12) is consistent only for . All the methods deduced in this case have linear convergence (the lower value for the asymptotic constant error is obtained for ). This fact together with a number of function evaluations equals to four, makes this method uninteresting from an efficiency point of view.
Something similar happens with Heun’s method given in Equation (7) and Runge-Kutta method of second order given in Equation (8). They have different iteration maps, respectively
and
, where
In both cases, we have
for a simple root
of
. So, as in the case of the refined Euler’s method, only linear convergence is achieved for
and then these two methods are inefficient from a numerical perspective.
The study of the Runge-Kutta method of order fourth defined in Equation (9) applied to Equation (4) leads us to the iteration scheme
, where
and
Note that, for a simple root
, we have
,
,
,
,
,
and then
There are no real values of h such that , then only linear convergence can be attained. In addition, we obtain consistent methods, that is is an attracting fixed point of if . These inequalities happens for where is, approximately, the only real root of the polynomial . The optimum value for h, for which the asymptotic error constant has the lowest value, is . In this case .
The analysis of the Adams-Bahforth second order method given in Equation (10) leads us to the following two-step multipoint method:
To study the local order of convergence related to Equation (14), we consider a simple root
of
and the error in the
n-th step
. Then,
where the terms of order higher than two in the error have been neglected. This approached formula for the errors generates a linear recurrence of second order, whose characteristic equation is
Consequently, the method Equation (14) is consistent if the two roots of the previous equation,
have module less than one. Note that
for all
but
for
. So, the consistency condition is satisfied only if
. In this case,
and
. Taking into account that
is a decreasing function for
and
is an increasing function for
, we can then obtain the best convergence rate when
, that is, for
.
In
Table 1 we show, in brief, the numerical information that we have deduced for methods Equations (5)–(9) considered by Jacobsen
et al. in [
3]. In fact, for each method, we show the asymptotic error constant (A.E.C.), the interval of values of
h for which consistent methods are obtained (I.C.) and the optimal value for
h regarding the order of convergence,
. In addition, the Adams-Basforth method given in Equation (10) is consistent for
with
. As a conclusion, we can say that, despite the order of the numerical methods for solving differential equations and the size of the step
h, the root-finding algorithms derived from their application to continuous Newton’s method Equation (
2) have only a linear order of convergence, with the exception of Euler’s method with
, where the convergence is quadratic. In this sense, we conclude that the numerical efficiency of these methods is poor. However, the study of the aforementioned methods can be interesting from other points of view, that reveals other topological or dynamical aspects as, for instance, the impact of the stepsize on the fractal dimension of the boundaries of the basins of attraction for the associated roots.
Table 1.
Some numerical properties of the root-finding methods obtained after applying methods Equations (5)–(9) to continuous Newton’s method Equation (
2).
Table 1.
Some numerical properties of the root-finding methods obtained after applying methods Equations (5)–(9) to continuous Newton’s method Equation (2).
| Method | A.E.C. | I.C. | |
|---|
| Euler Equation (5) | | | 1 |
| Refined Euler Equation (6) | | | 1 |
| Heun Equation (7) | | | 1 |
| Runge-Kutta 2 Equation (8) | | | 1 |
| Runge-Kutta 4 Equation (9) | | | |
3. Numerical Algorithms with Non-Constant Step Size
As we can see, the application of the numerical algorithms considered in [
3] to the continuous Newton’s method Equation (
2) generates iterative root finding methods that does not present a high numerical efficiency. The situation does not improve if we consider higher order numerical methods for the initial value problem Equation (
2). In fact, if we consider the second order Taylor’s method
we obtain the following iterative method
where
has been defined in Equation (13). But, once again,
so that the convergence of the method is just linear although the number of functional evaluations have been increased.
To avoid these difficulties, we can consider iterative methods with a non-constant step size. For instance, instead of considering method Equation (12) derived from Euler’s method, we consider methods where the step
h is substituted by a non-constant function
:
As in the previous section, if we consider a simple root
of
, we have
. In addition,
So, if we consider a function
H that satisfies conditions Equations (16) and (17), we can obtain iterative methods with at least cubic convergence. One choice (not the only one) for function
H that fulfills Equations (16) and (17) is
that leads us to the well-known Chebyshev’s method ([
4,
5]):
Even more, if we choose
we deduce the well-known Chebyshev-Halley family of methods ([
4,
5]):
Note that Chebyshev’s iterative method defined in Equation (18) is one of the methods defined in Equation (19), actually for
. Other methods belonging to this family are Halley’s method (
) or super-Halley’s method (
). The dynamical behavior of methods in the family Equation (19) have been studied in detail in the work of Cordero
et al. [
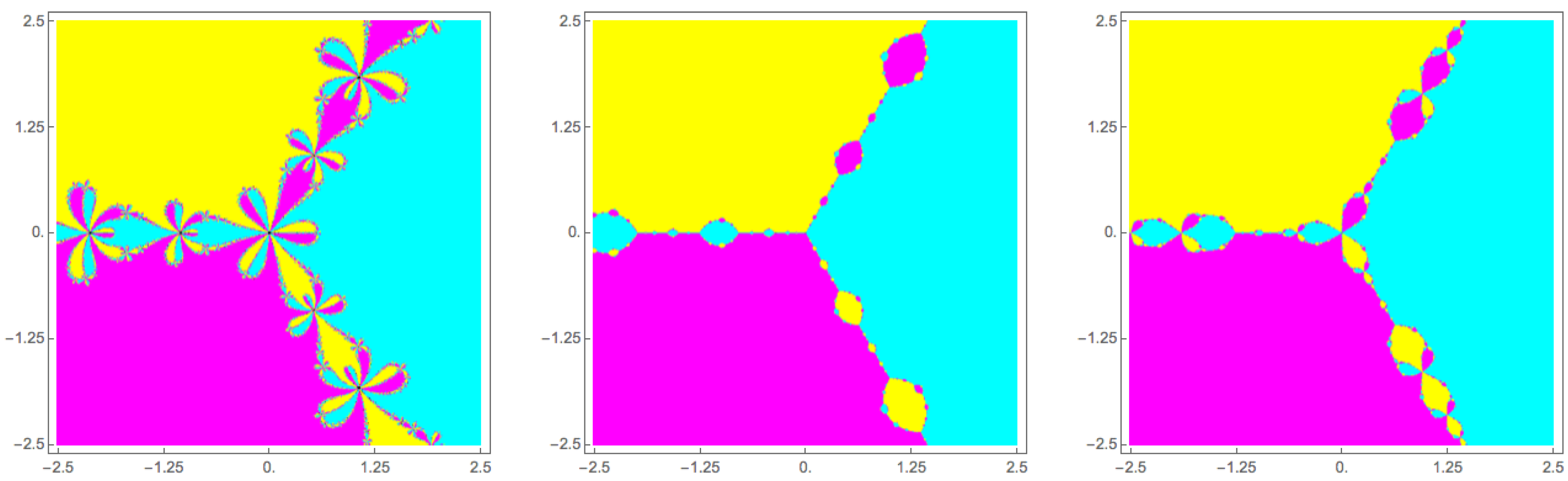
6]. The structure and dynamical properties of the basins of attraction of the roots of a given function changes depending on the choice of the iterative method considered for solving the equation. As a visual sample we show in
Figure 2 the basins of attraction of three methods in family Equation (19) when they applied to the polynomial
.
Figure 2.
Basins of attraction of the Chebyshev, Halley and super-Halley methods (, and , respectively, in Equation (19)) applied to the polynomial .
Figure 2.
Basins of attraction of the Chebyshev, Halley and super-Halley methods (, and , respectively, in Equation (19)) applied to the polynomial .
We can generalize family Equation (19) to obtain the general form of methods with cubic convergence given by Gander in [
7]. In fact, the iteration given by
where
H is a function satisfying
,
and
, has cubic convergence to simple roots of
p. The task of extending in this way Gander’s result to a higher order of convergence seems to be difficult. An approach for the quadratic case was given by Romero
et al. in [
8].