Model Equivalence-Based Identification Algorithm for Equation-Error Systems with Colored Noise
Abstract
:1. Introduction
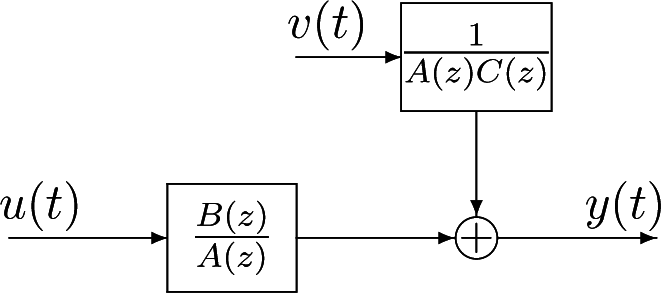
2. The Identification Model for an EEAR System
3. The Recursive Generalized Least Squares Algorithm
4. The Model Equivalence-Based Recursive Least Squares Algorithm
5. The Parameter Estimation of the Original System
6. Numerical Example
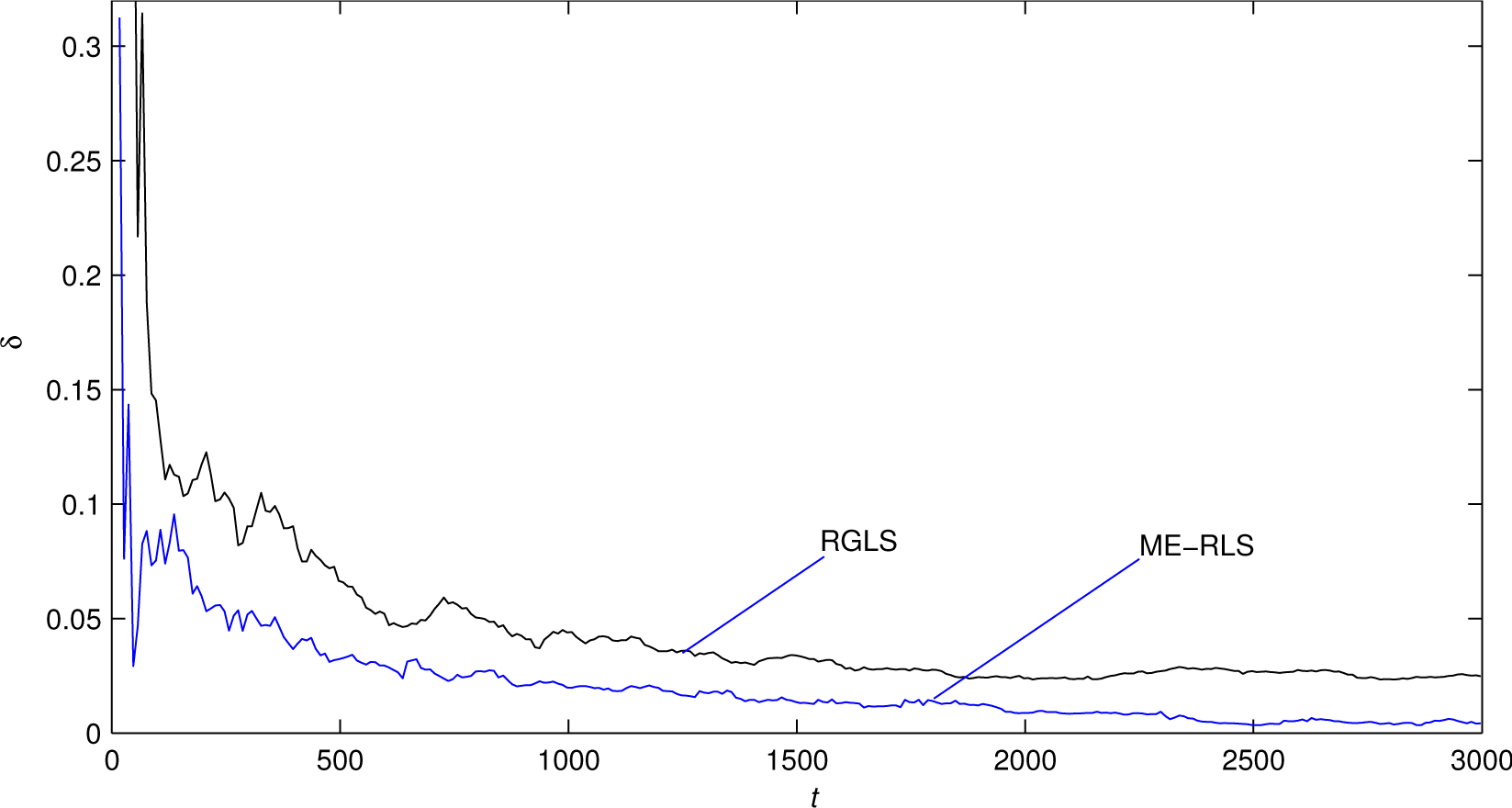
- The estimation errors of the ME-RLS algorithm become smaller, and the estimates converge to their true values with the data length increasing (i.e., the proposed algorithm works well).
- The estimation errors of the ME-RLS algorithm are smaller than those of the RGLS algorithm, which means that the parameter estimates given by the ME-RLS algorithm have higher accuracy than the RGLS algorithm for CARAR systems.
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Scarpiniti, M.; Comminiello, D.; Parisi, R.; Uncini, A. Nonlinear system identification using IIR Spline Adaptive Filtering. Signal Process. 2015, 108, 30–35. [Google Scholar]
- Li, H.; Shi, Y. Robust H-infty filtering for nonlinear stochastic systems with uncertainties and random delays modeled by Markov chains. Automatica 2012, 48, 159–166. [Google Scholar]
- Zhang, L.; Wang, Z.P.; Sun, F.C.; Dorrell, D.G. Online parameter identification of ultracapacitor models using the extended kalman filter. Algorithms 2014, 7, 3204–3217. [Google Scholar]
- Viegas, D.; Batista, P.; Oliveira, P.; Silvestre, C.; Chen, C.L.P. Distributed state estimation for linear multi-agent systems with time-varying measurement topology. Automatica 2015, 54, 72–79. [Google Scholar]
- Fang, H.; Wu, J.; Shi, Y. Genetic adaptive state estimation with missing input/output data. Proc. Inst. Mech. Eng. Part I: J. Syst. Control Eng. 2010, 224, 611–617. [Google Scholar]
- Fang, H.Z.; Shi, Y.; Yi, J.G. On stable simultaneous input and state estimation for discrete-time linear systems. Int. J. Adapt. Control Signal Process. 2011, 25, 671–686. [Google Scholar]
- Chen, F.W.; Garnier, H.; Gilson, M. Robust identification of continuous-time models with arbitrary time-delay from irregularly sampled data. J. Process Control 2015, 25, 19–27. [Google Scholar]
- Na, J.; Yang, J.; Wu, X.; Guo, Y. Robust adaptive parameter estimation of sinusoidal signals. Automatica 2015, 53, 376–384. [Google Scholar]
- Rincón, F.D.; Roux, G.A.C.L.; Lima, F.V. A novel ARX-based approach for the steady-state identification analysis of industrial depropanizer column datasets. Algorithms 2015, 3, 257–285. [Google Scholar]
- Upadhyay, P.; Kar, R.; Mandal, D.; Ghoshal, S.P.; Mukherjee, V. A novel design method for optimal IIR system identification using opposition based harmony search algorithm. J. Frankl. Inst. 2014, 351, 2454–2488. [Google Scholar]
- Scarpiniti, M.; Comminiello, D.; Parisi, R.; Uncini, A. Nonlinear spline adaptive filtering. Signal Process. 2013, 93, 772–783. [Google Scholar]
- Zhuang, L.F.; Pan, F.; Ding, F. Parameter and state estimation algorithm for single-input single-output linear systems using the canonical state space models. Appl. Math. Model. 2012, 36, 3454–3463. [Google Scholar]
- Khan, N.; Khattak, M.I.; Gu, D. Robust state estimation and its application to spacecraft control. Automatica 2012, 48, 3142–3150. [Google Scholar]
- Ding, F.; Liu, X.P.; Liu, G. Gradient based and least-squares based iterative identification methods for OE and OEMA systems. Digit. Signal Process. 2010, 20, 664–677. [Google Scholar]
- Ma, X.Y.; Ding, F. Gradient-based parameter identification algorithms for observer canonical state space systems using state estimates. Circuits Syst. Signal Process. 2015, 34, 1697–1709. [Google Scholar]
- Cao, Y.N.; Liu, Z.Q. Signal frequency and parameter estimation for power systems using the hierarchical dentification principle. Math. Comput. Model. 2010, 51, 854–861. [Google Scholar]
- Ding, F. Hierarchical parameter estimation algorithms for multivariable systems using measurement information. Inf. Sci. 2014, 227, 396–405. [Google Scholar]
- Liu, Y.J.; Ding, F.; Shi, Y. Least squares estimation for a class of non-uniformly sampled systems based on the hierarchical identification principle. Circuits Syst. Signal Process. 2012, 31, 1985–2000. [Google Scholar]
- Ding, J.; Fan, C.X.; Lin, J.X. Auxiliary model based parameter estimation for dual-rate output error systems with colored noise. Appl. Math. Model. 2013, 37, 4051–4058. [Google Scholar]
- Liu, Y.J.; Xiao, Y.S.; Zhao, X.L. Multi-innovation stochastic gradient algorithm for multiple-input single-output systems using the auxiliary model. Appl. Math. Comput. 2009, 215, 1477–1483. [Google Scholar]
- Hu, Y.B.; Liu, B.L.; Zhou, Q. A multi-innovation generalized extended stochastic gradient algorithm for output nonlinear autoregressive moving average systems. Appl. Math. Comput. 2014, 247, 218–224. [Google Scholar]
- Wang, C.; Tang, T. Recursive least squares estimation algorithm applied to a class of linear-in-parameters output error moving average systems. Appl. Math. Lett. 2014, 29, 36–41. [Google Scholar]
- Dehghan, M.; Hajarian, M. The generalized QMRCGSTAB algorithm for solving Sylvester-transpose matrix equations. Appl. Math. Lett. 2013, 26, 1013–1017. [Google Scholar]
- Hu, Y.B.; Liu, B.L.; Zhou, Q.; Yang, C. Recursive extended least squares parameter estimation for Wiener nonlinear systems with moving average noises. Circuits Syst. Signal Process. 2014, 33, 655–664. [Google Scholar]
- Wang, C.; Tang, T. Several gradient-based iterative estimation algorithms for a class of nonlinear systems using the filtering technique. Nonlinear Dyn. 2014, 77, 769–780. [Google Scholar]
- Hu, Y.B. Iterative and recursive least squares estimation algorithms for moving average systems. Simul. Model. Pract. Theory 2013, 34, 12–19. [Google Scholar]
- Zhang, W.G. Decomposition based least squares iterative estimation for output error moving average systems. Eng. Comput. 2014, 31, 709–725. [Google Scholar]
- Ding, F. System Identification—New Theory and Methods; Science Press: Beijing, China, 2013. [Google Scholar]
- Yu, F.; Mao, Z.Z.; Jia, M.X.; Yuan, P. Recursive parameter identification of Hammerstein-Wiener systems with measurement noise. Signal Process. 2014, 105, 137–147. [Google Scholar]
- Filipovic, V.Z. Consistency of the robust recursive Hammerstein model identification algorithm. J. Frankl. Inst. 2015, 352, 1932–1945. [Google Scholar]
- Cao, Z.X.; Yang, Y.; Lu, J.Y.; Gao, F.R. Constrained two dimensional recursive least squares model identification for batch processes. J. Process Control 2014, 24, 871–879. [Google Scholar]
- Liu, X.G.; Lu, J. Least squares based iterative identification for a class of multirate systems. Automatica 2010, 46, 549–554. [Google Scholar]
- Kon, J.; Yamashita, Y.; Tanaka, T.; Tashiro, A.; Daiguji, M. Practical application of model identification based on ARX models with transfer functions. Control Eng. Pract. 2013, 21, 195–203. [Google Scholar]
- Shardt, Y.A.W.; Huang, B. Closed-loop identification condition for ARMAX models using routing operating data. Automatica 2011, 47, 1534–1537. [Google Scholar]
- Chen, H.B.; Ding, F. Hierarchical least squares identification for Hammerstein nonlinear controlled autoregressive systems. Circuits Syst. Signal Process. 2015, 34, 61–75. [Google Scholar]
- Xiao, Y.S.; Yue, N. Parameter estimation for nonlinear dynamical adjustment models. Math. Comput. Model. 2011, 54, 1561–1568. [Google Scholar]
- Li, J.H. Parameter estimation for Hammerstein CARARMA systems based on the Newton iteration. Appl. Math. Lett. 2013, 26, 91–96. [Google Scholar]
| t | p1 | p2 | p3 | p4 | q1 | q2 | q3 | q4 | δ (%) |
|---|---|---|---|---|---|---|---|---|---|
| 100 | −2.08475 | 2.00319 | −1.31058 | 0.46149 | 0.64205 | −0.64349 | 0.52244 | −0.25044 | 8.32032 |
| 200 | −2.05787 | 1.93093 | −1.19902 | 0.39471 | 0.64234 | −0.62503 | 0.49950 | −0.21433 | 5.72365 |
| 500 | −2.12143 | 2.01030 | −1.18986 | 0.36351 | 0.64167 | −0.66963 | 0.50619 | −0.19317 | 3.17127 |
| 1000 | −2.12381 | 1.97065 | −1.13217 | 0.34035 | 0.64041 | −0.67566 | 0.48170 | −0.18376 | 1.96727 |
| 2000 | −2.13697 | 1.99482 | −1.12626 | 0.32412 | 0.64233 | −0.68648 | 0.48887 | −0.16974 | 0.87634 |
| 3000 | −2.14903 | 2.01217 | −1.12549 | 0.31735 | 0.64077 | −0.69361 | 0.49182 | −0.16431 | 0.43027 |
| True values | −2.15000 | 2.01000 | −1.11500 | 0.31020 | 0.64000 | −0.69200 | 0.48780 | −0.15980 | |
| t | a1 | a2 | b1 | b2 | c1 | c2 | δ1 (%) |
|---|---|---|---|---|---|---|---|
| 100 | −1.72608 | 0.78068 | 0.64169 | −0.40895 | −0.36228 | 0.59524 | 8.32032 |
| 200 | −1.77617 | 0.82717 | 0.64094 | −0.44197 | −0.31792 | 0.52245 | 5.72365 |
| 500 | −1.72733 | 0.78537 | 0.64185 | −0.41403 | −0.41615 | 0.49611 | 3.17127 |
| 1000 | −1.69531 | 0.75136 | 0.64083 | −0.39851 | −0.43859 | 0.47136 | 1.96727 |
| 2000 | −1.61778 | 0.67729 | 0.64252 | −0.35225 | −0.51871 | 0.47880 | 0.87634 |
| 3000 | −1.58944 | 0.64860 | 0.64075 | −0.33525 | −0.55603 | 0.48171 | 0.43027 |
| True values | −1.60000 | 0.66000 | 0.64000 | −0.34000 | −0.55000 | 0.47000 | |
| t | a1 | a2 | b1 | b2 | c1 | c2 | δ2 (%) |
|---|---|---|---|---|---|---|---|
| 100 | −1.42838 | 0.50276 | 0.65682 | −0.24579 | −0.51676 | 0.44419 | 12.68831 |
| 200 | −1.45138 | 0.52495 | 0.64732 | −0.25074 | −0.58370 | 0.40453 | 11.53063 |
| 500 | −1.51420 | 0.58095 | 0.64157 | −0.28291 | −0.51480 | 0.46001 | 6.71055 |
| 1000 | −1.54163 | 0.60665 | 0.63846 | −0.30402 | −0.54078 | 0.47384 | 4.34927 |
| 2000 | −1.57741 | 0.63814 | 0.64101 | −0.32634 | −0.52490 | 0.49242 | 2.38922 |
| 3000 | −1.56865 | 0.63248 | 0.63924 | −0.32090 | −0.53319 | 0.48230 | 2.50582 |
| True values | −1.60000 | 0.66000 | 0.64000 | −0.34000 | −0.55000 | 0.47000 | |
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, D.; Ding, F. Model Equivalence-Based Identification Algorithm for Equation-Error Systems with Colored Noise. Algorithms 2015, 8, 280-291. https://doi.org/10.3390/a8020280
Meng D, Ding F. Model Equivalence-Based Identification Algorithm for Equation-Error Systems with Colored Noise. Algorithms. 2015; 8(2):280-291. https://doi.org/10.3390/a8020280
Chicago/Turabian StyleMeng, Dandan, and Feng Ding. 2015. "Model Equivalence-Based Identification Algorithm for Equation-Error Systems with Colored Noise" Algorithms 8, no. 2: 280-291. https://doi.org/10.3390/a8020280
APA StyleMeng, D., & Ding, F. (2015). Model Equivalence-Based Identification Algorithm for Equation-Error Systems with Colored Noise. Algorithms, 8(2), 280-291. https://doi.org/10.3390/a8020280





