Predicting Student Academic Performance: A Comparison of Two Meta-Heuristic Algorithms Inspired by Cuckoo Birds for Training Neural Networks

Abstract

Predicting student academic performance with a high accuracy facilitates admission decisions and enhances educational services at educational institutions. This raises the need to propose a model that predicts student performance, based on the results of standardized exams, including university entrance exams, high school graduation exams, and other influential factors. In this study, an approach to the problem based on the artificial neural network (ANN) with the two meta-heuristic algorithms inspired by cuckoo birds and their lifestyle, namely, Cuckoo Search (CS) and Cuckoo Optimization Algorithm (COA) is proposed. In particular, we used previous exam results and other factors, such as the location of the student’s high school and the student’s gender as input variables, and predicted the student academic performance. The standard CS and standard COA were separately utilized to train the feed-forward network for prediction. The algorithms optimized the weights between layers and biases of the neuron network. The simulation results were then discussed and analyzed to investigate the prediction ability of the neural network trained by these two algorithms. The findings demonstrated that both CS and COA have potential in training ANN and ANN-COA obtained slightly better results for predicting student academic performance in this case. It is expected that this work may be used to support student admission procedures and strengthen the service system in educational institutions.

1. Introduction

Predicting student academic performance has long been an important research topic [1,2]. Among the issues of higher education institutions, questions concerning admissions remain important. The main objective of the admission system is to determine the candidates who would likely perform well after being accepted into the university. The quality of admitted students has a great influence on the level of research and training within the institution. The failure to perform an accurate admission decision may result in an unsuitable student being admitted to the program. Hence, admission officers want to know more about the academic potential of each student. Accurate predictions help admission officers to distinguish between suitable and unsuitable candidates for an academic program, and identify candidates who would likely do well in the university. The results obtained from the prediction of academic performance may be used for classifying students, which enables educational managers to offer them additional support, such as customized assistance and tutoring resources. The results of this prediction can also be used by instructors to specify the most suitable teaching actions for each group of students, and provide them with further assistance tailored to their needs. In addition, the prediction results may help students develop a good understanding of how well or how poorly they would perform, and then develop a suitable learning strategy. Accurate prediction of student achievement is one way to enhance the quality of education and provide better educational services.

Different approaches have been applied to predicting student academic performance, including traditional mathematical models [3,4] and modern data mining techniques [5,6,7]. In these approaches, a set of mathematical formulas was used to describe the quantitative relationships between outputs and inputs (i.e., predictor variables). The prediction is accurate if the error between the predicted and actual values is within a small range.

The artificial neural network (ANN), a soft computing technique, has been successfully applied in different fields of science, such as pattern recognition, fault diagnosis, forecasting and prediction. However, as far as we are aware, not much research on predicting student academic performance takes advantage of ANN. Kanakana and Olanrewaju [8] utilized a multilayer perception neural network to predict student performance. They used the average point scores of grade 12 students as inputs and the first year college results as output. The research showed that an ANN based model is able to predict student performance in the first semester with high accuracy. A multiple feed-forward neural network was proposed [6] to predict the students’ final achievement and to classify them into two groups. In their work, a student achievement prediction method was applied to a 10-week course. The results showed that accurate prediction is possible at an early stage, and more specifically at the third week of the 10-week course. Oladokun et al. [9] used an ANN model to predict the performance of a candidate being considered for admission into university. The results indicated that the ANN model is able to correctly predict the performance of more than 70% of the prospective students. The aforementioned studies revealed the great success of neural networks in the prediction of student academic performance.

Training algorithms play an important role in enhancing the quality of ANNs. Our aim is to use the efficient training algorithm for constructing a neural network that accurately predicts students’ academic performance. When a neural network is structured for a particular application, it must be trained before being used to classify test data. The aim of the training phase is to minimize a cost function defined as the mean squared error or sum squared error between its actual and target outputs by adjusting weights and biases. Presenting a satisfactory and efficient training algorithm has always been a challenging subject. The training phase may consist of several epochs. A popular approach used in the training phase is back-propagation learning; however, researchers have pointed out that some commonly used learning algorithms have disadvantages [10,11]. Several heuristic algorithms, including genetic algorithm (GA) [12], particle swarm optimization (PSO) [13] and ant colony optimization (ACO) [14] have been proposed for the purpose of training neural networks. Recently, two meta-heuristic algorithms inspired by the lifestyle of cuckoo birds were developed for solving optimization problems. Through some benchmarking studies, these two algorithms have been proven to be powerful meta-heuristic ones. Cuckoo Search (CS), proposed by Yang and Deb [15,16], was inspired by the particular egg laying and breeding characteristics of the cuckoo bird. Since then, CS has been used in solving various problems, and is considered to outperform other algorithms such as PSO and GA [16,17,18,19]. The other algorithm is the Cuckoo Optimization Algorithm (COA), developed by Rajabioun [20]. The comparison of the COA with standard versions of PSO and GA in some problems showed that the COA has superiority in fast convergence and global optimal achievement [20,21]. The purpose of this study is to use CS and COA for training neural networks in predicting students’ academic performance.

Taking into account the available literature, there is still room for improvement of ANN and the prediction model. This leads to the new approach proposed in this work for accomplishing a successful prediction of a student academic performance. The merit of the CS and COA algorithm and the success of ANN in the prediction of student academic performance have encouraged us to combine ANN and these algorithms. In this study, we propose an approach based on the multilayer feed-forward network improved by the CS and COA algorithms for predicting academic performance, which makes use of the optimizing ability of the two algorithms. We also compare the prediction performances of neural networks trained by these two algorithms. In general, the scientific contribution provided by the current research is the new approach applied herein. To the best of our knowledge, this combination of the two artificial intelligence techniques is applied for the first time in this research.

The paper is organized into seven sections. After the introduction in Section 1, the CS algorithm is presented in Section 2. Section 3 describes the COA algorithm. Section 4 is dedicated to describing the process of neural network training. The research design is provided in Section 5 and the results are in Section 6. Finally, Section 7 presents the conclusion.

2. Cuckoo Search

Cuckoo search is an optimization algorithm introduced by Yang and Deb [15,16]. This algorithm was inspired by the special lifestyle of the cuckoo species. The cuckoo bird lays its eggs in the nest of a host bird; however, in the process, they may remove the eggs of the host bird. Some of these eggs, which look similar to the host bird’s eggs, have the opportunity to grow up and become adult cuckoos. In other cases, the eggs are discovered by host birds and the host birds will throw them away or leave their nests and find other places to build new ones. The aim of the CS is to maximize the survival rate of the eggs. Each egg in a nest represents a solution, and a cuckoo egg stands for a new solution. The CS uses new and potentially better solutions to replace inadequate solutions in the nests. The CS is based on the following rules: (1) each cuckoo lays one egg at a time, and dumps this egg in a randomly chosen nest; (2) the best nests with high quality eggs (solutions) will carry over to the next generation; (3) the number of available host nests is fixed, and a host bird can detect an alien egg with a probability of p_a $\in$ [0, 1]. In this case, the host bird can either throw the egg away, or abandon the nest to build a new one in a new place. The last assumption can be estimated by the fraction p_a of the n nests being replaced by new nests (with new random solutions). For a maximization problem, the quality or fitness of a solution can be proportional to the objective function. Other forms of fitness can be defined in a similar way to the fitness function in genetic algorithms [15]. Based on the above-mentioned rules, the steps of the CS can be described as the pseudocode in Figure 1. The algorithm can be extended when each nest has multiple eggs representing a set of solutions.

Figure 1. Pseudocode of the Cuckoo Search (CS).

Figure 1. Pseudocode of the Cuckoo Search (CS).

In the CS algorithm, a balanced combination of a local random walk and the global explorative random walk by a parameter p_a. The local random walk is performed as follows:

x_i^{(t + 1)}=x_i^(t) + α s ⊗ H(p_a − ε) ⊗ (x^t_j − x^t_k)

(1)

Where x^t_j and x^t_k are two different solutions that are selected randomly by random permutation. H (u) is a Heaviside function, $\mathsf{\epsilon }$ is a random number derived from a uniform distribution, and s is the step size.

The global random walk is performed by the use of Lévy flights:

x_i^{(t + 1)}=x_i^(t) + α Lévy (λ)

(2)

Where $\mathsf{\alpha }$ > 0 is the step size, which depends on the scale of the problem. Lévy flights provide a random walk. The Lévy flight is a probability distribution, which has an infinite variance with an infinite mean. It is represented by:

Lévy ~ u = t^−λ , (1 < λ ≤ 3)

(3)

There are several ways to achieve random numbers in Lévy flights; however, a Mantegna algorithm is the most efficient [16]. In this study, the Mantegna algorithm is utilized to calculate this step length. In the Mantegna algorithm, the step length s is calculated by:

$$s=\frac{\mathsf{\mu }}{{\left|v\right|}^{1/\mathsf{\beta }}}$$

(4)

Where β is a parameter between [1,2], and μ and ν are from normal distribution as:

μ ~ N(0, σ_μ²) and ν ~ N(0, σ_ν²)

(5)

with

$${\mathsf{\sigma }}_{\mathsf{\mu }}={\left(\frac{\mathsf{\Gamma }(1+\mathsf{\beta })\sin (\mathsf{\pi \beta }/2)}{\mathsf{\Gamma }[(1+\mathsf{\beta })/2]\mathsf{\beta }{2}^{(\mathsf{\beta }-1)/2}}\right)}^{1/\mathsf{\beta }},{\mathsf{\sigma }}_{\mathsf{\nu }}=1$$

(6)

Studies have shown that CS is very efficient in dealing with optimization problems. However, several recent studies made some improvements to make the CS more practical for a wider range of applications without losing the advantages of the standard CS [22,23,24]. Notably, Walton et al. [25] have made two modifications to increase the convergence rate of the CS. The first modification was made to the size of the step size α. In the standard CS, α is constant; whereas, in the modified CS, α decreases when the number of generations increases. The second modification was to add an information exchange between the eggs to speed up convergence to a minimum. In the standard CS, the searches are performed independently and there is no information exchange between individuals. However, in the modified CS, there is a fraction of eggs with the best fitness that are put into a group of top eggs. It has also been indicated that adding the random biased walk to modified CS results in an efficient optimization algorithm [26]. However, in this study, we use the standard CS for training neural networks to predict student academic performance.

3. Cuckoo Optimization Algorithm

Rajabioun [20] developed another algorithm based on the cuckoo’s lifestyle, named the Cuckoo Optimization Algorithm. The fast convergence and global optima achievement of the algorithm have been proven through some benchmark problems. The lifestyle of the cuckoo species and their characteristics has also been the basic motivation for the development of this evolutionary optimization algorithm. The pseudocode of the COA is represented in Figure 2.

Figure 2. Pseudocode of the Cuckoo Optimization Algorithm (COA).

Figure 2. Pseudocode of the Cuckoo Optimization Algorithm (COA).

Cuckoos lay eggs within a maximum distance from their habitat. This range is called the Egg Laying Radius (ELR). In the algorithm, ELR is defined as:

$$ELR=\mathsf{\alpha }\times \frac{Numberofcurrentcuckoo’seggs}{Totalnumberofeggs}\times (varhi-varlow)$$

(7)

Where $\mathsf{\alpha }$ is an integer to handle the maximum value of ELR, and var_hi and var_low are the upper limit and lower limit for variables, respectively.

When the cuckoo groups are formed in different areas, the society with best profit value is then selected as the goal point for other cuckoos to immigrate to. In order to recognize which cuckoo belongs to which group, cuckoos are grouped by the K-means clustering method. When moving toward the goal point, the cuckoos only fly a part of the way and have a deviation. Specifically, each cuckoo only flies λ% of all distances and has a deviation of φ radians. The parameters for each cuckoo are defined as follows:

λ ~ U (0, 1)

φ ~ U (−ω, ω)

Where λ ~ U (0, 1) represents that λ is a random number (uniform distribution) between 0 and 1. ω is a parameter to constrain the deviation from goal habitat. A ω of π/6 is supposed to be enough for good convergence. Kahramanli [27] presented a modified COA that yielded better solutions to engineering problems. In the modified COA, a new ELR equation was proposed. However, in this study, we utilize the standard COA for training neural networks to predict student academic performance.

4. Artificial Neural Network

An artificial neural network (ANN) has two types of basic components, namely, neuron and link. A neuron is a processing element and a link is used to connect one neuron with another. Each link has its own weight. Each neuron receives stimulation from other neurons, processes the information, and produces an output. Neurons are organized into a sequence of layers. The first and the last layers are called input and output layers, respectively, and the middle layers are called hidden layers. The input layer is a buffer that presents data to the network. It is not a neural computing layer because it has no input weights and no activation functions. The hidden layer has no connections to the outside world. The output layer presents the output response to a given input. The activation coming into a neuron from other neurons is multiplied by the weights on the links over which it spreads, and then is added together with other incoming activations. A neural network in which activations spread only in a forward direction from the input layer through one or more hidden layers to the output layer is known as a multilayer feed-forward network. For a given set of data, a multi-layer feed-forward network can provide a good non-linear relationship. Studies have shown that a feed-forward network, even with only one hidden layer, can approximate any continuous function [28]. Therefore, a feed-forward network is an attractive approach [29]. Figure 3 shows an example of a feed-forward network with three layers. In Figure 3, R, N, and S are the numbers of input, hidden neurons, and output, respectively; iw and hw are the input and hidden weights matrices, respectively; hb and ob are the bias vectors of the hidden and output layers, respectively; x is the input vector of the network; ho is the output vector of the hidden layer; and y is the output vector of the network. The neural network in Figure 1 can be expressed through the following equations:

$$h{o}_i=f({\displaystyle \sum _{j=1}^{R}i{w}_{i,j}.x_j}+hbi), for i=1,..,N$$

(8)

$$y_i=f({\displaystyle \sum _{k=1}^{N}h{w}_{i,k}.h{o}_k}+obi), for i=1,..,S$$

(9)

Where f is an activation function.

Figure 3. A feed-forward network with three layers.

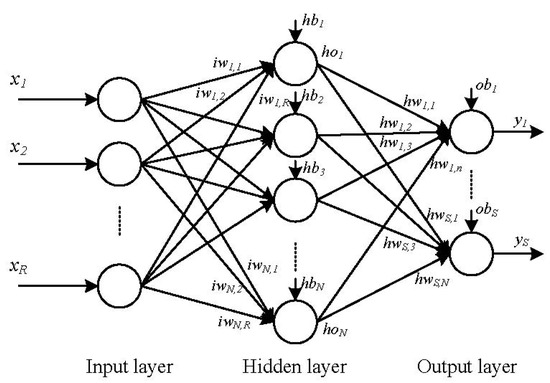
Figure 3. A feed-forward network with three layers.

When implementing a neural network, it is necessary to determine the structure in terms of number of layers and number of neurons in the layers. The larger the number of hidden layers and nodes, the more complex the network will be. A network with a structure that is more complicated than necessary over fits the training data [30]. This means that it performs well on data included in the training dataset, but may perform poorly on that in a testing dataset.

Once a network has been structured for a particular application, it is ready for training. Training a network means finding a set of weights and biases that will give desired values at the network’s output when presented with different patterns at its input. When network training is initiated, the iterative process of presenting the training data set to the network’s input continues until a given termination condition is satisfied. This usually happens based on a criterion indicating that the current achieved solution is good enough to stop training. Some of the common termination criteria are sum squared error (SSE) and mean squared error (MSE). Through continuous iterations, the optimal or near-optimal solution is finally achieved, which is regarded as the weights and biases of a neural network. Suppose that there are m input-target sets, x_k – t_k for k = 1, 2, …, m, for neural network training. Thus, network variables arranged as iw, hw, hb, and ob are to be changed to minimize a cost function. E, such as the SSE between network outputs, y_k, and desired targets, t_k, is as follows:

$$E={\displaystyle \sum _{k=1}^m{e}_k^2}={\displaystyle \sum _{k=1}^m{(t_k-y_k)}^2}$$

(10)

5. Research Design

This section represents the proposed model for the prediction of student academic performance. In this study, an application related to the context of Vietnam was used as an illustration.

5.1. Identifying Input and Output Variables

Through a literature review and discussion with admission officers and experts, a number of academic, social-economic, and other related factors that are considered to have an influence on the students’ academic performance were determined and chosen as input variables (i.e., independent variables, or predictor variables). The input variables were obtained from the admission registration profile and are as follows: University entrance exam results (normally, in Vietnam, candidates take three exams for the fixed group of subjects they choose), the overall average score from a high school graduation examination, elapsed time between graduating from high school and obtaining university admission, location of high school (there are four regions, as defined by the government of Vietnam: Region 1, Region 2, Region 3 and Region 4. Region 1 includes localities with difficult economic and social conditions; Region 2 is rural areas; Region 3 consists of provincial cities; and Region 4 includes central cities), type of high school attended (private or public), and gender (male or female). The average score of the first academic year was chosen as the output variable (i.e., dependent variable) since the first year in college is a time for adjustment [2]. It is based on the current grading system used by the university. In our study, the domain of output variables has its range from 0 to 10 (nominal scores). The output variable can be changed to predict students’ performance in their first through fourth year at an academic institution. In brief, there are eight input variables and one output variable in the proposed model.

Input and output variables must be pre-processed to be suitable for neural networks. The input variables and ranges are presented in Table 1. The output variable has a range from 0 to 10.

Table 1. Input variables.

Input Variable		Range
University entrance examination score	X1—Subject 1	0.5–10
	X2—Subject 2	0.5–10
	X3—Subject 3	0.5–10
X4—The average overall score of high school graduation examination		5–10
X5—Elapsed time between graduating from high school and obtaining university admission (0 year: 0; 1 year: 1; 2 years: 2; and 3 years–above: 3)		0, 1, 2, 3
X6—Location of student’s high school (Region 1: 0; Region 2: 1; Region 3: 2; Region 4: 3)		0, 1, 2, 3
X7—Type of high school attended (private:0; public:1)		0, 1
X8—Student’s gender (male:0; female:1)		0, 1

Table 1. Input variables.

Input Variable		Range
University entrance examination score	X1—Subject 1	0.5–10
	X2—Subject 2	0.5–10
	X3—Subject 3	0.5–10
X4—The average overall score of high school graduation examination		5–10
X5—Elapsed time between graduating from high school and obtaining university admission (0 year: 0; 1 year: 1; 2 years: 2; and 3 years–above: 3)		0, 1, 2, 3
X6—Location of student’s high school (Region 1: 0; Region 2: 1; Region 3: 2; Region 4: 3)		0, 1, 2, 3
X7—Type of high school attended (private:0; public:1)		0, 1
X8—Student’s gender (male:0; female:1)		0, 1

5.2. Dataset

We obtained our data from the University of Transport Technology, which is a public university in Vietnam. We used a real dataset from students in the Department of Bridge Construction as input variables and their achievements from the 2011–2012 academic year as output variables. The dataset consisted of 653 cases and was divided into two groups. The first group (about 60%) was used for training the model. The second group (about 40%) was employed to test the model. The training dataset served in model building, while the other group was used for the validation of the developed model.

5.3. Structure of the Neural Network

The structure of an ANN is dictated by the choice of the number in the input, hidden, and output layers. Each data set has its own particular structure, and therefore determines the specific ANN structure. The number of neurons comprised in the input layer is equal to the number of features (input variables) in the data. The number of neurons in the output layer is equal to the number of output variables. In this study, the data set includes eight input variables and one output variable; hence, the numbers of neurons in the input and output layers are eight and one, respectively. The three layer feed-forward neural network is utilized in this work since it can be used to approximate any continuous function [31,32]. Regarding the number of hidden neurons, the choice of an optimal size of hidden layer has often been studied, but a rigorous generalized method has not been found [33]. In this study, the choice is made through extensive simulation with different choices of the number of hidden nodes. For each choice, we obtained the performance of the concerned neural networks, and the number of hidden nodes providing the best performance was used for presenting results. The activation function from input to hidden is sigmoid. With no loss of generality, a commonly used form, f (n) = 2/(1 + e⁻²ⁿ) – 1, is utilized; while a linear function is used from the hidden to output layer.

5.4. Training Neural Networks

The objective function is to minimize SSE. The two aforementioned optimization algorithms are utilized to search optimal weights and biases of neural networks. The amount of errors is determined by the squared difference between the target output and actual output. In the implementation of the optimization algorithm to train a neural network, all training parameters, θ = {iw, hw, hb, ob}, are converted into a single vector of real numbers, as shown in Figure 4.

Figure 4. The vector of training parameters.

Figure 4. The vector of training parameters.

The aim of the training algorithm is to identify the optimal or near-optimal parameter, θ *, from the cost function E (θ). The parameters for the CS algorithm were set as follows: The number of nests was 20; the step size was 0.01; and the net discovery rate (p_a) was 0.1. The parameters for the COA algorithm were set as follows: The number of initial population was 20 and p% was 10%.

5.5. Examining the Performance

To examine the performance of a neural network, several criteria are used. These criteria are applied to the trained neural network to determine how well the network works. The criteria were used to compare predicted values and actual values. They are as follows:

Root mean squared error (RMSE): This index estimates the residual between the actual value and predicted value. A model has better performance if it has a smaller RMSE. An RMSE equal to zero represents a perfect fit.

$$RMSE=\sqrt{\frac{1}{m}{\displaystyle \sum _{k=1}^m{\left(t_k-y_k\right)}^2}}$$

(11)

Where t_k is the actual value, y_k is the predicted value produced by the model, and m is the total number of observations.

Mean absolute percentage error (MAPE): This index indicates an average of the absolute percentage errors; the lower the MAPE the better.

$$MAPE=\frac{1}{m}{\displaystyle \sum _{k=1}^m\left|\frac{t_k-y_k}{t_k}\right|}$$

(12)

Correlation coefficient (R): This criterion reveals the strength of relationships between actual values and predicted values. The correlation coefficient has a range from 0 to 1, and a model with a higher R means it has better performance.

$$R=\frac{{\displaystyle \sum _{k=1}^m\left(t_k-\overline{t}\right)\left(y_k-\overline{y}\right)}}{\sqrt{{\displaystyle \sum _{k=1}^m{\left(t_k-\overline{t}\right)}^2}.{\displaystyle \sum _{k=1}^m{\left(y_k-\overline{y}\right)}^2}}}$$

(13)

Where $\overline{t}=\frac{1}{m}{\displaystyle \sum _{k=1}^m{t}_k}$ and $\overline{y}=\frac{1}{m}{\displaystyle \sum _{k=1}^m{y}_k}$ are the average values of t_k and y_k, respectively.

In addition to the mentioned criteria, the number of iterations required by individual training algorithms to reach the certain output accuracy was also used to evaluate the performance of the training algorithms.

6. Results and Discussions

The CS implementation by Yang and Deb [15,16] was utilized in this study. Walton et al. [26] indicated that a slight variation in CS implementations may cause differences in results. Therefore, the results may not agree with the findings of the previous studies. The model was coded and implemented in the Matlab environment (Matlab R2011b) and simulation results were then obtained. A 10-fold cross validation method was used to avoid over-fitting. For this problem, the best performing architecture was 8-6-1, that is, with one hidden layer and six neurons, which resulted in a total of 54 weights and 7 biases. Hence, this architecture was applied to this study. In a real world application of an optimization technique, it is very difficult to define a stopping criterion. Moreover, in this study, there is an uncertainty in both the inputs and the output of the objective function. The number of iterations, when the obtained results reached an acceptable accuracy of prediction, was chosen as the stopping criterion. The number of objective function evaluations in the implementations of CS and COA in each iteration is the same. Figure 5 depicts the SSE values for the two algorithms in 100 iterations. It is clearly seen that the COA has a faster convergence than the CS. During the first five iterations, the convergence by the COA was very fast. At the 100th iteration, the SSE values of the neural network trained by the COA and CS were 171.5908 and 768.6833, respectively.

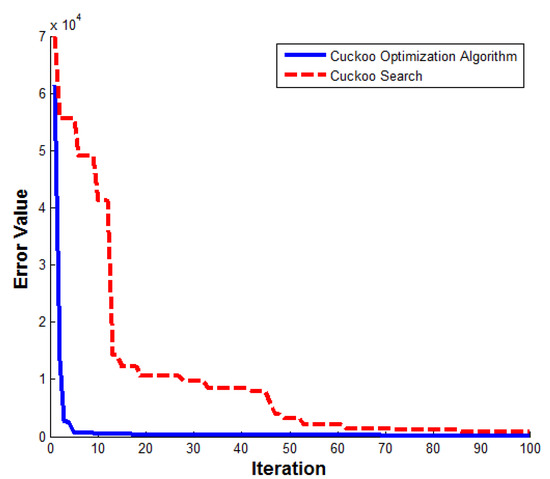
Figure 5. Sum squared error values in 100 iterations.

Figure 5. Sum squared error values in 100 iterations.

Table 2 represents the comparison of performance criteria values of the neural networks trained by CS (ANN-CS) and COA (ANN-COA) at different iterations. Theoretically, a prediction model is accepted as ideal when RMSE and MAPE are small and R is close to 1. As can be seen from Table 2, the ANN-COA has smaller RMSE and MAPE values as well as bigger R values for both the training and testing datasets. The results show that the ANN-COA has a better overall performance in all criteria. However, when compared with results from other studies on prediction, the obtained performance criteria values from the ANN-CS after 500 iterations are also satisfactory.

Table 2. Comparison of ANN-CS and the ANN-COA.

Iteration	Model	Training dataset			Testing dataset
		RMSE	MAPE	R	RMSE	MAPE	R
200	ANN-CS	1.0269	0.1348	0.5960	1.0577	0.1387	0.5877
	ANN-COA	0.5102	0.0677	0.9185	0.5264	0.0694	0.9087
500	ANN-CS	0.6628	0.0861	0.8479	0.7097	0.0975	0.8215
	ANN-COA	0.4613	0.0669	0.9269	0.4984	0.0702	0.9184
1000	ANN-CS	0.5385	0.0708	0.9166	0.6096	0.0719	0.8769
	ANN-COA	0.4366	0.0633	0.9412	0.4819	0.0692	0.9223

Table 2. Comparison of ANN-CS and the ANN-COA.

Iteration	Model	Training dataset			Testing dataset
		RMSE	MAPE	R	RMSE	MAPE	R
200	ANN-CS	1.0269	0.1348	0.5960	1.0577	0.1387	0.5877
	ANN-COA	0.5102	0.0677	0.9185	0.5264	0.0694	0.9087
500	ANN-CS	0.6628	0.0861	0.8479	0.7097	0.0975	0.8215
	ANN-COA	0.4613	0.0669	0.9269	0.4984	0.0702	0.9184
1000	ANN-CS	0.5385	0.0708	0.9166	0.6096	0.0719	0.8769
	ANN-COA	0.4366	0.0633	0.9412	0.4819	0.0692	0.9223

Figure 6 and Figure 7 present two scatter diagrams that illustrate the degree of correlation between actual values and predicted values obtained by the model using the two algorithms after 1000 iterations. In each figure, an identity line was drawn as a reference of perfect agreement. In this problem, the identity line represents that the two sets of data are identical. The more the two datasets agree, the more the points tend to concentrate in the vicinity of the identity line. Here the training dataset and testing dataset were used to test the neural network performance. It may be observed that most predicted values are close to the actual values. This trend indicates a good agreement between the two model predictions and the actual values.

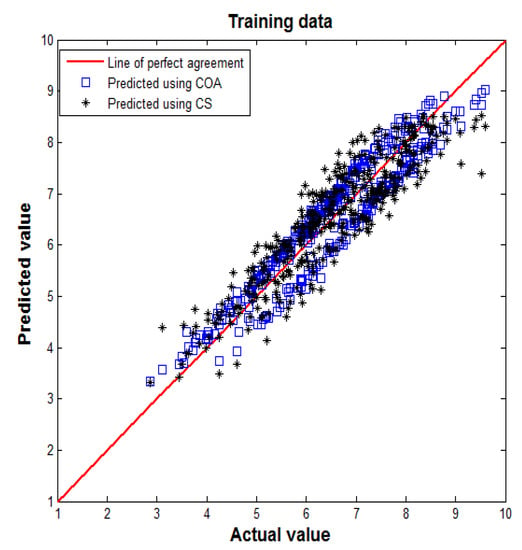
Figure 6. Comparison between actual and predicted values in training dataset.

Figure 6. Comparison between actual and predicted values in training dataset.

Figure 7. Comparison between actual and predicted values in testing dataset.

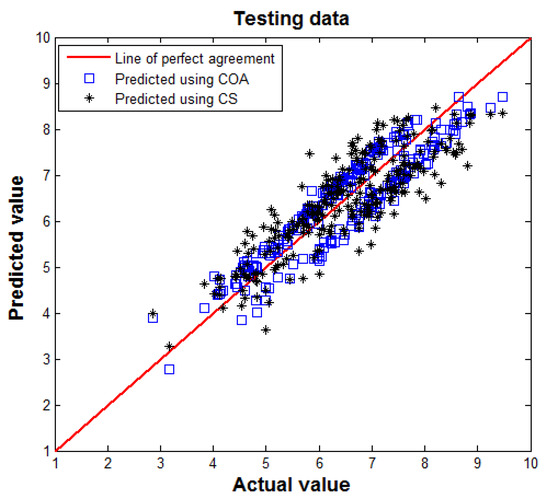
Figure 7. Comparison between actual and predicted values in testing dataset.

In order to evaluate the performance of the proposed approach, the Multiple Linear Regression (MLR) method was applied to the studied problem. Coefficients derived from the MLR method are presented in Table 3. The performance criteria RMSE, MAPE, and R for the training dataset were calculated as 0.5642, 0.0769, and 0.8904, respectively; while those for the testing dataset were calculated as 0.6174, 0.0753, and 0.8632, respectively. When comparing with the results in Table 2, the ANN-CS and ANN-COA at the 1000th iteration have smaller RMSE and MAPE values than those obtained from the MLR method as well as bigger R values for both the training and testing datasets. It can be concluded that the ANN-CS and ANN-COA have a better overall performance than the MLR method in predicting student academic performance.

Table 3. Coefficient values for MLR.

Variable	Coefficient
Intercept	−0.4325
X1	0.3471
X2	0.2758
X3	0.1388
X4	0.2916
X5	−0.0090
X6	0.0060
X7	0.0029
X8	−0.0798

Table 3. Coefficient values for MLR.

Variable	Coefficient
Intercept	−0.4325
X1	0.3471
X2	0.2758
X3	0.1388
X4	0.2916
X5	−0.0090
X6	0.0060
X7	0.0029
X8	−0.0798

Based on the obtained results, it can be concluded that the ANN-COA and ANN-CS can be used to predict student academic performance. However, when prediction accuracy and convergence speed are simultaneously desired, the COA algorithm is found to be more appropriate. The results show that the prediction outcome of the ANN-COA model is more accurate and reliable. Hence, the ANN-COA may be acceptable in serving as a predictor of student academic performance.

7. Conclusions

The accurate prediction of student academic performance is of importance for making admission decisions as well as providing better educational services. In this study, the feed-forward neural network was utilized to predict student academic performance. This study used the two powerful meta-heuristic algorithms, including CS and COA, based on the lifestyle of cuckoo birds to train ANNs for predicting students’ academic performance. The results of the ANN-COA were then compared against those of the ANN-CS in terms of RMSE, MAPE, and R achieved. The ANN-COA was found to have slightly better results for predicting student academic performance in this case. The findings demonstrated the remarkable advantage of the COA and CS in training ANN and the potential of the ANN in the prediction of students’ performance. In this study, the abilities to search for the optimal or near-optimal solutions of the two algorithms were also investigated. The results of the present study also reinforce the fact that a comparative analysis of different training algorithms is always supportive in enhancing the performance of a neural network. It is expected that this work may be used as a reference for decision making in the admission process and to provide better educational services by offering customized assistance according to students’ predicted academic performance. To improve prediction accuracy, future research should focus on other factors that may affect student academic performance, such as character, intelligence, and psychological factors. Moreover, we will develop and incorporate our model in a user-friendly software tool for the prediction of student academic performance in order to make this task easier for educators. Another future research direction is to use the improved and modified CS and COA in training neural networks.