Sparse Signal Recovery from Fixed Low-Rank Subspace via Compressive Measurement
Abstract
:1. Introduction
2. Model and Algorithm
2.1. The Model
 . In application of interest we always suppose d ≪ n, say
. In application of interest we always suppose d ≪ n, say  is a fixed low-rank subspace. Let the columns of an n × d matrix U be orthonormal and span
is a fixed low-rank subspace. Let the columns of an n × d matrix U be orthonormal and span  . {𝒜|ℝn → ℝm, m < n} is a linear compressive measurement operator which should satisfy the restricted isometry property (RIP) [2] with constant δK
. {𝒜|ℝn → ℝm, m < n} is a linear compressive measurement operator which should satisfy the restricted isometry property (RIP) [2] with constant δK
2.2. Variant of CoSaMP for Fixed Subspace
Algorithm 1. Given a fixed subspace  spanned by the column space of an n × d orthonormal matrix U, the variant of CoSaMP solver for the sparse recovery problem Equation (1). (s*, w*) = CoSaMP_subspace(v, U, 𝒜, 𝒜*, K, ε, maxIter). spanned by the column space of an n × d orthonormal matrix U, the variant of CoSaMP solver for the sparse recovery problem Equation (1). (s*, w*) = CoSaMP_subspace(v, U, 𝒜, 𝒜*, K, ε, maxIter). | |
| 1: | Initialize s,w,u: s0 =0, w0 =0, u0 =0. |
| 2: | while  and k < maxIter do and k < maxIter do |
| 3: | Estimate weights w: wk+1 = (U))−1(v − 𝒜(sk)) |
| 4: | Form signal proxy: y = 𝒜*(uk) |
| 5: | Support identification: Ω = supp(y; 2K) |
| 6: | Merge support:  |
| 7: | Signal estimation by least squares: |
| 8: | Update residue:  |
| 9: | k = k + 1 |
| 10: | end while |
| 11: | (s*, w*) = (sk, wk) |
2.3. Relation to Ordinary CS

3. Experiments Evaluation
 as the CS measurement ratio. U is an n × d matrix whose d columns are realizations of i.i.d. (0,In) random variables that are then orthornomalized. The weight vector w is a d × 1 vector whose entries are realizations of i.i.d. (0,In) random variables, which are Gaussian distributed with mean zero and variance 1. The K-sparse signal s is an n × 1 vector whose supports are chosen uniformly at random without replacement and we denote
as the CS measurement ratio. U is an n × d matrix whose d columns are realizations of i.i.d. (0,In) random variables that are then orthornomalized. The weight vector w is a d × 1 vector whose entries are realizations of i.i.d. (0,In) random variables, which are Gaussian distributed with mean zero and variance 1. The K-sparse signal s is an n × 1 vector whose supports are chosen uniformly at random without replacement and we denote  as the sparsity of the signal. We use relative error to quantify the sparse recovery performance as follows:
as the sparsity of the signal. We use relative error to quantify the sparse recovery performance as follows:

3.1. Algorithm Behavior on Simulated Data
3.1.1. Recovery on Signal Sparsity
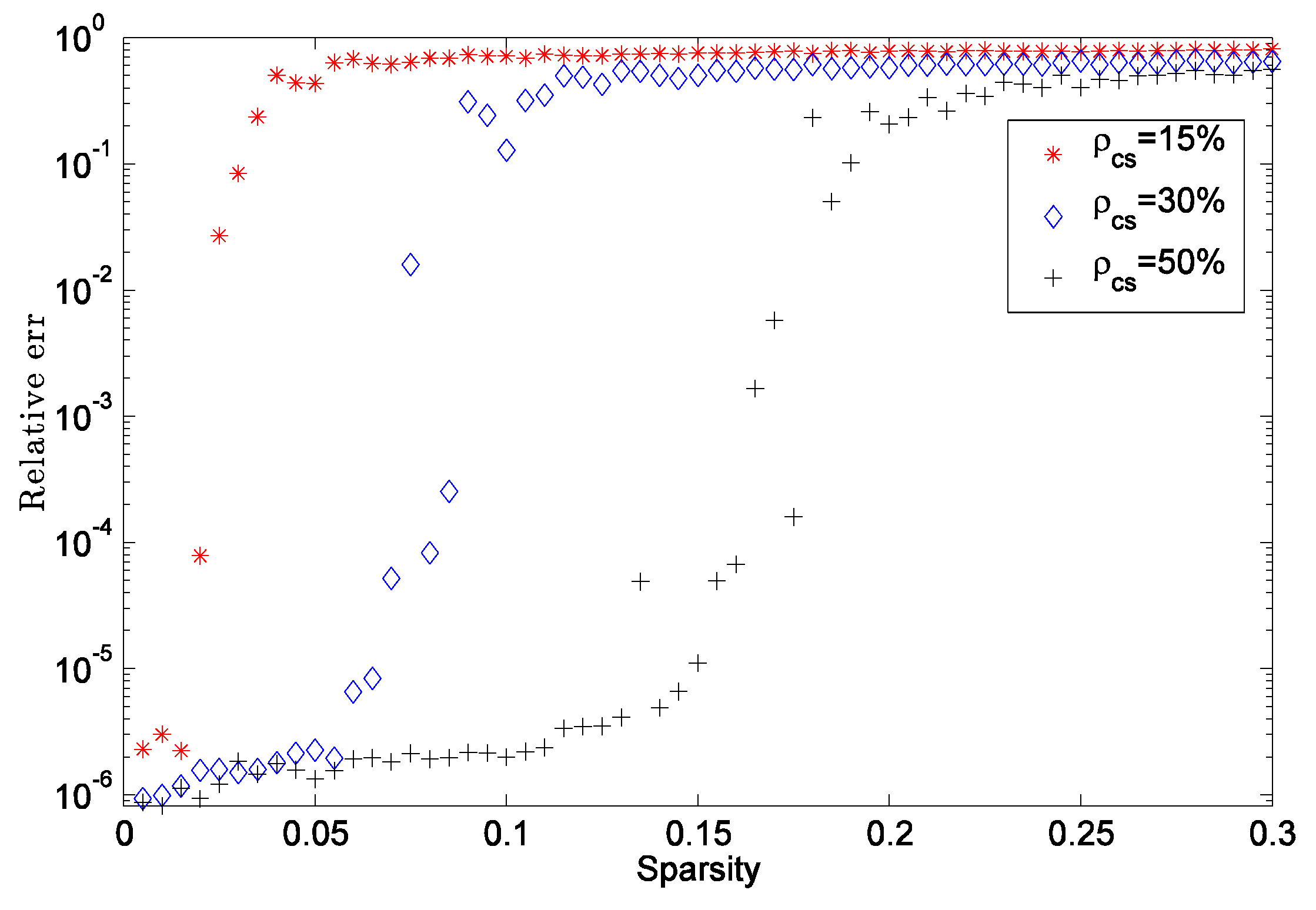
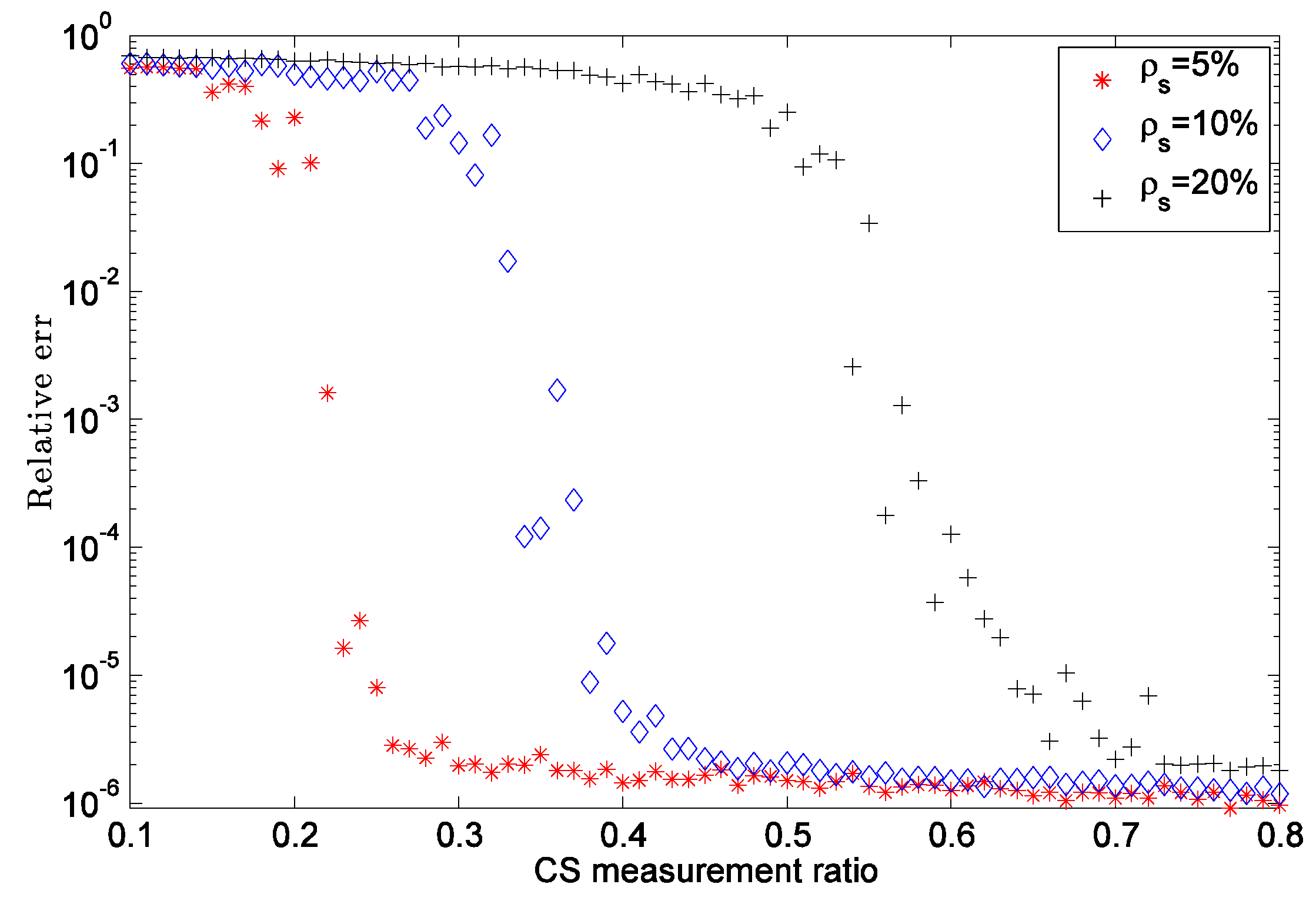
3.1.2. Recovery on CS Measurements
3.1.3. Recovery on the Rank of Fixed Subspace
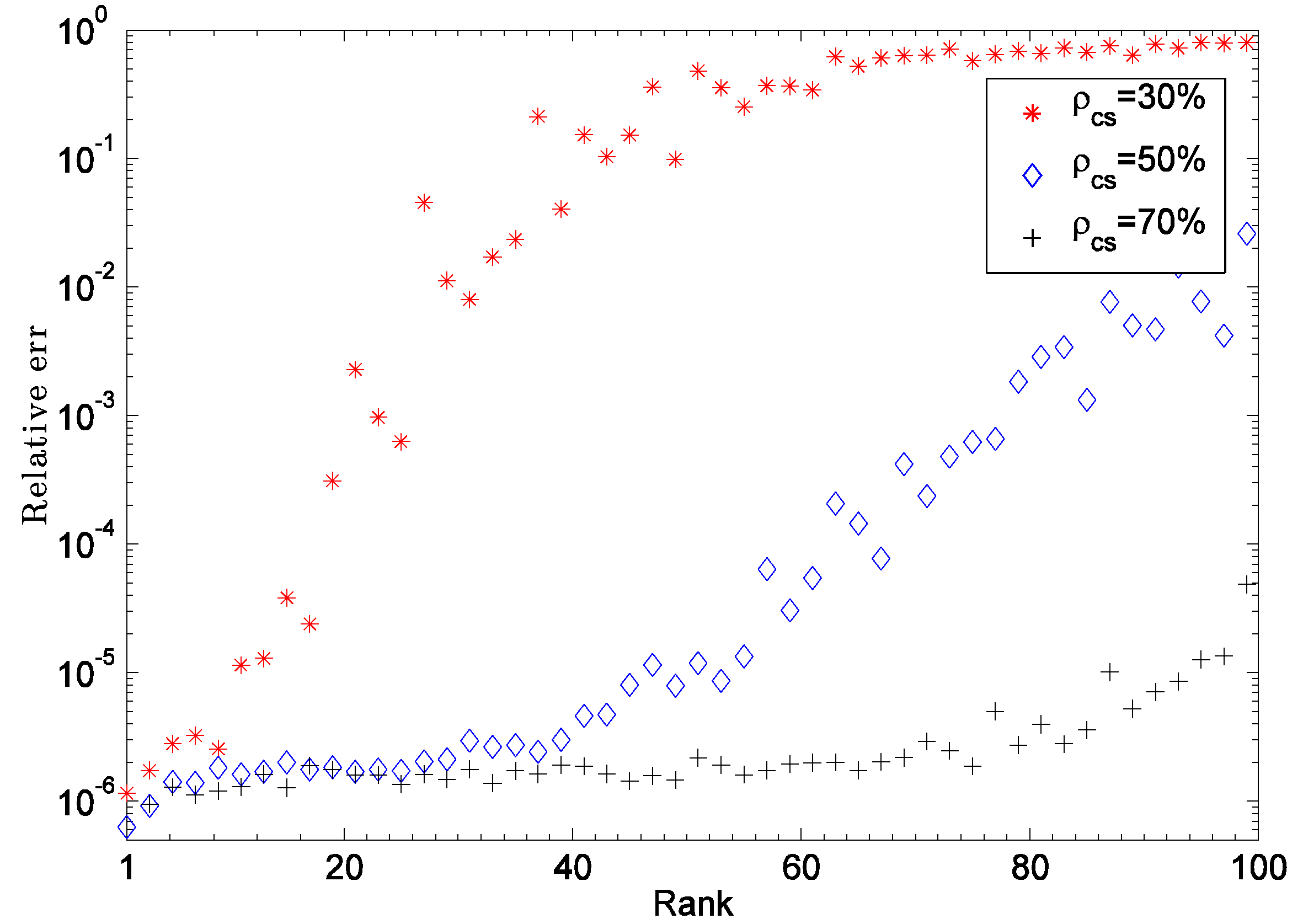
3.2. Comparisons with Ordinary CS
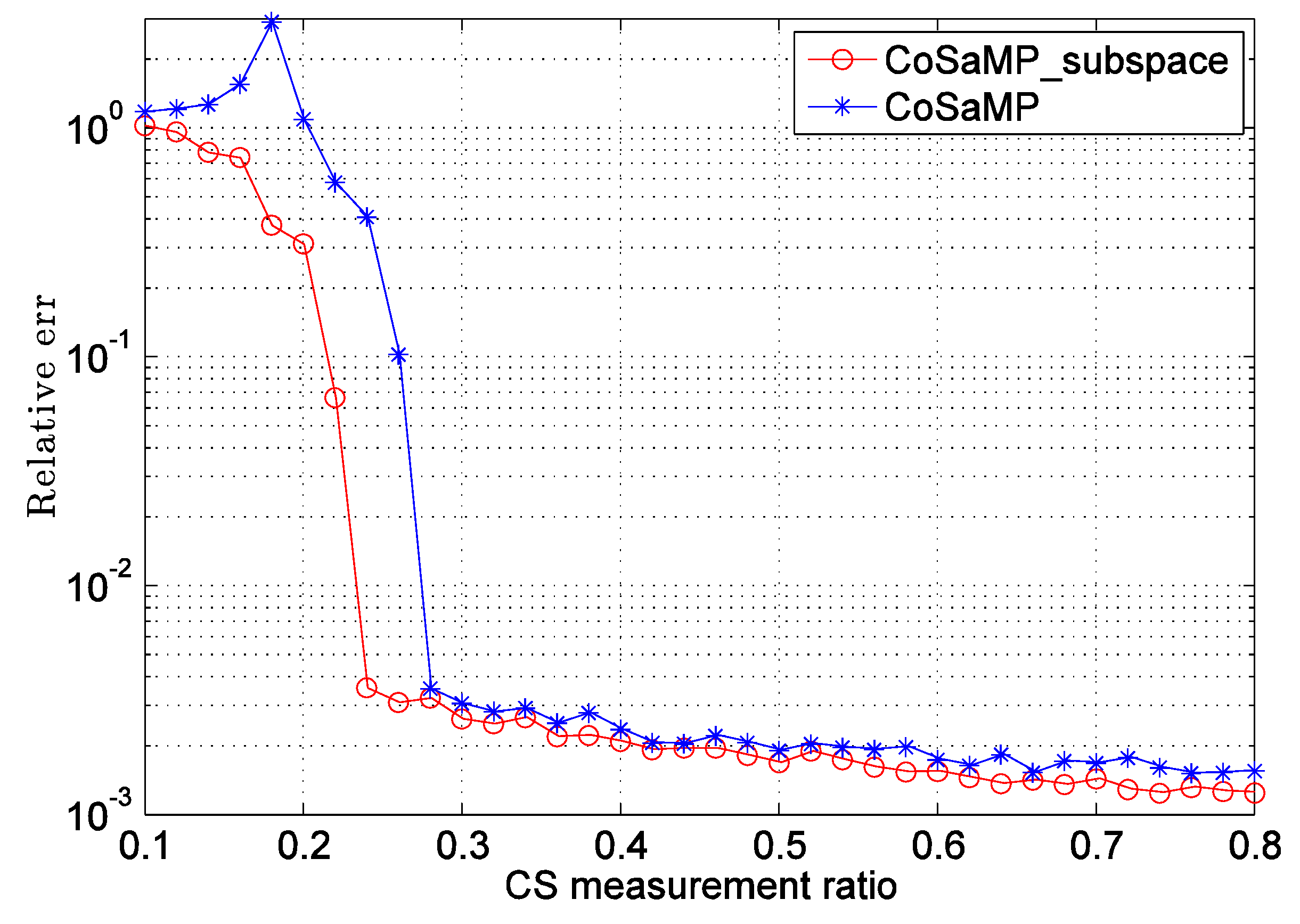
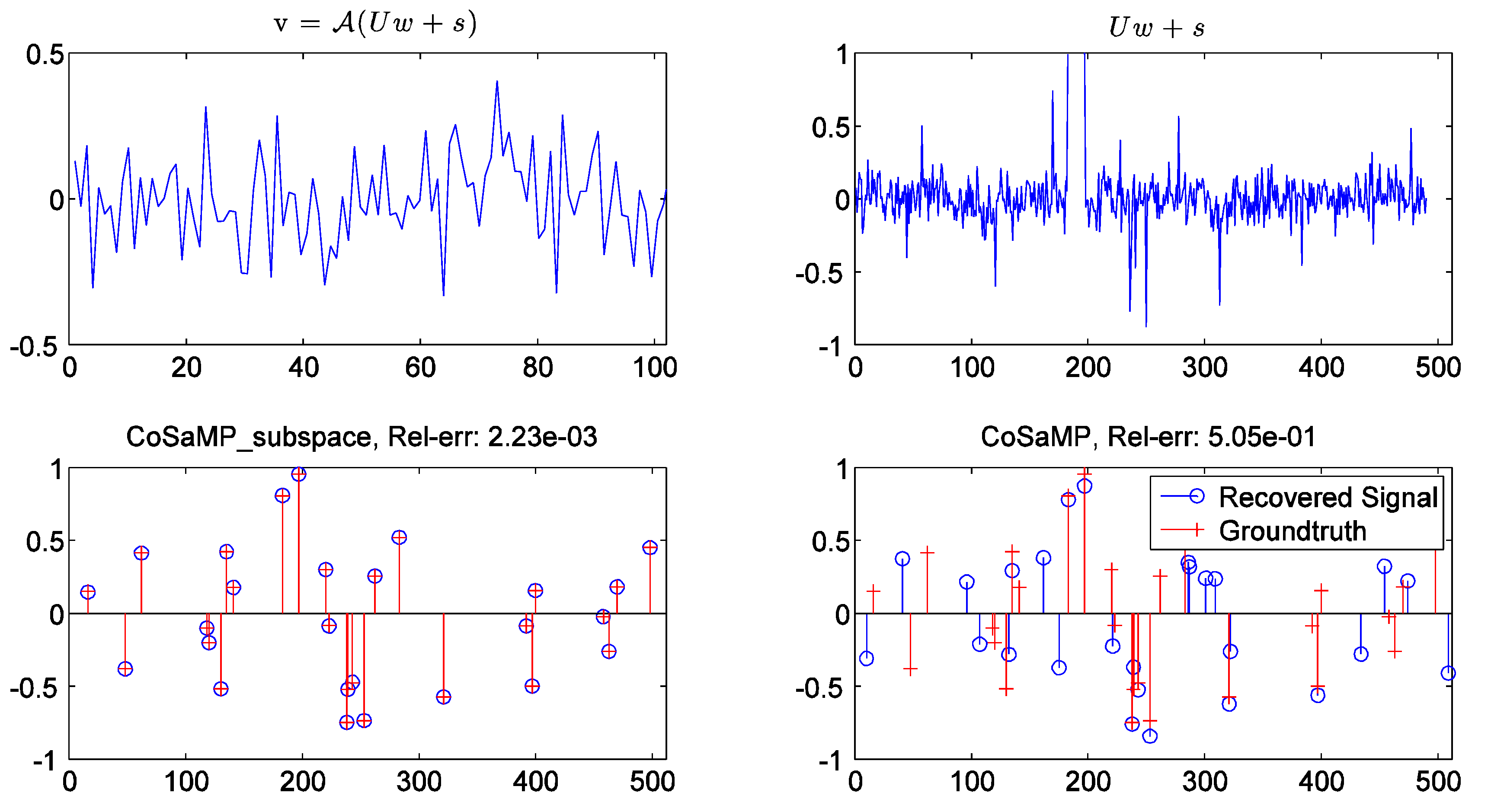
3.3. Video Compressive Sensing


4. Conclusions and Future Works
Acknowledgments
Conflicts of Interest
References
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Candès, E.J. The restricted isometry property and its implications for compressed sensing. Comptes Rendus Math. 2008, 346, 589–592. [Google Scholar] [CrossRef]
- Candès, E.J.; Wakin, M.B. An introduction to compressive sampling. IEEE Signal Process. Mag. 2008, 25, 21–30. [Google Scholar] [CrossRef]
- Candès, E.J.; Romberg, J.; Tao, T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 2006, 52, 489–509. [Google Scholar] [CrossRef]
- Baraniuk, R.G. Compressive sensing [lecture notes]. IEEE Signal Process. Mag. 2007, 24, 118–121. [Google Scholar] [CrossRef]
- Lustig, M.; Donoho, D.; Pauly, J.M. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn. Reson. Med. 2007, 58, 1182–1195. [Google Scholar] [CrossRef] [PubMed]
- Haupt, J.; Bajwa, W.U.; Rabbat, M.; Nowak, R. Compressed sensing for networked data. IEEE Signal Process. Mag. 2008, 25, 92–101. [Google Scholar] [CrossRef]
- Quer, G.; Masiero, R.; Munaretto, D.; Rossi, M.; Widmer, J.; Zorzi, M. On the Interplay between Routing and Signal Representation for Compressive Sensing in Wireless Sensor Networks. In Proceedings of the IEEE Information Theory and Applications Workshop, La Jolla, CA, USA, 8–13 February 2009; pp. 206–215.
- Ji, S.; Xue, Y.; Carin, L. Bayesian compressive sensing. IEEE Trans. Signal Process. 2008, 56, 2346–2356. [Google Scholar] [CrossRef]
- Ji, S.; Dunson, D.; Carin, L. Multitask compressive sensing. IEEE Trans. Signal Process. 2009, 57, 92–106. [Google Scholar] [CrossRef]
- Needell, D.; Tropp, J.A. CoSaMP: Iterative signal recovery from incomplete and inaccurate samples. Appl. Comput. Harmon. Anal. 2009, 26, 301–321. [Google Scholar] [CrossRef]
- Donoho, D.L.; Tsaig, Y. Fast Solution of l1-Norm Minimization Problems When the Solution May Be Sparse; Department of Statistics, Stanford University: Stanford, CA, USA, 2006. [Google Scholar]
- Qiu, C.; Vaswani, N. Recursive Sparse Recovery in Large but Correlated Noise. In Proceedings of the IEEE 2011 49th Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 28–30 September 2011; pp. 752–759.
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends Mach. Learn. 2011, 3, 1–122. [Google Scholar] [CrossRef]
- Coifman, R.; Geshwind, F.; Meyer, Y. Noiselets. Appl. Comput. Harmon. Anal. 2001, 10, 27–44. [Google Scholar] [CrossRef]
- Romberg, J. Imaging via compressive sampling. IEEE Signal Process. Mag. 2008, 25, 14–20. [Google Scholar] [CrossRef]
- Candès, E.J.; Li, X.; Ma, Y.; Wright, J. Robust principal component analysis? J. ACM 2011, 58, 11. [Google Scholar] [CrossRef]
- He, J.; Balzano, L.; Szlam, A. Incremental Gradient on the Grassmannian for Online Foreground and Background Separation in Subsampled Video. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Providence, RI, USA, 16–21 June 2012; pp. 1568–1575.
- Cevher, V.; Sankaranarayanan, A.; Duarte, M.F.; Reddy, D.; Baraniuk, R.G.; Chellappa, R. Compressive Sensing for Background Subtraction. In Computer Vision–ECCV 2008; Springer: Marseille, France, 2008; pp. 155–168. [Google Scholar]
- Duarte, M.F.; Davenport, M.A.; Takhar, D.; Laska, J.N.; Sun, T.; Kelly, K.F.; Baraniuk, R.G. Single-pixel imaging via compressive sampling. IEEE Signal Process. Mag. 2008, 25, 83–91. [Google Scholar] [CrossRef]
- Lin, Z.; Chen, M.; Ma, Y. The augmented lagrange multiplier method for exact recovery of corrupted low-rank matrices. 2010. arXiv preprint arXiv:1009.5055. arXiv.org e-Print archive. Available online: http://arxiv.org/abs/1009.5055 (accessed on 10 September 2013).
- Waters, A.E.; Sankaranarayanan, A.C.; Baraniuk, R. SpaRCS: Recovering Low-Rank and Sparse Matrices from Compressive Measurements. In Proceedings of the Advances in Neural Information Processing Systems, Granada, Spain, 12–14 December 2011; pp. 1089–1097.
- Zhan, J.; Vaswani, N.; Atkinson, I. Separating Sparse and Low-Dimensional Signal Sequences from Time-Varying Undersampled Projections of Their Sums. In Proceedings of the 2013 IEEE International Conference on Acoustics,Speech and Signal Processing (ICASSP), Vancouver, BC, Canada, 26–31 May 2013; pp. 5905–5909.
- Wright, J.; Ganesh, A.; Min, K.; Ma, Y. Compressive principal component pursuit. Inf. Inference 2013, 2, 32–68. [Google Scholar] [CrossRef]
- Balzano, L.; Nowak, R.; Recht, B. Online Identification and Tracking of Subspaces from Highly Incomplete Information. In Proceedings of the IEEE 2010 48th Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 29 September–1 October 2010; pp. 704–711.
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/
Share and Cite
He, J.; Gao, M.-W.; Zhang, L.; Wu, H. Sparse Signal Recovery from Fixed Low-Rank Subspace via Compressive Measurement. Algorithms 2013, 6, 871-882. https://doi.org/10.3390/a6040871
He J, Gao M-W, Zhang L, Wu H. Sparse Signal Recovery from Fixed Low-Rank Subspace via Compressive Measurement. Algorithms. 2013; 6(4):871-882. https://doi.org/10.3390/a6040871
Chicago/Turabian StyleHe, Jun, Ming-Wei Gao, Lei Zhang, and Hao Wu. 2013. "Sparse Signal Recovery from Fixed Low-Rank Subspace via Compressive Measurement" Algorithms 6, no. 4: 871-882. https://doi.org/10.3390/a6040871
APA StyleHe, J., Gao, M.-W., Zhang, L., & Wu, H. (2013). Sparse Signal Recovery from Fixed Low-Rank Subspace via Compressive Measurement. Algorithms, 6(4), 871-882. https://doi.org/10.3390/a6040871



