Monitoring Threshold Functions over Distributed Data Streams with Node Dependent Constraints
Abstract
:1. Introduction
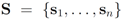 be a set of data streams collected at n nodes. Let v1(t),...,vn(t) be d dimensional real time varying vectors derived from the streams. For a function
be a set of data streams collected at n nodes. Let v1(t),...,vn(t) be d dimensional real time varying vectors derived from the streams. For a function 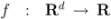 we would like to confirm the inequality
we would like to confirm the inequality 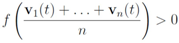
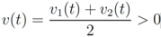
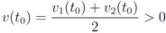 and to keep both nodes silent while
and to keep both nodes silent while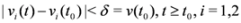
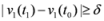 the nodes communicate, the mean v(t1) is computed, the local constraint δ is updated and made available to the nodes, and nodes are kept silent as long as the inequalities hold.
the nodes communicate, the mean v(t1) is computed, the local constraint δ is updated and made available to the nodes, and nodes are kept silent as long as the inequalities hold.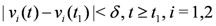
- 1. This approach works for a non-linear monitoring function f.
- 2. The results depend on the choice of a norm, and the numerical results reported show that l2 is probably not the best norm when one aims to minimize communication between nodes. In addition to the numerical results presented we also provide a simple illustrative example that highlights this point (see Remark 4.2).
- 3. Selection of node dependent local constraints may decrease communication between the nodes.
2. Text Mining Application
- 1. R–the set of “relevant" texts (text not labeled as spam),
- 2. F–the set of texts that contain a “feature" (word or term for example).
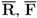 respectably (i.e.,
respectably (i.e., 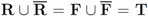 ), and consider the relative size of the four sets
), and consider the relative size of the four sets 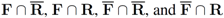 as follows:
as follows: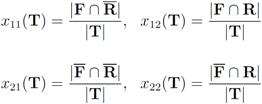
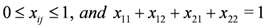
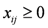 ,
, 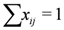 ), and given by
), and given by 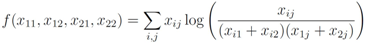
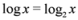 throughout the paper. We next relate empirical version of information gain Equation (3) and the information gain (see e.g., [12]).
throughout the paper. We next relate empirical version of information gain Equation (3) and the information gain (see e.g., [12]).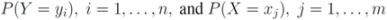
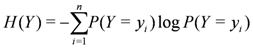
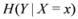 is defined by
is defined by 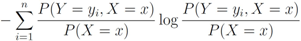
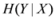 and information gain
and information gain 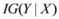 are given by
are given by 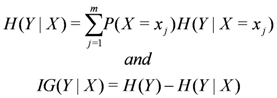
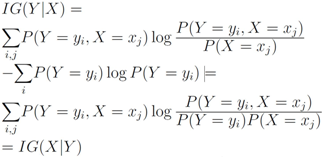
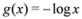 , information gain is non-negative
, information gain is non-negative 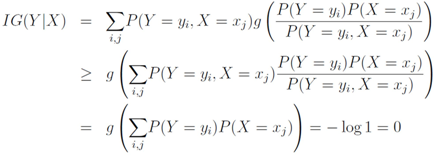
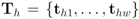 be the last w texts received at the
be the last w texts received at the 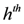 server, with
server, with 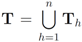 . Note that
. Note that 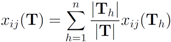
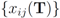 are the average of the local contingency tables
are the average of the local contingency tables 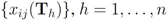 .
.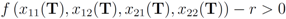
3. Non-Linear Threshold Function: An Example
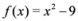 , and
, and  ,
, 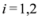 are scalar values stored at two distinct nodes. Note that if
are scalar values stored at two distinct nodes. Note that if 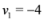 , and
, and 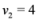 , then
, then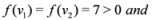
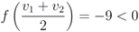
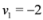 , and
, and 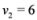 , then
, then 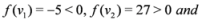
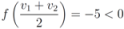
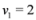 , and
, and 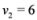 one has
one has 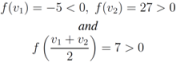
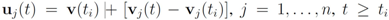 and to monitor the values of f on the convex hull conv
and to monitor the values of f on the convex hull conv  instead of the value of f at the average Equation (1). This strategy leads to sufficient conditions for Equation (1), and may be conservative.
instead of the value of f at the average Equation (1). This strategy leads to sufficient conditions for Equation (1), and may be conservative. without communication between the nodes are based on the following two observations:
without communication between the nodes are based on the following two observations: - 1. Convexity property. The mean v(t) is given by
, i.e., the mean v(t) is in the convex hull of
, and
is available to node j without much communication with other nodes.
- 2. If
is an l2 ball of radius
centered at
, then
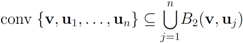
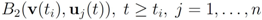
 into n independent tasks executed by the n nodes separately and without communication.
into n independent tasks executed by the n nodes separately and without communication.
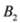 is substituted by
is substituted by 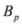 with
with 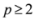 as we show later (see Remark 4.3) the inclusion fails when, for example,
as we show later (see Remark 4.3) the inclusion fails when, for example, 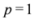 (for experimental results obtained with different norms see Section 5).
(for experimental results obtained with different norms see Section 5).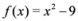 , and assignment provided by Equation (7). Let δ be a positive number. Consider two intervals of radius δ centered at
, and assignment provided by Equation (7). Let δ be a positive number. Consider two intervals of radius δ centered at 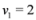 and
and 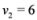 , i.e., we are interested in the intervals
, i.e., we are interested in the intervals 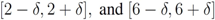
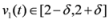 ,
, 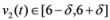 , and δ is small, then the average
, and δ is small, then the average 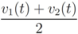 is not far from
is not far from 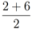 , and
, and 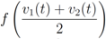 is not far from 7 (hence positive). In fact the sum of the intervals is the interval
is not far from 7 (hence positive). In fact the sum of the intervals is the interval 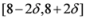 , and
, and 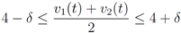
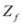 of f are -3 and 3, and as soon as δ is large enough so that the interval
of f are -3 and 3, and as soon as δ is large enough so that the interval 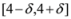 “hits" a point where f vanishes, communication between the nodes is required in order to verify Equation (1). In this particular example as long as
“hits" a point where f vanishes, communication between the nodes is required in order to verify Equation (1). In this particular example as long as 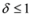 , and, therefore,
, and, therefore, 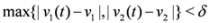
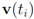 should not be transmitted (hence communication savings are possible), and there is no need to compute the distance from the center of each ball
should not be transmitted (hence communication savings are possible), and there is no need to compute the distance from the center of each ball 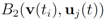 ,
, 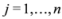 ,
, 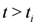 to the zero set
to the zero set 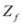 . For detailed comparison of results we refer the reader to [10].
. For detailed comparison of results we refer the reader to [10].4. Convex Minimization Problem
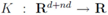 concave with respect to the first d variables
concave with respect to the first d variables 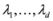 and convex with respect to the last nd variables
and convex with respect to the last nd variables 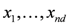 , solve
, solve 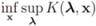
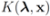 concludes the section.
concludes the section.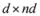 matrix made of n blocks, where each block is the
matrix made of n blocks, where each block is the 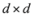 identity matrix multiplied by
identity matrix multiplied by  , so that for a set of n vectors
, so that for a set of n vectors  in
in 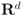 one has
one has 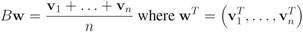
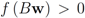 . We are looking for a vector x “nearest" to w so that
. We are looking for a vector x “nearest" to w so that 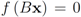 , i.e.,
, i.e., 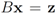 for some
for some 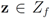 (where
(where 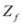 is the zero set of f, i.e.,
is the zero set of f, i.e.,  ). We now fix z
). We now fix z 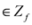 and denote the distance from w to the set
and denote the distance from w to the set 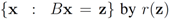 . Note that for each y inside the ball of radius
. Note that for each y inside the ball of radius 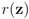 centered at w, one has
centered at w, one has 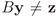 . If y belongs to a ball of radius
. If y belongs to a ball of radius 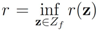 centered at w, then the inequality
centered at w, then the inequality 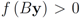 holds true.
holds true.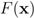 be a “norm" on
be a “norm" on 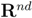 (specific functions F we run the numerical experiments with will be described later). The nearest “bad" vector problem described above is the following.
(specific functions F we run the numerical experiments with will be described later). The nearest “bad" vector problem described above is the following.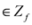 identify
identify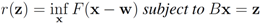
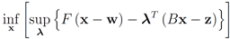 The function
The function 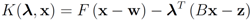
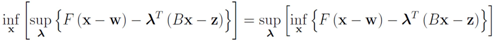
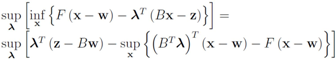
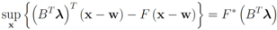
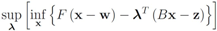
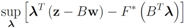
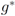 can be easily computed. Next we list conjugate functions for the most popular norms
can be easily computed. Next we list conjugate functions for the most popular norms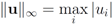
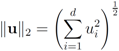
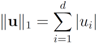
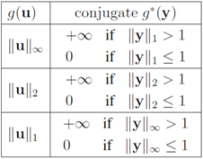
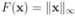 , and show below that in this case
, and show below that in this case 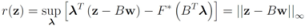
 the problem
the problem 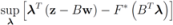 becomes
becomes 
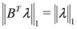 the problem reduces to
the problem reduces to 
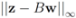 . Analogously, when
. Analogously, when 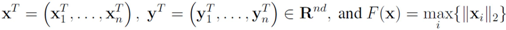
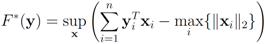 Assuming
Assuming 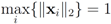 one has to look at
one has to look at 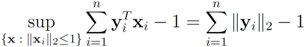
 . Finally the value for
. Finally the value for  is given by
is given by  . When
. When 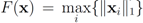 one has
one has 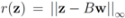 . For clarity sake we collect the above results in Table 1.
. For clarity sake we collect the above results in Table 1.| F(x) | r(z) |
|---|---|
 | ||z − Bw||1 |
 | ||z − Bw||2 |
 | ||z − Bw||∞ |
 (numerical experiments presented in Section 5 are conducted with all three norms). The monitoring algorithm we propose is the following.
(numerical experiments presented in Section 5 are conducted with all three norms). The monitoring algorithm we propose is the following.- 1. Set
.
- 2. Until end of stream.
- 3. Set
,
(i.e., remember “initial" values for the vectors).
- 4. Set
(for definition of w see Equation (12)).
- 5. Set
.
- 6. If
for each
go to step 5elsego to step 3
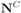 , and the set of nodes violating the constraint by
, and the set of nodes violating the constraint by 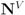 (so that
(so that 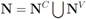 ). The cardinality of the sets is denoted by
). The cardinality of the sets is denoted by 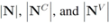 respectively, so that
respectively, so that 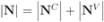 . Assuming
. Assuming 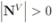 one has the following:
one has the following:- 1.
nodes violators transmit their scalar ID and new coordinates to the root (
messages).
- 2. the root sends scalar requests for new coordinates to the complying
nodes (
messages).
- 3. the
complying nodes transmit new coordinates to the root (
messages).
- 4. root updates itself, computes new distance δ to the surface, and sends δ to each node (
messages).
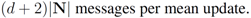
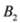 is substituted by
is substituted by 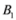 . Significance of this negative result becomes clear in Section 5.
. Significance of this negative result becomes clear in Section 5.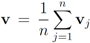 ,and
,and 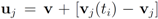 . If the Step 6 inequality holds for each node, then each point of the ball centered at
. If the Step 6 inequality holds for each node, then each point of the ball centered at 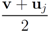 with radius
with radius 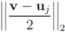 is contained in the l2 ball of radius δ centered at v (see Figure 2). Hence the sufficient condition offered by Algorithm 4.1 is more conservative than the one suggested in [8].
is contained in the l2 ball of radius δ centered at v (see Figure 2). Hence the sufficient condition offered by Algorithm 4.1 is more conservative than the one suggested in [8]. 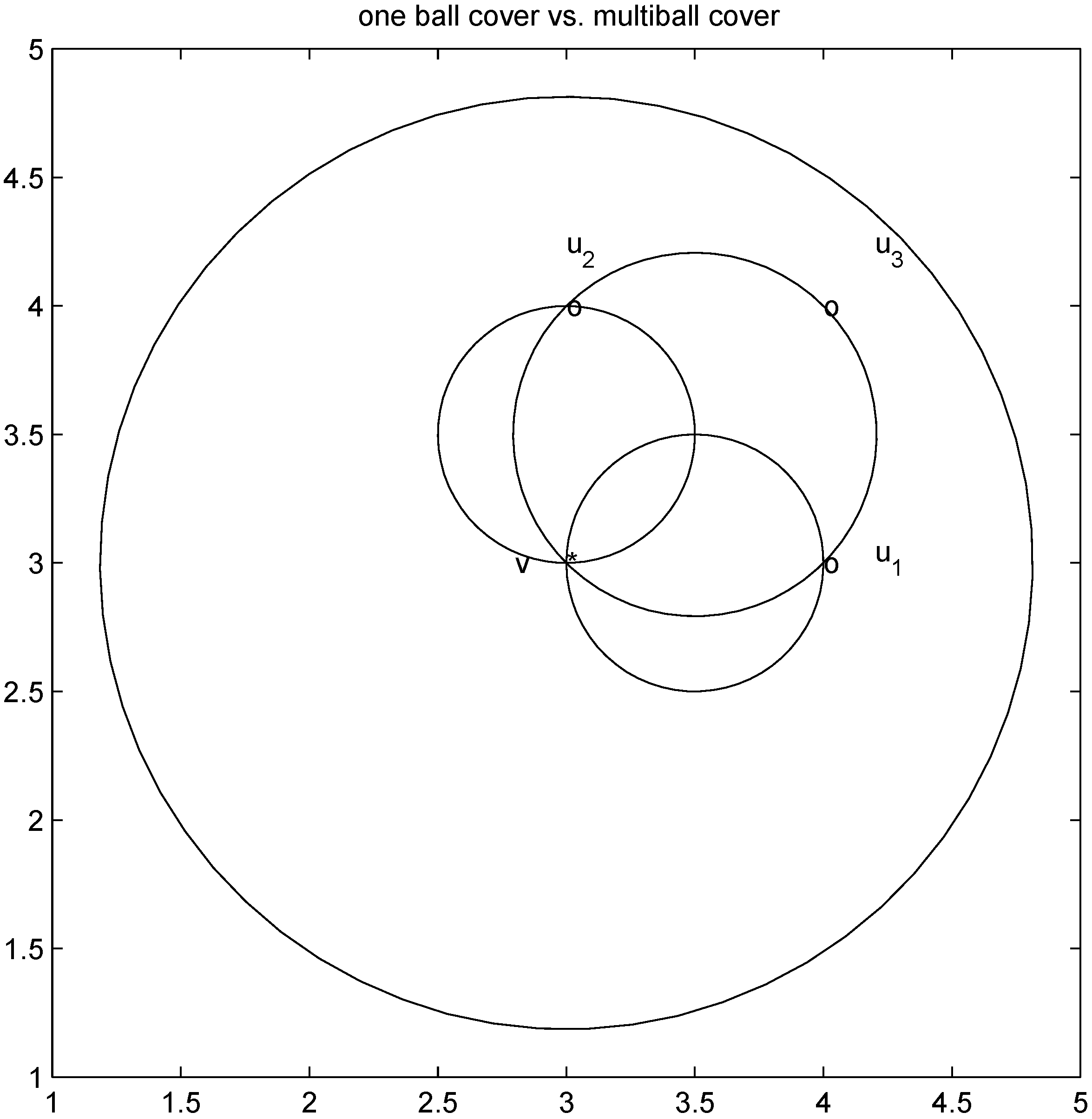
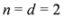 ,
,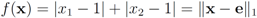
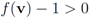 . Let
. Let 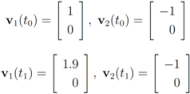
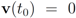 with
with 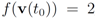 , and
, and 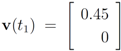 with
with 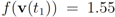 . At the same time
. At the same time 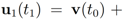
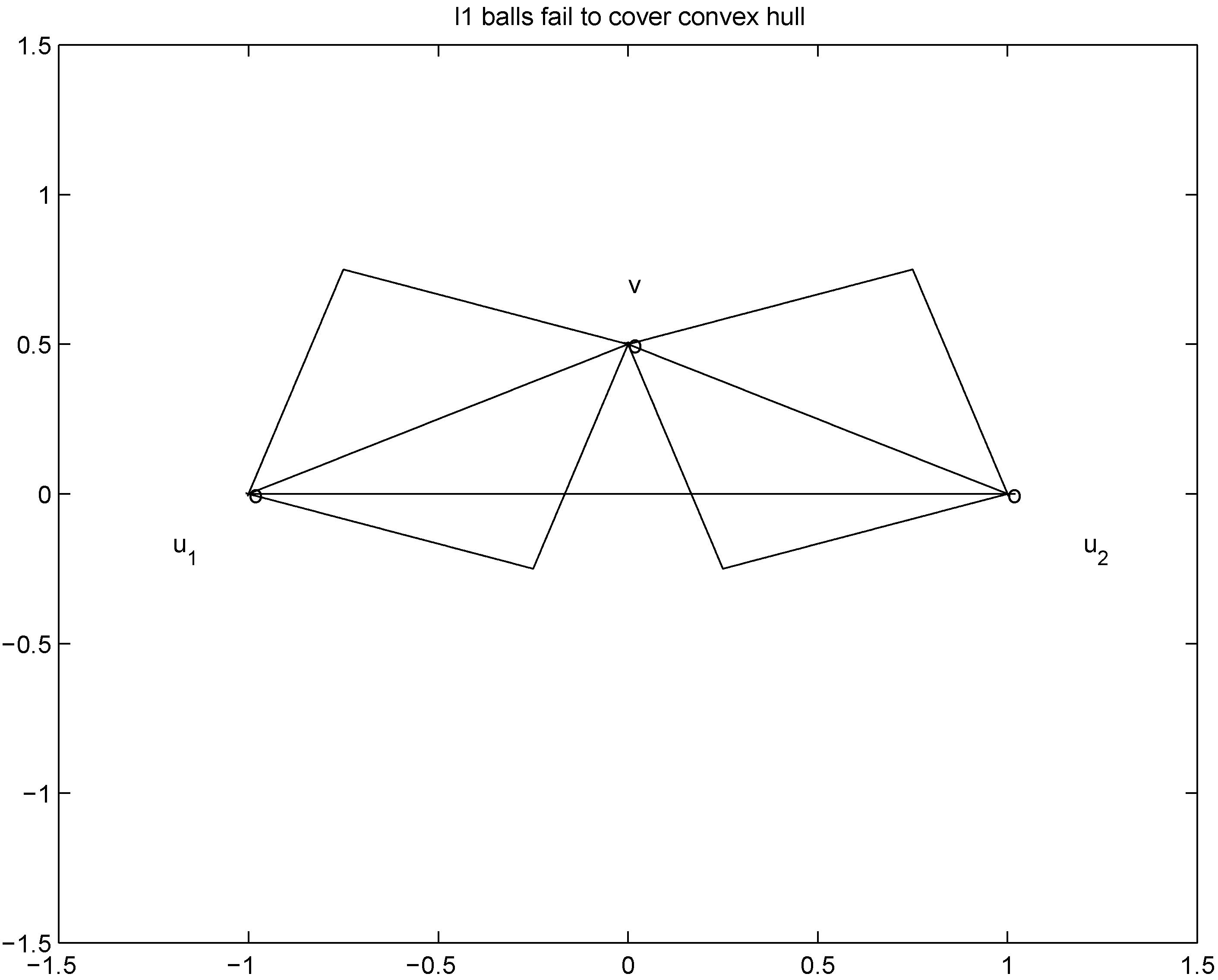
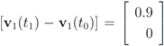 . It is easy to see that the l2 ball of radius
. It is easy to see that the l2 ball of radius 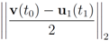 centered at
centered at 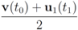 intersects the l1 ball of radius 1 centered at
intersects the l1 ball of radius 1 centered at  (see Figure 3). Hence the algorithm suggested in [8] requires nodes to communicate at time t1.
(see Figure 3). Hence the algorithm suggested in [8] requires nodes to communicate at time t1.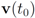 to the set
to the set  is 1, and since
is 1, and since 
 is an l1 ball of radius
is an l1 ball of radius 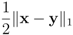 centered at
centered at 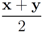 . Indeed, when, for example,
. Indeed, when, for example, 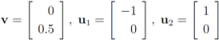
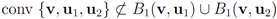
5. Experimental Results
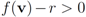 while minimizing communication between the nodes. From now on we shall assume simultaneous arrival of a new text at each node.
while minimizing communication between the nodes. From now on we shall assume simultaneous arrival of a new text at each node.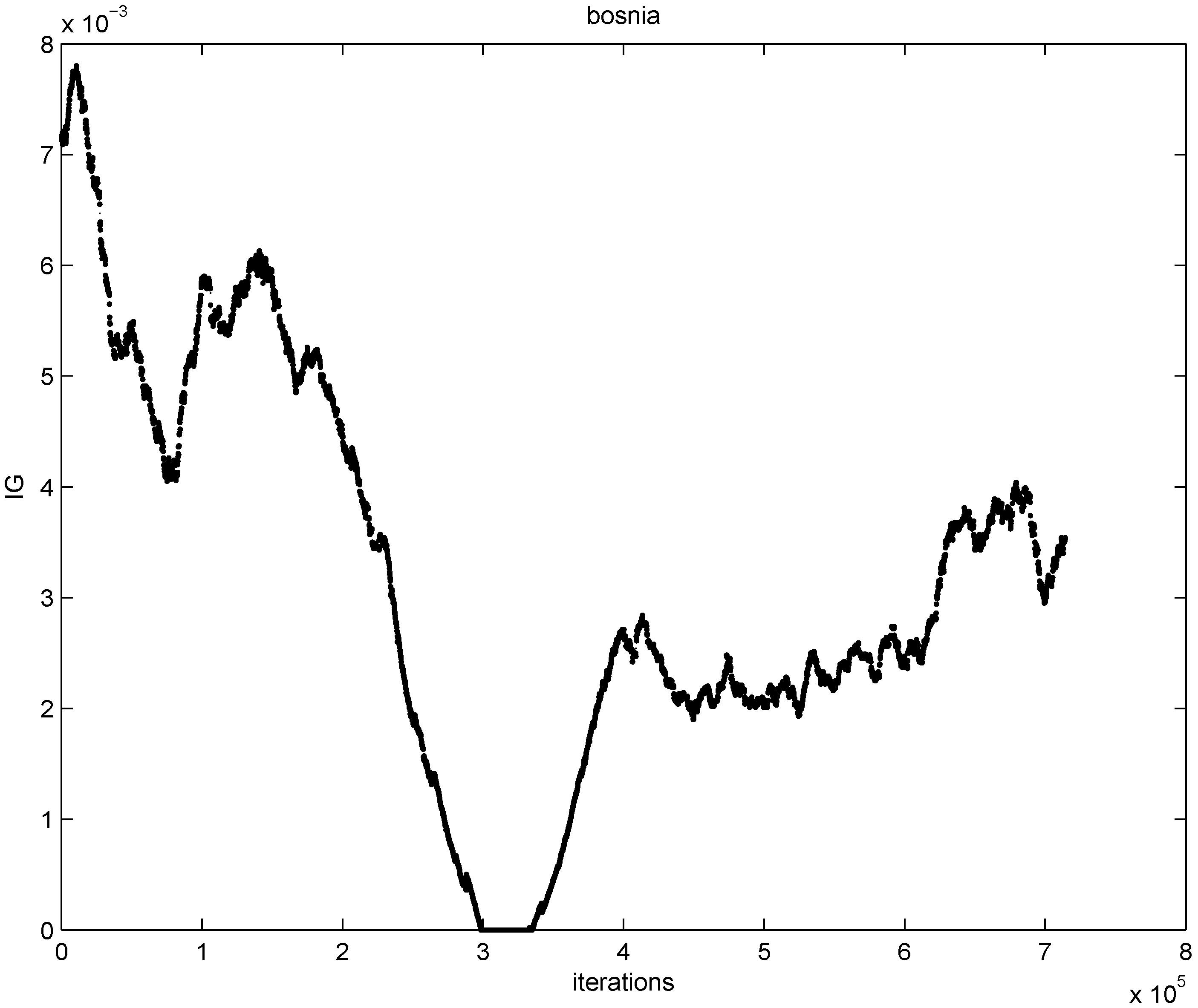
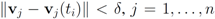 ) at each node is verified. If at least one node violates the local constraint, the average
) at each node is verified. If at least one node violates the local constraint, the average 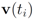 is updated. Our numerical experiment with the feature “bosnia", the l2 norm, and the threshold
is updated. Our numerical experiment with the feature “bosnia", the l2 norm, and the threshold 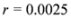 (reported in [8] as the threshold for feature “bosnia" incurring the highest communication cost) shows overall 4006 computation of the mean vector. An application of Equation (14) yields 240,360 messages. We repeat this experiment with l∞, and l1 norms. The results obtained and collected in Table 2 show that the smallest number of the mean updates is required for the l1 norm.
(reported in [8] as the threshold for feature “bosnia" incurring the highest communication cost) shows overall 4006 computation of the mean vector. An application of Equation (14) yields 240,360 messages. We repeat this experiment with l∞, and l1 norms. The results obtained and collected in Table 2 show that the smallest number of the mean updates is required for the l1 norm.  .
.
| Distance | Mean Comps | Messages | LL | LG | GL | GG |
|---|---|---|---|---|---|---|
| l2 | 4006 | 240,360 | 959 | 2 | 2 | 3043 |
| l∞ | 3801 | 228,060 | 913 | 2 | 2 | 2884 |
| l1 | 3053 | 183,180 | 805 | 2 | 2 | 2244 |
 goes through a sequence of updates, and the values
goes through a sequence of updates, and the values 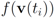 may be larger than, equal to, or less than the threshold r. We monitor the case
may be larger than, equal to, or less than the threshold r. We monitor the case 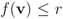 the same way as that of
the same way as that of 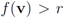 . In addition to the number of mean computations, we collect statistics concerning “crossings" (or lack of thereof), i.e., number of instances when the location of the mean v and its update
. In addition to the number of mean computations, we collect statistics concerning “crossings" (or lack of thereof), i.e., number of instances when the location of the mean v and its update 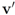 relative to the surface
relative to the surface 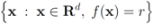 are either identical or different. Specifically over the monitoring period we denote by:
are either identical or different. Specifically over the monitoring period we denote by:- 1. “LL" the number of instances when
and
,
- 2. “LG" the number of instances when
and
,
- 3. “GL" the number of instances when
and
,
- 4. “GG" the number of instances when
and
.
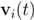 does not have to be uniform. Taking on account distribution of signals at each node may lead to additional communication savings. We illustrate this statement by a simple example involving just two nodes. If, for example, there is a reason to believe that
does not have to be uniform. Taking on account distribution of signals at each node may lead to additional communication savings. We illustrate this statement by a simple example involving just two nodes. If, for example, there is a reason to believe that 
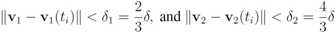
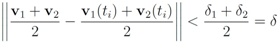
- 1. Start with the initial set of weights
- 2. As texts arrive at the next time instance
each node computes
If at timea local constraint is violated, then, in addition to
messages (see Equation (14)), each node j broadcasts
to the root, the root computes
, and transmits the updated weights
back to node j.
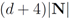
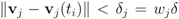 the number of mean computations is reported in Table 3.
the number of mean computations is reported in Table 3.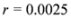 as the threshold value that incurred the highest communication cost, the paper leaves the concept of “communication cost" undefined (we define transmission of a double precision real number as a single “message"). In addition [9] provides a graph of “Messages vs. Threshold" only. It appears that the maximal value of “bosnia Messages vs. Threshold" graph is somewhere between 100,000 and 200,000.
as the threshold value that incurred the highest communication cost, the paper leaves the concept of “communication cost" undefined (we define transmission of a double precision real number as a single “message"). In addition [9] provides a graph of “Messages vs. Threshold" only. It appears that the maximal value of “bosnia Messages vs. Threshold" graph is somewhere between 100,000 and 200,000.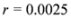 , and stream dependent local constraint
, and stream dependent local constraint 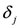 .
.
| Distance | Mean Comps | Messages | LL | LG | GL | GG |
|---|---|---|---|---|---|---|
| l2 | 2388 | 191,040 | 726 | 2 | 2 | 1658 |
| l∞ | 2217 | 177,360 | 658 | 2 | 2 | 1555 |
| l1 | 1846 | 147,680 | 611 | 2 | 2 | 1231 |
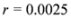 , and stream dependent local constraint
, and stream dependent local constraint 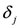 .
.
| Distance | Mean Comps | Messages |
|---|---|---|
| l2 | 1491 | 119,280 |
| l∞ | 1388 | 111,040 |
| l1 | 1304 | 104,320 |
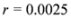 , and stream dependent local constraint
, and stream dependent local constraint 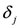 .
.
| Distance | Mean Comps | Messages |
|---|---|---|
| l2 | 7656 | 612,480 |
| l∞ | 7377 | 590,160 |
| l1 | 6309 | 504,720 |
6. Future Research Directions
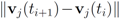 over time contribute uniformly to local constraints. Attaching more weight to recent changes than to older ones may contribute to further improvement of monitoring process.
over time contribute uniformly to local constraints. Attaching more weight to recent changes than to older ones may contribute to further improvement of monitoring process.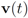 is updated because of a single node violation. This observation naturally leads to the idea of clustering nodes, and independent monitoring of the node clusters equipped with a coordinator. The monitoring will become a two step procedure. At the first step node violations are checked in each node separately. If a node violates its local constraint, the corresponding cluster computes updated cluster coordinator. At the second step, violations of local constraints by coordinators are checked, and if at least one violation is detected the root is updated. Table 6 indicates that in most of the instances only one coordinator will be effected, and, since communication within cluster requires less messages, the two step procedure briefly described above has a potential to bring additional savings.
is updated because of a single node violation. This observation naturally leads to the idea of clustering nodes, and independent monitoring of the node clusters equipped with a coordinator. The monitoring will become a two step procedure. At the first step node violations are checked in each node separately. If a node violates its local constraint, the corresponding cluster computes updated cluster coordinator. At the second step, violations of local constraints by coordinators are checked, and if at least one violation is detected the root is updated. Table 6 indicates that in most of the instances only one coordinator will be effected, and, since communication within cluster requires less messages, the two step procedure briefly described above has a potential to bring additional savings.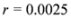 , and l2 norm
, and l2 norm
| nodes | violations |
|---|---|
| 1 | 3034 |
| 2 | 620 |
| 3 | 162 |
| 4 | 70 |
| 5 | 38 |
| 6 | 26 |
| 7 | 34 |
| 8 | 17 |
| 9 | 5 |
| 10 | 0 |
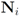 so that the total change within cluster
so that the total change within cluster 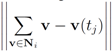 is minimized, i.e., nodes with different variations
is minimized, i.e., nodes with different variations 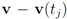 that cancel out each other as much as possible should be assigned to the same cluster. Hence, unlike classical clustering procedures, one needs to combine “dissimilar" nodes together. This is a challenging new type of a difficult clustering problem.
that cancel out each other as much as possible should be assigned to the same cluster. Hence, unlike classical clustering procedures, one needs to combine “dissimilar" nodes together. This is a challenging new type of a difficult clustering problem.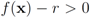 should be conducted with an error margin (i.e., the inequality
should be conducted with an error margin (i.e., the inequality 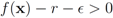 should be investigated, see [9]). A possible effect of an error margin on the required communication load is another direction of future research.
should be investigated, see [9]). A possible effect of an error margin on the required communication load is another direction of future research. 7. Conclusions
Acknowledgments
References
- Madden, S.; Franklin, M.J. An Architecture for Queries Over Streaming Sensor Data. In Proceedings of the ICDE 02, San Jose, CA, 26 February–1 March 2002; pp. 555–556.
- Dilman, M.; Raz, D. Efficient Reactive Monitoring. In Proceedings of the Twentieth Annual Joint Conference of the IEEE Computer and Communication Societies, Anchorage, Alaska, 2001; pp. 1012–1019.
- Zhu, Y.; Shasha, D. Statestream: Statistical Monitoring of Thousands of Data Streamsin Real Time. In Proceeding of the 28th international conference on Very Large Data Bases (VLDB), Hong Kong, China, 2002; pp. 358–369.
- Yi, B.-K.; Sidiropoulos, N.; Johnson, T.; Jagadish, H.V.; Faloutsos, C.; Biliris, A. Online Datamining for Co–Evolving Time Sequences. In Proceedings of ICDE 00IEEE Computer Society, San Diego, CA, 2000; pp. 13–22.
- Manjhi, A.; Shkapenyuk, V.; Dhamdhere, K.; Olston, C. Finding (Recently) Frequent Items in Distributed Data Streams. In Proceedings of the 21st International Conference on Data Engineering (ICDE 05), Tokyo, Japan, 2005; pp. 767–778.
- Wolff, R.; Bhaduri, K.; Kargupta, H. Local L2-Thresholding Based Data Mining in Peer-to-Peer Systems. In Proceedings of the SIAM International Conference on Data Mining (SDM 06), Bethesda, MD, USA, 2006; pp. 430–441.
- Wolff, R.; Bhaduri, K.; Kargupta, H. A generic local algorithm with applications for data mining in large distributed systems. IEEE Trans. Knowl. Data Eng. 2009, 21, 465–478. [Google Scholar] [CrossRef]
- Sharfman, I.; Schuster, A.; Keren, D. A geometric approach to monitoring threshold functions over distributed data streams. ACM Trans. Database Syst. 2007, 23, 23–29. [Google Scholar]
- Sharfman, I.; Schuster, A.; Keren, D. A Geometric Approach to Monitoring Threshold Functions over Distributed Data Streams. In Ubiquitous Knowledge Discovery; May, M., Saitta, L., Eds.; Springer–Verlag: New York, NY, USA, 2010; pp. 163–186. [Google Scholar]
- Kogan, J. Feature Selection over Distributed Data Streams through Convex Optimization. In Proceedings of the Twelfth SIAM International Conference on Data Mining (SDM 2012), Anaheim, CA, USA, 2012; pp. 475–484.
- Keren, D.; Sharfman, I.; Schuster, A.; Livne, A. Shape sensitive geometric monitoring. IEEE Trans. Knowl. Data Eng. 2012, 24, 1520–1535. [Google Scholar] [CrossRef]
- Gray, R.M. Entropy and Information Theory; Springer–Verlag: New York, NY, USA, 1990; pp. 119–162. [Google Scholar]
- Hinrichsen, D.; Pritchard, A.J. Real and Complex Stability Radii: A Survey. In Controlof Uncertain Systems; Hinrichsen, D., Pritchard, A.J., Eds.; Birkhauser: Boston, MA, USA, 1990; pp. 119–162. [Google Scholar]
- Rudin, W. Principles of Mathematical Analysis; McGraw-Hill: New York, NY, USA, 1976. [Google Scholar]
- Rockafellar, R.T. Convex Analysis; Princeton University Press: Princeton, NJ, USA, 1970. [Google Scholar]
- Bottou, L. Home Page. Available online: leon.bottou.org/projects/sgd (accessed on 14 September 2012).
- Mirkin, B. Clustering for Data Mining: A Data Recovery Approach; Chapman & Hall/CRC: Boca Raton, FL, USA, 2005. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Malinovsky, Y.; Kogan, J. Monitoring Threshold Functions over Distributed Data Streams with Node Dependent Constraints. Algorithms 2012, 5, 379-397. https://doi.org/10.3390/a5030379
Malinovsky Y, Kogan J. Monitoring Threshold Functions over Distributed Data Streams with Node Dependent Constraints. Algorithms. 2012; 5(3):379-397. https://doi.org/10.3390/a5030379
Chicago/Turabian StyleMalinovsky, Yaakov, and Jacob Kogan. 2012. "Monitoring Threshold Functions over Distributed Data Streams with Node Dependent Constraints" Algorithms 5, no. 3: 379-397. https://doi.org/10.3390/a5030379
APA StyleMalinovsky, Y., & Kogan, J. (2012). Monitoring Threshold Functions over Distributed Data Streams with Node Dependent Constraints. Algorithms, 5(3), 379-397. https://doi.org/10.3390/a5030379





































