Abstract
Monitoring data streams in a distributed system has attracted considerable interest in recent years. The task of feature selection (e.g., by monitoring the information gain of various features) requires a very high communication overhead when addressed using straightforward centralized algorithms. While most of the existing algorithms deal with monitoring simple aggregated values such as frequency of occurrence of stream items, motivated by recent contributions based on geometric ideas we present an alternative approach. The proposed approach enables monitoring values of an arbitrary threshold function over distributed data streams through stream dependent constraints applied separately on each stream. We report numerical experiments on a real-world data that detect instances where communication between nodes is required, and compare the approach and the results to those recently reported in the literature.
1. Introduction
In many emerging applications one needs to process a continuous stream of data in real time. Sensor networks [1], network monitoring [2], and real-time analysis of financial data [3,4] are examples of such applications. Monitoring queries is a particular class of queries in the context of data streams. Previous work in this area deals with monitoring simple aggregates [2], or term frequency occurrence in a set of distributed streams [5].
A general framework for efficient local algorithms monitoring l2 norm of the data average of large networks of computers, wireless sensors, or mobile devices was introduced in [6], and further developed in [7]. The current contribution is motivated by results recently reported in [8,9] with focus on a special case of the general model considered in [7]. This special case can be briefly described as follows:
Let 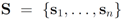 be a set of data streams collected at n nodes. Let v1(t),...,vn(t) be d dimensional real time varying vectors derived from the streams. For a function
be a set of data streams collected at n nodes. Let v1(t),...,vn(t) be d dimensional real time varying vectors derived from the streams. For a function 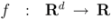 we would like to confirm the inequality
we would like to confirm the inequality
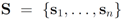 be a set of data streams collected at n nodes. Let v1(t),...,vn(t) be d dimensional real time varying vectors derived from the streams. For a function
be a set of data streams collected at n nodes. Let v1(t),...,vn(t) be d dimensional real time varying vectors derived from the streams. For a function 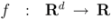 we would like to confirm the inequality
we would like to confirm the inequality 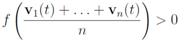
while minimizing communication between the nodes. Monitoring inequality (1), or monitoring geometric location of the mean is a problem that can be addressed using a variety of different mathematical tools. A specific choice of a monitoring tool is up to the user. We note that the problem as stated above does not specify any particular tool, l2, or any other norm that is required to address it.
The problem was recently addressed in [10], where the approach proposed imposes equal constraints on each node. In addition to previously used l2 norm (see, e.g., [6,7,8,9,11]) the paper provides theoretical framework for using a wide variety of convex functions, and, as an illustration, runs numerical experiments using l2, l1 and l∞ norms. In all numerical experiments reported in [10] an application of the same algorithm with l1 norm generates superior results. This paper extends results in [10] in a machine learning direction—a constraint imposed on each node depends on the stream history at the node.
As a simple illustration of the problem considered in the paper we focus on two scalar functions v1(t) and v2(t), and the identity function f (i.e., f(x) = x).We would like to guarantee the inequality
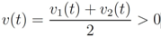
while keeping the nodes silent as much as possible. A possible strategy is to verify the initial inequality 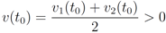 and to keep both nodes silent while
and to keep both nodes silent while
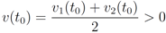 and to keep both nodes silent while
and to keep both nodes silent while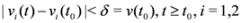
The first time t1 when one of the functions, say v1(t), crosses the boundary of the local constraint, i.e., 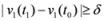 the nodes communicate, the mean v(t1) is computed, the local constraint δ is updated and made available to the nodes, and nodes are kept silent as long as the inequalities hold.
the nodes communicate, the mean v(t1) is computed, the local constraint δ is updated and made available to the nodes, and nodes are kept silent as long as the inequalities hold.
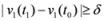 the nodes communicate, the mean v(t1) is computed, the local constraint δ is updated and made available to the nodes, and nodes are kept silent as long as the inequalities hold.
the nodes communicate, the mean v(t1) is computed, the local constraint δ is updated and made available to the nodes, and nodes are kept silent as long as the inequalities hold.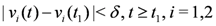
The main contributions of this paper are listed next. We demonstrate that:
- 1. This approach works for a non-linear monitoring function f.
- 2. The results depend on the choice of a norm, and the numerical results reported show that l2 is probably not the best norm when one aims to minimize communication between nodes. In addition to the numerical results presented we also provide a simple illustrative example that highlights this point (see Remark 4.2).
- 3. Selection of node dependent local constraints may decrease communication between the nodes.
- 4. The approach suggested in [10] and adopted in this paper paves the way to achieve further communication savings by clustering nodes, and monitoring cluster coordinators. Although this research direction is beyond the scope of this paper we address it briefly in Section 6.
In the next section we provide a text mining related example that leads to a non-linear threshold function f.
2. Text Mining Application
Let T be a finite text collection (for example a collection of mail or news items). We denote the size of the set T by |T|. We will be concerned with two subsets of T:
- 1. R–the set of “relevant" texts (text not labeled as spam),
- 2. F–the set of texts that contain a “feature" (word or term for example).
We denote complements of the sets by 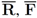 respectably (i.e.,
respectably (i.e., 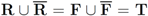 ), and consider the relative size of the four sets
), and consider the relative size of the four sets 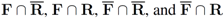 as follows:
as follows:
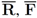 respectably (i.e.,
respectably (i.e., 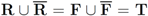 ), and consider the relative size of the four sets
), and consider the relative size of the four sets 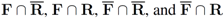 as follows:
as follows: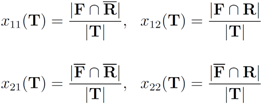
Note that
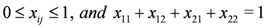
The function f is defined on the simplex (i.e., 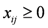 ,
, 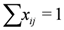 ), and given by
), and given by
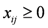 ,
, 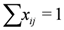 ), and given by
), and given by 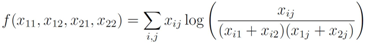
where 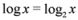 throughout the paper. We next relate empirical version of information gain Equation (3) and the information gain (see e.g., [12]).
throughout the paper. We next relate empirical version of information gain Equation (3) and the information gain (see e.g., [12]).
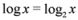 throughout the paper. We next relate empirical version of information gain Equation (3) and the information gain (see e.g., [12]).
throughout the paper. We next relate empirical version of information gain Equation (3) and the information gain (see e.g., [12]).Let Y and X be random variable with know distributions
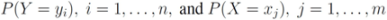
Entropy of Y is defined by
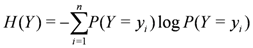
Entropy of Y conditional on X = x denoted by 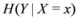 is defined by
is defined by
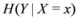 is defined by
is defined by 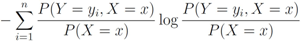
Conditional entropy 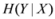 and information gain
and information gain 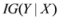 are given by
are given by
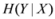 and information gain
and information gain 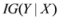 are given by
are given by 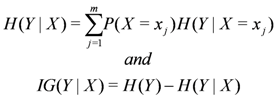
Information gain is symmetric, indeed
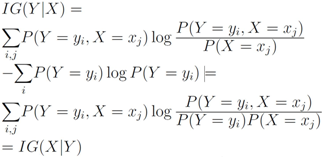
Due to convexity of 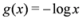 , information gain is non-negative
, information gain is non-negative
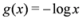 , information gain is non-negative
, information gain is non-negative 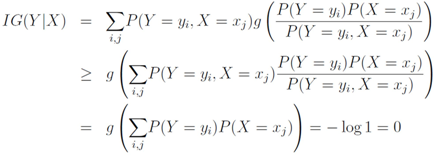
It is easy to see that Equation (3) provides information gain for the “feature".
As an example, we consider n agents installed on n different servers and a stream of texts arriving at the servers. Let 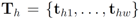 be the last w texts received at the
be the last w texts received at the 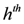 server, with
server, with 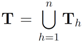 . Note that
. Note that
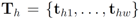 be the last w texts received at the
be the last w texts received at the 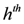 server, with
server, with 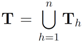 . Note that
. Note that 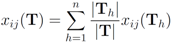
i.e., entries of the global contingency table 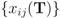 are the average of the local contingency tables
are the average of the local contingency tables 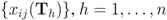 .
.
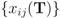 are the average of the local contingency tables
are the average of the local contingency tables 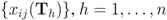 .
.For the given “feature" and a predefined positive threshold r we would like to verify the inequality
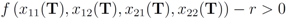
while minimizing communication between the servers. Note that Equation (3) is a nonlinear function. The case of a nonlinear monitoring function is different from that of linear one (in fact [8] calls the nonlinear monitoring function case “fundamentally different"). In the next section we demonstrate the difference, and describe an efficient way to handle the nonlinear case.
3. Non-Linear Threshold Function: An Example
We start with a slight modification of a simple one dimensional example presented in [8].
Example 3.1Let 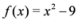 , and
, and  ,
, 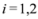 are scalar values stored at two distinct nodes. Note that if
are scalar values stored at two distinct nodes. Note that if 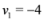 , and
, and 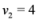 , then
, then
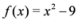 , and
, and  ,
, 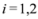 are scalar values stored at two distinct nodes. Note that if
are scalar values stored at two distinct nodes. Note that if 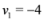 , and
, and 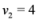 , then
, then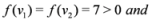
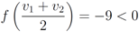
If 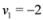 , and
, and 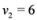 , then
, then
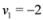 , and
, and 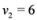 , then
, then 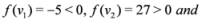
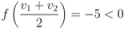
Finally, when 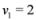 , and
, and 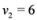 one has
one has
 , and
, and 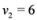 one has
one has 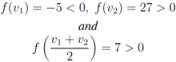
The simple illustrative example leads the authors of [8] to conclude that it is impossible to determine from the values of f at the nodes whether its value at the average is above the threshold or not. The remedy proposed is to consider the vectors 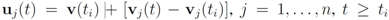 and to monitor the values of f on the convex hull conv
and to monitor the values of f on the convex hull conv  instead of the value of f at the average Equation (1). This strategy leads to sufficient conditions for Equation (1), and may be conservative.
instead of the value of f at the average Equation (1). This strategy leads to sufficient conditions for Equation (1), and may be conservative.
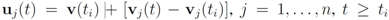 and to monitor the values of f on the convex hull conv
and to monitor the values of f on the convex hull conv  instead of the value of f at the average Equation (1). This strategy leads to sufficient conditions for Equation (1), and may be conservative.
instead of the value of f at the average Equation (1). This strategy leads to sufficient conditions for Equation (1), and may be conservative.The monitoring techniques for values of f on conv  without communication between the nodes are based on the following two observations:
without communication between the nodes are based on the following two observations:
 without communication between the nodes are based on the following two observations:
without communication between the nodes are based on the following two observations: - 1. Convexity property. The mean v(t) is given by
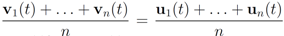 , i.e., the mean v(t) is in the convex hull of
, i.e., the mean v(t) is in the convex hull of 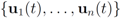 , and
, and 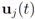 is available to node j without much communication with other nodes.
is available to node j without much communication with other nodes. - 2. If
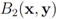 is an l2 ball of radius
is an l2 ball of radius 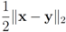 centered at
centered at 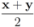 , then
, then
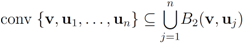
(see Figure 1). Since each ball
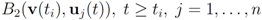
can be monitored by node j with no communication with other nodes, Equation (8) allows to split monitoring of conv  into n independent tasks executed by the n nodes separately and without communication.
into n independent tasks executed by the n nodes separately and without communication.
 into n independent tasks executed by the n nodes separately and without communication.
into n independent tasks executed by the n nodes separately and without communication.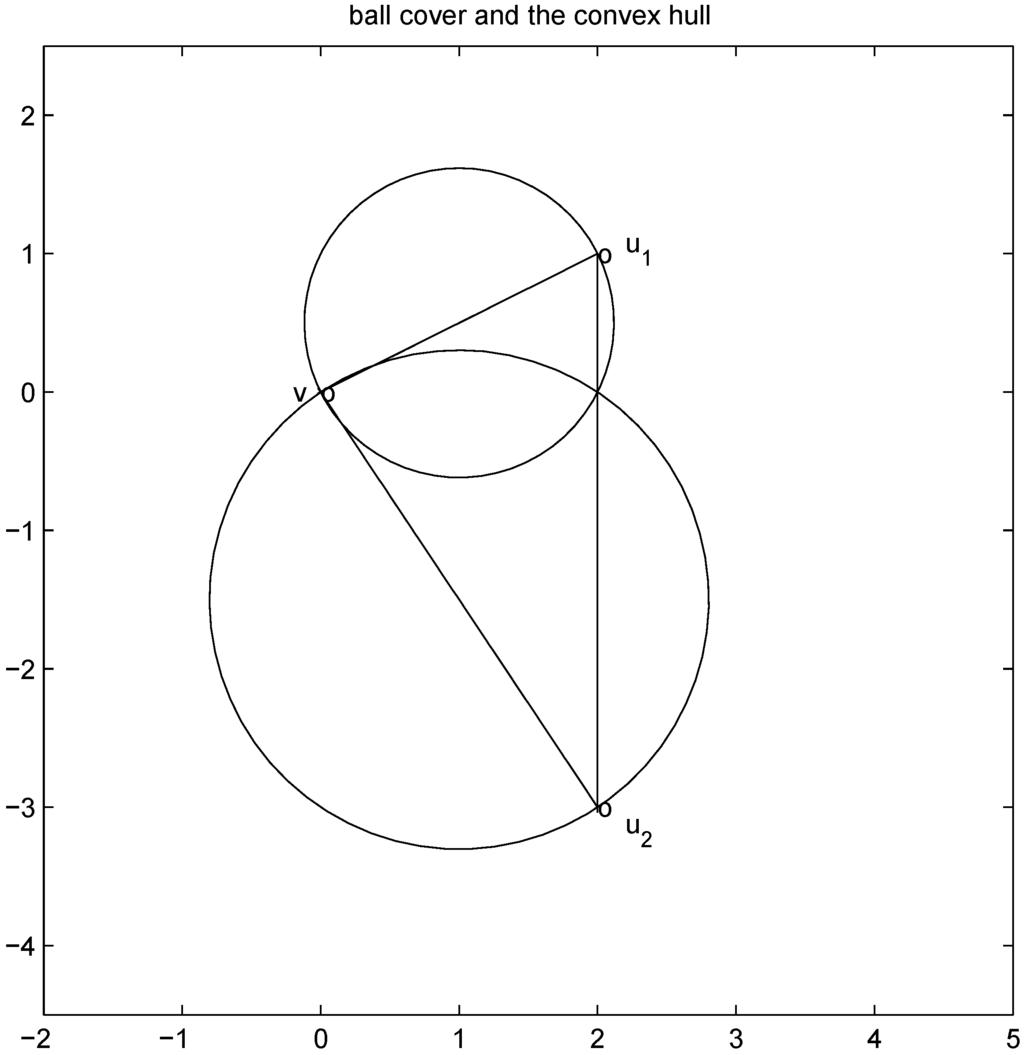
Figure 1.
ball cover.
While the inclusion Equation (8) holds when 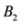 is substituted by
is substituted by 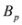 with
with 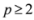 as we show later (see Remark 4.3) the inclusion fails when, for example,
as we show later (see Remark 4.3) the inclusion fails when, for example, 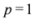 (for experimental results obtained with different norms see Section 5).
(for experimental results obtained with different norms see Section 5).
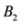 is substituted by
is substituted by 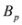 with
with 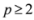 as we show later (see Remark 4.3) the inclusion fails when, for example,
as we show later (see Remark 4.3) the inclusion fails when, for example, 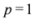 (for experimental results obtained with different norms see Section 5).
(for experimental results obtained with different norms see Section 5).In this paper we propose an alternative strategy that will be briefly explained next using Example 3.1, 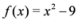 , and assignment provided by Equation (7). Let δ be a positive number. Consider two intervals of radius δ centered at
, and assignment provided by Equation (7). Let δ be a positive number. Consider two intervals of radius δ centered at 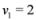 and
and 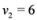 , i.e., we are interested in the intervals
, i.e., we are interested in the intervals
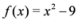 , and assignment provided by Equation (7). Let δ be a positive number. Consider two intervals of radius δ centered at
, and assignment provided by Equation (7). Let δ be a positive number. Consider two intervals of radius δ centered at 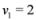 and
and 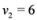 , i.e., we are interested in the intervals
, i.e., we are interested in the intervals 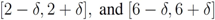
If 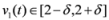 ,
, 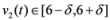 , and δ is small, then the average
, and δ is small, then the average 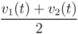 is not far from
is not far from 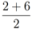 , and
, and 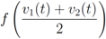 is not far from 7 (hence positive). In fact the sum of the intervals is the interval
is not far from 7 (hence positive). In fact the sum of the intervals is the interval 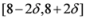 , and
, and
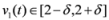 ,
, 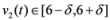 , and δ is small, then the average
, and δ is small, then the average 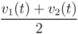 is not far from
is not far from 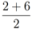 , and
, and 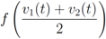 is not far from 7 (hence positive). In fact the sum of the intervals is the interval
is not far from 7 (hence positive). In fact the sum of the intervals is the interval 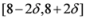 , and
, and 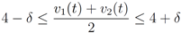
The “zero" points 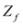 of f are -3 and 3, and as soon as δ is large enough so that the interval
of f are -3 and 3, and as soon as δ is large enough so that the interval 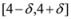 “hits" a point where f vanishes, communication between the nodes is required in order to verify Equation (1). In this particular example as long as
“hits" a point where f vanishes, communication between the nodes is required in order to verify Equation (1). In this particular example as long as 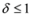 , and, therefore,
, and, therefore,
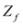 of f are -3 and 3, and as soon as δ is large enough so that the interval
of f are -3 and 3, and as soon as δ is large enough so that the interval 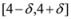 “hits" a point where f vanishes, communication between the nodes is required in order to verify Equation (1). In this particular example as long as
“hits" a point where f vanishes, communication between the nodes is required in order to verify Equation (1). In this particular example as long as 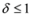 , and, therefore,
, and, therefore, 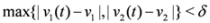
no communication is required between the nodes.
The condition presented above is a sufficient condition that guarantees Equation (1). As any sufficient condition is, this condition can be conservative. In fact when the distance is provided by the l2 norm, this sufficient condition is more conservative than the one provided by “ball monitoring" Equation (9) suggested in [8]. On the other hand, since only a scalar δ should be communicated to each node, the value of the updated mean 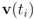 should not be transmitted (hence communication savings are possible), and there is no need to compute the distance from the center of each ball
should not be transmitted (hence communication savings are possible), and there is no need to compute the distance from the center of each ball 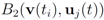 ,
, 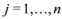 ,
, 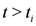 to the zero set
to the zero set 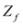 . For detailed comparison of results we refer the reader to [10].
. For detailed comparison of results we refer the reader to [10].
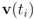 should not be transmitted (hence communication savings are possible), and there is no need to compute the distance from the center of each ball
should not be transmitted (hence communication savings are possible), and there is no need to compute the distance from the center of each ball 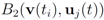 ,
, 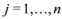 ,
, 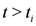 to the zero set
to the zero set 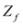 . For detailed comparison of results we refer the reader to [10].
. For detailed comparison of results we refer the reader to [10].We conclude the section by remarking that when inequality Equation (1) is reversed the same technique can be used to monitor the reversed inequality while minimizing communication between the nodes. We provide additional details in Section 5. In the next section we extend the above “monitoring with no communication" argument to the general vector setting. The approach suggested in the next section is motivated by an earlier research on robust stability of control systems (see e.g., [13]).
4. Convex Minimization Problem
In this section we state the monitoring problem as a convex minimization problem. For an appropriate analysis background we refer the interested reader to the classical monograph [14]. For the relevant convex analysis material see [15].
Consider the following optimization problem:
Problem 4.1For a function 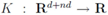 concave with respect to the first d variables
concave with respect to the first d variables 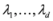 and convex with respect to the last nd variables
and convex with respect to the last nd variables 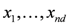 , solve
, solve
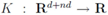 concave with respect to the first d variables
concave with respect to the first d variables 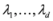 and convex with respect to the last nd variables
and convex with respect to the last nd variables 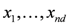 , solve
, solve 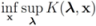
A solution for Problem 4.1 with appropriately selected 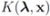 concludes the section.
concludes the section.
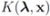 concludes the section.
concludes the section.The connection between Problem 4.1, and the monitoring problem is explained next. Let B be a 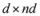 matrix made of n blocks, where each block is the
matrix made of n blocks, where each block is the 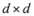 identity matrix multiplied by
identity matrix multiplied by  , so that for a set of n vectors
, so that for a set of n vectors  in
in 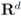 one has
one has
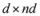 matrix made of n blocks, where each block is the
matrix made of n blocks, where each block is the 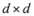 identity matrix multiplied by
identity matrix multiplied by  , so that for a set of n vectors
, so that for a set of n vectors  in
in 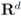 one has
one has 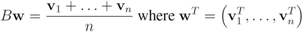
Assume that inequality Equation (1) holds for the vector w, i.e., 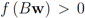 . We are looking for a vector x “nearest" to w so that
. We are looking for a vector x “nearest" to w so that 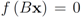 , i.e.,
, i.e., 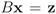 for some
for some 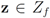 (where
(where 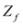 is the zero set of f, i.e.,
is the zero set of f, i.e.,  ). We now fix z
). We now fix z 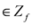 and denote the distance from w to the set
and denote the distance from w to the set 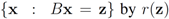 . Note that for each y inside the ball of radius
. Note that for each y inside the ball of radius 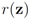 centered at w, one has
centered at w, one has 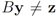 . If y belongs to a ball of radius
. If y belongs to a ball of radius 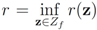 centered at w, then the inequality
centered at w, then the inequality 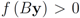 holds true.
holds true.
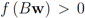 . We are looking for a vector x “nearest" to w so that
. We are looking for a vector x “nearest" to w so that 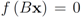 , i.e.,
, i.e., 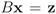 for some
for some 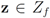 (where
(where 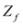 is the zero set of f, i.e.,
is the zero set of f, i.e.,  ). We now fix z
). We now fix z 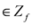 and denote the distance from w to the set
and denote the distance from w to the set 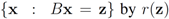 . Note that for each y inside the ball of radius
. Note that for each y inside the ball of radius 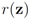 centered at w, one has
centered at w, one has 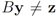 . If y belongs to a ball of radius
. If y belongs to a ball of radius 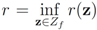 centered at w, then the inequality
centered at w, then the inequality 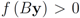 holds true.
holds true.Let 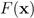 be a “norm" on
be a “norm" on 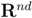 (specific functions F we run the numerical experiments with will be described later). The nearest “bad" vector problem described above is the following.
(specific functions F we run the numerical experiments with will be described later). The nearest “bad" vector problem described above is the following.
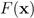 be a “norm" on
be a “norm" on 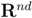 (specific functions F we run the numerical experiments with will be described later). The nearest “bad" vector problem described above is the following.
(specific functions F we run the numerical experiments with will be described later). The nearest “bad" vector problem described above is the following.Problem 4.2For 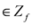 identify
identify
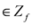 identify
identify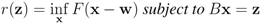
We note that Equation (13) is equivalent to 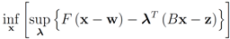 The function
The function
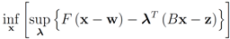 The function
The function 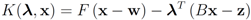
is concave (actually linear) in λ, and convex in x. Hence (see e.g., [15])
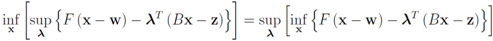
The right hand side of the above equality can be conveniently written as follows
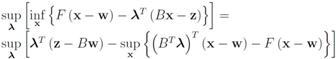
The conjugate 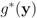 of a function
of a function 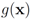 is defined by
is defined by 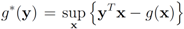 (see e.g., [15]). We note that
(see e.g., [15]). We note that
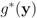 of a function
of a function 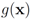 is defined by
is defined by 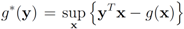 (see e.g., [15]). We note that
(see e.g., [15]). We note that 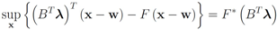
hence to compute
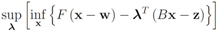
one has to deal with
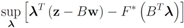
For many functions g the conjugate 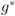 can be easily computed. Next we list conjugate functions for the most popular norms
can be easily computed. Next we list conjugate functions for the most popular norms
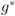 can be easily computed. Next we list conjugate functions for the most popular norms
can be easily computed. Next we list conjugate functions for the most popular norms1. 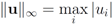
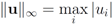
2. 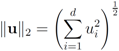
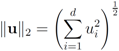
3. 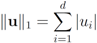
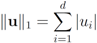
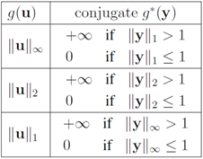
We note that some of the functions F we consider in this paper are different from lP norms (see Table 1 for the list of the functions). We first select 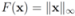 , and show below that in this case
, and show below that in this case
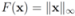 , and show below that in this case
, and show below that in this case 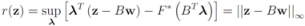
Note that with the choice  the problem
the problem 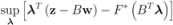 becomes
becomes
 the problem
the problem 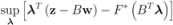 becomes
becomes 
Since 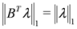 the problem reduces to
the problem reduces to
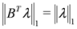 the problem reduces to
the problem reduces to 
The solution to this maximization problem is 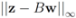 . Analogously, when
. Analogously, when
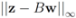 . Analogously, when
. Analogously, when 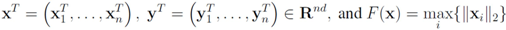
one has 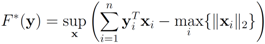 Assuming
Assuming 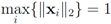 one has to look at
one has to look at
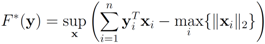 Assuming
Assuming 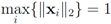 one has to look at
one has to look at 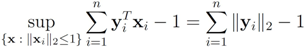
Hence
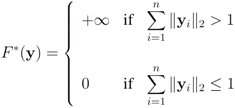
and 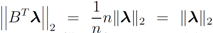 . Finally the value for
. Finally the value for  is given by
is given by 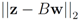 . When
. When 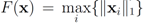 one has
one has 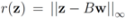 . For clarity sake we collect the above results in Table 1.
. For clarity sake we collect the above results in Table 1.
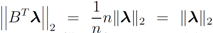 . Finally the value for
. Finally the value for 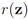 is given by
is given by 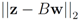 . When
. When 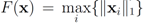 one has
one has 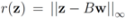 . For clarity sake we collect the above results in Table 1.
. For clarity sake we collect the above results in Table 1.
Table 1.
norm–ball radius correspondence for three different norms and fixed 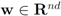 .
.
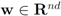 .
.
| F(x) | r(z) |
|---|---|
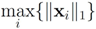 | ||z − Bw||1 |
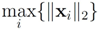 | ||z − Bw||2 |
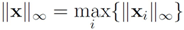 | ||z − Bw||∞ |
In the algorithm described below the norm is denoted just by  (numerical experiments presented in Section 5 are conducted with all three norms). The monitoring algorithm we propose is the following.
(numerical experiments presented in Section 5 are conducted with all three norms). The monitoring algorithm we propose is the following.
 (numerical experiments presented in Section 5 are conducted with all three norms). The monitoring algorithm we propose is the following.
(numerical experiments presented in Section 5 are conducted with all three norms). The monitoring algorithm we propose is the following.Algorithm 4.1Threshold monitoring algorithm.
- 1. Set
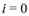 .
. - 2. Until end of stream.
- 3. Set
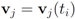 ,
, 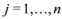 (i.e., remember “initial" values for the vectors).
(i.e., remember “initial" values for the vectors). - 4. Set
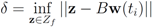 (for definition of w see Equation (12)).
(for definition of w see Equation (12)). - 5. Set
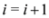 .
. - 6. If
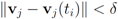 for each
for each 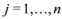 go to step 5elsego to step 3
go to step 5elsego to step 3
In what follows, we assume that transmission of a double precision real number amounts to broadcasting one message. The message computation is based on the assumption that all nodes are updated by a new text simultaneously. When mean update is required, a coordinator (root) requests and receives messages from the nodes.
We next count a number of messages that should be broadcast per one iteration if the local constraint δ is violated at least at one node. We shall denote the set of all nodes by N, the set of nodes complying with the constraint by 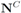 , and the set of nodes violating the constraint by
, and the set of nodes violating the constraint by 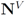 (so that
(so that 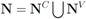 ). The cardinality of the sets is denoted by
). The cardinality of the sets is denoted by 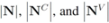 respectively, so that
respectively, so that 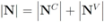 . Assuming
. Assuming 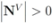 one has the following:
one has the following:
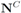 , and the set of nodes violating the constraint by
, and the set of nodes violating the constraint by 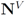 (so that
(so that 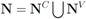 ). The cardinality of the sets is denoted by
). The cardinality of the sets is denoted by 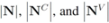 respectively, so that
respectively, so that 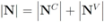 . Assuming
. Assuming 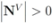 one has the following:
one has the following:- 1.
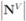 nodes violators transmit their scalar ID and new coordinates to the root (
nodes violators transmit their scalar ID and new coordinates to the root ( 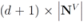 messages).
messages). - 2. the root sends scalar requests for new coordinates to the complying
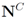 nodes (
nodes ( 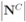 messages).
messages). - 3. the
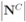 complying nodes transmit new coordinates to the root (
complying nodes transmit new coordinates to the root ( 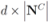 messages).
messages). - 4. root updates itself, computes new distance δ to the surface, and sends δ to each node (
 messages).
messages).
This leads to total of
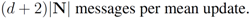
We conclude the section with three remarks. The first one compares conservatism of Algorithm 4.1 and the one suggested in [8]. The second one again compares the ball cover suggested in [8] and application of Algorithm 4.1 with l1 norm. The last one shows by an example that Equation (8) fails when 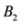 is substituted by
is substituted by 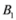 . Significance of this negative result becomes clear in Section 5.
. Significance of this negative result becomes clear in Section 5.
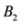 is substituted by
is substituted by 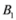 . Significance of this negative result becomes clear in Section 5.
. Significance of this negative result becomes clear in Section 5.Remark 4.1 Let 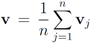 ,and
,and 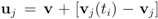 . If the Step 6 inequality holds for each node, then each point of the ball centered at
. If the Step 6 inequality holds for each node, then each point of the ball centered at 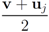 with radius
with radius 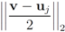 is contained in the l2 ball of radius δ centered at v (see Figure 2). Hence the sufficient condition offered by Algorithm 4.1 is more conservative than the one suggested in [8].
is contained in the l2 ball of radius δ centered at v (see Figure 2). Hence the sufficient condition offered by Algorithm 4.1 is more conservative than the one suggested in [8].
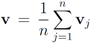 ,and
,and 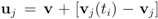 . If the Step 6 inequality holds for each node, then each point of the ball centered at
. If the Step 6 inequality holds for each node, then each point of the ball centered at 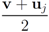 with radius
with radius 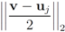 is contained in the l2 ball of radius δ centered at v (see Figure 2). Hence the sufficient condition offered by Algorithm 4.1 is more conservative than the one suggested in [8].
is contained in the l2 ball of radius δ centered at v (see Figure 2). Hence the sufficient condition offered by Algorithm 4.1 is more conservative than the one suggested in [8]. 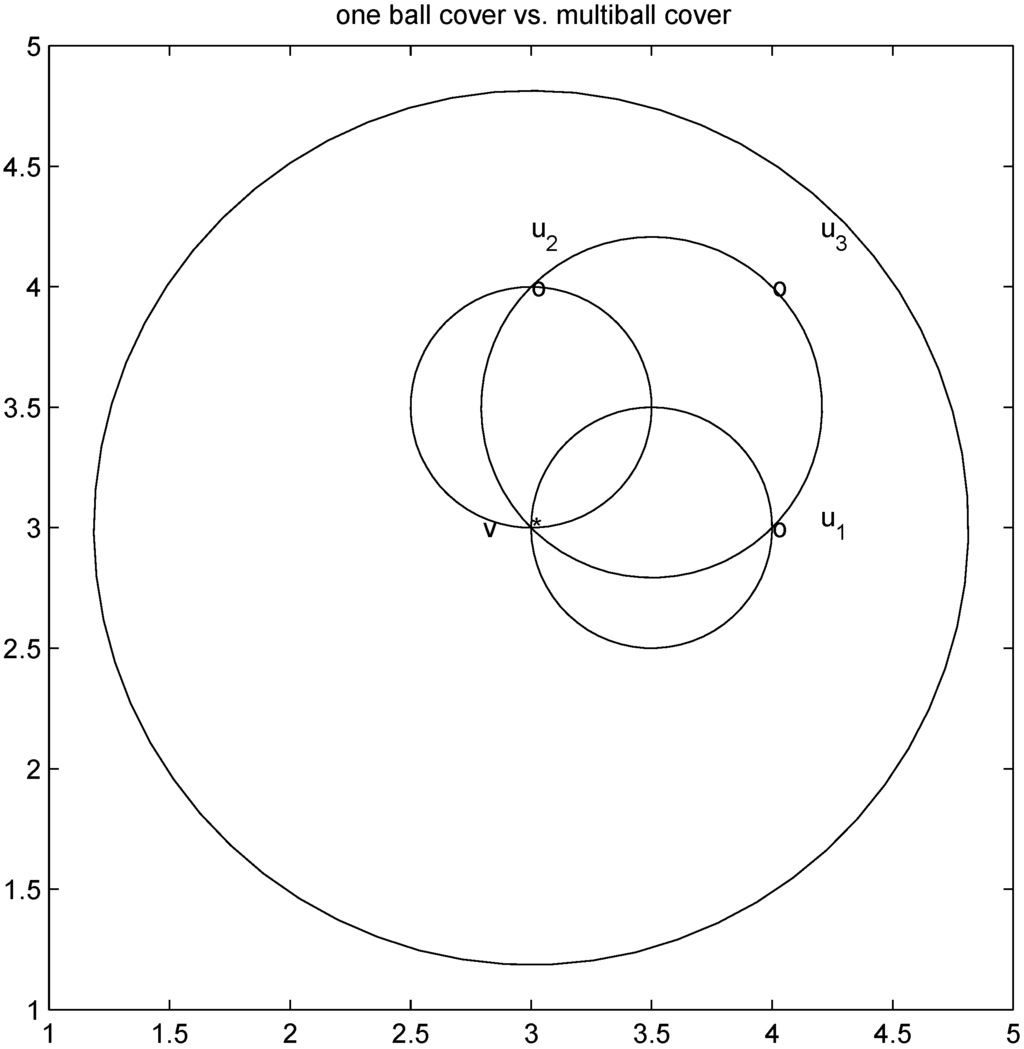
Figure 2.
conservative cover by a single l2 ball.
Algorithm 4.1 can be executed with a variety of different norms, and, as we show next, l2 might not be the best one when communication between the nodes should be minimized.
Remark 4.2 Let 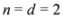 ,
,
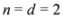 ,
,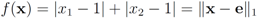
thedistance is given by the l1 norm, and the aim is to monitor the inequality 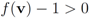 . Let
. Let
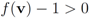 . Let
. Let 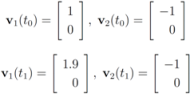
We first consider the “ball cover" construction suggested in [8]. With this data 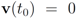 with
with 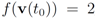 , and
, and 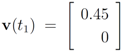 with
with 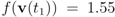 . At the same time
. At the same time 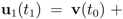
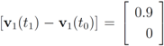 . It is easy to see that the l2 ball of radius
. It is easy to see that the l2 ball of radius 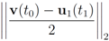 centered at
centered at 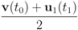 intersects the l1 ball of radius 1 centered at
intersects the l1 ball of radius 1 centered at  (see Figure 3). Hence the algorithm suggested in [8] requires nodes to communicate at time t1.
(see Figure 3). Hence the algorithm suggested in [8] requires nodes to communicate at time t1.
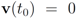 with
with 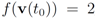 , and
, and 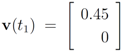 with
with 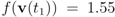 . At the same time
. At the same time 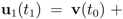
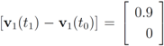 . It is easy to see that the l2 ball of radius
. It is easy to see that the l2 ball of radius 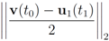 centered at
centered at 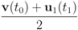 intersects the l1 ball of radius 1 centered at
intersects the l1 ball of radius 1 centered at  (see Figure 3). Hence the algorithm suggested in [8] requires nodes to communicate at time t1.
(see Figure 3). Hence the algorithm suggested in [8] requires nodes to communicate at time t1.On the other hand the l1 distance from 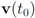 to the set
to the set  is 1, and since
is 1, and since
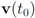 to the set
to the set  is 1, and since
is 1, and since 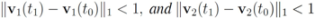
Algorithm 4.1 requires no communication between nodes at time t1. In this particular case the sufficient condition offered by Algorithm 4.1 is less conservative than the one suggested in [8].
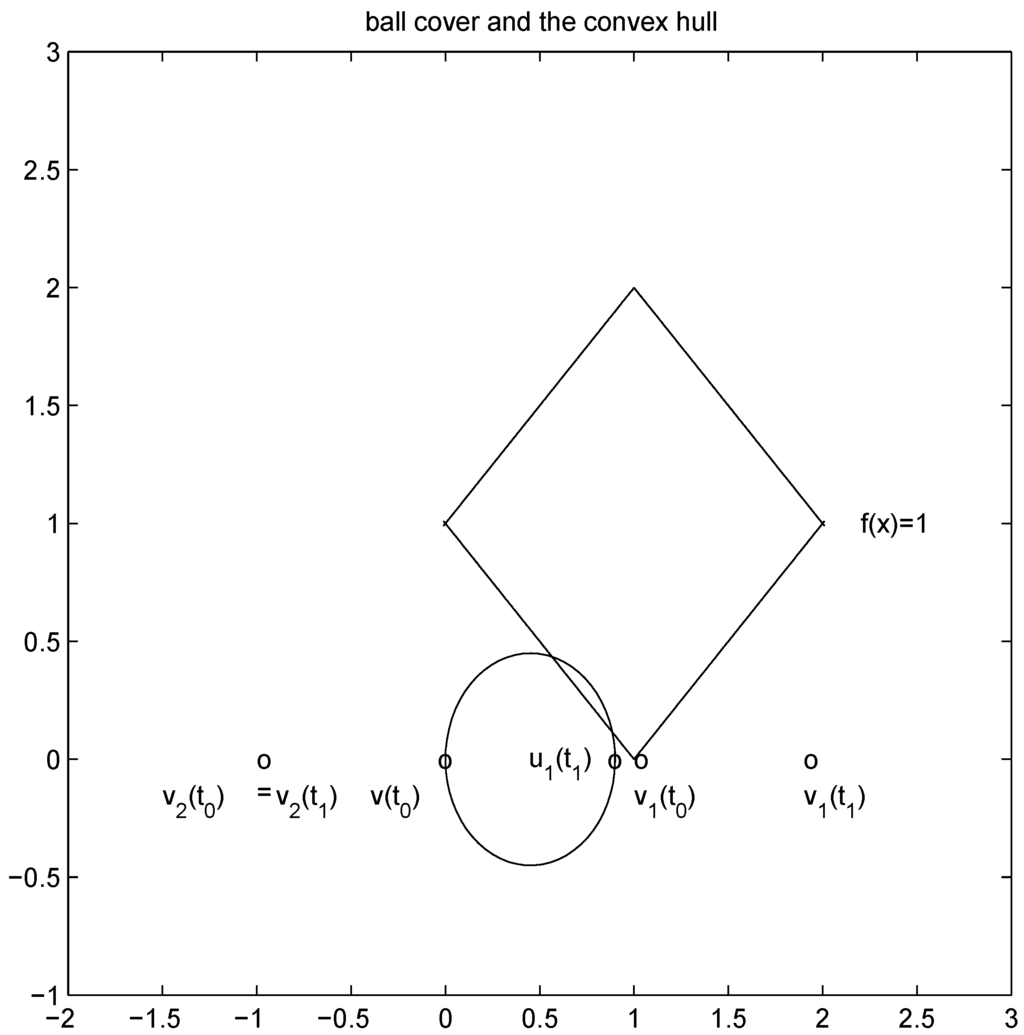
Figure 3.
l2 ball cover requires communication.
Remark 4.3It is easy to see that inclusion Equation (8) fails when  is an l1 ball of radius
is an l1 ball of radius 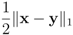 centered at
centered at 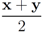 . Indeed, when, for example,
. Indeed, when, for example,
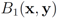 is an l1 ball of radius
is an l1 ball of radius 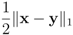 centered at
centered at 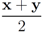 . Indeed, when, for example,
. Indeed, when, for example, 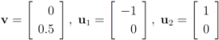
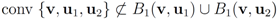
In the next section we apply Algorithm 4.1 to a real life data and report number of required mean computations.
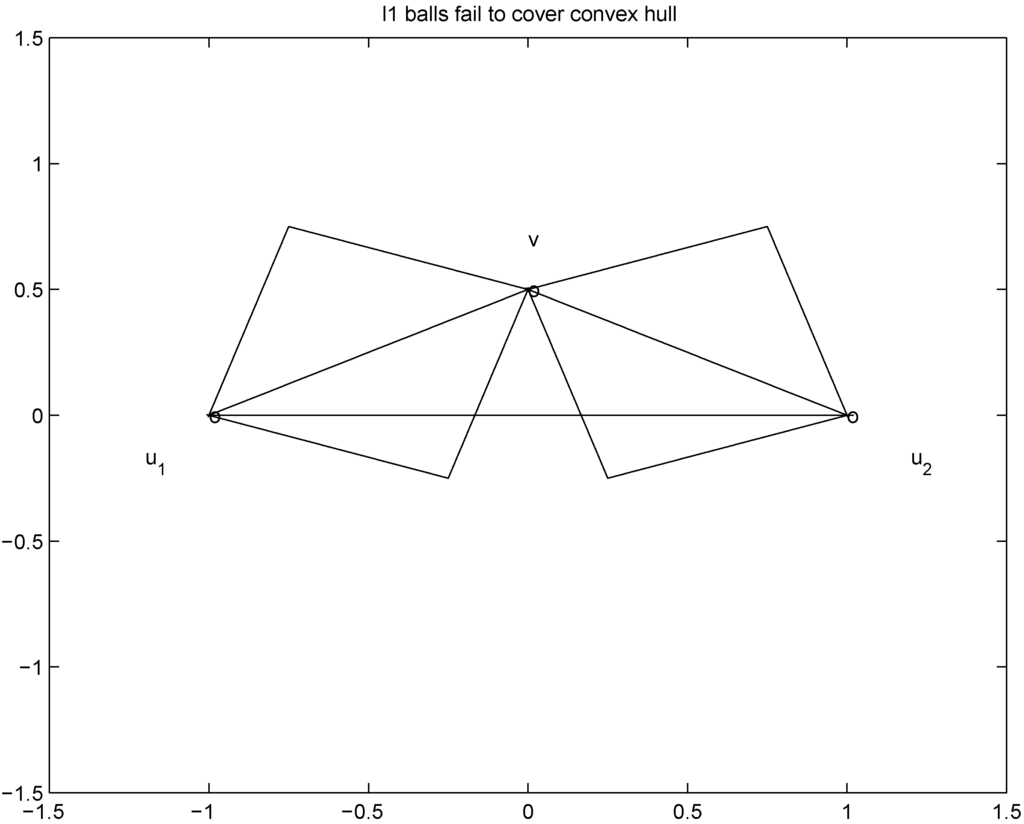
Figure 4.
failed cover by l1 balls.
5. Experimental Results
We apply Algorithm 4.1 to data streams generated from the Reuters Corpus RCV1–V2. The data is available from [16] and consists of 781,265 tokenized documents with DID (document ID) ranging from 2651 to 810596.
The methodology described below attempts to follow that presented in [8]. We simulate n streams by arranging the feature vectors in ascending order with respect to DID, and selecting feature vectors for the stream in the round robin fashion.
In the Reuters Corpus RCV1–V2 each document is labeled as belonging to one or more categories. We label a vector as “relevant" if it belongs to the “CORPORATE/INDUSTRIAL" (“CCAT") category, and “spam" otherwise. Following [9] we focus on three features: “bosnia", “ipo", and “febru". Each experiment was performed with 10 nodes, where each node holds a sliding window containing the last 6700 documents it received.
First we use 67,000 documents to generate initial sliding windows. The remaining 714,265 documents are used to generate data streams, hence the selected feature information gain is computed 714,265 times. Based on all the documents contained in the sliding window at each one of the 714,266 time instances, we compute and graph 714,266 information gain values for the feature “bosnia" (see Figure 5).
For the experiments described below the threshold value r is predefined, and the goal is to monitor the inequality 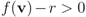 while minimizing communication between the nodes. From now on we shall assume simultaneous arrival of a new text at each node.
while minimizing communication between the nodes. From now on we shall assume simultaneous arrival of a new text at each node.
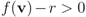 while minimizing communication between the nodes. From now on we shall assume simultaneous arrival of a new text at each node.
while minimizing communication between the nodes. From now on we shall assume simultaneous arrival of a new text at each node.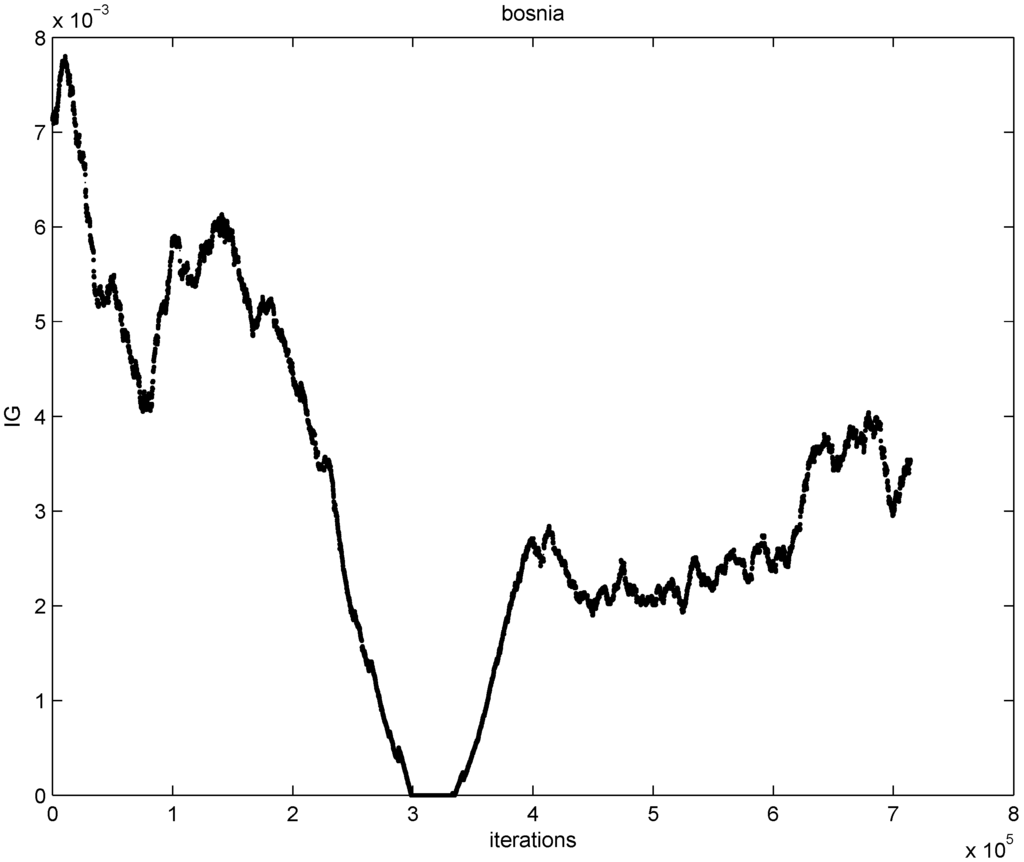
Figure 5.
information gain values for the feature “bosnia”.
As new texts arrive, the local constraint (i.e., inequalities 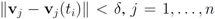 ) at each node is verified. If at least one node violates the local constraint, the average
) at each node is verified. If at least one node violates the local constraint, the average  is updated. Our numerical experiment with the feature “bosnia", the l2 norm, and the threshold
is updated. Our numerical experiment with the feature “bosnia", the l2 norm, and the threshold 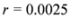 (reported in [8] as the threshold for feature “bosnia" incurring the highest communication cost) shows overall 4006 computation of the mean vector. An application of Equation (14) yields 240,360 messages. We repeat this experiment with l∞, and l1 norms. The results obtained and collected in Table 2 show that the smallest number of the mean updates is required for the l1 norm.
(reported in [8] as the threshold for feature “bosnia" incurring the highest communication cost) shows overall 4006 computation of the mean vector. An application of Equation (14) yields 240,360 messages. We repeat this experiment with l∞, and l1 norms. The results obtained and collected in Table 2 show that the smallest number of the mean updates is required for the l1 norm.
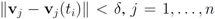 ) at each node is verified. If at least one node violates the local constraint, the average
) at each node is verified. If at least one node violates the local constraint, the average 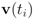 is updated. Our numerical experiment with the feature “bosnia", the l2 norm, and the threshold
is updated. Our numerical experiment with the feature “bosnia", the l2 norm, and the threshold 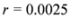 (reported in [8] as the threshold for feature “bosnia" incurring the highest communication cost) shows overall 4006 computation of the mean vector. An application of Equation (14) yields 240,360 messages. We repeat this experiment with l∞, and l1 norms. The results obtained and collected in Table 2 show that the smallest number of the mean updates is required for the l1 norm.
(reported in [8] as the threshold for feature “bosnia" incurring the highest communication cost) shows overall 4006 computation of the mean vector. An application of Equation (14) yields 240,360 messages. We repeat this experiment with l∞, and l1 norms. The results obtained and collected in Table 2 show that the smallest number of the mean updates is required for the l1 norm. 
Table 2.
number of mean computations, messages, and crossings per norm for feature “bosnia" with threshold 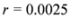 .
.
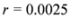 .
.
| Distance | Mean Comps | Messages | LL | LG | GL | GG |
|---|---|---|---|---|---|---|
| l2 | 4006 | 240,360 | 959 | 2 | 2 | 3043 |
| l∞ | 3801 | 228,060 | 913 | 2 | 2 | 2884 |
| l1 | 3053 | 183,180 | 805 | 2 | 2 | 2244 |
Throughout the iterations the mean 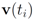 goes through a sequence of updates, and the values
goes through a sequence of updates, and the values 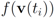 may be larger than, equal to, or less than the threshold r. We monitor the case
may be larger than, equal to, or less than the threshold r. We monitor the case 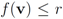 the same way as that of
the same way as that of 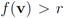 . In addition to the number of mean computations, we collect statistics concerning “crossings" (or lack of thereof), i.e., number of instances when the location of the mean v and its update
. In addition to the number of mean computations, we collect statistics concerning “crossings" (or lack of thereof), i.e., number of instances when the location of the mean v and its update 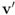 relative to the surface
relative to the surface 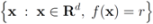 are either identical or different. Specifically over the monitoring period we denote by:
are either identical or different. Specifically over the monitoring period we denote by:
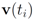 goes through a sequence of updates, and the values
goes through a sequence of updates, and the values 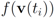 may be larger than, equal to, or less than the threshold r. We monitor the case
may be larger than, equal to, or less than the threshold r. We monitor the case 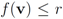 the same way as that of
the same way as that of 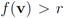 . In addition to the number of mean computations, we collect statistics concerning “crossings" (or lack of thereof), i.e., number of instances when the location of the mean v and its update
. In addition to the number of mean computations, we collect statistics concerning “crossings" (or lack of thereof), i.e., number of instances when the location of the mean v and its update 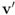 relative to the surface
relative to the surface 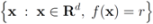 are either identical or different. Specifically over the monitoring period we denote by:
are either identical or different. Specifically over the monitoring period we denote by:- 1. “LL" the number of instances when
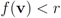 and
and 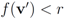 ,
, - 2. “LG" the number of instances when
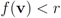 and
and 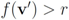 ,
, - 3. “GL" the number of instances when
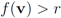 and
and 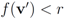 ,
, - 4. “GG" the number of instances when
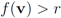 and
and 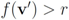 .
.
The number of “crossings" is reported in the last four columns of Table 2.
Note that variation of vectors 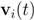 does not have to be uniform. Taking on account distribution of signals at each node may lead to additional communication savings. We illustrate this statement by a simple example involving just two nodes. If, for example, there is a reason to believe that
does not have to be uniform. Taking on account distribution of signals at each node may lead to additional communication savings. We illustrate this statement by a simple example involving just two nodes. If, for example, there is a reason to believe that
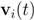 does not have to be uniform. Taking on account distribution of signals at each node may lead to additional communication savings. We illustrate this statement by a simple example involving just two nodes. If, for example, there is a reason to believe that
does not have to be uniform. Taking on account distribution of signals at each node may lead to additional communication savings. We illustrate this statement by a simple example involving just two nodes. If, for example, there is a reason to believe that 
then the number of node violations may be reduced by imposing node dependent constraints
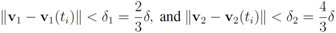
so that the faster varying signal at the second node enjoys larger “freedom" of change, while the inequality
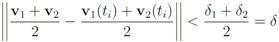
holds true. Assignments of “weighted" local constraints requires information provided by Equation (15). With no additional assumptions about signal distribution, this information is not available. Unlike [11] we refrain from making assumptions regarding possible underlying data distributions, instead we estimate the weights as follows:
- 1. Start with the initial set of weights
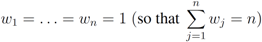
- 2. As texts arrive at the next time instance
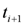 each node computes
each node computes 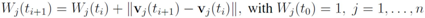 If at time
If at time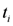 a local constraint is violated, then, in addition to
a local constraint is violated, then, in addition to 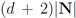 messages (see Equation (14)), each node j broadcasts
messages (see Equation (14)), each node j broadcasts 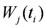 to the root, the root computes
to the root, the root computes 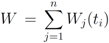 , and transmits the updated weights
, and transmits the updated weights 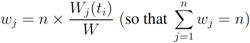 back to node j.
back to node j.
Broadcasts of weights cause increase of total number of messages per iteration to
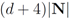
With inequalities in Step 6 of Algorithm 4.1 substituted by 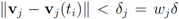 the number of mean computations is reported in Table 3.
the number of mean computations is reported in Table 3.
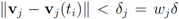 the number of mean computations is reported in Table 3.
the number of mean computations is reported in Table 3.It is of interest to compare results presented in Table 3 with those reported, for example, in [9]. The comparison, however, is not an easy task. While [9] reports the threshold 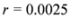 as the threshold value that incurred the highest communication cost, the paper leaves the concept of “communication cost" undefined (we define transmission of a double precision real number as a single “message"). In addition [9] provides a graph of “Messages vs. Threshold" only. It appears that the maximal value of “bosnia Messages vs. Threshold" graph is somewhere between 100,000 and 200,000.
as the threshold value that incurred the highest communication cost, the paper leaves the concept of “communication cost" undefined (we define transmission of a double precision real number as a single “message"). In addition [9] provides a graph of “Messages vs. Threshold" only. It appears that the maximal value of “bosnia Messages vs. Threshold" graph is somewhere between 100,000 and 200,000.
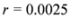 as the threshold value that incurred the highest communication cost, the paper leaves the concept of “communication cost" undefined (we define transmission of a double precision real number as a single “message"). In addition [9] provides a graph of “Messages vs. Threshold" only. It appears that the maximal value of “bosnia Messages vs. Threshold" graph is somewhere between 100,000 and 200,000.
as the threshold value that incurred the highest communication cost, the paper leaves the concept of “communication cost" undefined (we define transmission of a double precision real number as a single “message"). In addition [9] provides a graph of “Messages vs. Threshold" only. It appears that the maximal value of “bosnia Messages vs. Threshold" graph is somewhere between 100,000 and 200,000.
Table 3.
number of mean computations, messages, and crossings per norm for feature “bosnia" with threshold 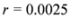 , and stream dependent local constraint
, and stream dependent local constraint 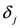 .
.
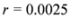 , and stream dependent local constraint
, and stream dependent local constraint 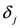 .
.
| Distance | Mean Comps | Messages | LL | LG | GL | GG |
|---|---|---|---|---|---|---|
| l2 | 2388 | 191,040 | 726 | 2 | 2 | 1658 |
| l∞ | 2217 | 177,360 | 658 | 2 | 2 | 1555 |
| l1 | 1846 | 147,680 | 611 | 2 | 2 | 1231 |
We repeat the experiments with “ipo" and “febru" and report the results in Table 4 and Table 5 respectively. The results obtained with stream dependent local constraints is a significant improvement over those presented in [10]. Consistent with the results in [10] l1 norm comes up as the norm that requires smallest number of mean updates in all reported experiments.

Table 4.
number of mean computations, messages, and crossings per norm for feature “febru" with threshold 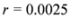 , and stream dependent local constraint
, and stream dependent local constraint 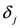 .
.
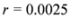 , and stream dependent local constraint
, and stream dependent local constraint 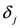 .
.
| Distance | Mean Comps | Messages |
|---|---|---|
| l2 | 1491 | 119,280 |
| l∞ | 1388 | 111,040 |
| l1 | 1304 | 104,320 |

Table 5.
number of mean computations, messages, and crossings per norm for feature “ipo" with threshold 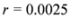 , and stream dependent local constraint
, and stream dependent local constraint 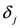 .
.
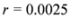 , and stream dependent local constraint
, and stream dependent local constraint 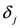 .
.
| Distance | Mean Comps | Messages |
|---|---|---|
| l2 | 7656 | 612,480 |
| l∞ | 7377 | 590,160 |
| l1 | 6309 | 504,720 |
6. Future Research Directions
In what follows we briefly outline a number of immediate research directions we plan to pursue.
The local constraints introduced in this paper depend on history of a data stream at each node, and variations 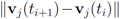 over time contribute uniformly to local constraints. Attaching more weight to recent changes than to older ones may contribute to further improvement of monitoring process.
over time contribute uniformly to local constraints. Attaching more weight to recent changes than to older ones may contribute to further improvement of monitoring process.
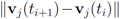 over time contribute uniformly to local constraints. Attaching more weight to recent changes than to older ones may contribute to further improvement of monitoring process.
over time contribute uniformly to local constraints. Attaching more weight to recent changes than to older ones may contribute to further improvement of monitoring process.Table 6 (borrowed from [10]) shows that in about 75% of instances (3034 out of 4006) the mean 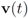 is updated because of a single node violation. This observation naturally leads to the idea of clustering nodes, and independent monitoring of the node clusters equipped with a coordinator. The monitoring will become a two step procedure. At the first step node violations are checked in each node separately. If a node violates its local constraint, the corresponding cluster computes updated cluster coordinator. At the second step, violations of local constraints by coordinators are checked, and if at least one violation is detected the root is updated. Table 6 indicates that in most of the instances only one coordinator will be effected, and, since communication within cluster requires less messages, the two step procedure briefly described above has a potential to bring additional savings.
is updated because of a single node violation. This observation naturally leads to the idea of clustering nodes, and independent monitoring of the node clusters equipped with a coordinator. The monitoring will become a two step procedure. At the first step node violations are checked in each node separately. If a node violates its local constraint, the corresponding cluster computes updated cluster coordinator. At the second step, violations of local constraints by coordinators are checked, and if at least one violation is detected the root is updated. Table 6 indicates that in most of the instances only one coordinator will be effected, and, since communication within cluster requires less messages, the two step procedure briefly described above has a potential to bring additional savings.
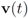 is updated because of a single node violation. This observation naturally leads to the idea of clustering nodes, and independent monitoring of the node clusters equipped with a coordinator. The monitoring will become a two step procedure. At the first step node violations are checked in each node separately. If a node violates its local constraint, the corresponding cluster computes updated cluster coordinator. At the second step, violations of local constraints by coordinators are checked, and if at least one violation is detected the root is updated. Table 6 indicates that in most of the instances only one coordinator will be effected, and, since communication within cluster requires less messages, the two step procedure briefly described above has a potential to bring additional savings.
is updated because of a single node violation. This observation naturally leads to the idea of clustering nodes, and independent monitoring of the node clusters equipped with a coordinator. The monitoring will become a two step procedure. At the first step node violations are checked in each node separately. If a node violates its local constraint, the corresponding cluster computes updated cluster coordinator. At the second step, violations of local constraints by coordinators are checked, and if at least one violation is detected the root is updated. Table 6 indicates that in most of the instances only one coordinator will be effected, and, since communication within cluster requires less messages, the two step procedure briefly described above has a potential to bring additional savings.
Table 6.
number of nodes simultaneously violating local constraints. for feature “bosnia" with threshold 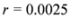 , and l2 norm
, and l2 norm
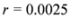 , and l2 norm
, and l2 norm
| nodes | violations |
|---|---|
| 1 | 3034 |
| 2 | 620 |
| 3 | 162 |
| 4 | 70 |
| 5 | 38 |
| 6 | 26 |
| 7 | 34 |
| 8 | 17 |
| 9 | 5 |
| 10 | 0 |
We note that a standard clustering problem is often described as “…finding and describing cohesive or homogeneous chunks in data, the clusters" (see e.g., [17]). The monitoring data streams problem requires to assign to the same cluster i nodes 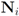 so that the total change within cluster
so that the total change within cluster 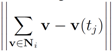 is minimized, i.e., nodes with different variations
is minimized, i.e., nodes with different variations 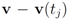 that cancel out each other as much as possible should be assigned to the same cluster. Hence, unlike classical clustering procedures, one needs to combine “dissimilar" nodes together. This is a challenging new type of a difficult clustering problem.
that cancel out each other as much as possible should be assigned to the same cluster. Hence, unlike classical clustering procedures, one needs to combine “dissimilar" nodes together. This is a challenging new type of a difficult clustering problem.
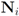 so that the total change within cluster
so that the total change within cluster 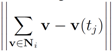 is minimized, i.e., nodes with different variations
is minimized, i.e., nodes with different variations 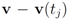 that cancel out each other as much as possible should be assigned to the same cluster. Hence, unlike classical clustering procedures, one needs to combine “dissimilar" nodes together. This is a challenging new type of a difficult clustering problem.
that cancel out each other as much as possible should be assigned to the same cluster. Hence, unlike classical clustering procedures, one needs to combine “dissimilar" nodes together. This is a challenging new type of a difficult clustering problem.Realistically, verification of inequality 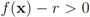 should be conducted with an error margin (i.e., the inequality
should be conducted with an error margin (i.e., the inequality 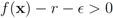 should be investigated, see [9]). A possible effect of an error margin on the required communication load is another direction of future research.
should be investigated, see [9]). A possible effect of an error margin on the required communication load is another direction of future research.
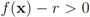 should be conducted with an error margin (i.e., the inequality
should be conducted with an error margin (i.e., the inequality 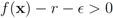 should be investigated, see [9]). A possible effect of an error margin on the required communication load is another direction of future research.
should be investigated, see [9]). A possible effect of an error margin on the required communication load is another direction of future research. 7. Conclusions
Monitoring streams over distributed systems is an important and challenging problem with a wide range of applications. In this paper we build on the approach for monitoring an arbitrary threshold functions suggested in [10], and introduce stream dependent local constraints that serve as a feedback monitoring mechanism. The obtained preliminary results indicate substantial improvement over those reported in [10], and demonstrate that monitoring with l1 norm requires fewer updates than that with l∞ or l2 norm.
Acknowledgments
The authors thank anonymous reviewers whose valuable comments greatly enhanced exposition of the results. The work of the first author was supported in part by 2012 UMBC Summer Faculty Fellowship grant.
References
- Madden, S.; Franklin, M.J. An Architecture for Queries Over Streaming Sensor Data. In Proceedings of the ICDE 02, San Jose, CA, 26 February–1 March 2002; pp. 555–556.
- Dilman, M.; Raz, D. Efficient Reactive Monitoring. In Proceedings of the Twentieth Annual Joint Conference of the IEEE Computer and Communication Societies, Anchorage, Alaska, 2001; pp. 1012–1019.
- Zhu, Y.; Shasha, D. Statestream: Statistical Monitoring of Thousands of Data Streamsin Real Time. In Proceeding of the 28th international conference on Very Large Data Bases (VLDB), Hong Kong, China, 2002; pp. 358–369.
- Yi, B.-K.; Sidiropoulos, N.; Johnson, T.; Jagadish, H.V.; Faloutsos, C.; Biliris, A. Online Datamining for Co–Evolving Time Sequences. In Proceedings of ICDE 00IEEE Computer Society, San Diego, CA, 2000; pp. 13–22.
- Manjhi, A.; Shkapenyuk, V.; Dhamdhere, K.; Olston, C. Finding (Recently) Frequent Items in Distributed Data Streams. In Proceedings of the 21st International Conference on Data Engineering (ICDE 05), Tokyo, Japan, 2005; pp. 767–778.
- Wolff, R.; Bhaduri, K.; Kargupta, H. Local L2-Thresholding Based Data Mining in Peer-to-Peer Systems. In Proceedings of the SIAM International Conference on Data Mining (SDM 06), Bethesda, MD, USA, 2006; pp. 430–441.
- Wolff, R.; Bhaduri, K.; Kargupta, H. A generic local algorithm with applications for data mining in large distributed systems. IEEE Trans. Knowl. Data Eng. 2009, 21, 465–478. [Google Scholar] [CrossRef]
- Sharfman, I.; Schuster, A.; Keren, D. A geometric approach to monitoring threshold functions over distributed data streams. ACM Trans. Database Syst. 2007, 23, 23–29. [Google Scholar]
- Sharfman, I.; Schuster, A.; Keren, D. A Geometric Approach to Monitoring Threshold Functions over Distributed Data Streams. In Ubiquitous Knowledge Discovery; May, M., Saitta, L., Eds.; Springer–Verlag: New York, NY, USA, 2010; pp. 163–186. [Google Scholar]
- Kogan, J. Feature Selection over Distributed Data Streams through Convex Optimization. In Proceedings of the Twelfth SIAM International Conference on Data Mining (SDM 2012), Anaheim, CA, USA, 2012; pp. 475–484.
- Keren, D.; Sharfman, I.; Schuster, A.; Livne, A. Shape sensitive geometric monitoring. IEEE Trans. Knowl. Data Eng. 2012, 24, 1520–1535. [Google Scholar] [CrossRef]
- Gray, R.M. Entropy and Information Theory; Springer–Verlag: New York, NY, USA, 1990; pp. 119–162. [Google Scholar]
- Hinrichsen, D.; Pritchard, A.J. Real and Complex Stability Radii: A Survey. In Controlof Uncertain Systems; Hinrichsen, D., Pritchard, A.J., Eds.; Birkhauser: Boston, MA, USA, 1990; pp. 119–162. [Google Scholar]
- Rudin, W. Principles of Mathematical Analysis; McGraw-Hill: New York, NY, USA, 1976. [Google Scholar]
- Rockafellar, R.T. Convex Analysis; Princeton University Press: Princeton, NJ, USA, 1970. [Google Scholar]
- Bottou, L. Home Page. Available online: leon.bottou.org/projects/sgd (accessed on 14 September 2012).
- Mirkin, B. Clustering for Data Mining: A Data Recovery Approach; Chapman & Hall/CRC: Boca Raton, FL, USA, 2005. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).