Abstract
A disentanglement puzzle consists of mechanically interlinked pieces, and the puzzle is solved by disentangling one piece from another set of pieces. A string puzzle consists of strings entangled with one or more wooden pieces. We consider the generalized string puzzle problem whose input is the layout of strings and a wooden board with holes embedded in the 3-dimensional Euclidean space. We present a polynomial-time transformation from an arbitrary instance f of the 3SAT problem to a string puzzle s such that f is satisfiable if and only if s is solvable. Therefore, the generalized string puzzle problem is NP-hard.
1. Introduction
A disentanglement puzzle consists of mechanically interlinked pieces, and the puzzle is solved by disentangling one piece or a set of pieces from another set of pieces. A typical disentanglement puzzle is a wire puzzle, which is one of the most fundamental and popular playthings.
A wire puzzle consists of two or more entangled stiff wires. Wires may or may not be closed loops, and they have complex shapes. Normally, wire puzzles are solved by disentangling one piece from another set of pieces without cutting or bending the wires.
A string puzzle is also a disentanglement puzzle, which is an intellectual training toy especially for young children. To avoid accidental injury, it is composed entirely of natural materials, instead of stiff sharp wires. Most string puzzles consist of soft strings entangled with wooden pieces. The strings are closed loops or unclosed strings. Unclosed strings usually have wooden balls attached to their ends. Usually, one of the wooden pieces is a board with holes. Strings are entangled with each other and with wooden pieces through the holes. Sometimes, a string may have a wooden ring which can slide along the string.
In this paper, we investigate the computational complexity of string puzzles. We consider the simplest version of a string puzzle, which consists of a single wooden rectangular board with holes and looped strings entangled with the board through the holes. The goal of the puzzle is to disentangle the target string from the wooden board and another set of strings.
We define the generalized string puzzle problem whose input is the initial layout of looped strings and a rectangular board with holes embedded in the 3-dimensional Euclidean space. We present a polynomial-time transformation from an arbitrary instance f of the 3SAT problem to a string puzzle s such that f is satisfiable if and only if s is solvable. Therefore, the generalized string puzzle problem is NP-hard.
There has been a huge amount of literature on the computational complexities of games and puzzles. For example, Hashiwokakero [1], Hiroimono [2], Minesweeper [3], Solitaire [4], Tetravex [5], and Tetris [6] are known to be NP-hard. Uehara proved that deciding whether a given pop-up book can be opened (or closed) is NP-hard [7].
As for higher complexity classes, Amazons [8,9], Othello [10], Rush Hour [11] are PSPACE-hard. (Fernau et al. [12] studied the parameterized complexity of a generalized version of Rush Hour.) Uno et al. showed that an uncooperative two-player (resp. a single-player) version of UNO is PSPACE-hard (resp. NP-hard). [13]. Chess [14] and Go [15] are known to be EXPTIME-hard. The current authors constructed a cast puzzle (a disentanglement puzzle consisting of zinc die-casting alloys) whose complexity is k-EXPSPACE-hard [16]. More information on games and puzzles can be found in [17].
2. Definitions and Main Results
A string puzzle is composed of looped strings and a rectangular board with holes embedded in the 3-dimensional Euclidean space. Strings are entangled with each other and with the board through the holes. One of the strings is called the target string. A string puzzle is said to be solvable if the target string can be disentangled from the board and another set of strings without cutting strings or deforming, whittling, or breaking the board.
We can freely bend and fold strings into desired shapes, but we cannot cut any string. We assume that the diameter of every string is negligibly small. Nevertheless, we further assume that the length of any string cannot be increased even under high tension.
The input of the generalized string puzzle problem is the initial layout of the board and strings, which must be represented by a sequence over on the input tape of a Turing machine. The layout of the rectangular board is represented by the coordinates of the eight vertices (corners) in the 3-dimensional Euclidean space. Holes of the board in this paper are empty spaces in the board whose shapes are polyhedrons such that each polyhedron has one face in the surface of the board and has another face in the reverse face of the board. All vertices of the hole-polyhedrons are supposed to be on the face of the board and not inside. (For example, holes of the board of Figure 1(a) are rectangular prisms, and those of Figure 1(c) are a 10-hedron and a rectangular prism.) Each polyhedron is represented by a set of its faces, where each face is represented by a sequence of the coordinates of the vertices.
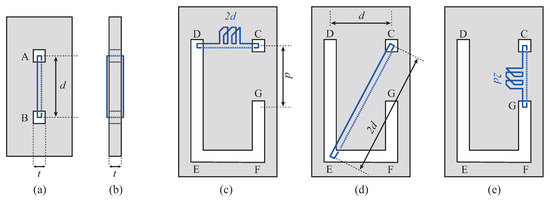
Figure 1.
(a) A board having two holes. A looped string goes through A and B; (b) Lateral view of (a); (c) A board having hole C and a corridor connecting D to G; (d) The string can be moved from D to E by smoothing out the slack ; (e) The string is moved from E to G. The amount of slack becomes when the string reaches G.
The initial layout of strings is given as follows. We assume that a string is initially strained and folded at points on the string (see red and blue strings of Figure 2(a)). A string is represented as a sequence of line segments. Every segment extreme is shared by exactly one other segment (adjacent segment). Thus, every string can be represented by a sequence of the coordinates of segment extremes. We consider a string puzzle of which the board, holes, and strings have integral coordinates.
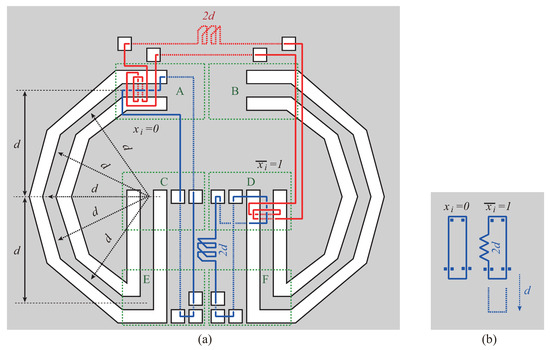
Figure 2.
(a) A gadget simulating variable ; (b) Simplified illustration of (a).
Now we are ready to present our main result.
Theorem 1
There is a polynomial-time transformation from an arbitrary instance f of the 3SAT problem to a string puzzle s such that f is satisfiable if and only if s is solvable.
Corollary 1
The generalized string puzzle problem is NP-hard.
The proof of Theorem 1 is given in the following section.
3. Transformation from 3SAT-Instances to String Puzzles
In this section, we will prove Theorem 1. We present a polynomial-time transformation from an arbitrary instance f of the 3SAT problem to a string puzzle such that f is satisfiable if and only if the string puzzle is solvable.
3.1. 3SAT Problem
The definition of 3SAT is mostly from [18]. Let be a set of Boolean variables. Boolean variables take on values 0 (false) and 1 (true). If x is a variable in U, then x and are literals over U. The value of is 1 (true) if and only if x is 0 (false). A clause over U is a set of literals over U, such as . It represents the disjunction of those literals and is satisfied by a truth assignment if and only if at least one of its members is true under that assignment.
An instance of 3SAT is a collection of clauses over U such that for . The 3SAT problem asks whether there exists some truth assignment for U that simultaneously satisfies all the clauses in f. For example, , , and , , provide an instance of 3SAT. For this instance, the answer is “yes”, since there is a truth assignment satisfying all clauses.
3.2. A Board, Holes, and Corridors
In order to transform the instance of 3SAT, we will design holes on a board and construct strings entangled with the board through the holes.
There are two types of holes, square holes and corridors. In Figure 1(a), a looped string goes through square holes A and B. Each square hole has length t in height, width, and depth. The thickness of the board is also t (see Figure 1(b)). Let d be the distance between the centers of square holes A and B. In this paper, we assume that the value of t is regarded to be negligibly small as compared with d. Under this assumption, we say that the length of the looped string is at least , and the string is tight if its length is exactly . In the following, square holes are simply called holes.
Consider the board of Figure 1(c). This is a board with hole C and corridor connecting D to G through E and F. The distances from C to D and from C to G are both d, and the distance from C to E is . Suppose the looped string goes through C and D, and the length of the string is . The coil-like portion labeled with in Figure 1(c) represents string slack.
We can move the string from D to E (see Figure 1(d)). When the string reaches E, the amount of the slack is zero, and the string is tight. Furthermore, we can move the string from E to G (see Figure 1(e)). At position G, the amount of the slack is . A slack whose amount is is simply called a “slack ”. (Figure 1 is used only for explanations of holes, corridors, strings, slacks, and so on.)
3.3. A Gadget for
We first construct a gadget simulating variable on a board. In Figure 2(a), there are four corridors and 14 holes in the gadget. Corridors and holes of the gadget are left-right symmetric. On the left half of the gadget, there are two corridors which are composed of C-shaped corridors followed by vertical corridors. Each C-shaped corridor is composed of many short straight corridors so that any point in the C-shaped corridors is almost equidistant d from the top end of the vertical corridors.
In Figure 2(a), there are two blue strings and a red string. Each blue string goes through holes and corridors six times, and the red string goes through holes and corridors 12 times. The red string twines around each blue string (see green quadrilateral areas A and D). We assume that the six areas A through F are negligibly small compared with the value of d. (In the figure, distance d is not so long due to space limitation. However, one can see that constructing the gadget of Figure 2(a) for a sufficiently large d is not difficult.)
Since the quadrilateral areas are negligibly small, the part of a string in a quadrilateral area also has negligibly small length. Hence, we can regard the length of the left blue string as . The right blue string also has length , since it has slack and it connects D and F. The red string is entangled with the left blue string in area A and with the right blue string in area D. The left blue string has no slack, and the right blue string has slack . This situation represents and .
In Figure 2(a), 14 holes are rectangular prisms, and four corridors are polyhedrons of 17 or 18 faces. Each such polyhedron can be represented by a set of its faces, where each face is represented by a sequence of the coordinates of the vertices. Thus, holes and corridors of Figure 2(a) can be encoded into sequences. The left blue string of Figure 2(a) is composed of 17 line segments. (Note that six of the 17 segments are vertical segments between the surface and the reverse surface of the board.) The left blue string can be represented by a sequence of the coordinates of 17 segment extremes. In this way, blue and red strings of Figure 2(a) can also be encoded into sequences.
A gadget of Figure 2(a) is embedded in an area of size constant, and n such gadgets for variables can be embedded in an area of size polynomial in n. Arbitrary points in the polynomial-size area can be represented by bit-sequences of length if they have integral coordinates. Therefore, all n gadgets can be encoded into a sequence of length polynomial. Hence, the transformation from the set of n variables to the sequence representing n gadgets can be computed in polynomial time.
In the following, the gadget in Figure 2(a) is simply illustrated as Figure 2(b). In this figure, the jagged-shape portion labeled with is the slack, and the height of the right blue looped string is increased by d when the slack is smoothed out.
The red string has slack in Figure 2(a). If the entanglement in D is moved to F (see the down-pointing arrow in Figure 3), then the amount of the slack of the red string changes from to 0 (and the red string becomes tight). At the same time, the amount of the slack of the right blue string also changes from to 0. Furthermore, if the entanglement is moved from F to B, the amount of the slack of the red string changes from 0 to (see the top two slacks in Figure 3). During the movement from F to B, the slack of the right blue string is almost zero, since any point in the corridor from F to B is almost equidistant d from D.
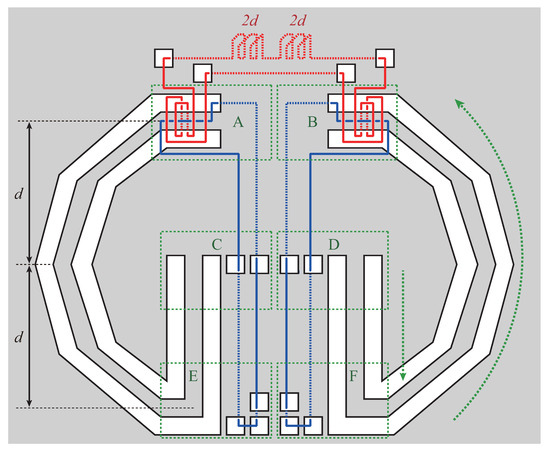
Figure 3.
Entanglement is moved from D to F, and then from F to B.
Now we can move the entanglement in area A to C via E (see Figure 4(a)). After this movement, the left blue string has slack , and the right blue string has no slack. This situation represents and .
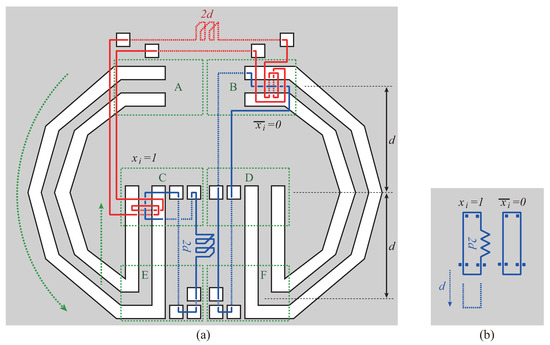
Figure 4.
Entanglement in A is moved to C via E.
It should be noted that, when the amount of the slack of the red string is (see Figure 2(a)), the entanglement in A cannot go to C. This is because the distance between A and E is (which requires slack ). Therefore, if the value of is 1 (i.e., the right blue string has slack ), then the value of is 0 (the left blue string has no slack). The right blue string can have slack only if the left blue string has no slack.
3.4. Disjunction Gadgets
Figure 5(a) is the left and right turns of a string. Suppose that a literal is true; namely, the gadget has slack . We can translate the slack to any place by using the gadget of Figure 5(a). When the slack of the blue string is smoothed out (see Figure 5(b)), the end of another string is moved down. Figure 5(c) is the simplified illustration of Figure 5(a). One of the purposes of the gadget is to use the slack from one string to extend the end of another string.
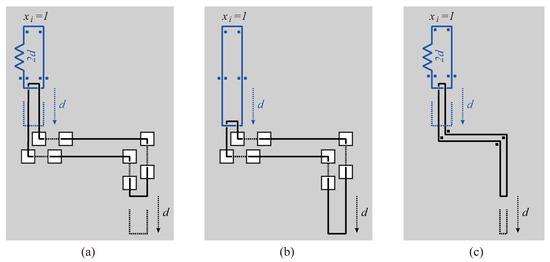
Figure 5.
(a) Left and right turn gadget; (b) When the slack of the blue string is smoothed out, the end of another string is moved down; (c) Simplified illustration of (a).
Figure 6(a) is a disjunction gadget. The red string has slack . This slack plays a key role in this gadget. For example, suppose there is a clause . This clause is satisfied if at least one of the three literals is true. In the figure, each of blue strings and has slack , and blue string has no slack. This is the case when the truth assignment is . In this case, if two slacks of blue strings and are smoothed out (see Figure 6(b)), then the corresponding two black strings obtain slacks of which the amount is in total. However, the amount of the slack of the red string was only . Thus, the amount of slack which the green string obtains is .
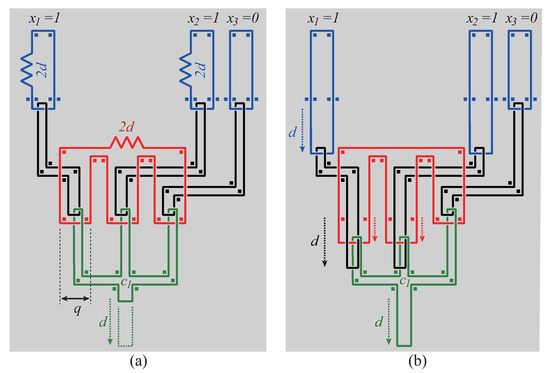
Figure 6.
(a) Disjunction gadget for clause ; (b) Two slacks labeled with in blue strings are translated to the same amount of two slacks in black strings. If at least one of the three blue strings has slack , then the green string obtains slack . The total length of two red arrows is d.
Therefore, if at least one of the three blue strings has slack , then the green string obtains slack . It should be noted that the amount of slack the green string obtains is at most . In Figure 6(a), we can suppose that the value of q is negligibly small, since the diameter of any string and the size of the holes of Figure 5(a) are assumed to be negligibly small.
We construct a gadget of Figure 6(a) for every clause . If a literal appears in k clauses, then the blue string is connected to k black strings.
The number of clauses is bounded by a polynomial in n. By an observation similar to variable gadgets, one can see that the transformation from the set of m clauses to the sequence representing m disjunction gadgets can be computed in polynomial time.
3.5. Conjunction Gadgets
The lower ends of the m green strings (see Figure 6) are grouped together (see the top of Figure 7(a)) by using left and right turn gadgets of Figure 5. Finally, we need one new red string and one new black string (see Figure 7(a)). The red string is connected to all the m green strings . The black string is the target string, which straddles the red string (see Figure 7(b)). Both ends of the target string are hooked on the U-shaped corridors. All the m green strings have slacks if and only if the target string can be disentangled from the board.
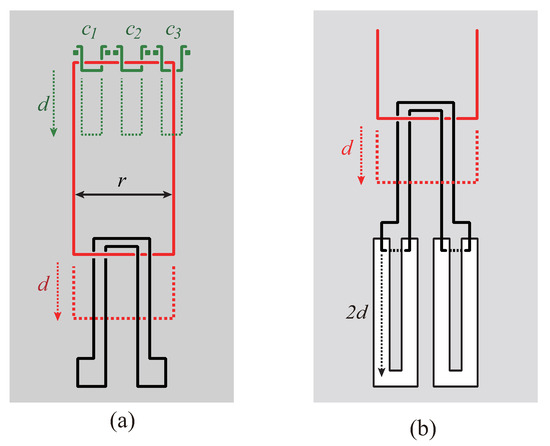
Figure 7.
(a) Conjunction gadget connected to all clause gadgets; (b) The target string can be disentangled from the board when the red string has slack .
In Figure 7(a), the value of r is negligibly small from the same reason as the value q in Figure 6(a). In Figure 7(b), the height of each U-shaped corridor is , and the width is negligibly small as compared with the height. The construction of the conjunction gadget can be done in polynomial time from the reason similar to disjunction gadgets.
Strictly speaking, the left blue string of Figure 2 is not tight, since it is entangled with the red string in area A. So, the lower end of the left blue string can move down slightly when it has no coil-like slack. Such a slight movement is transmitted to the target string of Figure 7 via disjunction gadgets of Figure 6. However, if we assume that the value of Figure 7(b) is sufficiently large compared to the amount of the slight movement, then the target string cannot be disentangled from the board when at least one of the clauses is not satisfied.
From this construction, (1) all the clauses of the 3SAT instance are satisfied if and only if the target string is disentangled from the board, and (2) the transformation of the 3SAT instance to the string puzzle can be done in polynomial time. This completes the proof of Theorem 1.
4. Conclusions
In this paper, we presented a polynomial-time transformation from an instance f of the 3SAT problem to a string puzzle s such that f is satisfiable if and only if s is solvable. Therefore, the generalized string puzzle problem is NP-hard. It is not known whether the problem is in NP. The puzzle movements used in this paper are the kind of shifting actions, such as shifting entanglements (Figure 3), smoothing out a slack of a string (Figure 4(b)), and transferring a slack from one string to the next string (Figure 5). Those actions are enough for proving the NP-hardness of the problem. However, for solving real string puzzles, we can actually perform complex movements, such as moving entanglements through holes, creating and removing knots, and so on. By using such complex movements, PSPACE-hard or EXPTIME-hard problems may be able to be reduced to string puzzles. We conjecture that the complexity of the generalized string puzzle problem is harder than NP.
Acknowledgements
We would like to thank anonymous referees for their constructive suggestions and comments on the initial draft of this paper.
References
- Andersson, D. Hashiwokakero is NP-complete. Inform. Process Lett. 2009, 109, 1145–1146. [Google Scholar] [CrossRef]
- Andersson, D. HIROIMONO is NP-complete. In Proceedings of the 4th International Conference on Fun with Algorithms (Lecture Notes in Computer Science 4475), Castiglioncello, Italy, 3–5 June 2007; pp. 30–39. [Google Scholar]
- Kaye, R. Minesweeper is NP-complete. Math. Intell. 2000, 22, 9–15. [Google Scholar] [CrossRef]
- Longpré, L.; McKenzie, P. The complexity of Solitaire. Theor. Comput. Sci. 2009, 410, 5252–5260. [Google Scholar] [CrossRef]
- Takenaga, T.; Walsh, T. TETRAVEX is NP-complete. Inform. Process Lett. 2006, 99, 171–174. [Google Scholar] [CrossRef]
- Breukelaar, R.; Demaine, E.D.; Hohenberger, S.; Hoogeboom, H.J.; Kosters, W.A.; Lieben-Nowell, D. Tetris is hard, even to approximate. Int. J. Comput. Geom. Appl. 2004, 14, 41–68. [Google Scholar] [CrossRef]
- Uehara, R.; Teramoto, S. Computational complexity of a pop-up book. In Proceedings of the 18th Canadian Conference on Computational Geometry, Kingston, ON, Canada, August 2006; pp. 3–6. [Google Scholar]
- Furtak, T.; Kiyomi, M.; Uno, T.; Buro, M. Generalized amazons is PSPACE-complete. In Proceedings of the 19th International Joint Conference on Artificial Intelligence (IJCAI), Edinburgh, Scotland, UK, 30 July–5 August 2005; pp. 132–137. [Google Scholar]
- Hearn, R.A. Amazons is PSPACE-complete. 2005. Available online: http://arxiv.org/abs/cs.CC/0502013 (accessed on 10 April 2011).
- Iwata, S.; Kasai, T. The Othello game on an n × n board is PSPACE-complete. Theor. Comput. Sci. 1994, 123, 329–340. [Google Scholar] [CrossRef]
- Flake, G.W.; Baum, E.B. Rush hour is PSPACE-complete, or why you should generously tip parking lot attendants. Theor. Comput. Sci. 2002, 270, 895–911. [Google Scholar] [CrossRef]
- Fernau, H.; Hagerup, T.; Nishimura, N.; Ragde, P.; Reinhardt, K. On the parameterized complexity of a generalized rush hour puzzle. In Proceedings of the 15th Canadian Conference on Computational Geometry, Halifax, NS, Canada, 11–13 August 2003; pp. 6–9. [Google Scholar]
- Demaine, E.D.; Demaine, M.L.; Uehara, R.; Uno, T.; Uno, Y. UNO is hard, even for a single player. In Proceedings of the 5th International Conference on Fun with Algorithms (FUN 2010) (Lecture Notes in Computer Science 6099), Ischia, Italy, 2–4 June 2010; pp. 133–144. [Google Scholar]
- Fraenkel, A.S.; Lichtenstein, D. Computing a perfect strategy for n × n chess requires time exponential in n. J. Comb. Theory A 1981, 31, 199–214. [Google Scholar] [CrossRef]
- Robson, J.M. The complexity of go. In Proceedings of the IFIP 9th World Computer Congress, Paris, France, 19–23 September 1983; pp. 413–417. [Google Scholar]
- Iwamoto, C.; Sasaki, K.; Nishio, K.; Morita, K. NP-hard and k-eXPSPACE-hard cast puzzles. IEICE Trans. Inf. Syst. 2010, E93-D, 2995–3004. [Google Scholar] [CrossRef]
- Hearn, R.A.; Demaine, E.D. Games, Puzzles, and Computation; A K Peters Ltd., Ed.; Wellesley: Massachusetts, MA, USA, 2009. [Google Scholar]
- Garey, M.R.; Johnson, D.S. Computers and Intractability: A Guide to the Theory of NP-Completeness; W.H. Freeman: New York, NY, USA, 1979. [Google Scholar]
© 2012 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (https://creativecommons.org/licenses/by/3.0/).