Abstract
Tantrix (Tantrix is a registered trademark of Colour of Strategy Ltd. in New Zealand, and of TANTRIX JAPAN in Japan, respectively, under the license of M. McManaway, the inventor.) is a puzzle to make a loop by connecting lines drawn on hexagonal tiles, and the objective of this research is to solve it by a computer. For this purpose, we first give a problem setting of solving Tantrix as making a loop on a given fixed board. We then formulate it as an integer program by describing the rules of Tantrix as its constraints, and solve it by a mathematical programming solver to have a solution. As a result, we establish a formulation that can solve Tantrix of moderate size, and even when the solutions are invalid only by elementary constraints, we achieved it by introducing additional constraints and re-solve it. By this approach we succeeded to solve Tantrix of size up to 60.
1. Introduction
Games and puzzles are entertainments for human beings, and solving puzzles or playing games are lots of fun for everybody. Such games and puzzles are often logical enough, and they have long been attracted interests of mathematicians and computer scientists not only for the pleasure but for their research [1]. Those may include Nim, Hex, Peg Solitaire, Tetris, Geography, Sudoku, Rubik’s Cube, Chess, Othello, Go, and so on [2,3,4,5,6].
There are also a lot of directions and objectives when games and puzzles are treated as research topics [1,7,8,9]. Some of those are investigating their mathematical structures [2,10,11], computational complexities [3,12], winning strategies [1,7], and so on. As computers evolve and their utilization methods expand, they are rapidly incorporated into these research areas [2,4,5,6]. That is, for example, to develop a computer program that can beat humans in playing games or can solve puzzles faster than humans.
In this paper, we focus on a puzzle called Tantrix to make a loop by connecting lines drawn on hexagonal tiles [13,14,15]. The objective of this research is to solve it by a computer. Specifically, we first give a simplified problem setting of solving Tantrix as making a loop on a given fixed board. We then formulate it as an integer program (IP) [16,17] by representing the rules or properties (necessary conditions) that solutions of Tantrix satisfy as its constraint conditions. We finally obtain a solution by solving that IP formulation by a commercial mathematical programming solver. After that, since we may not have valid solutions only by elementary constraints, we introduce new additional constraints in order to derive correct solutions. Furthermore, we give some observations and proposals for solving larger problems in less computational time. Finally we show the current best solution of Tantrix obtained by the proposed approach. Our approach of using IP formulation to solving puzzles seems unique, and to the best of our knowledge, this is one of very few cases that IP meets solving puzzles successfully.
In Section 2, we introduce a puzzle called Tantrix and explain its rules. Next in Section 3, we give a problem setting for solving Tantrix by a computer and terminology for IP formulations. Then in Section 4, we describe a framework for solving this problem by using integer programming and propose its formulations. We solve these formulations by a solver and show its experimental results. In Section 5, we develop some ideas to accelerate their computational time. Finally Section 6 presents some future work and concludes the paper.
2. Tantrix
Tantrix is a puzzle originally invented in 1988 by Mike McManaway of New Zealand [13]. Several variants of commercial Tantrix products have been sold so far, and among those a solitaire version is named “Tantrix Discovery” [13,14,15,18]. Throughout this paper, we only focus on this solitaire version, Tantrix Discovery, and we simply call it “Tantrix” in the rest of this paper.
Tantrix is played by 10 sorts of hexagonal tiles of the same size. A tile has two surfaces, which we call a top (surface) and a back (surface). On a top surface three lines are drawn in red, blue and yellow, respectively (Figure 1(a)), and on a back surface one of the numbers from 1 to 10 is drawn in either one of the three colors red, blue or yellow (Figure 1(b)). The 10 patterns of lines drawn on tops are all different from each other.
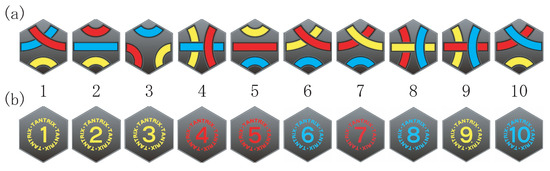
Figure 1.
(a) Tops of 10 sorts of tiles (with their orientations 1), and (b) their corresponding backs.
Tantrix is played by putting tiles in the form of hexagonal lattice and the goal is to make a loop in one designated color of the three colors according to the following rules.
- determine the number of tiles for the challenge (challenge number), which is greater than 2,
- prepare the tiles as many numbers as the challenge number consecutively starting from a tile with number 1 on its back (in case it is more than 10, start from 1 again),
- the designated color is the one in which the lowest digit of the challenge number is written (on the back of the tile),
- connect all the lines of the designated color (drawn on prepared tiles) so that they form a single loop,
- connect the lines of the other colors than the designated color so that their touching colors match.
Here such arrangements in which there is a hole (places without tiles surrounded by more than 5 tiles) (Figure 2(a)), or any one of the lines of the designated color is not a part of a loop (Figure 2(b)) are not allowed. When one completes making a loop according to the above rules, we say that we cleared that challenge number of Tantrix (To be authorized as an official record, an arrangement must satisfy the following condition: in the arrangement let one of the three directions (axes) that has the most number x of tiles be A, and the other two directions that cross A be B and C. Then there must be more tiles than 30% of x in more rows than 75% of those in directions B and C, respectively. This condition is set to exclude the so-called “4-tiles’ equation” discovered by C. Fraser of England. This information was once posted in [13], however, we can no longer find it on Nov. 15, 2011.).
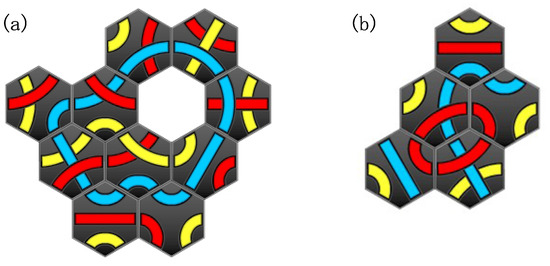
Figure 2.
Examples of “uncleared” arrangements although they satisfy rules from 1 to 5: (a) there is a hole; and (b) a line of the designated color (red) is not a part of a loop.
Suppose we try Tantrix of challenge number 5. The designated color of that number is red (Figure 1(b)). In Figure 3, a single loop of the designated color red is made by using all the red lines drawn on five tiles that have numbers from 1 to 5, and the colors of touching lines of the other colors also match (in this case blue only) at the same time. In addition there is no hole in this arrangement of tiles. Therefore, we say that we cleared Tantrix of challenge number 5.
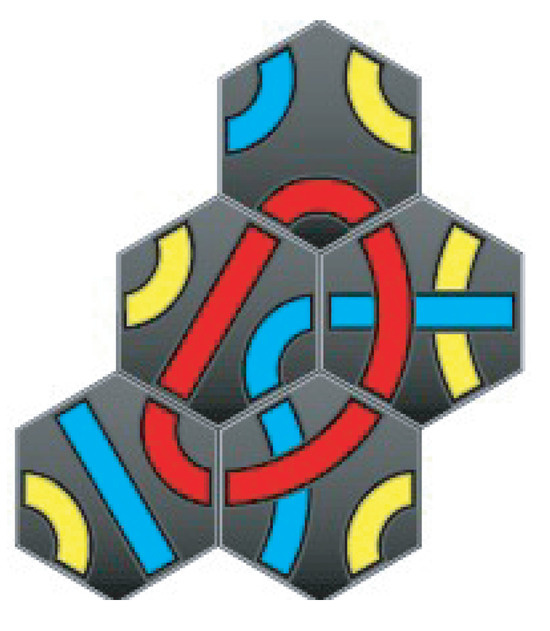
Figure 3.
An example of a “cleared” arrangement; a Tantrix solution of challenge number 5.
A solution (of challenge number n) is an arrangement how n tiles are placed, and a Tantrix solution is the one that satisfies all the above conditions (Figure 3). A shape of a solution is its boundary formed by n hexagonal tiles.
3. A Problem Setting and Terminology for Formulations
We attempt to solve this puzzle by formulating its solutions as an integer program and using mathematical programming solver for it. In this section, we give a simplified problem setting for this purpose and give some terminology for IP formulations.
3.1. A Problem Setting for Solving Tantrix by a Computer
Humans may play Tantrix on the table, on the floor or at any other places they like. For computers, however, we have to prepare artificially and appropriately a space where solutions are made. Consider an infinite hexagonal lattice plane (as shown in Figure 4), where the size of each hexagon is as the same as the one of a tile. When Tantrix is played by a computer, a tile is placed to fit on each hexagon, which we call a place (Figure 4(a)). In addition, a collection of multiple places where a solution is supposed to be made is called a board (Figure 4(b)). The size of a board is the number of hexagons that constitute it.
Figure 4.
A place (left) and an example of a board (of size 5) (right) on a hexagonal lattice plane.
When a human solves Tantrix, one may connect the lines of the designated color to make a single loop, while connecting lines of the other colors simultaneously, as well as arranging tiles so that they do not create a hole in its shape at the same time. Especially, one cannot supposed to imagine the final shape of a loop (and thus, a solution) in advance. In other words, even if once one determined the challenge number, the shape of a solution cannot be fixed uniquely. It is not so easy for computers to deal with this situation since they have to assume unfixed shapes of boards on an infinite hexagonal lattice plane. To avoid this difficulty, in this paper, we consider a following simplified setting of Tantrix, in which we also give as an input a fixed board of the same size as a challenge number and place tiles on that board.
- Fixed_Board TANTRIXInput: a challenge number n and a board of size n that satisfies the rules of Tantrix,Question: a Tantrix solution if there is on the input board, or no, otherwise.
Remark that on this problem setting, the shape of a solution always matches the shape of an input board. Furthermore, to concentrate on developing integer program formulations for making a loop that satisfies rules of Tantrix, we give a board whose shape is known to have a Tantrix solution (confirmed by humans) as an input. This implies that we do not have to consider “no” instances under this assumption.
In the subsequent sections, we solve this problem Fixed_Board TANTRIX by utilizing a mathematical programming solver after formulating it as an IP. We use IBM ILOG CPLEX 12.2 [19] as a solver, which is installed on a single PC of Intel Pentium Dual E2200 processor (2.2 GHz) with 1 GB RAM.
3.2. Terminology and Definitions for IP Formulation
We call a tile with number i on its back tile i. Remind that the designated color of a number is the one in which the number is written. We define an angle of a line as its central angle when we regard it as a circular arc of a circle, where we define the angle of a straight line to be . Then an angle of a line is either one of , or (Figure 5). For example, tile 2 is said to have a red line of an angle , blue line and yellow line (Figure 1(a)).
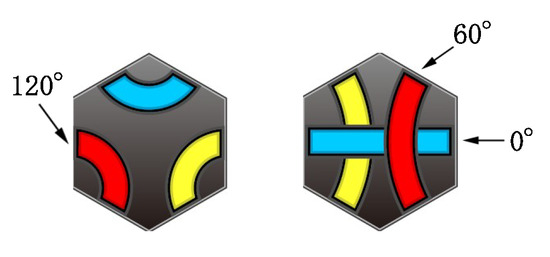
Figure 5.
Three angles of lines.
To distinguish places and orientations of tiles to be placed, we next assign numbers to them. For places of an input board (of the same size as a challenge number n), we give numbers from 1 to n appropriately (e.g., Figure 6). We also give numbers from 1 to 6 to the edges of each place counterclockwise as shown in Figure 7. The orientations of a tile to be placed take values from 1 to 6. We define it in the following way (Figure 8): place a tile showing its back and its number in the upright position; flip it horizontally, and it is orientation 1; every time we rotate it by clockwise, its orientations will be 2, 3, 4, 5 and 6, respectively. Figure 1(a) shows each tile in its orientation 1.
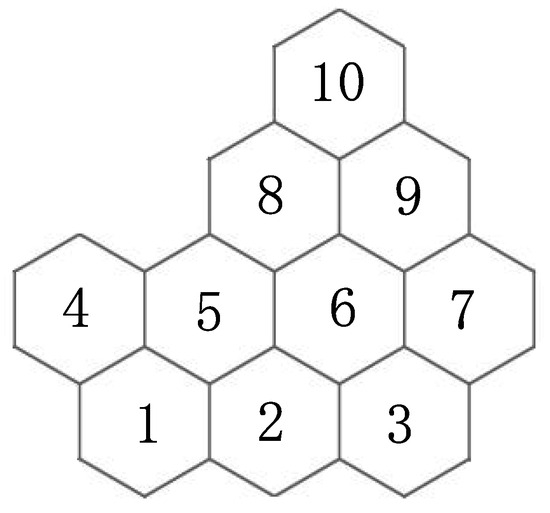
Figure 6.
An example of a board of size 10 and given numbers to its places.
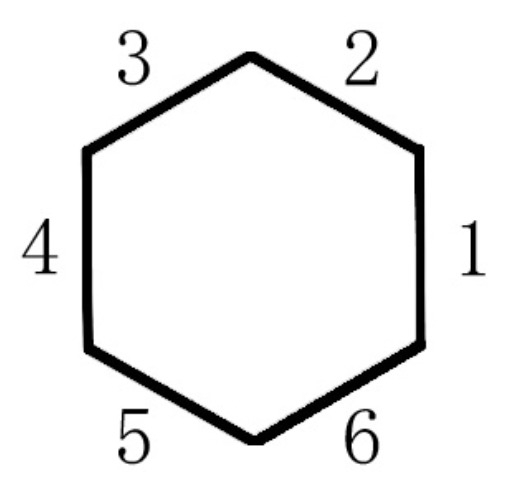
Figure 7.
Numbers of edges of a place.
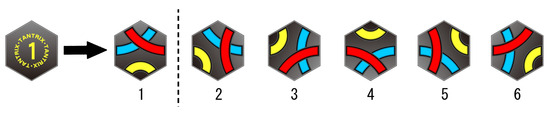
Figure 8.
Orientations of a tile.
Next, let be a function that returns the number of the place that is adjacent to place j with its edge ℓ, and returns 0 if such a place is out of a board. In Figure 6, for example, and . For simplicity, once a tile is (or supposed to be) placed on a certain place with a certain orientation, we allow to identify the tile with that place. That is, we alternatively say, for example, that the color of a line of an edge of a place instead of saying that the color of a line (of a placed tile) appearing on the corresponding edge (of the place where the tile is placed in a certain orientation), and so on.
4. An Integer Programming Formulation
In this section, we formulate Fixed_Board Tantrix as an integer program. We first introduce variables, and then explain constraints and an objective function. Then we show experimental results of solving this formulated IP by a solver.
4.1. Variables
We distinguish all the tiles prepared for challenge number n, that is, we number the tiles from 1 to n. Then we use the following two integral variables for our IP formulation.
First, for each tile i, for each place j and each orientation k, let a 0–1 variable be
Next for each place j and its edge ℓ, let a variable that expresses the color of its corresponding line (of a placed tile) be
Here we use values 1, 2 and 3 to indicate three colors of lines, and the value 3 is intended to denote the designated color. Remark here that if we define a function that returns the color of the line corresponding to edge ℓ when tile i is placed in orientation k (we can know it according to the top of tiles), the variable is represented by using and as the following:
4.2. Constraints and an Objective Function
We now describe the (necessary) conditions to hold for a Tantrix solution as constraints of an integer program. Based on the rules of Tantrix, we introduce the following four constrains.
- Constraint 1 (C1). Exactly one tile is placed on each place.Constraint 2 (C2). Each tile is used exactly once.Constraint 3 (C3). The color of a line of an edge that is on the boundary of a board is not the designated color.Constraint 4 (C4). The colors of lines whose corresponding edges are touching each other have to match.
Constraint 1 is required to hold for any place on a board that it cannot happen that no tiles or more than two tiles are placed, and it is represented by the following formula:
Constraint 2 can be set since we distinguish all the tiles. Each tile i is used exactly once and this is formulated as follows:
Constraint 3 implies that a line of the designated color of any tile cannot become adjacent to the boundary of a board, and it is expressed as follows:
Constraint 4 implies the rules 4 and 5 of Tantrix; that is, connect lines of the same color for every three colors. This condition is formulated as follows:
Remark here that, by C3 and C4, any line of the designated color must be a part of a loop, that is, they constitute a necessary and sufficient condition for that all the lines of the designated color form loops.
We call a loop of the designated color consists of less than n tiles a subloop. Then by C1–C4 we cannot avoid subloops. That is, they do not imply sufficient conditions that a loop of the designated color is unique, which must be satisfied by a Tantrix solution. It is, of course, not impossible to introduce constraints that eliminates all the probable subloops in a formulation as it is introduced for TSP formulations [16,17,20,21], however, it may require exponential number of constraints, which may also cause a long computational time. Therefore, to guarantee the uniqueness of the loop of the designated color, in our formulation, we add constraints for eliminating subloops every time they appear and re-solve it.
In our approach, since a (Tantrix) solution is formulated as constraints of an integer program, it suffices to find one of its feasible solutions. In such a case, an objective function is enough to be virtual, and therefore, we set it as , for a descriptive purpose.
4.3. Elementary Experiments and the Results
We solve the integer program formulated so far by a solver to obtain a solution and to examine the solution time. We use IBM ILOG CPLEX 12.2 [19] as a solver, which is installed on a single PC of Intel Pentium Dual E2200 processor (2.2 GHz) with 1 GB RAM. Since the computational time spent for solving a fixed formulation by a solver on a same computer is always the same in principle, we adopt the one by a single computation throughout our experiments.
We performed experiments for challenge numbers 5, 10, 15, 20, 25 and 30. Remind here that we give as an input an appropriate board on which it has a Tantrix solution. Table 1 shows its computational time and the number of loops in a solution for each challenge number. Figure 9 depicts the obtained solution for challenge number 10. We see that we can solve our formulation within 3 seconds up to challenge number 25. For challenge numbers 30 and 35, on the other hand, it requires approximately 100 and 13,000 seconds, respectively, and we can confirm that the computational time increases drastically. We can imagine that it is difficult to obtain solutions more than these challenge numbers under our current formulation.

Table 1.
Computational time (s) of solving IP formulations using constraints C1, C2, C3 and C4, and the number of loops in each solution.
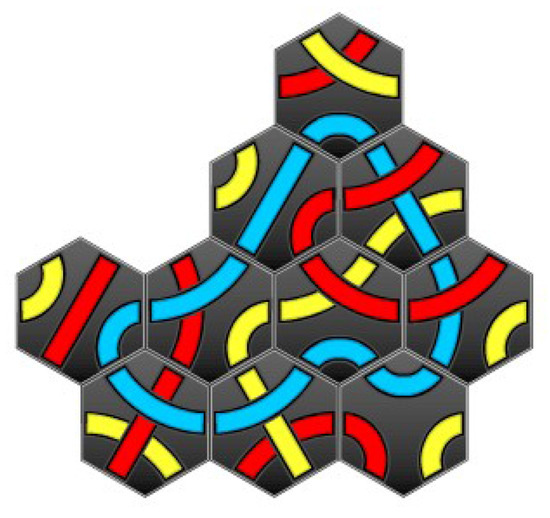
Figure 9.
The solution for challenge number 10, where we use a board in Figure 6.
As we mentioned, elementary constraints C1–C4 cannot eliminate subloops. In fact, for challenge numbers 20, 25 and 35, their solutions include subloops. We show in Figure 10(a) a board used for challenge number 20, and in Figure 10(b) the obtained solution. Hence, we have to eliminate these subloops to obtain a Tantrix solution.
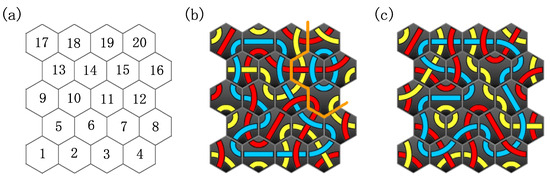
Figure 10.
(a) A board of size 20 used for challenge number 20; (b) a solution obtained by solving a formulation using C1–C4; including 2 subloops of its designated color blue, where an orange line is a cut defined by them; and (c) a final solution obtained by solving a formulation by adding C5.
4.4. Subloop Elimination
To eliminate subloops appearing in a solution, we introduce new constraints. We add them to the original formulation, and re-solve the updated one. We iterate this process every time subloops appear in a solution until we finally obtain a Tantrix solution. Now we call a border that divides a board into two parts a cut. Then if the loop of the designated color is unique, it crosses over an arbitrary cut more than once. Therefore, we introduce the following new constraint.
- Constraint 5 (C5). Lines of the designated color cross the cut over which they do not cross.
To describe this constraint, we introduce for convenience a new 0-1 variable .
More precisely, we define a cut K as a pair of place j and its edge ℓ, where one of the divided part by that cut is adjacent to. Then C5 can be formulated as follows:
and we give this constraint for all the cuts that lines of the designated color do not cross in a solution. For example, in a solution of challenge number 20 (Figure 10(b)), such a cut is K, , , , , , , and thus C5 for this cut becomes .
The value of this variable is, in fact, determined by those of the variable ; that is, if or 2 (i.e., not the designated color), or if (i.e., the designated color). In other words, possible combinations of values for and are ∈ . Therefore, can be represented by the following two inequalities:
For challenge numbers 20, 25 and 35, whose solutions include subloops, we iterated adding C5 to each of their formulations and re-solving it until we obtain a Tantrix solution. Table 2 is the results for this experiment, and it shows the computational time required in each iteration (#iteration) and the sum of those for all iterations (total). (We define the first trial of solving the original formulation without C5 as the 0th iteration.) Figure 10(c) depicts the final solution for challenge number 20, where we can confirm that a subloop in the original solution (Figure 10(b)) is eliminated and that there is a single loop. We are now able to obtain a Tantrix solution by formulations using C1, C2, C3, C4 with adding C5 if needed.

Table 2.
Computational time (s) of solving IP formulations using C1–C4 with adding C5 for challenge numbers 20, 25 and 35.
5. Improvement for Larger Challenge Number
According to the framework of IP formulations which we proposed in the previous section, we can at worst obtain Tantrix solutions unless we bother consuming time and spending work of re-solve. On the other hand, if we try to solve it for larger challenge numbers, the increase of computational time (as is observed in Table 2) and the re-solve due to subloops are still big issues to make it tractable. To cope with these problems, we propose some new ideas, and adopt them one by one if it is confirmed to be effective (in a way, trial and error).
5.1. Reduce Variables and Constraints
In general, introducing too many variables and constraints often causes the increase of computational time spent by a solver. Therefore, we first consider a direct way to eliminate some of the variables. For this purpose, we decide to use only 10 sorts of tiles (as is the original rules of Tantrix) instead of distinguishing all the tiles and give them numbers from 1 to n. More specifically, the number of tile i, used when challenge number is n, is . Hence we change C2 into the following:
- Constraint (C2). Each tile i is used times.
Thus, this constraint is formulated as follows:
where .
By this modification, the range of the index i of the variable becomes from 1 to , which was from 1 to n before the modification. We notice that is at most 10 (a constant). Then the number of variables is reduced from to , which is when the challenge number . Due to this reduction, the number of constraints for this variable is also reduced from n to . Table 3 shows computational results of solving a formulation using C1, C2, C3 and C4. By comparing it with the results in Table 1 and Table 2, we can confirm that the computational time is remarkably reduced. We consider this is due to the reduction of the number of variables and constraints, thus in the subsequent formulations, we always adopt C2 instead of C2.

Table 3.
Computational time (s) of solving IP formulations using C1, C2, C3 and C4 for challenge numbers 25, 30 and 35.
5.2. Fix Tiles with a Line of the Designated Color
By utilizing the assumption that a board is given as an input, there may be some places on the board where a tile that has a line of the designated color can be placed. Such a place is where four of its six adjacent places are not included in the board (Figure 11). Then we set this condition as the following constraint:
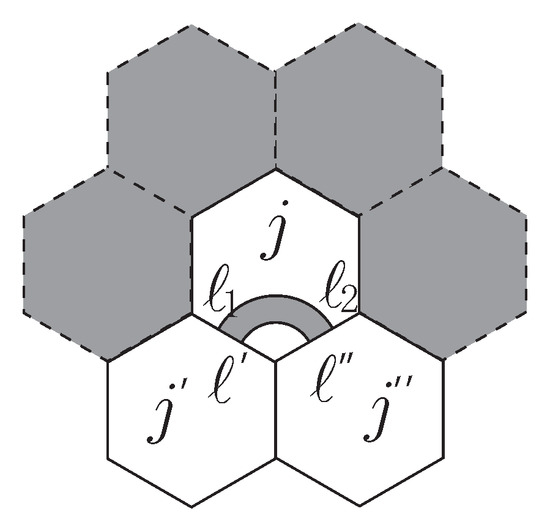
Figure 11.
A place where only a tile that has a line of the designated color can be placed.
- Constraint 6 (C6). Only a tile that has a line of the designated color is placed if a place is adjacent only to two places in a board.
If there exists such a place that satisfies the above condition, this constraint is realized by specifying the colors of the lines whose corresponding edges are touching to the adjacent places to be the designated color 3. That is, for such a place j and its two adjacent places and we add the following formulas:
Table 4 shows computational results of solving a formulation using C1, C2, C3, C4 and C6 for challenge numbers 30, 35 and 40. To verify the effect of C6, we compare the computational time with those in Table 3 in the case of challenge numbers 30 and 35. Then the overall solution time is reduced from 9.76 to 1.86 and from 1448.99 to 182.11, respectively, and we can confirm its effectiveness.

Table 4.
Computational time (s) of solving IP formulations using C1, C2, C3, C4 and C6 for challenge numbers 30, 35 and 40; and IP formulations adding C7, C8 and C9 to them as well for challenge number 40 (rightmost column).
On the other hand, we can see that the number of iterations for eliminating subloops seems to be increasing as the challenge number grows. In fact, in case of challenge number 40, it requires 14 re-solves. We consider this many iterations may be one of the main reasons for increasing computational time, and we develop a way for reducing it.
5.3. Eliminate Short Subloops in Advance
We show in Figure 12 some solutions of the previous experiments for challenge number 40. To observe these solutions, we can see that subloops consists of 3 or 4 tiles, and these are considered to cause multiple re-solves. Therefore, we attempt to reduce the number of iterations by eliminating these types of short subloops. More specifically, we eliminate subloops consists of 3, 4 or 5 tiles (for challenge number greater than 5):
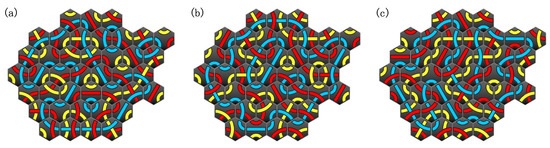
Figure 12.
Solutions obtained by solving IP formulations using C1, C2, C3, C4 and C6 for challenge number 40: after (a) 3rd, (b) 7th and (c) 14th iterations, respectively.
- Constraint 7 (C7). There are no loops consists of 3 tiles.Constraint 8 (C8). There are no loops consists of 4 tiles.Constraint 9 (C9). There are no loops consists of 5 tiles.
It is easy to see that C7 is equivalent to that none of the arrangements of lines of the designated color shown in Figure 13(a) appears on any two adjacent places on a board. Therefore, this constraint is realized by forbidding these types of tiles (having lines of the designated color) to become one of those arrangements.
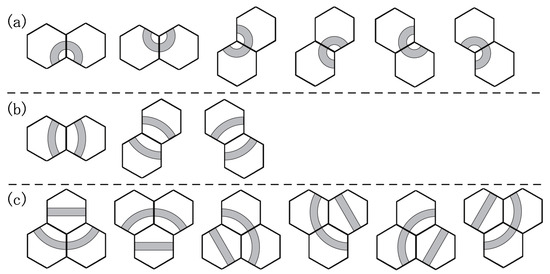
Figure 13.
Forbidden arrangements of lines of the designated color for challenge number greater than 5. These will force subloops consist of (a) 3, (b) 4 and (c) 5 tiles, respectively.
Suppose now that the designated color is red. We can see that tiles 2 and 3 have red lines (Figure 1). To forbid these two tiles to be placed in one of those arrangements simultaneously, we force the sum of corresponding to being these arrangements not to be greater than 1. Therefore, in this concrete case, the formulations become as follows. We can consider similarly in the case that the designated color is blue or yellow:
For constraint C8, we can deal with it in a similar way to C7. In fact, C8 is equivalent to that none of the three arrangements of lines of the designated color in Figure 13(b) appears on any two adjacent places on a board. Therefore, it is realized by forbidding these types of tiles (having lines of the designated color) to become one of those arrangements. It is also the case that we can represent this constraint by the corresponding variables , and in the case of the designated color is red, for example, it is formulated as follows (similarly for blue and yellow):
For C9, it is equivalent to that for lines of the designated color none of the six arrangements in Figure 13(c) appears on every mutually adjacent tree places on a board. Suppose the designated color is red, then tiles 5 and 9 have red lines and tiles 1, 4, 6, 7, 8 and 10 have red lines. Therefore, we can express by using variables corresponding to these tiles that they do not form any of the arrangements. Since they become too messy, we omit here to show the entire formulas to avoid it.
For challenge number 40, we show the results of solving formulations using C1, C2, C3, C4, C6 together with C7, C8 and C9, also in Table 4 (in the rightmost column). As a result, we can observe that the number of iterations is drastically reduced and we can obtain a Tantrix solution only after two iterations. Also as this consequence, its computational time is also reduced substantially.
5.4. Further Challenge
To summarize all the ideas, observations and experiments presented so far, it gives good experimental results that a formulation using constraints C1, C2, C3, C4, C6, C7, C8, C9 is solved by adding C5 until subloops disappear. Hence, under this formulation, we try to solve Fixed_Board Tantrix by increasing its challenge number as 45, 50, 55 and 60. Table 5 shows these experimental results. As a consequence, the current best result (in the challenge number) for Fixed_Board Tantrix is 60 which is solved in total time 6713.25 s. We also show the solution in Figure 14.

Table 5.
Computational time (s) for challenge numbers 45, 50, 55 and 60 under our current best formulation.
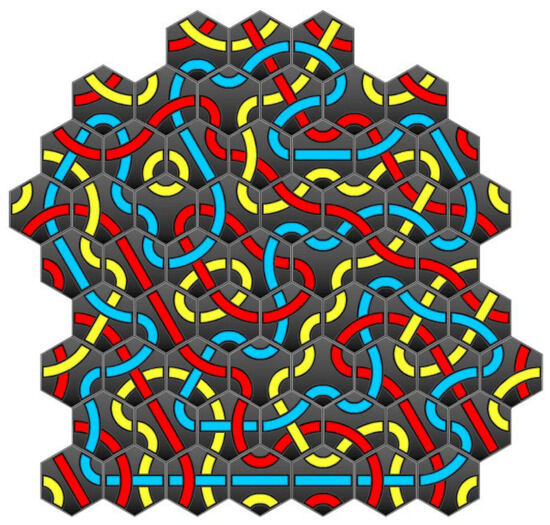
Figure 14.
A Tantrix solution of challenge number 60, which is obtained by solving IP formulations.
6. Conclusions
In this paper, we tried to solve Tantrix by a computer, and to the best of our knowledge, this is the first research report about solving Tantrix itself. The approach we adopted here is to formulate it as an IP and to solve it by a mathematical programming solver, and we consider that this approach to solving puzzles is quite unique and entertaining as well. Although our problem setting is a simplified one, we could successfully solve it with challenge number up to 60, which is more or less larger than we expected. The results in this paper show that an approach using IP to solving puzzles is probable and we believe that it may be valid for solving other puzzles. One of the important future work, of course, is to develop more effective formulations to solve Tantrix of larger challenge numbers.
In order to put the problem into our IP framework, we were forced to simplify the problem of solving Tantrix by restricting the shape and the size of boards. However, this restriction is quite unnatural for humans. Therefore, one more important future work is to give more natural problem setting like humans solve, and formulate it as an IP and solve it. We are approaching this in several ways and is now under progress.
Finally, we mention about the complexity issues about Tantrix. Some results are known with respect to the complexity of Tantrix; e.g., an artificial variant, called Tantrix rotation, is shown to be NP-complete [22]. However, the complexity of the original Tantrix has not been studied to the best of our knowledge, although it is easily conjectured to be intractable. Therefore, we pose here a problem of the complexity of Tantrix (the original Tantrix discovery) including a natural problem setting of Tantrix itself.
Acknowledgments
This research is partly supported by Grant-in-Aid for Scientific Research (KAKENHI), No. 23500022. We would also like to thank the anonymous referees for their careful reading and comments which greatly helped correct and improve this paper.
References
- Gardner, M. Mathematical Games: The Entire Collection of His Scientific American Columns; The Mathematical Association of America: Washington, DC, USA, 2005. [Google Scholar]
- Felgenhauer, B.; Jarvis, F. Sudoku enumeration problems. Available online: http://www.afjarvis.staff.shef.ac.uk/sudoku/ (accessed on 15 March 2012).
- Lichtenstein, D.; Sipser, M. GO is polynomial-space hard. J. ACM 1980, 27, 393–401. [Google Scholar] [CrossRef]
- Rokicki, T.; Kociemba, H.; Davidson, M.; Dethridge, J. God’s Number is 20. 2010. Available online: http://cube20.org/ (accessed on 15 March 2012).
- Rosenbloom, P.S. A world-championship-level Othello program. Artif. Intell. 1982, 19, 279–320. [Google Scholar] [CrossRef]
- Shanon, C.E. Programming a computer for playing Chess. Philos. Mag. 1950, 41, 256–275. [Google Scholar] [CrossRef]
- Albert, M.H.; Nowakowski, R.J.; Wolfe, D. Lessons in Play: An Introduction to Combinatorial Game Theory; A K Peters Ltd.: Wellesley, MA, USA, 2007. [Google Scholar]
- Demaine, E.D. Playing Games with Algorithms: Algorithmic Combinatorial Game Theory. In Proceedings of the 26th Symposium on Mathematical Foundations in Computer Science (MFCS ’01), Marianske Lazne, Czech Republic, 27–31 August 2001; Volume 2136, pp. 18–32. [Google Scholar]
- Hearn, R.A.; Demaine, E.D. Games, Puzzles, and Computation; A K Peters Ltd.: Wellesley, MA, USA, 2009. [Google Scholar]
- Lee, M.K. The graph for the Tower of Hanoi with four pegs. Pythagoras 2003, 57, 27–31. [Google Scholar]
- McGuire, G.; Tugemann, B.; Civario, G. There is no 16-clue sudoku: Solving the sudoku minimum number of clues problem. arXiv 2012, arXiv:1201.0749v1. [Google Scholar]
- Demaine, E.D.; Demaine, M.L.; Uehara, R.; Uno, T.; Uno, Y. UNO Is Hard, Even for a Single Player. In Proceedings of the 5th International Conference on Fun with Algorithms (FUN ’10), Ischia, Italy, 2–4 June 2010; Volume 6099, pp. 133–144. [Google Scholar]
- Tantrix Japan Official Homepage (in Japanese). Available online: http://www.tantrix.jp/ (accessed on 15 March 2012).
- Tantrix.com (a Tantrix website in New Zealand). Available online: http://www.tantrix.com/ (accessed on 15 March 2012).
- Tantrix in the UK and Ireland (a Tantrix website in the United Kingdom). Available online: http://www.tantrix.co.uk/ (accessed on 15 March 2012).
- Pataki, G. Teaching integer programming formulations using the traveling salesman problem. SIAM Rev. 2003, 45, 116–122. [Google Scholar] [CrossRef]
- Wolsey, L.A. Integer Programming; Wiley Interscience: Hoboken, NJ, USA, 1999. [Google Scholar]
- Tantrix UK Ltd. Tantrix teacher/parent guide. 2010. Available online: http://www.tantrix.co.uk/ (accessed on 15 March 2012).
- IBM ILOG CPLEX Optimizer (a website in IBM). Available online: http://www-01.ibm.com/software/integration/optimization/cplex-optimizer/ (accessed on 15 March 2012).
- Applegate, D.L.; Bixby, R.E.; Chvátal, V.; Cook, W.J. The Traveling Salesman Problem—A Computational Study; Saunders Publishing: Philadelphia, PA, USA, 2006. [Google Scholar]
- Cook, W.J.; Cunningham, W.H.; Pulleyblank, W.R.; Schrijver, A. Combinatorial Optimization; Wiley Interscience: Hoboken, NJ, USA, 1997. [Google Scholar]
- Holzer, M.; Holzer, W. Tantrix rotation puzzles are intractable. Discret. Appl. Math. 2004, 144, 345–358. [Google Scholar] [CrossRef]
© 2012 by the authors. licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/.)