1. Introduction
Continuum damage mechanics (CDM) failure models are well-known and implemented extensively in many engineering applications. The attraction to these models is partly based on the use of macroscopic fields to quantify the state of the microstructure of a material, thus allowing for damage models to be easily incorporated into existing commercial finite element analysis software. A large body of literature exists on the development and physical basis of continuum damage models; however, in this paper, we do not seek to add to it. Rather, we explore the use of adaptive mesh refinement techniques to address a common issue in the implementation of continuum damage models.
Damage models derived in the framework of continuum mechanics with internal state variables often employ evolution equations for the damage field(s) that are ordinary differential equations (ODEs) in time, and are thus without the action of any spatial differential operators on the damage field. The lack of these spatial differential operators induces localization and severe mesh dependence (see, e.g., [
1]) in the damage field. When not relying on a reformulation of the evolution equation(s), a simple approach to dealing with the localization problem is to define a physically-based minimum element size. However, even when this strategy is chosen, mesh dependence of the solution persists, and the level of mesh refinement necessary for resolving the damage field may be beyond the computational resources available. With this in mind, the main goal of this paper is to begin to explore whether or not, after having chosen a physically-based minimum element size, adaptive mesh refinement may offer an effective strategy to reduce the problem size while still resolving the damage morphology. Note that we are not proposing a method for eliminating the mesh-dependence of the system (see, for example, [
2,
3,
4]), but rather a technique for locally decreasing the mesh size in order to resolve the morphology of the damage while simultaneously containing the computational cost of the problem.
The algorithm is driven by refinement indicators directly related to the prediction of damage nucleation and evolution without any a priori considerations on the location of so-called damage “hot spots.” The refinement schemes are employed alongside a finite element formulation previously developed by the authors in which the basis for the damage field is discontinuous and the time stepping for the damage field is separate from that used to integrate the displacement and velocity fields. The preliminary results presented herein show that, to within a limited extent, it is possible to obtain visually similar damage solutions (for identical sets of initial and boundary conditions) even when starting from different initial meshes. In this sense, we are encouraged that further development of the algorithm and technique are warranted; however, we are as yet unable to make claims of convergence in the strict mathematical sense.
This paper is organized as follows: first, we briefly present the derivation of the equations of motion for a linear elastic material with simple microcracking, as a sample problem on which to apply the algorithm; second, we provide a detailed description of the numerical methods used in our simulations; third, we present two original h-refinement algorithms; and finally discuss sample calculations showing the effectiveness of the proposed approaches at resolving the damage morphology.
2. Linear Elasticity with Microcracking
A linear elastic body with isotropic microcracking is perhaps the simplest example of a continuum damage model based on the theory of internal state variables. While we view the damage field as describing the effects of microcracking, the numerical methods and adaptive meshing algorithms we discuss are largely independent of this assumption. That is, we make no claim that these techniques are intrinsically restricted to problems in linear elasticity, or to bodies which fail through microcracking and fracture.
Let
be a continuous body, and let
denote a chosen reference configuration, which, for convenience, we identify with the configuration at time
. By
we denote the deformed configuration at time
t, where
. The position of a material point relative to a fixed origin in an inertial reference frame is denoted by
X and
x for the reference and deformed configurations, respectively. In the reference configuration the body is assumed to have a mass density
. We denote by
the displacement field, i.e.,
The deformation and displacement gradients are, respectively,
Here we follow a Lagrangian formulation, and
denotes the gradient operator with respect to position in the reference configuration. The finite strain and symmetric small strain are defined, respectively, as
Microcracking is the only failure mechanism considered in this model. This assumption allows for the resulting IBVP to have a simple form, and is well accepted as being successfully modeled by continuum methods (see [
5]). Microcracking within the body is assumed to be isotropic, and we use a single scalar field to capture its effect. Let
be such a field and, as is often the case in CDM, let
ϕ be restricted to the interval
Here
and
correspond respectively to the absence of microcracking (a pristine material point), and a totally failed material point. We assume that the growth of microcracks, and hence the damage parameter, is irreversible,
We consider an evolution law for microcracking based on the Griffith criterion, as described by [
6]. Let the damage energy release rate be defined as
where
is the Helmholtz free energy per unit volume. For physically admissible damage evolutions, the energy release rate must be a positive quantity, since during such evolutions damage growth is expected to entail the expenditure of stored energy. As with the Griffith criterion, we posit that there is a critical energy release rate
that must be met before microcracking can evolve. This concept, coupled with the non-decreasing nature of the damage variable, suggests an evolution law of the form
where
is a crack propagation parameter, and the operator
returns the value of the argument if the argument is positive, and zero otherwise. In this manner, on a point by point basis, the damage variable can only be an increasing function of time, whose time rate of growth is related to the excess energy release rate required for microcracking to evolve. Notice that the presence of
in the damage evolution law serves the purpose of a built-in nucleation criterion. In addition, notice that the parameters
and
can be functions of damage. However, for simplicity, in this paper, the parameters
and
are assumed to be constant and uniform.
We treat the damage field
ϕ as an internal state variable (ISV), and as such derive the equations of motion according to the theory of continuous bodies with internal state variables (see, e.g., [
7] and [
8]). Following the Coleman-Noll procedure (see [
9]), we obtain the thermodynamic constraints
where
is the constitutive response function for the first Piola-Kirchhoff stress tensor,
is the constitutive response function for the second Piola-Kirchhoff stress tensor, and
represents the material frame indifferent constitutive response function (see any text on continuum mechanics, e.g., [
8] or [
10]) of the denoted quantity.
We can immediately verify that the third constraint in (8) is satisfied by the choice of damage evolution in (7). Because at any given point in the body
ϕ is an increasing function, there are two distinct cases for the third constraint in (8):
Following the traditional theory of linear elasticity, we will consider motions under which it is reasonable to assume that
Expanding the free energy about
, and retaining up to and including the terms of
, one has
Traditionally, when the body is deformation free, it is assumed that there is no stored energy available for work in the body, and that there is no residual stress in the body. However, in this case we must also assume that for the previous statement to hold, a non-uniform presence of damage also does not give rise to recoverable work or residual stress. Consequently, the first two terms of the expansion in (10) are equal to zero, and we are left with the free energy
is the fourth-order elasticity tensor. Note that the elastic moduli are now time-dependent via the damage variable. Borrowing from the large collection of damage mechanics literature, we choose a simple dependence on the elastic moduli on the damage variable,
where
are the elastic moduli when the material is undamaged and
. Combining (12), (11), the thermodynamic constraints in (8), and the definition of the energy release rate in (6), the free energy, stress, and energy release rate are
Substituting the stress and energy release rate into the balance of linear momentum and damage evolution equation, respectively, yields the equations of motion
where
is the body force per unit volume. Following the traditional methods of linear elasticity we retain only terms of order
δ in (14), and we retain terms only up to order
in (15), resulting in the final equations of motion for a linear elastic material with simple microcracking
The system in (16)–(17) is representative of many damage models, namely a hyperbolic PDE coupled to an ODE governing the evolution of the internal damage variable. It should be noted that the right-hand side of (17) is non-smooth, and that the choice of an ODE as the evolution law is specifically what creates the intrinsically mesh-dependent nature of the damage field. As discussed in the introduction, the general character of this model is not new, and non-local approaches have been proposed throughout the literature; however, the focus of this paper is not on the adopted damage evolution law, but the proposed adaptive mesh refinement algorithm. This algorithm could be applied to many damage models, and the one presented in this section is merely to provide a test case under which to demonstrate the
h-refinement performance in terms of resolving the damage morphology.
4. Adaptive Mesh Refinement Algorithm
The adaptive
h-refinement implemented in this work uses
a posteriori refinement indicators to determine which cells of the triangulation must be refined (see, for example, [
15] and [
16]).
4 For the damage model presented in this paper, we are primarily concerned with isolating the damage evolution to a small area of the domain, and adequately resolving the morphology of the damage solution. Therefore, the proposed scheme should be viewed as a tool for increasing the resolution of the damage field locally, while maintaining reasonable problems sizes. While it is hoped that this approach may be beneficial to producing repeatable results when the solutions are mesh dependent, it is not a cure or fix for such a condition. Rather, this is a first attempt by the authors at incorporating adaptive refinement into dynamic damage models.
We construct two refinement indicators, which subsequently require two separate algorithms. The first indicator is based exclusively on the damage variable
while the second is based on the excess energy release rate
where
c is a constant,
is the diameter of the
K-th cell and
is the minimum cell diameter allowed in the simulation. The use of a minimum mesh size is a simple and well-known method for addressing localization. Here we propose that it should be related to the particular microstructure of the body in question; however, we provide no relationship between
and any specific physics, as the point of this paper is not the physical model itself but rather numerical techniques. The constant
c in (39) allows us to adjust the excess energy release rate. In particular,
will cause
to be non-zero before damage growth occurs, and in effect preemptively refine the mesh. The complete mesh refinement algorithms are given in
Figure 1 and
Figure 2, for the damage based scheme and the energy release rate scheme, respectively. The minimum cell length defines the scale at which damage evolution will occur. Accordingly, each of the algorithms iterates through refinement cycles, within a given timestep, until each cell which has a non-zero refinement indicator has a diameter less than
. No mesh coarsening is implemented, as we do not want to have damage evolving at a mesh size greater than the minimum one.
Throughout the refinement process, the triangulation is changed, resulting in the need to resize the associated matrices and vectors, as well as transfer the solution from the previous triangulation to the new one. This require time and changing memory requirements, and are detrimental to the performance of the code. However, even with these performance issues, the resulting algorithm is still much faster than using a fine scale mesh from the onset of the simulation.
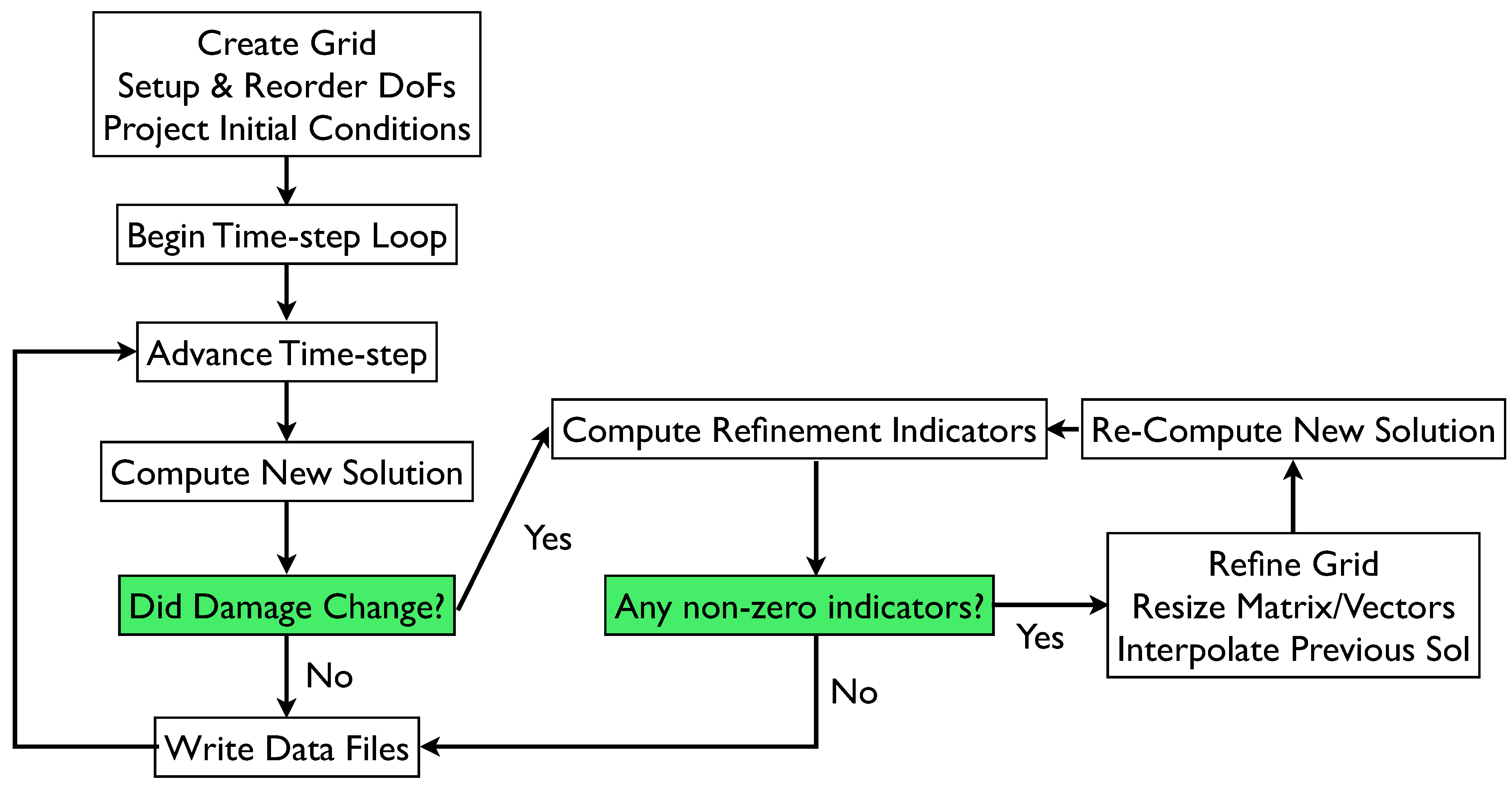
Figure 1.
Damage based refinement algorithm flow chart.
Figure 1.
Damage based refinement algorithm flow chart.
Figure 2.
Energy Release Rate based algorithm flow chart.
Figure 2.
Energy Release Rate based algorithm flow chart.
5. Numerical Experiments
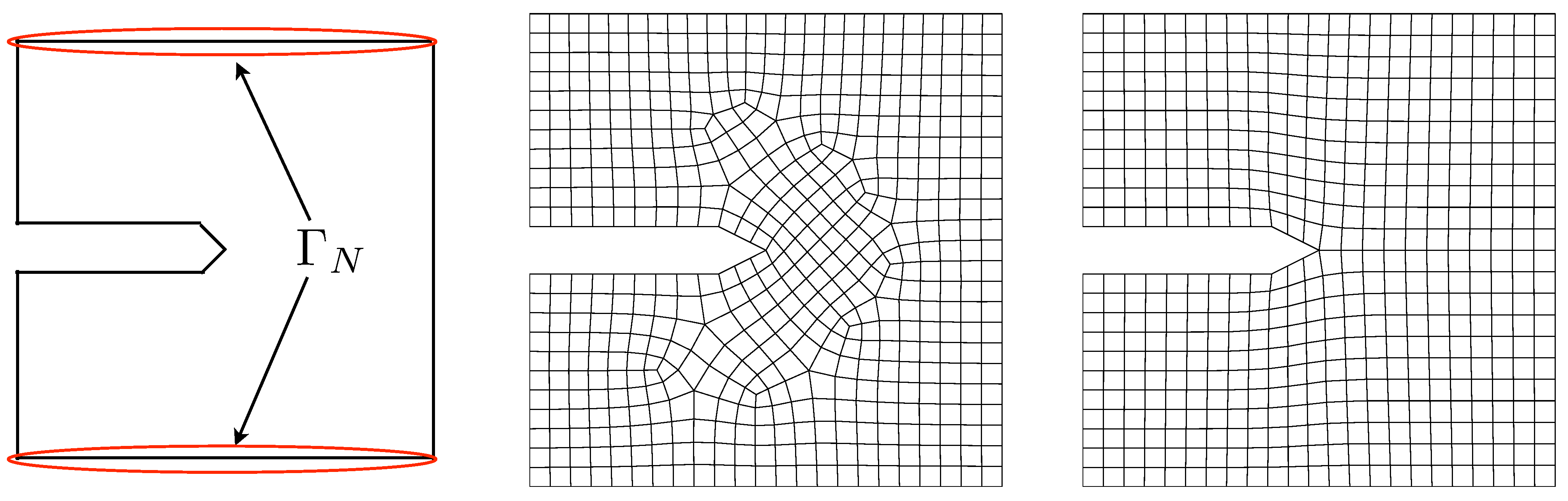
In this section we investigate the performance of the proposed algorithms. A simple example consisting of a two-dimensional bar fixed at one end and subjected to an applied load at the other is used to gain confidence that the proposed algorithms are functioning as desired. A more complicated example, consisting of a two-dimensional idealization of a compact test specimen is used to evaluate how well the algorithms address the use of different meshes, by visually comparing the resulting damage fields on each triangulation.
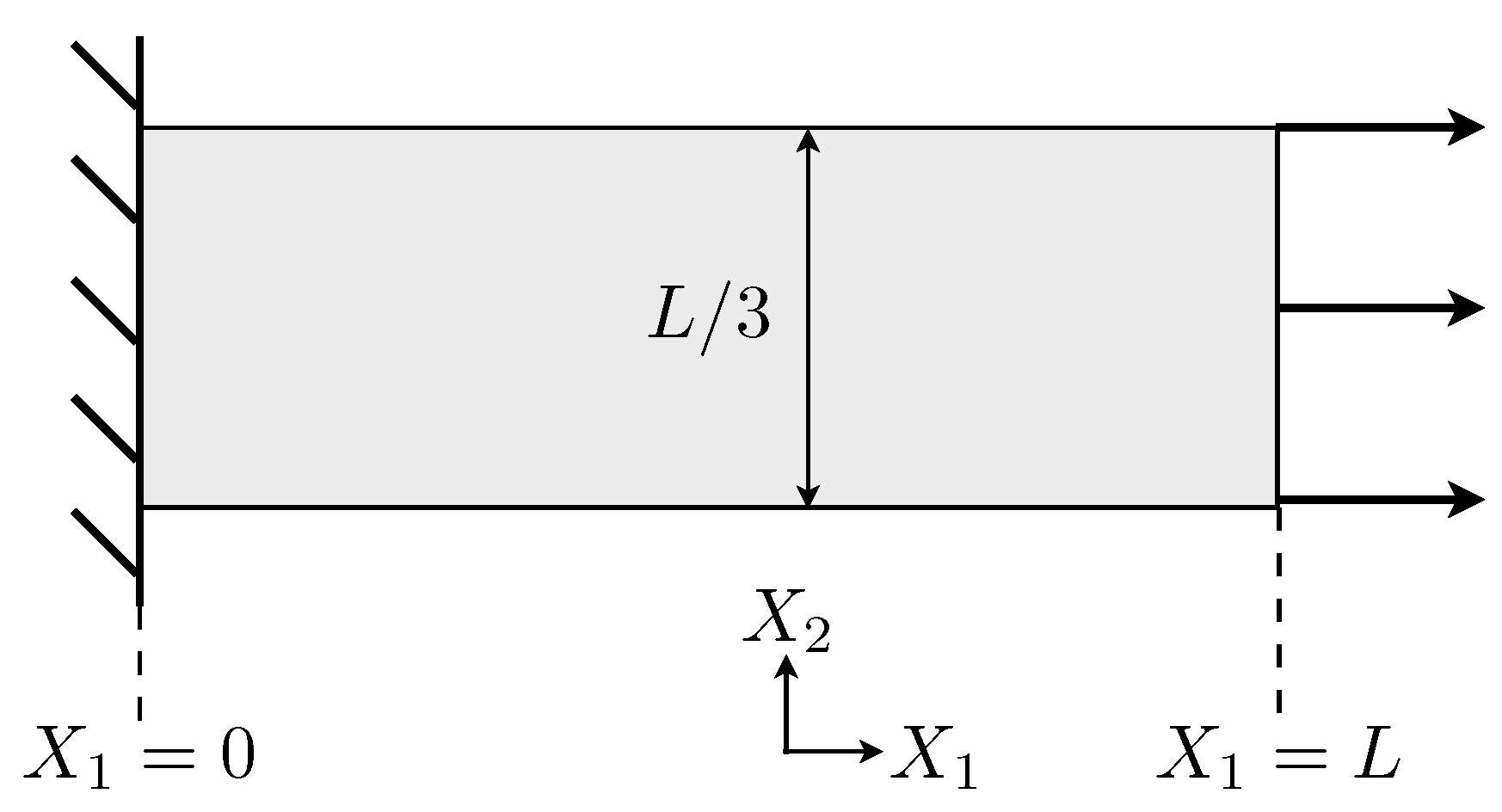
The geometry of a two-dimensional bar fixed at one end and subjected to a Neumann (traction) boundary condition at the other is given in
Figure 3.
Figure 3.
Geometry and boundary conditions of a two-dimensional bar fixed at and subject to an applied traction at .
Figure 3.
Geometry and boundary conditions of a two-dimensional bar fixed at and subject to an applied traction at .
The essential boundary conditions are
and
, and the applied traction force is defined as the smooth function
where
. The initial conditions are
,
, and
. This simple initial boundary value problem corresponds to a two-dimensional bar which is clamped at one end, and initially at rest with uniform damage, being smoothly loaded up to a particular load at which time the load is held constant. Thus, a wave will propagate along the bar, eventually striking the fixed end. The particular material properties and parameters for the following simulations are given in
Table 1, and have been chosen to be representative of a brittle material.
Table 1.
Material properties representative of a brittle material, and the loading parameters.
Table 1.
Material properties representative of a brittle material, and the loading parameters.
| Elastic Modulus | 9 ×109 Pa | Density | 1.7 × 103 kg/m3 |
| Poisson Ratio | 0.3 | Gcr | 3 × 107 J/m3 |
| ηc | 0.1 m3/J·s | β | 2 |
| τ | 20 μs | sx | 5× 107 Pa |
Figure 4.
Damage-based refinement scheme: from top to bottom, triangulations of the two-dimensional bar at times , 88.5 μs, 106.1 μs, and 115.9 μs. The refinement is concentrated at the fixed end of the bar, which is where we expect the damage to increase.
Figure 4.
Damage-based refinement scheme: from top to bottom, triangulations of the two-dimensional bar at times , 88.5 μs, 106.1 μs, and 115.9 μs. The refinement is concentrated at the fixed end of the bar, which is where we expect the damage to increase.
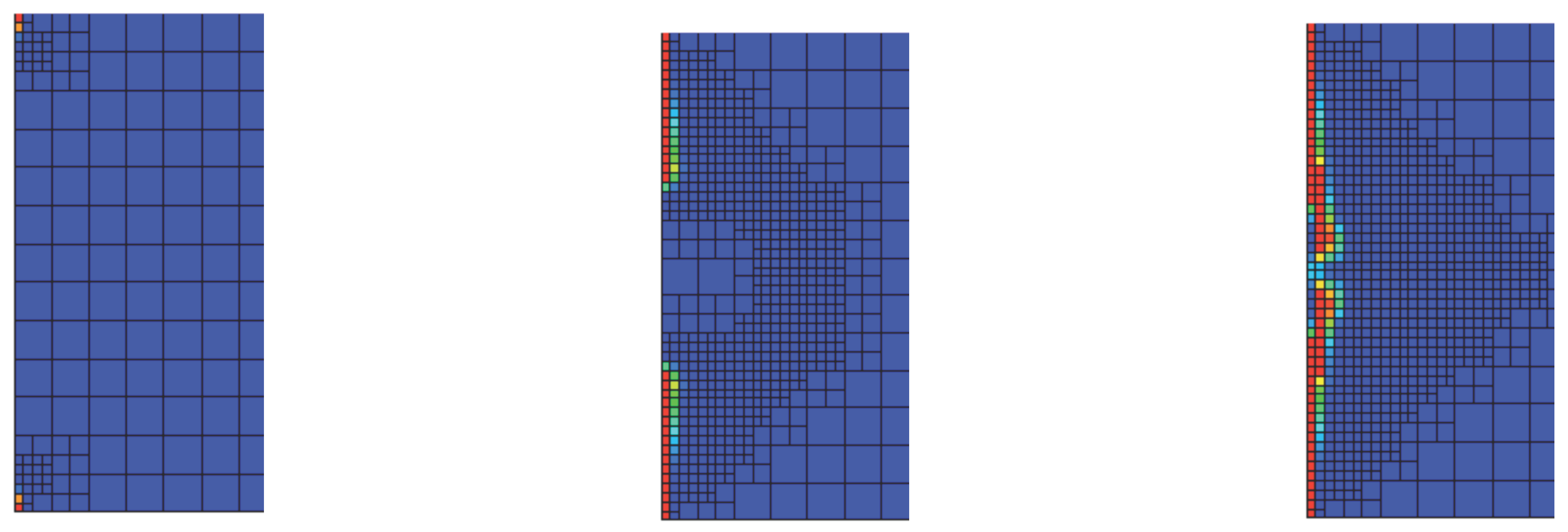
We see in
Figure 4 that the mesh refinement is localized to the fixed (left) end of the bar, indicating that this is where the damage is increasing. This is expected, because as the wave strikes the fixed end of the bar, we expect from the theory of linear elasticity to have very high strains at the corners of the domain, and thus an energy release rate that is higher than other locations in the domain. We plot the values of the damage variable in
Figure 5, and see that the damage nucleates at the corners of the domain, and subsequently, as the corner cells become fully damaged we see the adjacent cell become damaged, and so on. The damage-based refinement scheme only allows for damage evolution at the smallest mesh size. We can see this in
Figure 5, where the piecewise constant damage is clearly localized to an individual cell at the smallest refinement level. We see that there is no damage evolution in larger cells, as desired. We now want to compare the performance of the damage based and energy release rate based error estimation schemes.
Figure 5.
Damage based refinement: from left to right, zoom-in images of the damage at the fixed-end of the bar , at 88.5 μs, 106.1 μs, and 115.9 μs. The damage nucleates at the corners of the bar, and progresses towards the center.
Figure 5.
Damage based refinement: from left to right, zoom-in images of the damage at the fixed-end of the bar , at 88.5 μs, 106.1 μs, and 115.9 μs. The damage nucleates at the corners of the bar, and progresses towards the center.
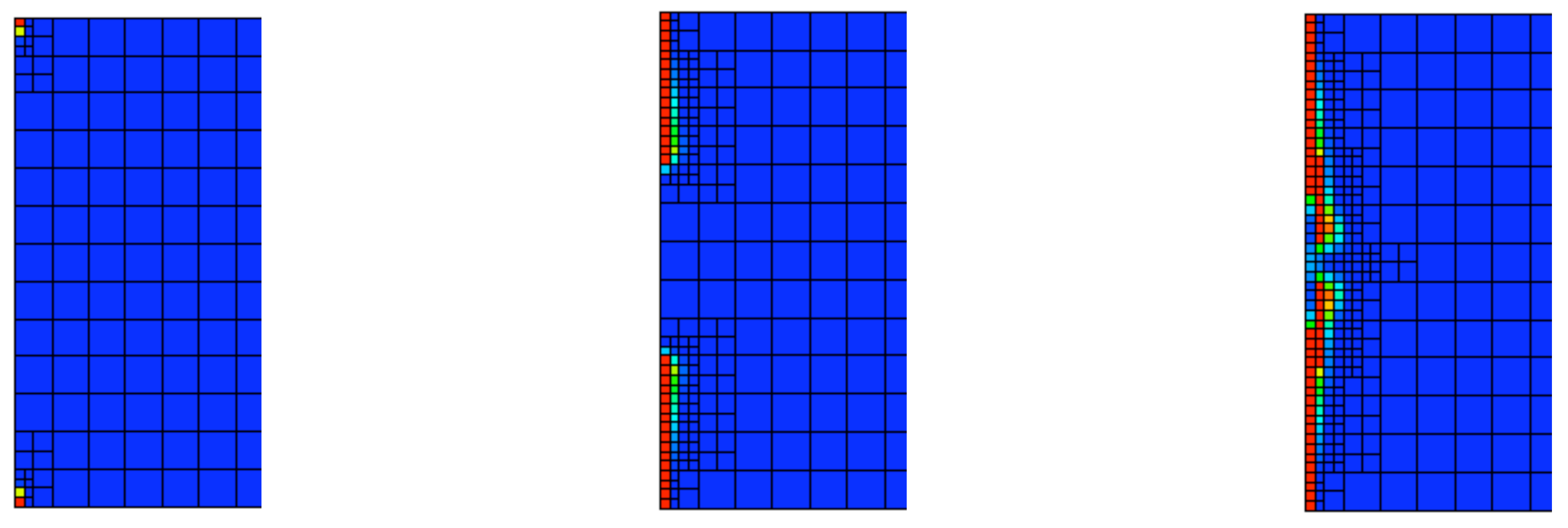
Figure 6.
Energy release rate based refinement, with : from left to right, zoom-in images of the damage at the fixed-end of the bar , at 88.5 μs, 106.1 μs, and 115.9 μs.
Figure 6.
Energy release rate based refinement, with : from left to right, zoom-in images of the damage at the fixed-end of the bar , at 88.5 μs, 106.1 μs, and 115.9 μs.
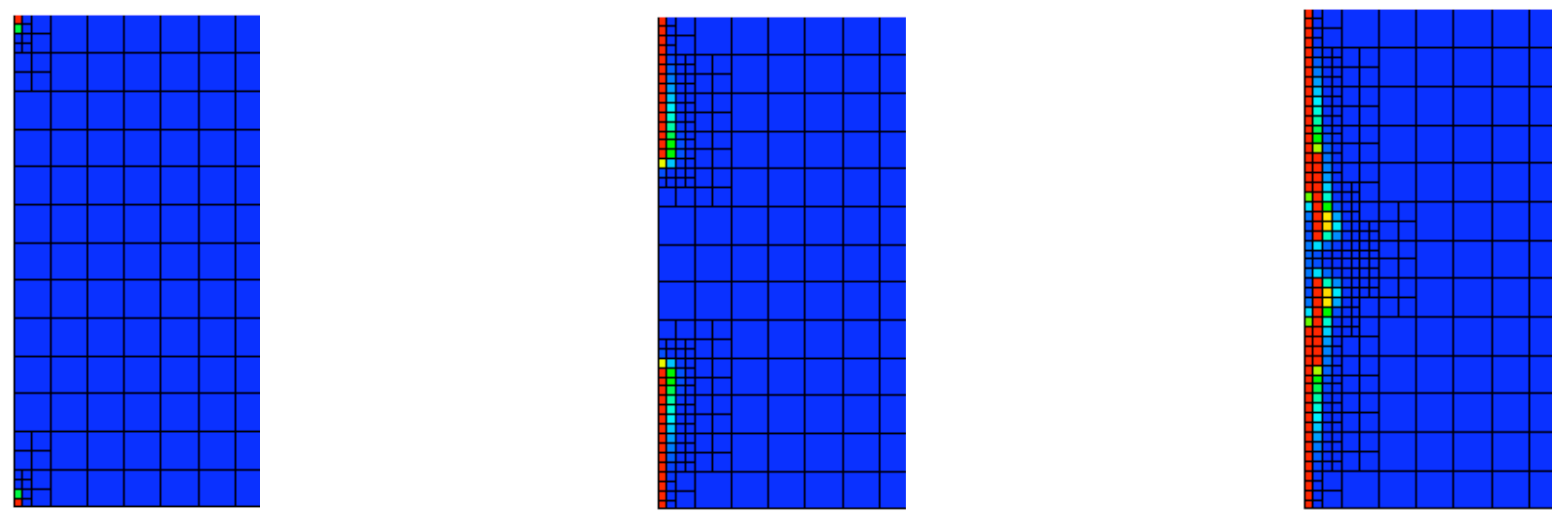
Figure 7.
Energy release rate based refinement,
: The same simulation as in
Figure 6, but now with the refinement indicator parameter
. Note the difference in the mesh pattern, specifically the refinement of cells in which damage is not evolving.
Figure 7.
Energy release rate based refinement,
: The same simulation as in
Figure 6, but now with the refinement indicator parameter
. Note the difference in the mesh pattern, specifically the refinement of cells in which damage is not evolving.
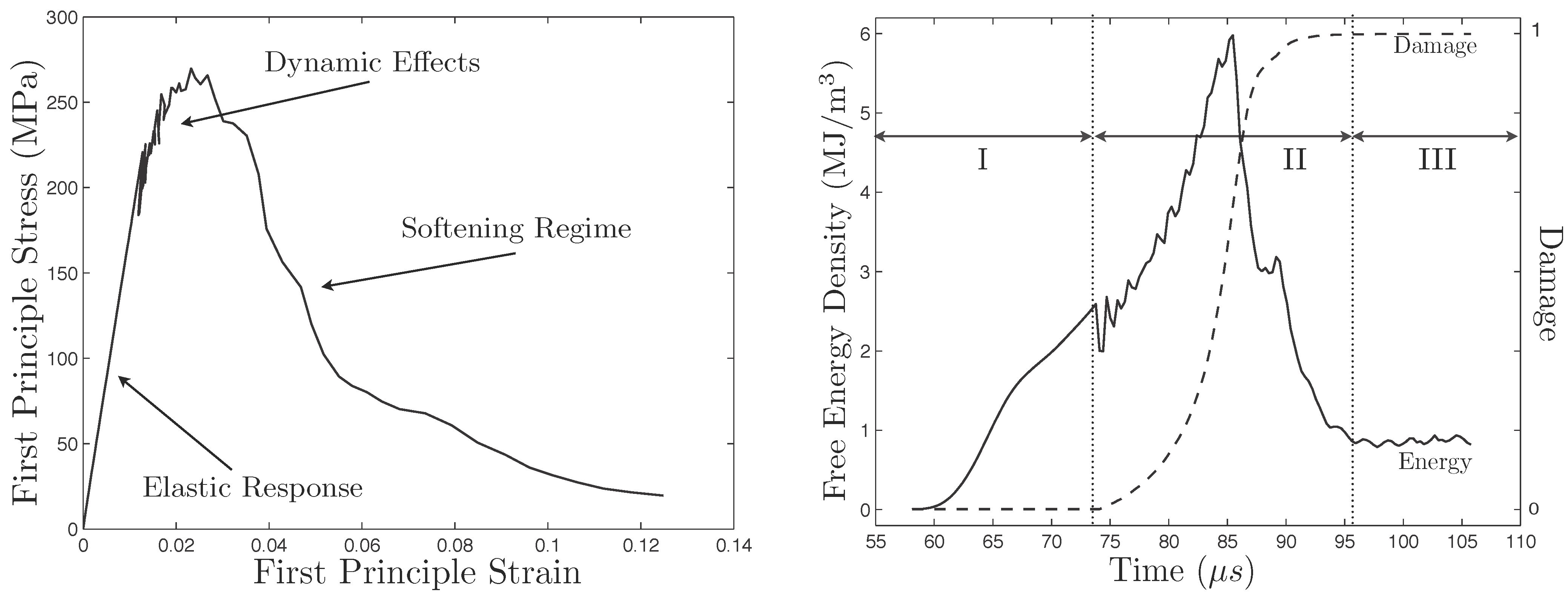
Figure 8.
The first principle stress versus the first principle strain at a point which becomes fully damaged (left) and the corresponding time series of the damage variable and Helmholtz free energy density (right). Dynamic effects can be observed in both data sets. On the right, region I corresponds to the response before damage evolution, region II to the brief period of damage evolution, and region III to the period when the material is fully damaged.
Figure 8.
The first principle stress versus the first principle strain at a point which becomes fully damaged (left) and the corresponding time series of the damage variable and Helmholtz free energy density (right). Dynamic effects can be observed in both data sets. On the right, region I corresponds to the response before damage evolution, region II to the brief period of damage evolution, and region III to the period when the material is fully damaged.
To serve as a check that the simple damage model we have chosen to use for demonstration purposes is functioning correctly, in
Figure 8 we provide a plot of the first principle stress versus the first principle strain at a point which becomes fully damaged (left) and the corresponding time series of the damage variable and Helmholtz free energy density (right). The point we have chosen is the center of the bottom left cell in
Figure 7. Note that both the parametric (in time) stress/strain plot and time series plot of the damage and energy are simply records of the motion of a point which becomes fully damaged, and are not comparable to the usual uniaxial stress strain curves.
Figure 6 shows the damage solution of the same problem, but now using the refinement indicators based on the excess energy release rate with the parameter
c in (39) set equal to one. We observe that the damage solution in
Figure 6, while not identical to that in
Figure 5, is quite similar to it. We attribute the similarity in the damage solutions to the fact that we have set
in (39), and hence the energy release rate refinement indicator is the same as the damage based indicator and produces similar results. To illustrate the effect of adjusting the constant
c, in
Figure 7 we show the damage solution and mesh refinement for the same problem, but this time obtained using an energy release based refinement indicator with the parameter
. Preemptive mesh refinement is now clearly visible in
Figure 7, however, the damage field is still essentially the same as in
Figure 5 and
Figure 6. Thus, in this circumstance, it appears that either the damage based or energy release rate based schemes would provide adequate performance.
5.1. Idealized Compact Test Specimen
To further test and demonstrate the capabilities of the proposed algorithm, we choose to model the well known experiment of a compact test specimen in tension, in order to simulate conditions under which Mode I failure would normally occur. However, unlike many experiments of this nature, the loading on the specimen is monotonic and highly dynamic (as opposed to standard fatigue tests with slow, cyclic loading). The geometry and initial meshes for the simulations are given in
Figure 9, and the boundary conditions are
where
. The initial conditions are
,
, and
, and the material properties are listed in
Table 1, with the exception that now we take
and
.
Figure 9.
Geometry and initial meshes for the simulations of an idealized 2D compact test specimen. Vertical traction loading is applied to the faces denoted as
, creating a situation likely to result in Mode I failure. The meshes were created using the
pave (left) and
submap (right) methods in Cubit [
17].
Figure 9.
Geometry and initial meshes for the simulations of an idealized 2D compact test specimen. Vertical traction loading is applied to the faces denoted as
, creating a situation likely to result in Mode I failure. The meshes were created using the
pave (left) and
submap (right) methods in Cubit [
17].
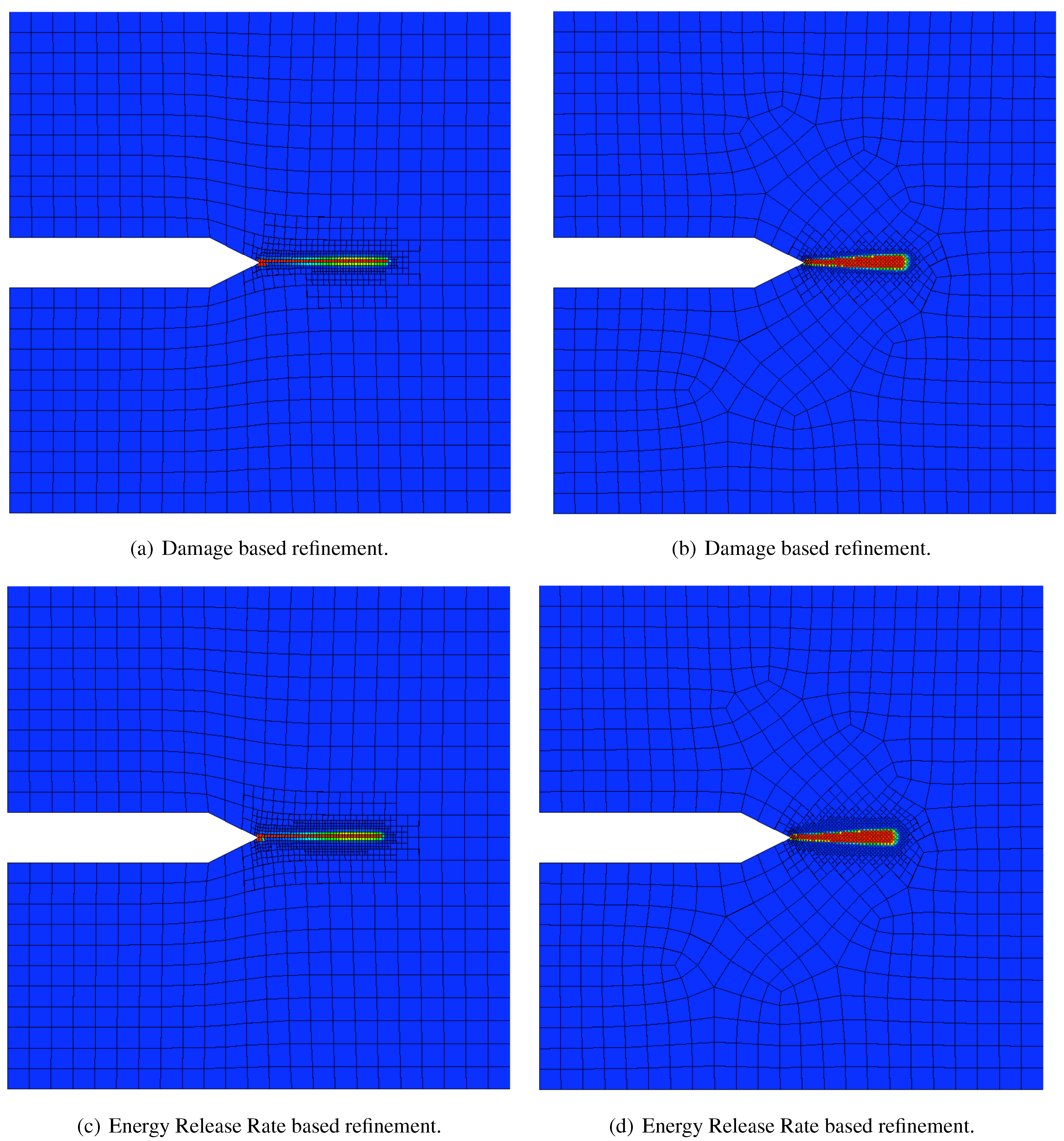
For this specific loading condition and set of material properties (including
), we see in
Figure 10 that both the damage and energy release rate based refinement schemes show similar results for the damage solution on both initial meshes, thus demonstrating that the solution is somewhat independent of the mesh. By this we mean that, while the two damage distributions are clearly not identical, they do concentrate on the horizontal symmetry line of the compact specimen, as expected. As it turns out, the differences between the solutions obtained using different initial grids can be traced to the specific values used for the parameter
in relation to that of the parameter
. Before addressing this issue, we remark that for the results shown in
Figure 10, the parameter in the energy release rate based refinement algorithm is
, and as such, we notice that the corresponding solutions in
Figure 10(c) and
Figure 10(d) have a slightly greater extent of refinement. However, comparing the damage solutions in
Figure 10(a) and
Figure 10(b) with those in
Figure 10(c) and
Figure 10(d), we see that the preemptive refinement of the energy release rate based algorithm yielded essentially the same damage solution as that produced by the refinement indicator based on the time rate of change of the damage. Therefore, we conclude again that in this instance, either scheme is adequate.
Going back to discussing the mesh dependence issue, the most noticeable difference between the solutions on the grid in
Figure 10(a) and
Figure 10(c) and the grid in
Figure 10(b) and
Figure 10(d) is the degree of localization of the damage solution. In the first set of aforementioned figures, the damage is localized to a single cell, while in the second set the damage is clearly spread over numerous cells across the horizontal mid-line of the solution domain.
Figure 11(a) and
Figure 11(b) show the region of interest in
Figure 10(a) and
Figure 10(b), respectively. It is clear in these figures that, with the choice of piecewise constant elements, the damage solution seems to evolve in cells that are adjacent to the face of an already damaged cell, as opposed to one which is connected only at a corner. We discovered that this effect becomes more pronounced as we increase the value of
while keeping the value of
fixed.
In fact, taking the value of
, which is three times the value used to produce the solutions in
Figure 10(a)–
Figure 10(d), we see in
Figure 12 that the ability of the algorithm to address the mesh-dependency of the solution is diminished (again, keeping in mind that the value of
is held constant) to the point that two completely different physical failure patters are obtained. We suspect that to obtain physically comparable solutions on different initial meshes, we would need to determine the influence the values of
and
have on each other. However, this may not be an acceptable solution due to the fact that the value used for
should be physical-based, that is, as though
were a constitutive parameter. Clearly this also means that comparing solutions with vastly different values of
while keeping
fixed may be questionable. With this in mind, we feel that the results presented in this paper demonstrate that the proposed algorithm is well suited for locally refining the mesh in areas of evolving damage, but could certainly be more robust. Specifically, the authors feel that more careful study of the combination of solution space choices for the damage variable, error estimates, and refinement strategies are necessary before any more general claims can be made about the viability of using adaptive
h-refinement for addressing mesh dependency of damage models prone to localization.
Figure 10.
Damage solutions on two very different meshes with the two proposed refinement algorithms. In these simulations, the constant in (39) is
, leading to the preemptive refinement of non-damaged cells in
Figure 10(c) and
Figure 10(d). In general, the solutions are all similar, thus we are encouraged that adaptive mesh refinement may be able to help control mesh-dependency issues; however, it is clear that the extent of localization is different between the two meshes and not yet to a point of mathematical comparison.
Figure 10.
Damage solutions on two very different meshes with the two proposed refinement algorithms. In these simulations, the constant in (39) is
, leading to the preemptive refinement of non-damaged cells in
Figure 10(c) and
Figure 10(d). In general, the solutions are all similar, thus we are encouraged that adaptive mesh refinement may be able to help control mesh-dependency issues; however, it is clear that the extent of localization is different between the two meshes and not yet to a point of mathematical comparison.
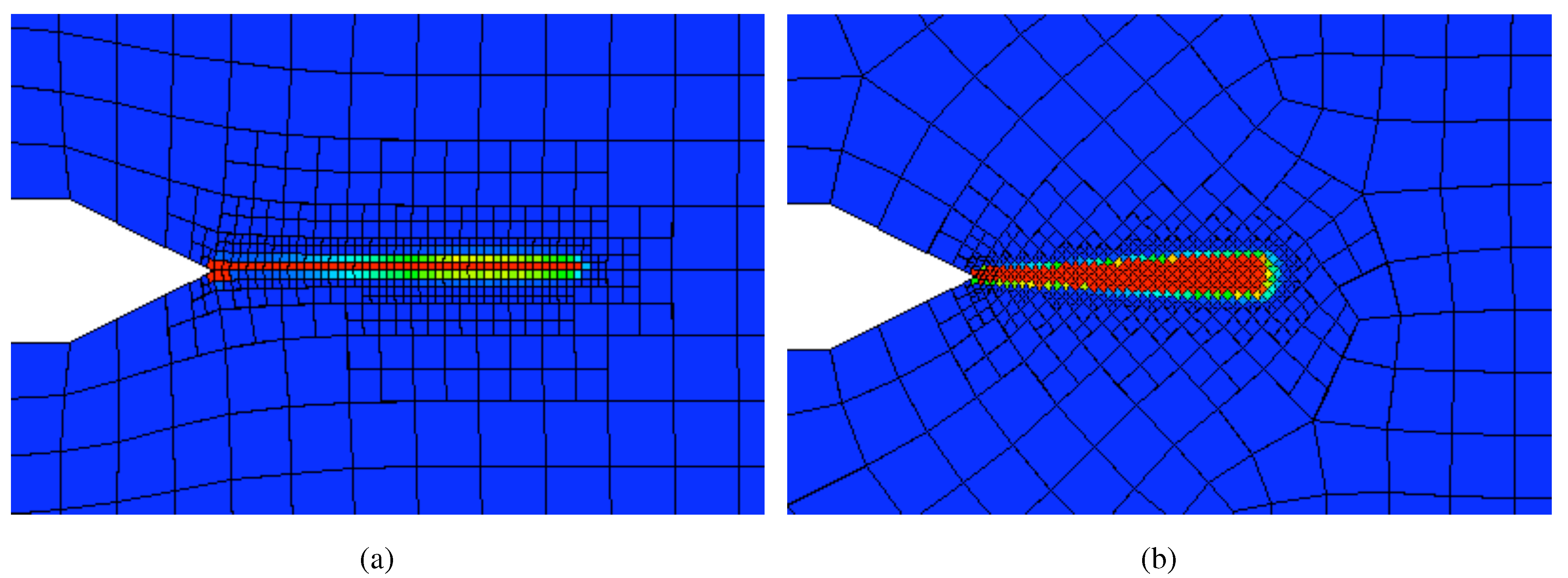
Figure 11.
Zoom-in of the damage solutions in
Figure 10(a) and
Figure 10(b), respectively, showing the damage field solution produced by the damage-based refinement algorithm. The extent to which the damage is localized is clearly visible, and, for this first attempt, is considered thus far to be sucessful.
Figure 11.
Zoom-in of the damage solutions in
Figure 10(a) and
Figure 10(b), respectively, showing the damage field solution produced by the damage-based refinement algorithm. The extent to which the damage is localized is clearly visible, and, for this first attempt, is considered thus far to be sucessful.
Figure 12.
Damage field solutions using the energy release rate refinement algorithm, but with
three times larger than the value used to find the solutions in
Figure 10(c)–
Figure 10(d). Clearly, the ability of the algorithm to mitigate the mesh dependence is diminished.
Figure 12.
Damage field solutions using the energy release rate refinement algorithm, but with
three times larger than the value used to find the solutions in
Figure 10(c)–
Figure 10(d). Clearly, the ability of the algorithm to mitigate the mesh dependence is diminished.