Automated Modelling of Evolving Discontinuities
Abstract
:1. Introduction
2. Automated Mathematical Modelling
element = FiniteElement("Lagrange", "tetrahedron", 1)
v = TestFunction(element)
u = TrialFunction(element)
w = Function(element)
f = Function(element)
a = w*dot(grad(v), grad(u))*dx
L = v*f*dx
|
3. Extended Finite Element Method: Review
3.1. Incorporating Discontinuities into Finite Element Spaces
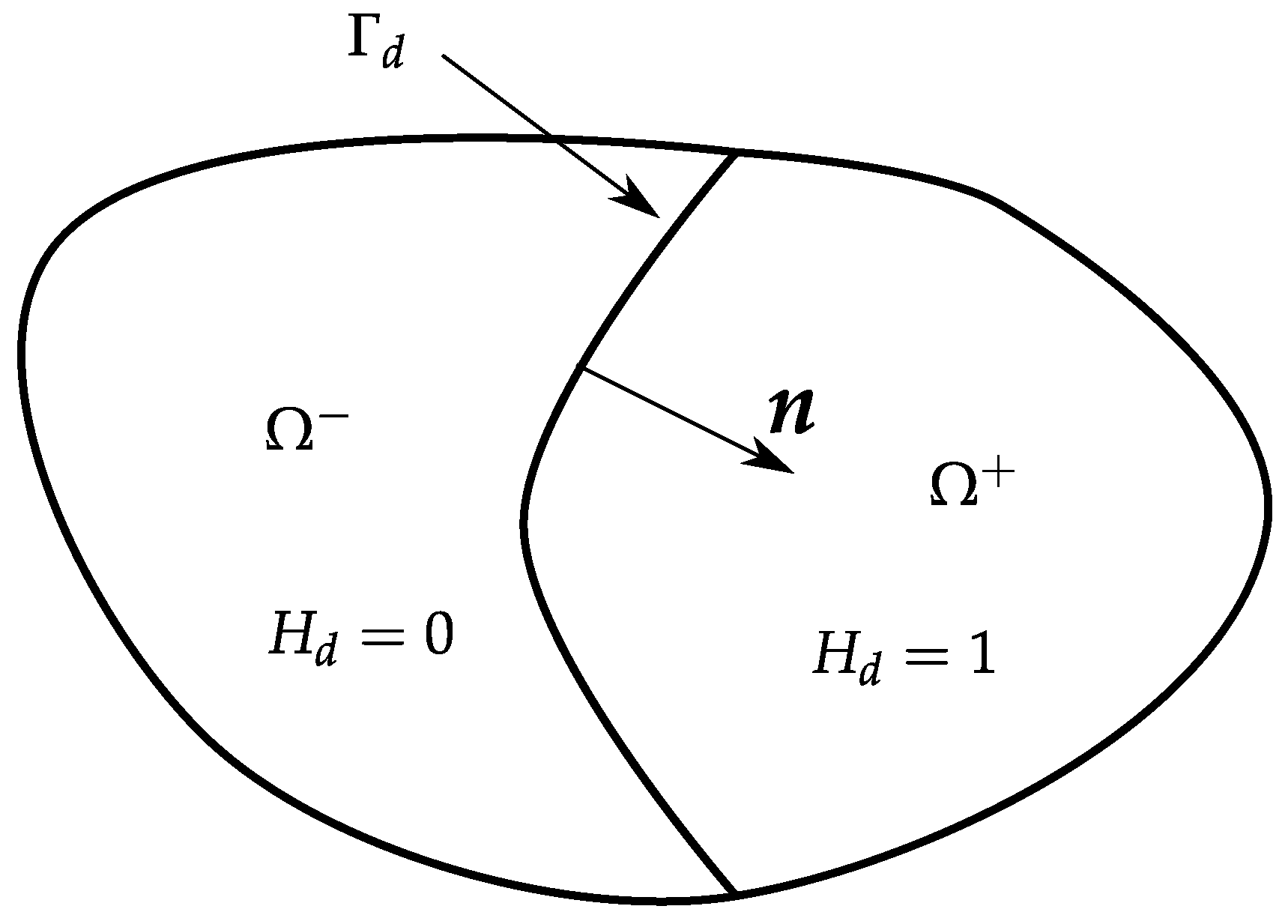
3.2. Example: Poisson Equation
4. Automated Modelling of Discontinuities
4.1. Domain-Specific Language Extensions
elem_cont = FiniteElement(type, shape, order) elem_discont = DiscontinuousFiniteElement(type, shape, order) element = elem_cont + element_discont |
v = TestFunctionPUM(element) u = TrialFunctionPUM(element) f = Function(elem_cont) |
# Finite element spaces
elem_cont = FiniteElement("Lagrange", "triangle", 2)
elem_discont = DiscontinuousFiniteElement("Lagrange", "triangle", 2)
element = elem_cont + elem_discont
# Test and trial functions
v = TestFunctionPUM(element)
u = TrialFunctionPUM(element)
# Source term
f = Function(elem_cont)
# Interface flux parameter
k = Constant("triangle")
# Bilinear and linear forms
a = dot(grad(v), grad(u))*dx + k*djump(v)*djump(u)*dc
L = v*f*dx
|
4.2. Specialised Generated Code
UFC_PoissonBilinearForm a(pum); UFC_PoissonLinearForm L(pum); |
Poisson_dof_map_0 dof_map(pum); |
Poisson_cell_integral_0 cell_integral(pum); |
4.3. Solver Environment
Surface representation
Interface to the generated code and local extension of the finite element basis management
std::vector<const Surface*> surfaces; PUM pum(surfaces, mesh, standard_dof_map); |
Function spaces and variational forms
Poisson::FunctionSpace V(mesh, pum_objects); Poisson::BilinearForm a(V, V); Poisson::LinearForm L(V); |
std::vector<const GenericPUM*> pum_objects; pum_objects.push_back(&pum_u); pum_objects.push_back(&pum_u); pum_objects.push_back(&pum_u); pum_objects.push_back(&pum_p); Incompressible3D::FunctionSpace V(mesh, pum_objects); |
Matrix A; Vector b; Assembler::assemble(A, a); Assembler::assemble(b, L); |
5. Examples
5.1. Weighted Poisson Equation


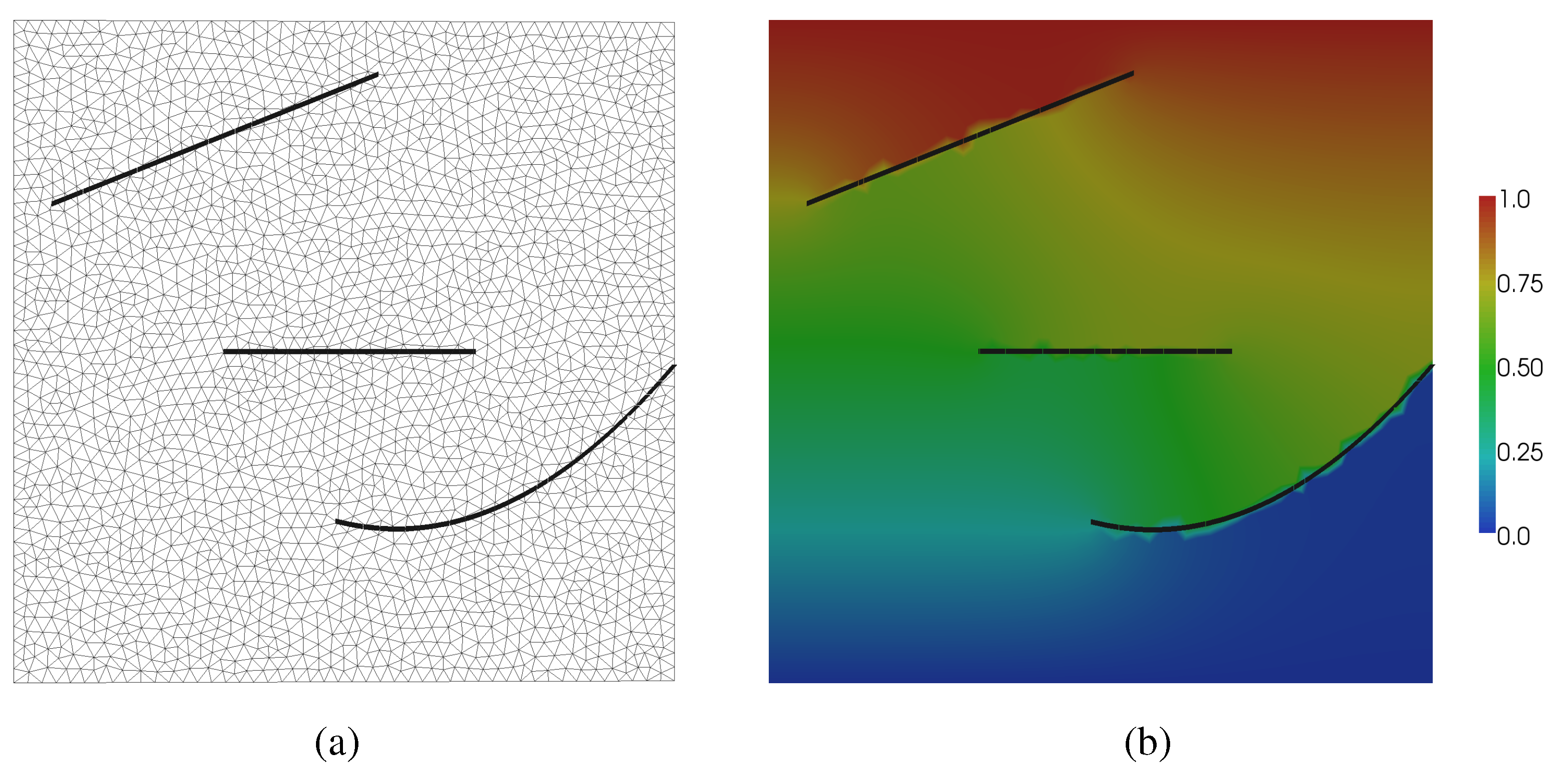

5.2. Three-dimensional elasticity
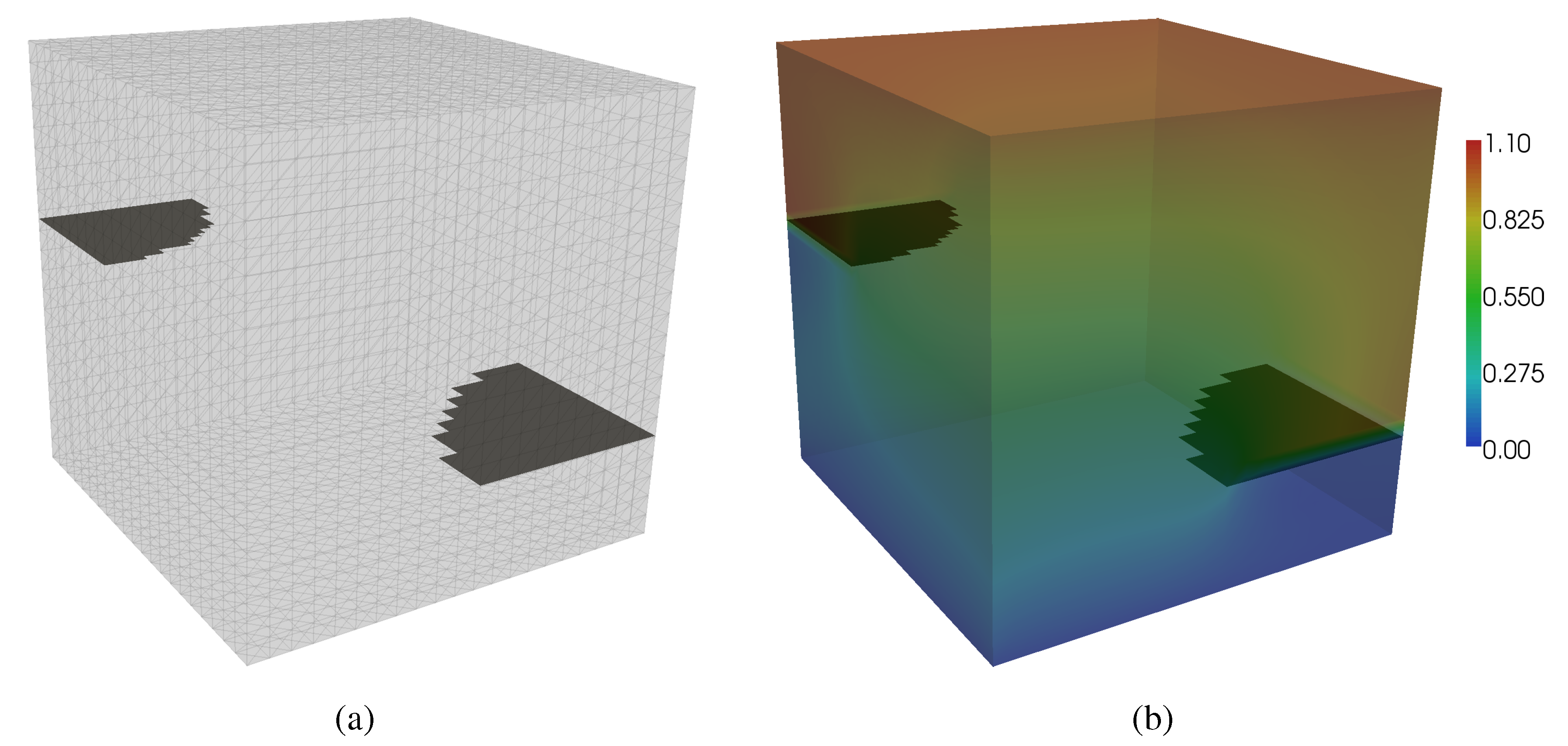
5.3. Incompressible elasticity with cohesive discontinuity surfaces


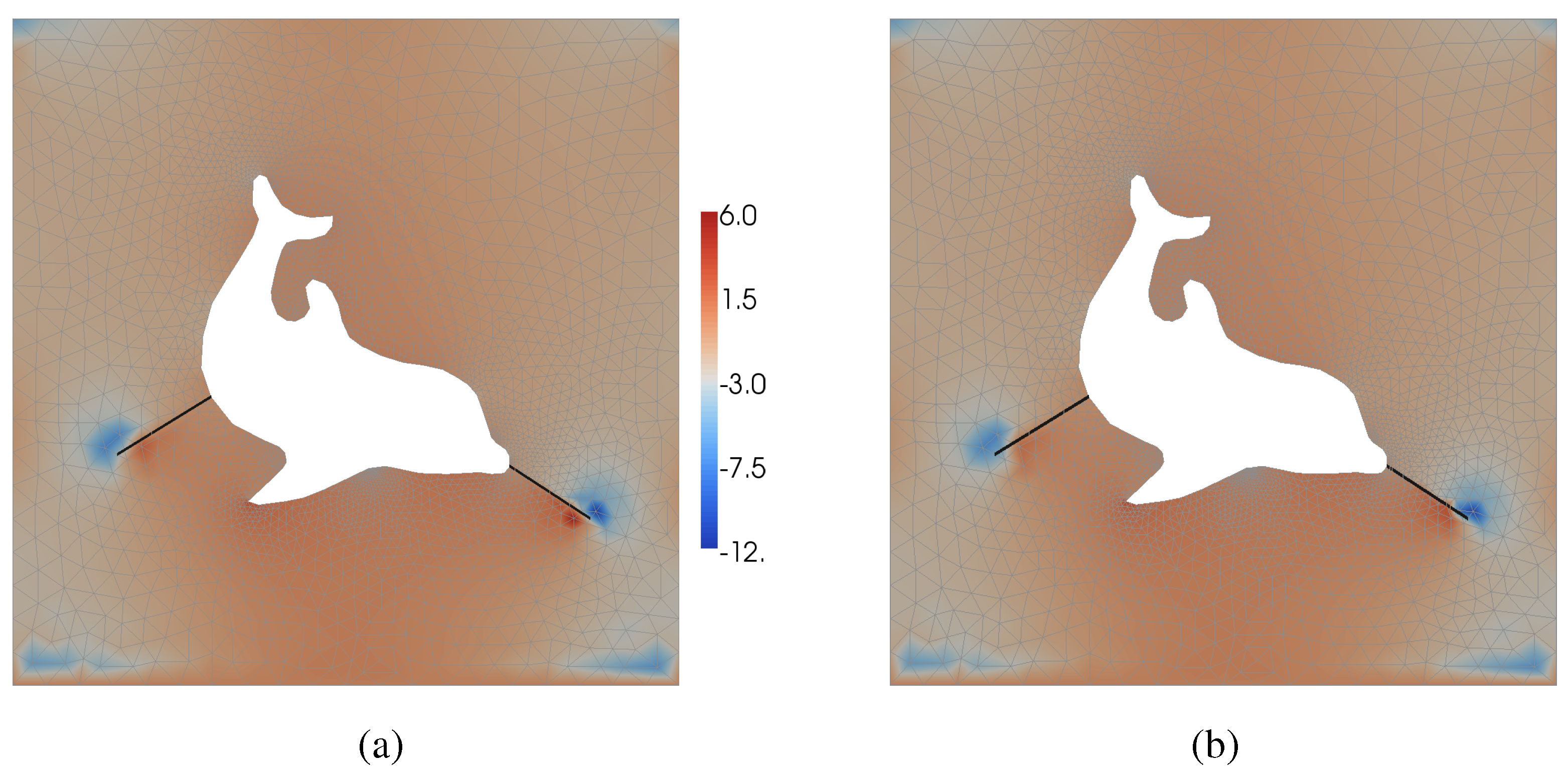
6. Conclusions
Acknowledgements
References
- Melenk, J. M.; Babuska, I. The partition of unity finite element method: Basic theory and applications. Comput. Method. Appl. Mech. Eng. 1996, 139, 289–314. [Google Scholar] [CrossRef]
- Moës, N.; Dolbow, J.; Belytschko, T. A finite element method for crack growth without remeshing. Int. J. Numer. Method. Eng. 1999, 46, 231–150. [Google Scholar] [CrossRef]
- Belytschko, T.; N. Moës, S. U.; Parimik, C. Arbitrary discontinuities in finite elements. Int. J. Numer. Method. Eng. 2001, 50, 993–1013. [Google Scholar] [CrossRef]
- Strouboulis, T.; Copps, K.; Babuška, I. The generalized finite element method. Comput. Method. Appl. Mech. Eng. 2001, 190, 4081–4193. [Google Scholar] [CrossRef]
- Bordas, S.; Nguyen, P. V.; Dunant, C.; Guidoum, A.; Nguyen-Dang, H. An extended finite element library. Int. J. Numer. Method. Eng. 2007, 71, 703–732. [Google Scholar] [CrossRef]
- Kirby, R. C.; Logg, A. A compiler for variational forms. ACM Trans. Math. Software 2006, 32, 417–444. [Google Scholar] [CrossRef]
- Logg, A.; Wells, G. N. DOLFIN: Automated finite element modelling, 2009. Available online: http://www.dspace.cam.ac.uk/handle/1810/214787.
- Ølgaard, K. B.; Logg, A.; Wells, G. N. Automated code generation for discontinuous Galerkin methods. SIAM J. Sci. Comput. 2008, 31, 849–864. [Google Scholar] [CrossRef]
- Rognes, M. E.; Kirby, R. C.; Logg, A. Efficient assembly of H(div) and H(curl) conforming finite elements. 2009; Submitted. [Google Scholar]
- Ølgaard, K. B.; Wells, G. N. Optimisations for quadrature representations of finite element tensors through automated code generation. ACM Trans. Math. Software 2010, 37. Available online: http://www.dspace.cam.ac.uk/handle/1810/218613. [Google Scholar] [CrossRef]
- FEniCS. FEniCS Project 2009. Available online: http://www.fenics.org/.
- Nikbakht, M.; Wells, G. N. Supporting material 2009. Available online: http://www.dspace.cam.ac.uk/handle/1810/218650.
- Logg, A.; others. FEniCS Form Compiler 2009. Available online: http://www.fenics.org/ffc.
- Alnæs, M. S.; Logg, A.; Mardal, K.-A.; Skavhaug, O.; Langtangen, H. P. UFC Specification User Manual. 2009. Available online: http://www.fenics.org/ufc/.
- Alnæs, M. S.; Logg, A.; Mardal, K.-A.; Skavhaug, O.; Langtangen, H. P. Unified framework for finite element assembly. Int. J. Computat. Sci. Eng. 2009. Available online: http://simula.no/research/scientific/publications/Simula.SC.96/simula_pdf_file.
- Logg, A.; Wells, G. N.; others. DOLFIN 2009. Available online: http://www.fenics.org/dolfin.
- Babuška, I.; Melenk, J. M. The Partition of Unity Method. Int. J. Numer. Method. Eng. 1997, 40, 727–758. [Google Scholar] [CrossRef]
- Belytschko, T.; Black, T. Elastic crack growth in finite elements with minimal remeshing. Int. J. Numer. Method. Eng. 1999, 45, 601–620. [Google Scholar] [CrossRef]
- Wells, G. N.; Sluys, L. J. A new method for modelling cohesive cracks using finite elements. Int. J. Numer. Method. Eng. 2001, 50, 2667–2682. [Google Scholar] [CrossRef]
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Nikbakht, M.; Wells, G.N. Automated Modelling of Evolving Discontinuities. Algorithms 2009, 2, 1008-1030. https://doi.org/10.3390/a2031008
Nikbakht M, Wells GN. Automated Modelling of Evolving Discontinuities. Algorithms. 2009; 2(3):1008-1030. https://doi.org/10.3390/a2031008
Chicago/Turabian StyleNikbakht, Mehdi, and Garth N. Wells. 2009. "Automated Modelling of Evolving Discontinuities" Algorithms 2, no. 3: 1008-1030. https://doi.org/10.3390/a2031008
APA StyleNikbakht, M., & Wells, G. N. (2009). Automated Modelling of Evolving Discontinuities. Algorithms, 2(3), 1008-1030. https://doi.org/10.3390/a2031008



