A Heuristics-Guided Simplified Discrete Harmony Search Algorithm for Solving 0-1 Knapsack Problem
Abstract
1. Introduction
2. Preliminaries
2.1. Problem Formulation
2.2. The Harmony Search Algorithm
| Algorithm 1 The basic HS algorithm. |
| 1: Initialize the parameters of the HS algorithm 2: Initialize the harmonies (solutions) in harmony memory 3: while Stop condition is not met do 4: for each dimension j from 1 to n do 5: if rand() < hmcr then // Memory Consideration Operator 6: , where i is randomly selected from 1 to hms 7: if rand() < par then // Pitch Adjustment Operator 8: Adjust 9: end if 10: else // Random Search Operator 11: Randomly create a value for 12: end if 13: end for 14: Use to update harmony memory 15: end while |
2.3. Discrete HS Algorithms for the 0-1KP
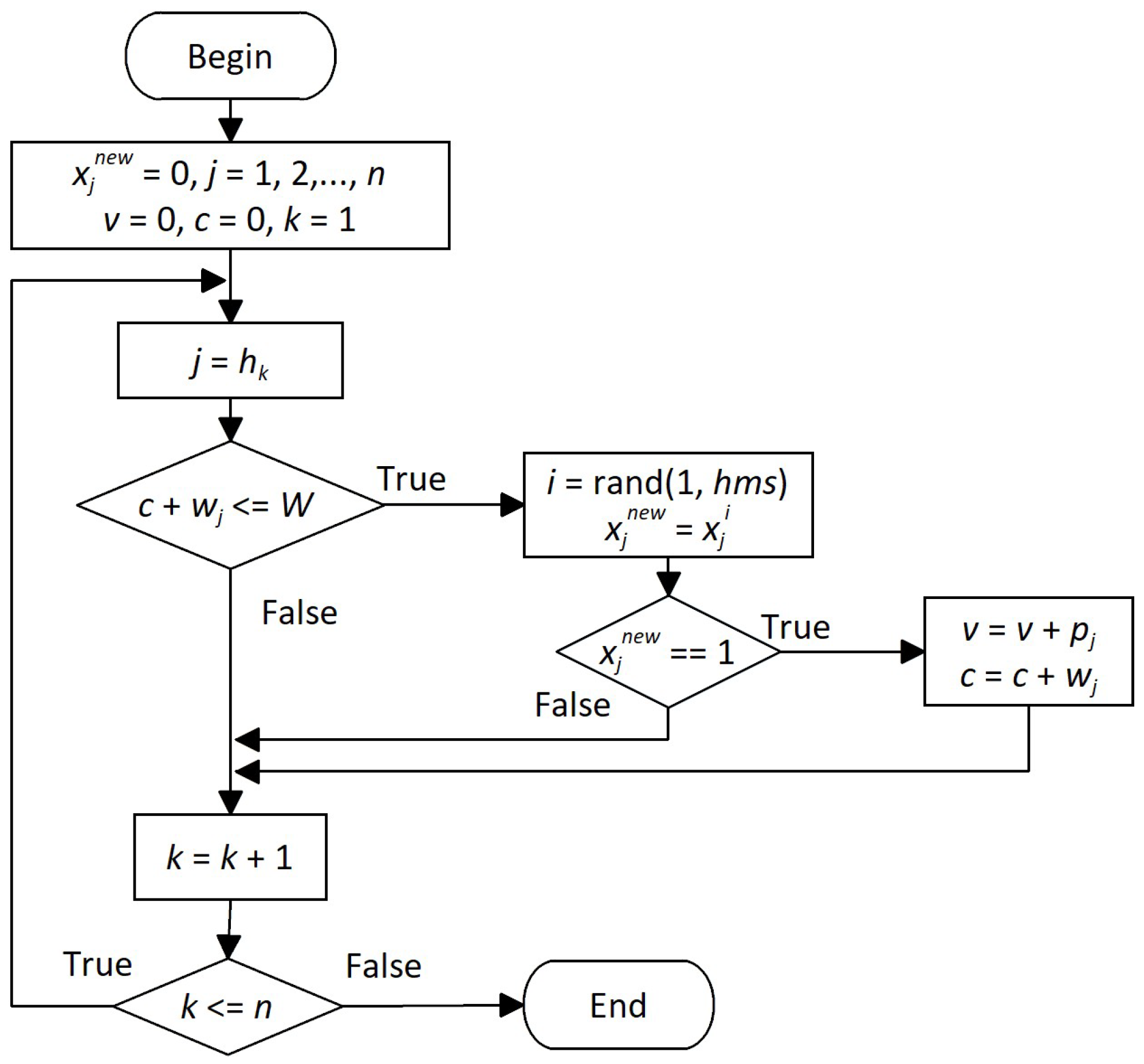
3. Simplified Discrete Harmony Search Algorithm for the 0-1KP
3.1. Discussions of the HS Algorithm
3.2. Description of the SDHS Algorithm
| Algorithm 2 Pseudo code of the SDHS algorithm for the 0-1KP. |
| Require: Ensure: best solution found; 1: Initialize every for the harmony memory, where 2: the best harmony in harmony memory 3: while do //Memory consideration 4: Call Algorithm 3 to construct a solution //Pitch adjustment 5: Call Algorithm 4 to enhance the solution //Update the harmony memory 6: if is better than the worst solution in the harmony memory then 7: Remove the worst solution in the harmony memory 8: Append into the harmony memory 9: end if 10: if is better than then 11: 12: end if 13: 14: end while 15: return |
3.3. Memory Consideration Operator
| Algorithm 3 The memory consideration operator. |
| 1: , for 2: 3: 4: for to n do 5: 6: if then 7: Randomly select a harmony from the harmony memory 8: 9: if then 10: 11: 12: end if 13: end if 14: end for |
3.4. Solution-Level Pitch Adjustment Operator
| Algorithm 4 Solution-level pitch adjustment operator. |
| Require: //A feasible solution 1: the sorted items in non-ascending order of profit 2: for to n do 3: 4: if and then 5: 6: 7: 8: end if 9: end for 10: return |
4. Behavior Analysis
4.1. Effect of Heuristics and Parameter on Performance
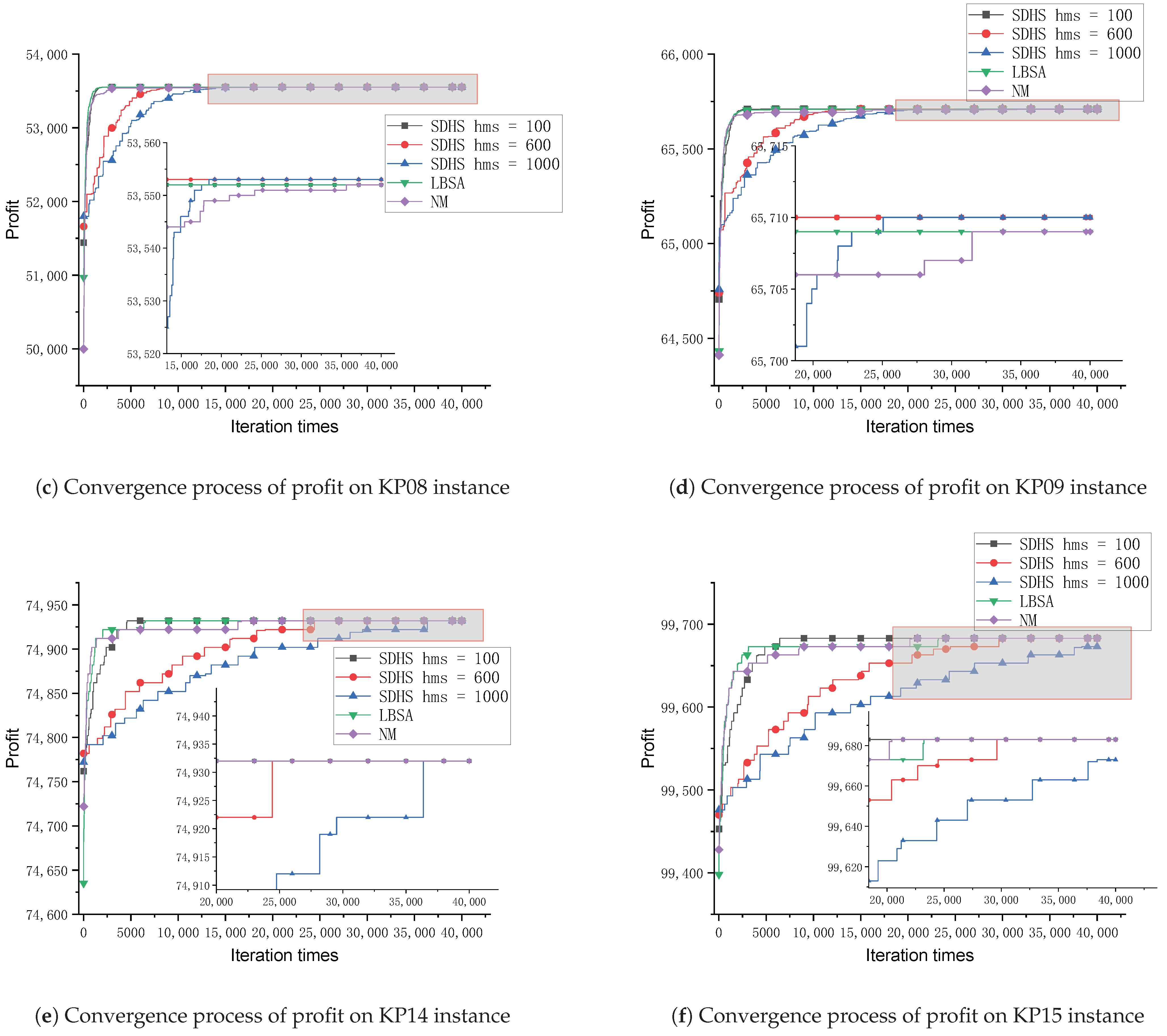
4.2. Effect of Parameter hms on the Convergence Process
4.3. Effect of Parameter hms on the Diversity
4.4. The Running Time of SDHS
5. Comparative Experiments
5.1. Experiment on the First Set of Large-Scale 0-1KP Instances
5.2. Experiment on the Second Set of Large-Scale 0-1KP Instances
5.3. Experiment on the Third Set of Large-Scale 0-1KP Instances
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Taillandier, F.; Fernandez, C.; Ndiaye, A. Real estate property maintenance optimization based on multiobjective multidimensional knapsack problem. Comput.-Aided Civ. Infrastruct. Eng. 2017, 32, 227–251. [Google Scholar] [CrossRef]
- Karaboghossian, T.; Zito, M. Easy knapsacks and the complexity of energy allocation problems in the smart grid. Optim. Lett. 2018, 12, 1553–1568. [Google Scholar] [CrossRef]
- Brandt, F.; Nickel, S. The air cargo load planning problem—A consolidated problem definition and literature review on related problems. Eur. J. Oper. Res. 2019, 275, 399–410. [Google Scholar] [CrossRef]
- Liu, J.; Bi, J.; Xu, S. An improved attack on the basic Merkle–Hellman Knapsack cryptosystem. IEEE Access 2019, 7, 59388–59393. [Google Scholar] [CrossRef]
- Yates, J.; Lakshmanan, K. A constrained binary knapsack approximation for shortest path network interdiction. Comput. Ind. Eng. 2011, 61, 981–992. [Google Scholar] [CrossRef]
- Tavana, M.; Keramatpour, M.; Santos-Arteaga, F.J.; Ghorbaniane, E. A fuzzy hybrid project portfolio selection method using data envelopment analysis, TOPSIS and integer programming. Expert Syst. Appl. 2015, 42, 8432–8444. [Google Scholar] [CrossRef]
- Wang, X.; He, Y. Evolutionary Algorithms for Knapsack Problems. J. Softw. 2017, 28, 1–16. [Google Scholar]
- Gherboudj, A.; Layeb, A.; Chikhi, S. Solving 0-1 knapsack problems by a discrete binary version of cuckoo search algorithm. Int. J. Bio-Inspired Comput. 2012, 4, 229–236. [Google Scholar] [CrossRef]
- Feng, Y.; Wang, G.G.; Gao, X.Z. A novel hybrid cuckoo search algorithm with global harmony search for 0-1 knapsack problems. Int. J. Comput. Intell. Syst. 2016, 9, 1174–1190. [Google Scholar] [CrossRef]
- Bhattacharjee, K.K.; Sarmah, S.P. Modified swarm intelligence based techniques for the knapsack problem. Appl. Intell. 2017, 46, 158–179. [Google Scholar] [CrossRef]
- Nguyen, P.H.; Wang, D.; Truong, T.K. A Novel Binary Social Spider Algorithm for 0-1 Knapsack Problem. Int. J. Innov. Comput. Inf. Control 2017, 13, 2039–2049. [Google Scholar]
- Kulkarni, A.J.; Shabir, H. Solving 0-1 knapsack problem using cohort intelligence algorithm. Int. J. Mach. Learn. Cybern. 2016, 7, 427–441. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, X.; Zhou, G. An improved monkey algorithm for a 0-1 knapsack problem. Appl. Soft Comput. 2016, 38, 817–830. [Google Scholar] [CrossRef]
- Wu, H.; Zhang, F.; Zhan, R.; Wang, S.; Zhang, C. A binary wolf pack algorithm for solving 0-1 knapsack problem. Syst. Eng. Electron. 2014, 36, 1660–1667. [Google Scholar]
- Yassien, E.; Masadeh, R.; Alzaqebah, A.; Shaheen, A. Grey Wolf Optimization Applied to the 0/1 Knapsack Problem. Int. J. Comput. Appl. 2017, 169, 11–15. [Google Scholar] [CrossRef]
- Gao, Y.; Zhang, F.; Zhao, Y.; Li, C. Quantum-Inspired Wolf Pack Algorithm to Solve the 0-1 Knapsack Problem. Math. Probl. Eng. 2018, 2018, 5327056. [Google Scholar] [CrossRef]
- Erdoğan, F.; Karakoyun, M.; Gülcü, Ş. An effective binary dynamic grey wolf optimization algorithm for the 0-1 knapsack problem. Multimed. Tools Appl. 2024. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, W. Quantum-inspired differential evolution with grey wolf optimizer for 0-1 knapsack problem. Mathematics 2021, 9, 1233. [Google Scholar] [CrossRef]
- Rizk-Allah, R.M.; Hassanien, A.E. New binary bat algorithm for solving 0-1 knapsack problem. Complex Intell. Syst. 2018, 4, 31–53. [Google Scholar] [CrossRef]
- Yampolskiy, R.V.; El-Barkouky, A. Wisdom of artificial crowds algorithm for solving NP-hard problems. Int. J. Bio-Inspired Comput. 2011, 3, 358–369. [Google Scholar] [CrossRef]
- Wu, H.; Zhou, Y.; Luo, Q. Hybrid symbiotic organisms search algorithm for solving 0-1 knapsack problem. Int. J. Bio-Inspired Comput. 2018, 12, 23–53. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Zhou, Y. An elite opposition-flower pollination algorithm for a 0-1 knapsack problem. Int. J. Bio-Inspired Comput. 2018, 11, 46–53. [Google Scholar] [CrossRef]
- Truong, T.K.; Li, K.; Xu, Y. Chemical reaction optimization with greedy strategy for the 0-1 knapsack problem. Appl. Soft Comput. 2013, 13, 1774–1780. [Google Scholar] [CrossRef]
- Truong, T.K.; Li, K.; Xu, Y.; Ouyang, A.; Nguyen, T.T. Solving 0-1 knapsack problem by artificial chemical reaction optimization algorithm with a greedy strategy. J. Intell. Fuzzy Syst. 2015, 28, 2179–2186. [Google Scholar] [CrossRef]
- Zhao, J.; Huang, T.; Pang, F.; Liu, Y. Genetic Algorithm Based on Greedy Strategy in the 0-1 Knapsack Problem. In Proceedings of the Third International Conference on Genetic and Evolutionary Computing, Guilin, China, 14–16 October 2009; pp. 105–107. [Google Scholar]
- Umbarkar, A.J.; Joshi, M.S. 0/1 knapsack problem using diversity based dual population genetic algorithm. Int. J. Intell. Syst. Appl. 2014, 6, 34–40. [Google Scholar] [CrossRef]
- Feng, Y.; Wang, G.G.; Deb, S.; Lu, M.; Zhao, X.J. Solving 0-1 knapsack problem by a novel binary monarch butterfly optimization. Neural Comput. Appl. 2017, 28, 1619–1634. [Google Scholar] [CrossRef]
- Feng, Y.; Wang, G.G.; Dong, J.; Wang, L. Opposition-based learning monarch butterfly optimization with Gaussian perturbation for large-scale 0-1 knapsack problem. Comput. Electr. Eng. 2018, 67, 454–468. [Google Scholar] [CrossRef]
- Feng, Y.; Yang, J.; Wu, C.; Lu, M.; Zhao, X.J. Solving 0-1 knapsack problems by chaotic monarch butterfly optimization algorithm with Gaussian mutation. Memetic Comput. 2018, 10, 135–150. [Google Scholar] [CrossRef]
- Bansal, J.C.; Deep, K. A Modified Binary Particle Swarm Optimization for Knapsack Problems. Appl. Math. Comput. 2012, 218, 11042–11061. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; El-Shahat, D.; Sangaiah, A.K. A modified nature inspired meta-heuristic whale optimization algorithm for solving 0-1 knapsack problem. Int. J. Mach. Learn. Cybern. 2019, 10, 495–514. [Google Scholar] [CrossRef]
- Bhattacharjee, K.K.; Sarmah, S.P. Shuffled frog leaping algorithm and its application to 0/1 knapsack problem. Appl. Soft Comput. 2014, 19, 252–263. [Google Scholar] [CrossRef]
- Zhang, J.; Jiang, W.; Zhao, K. An improved Shuffled frog-leaping algorithm to solving 0-1 knapsack problem. IEEE Access 2024, 12, 148155–148166. [Google Scholar] [CrossRef]
- Abdollahzadeh, B.; Barshandeh, S.; Javadi, H.; Epicoco, N. An enhanced binary slime mould algorithm for solving the 0-1 knapsack problem. Eng. Comput. 2022, 38, 3423–3444. [Google Scholar] [CrossRef]
- Shu, Z.; Ye, Z.; Zong, X.; Liu, S.; Zhang, D.; Wang, C.; Wang, M. A modified hybrid rice optimization algorithm for solving 0-1 knapsack problem. Appl. Intell. 2022, 52, 5751–5769. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Saber, S.; Hezam, I.M.; Sallam, K.M.; Hameed, I.A. Binary metaheuristic algorithms for 0-1 knapsack problems: Performance analysis, hybrid variants, and real-world application. J. King Saud Univ. Comput. Inf. Sci. 2024, 36, 102093. [Google Scholar] [CrossRef]
- Yildizdan, G.; Baş, E. A novel binary artificial jellyfish search algorithm for solving 0-1 knapsack problems. Neural Process. Lett. 2023, 55, 8605–8671. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Hezam, I.M.; Sallam, K.M.; Alshamrani, A.M.; Hameed, I.A. A novel binary Kepler optimization algorithm for 0-1 knapsack problems: Methods and applications. Alex. Eng. J. 2023, 82, 358–376. [Google Scholar] [CrossRef]
- Zou, D.; Gao, L.; Li, S.; Wu, J. Solving 0-1 knapsack problem by a novel global harmony search algorithm. Appl. Soft Comput. 2011, 11, 1556–1564. [Google Scholar] [CrossRef]
- Layeb, A. A hybrid quantum inspired harmony search algorithm for 0-1 optimization problems. J. Comput. Appl. Math. 2013, 253, 14–25. [Google Scholar] [CrossRef]
- Wang, L.; Yang, R.; Xu, Y.; Niu, Q.; Pardalos, P.M.; Fei, M. An improved adaptive binary Harmony Search algorithm. Inf. Sci. 2013, 232, 58–87. [Google Scholar] [CrossRef]
- Ouyang, H.B.; Gao, L.Q.; Kong, X.Y.; Liu, H.Z. A binary modified harmony search algorithm for 0-1 knapsack problem. Control Decis. 2014, 29, 1174–1180. [Google Scholar]
- Tuo, S.; Yong, L.; Deng, F.A. A novel harmony search algorithm based on teaching-learning strategies for 0-1 knapsack problems. Sci. World J. 2014, 2014, 637412. [Google Scholar] [CrossRef] [PubMed]
- Xiang, W.L.; An, M.Q.; Li, Y.Z.; He, R.C.; Zhang, J.F. A novel discrete global-best harmony search algorithm for solving 0-1 knapsack problems. Discret. Dyn. Nat. Soc. 2014, 2014, 573731. [Google Scholar] [CrossRef]
- Kong, X.; Gao, L.; Ouyang, H.; Li, S. A simplified binary harmony search algorithm for large scale 0-1 knapsack problems. Expert Syst. Appl. 2015, 42, 5337–5355. [Google Scholar] [CrossRef]
- Liu, K.; Ouyang, H.; Li, S.; Gao, L. A Hybrid Harmony Search Algorithm with Distribution Estimation for Solving the 0-1 Knapsack Problem. Math. Probl. Eng. 2022, 2022, 8440165. [Google Scholar] [CrossRef]
- Zhan, S.; Zhang, Z.; Wang, L.; Zhong, Y. List-Based Simulated Annealing Algorithm With Hybrid Greedy Repair and Optimization Operator for 0-1 Knapsack Problem. IEEE Access 2018, 6, 54447–54458. [Google Scholar] [CrossRef]
- Zhan, S.; Wang, L.; Zhang, Z.; Zhong, Y. Noising methods with hybrid greedy repair operator for 0-1 knapsack problem. Memetic Comput. 2020, 12, 37–50. [Google Scholar] [CrossRef]
- Wu, L.; Lin, K.; Lin, X.; Lin, J. List-based threshold accepting algorithm with improved neighbor operator for 0-1 knapsack problem. Algorithms 2024, 17, 478. [Google Scholar] [CrossRef]
- Feng, Y.; Jia, K.; He, Y. An improved hybrid encoding cuckoo search algorithm for 0-1 knapsack problems. Comput. Intell. Neurosci. 2014, 2014, 970456. [Google Scholar] [CrossRef]
- Feng, Y.; Wang, G.G.; Feng, Q.; Zhao, X.J. An effective hybrid cuckoo search algorithm with improved shuffled frog leaping algorithm for 0-1 knapsack problems. Comput. Intell. Neurosci. 2014, 2014, 857254. [Google Scholar] [CrossRef]
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. A New Heuristic Optimization Algorithm: Harmony Search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Zhang, T.; Geem, Z.W. Review of harmony search with respect to algorithm structure. Swarm Evol. Comput. 2019, 48, 31–43. [Google Scholar] [CrossRef]
- Ouyang, H.; Wu, W.; Zhang, C.L.; Li, S.; Zou, D.; Liu, G. Improved harmony search with general iteration models for engineering design optimization problems. Soft Comput. 2019, 23, 10225–10260. [Google Scholar] [CrossRef]
- Nazariheris, M.; Mohammadiivatloo, B.; Asadi, S.; Kim, J.; Geem, Z.W. Harmony search algorithm for energy system applications: An updated review and analysis. J. Exp. Theor. Artif. Intell. 2019, 31, 723–749. [Google Scholar] [CrossRef]
- Yi, J.; Gao, L.; Li, X.; Shoemaker, C.A.; Lu, C. An on-line variable-fidelity surrogate-assisted harmony search algorithm with mul-ti-level screening strategy for expensive engineering design optimization. Knowl. Based Syst. 2019, 170, 1–19. [Google Scholar] [CrossRef]
- Lenin, N.; Siva Kumar, M. Harmony search algorithm for simultaneous minimization of bi-objectives in multi-row parallel machine layout problem. Evol. Intell. 2021, 14, 1495–1522. [Google Scholar] [CrossRef]
- Luo, K. A sequence learning harmony search algorithm for the flexible process planning problem. Int. J. Prod. Res. 2022, 60, 3182–3200. [Google Scholar] [CrossRef]
- Gong, J.; Zhang, Z.; Liu, J.; Guan, C.; Liu, S. Hybrid algorithm of harmony search for dynamic parallel row ordering problem. J. Manuf. Syst. 2021, 58, 159–175. [Google Scholar] [CrossRef]
- Geem, Z.W.; Sim, K. Parameter-setting-free harmony search algorithm. Appl. Math. Comput. 2010, 217, 3881–3889. [Google Scholar] [CrossRef]
- Luo, K.; Ma, J.; Zhao, Q. Enhanced self-adaptive global-best harmony search without any extra statistic and external archive. Inf. Sci. 2019, 482, 228–247. [Google Scholar] [CrossRef]
- Pisinger, D. Where are the hard knapsack problems? Comput. Oper. Res. 2005, 32, 2271–2284. [Google Scholar] [CrossRef]





| Operator | Algorithm | Time Complexity | Parameters | Num Params |
|---|---|---|---|---|
| Initialization | HS | O() | Size of the harmony memory () | 1 |
| SDHS | O() | Size of the harmony memory () | 1 | |
| Memory Consideration | HS | O(n) | Harmony Memory Consideration Rate () | 1 |
| SDHS | O(n) | None | 0 | |
| Pitch Adjustment | HS | O(n) | Pitch Adjustment Rate (), Bandwidth () | 2 |
| SDHS | O(n) | None | 0 | |
| Random Selection | HS | O(n) | None | 0 |
| SDHS | None | None | 0 | |
| Update Harmony Memory | HS | O() | None | 0 |
| SDHS | O() | None | 0 | |
| Overall per iteration | HS | O() | ||
| SDHS | O() |
| Correlation | Weight | Value | Capacity W |
|---|---|---|---|
| Uncorrelated | rand (10, 100) | rand (10, 100) | 0.75 × sum of weights |
| Weakly correlated | rand (10, 100) | rand (, ) | 0.75 × sum of weights |
| Strongly correlated | rand (10, 100) | 0.75 × sum of weights |
| hms | KP01 | KP04 | ||||
|---|---|---|---|---|---|---|
| SDHS | SDHS1 | SDHS2 | SDHS | SDHS1 | SDHS2 | |
| 100 | 0.335 | 54.28 | 0.72 | 0.23 | 72.95 | 0.13 |
| 200 | 0.065 | 44.64 | 0.31 | 0.02 | 60.09 | 0.025 |
| 300 | 0.01 | 40.395 | 0.245 | 0 | 53.58 | 0 |
| 400 | 0.005 | 38.29 | 0.145 | 0 | 48.3 | 0 |
| 500 | 0 | 36.015 | 0.135 | 0 | 47.19 | 0 |
| 600 | 0 | 34.775 | 0.04 | 0 | 49.395 | 0 |
| 700 | 0 | 33.785 | 0.05 | 0 | 58.07 | 0 |
| 800 | 0 | 36.195 | 0.05 | 0 | 71.645 | 0 |
| 900 | 0 | 40.72 | 0.035 | 0 | 85.055 | 0 |
| 1000 | 0 | 47.105 | 0.02 | 0 | 94.865 | 0 |
| 1100 | 0 | 53.61 | 0.02 | 0 | 101.725 | 0 |
| 1200 | 0 | 61.65 | 0.005 | 0 | 109.82 | 0 |
| 1300 | 0 | 68.865 | 0.015 | 0 | 118.995 | 0 |
| 1400 | 0 | 75.695 | 0.01 | 0 | 127.94 | 0 |
| 1500 | 0 | 81.925 | 0.005 | 0 | 137.22 | 0 |
| 1600 | 0 | 87.77 | 0.005 | 0 | 148.42 | 0 |
| 1700 | 0 | 93.475 | 0 | 0 | 158.79 | 0 |
| 1800 | 0 | 99.535 | 0 | 0 | 172.145 | 0 |
| 1900 | 0 | 105.115 | 0 | 0 | 186.245 | 0 |
| 2000 | 0 | 111.095 | 0 | 0 | 199.61 | 0 |
| Average | 0.021 | 62.247 | 0.091 | 0.013 | 105.103 | 0.008 |
| hms | KP08 | KP09 | ||||
|---|---|---|---|---|---|---|
| SDHS | SDHS1 | SDHS2 | SDHS | SDHS1 | SDHS2 | |
| 100 | 0.18 | 45.335 | 0.26 | 0.385 | 144.19 | 0.28 |
| 200 | 0.01 | 36.445 | 0.035 | 0.155 | 132.495 | 0.045 |
| 300 | 0 | 32.74 | 0.01 | 0.07 | 130.785 | 0.01 |
| 400 | 0 | 29.99 | 0 | 0.01 | 131.775 | 0 |
| 500 | 0 | 28.76 | 0.005 | 0 | 133.07 | 0 |
| 600 | 0 | 29.47 | 0 | 0 | 138.56 | 0 |
| 700 | 0 | 34.585 | 0 | 0 | 146.825 | 0 |
| 800 | 0 | 44.16 | 0 | 0 | 157.915 | 0 |
| 900 | 0 | 55.18 | 0 | 0 | 169.455 | 0 |
| 1000 | 0 | 65.18 | 0 | 0 | 182.29 | 0 |
| 1100 | 0 | 72.32 | 0 | 0 | 195.82 | 0 |
| 1200 | 0 | 79.75 | 0 | 0 | 209.89 | 0 |
| 1300 | 0 | 85.14 | 0 | 0.005 | 226.31 | 0 |
| 1400 | 0 | 91.58 | 0 | 0.02 | 242.24 | 0 |
| 1500 | 0 | 98.17 | 0 | 0.425 | 259.445 | 0 |
| 1600 | 0 | 105.375 | 0 | 0.905 | 276.425 | 0 |
| 1700 | 0 | 114.675 | 0 | 1.285 | 295.605 | 0 |
| 1800 | 0 | 126.37 | 0 | 2.55 | 313.225 | 0 |
| 1900 | 0 | 138.885 | 0 | 4.265 | 331.26 | 0 |
| 2000 | 0 | 153.075 | 0 | 6.78 | 348.215 | 0 |
| Average | 0.010 | 73.359 | 0.016 | 0.843 | 208.290 | 0.017 |
| hms | KP14 | KP15 | ||||
|---|---|---|---|---|---|---|
| SDHS | SDHS1 | SDHS2 | SDHS | SDHS1 | SDHS2 | |
| 100 | 0 | 72.59 | 0.46 | 0 | 106.425 | 8.285 |
| 200 | 0 | 85.455 | 0.01 | 0 | 121.04 | 3.37 |
| 300 | 0 | 95.335 | 0.005 | 0 | 134.045 | 2.035 |
| 400 | 0 | 103.92 | 0 | 0 | 147.27 | 1.365 |
| 500 | 0 | 110.86 | 0 | 0 | 155.245 | 1.115 |
| 600 | 0 | 117.69 | 0 | 0 | 162.93 | 1.035 |
| 700 | 0 | 121.46 | 0 | 0 | 169.12 | 0.995 |
| 800 | 0 | 125.785 | 0 | 2.015 | 173.815 | 0.78 |
| 900 | 0 | 128.85 | 0 | 9.85 | 177.06 | 1.22 |
| 1000 | 1.095 | 130.995 | 0 | 10.015 | 180.01 | 2.56 |
| 1100 | 8.745 | 134.57 | 0 | 17.455 | 182.77 | 5.565 |
| 1200 | 9.955 | 136.355 | 0.01 | 20.03 | 184.91 | 9.9 |
| 1300 | 10.665 | 137.585 | 0.03 | 25.835 | 186.475 | 10 |
| 1400 | 16.435 | 137.82 | 0.11 | 29.675 | 187.975 | 10 |
| 1500 | 19.11 | 139.77 | 1.14 | 34.565 | 188.55 | 10 |
| 1600 | 20.47 | 139.21 | 6.765 | 39.56 | 190.01 | 10.325 |
| 1700 | 24.65 | 140.48 | 9.225 | 42.86 | 189.42 | 13.81 |
| 1800 | 28.39 | 140.915 | 9.975 | 48.145 | 190.145 | 17.88 |
| 1900 | 29.91 | 141.395 | 10 | 50.53 | 189.98 | 19.53 |
| 2000 | 33.585 | 142.14 | 10.005 | 55.785 | 190.21 | 19.775 |
| Average | 10.151 | 124.159 | 2.387 | 19.316 | 170.370 | 7.477 |
| Type | R = 100 | R = 1000 | R = 10,000 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| > | = | < | p | > | = | < | p | > | = | < | p | |
| UC | 14 | 94 | 2 | 1.5 × 10−3 | 48 | 38 | 24 | 1.3 × 10−2 | 60 | 30 | 20 | 2.8 × 10−6 |
| WC | 1 | 109 | 0 | 1.0 | 32 | 33 | 45 | 6.6 × 10−1 | 53 | 9 | 48 | 4.1 × 10−1 |
| SC | 66 | 44 | 0 | 1.7 × 10−12 | 78 | 32 | 0 | 1.7 × 10−14 | 101 | 9 | 0 | 2.7 × 10−18 |
| MSC | 61 | 49 | 0 | 1.1 × 10−11 | 72 | 38 | 0 | 1.7 × 10−13 | 85 | 25 | 0 | 1.2 × 10−15 |
| PC | 0 | 110 | 0 | - | 0 | 110 | 0 | - | 8 | 69 | 33 | 5.0 × 10−4 |
| CI | 105 | 0 | 5 | 3.6 × 10−19 | 110 | 0 | 0 | 8.9 × 10−20 | 110 | 0 | 0 | 8.9 × 10−20 |
| 0-1KP Instances | Data Set Classification | Item Number | Algorithms |
|---|---|---|---|
| The first instance set | 16 uncorrelated instances | 500–6400 | NGHS [39], ABHS [41], SBHS [45] |
| The second instance set | 5 uncorrelated instances | 800–2000 | CSGHS [9], BMBO [27], |
| 5 weakly correlated instances | 800–2000 | CMBO [29], OMBO [28], | |
| 5 strongly correlated instances | 800–2000 | NM [48], LBSA [47] | |
| The third instance set | 5 weakly correlated instances | 200–1000 | CGMA [13], MBPSO [30], |
| 5 strongly correlated instances | 200–1000 | DGHS [44], HSOSHS [21] | |
| 5 multiple strongly correlated instances | 300–1200 | ||
| 5 profit ceiling instances | 300–1200 | ||
| 4 uncorrelated instances | 3000–10,000 |
| Method | Ins | Best | Worst | Mean | Time (s) | Ins | Best | Worst | Mean | Time (s) |
|---|---|---|---|---|---|---|---|---|---|---|
| NGHS | LKP01 | 61.82 | 61.11 | 61.5 | - | LKP09 | 1133.44 | 1125.69 | 1129.02 | - |
| ABHS | 62.01 | 61.71 | 61.9 | - | 1140.69 | 1133.22 | 1136.57 | - | ||
| SBHS | 62.08 | 61.97 | 62.04 | - | 1155.65 | 1155.35 | 1155.57 | - | ||
| SDHS | 62.08 | 62.08 | 62.08 | 0.02 | 1155.68 | 1155.68 | 1155.68 | 1.04 | ||
| NGHS | LKP02 | 128.34 | 126.87 | 127.66 | - | LKP10 | 1257.45 | 1249.74 | 1252.86 | - |
| ABHS | 129.31 | 128.51 | 128.94 | - | 1263.67 | 1257.85 | 1260.46 | - | ||
| SBHS | 129.44 | 129.27 | 129.37 | - | 1283.92 | 1283.26 | 1283.79 | - | ||
| SDHS | 129.44 | 129.44 | 129.44 | 0.04 | 1283.92 | 1283.92 | 1283.92 | 1.16 | ||
| NGHS | LKP03 | 190.18 | 187.9 | 189.23 | - | LKP11 | 1615.64 | 1604.28 | 1610.5 | - |
| ABHS | 191.49 | 190.32 | 191.04 | - | 1623.3 | 1613.54 | 1618.77 | - | ||
| SBHS | 192.02 | 191.85 | 192.01 | - | 1653.72 | 1653.43 | 1653.64 | - | ||
| SDHS | 192.02 | 192.02 | 192.02 | 0.07 | 1653.76 | 1653.76 | 1653.76 | 1.64 | ||
| NGHS | LKP04 | 310.16 | 305.67 | 308.33 | - | LKP12 | 1877.6 | 1868.31 | 1872.43 | - |
| ABHS | 312.51 | 310.67 | 311.79 | - | 1879.12 | 1868.61 | 1874.04 | - | ||
| SBHS | 314.23 | 314.1 | 314.19 | - | 1917.49 | 1917.23 | 1917.42 | - | ||
| SDHS | 314.23 | 314.23 | 314.23 | 0.12 | 1917.58 | 1917.57 | 1917.57 | 1.96 | ||
| NGHS | LKP05 | 442.32 | 436.45 | 440.83 | - | LKP13 | 2200.57 | 2191.68 | 2196.15 | - |
| ABHS | 446.3 | 444.42 | 445.43 | - | 2203.56 | 2193.78 | 2199.31 | - | ||
| SBHS | 448.65 | 448.46 | 448.6 | - | 2248.27 | 2247.77 | 2248.12 | - | ||
| SDHS | 448.65 | 448.65 | 448.65 | 0.27 | 2248.30 | 2248.30 | 2248.30 | 2.42 | ||
| NGHS | LKP06 | 626.77 | 619.15 | 623.87 | - | LKP14 | 3061.12 | 3047.8 | 3054.33 | - |
| ABHS | 632.38 | 628.65 | 630.34 | - | 3055.47 | 3040.32 | 3046.91 | - | ||
| SBHS | 638.14 | 638 | 638.09 | - | 3135.71 | 3135.29 | 3135.58 | - | ||
| SDHS | 638.14 | 638.14 | 638.14 | 0.45 | 3135.77 | 3135.77 | 3135.77 | 3.83 | ||
| NGHS | LKP07 | 750.67 | 745.05 | 747.66 | - | LKP15 | 3625.86 | 3609.96 | 3617.04 | - |
| ABHS | 756.08 | 752.10 | 754.26 | - | 3615.85 | 3601.58 | 3607.61 | - | ||
| SBHS | 763.81 | 763.39 | 763.71 | - | 3707.39 | 3706.98 | 3707.29 | - | ||
| SDHS | 763.83 | 763.83 | 763.83 | 0.68 | 3707.45 | 3707.44 | 3707.44 | 4.99 | ||
| NGHS | LKP08 | 945.20 | 938.31 | 941.97 | - | LKP16 | 4009.33 | 3995.04 | 4003.40 | - |
| ABHS | 950.70 | 947.36 | 949.17 | - | 4009.08 | 3993.47 | 4001.41 | - | ||
| SBHS | 964.91 | 964.70 | 964.85 | - | 4090.83 | 4090.36 | 4090.64 | - | ||
| SDHS | 964.92 | 964.91 | 964.92 | 0.97 | 4090.87 | 4090.86 | 4090.87 | 5.64 |
| Algorithm | Rank | Gap (%) | p-Value | p-Holm | Sum of |
|---|---|---|---|---|---|
| SDHS | 1 | - | - | - | - |
| NGHS | 3.81 | 2.128 | 0/0/16 | ||
| ABHS | 3.19 | 1.565 | 0/0/16 | ||
| SBHS | 2 | 0.015 | 0.126 | 0.126 | 0/0/16 |
| Ins | Opt | Method | Best | Worst | Mean | Median | Std | Time (s) |
|---|---|---|---|---|---|---|---|---|
| KP01 | 40,686 | CSGHS | 40,342 | 40,056 | 40,182 | 40,190 | 68.87 | - |
| BMBO | 40,232 | 39,765 | 40,035 | 40,036 | 105.8 | - | ||
| CMBO | 40,686 | 40,683 | 40,683 | 40,683 | 0.71 | - | ||
| OMBO | 40,686 | 40,683 | 40,684 | 40,683 | 0.86 | - | ||
| NM | 40,685 | 40,684 | 40,684.88 | 40,685 | 0.22 | - | ||
| LBSA | 40,686 | 40,684 | 40,684.9 | 40,685 | 0.18 | - | ||
| SDHS | 40,686 | 40,686 | 40,686 | 40,686 | 0 | 0.38 | ||
| KP02 | 50,592 | CSGHS | 50,027 | 49,717 | 49,846 | 49,835 | 84.36 | - |
| BMBO | 50,024 | 49,336 | 49,699 | 49,689 | 135.3 | - | ||
| CMBO | 50,592 | 50,590 | 50,590 | 50,590 | 0.49 | - | ||
| OMBO | 50,592 | 50,590 | 50,590 | 50,590 | 0.70 | - | ||
| NM | 50,592 | 50,592 | 50,592 | 50,592 | 0 | - | ||
| LBSA | 50,592 | 50,591 | 50,591.98 | 50,592 | 0.04 | - | ||
| SDHS | 50,592 | 50,592 | 50,592 | 50,592 | 0 | 0.55 | ||
| KP03 | 61,846 | CSGHS | 60,951 | 60,616 | 60,788 | 60,791 | 79.79 | - |
| BMBO | 61,109 | 60,214 | 60,677 | 60,660 | 165.8 | - | ||
| CMBO | 61,845 | 61,840 | 61,841 | 61,840 | 1.38 | - | ||
| OMBO | 61,845 | 61,840 | 61,842 | 61,843 | 1.82 | - | ||
| NM | 61,846 | 61,845 | 61,845.32 | 61,845 | 0.44 | - | ||
| LBSA | 61,846 | 61,845 | 61,845.27 | 61,845 | 0.40 | - | ||
| SDHS | 61,846 | 61,846 | 61,846 | 61,846 | 0 | 0.79 | ||
| KP04 | 77,033 | CSGHS | 75,889 | 75,452 | 75,639 | 75,631 | 112.3 | - |
| BMBO | 75,761 | 75,062 | 75,464 | 75,482 | 193.3 | - | ||
| CMBO | 77,033 | 77,031 | 77,031 | 77,031 | 0.31 | - | ||
| OMBO | 77,033 | 77,031 | 77,031 | 77,031 | 0.56 | - | ||
| NM | 77,033 | 77,032 | 77,032.92 | 77,033 | 0.15 | - | ||
| LBSA | 77,033 | 77,032 | 77,032.76 | 77,033 | 0.37 | - | ||
| SDHS | 77,033 | 77,033 | 77,033 | 77,033 | 0 | 0.9 | ||
| KP05 | 102,316 | CSGHS | - | - | - | - | - | - |
| BMBO | - | - | - | - | - | - | ||
| CMBO | 102,316 | 102,313 | 102,314 | 102,313 | 0.93 | - | ||
| OMBO | 102,316 | 102,313 | 102,314 | 102,313 | 1.11 | - | ||
| NM | 102,316 | 102,316 | 102,316 | 102,316 | 0 | - | ||
| LBSA | 102,316 | 102,315 | 102,315.9 | 102,316 | 0.20 | - | ||
| SDHS | 102,316 | 102,316 | 102,316 | 102,316 | 0 | 1.15 |
| Ins | Opt | Method | Best | Worst | Mean | Median | Std | Time (s) |
|---|---|---|---|---|---|---|---|---|
| KP06 | 35,069 | CSGHS | 34,850 | 34,795 | 34,824 | 34,825 | 14.00 | - |
| BMBO | 34,860 | 34,681 | 34,786 | 34,784 | 35.01 | - | ||
| CMBO | 35,069 | 35,064 | 35,067 | 35,067 | 1.45 | - | ||
| OMBO | 35,069 | 35,064 | 35,067 | 35,068 | 1.47 | - | ||
| NM | 35,069 | 35,069 | 35,069 | 35,069 | 0 | - | ||
| LBSA | 35,069 | 35,068 | 35,068.99 | 35,069 | 0.02 | - | ||
| SDHS | 35,069 | 35,069 | 35,069 | 35,069 | 0 | 0.38 | ||
| KP07 | 43,786 | CSGHS | 43,484 | 43,386 | 43,440 | 43,442 | 22.39 | - |
| BMBO | 43,491 | 43,359 | 43,412 | 43,413 | 31.36 | - | ||
| CMBO | 43,786 | 43,781 | 43,784 | 43,784 | 1.34 | - | ||
| OMBO | 43,786 | 43,782 | 43,785 | 43,785 | 1.03 | - | ||
| NM | 43,786 | 43,785 | 43,785.96 | 43,786 | 0.08 | - | ||
| LBSA | 43,786 | 43,785 | 43,785.97 | 43,786 | 0.06 | - | ||
| SDHS | 43,786 | 43,786 | 43,786 | 43,786 | 0 | 0.63 | ||
| KP08 | 53,553 | CSGHS | 52,711 | 52,354 | 52,556 | 52,565 | 76.89 | - |
| BMBO | 52,774 | 52,110 | 52,425 | 52,390 | 158.2 | - | ||
| CMBO | 53,552 | 53,552 | 53,552 | 53,552 | 0 | - | ||
| OMBO | 53,553 | 53,552 | 53,552 | 53,552 | 1.82 | - | ||
| NM | 53,553 | 53,552 | 53,552.02 | 53,552 | 0.04 | - | ||
| LBSA | 53,553 | 53,552 | 53,552.03 | 53,552 | 0.06 | - | ||
| SDHS | 53,553 | 53,553 | 53,553 | 53,553 | 0 | 0.69 | ||
| KP09 | 65,710 | CSGHS | 65,116 | 64,980 | 65,045 | 65,044 | 38.14 | - |
| BMBO | 65,123 | 64,916 | 65,022 | 65,012 | 56.38 | - | ||
| CMBO | 65,710 | 65,708 | 65,709 | 65,708 | 0.58 | - | ||
| OMBO | 65,710 | 65,708 | 65,709 | 65,709 | 0.52 | - | ||
| NM | 65,709 | 65,709 | 65,709 | 65,709 | 0 | - | ||
| LBSA | 65,709 | 65,709 | 65,709 | 65,709 | 0 | - | ||
| SDHS | 65,710 | 65,710 | 65,710 | 65,710 | 0 | 0.76 | ||
| KP10 | 108,200 | CSGHS | - | - | - | - | - | - |
| BMBO | - | - | - | - | - | - | ||
| CMBO | 108,200 | 108,200 | 108,200 | 108,200 | 0 | - | ||
| OMBO | 108,200 | 108,200 | 108,200 | 108,200 | 0 | - | ||
| NM | 108,200 | 108,200 | 108,200 | 108,200 | 0 | - | ||
| LBSA | 108,200 | 108,200 | 108,200 | 108,200 | 0 | - | ||
| SDHS | 108,200 | 108,200 | 108,200 | 108,200 | 0 | 1.14 |
| Ins | Opt | Method | Best | Worst | Mean | Median | Std | Time (s) |
|---|---|---|---|---|---|---|---|---|
| KP11 | 40,167 | CSGHS | 40,147 | 40,126 | 40,132 | 40,130 | 5.54 | - |
| BMBO | 40,127 | 40,107 | 40,116 | 40,117 | 4.52 | - | ||
| CMBO | 40,167 | 40,166 | 40,167 | 40,167 | 0.14 | - | ||
| OMBO | 40,167 | 40,167 | 40,167 | 40,167 | 0 | - | ||
| NM | 40,167 | 40,167 | 40,167 | 40,167 | 0 | - | ||
| LBSA | 40,167 | 40,167 | 40,167 | 40,167 | 0 | - | ||
| SDHS | 40,167 | 40,167 | 40,167 | 40,167 | 0 | 0.65 | ||
| KP12 | 49,443 | CSGHS | 49,403 | 49,383 | 49,393 | 49,393 | 6.52 | - |
| BMBO | 49,393 | 49,353 | 49,378 | 49,382 | 10.12 | - | ||
| CMBO | 49,433 | 49,433 | 49,422 | 49,433 | 2.49 | - | ||
| OMBO | 49,443 | 49,441 | 49,443 | 49,443 | 0.34 | - | ||
| NM | 49,443 | 49,443 | 49,443 | 49,443 | 0 | - | ||
| LBSA | 49,443 | 49,443 | 49,443 | 49,443 | 0 | - | ||
| SDHS | 49,443 | 49,443 | 49,443 | 49,443 | 0 | 0.85 | ||
| KP13 | 60,640 | CSGHS | 60,587 | 60,567 | 60,573 | 60,570 | 5.32 | - |
| BMBO | 60,588 | 60,530 | 60,562 | 60,560 | 11.98 | - | ||
| CMBO | 60,640 | 60,639 | 60,640 | 60,640 | 0.14 | - | ||
| OMBO | 60,640 | 60,640 | 60,640 | 60,640 | 0 | - | ||
| NM | 60,640 | 60,640 | 60,640 | 60,640 | 0 | - | ||
| LBSA | 60,640 | 60,640 | 60,640 | 60,640 | 0 | - | ||
| SDHS | 60,640 | 60,640 | 60,640 | 60,640 | 0 | 0.74 | ||
| KP14 | 74,932 | CSGHS | 74,858 | 74,817 | 74,835 | 74,832 | 9.31 | - |
| BMBO | 74,842 | 74,772 | 74,818 | 74,821 | 15.80 | - | ||
| CMBO | 74,932 | 74,931 | 74,932 | 74,932 | 0.27 | - | ||
| OMBO | 74,932 | 74,931 | 74,932 | 74,932 | 0.14 | - | ||
| NM | 74,932 | 74,932 | 74,932 | 74,932 | 0 | - | ||
| LBSA | 74,932 | 74,932 | 74,932 | 74,932 | 0 | - | ||
| SDHS | 74,932 | 74,932 | 74,932 | 74,932 | 0 | 0.88 | ||
| KP15 | 99,683 | CSGHS | - | - | - | - | - | - |
| BMBO | - | - | - | - | - | - | ||
| CMBO | 99,683 | 99,672 | 99,682 | 99,683 | 2.23 | - | ||
| OMBO | 99,683 | 99,679 | 99,683 | 99,683 | 0.58 | - | ||
| NM | 99,683 | 99,683 | 99,683 | 99,683 | 0 | - | ||
| LBSA | 99,683 | 99,683 | 99,683 | 99,683 | 0 | - | ||
| SDHS | 99,683 | 99,683 | 99,683 | 99,683 | 0 | 1.25 |
| Algorithm | Rank | Gap (%) | p-Value | p-Holm | Sum of |
|---|---|---|---|---|---|
| SDHS | 1.71 | - | - | - | - |
| CSGHS | 7 | 0.932 | 0/0/12 | ||
| BMBO | 6 | 1.071 | 0/0/12 | ||
| CMBO | 4.21 | 0.005 | 0.069 | 0.275 | 0/3/9 |
| OMBO | 3.75 | 0.002 | 0.237 | 0.71 | 0/4/8 |
| NM | 2.58 | 0.0005 | 0.956 | 1 | 0/7/5 |
| LBSA | 2.75 | 0.0005 | 0.901 | 1 | 0/7/5 |
| Dim | Opt | Method | Best | Worst | Mean | Median | Std | Time (s) |
|---|---|---|---|---|---|---|---|---|
| 200 | 8714 | CGMA | 8714 | 8710 | 8713.00 | 8714 | 1.2318 | - |
| MBPSO | 8699 | 8685 | 8692.13 | 8692 | 3.2772 | - | ||
| DGHS | 8672 | 8642 | 8652.80 | 8651 | 6.3702 | - | ||
| HSOSHS | 8714 | 8710 | 8711.47 | 8711 | 1.1366 | - | ||
| SDHS | 8714 | 8714 | 8714 | 8714 | 0 | 0.06 | ||
| 300 | 12,632 | CGMA | 12,632 | 12,626 | 12,629.50 | 12,629 | 1.5702 | - |
| MBPSO | 12,588 | 12,570 | 12,577.27 | 12,576 | 4.6382 | - | ||
| DGHS | 12,532 | 12,502 | 12,516.13 | 12,516.5 | 8.4598 | - | ||
| HSOSHS | 12,632 | 12,626 | 12,629.97 | 12,630 | 1.4735 | - | ||
| SDHS | 12,632 | 12,632 | 12,632 | 12,632 | 0 | 0.08 | ||
| 500 | 22,147 | CGMA | 22,141 | 22,128 | 22,135.40 | 22,136 | 3.5292 | - |
| MBPSO | 22,053 | 22,010 | 22,025.57 | 22,024.5 | 10.2071 | - | ||
| DGHS | 21,965 | 21,917 | 21,934.33 | 21,930.5 | 12.1324 | - | ||
| HSOSHS | 22,147 | 22,131 | 22,141.47 | 22,142 | 3.7207 | - | ||
| SDHS | 22,148 | 22,148 | 22,148 | 22,148 | 0 | 0.14 | ||
| 800 | 35,749 | CGMA | 35,734 | 35,695 | 35,717.03 | 35,719 | 9.9186 | - |
| MBPSO | 35,564 | 35,499 | 35,516.83 | 35,512.5 | 15.7854 | - | ||
| DGHS | 35,469 | 35,368 | 35,394.27 | 35,391 | 20.2006 | - | ||
| HSOSHS | 35,749 | 35,730 | 35,739.23 | 35,740 | 5.7095 | - | ||
| SDHS | 35,762 | 35,762 | 35,762 | 35,762 | 0 | 0.26 | ||
| 1000 | 44,063 | CGMA | 44,042 | 43,996 | 44,018.03 | 44,015.5 | 11.3820 | - |
| MBPSO | 43,788 | 43,713 | 43,741.30 | 43,740 | 15.7045 | - | ||
| DGHS | 43,626 | 43,571 | 43,598.87 | 43,598.5 | 15.4334 | - | ||
| HSOSHS | 44,063 | 44,024 | 44,047.87 | 44,047.5 | 7.9816 | - | ||
| SDHS | 44,092 | 44,092 | 44,092 | 44,092 | 0 | 0.36 |
| Dim | Opt | Method | Best | Worst | Mean | Median | Std | Time (s) |
|---|---|---|---|---|---|---|---|---|
| 200 | 9775 | CGMA | 9775 | 9775 | 9775 | 9775 | 0 | - |
| MBPSO | 9775 | 9775 | 9775 | 9775 | 0 | - | ||
| DGHS | 9775 | 9766 | 9772.77 | 9773 | 2.5955 | - | ||
| HSOSHS | 9775 | 9775 | 9775 | 9775 | 0 | - | ||
| SDHS | 9775 | 9775 | 9775 | 9775 | 0 | 0.07 | ||
| 300 | 14,760 | CGMA | 14,760 | 14,750 | 14,751.00 | 14,750 | 3.0513 | - |
| MBPSO | 14,760 | 14,750 | 14,751.77 | 14,750 | 3.2872 | - | ||
| DGHS | 14,750 | 14,738 | 14,743.00 | 14,740 | 4.1936 | - | ||
| HSOSHS | 14,760 | 14,750 | 14,759.33 | 14,760 | 2.5371 | - | ||
| SDHS | 14,760 | 14,760 | 14,760 | 14,760 | 0 | 0.1 | ||
| 500 | 25,597 | CGMA | 25,587 | 25,577 | 25,578.33 | 25,577 | 3.4575 | - |
| MBPSO | 25,587 | 25,577 | 25,578.57 | 25,577 | 3.2872 | - | ||
| DGHS | 25,567 | 25,554 | 25,561.40 | 25,563 | 4.4613 | - | ||
| HSOSHS | 25,597 | 25,587 | 25,590.67 | 25,587 | 4.9013 | - | ||
| SDHS | 25,597 | 25,597 | 25,597 | 25,597 | 0 | 0.19 | ||
| 800 | 39,940 | CGMA | 39,920 | 39,910 | 39,914.33 | 39,910 | 5.0401 | - |
| MBPSO | 39,920 | 39,900 | 39,904.17 | 39,901 | 5.0860 | - | ||
| DGHS | 39,894 | 39,867 | 39,877.20 | 39,877.5 | 5.8804 | - | ||
| HSOSHS | 39,940 | 39,930 | 39,931.33 | 39,930 | 3.4575 | - | ||
| SDHS | 39,940 | 39,940 | 39,940 | 39,940 | 0 | 0.28 | ||
| 1000 | 48,763 | CGMA | 48,743 | 48,713 | 48,728.27 | 48,732 | 6.2419 | - |
| MBPSO | 48,723 | 48,703 | 48,712.40 | 48,712 | 4.4303 | - | ||
| DGHS | 48,699 | 48,671 | 48,679.67 | 48,678 | 8.3101 | - | ||
| HSOSHS | 48,763 | 48,743 | 48,752.33 | 48,753 | 3.6515 | - | ||
| SDHS | 48,763 | 48,763 | 48,763 | 48,763 | 0 | 0.35 |
| Dim | Opt | Method | Best | Worst | Mean | Median | Std | Time (s) |
|---|---|---|---|---|---|---|---|---|
| 300 | 17,259 | CGMA | 17,259 | 17,239 | 17,253.67 | 17,259 | 8.9955 | - |
| MBPSO | 17,259 | 17,257 | 17,258.83 | 17,259 | 0.5307 | - | ||
| DGHS | 17,239 | 17,219 | 17,234.13 | 17,236 | 5.7878 | - | ||
| HSOSHS | 17,259 | 17,259 | 17,259 | 17,259 | 0 | - | ||
| SDHS | 17,259 | 17,259 | 17,259 | 17,259 | 0 | 0.09 | ||
| 500 | 29,775 | CGMA | 29,755 | 29,735 | 29,752.33 | 29,755 | 6.9149 | - |
| MBPSO | 29,755 | 29,735 | 29,752.13 | 29,755 | 6.1180 | - | ||
| DGHS | 29,735 | 29,697 | 29,714.93 | 29,712 | 9.7660 | - | ||
| HSOSHS | 29,775 | 29,755 | 29,772.33 | 29,775 | 6.9149 | - | ||
| SDHS | 29,775 | 29,775 | 29,775 | 29,775 | 0 | 0.15 | ||
| 800 | 47,153 | CGMA | 47,133 | 47,113 | 47,120.33 | 47,113 | 9.8027 | - |
| MBPSO | 47,113 | 47,092 | 47,106.57 | 47,111 | 7.8111 | - | ||
| DGHS | 47,079 | 47,033 | 47,053.30 | 47,052 | 11.0365 | - | ||
| HSOSHS | 47,153 | 47,133 | 47,151.67 | 47,153 | 5.0742 | - | ||
| SDHS | 47,173 | 47,153 | 47,167.83 | 47,172 | 7.1609 | 0.28 | ||
| 1000 | 59,575 | CGMA | 59,555 | 59,495 | 59,516.33 | 59,515 | 12.7937 | - |
| MBPSO | 59,513 | 59,475 | 59,490.33 | 59,492 | 8.8213 | - | ||
| DGHS | 59,455 | 59,403 | 59,427.83 | 59,431 | 12.6248 | - | ||
| HSOSHS | 59,575 | 59,555 | 59,566.33 | 59,575 | 10.0801 | - | ||
| SDHS | 59,595 | 59,575 | 59,578.2 | 59,575 | 5.5172 | 0.37 | ||
| 1200 | 69,122 | CGMA | 69,062 | 69,021 | 69,037.67 | 69,042 | 13.9243 | - |
| MBPSO | 69,012 | 68,980 | 68,996.53 | 68,998.5 | 6.9319 | - | ||
| DGHS | 68,949 | 68,892 | 68,916.10 | 68,917.5 | 12.8529 | - | ||
| HSOSHS | 69,122 | 69,082 | 69,103.33 | 69,102 | 8.9955 | - | ||
| SDHS | 69,122 | 69,122 | 69,122 | 69,122 | 0 | 0.43 |
| Dim | Opt | Method | Best | Worst | Mean | Median | Std | Time (s) |
|---|---|---|---|---|---|---|---|---|
| 300 | 13,143 | CGMA | 13,143 | 13,140 | 13,142.20 | 13,143 | 1.3493 | - |
| MBPSO | 13,143 | 13,140 | 13,141.40 | 13,140 | 1.5222 | - | ||
| DGHS | 13,137 | 13,131 | 13,134.30 | 13,134 | 1.2077 | - | ||
| HSOSHS | 13,143 | 13,143 | 13,143 | 13,143 | 0 | - | ||
| SDHS | 13,143 | 13,143 | 13,143 | 13,143 | 0 | 0.09 | ||
| 500 | 21,069 | CGMA | 21,069 | 21,063 | 21,068.00 | 21,069 | 1.6400 | - |
| MBPSO | 21,069 | 21,063 | 21,066.10 | 21,066 | 1.4704 | - | ||
| DGHS | 21,060 | 21,054 | 21,056.00 | 21,057 | 1.8194 | - | ||
| HSOSHS | 21,069 | 21,069 | 21,069 | 21,069 | 0 | - | ||
| SDHS | 21,069 | 21,069 | 21,069 | 21,069 | 0 | 0.16 | ||
| 800 | 34,227 | CGMA | 34,227 | 34,221 | 34,223.90 | 34,224 | 2.2947 | - |
| MBPSO | 34,221 | 34,215 | 34,216.40 | 34,215 | 2.1909 | - | ||
| DGHS | 34,209 | 34,197 | 34,201.50 | 34,200 | 2.4600 | - | ||
| HSOSHS | 34,227 | 34,227 | 34,227 | 34,227 | 0 | - | ||
| SDHS | 34,227 | 34,227 | 34,227 | 34,227 | 0 | 0.27 | ||
| 1000 | 42,108 | CGMA | 42,108 | 42,108 | 42,108 | 42,108 | 0 | - |
| MBPSO | 42,108 | 42,099 | 42,104.10 | 42,105 | 2.1066 | - | ||
| DGHS | 42,096 | 42,084 | 42,088.00 | 42,087 | 2.9827 | - | ||
| HSOSHS | 42,108 | 42,108 | 42,108 | 42,108 | 0 | - | ||
| SDHS | 42,108 | 42,108 | 42,108 | 42,108 | 0 | 0.36 | ||
| 1200 | 51,585 | CGMA | 51,585 | 51,582 | 51,583.80 | 51,585 | 1.4948 | - |
| MBPSO | 51,576 | 51,570 | 51,572.20 | 51,573 | 2.0745 | - | ||
| DGHS | 51,558 | 51,549 | 51,553.80 | 51,552 | 2.4410 | - | ||
| HSOSHS | 51,585 | 51,585 | 51,585 | 51,585 | 0 | - | ||
| SDHS | 51,585 | 51,585 | 51,585 | 51,585 | 0 | 0.45 |
| Dim | Opt | Method | Best | Worst | Mean | Median | Std | Time (s) |
|---|---|---|---|---|---|---|---|---|
| 3000 | 1914.62 | CGMA | 1905.08 | 1901.03 | 1902.49 | 1902.28 | 1.0721 | - |
| MBPSO | 1887.61 | 1884.12 | 1885.70 | 1885.38 | 0.9509 | - | ||
| DGHS | 1915.72 | 1874.84 | 1878.48 | 1876.60 | 8.8626 | - | ||
| HSOSHS | 1914.62 | 1912.41 | 1913.55 | 1913.65 | 0.5508 | - | ||
| SDHS | 1918.25 | 1918.24 | 1918.24 | 1918.24 | 0.0014 | 1.26 | ||
| 5000 | 3198.62 | CGMA | 3174.57 | 3167.25 | 3171.66 | 3171.79 | 1.5624 | - |
| MBPSO | 3149.96 | 3144.21 | 3146.81 | 3146.76 | 1.1317 | - | ||
| DGHS | 3136.95 | 3130.92 | 3133.70 | 3133.39 | 1.8258 | - | ||
| HSOSHS | 3198.62 | 3193.24 | 3195.30 | 3195.17 | 1.4499 | - | ||
| SDHS | 3210.52 | 3210.47 | 3210.50 | 3210.50 | 0.0096 | 2.52 | ||
| 7000 | 4444.40 | CGMA | 4410.22 | 4399.96 | 4406.19 | 4406.11 | 2.4319 | - |
| MBPSO | 4379.24 | 4373.04 | 4375.35 | 4375.22 | 1.9022 | - | ||
| DGHS | 4366.02 | 4356.18 | 4359.12 | 4358.52 | 2.5196 | - | ||
| HSOSHS | 4444.40 | 4436.23 | 4438.50 | 4438.28 | 2.1447 | - | ||
| SDHS | 4469.43 | 4469.24 | 4469.34 | 4469.34 | 0.0348 | 4.16 | ||
| 10000 | 6340.18 | CGMA | 6294.93 | 6284.56 | 6288.19 | 6287.12 | 2.7812 | - |
| MBPSO | 6251.53 | 6246.10 | 6249.05 | 6249.12 | 1.6007 | - | ||
| DGHS | 6235.64 | 6227.47 | 6231.33 | 6230.79 | 2.0268 | - | ||
| HSOSHS | 6340.18 | 6327.39 | 6333.76 | 6334.03 | 3.2233 | - | ||
| SDHS | 6387.25 | 6386.69 | 6387.02 | 6387.00 | 0.1138 | 7.19 |
| Algorithm | Rank | Gap | p-Value | p-Holm | Sum of |
|---|---|---|---|---|---|
| SDHS | 1.21 | - | - | - | - |
| CGMA | 3.02 | 0.257 | 0/2/22 | ||
| MBPOS | 3.81 | 0.491 | 0/1/23 | ||
| DGHS | 5 | 0.685 | 0/0/24 | ||
| HSOSHS | 1.96 | 0.111 | 0/6/18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, F.; Cheng, K.; Yang, K.; Li, N.; Lin, Y.; Zhong, Y. A Heuristics-Guided Simplified Discrete Harmony Search Algorithm for Solving 0-1 Knapsack Problem. Algorithms 2025, 18, 295. https://doi.org/10.3390/a18050295
Zheng F, Cheng K, Yang K, Li N, Lin Y, Zhong Y. A Heuristics-Guided Simplified Discrete Harmony Search Algorithm for Solving 0-1 Knapsack Problem. Algorithms. 2025; 18(5):295. https://doi.org/10.3390/a18050295
Chicago/Turabian StyleZheng, Fuyuan, Kanglong Cheng, Kai Yang, Ning Li, Yu Lin, and Yiwen Zhong. 2025. "A Heuristics-Guided Simplified Discrete Harmony Search Algorithm for Solving 0-1 Knapsack Problem" Algorithms 18, no. 5: 295. https://doi.org/10.3390/a18050295
APA StyleZheng, F., Cheng, K., Yang, K., Li, N., Lin, Y., & Zhong, Y. (2025). A Heuristics-Guided Simplified Discrete Harmony Search Algorithm for Solving 0-1 Knapsack Problem. Algorithms, 18(5), 295. https://doi.org/10.3390/a18050295






