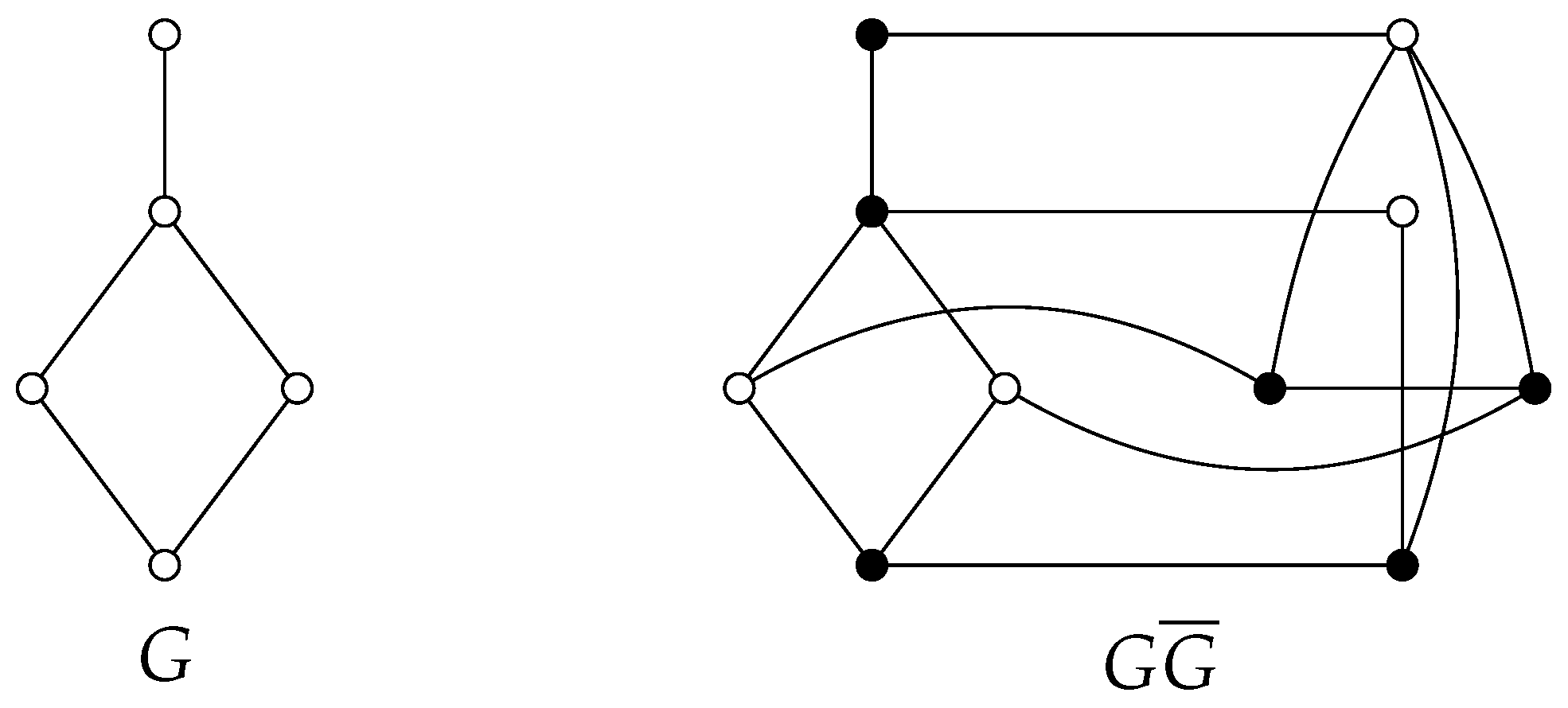
1. Introduction
The study of domination problems constitutes a fundamental line of research within graph theory, offering both deep theoretical insights and practical applications. Over recent decades, attention in this field has grown significantly due to its wide range of applications across various scientific disciplines, including social sciences, linear algebra, computational complexity, communication networks, algorithm design, optimization problems, and complex ecosystems (see [
1,
2]). In this context, several domination parameters have been introduced in previous studies, often involving the combination of multiple parameters [
1,
3,
4,
5]. This paper examines a particular parameter that combines the well-known notions of independence and total domination. Furthermore, we investigate the properties of this parameter from both computational and combinatorial perspectives.
In this paper, we consider simple graphs with size and order , where A is a subset of and is a vertex. The subgraph induced by A is represented as . The symbol denotes the set of neighbors of x contained within A, formally defined as . Furthermore, represents the closed neighborhood of x within A, defined as . We also define as the cardinality of , i.e., . The degree of x is denoted as . For ease of notation, we will often use and to refer to and , respectively. The maximum degree of is defined as , and the minimum degree as . Vertices are leaf vertices if , while support vertices are any vertices adjacent to leaf vertices. and denote the sets of support and leaf vertices, respectively.
A set
is an independent set of
if
is an edgeless graph, and
, the independence number, is the size of the largest independent set in
[
6,
7,
8].
A nonempty set
T is called a
total dominating set (TDS) if, for every
, there exists an edge
such that
. The
total domination number, denoted by
, is the smallest number of elements in any TDS of
. A TDS containing exactly
vertices is referred to as a
-
set. Since total domination cannot be defined for graphs containing isolated vertices, all graphs considered in this paper are assumed to have no isolated vertices. Please note that by the previous definitions,
. For additional details on total domination, refer to [
3,
8,
9,
10,
11].
If
T is a TDS such that the subgraph induced by
forms an independent set, then
T is called a
total outer-independent dominating set (TOIDS). The
total outer-independent domination number, represented as
, refers to the smallest cardinality of any TOIDS. A TOIDS with cardinality
is called a
-
set. This concept was first presented in [
12] and was briefly studied in [
13], where it was referred to as the total co-independent domination number. Please note that by the previous definitions,
, for
.
If , , …, with are the connected components of a graph with , then any TOIDS of is the union of TOIDSs from each connected component , for . This is expressed in the following simple result.
Remark 1. Let , , …, with be the components of a non-connected graph that has no isolated vertices. Then Aligned with the previous remark, we will henceforth restrict our analysis to TOIDS in nontrivial connected graphs.
The study of TOIDS has gained considerable attention in recent years, owing to their valuable practical applications and extensive theoretical properties [
4,
12,
13,
14,
15]. The objective is to identify a TOIDS with the smallest cardinality, which is an
optimal total outer-independent dominating set. However, as demonstrated in [
4], this problem has been proven to be
-complete. A problem is considered NP-complete if it is part of the NP class (nondeterministic polynomial time), and every other NP problem can be reduced to it in polynomial time. In simpler terms, an NP-complete problem is as hard as any other problem within NP. If a polynomial-time solution is discovered for any NP-complete problem, then all problems in NP would be solvable in polynomial time. Since no polynomial-time algorithm is currently known for NP-complete problems, research often focuses on approximation algorithms, heuristics, and integer programming formulations to obtain efficient solutions for practical instances.
In [
5], a polynomial-time algorithm is proposed to compute
for trees. In addition, refs. [
4,
14,
15,
16] have presented various upper and lower bounds for the problem. As far as we know, no further results have been reported concerning this issue. In particular, to the best of our knowledge, no exact or approximation algorithms have been previously suggested for the TOIDS problem in general graph classes.
This paper presents new lower and upper bounds for
. We also propose an exact solution approach using an integer linear programming (ILP) formulation alongside a heuristic method and a purification procedure to reduce the size of the total outer-independent dominating set produced by the heuristic. Additionally, we provide experimental results and computational analyses to assess the performance of both the ILP and heuristic methods across 500 graph instances. Our ILP approach successfully found optimal solutions for graphs with up to 9100 vertices. Specifically, we computed
for the 500 graph with
, which were randomly generated and can now be used as benchmarks for future research. These
values and the corresponding instances are publicly available in [
17]. Interestingly, in about 28.69% of the cases where the exact algorithm produced an optimal solution, the heuristic also yielded an optimal result. For the remaining instances, the average absolute error was roughly 1.012 vertices, with an average approximation ratio of 1.0032.
In summary, our work contributes to the understanding and advancement of the total outer-independent dominating set problem, offering insights into its structural properties and providing a practical algorithm for its computation.
Section 2 explores new upper and lower bounds for
and establishes relationships with other domination and independence parameters, along with an ILP formulation.
Section 3 presents our heuristic, defines several graph families for which it provides an optimal solution, and outlines a purification process. Finally,
Section 4 provides a detailed overview of our experimental results.
3. Heuristic Algorithm
Now, we present our heuristic for approximating a total outer-independent dominating set. This heuristic is divided into two stages: Stage 1 follows a greedy methodology to find a TOIDS, and Stage 2 consists of a purification procedure that delivers a minimal TOIDS. Stage 1 is further divided into two fundamental parts: the first part constructs a total dominating set, and the second part updates this set to ensure that its complement is independent.
We need a few definitions to describe our heuristic. We denote by the TOIDS formed by the heuristic in iteration h. The dominated set in iteration h is denoted by ; this vertex set is formed by the vertices that have at least one neighbor in . Please note that in the final iteration of Stage 1, the set is an independent set. Finally, denotes the vertex set that has no neighbors in in iteration h, i.e., .
In general, our heuristic is a greedy algorithm that runs over several iterations. The iterative process in Stage 1 is guaranteed to converge, as in each iteration, a vertex is selected from and added to , reducing the size of or . Since these sets are subsets of , the number of iterations is at most n, ensuring termination in a finite number of steps. Below, we provide a detailed description of our heuristic.
First, we select two vertices where u is the vertex with the highest degree in and v is its neighbor with the highest number of neighbors not dominated by u. Thus, initially , and . Notice that these are disjoint sets and .
Remark 2. The sets , and are disjoint and .
Lemma 1. If then and is a minimum total dominating set.
Proof. By Remark 2 and , it follows immediately that . This implies that all vertices in have a neighbor in . Please note that by the construction of the algorithm, . Since , then is minimum, a TDS cannot contain fewer than two vertices. □
A direct consequence of the previous lemma is the following observation.
Remark 3. If and is an independent set, then is a minimum TOIDS.
The initial sets are updated iteratively at each iteration , resulting in the current sets of vertices , , and , where is the partial total outer-independent dominating set. Each iteration begins if or is not an independent set. In the first iterative part of Stage 1, for each iteration, we choose a vertex such that is as large as possible. Then, we add v to , i.e., . Please note that v is chosen to maximize the number of adjacent vertices among those that do not yet have neighbors in . At this point, the sets and are updated accordingly.
In the second iterative part of Stage 1, each iteration runs if the set is not yet an independent set. Thus, we choose a vertex such that is as large as possible, then we add u to , i.e., . Please note that u is the vertex that has the most neighbors in . At this point, the sets and are updated accordingly.
At the end of Stage 1, we obtain a TOIDS of the graph
G in
. Up to this point, the algorithm may have included redundant vertices in
. Therefore, in Stage 2, we proceed to apply a purification procedure that yields a minimal TOIDS of
G. The purification procedure is described in
Section 3. The pseudo-code for the heuristic is shown as follows (see Algorithm 1).
| Algorithm 1 Heuristic TOID |
Input: A graph . Output: A minimal total outer-independent dominating set . ; is the vertex with the maximum degree in ; is a vertex in such that be maximum; ; ; ; {first iterative part of Stage 1} while
do ; a vertex such that be maximum; ; ; ; end while {second iterative part of Stage 1} while is not an independent set do ; a vertex such that be maximum; ; ; end while {Stage 2} Purify(G,);
|
Theorem 5. Stage 1 of the Heuristic TOID runs in at most iterations, taking time.
Proof. The total number of iterations in the loops of Stage 1 is bounded by . Please note that the bound is reached for the graph and . Then, Stage 1 performs iterations.
In iteration , for each vertex , the neighborhood is determined by summing all the entries equal to 1 in the row associated with vertex u. The selection of the maximum takes time. Similarly, for each vertex , the value is computed by summing all the entries equal to 1 in the row corresponding to vertex v, provided that the entries for vertex u are not both 1.
In each iteration, , is calculated for every vertex by counting all the 1 entries in the row corresponding to that vertex, if the entries are simultaneously 1 in . Similarly, is calculated for every vertex . Given that each row consists of n entries and there are fewer than n rows to check, the computation of or , along with the selection of the maximum, requires time. Following the same idea, we can determine if the set is independent if, for every vertex , it holds that .
Please note that and . Therefore, the total number of iterations in the loops of Stage 1 is bounded by n. Hence, Stage 1 finds a total outer-independent dominating set in time. □
Proposition 5. Let G be a connected split graph with maximum clique K and independent set I. Then, the Heuristic TOID finds an optimal solution for the graph G if, in iteration i of the second iterative part of Stage 1, there is no vertex such that .
Proof. Clearly, every vertex in K has a higher degree than the vertices in . Then, in iteration , Heuristic TOID will select the vertices such that is maximized, forming the set . Since dominates all the vertices in K, and is an independent set, in every iteration of the first iterative part of Stage 1, is a vertex in with the largest number of undominated neighbors in , and is updated as . The first iterative part stops when all the vertices in are dominated.
If , then is an independent set, and the second iterative part of Stage 1 is skipped, proceeding directly to Stage 2. If there exists a vertex such that , the procedure removes this vertex from the set and returns a set with vertices. Otherwise, the cardinality of cannot be reduced, and . In either case, by the proof of Proposition 2, this is an optimal solution.
If , then is not an independent set and has vertices from K in . Please note that these r vertices form a graph. Therefore, in the second iterative part of Stage 1, since in every iteration , there is no vertex such that , vertices from the set are removed from and added to to ensure that becomes an independent set. Then, . The current set does not allow purification by the proof of Proposition 2, and is an optimal solution. □
Purify Procedure
In Theorem 2.3 of [
13], Soner et al. demonstrate that:
Lemma 2. Let T be a TOIDS. T is a minimal set if and only if, for each vertex , one of the following conditions holds:
- (i)
There exists a vertex such that .
- (ii)
There exists a vertex that is adjacent to x.
Following these ideas, the objective of this subsection is to propose a purification procedure that yields a minimal total outer-independent domination set (see Algorithm 2). Below are two definitions that we will use in the purification procedure. The
private neighborhood of a vertex
, denoted by
, is given by
A vertex in
is referred to as a
private neighbor of
x. These definitions are equivalent to condition
in Lemma 2.
Please note that all vertices in the set formed in this way satisfy one of the conditions proposed in Lemma 2, making it a minimal total outer-independent dominating set for the graph G. Using similar reasoning as in the proof of Theorem 5, it follows that the purification procedure can be executed in time .
Theorem 6. Purify runs in at most k iterations, and its time complexity is .
| Algorithm 2 Purify |
Input: A TOIDS and a graph . Output: A minimal TOIDS . ; {vertices of in the sequence in which they were included by Stage 1} ; while
do if then ; {we purify vertex } end if ; end while
|
4. Experimental Results
This section provides an overview of our computational analysis. We implemented the ILP formulation and Heuristic TOID in C++ using the CPLEX library, both running on a Windows 11 operating system for 64-bit architecture. The experiments were conducted on a personal computer equipped with an Intel Core i7-9750H processor (2.6 GHz) and 16 GB of DDR4 RAM. Our algorithm was tested on a set of 500 benchmark instances from [
17,
32,
33].
Since no benchmark instances for the TOIDS problem previously existed, we used optimal values from CPLEX alongside established upper and lower bounds to evaluate heuristic performance. While our computational experiments provide valuable insights into the performance of the proposed heuristic and ILP formulation, some limitations should be considered. First, since no standard benchmark instances existed for this problem, the generated dataset may not fully represent the characteristics of real-world graphs. Second, computational constraints limited the exact resolution of larger instances using CPLEX, which may affect the evaluation of the heuristic’s performance in such cases. Finally, further experiments on graphs from real-world applications would be necessary to assess the generalizability of our approach beyond the tested instances.
Table 1 presents the values of
for 39 instances out of the 500 analyzed using CPLEX. These instances were randomly selected from the full dataset. Additionally,
T and
represent the solutions provided by our heuristic in Stages 1 and 2, respectively. The values of
shown in
Table 1 can be compared with the solutions obtained by the heuristic. This comparison enables an assessment of the accuracy and effectiveness of the heuristic in estimating
for the analyzed instances.
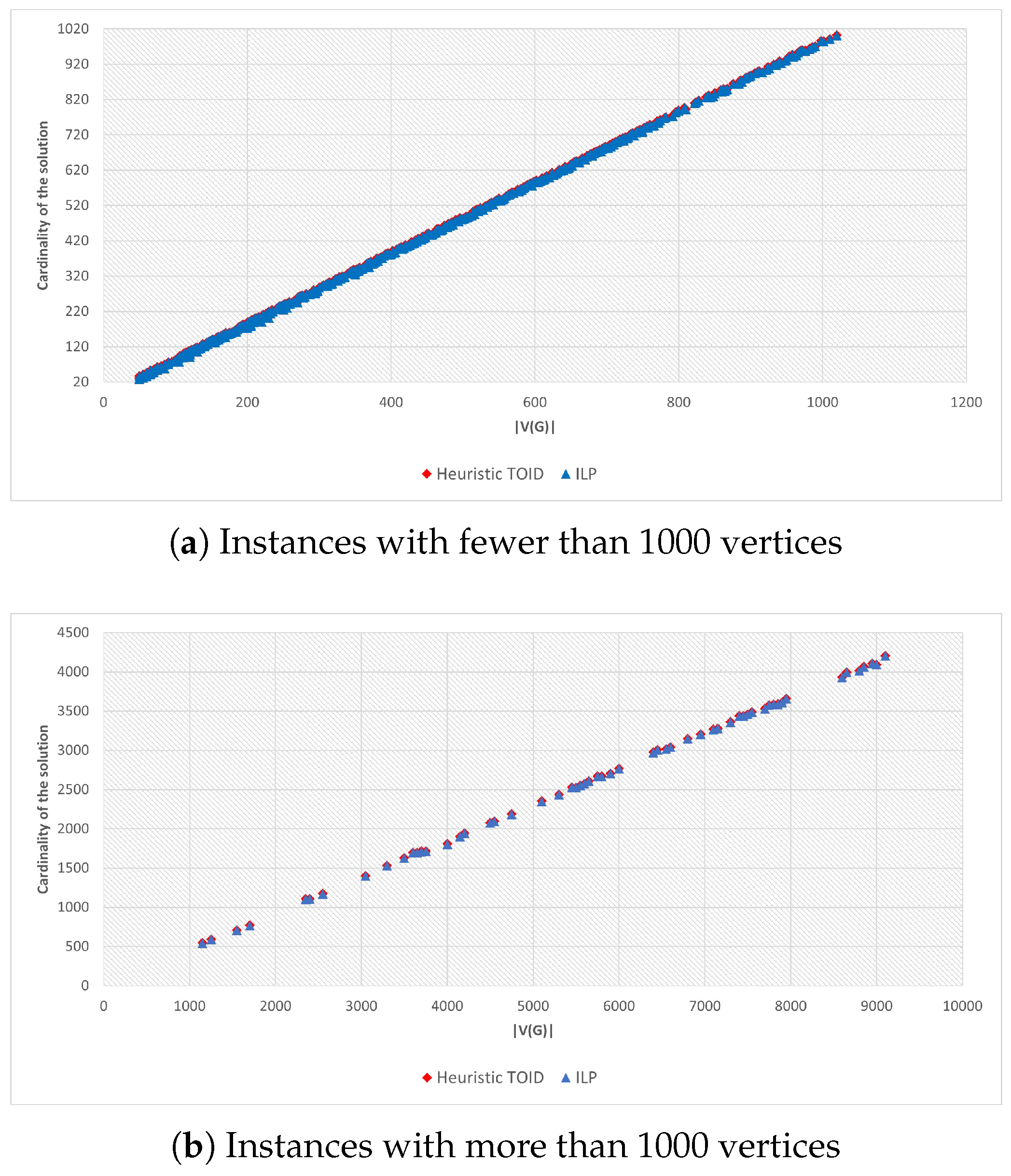
Figure 3 presents a comparison between the solutions produced by our Heuristic TOID and the optimal values obtained by CPLEX for instances with up to 9100 vertices. Our heuristic successfully found the optimal solution in 28.69% of the instances. For the cases where the optimal solution was not achieved, the average absolute error was approximately 1.012 vertices.
Figure 4 shows the approximation ratio of our heuristic in those instances where the optimal solution was not found. For these instances, the minimum approximation ratio was 1.00028, the maximum was 1.05555, and the average was 1.0032.
Figure 4 also reveals a clear trend toward reducing the approximation ratio as the number of vertices increases. This result highlights the strong performance of our heuristic in terms of approximation ratio for instances with a larger number of vertices. The low approximation ratios demonstrate the high quality of our heuristic in efficiently providing near-optimal solutions.
The execution time of CPLEX and the heuristic varies depending on the density of the analyzed instances. In our analysis, graph density is defined as
.
Figure 5a,b compare the time taken by CPLEX to find
with the time taken by the heuristic to find a feasible solution, considering graph density.
Figure 5a shows the execution time for instances with a density of less than
. For these instances, CPLEX performed better; on average, it was approximately
times faster than the heuristic. CPLEX successfully solved instances of this type with up to 9100 vertices. However, for instances with more than 9100 vertices, CPLEX ran out of available memory on the system and failed to find the optimal solution. Whereas the heuristic was not constrained by memory capacity, successfully solving instances with more than 14,000 vertices.
Figure 5b shows the execution time for instances with a density greater than
. For these instances, the heuristic outperformed CPLEX, being approximately
times faster on average. CPLEX was able to solve instances of this type with up to 1100 vertices, while the heuristic successfully solved instances with up to 14,100 vertices in less than two hours without reaching the memory limit (see BD4_xx instances in
Table 1). In instances where the heuristic identified the optimal solution, i.e., a
-set, regardless of the instance density, the heuristic was, on average, 594 times faster than CPLEX. These findings, along with the excellent approximation ratios shown in
Figure 4, emphasize the critical role of heuristics in solving large-scale problems that are computationally infeasible for exact methods.
The results reported for our heuristic include the purification stage (Stage 2). The purification process proved effective in practice, as illustrated in
Figure 6. In this figure,
and
represent the number of vertices in the TOIDS before and after purification, respectively. In 99.59% of the analyzed instances, Stage 1 did not yield minimal TOIDS, i.e., Stage 1 produced TOIDS with redundant vertices. The purification process in Stage 2 of our heuristic exhibited different behaviors depending on the graph density. For graphs with a density lower than 0.1, an average of 191.68 vertices were removed, with a minimum of 28 and a maximum of 316. In these instances, on average, 6.81% of the vertices provided by Stage 1 were eliminated. In contrast, for graphs with a density greater than 0.1, the purification process had a significantly smaller impact. The average number of vertices removed was only 2.80, with a minimum of 0 and a maximum of 5. In these cases, the purification step reduced, on average, only 1.09% of the vertices provided by Stage 1. These results highlight that the purification procedure is notably more effective in sparse graphs, where a larger proportion of vertices can be removed, while in denser graphs, the final solution remains almost unchanged after Stage 2.
Figure 7a,b display boxplots illustrating the distribution of purified vertices in graphs with varying densities. The box represents the interquartile range (IQR), encompassing the central 50% of the data. The line within the box marks the median, which is the middle value. The whiskers represent the range of data that is not considered outliers, while any points outside this range are considered outliers. In
Figure 7a, which corresponds to graphs with a density of 0.1 or higher, we observe that the purified vertices are concentrated between 0 and 3. This suggests that the number of purified vertices is generally low in high-density graphs, indicating a better quality of the solution delivered by Stage 1. However, Stage 2 is still needed to guarantee a minimal TOIDS.
In contrast,
Figure 7b, representing graphs with very low density (almost trees), shows a much wider spread in the values. The number of purified vertices is significantly higher, ranging from 28 to 316 vertices. This indicates that in low-density graphs, where the structure is more dispersed and less connected, the purification process has a much more significant impact. In these cases, it is more likely that many redundant or non-essential vertices can be removed. In summary, Stage 1 of our heuristic tends to be more effective in higher-density graphs, while it faces greater challenges in very low-density graphs.
5. Conclusions
In this work, we introduced new lower and upper bounds for and presented both an ILP formulation and a heuristic algorithm for addressing the total outer-independent domination problem. As no prior algorithm had been developed for this specific problem, we utilized the optimal solutions generated by CPLEX for our ILP model as a basis for evaluating the performance of our heuristic. Our experiments employed well-established benchmark instances originally designed for the classical domination problem. CPLEX successfully solved 500 of these instances, which included graphs with up to 9100 vertices. In addition, our heuristic consistently produced high-quality solutions for the same benchmarks, achieving an average error of 1.012 vertices across all tested instances. We also identified certain families of graphs where our heuristic guarantees optimal solutions. Looking ahead, we believe this research can be extended to tackle more complex variants of domination problems, such as k-tuple domination, secure domination, alliance domination, and total outer k-independent domination, opening new lines of research.
In addition to the results presented in this paper, several open problems remain related to . One significant direction for future research is the study of this parameter in the context of various graph operators and transformations. Specifically, the behavior of under graph product operators (e.g., corona product, lexicographic product) and graph transformations (e.g., edge contractions, vertex deletions) remains largely unexplored. Investigating these operators could provide valuable insights and inspire further research in domination theory. Moreover, a comparative analysis with existing domination parameters across various graph families would offer deeper insights into the advantages and limitations of . Such comparisons could highlight the applicability of in relation to well-established parameters, including the powerful k-alliance number, 2-packing number, global offensive k-alliance number, independence number, and independent domination number. Exploring these areas will not only expand our understanding of but could also reveal new relationships between domination parameters in different graph families. We believe that addressing these open problems will significantly contribute to the theory of domination in graphs and inspire future research in this area.