Simplified Integrity Checking for an Expressive Class of Denial Constraints
Abstract
1. Introduction
2. Related Work
3. Relational and Deductive Databases
4. A Simplification Procedure for Obtaining a Pre-Test
4.1. The Core Language
Generating Weakest Preconditions in
- Let us indicate with a copy of Γ in which any atom is simultaneously replaced by the expression and every intensional predicate q is simultaneously replaced by a new intensional predicate defined in below.
- Similarly, let us indicate with a copy of in which the same replacements are simultaneously made, and let be the biggest subset of including only definitions of predicates on which depends.
- replace, in Γ, each atom by , where is p’s defining formula and its head variables. If no replacement was made, then stop;
- transform the result into a set of denials according to the following patterns:
- is replaced by and ;
- is replaced by ;
- is replaced by and .
4.2. Simplification in
5. Denials with Negated Existential Quantifiers
- replace, in Γ, each occurrence of a literal of the form by and of a literal of the form by , where is p’s defining formula, its head variables and its non-distinguished variables. If no replacement was made, stop;
- transform the resulting formula into a set of extended denials according to the following patterns; is an expression indicating the body of an NEE in which occurs; and are disjoint sequences of variables:
- is replaced by and ;
- is replaced by ;
- is replaced by and ;
- is replaced by.
- (1)
- subsumes with substitution σ.
- (2)
- For every NEE in B, there is an NEE in D such that is extended-subsumed by .
Practical Applications
- The proposed operators work at the schema (program) level, not at the data level, so the synthetic generation would need to concern schemas (and update patterns) instead of datasets.
- Although a few efforts exist to generate schemas, such as [95], there is no proper benchmark that comes with the generation of integrity constraints or update patterns and, even more importantly, with a ground truth indicating the ideal kind of simplification that one should aim to obtain.
- Although data-independent measures of the quality of a simplification could be defined, there is no univocally correct way of doing this, as was shown in [15]. The “easy way” is to just count the remaining literals in the simplified formula, with no guarantee, however, that the obtained formula is indeed easier to check. To this end, the (non-)equality elimination steps shown in Definition 18 naturally follow in this direction by consistently reducing the number of literals in higher-level NEEs.
- Database schema design activities require expertise and finesse that would be annihilated by a synthetic generation, leading to results of questionable utility.
- Datasets would of course come into play when checking the (simplified) integrity constraints against data proper, and a comparison with other techniques at that level could certainly provide favorable time measurements each time an illegal update is encountered, since its execution and retraction would be completely avoided with our preventive approach. However, even ignoring all the previous considerations on the lack of suitable synthetically generated tests, the number and incidence of illegal updates in such tests could be increased at will, thereby unfairly magnifying the advantages of our technique as well.
- In light of all the above considerations, we have preferred to focus on the few examples existing in the literature of simplification procedures that work on constraints outside the (simpler) language and show that, even in those ad hoc built cases, our general procedure produces similar or identical simplified checks (with the additional advantage of guaranteeing the possibility of a preventive approach).
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nicolas, J.M. Logic for Improving Integrity Checking in Relational Data Bases. Acta Inform. 1982, 18, 227–253. [Google Scholar] [CrossRef]
- Bernstein, P.A.; Blaustein, B.T. Fast Methods for Testing Quantified Relational Calculus Assertions. In Proceedings of the 1982 ACM SIGMOD International Conference on Management of Data, Orlando, FL, USA, 2–4 June 1982; Schkolnick, M., Ed.; ACM Press: New York, NY, USA, 1982; pp. 39–50. [Google Scholar]
- Henschen, L.; McCune, W.; Naqvi, S. Compiling Constraint-Checking Programs from First-Order Formulas. In Proceedings of the Advances in Database Theory, Los Angeles, CA, USA, 1–5 February 1988; Gallaire, H., Minker, J., Nicolas, J.M., Eds.; Plenum Press: New York, NY, USA, 1984; Volume 2, pp. 145–169. [Google Scholar]
- Hsu, A.; Imielinski, T. Integrity Checking for Multiple Updates. In Proceedings of the 1985 ACM SIGMOD International Conference on Management of Data, Austin, TX, USA, 28–31 May 1985; Navathe, S.B., Ed.; ACM Press: New York, NY, USA, 1985; pp. 152–168. [Google Scholar]
- Lloyd, J.W.; Sonenberg, L.; Topor, R.W. Integrity Constraint Checking in Stratified Databases. J. Log. Program. 1987, 4, 331–343. [Google Scholar] [CrossRef]
- Qian, X. An Effective Method for Integrity Constraint Simplification. In Proceedings of the Fourth International Conference on Data Engineering, Los Angeles, CA, USA, 1–5 February 1988; IEEE Computer Society: Washington, DC, USA, 1988; pp. 338–345. [Google Scholar]
- Sadri, F.; Kowalski, R. A Theorem-Proving Approach to Database Integrity. In Foundations of Deductive Databases and Logic Programming; Minker, J., Ed.; Morgan Kaufmann: Los Altos, CA, USA, 1988; pp. 313–362. [Google Scholar]
- Chakravarthy, U.S.; Grant, J.; Minker, J. Logic-based approach to semantic query optimization. ACM Trans. Database Syst. TODS 1990, 15, 162–207. [Google Scholar] [CrossRef]
- Decker, H.; Celma, M. A Slick Procedure for Integrity Checking in Deductive Databases. In Logic Programming, Proceedings of the 11th International Conference on Logic Programming, Santa Margherita Ligure, Italy, 13–18 June 1994; Van Hentenryck, P., Ed.; MIT Press: Cambridge, MA, USA, 1994; pp. 456–469. [Google Scholar]
- Lee, S.Y.; Ling, T.W. Further Improvements on Integrity Constraint Checking for Stratifiable Deductive Databases. In Proceedings of the VLDB’96, Proceedings of 22th International Conference on Very Large Data Bases, Mumbai, India, 3–6 September 1996; Vijayaraman, T.M., Buchmann, A.P., Mohan, C., Sarda, N.L., Eds.; Morgan Kaufmann: San Francisco, CA, USA, 1996; pp. 495–505. [Google Scholar]
- Leuschel, M.; de Schreye, D. Creating Specialised Integrity Checks Through Partial Evaluation of Meta-Interpreters. J. Log. Program. 1998, 36, 149–193. [Google Scholar] [CrossRef]
- Seljée, R.; de Swart, H.C.M. Three Types of Redundancy in Integrity Checking: An Optimal Solution. Data Knowl. Eng. 1999, 30, 135–151. [Google Scholar] [CrossRef]
- Decker, H. Translating advanced integrity checking technology to SQL. In Database Integrity: Challenges and Solutions; Doorn, J.H., Rivero, L.C., Eds.; Idea Group Publishing: Hershey, PA, USA, 2002; pp. 203–249. [Google Scholar]
- Ceri, S.; Bernasconi, A.; Gagliardi, A.; Martinenghi, D.; Bellomarini, L.; Magnanimi, D. PG-Triggers: Triggers for Property Graphs. In Proceedings of the Companion of the 2024 International Conference on Management of Data, SIGMOD/PODS 2024, Santiago, Chile, 9–15 June 2024; Barceló, P., Sánchez-Pi, N., Meliou, A., Sudarshan, S., Eds.; ACM: New York, NY, USA, 2024; pp. 373–385. [Google Scholar] [CrossRef]
- Martinenghi, D. Advanced Techniques for Efficient Data Integrity Checking. Ph.D. Thesis, Department of Computer Science, Roskilde University, Roskilde, Denmark, 2005. [Google Scholar]
- Christiansen, H.; Martinenghi, D. Simplification of Database Integrity Constraints Revisited: A Transformational Approach. In Logic Based Program Synthesis and Transformation, Proceedings of the 13th International Symposium LOPSTR 2003, Uppsala, Sweden, 25–27 August 2003; Lecture Notes in Computer Science; Revised Selected Papers; Bruynooghe, M., Ed.; Springer: Berlin/Heidelberg, Germany, 2003; Volume 3018, pp. 178–197. [Google Scholar] [CrossRef]
- Chandra, A.K.; Merlin, P.M. Optimal implementation of conjunctive queries in relational databases. In Proceedings of the 9th Annual ACM Symposium on Theory of Computing, ACM, Boulder, CO, USA, 4–6 May 1977; pp. 77–90. [Google Scholar]
- Shmueli, O. Decidability and expressiveness aspects of logic queries. In Proceedings of the Sixth ACM SIGACT-SIGMOD-SIGART Symposium on Principles of Database Systems, San Diego, CA, USA, 23–25 March 1987; pp. 237–249. [Google Scholar] [CrossRef]
- Calì, A.; Martinenghi, D. Conjunctive Query Containment under Access Limitations. In Proceedings of the Conceptual Modeling—ER 2008, 27th International Conference on Conceptual Modeling, Barcelona, Spain, 20–24 October 2008; Lecture Notes in Computer Science; Proceedings. Li, Q., Spaccapietra, S., Yu, E.S.K., Olivé, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; Volume 5231, pp. 326–340. [Google Scholar] [CrossRef]
- Chomicki, J. Efficient Checking of Temporal Integrity Constraints Using Bounded History Encoding. ACM Trans. Database Syst. TODS 1995, 20, 149–186. [Google Scholar] [CrossRef]
- Cowley, W.; Plexousakis, D. Temporal Integrity Constraints with Indeterminacy. In Proceedings of the VLDB 2000—26th International Conference on Very Large Data Bases, Cairo, Egypt, 10–14 September 2000; Abbadi, A.E., Brodie, M.L., Chakravarthy, S., Dayal, U., Kamel, N., Schlageter, G., Whang, K.Y., Eds.; Morgan Kaufmann: Los Altos, CA, USA, 2000; pp. 441–450. [Google Scholar]
- Carmo, J.; Demolombe, R.; Jones, A.J.I. An Application of Deontic Logic to Information System Constraints. Fundam. Inform. 2001, 48, 165–181. [Google Scholar]
- Godfrey, P.; Gryz, J.; Zuzarte, C. Exploiting constraint-like data characterizations in query optimization. In Proceedings of the SIGMOD ’01: 2001 ACM SIGMOD International Conference on Management of Data, Santa Barbara, CA, USA, 21–24 May 2001; Aref, W.G., Ed.; ACM Press: New York, NY, USA, 2001; pp. 582–592. [Google Scholar] [CrossRef]
- Krr, N.; Zilberstein, S. Scoring-based methods for preference representation and reasoning. In Proceedings of the 21st National Conference on Artificial Intelligence (AAAI), Boston, MA, USA, 16–20 July 2006; pp. 539–545. [Google Scholar]
- Brafman, R.I.; Domshlak, C. Preference handling: An AI perspective. AI Mag. 2006, 28, 58–68. [Google Scholar]
- Parsons, S.; Wooldridge, M. Scoring functions for user preference modeling. In Proceedings of the ACM International Conference on Intelligent User Interfaces (IUI), San Francisco, CA, USA, 13–16 January 2002; pp. 19–26. [Google Scholar]
- Faulkner, L.; Kersten, M.L. Preference handling in database systems. VLDB J. 2016, 25, 573–600. [Google Scholar]
- Kiessling, W. Foundations of preferences in database systems. In Proceedings of the 28th International Conference on Very Large Databases (VLDB), Hong Kong, China, 20–23 August 2002; Morgan Kaufmann: Los Altos, CA, USA, 2002; pp. 311–322. [Google Scholar]
- Chomicki, J. Preference formulas in relational queries. ACM Trans. Database Syst. TODS 2003, 28, 427–466. [Google Scholar] [CrossRef]
- Agrawal, R.; Wimmers, E.L. Preference SQL: Flexible preference queries in databases. In Proceedings of the 2005 ACM SIGMOD International Conference on Management of Data, Baltimore, MD, USA, 14–16 June 2005; pp. 560–572. [Google Scholar]
- Bárány, V.; Benedikt, M.; Bourhis, P. Access patterns and integrity constraints revisited. In Proceedings of the Joint 2013 EDBT/ICDT Conferences, ICDT ’13 Proceedings, Genoa, Italy, 18–22 March 2013; Tan, W., Guerrini, G., Catania, B., Gounaris, A., Eds.; ACM: New York, NY, USA, 2013; pp. 213–224. [Google Scholar] [CrossRef]
- Codd, E.F. Further normalization of the database relational model. In Proceedings of the Courant Computer Science Symposium 6: Data Base Systems, New York, NY, USA, 24–25 May 1971; Rustin, R., Ed.; Prentice-Hall: Englewood Cliffs, NJ, USA, 1972; pp. 33–64. [Google Scholar]
- Fagin, R. Multivalued Dependencies and a New Normal Form for Relational Databases. ACM Trans. Database Syst. TODS 1977, 2, 262–278. [Google Scholar] [CrossRef]
- Fagin, R. Horn clauses and database dependencies. J. ACM 1982, 29, 952–985. [Google Scholar] [CrossRef]
- Beeri, C.; Vardi, M.Y. A Proof Procedure for Data Dependencies. J. ACM 1984, 31, 718–741. [Google Scholar] [CrossRef]
- Fagin, R.; Kolaitis, P.G.; Miller, R.J.; Popa, L. Data exchange: Semantics and query answering. Theor. Comput. Sci. 2005, 336, 89–124. [Google Scholar] [CrossRef]
- Ullman, J.D. Principles of Database and Knowledge-Base Systems, Volume I; Computer Science Press: New York, NY, USA, 1988. [Google Scholar]
- Ullman, J.D. Principles of Database and Knowledge-Base Systems, Volume II; Computer Science Press: New York, NY, USA, 1989. [Google Scholar]
- Grefen, P.W.P.J. Combining Theory and Practice in Integrity Control: A Declarative Approach to the Specification of a Transaction Modification Subsystem. In Proceedings of the 19th International Conference on Very Large Data Bases, Dublin, Ireland, 24–27 August 1993; Agrawal, R., Baker, S., Bell, D.A., Eds.; Morgan Kaufmann: Los Altos, CA, USA, 1993; pp. 581–591. [Google Scholar]
- Arenas, M.; Bertossi, L.E.; Chomicki, J. Consistent Query Answers in Inconsistent Databases. In Proceedings of the Eighteenth ACM SIGACT-SIGMOD-SIGART Symposium on Principles of Database Systems, Philadelphia, PA, USA, 31 May–2 June 1999; pp. 68–79. [Google Scholar]
- Calì, A.; Lembo, D.; Rosati, R. On the decidability and complexity of query answering over inconsistent and incomplete databases. In Proceedings of the PODS ’03: Twenty-Second ACM SIGMOD-SIGACT-SIGART Symposium on Principles of Database Systems, New York, NY, USA, 9–12 June 2003; pp. 260–271. [Google Scholar] [CrossRef]
- Arieli, O.; Denecker, M.; Nuffelen, B.V.; Bruynooghe, M. Database Repair by Signed Formulae. In Proceedings of the Foundations of Information and Knowledge Systems, Third International Symposium (FoIKS 2004), Wilhelminenburg Castle, Austria, 17–20 February 2004; Lecture Notes in Computer Science. Seipel, D., Torres, J.M.T., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; Volume 2942, pp. 14–30. [Google Scholar]
- Bertossi, L.E. Database Repairing and Consistent Query Answering; Synthesis Lectures on Data Management; Morgan & Claypool Publishers: San Rafael, CA, USA, 2011. [Google Scholar] [CrossRef]
- Bertossi, L.E. Database Repairs and Consistent Query Answering: Origins and Further Developments. In Proceedings of the 38th ACM SIGMOD-SIGACT-SIGAI Symposium on Principles of Database Systems, PODS, Amsterdam, The Netherlands, 30 June–5 July 2019; Suciu, D., Skritek, S., Koch, C., Eds.; ACM: New York, NY, USA, 2019; pp. 48–58. [Google Scholar] [CrossRef]
- Decker, H.; Martinenghi, D. A Relaxed Approach to Integrity and Inconsistency in Databases. In Proceedings of the Logic for Programming, Artificial Intelligence, and Reasoning, 13th International Conference, LPAR 2006, Phnom Penh, Cambodia, 13–17 November 2006; Lecture Notes in Computer Science; Proceedings. Hermann, M., Voronkov, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; Volume 4246, pp. 287–301. [Google Scholar] [CrossRef]
- Decker, H.; Martinenghi, D. Avenues to Flexible Data Integrity Checking. In Proceedings of the 17th International Workshop on Database and Expert Systems Applications (DEXA 2006), Krakow, Poland, 4–8 September 2006; IEEE Computer Society: Washington, DC, USA, 2006; pp. 425–429. [Google Scholar] [CrossRef]
- Decker, H.; Martinenghi, D. Getting Rid of Straitjackets for Flexible Integrity Checking. In Proceedings of the 18th International Workshop on Database and Expert Systems Applications (DEXA 2007), Regensburg, Germany, 3–7 September 2007; IEEE Computer Society: Washington, DC, USA, 2007; pp. 360–364. [Google Scholar] [CrossRef]
- Grant, J.; Hunter, A. Measuring inconsistency in knowledgebases. J. Intell. Inf. Syst. 2006, 27, 159–184. [Google Scholar] [CrossRef]
- Grant, J.; Hunter, A. Measuring the Good and the Bad in Inconsistent Information. In Proceedings of the IJCAI 2011, Proceedings of the 22nd International Joint Conference on Artificial Intelligence, Barcelona, Catalonia, Spain, 16–22 July 2011; Walsh, T., Ed.; IJCAI/AAAI: Montreal, QC, Canada, 2011; pp. 2632–2637. [Google Scholar] [CrossRef]
- Grant, J.; Hunter, A. Distance-Based Measures of Inconsistency. In Proceedings of the Symbolic and Quantitative Approaches to Reasoning with Uncertainty—12th European Conference, ECSQARU 2013, Utrecht, The Netherlands, 8–10 July 2013; Lecture Notes in Computer Science, Proceedings. van der Gaag, L.C., Ed.; Springer: Berlin/Heidelberg, Germany, 2013; Volume 7958, pp. 230–241. [Google Scholar] [CrossRef]
- Grant, J.; Hunter, A. Analysing inconsistent information using distance-based measures. Int. J. Approx. Reason. 2017, 89, 3–26. [Google Scholar] [CrossRef]
- Grant, J.; Hunter, A. Semantic inconsistency measures using 3-valued logics. Int. J. Approx. Reason. 2023, 156, 38–60. [Google Scholar] [CrossRef]
- Christiansen, H.; Martinenghi, D. Simplification of Integrity Constraints for Data Integration. In Proceedings of the Foundations of Information and Knowledge Systems, Third International Symposium, FoIKS 2004, Wilhelminenberg Castle, Austria, 17–20 February 2004; Lecture Notes in Computer Science; Proceedings. Seipel, D., Torres, J.M.T., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; Volume 2942, pp. 31–48. [Google Scholar] [CrossRef]
- Martinenghi, D. Simplification of Integrity Constraints with Aggregates and Arithmetic Built-Ins. In Proceedings of the Flexible Query Answering Systems, 6th International Conference, FQAS 2004, Lyon, France, 24–26 June 2004; Lecture Notes in Computer Science; Proceedings. Christiansen, H., Hacid, M., Andreasen, T., Larsen, H.L., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; Volume 3055, pp. 348–361. [Google Scholar] [CrossRef]
- Samarin, S.D.; Amini, M. Integrity Checking for Aggregate Queries. IEEE Access 2021, 9, 74068–74084. [Google Scholar] [CrossRef]
- Martinenghi, D.; Christiansen, H. Transaction Management with Integrity Checking. In Proceedings of the Database and Expert Systems Applications, 16th International Conference, DEXA 2005, Copenhagen, Denmark, 22–26 August 2005; Lecture Notes in Computer Science; Proceedings. Andersen, K.V., Debenham, J.K., Wagner, R.R., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; Volume 3588, pp. 606–615. [Google Scholar] [CrossRef]
- Christiansen, H.; Martinenghi, D. Symbolic Constraints for Meta-Logic Programming. Appl. Artif. Intell. 2000, 14, 345–367. [Google Scholar] [CrossRef]
- Kenig, B.; Suciu, D. Integrity Constraints Revisited: From Exact to Approximate Implication. In Proceedings of the 23rd International Conference on Database Theory, ICDT 2020, Copenhagen, Denmark, 30 March–2 April 2020; LIPIcs. Lutz, C., Jung, J.C., Eds.; Schloss Dagstuhl-Leibniz-Zentrum für Informatik: Wadern, Germany, 2020; Volume 155, pp. 18:1–18:20. [Google Scholar] [CrossRef]
- Yu, H.; Hu, Q.; Yang, Z.; Liu, H. Efficient Continuous Big Data Integrity Checking for Decentralized Storage. IEEE Trans. Netw. Sci. Eng. 2021, 8, 1658–1673. [Google Scholar] [CrossRef]
- Yang, C.; Tao, X.; Wang, S.; Zhao, F. Data Integrity Checking Supporting Reliable Data Migration in Cloud Storage. In Proceedings of the Wireless Algorithms, Systems, and Applications—15th International Conference, WASA 2020, Qingdao, China, 13–15 September 2020; Lecture Notes in Computer Science; Proceedings, Part I. Yu, D., Dressler, F., Yu, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2020; Volume 12384, pp. 615–626. [Google Scholar] [CrossRef]
- Masciari, E. Trajectory Clustering via Effective Partitioning. In Proceedings of the Flexible Query Answering Systems, 8th International Conference, FQAS 2009, Roskilde, Denmark, 26–28 October 2009; Lecture Notes in Computer Science; Proceedings. Andreasen, T., Yager, R.R., Bulskov, H., Christiansen, H., Larsen, H.L., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5822, pp. 358–370. [Google Scholar] [CrossRef]
- Masciari, E.; Mazzeo, G.M.; Zaniolo, C. Analysing microarray expression data through effective clustering. Inf. Sci. 2014, 262, 32–45. [Google Scholar] [CrossRef]
- Masciari, E.; Moscato, V.; Picariello, A.; Sperlì, G. A Deep Learning Approach to Fake News Detection. In Proceedings of the Foundations of Intelligent Systems—25th International Symposium, ISMIS 2020, Graz, Austria, 23–25 September 2020; Lecture Notes in Computer Science. Helic, D., Leitner, G., Stettinger, M., Felfernig, A., Ras, Z.W., Eds.; Springer: Berlin/Heidelberg, Germany, 2020; Volume 12117, pp. 113–122. [Google Scholar] [CrossRef]
- Masciari, E.; Moscato, V.; Picariello, A.; Sperlì, G. Detecting fake news by image analysis. In Proceedings of the IDEAS 2020: 24th International Database Engineering & Applications Symposium, Seoul, Republic of Korea, 12–14 August 2020; Desai, B.C., Cho, W., Eds.; ACM: New York, NY, USA, 2020; pp. 27:1–27:5. [Google Scholar] [CrossRef]
- Fazzinga, B.; Flesca, S.; Masciari, E.; Furfaro, F. Efficient and effective RFID data warehousing. In Proceedings of the International Database Engineering and Applications Symposium (IDEAS 2009), Cetraro, Italy, 16–18 September 2009; International Conference Proceeding Series. Desai, B.C., Saccà, D., Greco, S., Eds.; ACM: New York, NY, USA, 2009; pp. 251–258. [Google Scholar] [CrossRef]
- Fazzinga, B.; Flesca, S.; Furfaro, F.; Masciari, E. RFID-data compression for supporting aggregate queries. ACM Trans. Database Syst. 2013, 38, 11. [Google Scholar] [CrossRef]
- Masciari, E.; Gao, S.; Zaniolo, C. Sequential pattern mining from trajectory data. In Proceedings of the 17th International Database Engineering & Applications Symposium, IDEAS ’13, Barcelona, Spain, 9–11 October 2013; Desai, B.C., Larriba-Pey, J.L., Bernardino, J., Eds.; ACM: New York, NY, USA, 2013; pp. 162–167. [Google Scholar] [CrossRef]
- Galli, L.; Fraternali, P.; Martinenghi, D.; Tagliasacchi, M.; Novak, J. A Draw-and-Guess Game to Segment Images. In Proceedings of the 2012 International Conference on Privacy, Security, Risk and Trust, PASSAT 2012, and 2012 International Confernece on Social Computing, SocialCom 2012, Amsterdam, The Netherlands, 3–5 September 2012; IEEE Computer Society: Washington, DC, USA, 2012; pp. 914–917. [Google Scholar] [CrossRef]
- Bozzon, A.; Catallo, I.; Ciceri, E.; Fraternali, P.; Martinenghi, D.; Tagliasacchi, M. A Framework for Crowdsourced Multimedia Processing and Querying. In Proceedings of the First International Workshop on Crowdsourcing Web Search, Lyon, France, 17 April 2012; CEUR Workshop Proceedings. Volume 842, pp. 42–47. [Google Scholar]
- Loni, B.; Menendez, M.; Georgescu, M.; Galli, L.; Massari, C.; Altingövde, I.S.; Martinenghi, D.; Melenhorst, M.; Vliegendhart, R.; Larson, M. Fashion-focused creative commons social dataset. In Proceedings of the Multimedia Systems Conference 2013, MMSys ’13, Oslo, Norway, 27 February–1 March 2013; pp. 72–77. [Google Scholar]
- Costa, G.; Manco, G.; Masciari, E. Dealing with trajectory streams by clustering and mathematical transforms. J. Intell. Inf. Syst. 2014, 42, 155–177. [Google Scholar] [CrossRef]
- Wang, H.; He, D.; Yu, J.; Xiong, N.N.; Wu, B. RDIC: A blockchain-based remote data integrity checking scheme for IoT in 5G networks. J. Parallel Distrib. Comput. 2021, 152, 1–10. [Google Scholar] [CrossRef]
- Srivastava, S.S.; Atre, M.; Sharma, S.; Gupta, R.; Shukla, S.K. Verity: Blockchains to Detect Insider Attacks in DBMS. arXiv 2019, arXiv:1901.00228. [Google Scholar]
- Ji, Y.; Shao, B.; Chang, J.; Bian, G. Flexible identity-based remote data integrity checking for cloud storage with privacy preserving property. Clust. Comput. 2022, 25, 337–349. [Google Scholar] [CrossRef]
- Bienvenu, M.; Bourgaux, C. Inconsistency Handling in Prioritized Databases with Universal Constraints: Complexity Analysis and Links with Active Integrity Constraints. arXiv 2023, arXiv:2306.03523. [Google Scholar]
- Nilsson, U.; Małuzyński, J. Logic, Programming and Prolog, 2nd ed.; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 1995. [Google Scholar]
- Lloyd, J. Foundations of Logic Programming, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1987. [Google Scholar]
- Apt, K.R.; Blair, H.A.; Walker, A. Towards a Theory of Declarative Knowledge. In Foundations of Deductive Databases and Logic Programming; Minker, J., Ed.; Morgan Kaufmann: Los Altos, CA, USA, 1988; pp. 89–148. [Google Scholar]
- Apt, K.R.; Bol, R.N. Logic Programming and Negation: A Survey. J. Log. Program. 1994, 19/20, 9–71. [Google Scholar] [CrossRef]
- Przymusinski, T.C. On the declarative semantics of deductive databases and logic programming. In Foundations of Deductive Databases and Logic Programming; Minker, J., Ed.; Morgan Kaufmann: Los Altos, CA, USA, 1988; pp. 193–216. [Google Scholar]
- Gelfond, M.; Lifschitz, V. Minimal Model Semantics for Logic Programming. In Logic Programming: Proceedings of the Fifth Logic Programming Symposium; Kowalski, R., Bowen, K., Eds.; MIT Press: Cambridge, MA, USA, 1988; pp. 1070–1080. [Google Scholar]
- van Gelder, A.; Ross, K.; Schlipf, J.S. Unfounded sets and well-founded semantics for general logic programs. In Proceedings of the ACM SIGACT-SIGMOD-SIGART Symposium on Principles of Database Systems (PODS 88), Austin, TX, USA, 21–23 March 1988; pp. 221–230. [Google Scholar]
- Dijkstra, E.W. A Discipline of Programming; Prentice-Hall: Hoboken, NJ, USA, 1976. [Google Scholar]
- Hoare, C. An axiomatic basis for computer programming. Commun. ACM 1969, 12, 576–580. [Google Scholar] [CrossRef]
- Bol, R.N. Loop checking in partial deduction. J. Log. Program. 1993, 16, 25–46. [Google Scholar] [CrossRef][Green Version]
- Grant, J.; Minker, J. The impact of logic programming on databases. Commun. ACM CACM 1992, 35, 66–81. [Google Scholar] [CrossRef]
- Grant, J.; Minker, J. Integrity Constraints in Knowledge Based Systems. In Knowledge Engineering Vol II, Applications; Adeli, H., Ed.; McGraw-Hill: New York, NY, USA, 1990; pp. 1–25. [Google Scholar]
- Eisinger, N.; Ohlbach, H.J. Deduction Systems Based on Resolution. In Handbook of Logic in Artificial Intelligence and Logic Programming—Vol 1: Logical Foundations; Gabbay, D.M., Hogger, C.J., Robinson, J.A., Eds.; Clarendon Press: Oxford, UK, 1993; pp. 183–271. [Google Scholar]
- Robinson, J.A. A Machine-Oriented Logic Based on the Resolution Principle. J. ACM 1965, 12, 23–41. [Google Scholar] [CrossRef]
- Chang, C.L.; Lee, R.C. Symbolic Logic and Mechanical Theorem Proving; Academic Press: Cambridge, MA, USA, 1973. [Google Scholar]
- Topor, R.W. Domain-Independent Formulas and Databases. Theor. Comput. Sci. 1987, 52, 281–306. [Google Scholar] [CrossRef][Green Version]
- Lloyd, J.W.; Topor, R.W. Making Prolog more Expressive. J. Log. Program. 1984, 3, 225–240. [Google Scholar] [CrossRef]
- Information Technology—Database Languages—GQL. 2024. Available online: https://www.iso.org/standard/76120.html (accessed on 17 February 2025).
- Magnanimi, D.; Bellomarini, L.; Ceri, S.; Martinenghi, D. Reactive Company Control in Company Knowledge Graphs. In Proceedings of the 39th IEEE International Conference on Data Engineering, ICDE 2023, Anaheim, CA, USA, 3–7 April 2023; pp. 3336–3348. [Google Scholar] [CrossRef]
- Baldazzi, T.; Sallinger, E. iWarded. 2022. Available online: https://github.com/joint-kg-labs/iWarded (accessed on 17 February 2025).
- Cole, R.L.; Graefe, G. Optimization of Dynamic Query Evaluation Plans. In Proceedings of the 1994 ACM SIGMOD International Conference on Management of Data, Minneapolis, MN, USA, 24–27 May 1994; Snodgrass, R.T., Winslett, M., Eds.; ACM Press: New York, NY, USA, 1994; pp. 150–160. [Google Scholar]
- Seshadri, P.; Hellerstein, J.M.; Pirahesh, H.; Leung, T.Y.C.; Ramakrishnan, R.; Srivastava, D.; Stuckey, P.J.; Sudarshan, S. Cost-Based Optimization for Magic: Algebra and Implementation. In Proceedings of the 1996 ACM SIGMOD International Conference on Management of Data, Montreal, QC, Canada, 4–6 June 1996; Jagadish, H.V., Mumick, I.S., Eds.; ACM Press: New York, NY, USA, 1996; pp. 435–446. [Google Scholar]
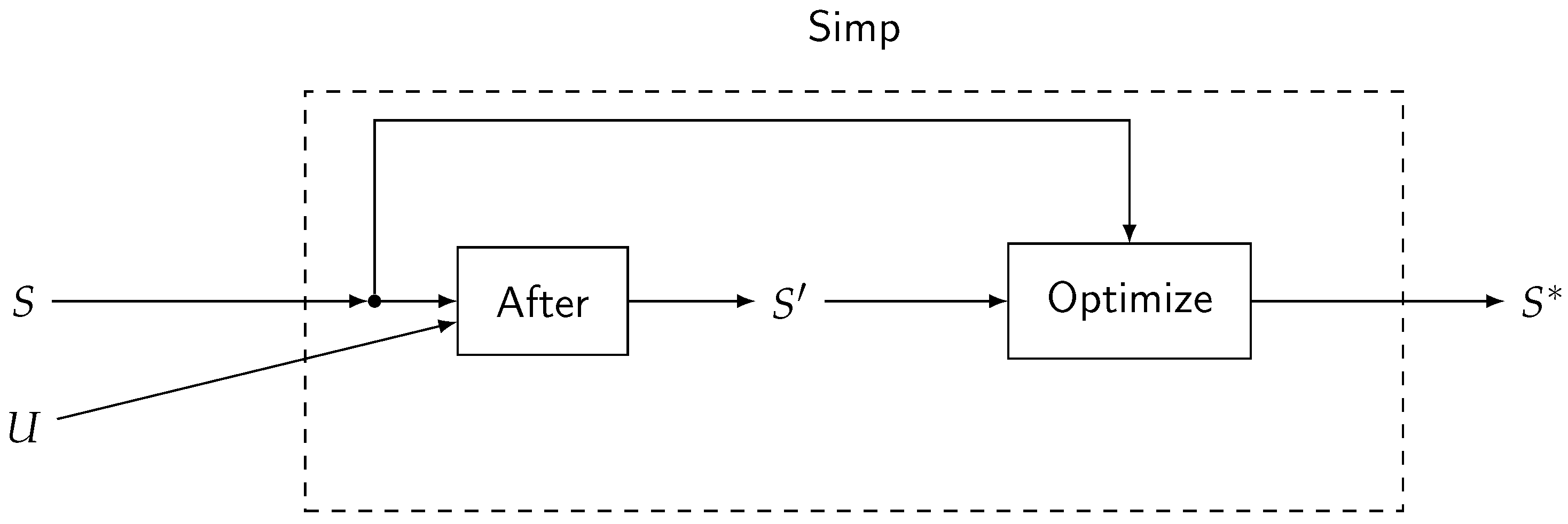

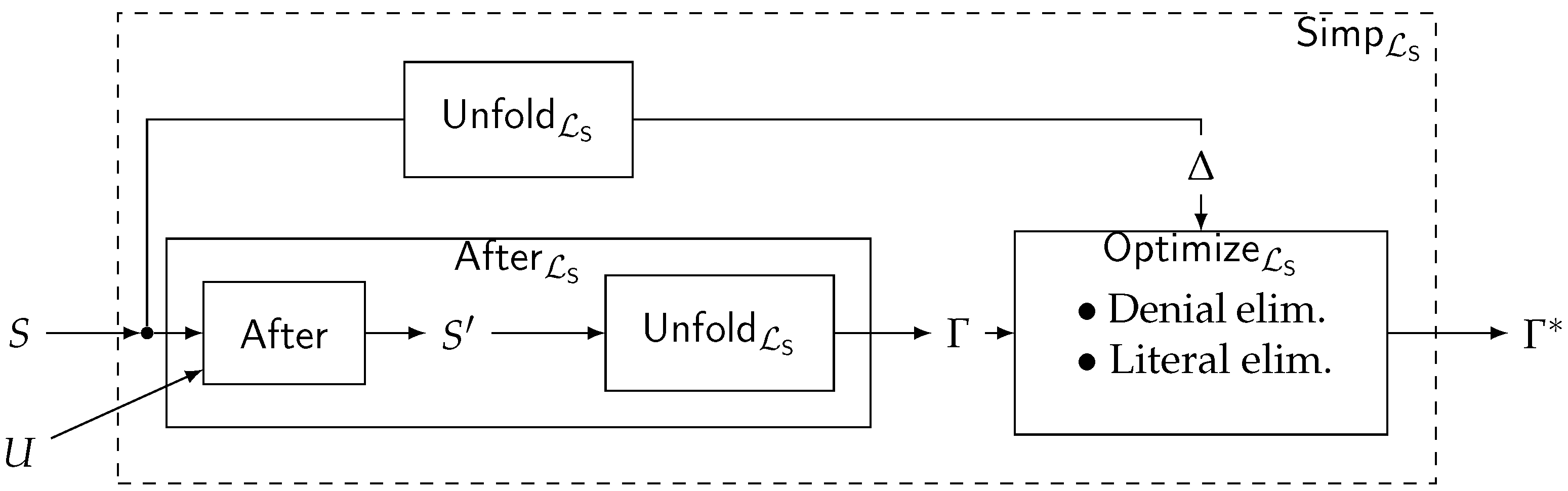
| Notation | Explanation |
|---|---|
| Schema is a WP of schema S wrt update U (Definition 7) | |
| A class of schemata that can be unfolded as a set of denials (Definition 6) | |
| For a schema , is the unfolding of wrt (Definition 8) | |
| The set of denials is a WP of schema wrt update U, and is defined as | |
| Denial subsumes denial (Definition 9) | |
| Denial strictly subsumes denial (Definition 9) | |
| Reduction: same as denial but without redundancies (Definition 10) | |
| , | Expansion: same as denial (or set of denials ) with constants and repeated variables replaced by new variables and equalities; see [8] |
| Denial is derived from the set of denials . In particular, there is a resolution derivation of a denial from such that (Definition 11) | |
| is the result of applying denial elimination and literal elimination from the set of denials as long as possible by trusting the set of denials (Definition 12) | |
| The set of denials is a CWP of schema wrt update U computed through and (Definition 13) |
| Notation | Explanation |
|---|---|
| A class of schemata that can be unfolded as a set of extended denials (Definition 14) | |
| For a schema , is the unfolding of wrt (Definition 16) | |
| The set of extended denials is a WP of schema wrt update U (Definition 17) | |
| Extended denial extended-subsumes extended denial (Definition 19) | |
| Reduction: same as extended denial but without redundancies (Definition 20) | |
| is the result of applying (possibly nested) extended denial elimination and general literal elimination from constraint theory as long as possible by trusting constraint theory (Definition 21) | |
| The set of extended denials is a CWP of schema wrt update U computed through and (Definition 22) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martinenghi, D. Simplified Integrity Checking for an Expressive Class of Denial Constraints. Algorithms 2025, 18, 123. https://doi.org/10.3390/a18030123
Martinenghi D. Simplified Integrity Checking for an Expressive Class of Denial Constraints. Algorithms. 2025; 18(3):123. https://doi.org/10.3390/a18030123
Chicago/Turabian StyleMartinenghi, Davide. 2025. "Simplified Integrity Checking for an Expressive Class of Denial Constraints" Algorithms 18, no. 3: 123. https://doi.org/10.3390/a18030123
APA StyleMartinenghi, D. (2025). Simplified Integrity Checking for an Expressive Class of Denial Constraints. Algorithms, 18(3), 123. https://doi.org/10.3390/a18030123






