Three-Dimensional Object Recognition Using Orthogonal Polynomials: An Embedded Kernel Approach

Abstract

Computer vision seeks to mimic the human visual system and plays an essential role in artificial intelligence. It is based on different signal reprocessing techniques; therefore, developing efficient techniques becomes essential to achieving fast and reliable processing. Various signal preprocessing operations have been used for computer vision, including smoothing techniques, signal analyzing, resizing, sharpening, and enhancement, to reduce reluctant falsifications, segmentation, and image feature improvement. For example, to reduce the noise in a disturbed signal, smoothing kernels can be effectively used. This is achievedby convolving the distributed signal with smoothing kernels. In addition, orthogonal moments (OMs) are a crucial technique in signal preprocessing, serving as key descriptors for signal analysis and recognition. OMs are obtained by the projection of orthogonal polynomials (OPs) onto the signal domain. However, when dealing with 3D signals, the traditional approach of convolving kernels with the signal and computing OMs beforehand significantly increases the computational cost of computer vision algorithms. To address this issue, this paper develops a novel mathematical model to embed the kernel directly into the OPs functions, seamlessly integrating these two processes into a more efficient and accurate approach. The proposed model allows the computation of OMs for smoothed versions of 3D signals directly, thereby reducing computational overhead. Extensive experiments conducted on 3D objects demonstrate that the proposed method outperforms traditional approaches across various metrics. The average recognition accuracy improves to 83.85% when the polynomial order is increased to 10. Experimental results show that the proposed method exhibits higher accuracy and lower computational costs compared to the benchmark methods in various conditions for a wide range of parameter values.

1. Introduction

Three-dimensional object recognition is considered an important research area in computer vision and artificial intelligence. It focuses on the identification and classification of objects in three-dimensional space. In contrast to 2D, 3D object recognition makes use of depth data, spatial relationships, and geometric features, which lead to a better understanding of the object in the real world [1]. This capability is considered essential for applications where both perception accuracy and real-world interaction are required [2].

The importance of 3D object recognition arises from its wide range of applications across various industries. In augmented and virtual reality, 3D recognition improves the user experiences by allowing for simple interactions with virtual objects in the real world [3]. In robotics, 3D object recognition enables machines to navigate and process objects efficiently, facilitating several tasks such as autonomous navigation and object grasping [4,5]. In healthcare, 3D object recognition enhances advanced medical imaging and surgical planning by providing detailed 3D reconstructions of anatomical structures [6]. In addition, in security and surveillance, 3D recognition improves object detection and tracking in complex environments, which enhances the capabilities of safety and monitoring [7]. Moreover, accurate recognition and interpretation of 3D objects is crucial for advancements in autonomous vehicles, where understanding the 3D structure of the environment is important for safe navigation [8].

Three-dimensional object recognition is important for bridging the gap between digital systems and the real world. As this technology continues to develop, 3D object recognition reveals exciting new possibilities, making it significant in the field of modern computer vision and AI research.

After capturing visual data, image processing algorithms are utilized to identify 3D objects, and areas of interest. These algorithms play a crucial role in extracting meaningful information from visual inputs. This is essential for tasks such as 3D object detection, classification, and scene understanding. Utilizing advanced algorithms, systems can interpret and analyze visual data efficiently across various domains [9]. Within this context, orthogonal polynomials (OPs) can be used, which serve as powerful mathematical tools that significantly enhance the overall performance of the system [10,11,12]. The application of OPs in image preprocessing ensures accurate and efficient processing, making them indispensable for achieving reliable and precise navigation in autonomous robotic systems [13]. A great deal of progress in the OPs field has been made recently in relation to significant analysis branches because OPs are connected to different functions, such as hypergeometric, trigonometric, and elliptic functions. In addition, OPs are related to continued fractions theory, as well as to problems of interpolation, mechanical quadrature, and their occurrence in the theory of integral and differential equations. Moreover, OPs provide instructive illustrations of some situations in the theory of orthogonal systems. In addition, some OPs have recently played important roles in mathematical statistics and quantum mechanics [14]. Moments are considered as the projection of OPs on the signal domain [15].

Discrete moments, also known as discrete orthogonal moments, have been utilized in various signal processing fields such as speech, image, and video processing [16,17,18,19]. They are commonly used as a shape descriptor and are applied in different tasks such as face recognition [20], image classification [21], differential equations [22,23,24,25], speech enhancement [26], and edge detection [27]. Moreover, orthogonal moments have been utilized in other areas such as speech enhancement [28,29], watermarking [30], medical image analysis [31,32,33], and shot boundary detection [34].

In general, moments are quantities that are used to represent 1D, 2D, and 3D data without redundancy, making them an effective and efficient data descriptor. This means that moments have the capability to describe data while avoiding duplication [35,36,37]. Signal preprocessing techniques play a crucial role in enhancing the performance of computer vision algorithms by improving the quality of input data [38]. For instance, noise is removed from signals by utilizing smoothing kernels, such as averaging kernels. This is performed to obtain a more clean and reliable data for the remaining processing steps [19,39]. Furthermore, gradient kernels are usually used to calculate the gradients in the x-direction for 1D signals, x- and y-directions for 2D signals, and x-, y- and z-directions for 3D signals to determine intensity changes in the aforementioned directions, respectively. Extracting moments from images following preprocessing with smoothing and/or gradient image kernels is an effective approach to represent signals [40,41]. However, some existing works are required to reduce the spectral data space and, consequently, the computational load. More improvement is required to obtain more robust and accurate methods.

In order to obtain a smoothed and gradient version of a 3D signal f, kernels $h_s$ and $h_g$ are convolved with the signal. The convolution process is carried out separately for each required version of the 3D signal. Once the smoothed and gradient versions of the 3D signal are obtained, moments can be extracted from them. However, performing these operations for each signal significantly increases the computational cost of a feature extraction algorithm, such as for 3D object recognition. Recently, 3D object recognition has emerged as a transformative technology with significant potential in fields such as virtual reality, autonomous driving, and commercial manufacturing. While advanced feature extraction methods, including deep learning models, have achieved impressive results in this domain, their high computational cost poses a substantial challenge, particularly for resource-constrained mobile applications [42]. Three-dimensional object recognition is a complex process because 3D objects provide a large variety of projected images based on viewing direction, illumination, distance, and other viewing conditions [43]. To deal with viewing direction effects, in [43], a computational work is demonstrated using sets of a small number of object viewpoints. However, this approach leaves many problems unanswered. The main problems include the use of abstractions, class-based recognition, and the classification problem, which requires a large experimental and computational research. Basically, computer vision is an active task and plays a crucial role in making the computer system see and identify the visual world automatically based on simulating the basic biological ability of human visual perception. Therefore, to achieve a high potential, the focus is on having an accurate algorithm with a lower computational cost [44,45].

Therefore, the aim of this paper is to obtain an accurate algorithm with a lower computational cost by addressing the aforementioned issues. To this end, we propose a new mathematical model for 3D object recognition that computes preprocessed signal moments by combining two operations into one, thereby reducing the cost of clustering. This model can be effectively used in mobile robot applications. To achieve this, we have embedded a smoothing kernel operator into OP functions to extract features quickly and efficiently. Our contributions are as follows:

• We presented a mathematical model that integrates image kernels directly into orthogonal polynomial (OP) functions, eliminating the need for separate convolution and orthogonal moment (OM) computation processes. This innovation significantly reduces computational overhead while maintaining accuracy.
• The presented mathematical model shows a reduction in computational cost, making it suitable for applications and large-scale 3D signal processing. Moreover, the method not only enhances efficiency but also achieves an improvement in recognition accuracy. In addition, the presented approach can be used with any discrete orthogonal polynomials.
• We conducted extensive experiments using the well-known McGill benchmark dataset to validate the effectiveness of the presented approach. These experiments were performed under various noisy environments to evaluate the robustness and reliability of the approach.

This paper is organized as follows: Section 2 discusses the preliminaries related to the orthogonal polynomial (OP) used in this paper and the formulation of the squared Krawtchouk–Tchebichef polynomial. In Section 3, the methodology of the proposed approach is given. Section 4 carries out the performance evaluation of the proposed recognition system based on the proposed technique. Finally, the paper concludes with a summary of findings and future directions in Section 5.

2. Preliminaries

This section describes the OP used in this paper, as well as the process of computing moments, which will be used in the vision and control system of mobile robots to ensure safe navigation in environments. Moments have a significant role in the process of feature extraction. Feature selection is the process of choosing a subset of relevant features from a larger set for a particular task, such as classification. The length of the feature vector is important in the performance of machine learning algorithms. Forming a feature vector using too few features may not capture enough information, which affects the recognition accuracy. On the other hand, constructing a feature vector using too many features can lead to overfitting. Therefore, finding the optimal feature vector length is essential.

Features that possess energy compaction and localization properties in the moment domain are able to simplify feature handling and have a significant impact on processing steps [46]. This is because they allow the signal to be expressed using a small number of moments, reducing computational complexity. Moreover, the localization property in space identifies the region of interest, which speeds up the computation and improves feature classification [47]. To achieve these properties, this paper uses the squared Krawtchouk–Tchebichef polynomial (SKTP) as a discrete transform. The SKTP has been shown to have robust performance in different applications, demonstrating its powerful energy compaction and localization properties [46]. Moreover, its localization property in space contributes an additional reduction in computation and feature classification by locating the region of interest (ROI) [48].

2.1. Formulation of the Squared Krawtchouk–Tchebichef Polynomial

The SKTP is a mathematical function that is generated by combining two orthogonal polynomials according to a defined mathematical operation. This method is efficiently applicable because when two orthogonal polynomials are multiplied, the result is also an orthogonal polynomial. This means that the properties of the original polynomials are maintained in the newly generated polynomial, as explained in [28,46,49]. To this end, the SKTP can be expressed as the nth order of the polynomial $R_n^p(x;N)$, where p is a parameter that determines the shift of the polynomial and N is the maximum degree of the polynomial so that

$$R_n^p(x;N)=\sum _{i=0}^{N-1}{A}_i^p(x;N)B_i^p(n;N),$$

(1)

where $A_n^p(x;N)$, and $B_n^p(x;N)$ represent the discrete Krawtchouk–Tchebichef polynomial (DKTP) [28] and discrete Tchebichef–Krawtchouk polynomial (DTKP) [49], respectively. The aforementioned polynomials are also formed from two orthogonal polynomials, which are defined by [28,49] as follows:

$$\begin{array}{cc}\hfill A_n^p(x;N)& =\sum _{i=0}^{N-1}{K}_i^p(n;N)T_i(x;N),\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill B_n^p(x;N)& =\sum _{i=0}^{N-1}{K}_i^p(x;N)T_i(n;N),\hfill \end{array}$$

(3)

where $K_n^p(x;N)$ and $T_n(x;N)$ are the Krawtchouk and Tchebichef polynomials, respectively. Note that p represents the parameter of the Krawtchouk polynomials. From (2) and (3), the SKTP that is defined in (1) can also be written as follows:

$$R_n^p(x;N)=\sum _{i=0}^{N-1}\sum _{j=0}^{N-1}\sum _{l=0}^{N-1}{K}_j^p(i;N)T_j(x;N)K_l^p(n;N)T_l(i;N).$$

(4)

The matrix of SKTP, $\mathbf{R}$, can be represented by multiplying the Krawtchouk and Tchebichef polynomials using matrix multiplication properties as

$$\mathbf{R}={\left(\mathbf{K}\mathbf{T}\right)}^2$$

(5)

2.2. Computation of 3D Moments

In the literature, there are different methods proposed for computing 3D moments. Examples of these methods are the direct method, cubes method, and matrix product method, as well as Kronecker tensor and matrix product method [50]. The primary goal of these methods is to minimize computation time while maintaining accuracy. However, the computational complexity of these methods varies. For example, the direct method has a computational complexity of $\mathcal{O}\left(n^6\right)$, while the cubes method has a complexity of $\mathcal{O}\left({\left({\displaystyle \frac{n}{Cubos}}\right)}^6\right)$, the matrix product method has a complexity of $\mathcal{O}\left({\left({\displaystyle \frac{n}{8}}\right)}^6\right)$, and finally, the Kronecker tensor and matrix product method has a complexity of $\mathcal{O}\left(n^{3.81}\right)$ [50]. As illustrated above, the computational complexity burden could be very high, especially with 3D signals. To overcome this issue, this paper proposes an efficient method of using the Kronecker tensor as well as the matrix multiplication method to compute the moments in an efficient way with lower computational complexity. To this end, for a 3D signal $f(x,y,z)$, the moments $\mathbf{M}$ can be computed as follows [50]:

$$\begin{array}{cc}\hfill {\mathbf{M}}_{:,k}& =\sum _z{\mathbf{R}}_{k,z}\otimes \left[{\mathbf{R}}_{n,x}\mathbf{F}{\mathbf{R}}_{m,y}\right]\hfill \\ \hfill & n,m,k=0,1,\dots ,Ord,\hfill \end{array}$$

(6)

where $Ord$ represents the order, and ${\mathbf{M}}_{n,m,k}\in {\mathbb{R}}^{L\times L\times L}\leftarrow {\mathbf{M}}_{:,k}\in {\mathbb{R}}^{L^2\times L}$.

3. Research Design and Methodology

This section describes the methodology of the proposed method. Suppose we have a 3D object, denoted by $f(x,y,z)$, with dimensions $N_x\times N_y\times N_z$. Let us also consider a kernel, denoted by $h(u,v,w)$, that we convolve with $f(x,y,z)$ resulting in a new 3D object of size $N_x\times N_y\times N_z$, denoted by $g(x,y,z)$ that can be written as:

$$\begin{array}{cc}\hfill g(x,y,z)& =f(x,y,z)\ast h(u,v,w)\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill g(x,y,z)& =\sum _{u=-a}^a\sum _{v=-b}^b\sum _{w=-c}^{c}f(x,y,z)h(u-x,v-y,w-z).\hfill \end{array}$$

(8)

When convolving a kernel of size $A\times B\times C$ with a function $f(x,y,z)$, it is possible to decompose the convolution operation into three separate operations. This approach is called spatially separable convolution. In this method, the kernel of size $A\times B\times C$ is split into three separate kernels: an $A\times 1\times 1$ kernel, a $1\times B\times 1$ kernel, and a $1\times 1\times C$ kernel.

In the spatially separable convolution process, the first kernel, i.e., the $A\times 1\times 1$ kernel, is convolved with $f(x,y,z)$, followed by convolving the result with the $1\times B\times 1$ kernel and then convolving the output of the previous step with the $1\times 1\times C$ kernel. This technique has been explained in detail in [51]. As a result of this decomposition, the original convolution equation, represented by (7), can be rewritten as follows:

$$g(x,y,z)=\sum _{u=-a}^a\left[\sum _{v=-b}^b\left[\sum _{w=-c}^{c}f(x,y,z)h(w-z)\right]h(v-y)\right]h(u-x).$$

(9)

To calculate the moments of the function $g(x,y,z)$, we can use Equation (6). This equation will yield the moments (${\mathbf{MC}}_{n,m,k}$) of the original function $f(x,y,z)$ after it has been convolved with the kernel and can be expressed, in the form of a matrix, as follows:

$$\begin{array}{cc}\hfill {\mathbf{MC}}_{:,k}& =\sum _z{\mathbf{R}}_{k,z}\otimes \left[{\mathbf{R}}_{n,x}\mathbf{G}{\mathbf{R}}_{m,y}^T\right]\hfill \\ \hfill & n,m,k=0,1,\dots ,Ord,\hfill \end{array}$$

(10)

where $\mathbf{G}$ denotes the matrix form of the function $g(x,y,z)$ and ⊗ represents the mathematical kronecker product. In what follows, we provide proof of the above expression.

Proposition 1. 

Suppose we have a function $\mathbf{p}$ that is convolved with a kernel $\mathbf{h}$. The outcome of this convolution operation is a new function $\mathbf{q}$, which can be expressed as follows:

$$\mathbf{q}=\mathbf{p}\ast \mathbf{h}.$$

(11)

Typically, the convolution operation presented above can be reformulated using the properties of matrix multiplication. The resulting matrix can be expressed as follows:

$$\mathbf{Q}=\mathbf{H}\mathbf{P},$$

(12)

In the equation mentioned above, the matrix H represents the Toeplitz matrix of the kernel $\mathbf{h}$. Using this equation, we can compute the moments Φ as a function of $\mathbf{Q}$ as follows:

$$\mathbf{\Phi }=\mathbf{R}\mathbf{Q}.$$

(13)

To this end, we can substitute matrix $\mathbf{P}$ given above into the moment function Φ. The resulting moment function Φ can be written as follows:

$$\begin{array}{cc}\hfill \mathbf{\Phi }& =\mathbf{R}\mathbf{H}\mathbf{P}\hfill \end{array}$$

(14)

Let us assume that ${\mathbf{R}}_{\mathbf{e}}=\mathbf{R}\mathbf{H}$, which represents the orthogonal polynomials embedded with the kernel $\mathbf{H}$ so that we have the following:

$$\begin{array}{cc}\hfill \mathbf{\Phi }& ={\mathbf{R}}_{\mathbf{e}}\mathbf{P}\hfill \end{array}$$

(15)

The concept we discussed above can also be extended to multidimensional signals. In other words, we can use the same approach to compute moments for signals with more than two dimensions. To achieve this, we can substitute Equation (14) into (10), which yields the following formula:

$${\mathbf{MC}}_{:,k}=\sum _z{\mathbf{R}}_{e(k,z)}\otimes \left[{\mathbf{R}}_{e(n,x)}\mathbf{F}{\mathbf{R}}_{e(m,y)}^T\right].$$

(16)

From the formula (16), we can observe that the moments of the function g can be calculated using the original function f and the orthogonal polynomials that contain the kernels within them. These orthogonal polynomials are denoted as ${\mathbf{R}}_{e(n,x)}$, ${\mathbf{R}}_{e(m,y)}$, and ${\mathbf{R}}_{e(k,z)}$ for the x, y, and z dimensions, respectively. Here, ${\mathbf{R}}_e$ is the embedded version of the orthogonal polynomials and is obtained by multiplying $\mathbf{R}$ (the standard orthogonal polynomial matrix) with the Toeplitz matrix H of the corresponding kernel ($h_x$, $h_y$, or $h_z$). It is important to note that the Toeplitz matrix H represents the convolution kernel.

Remark 1. 

The current formula for computing moments is faster than the formula that first applies the convolution operation and then computes the moments. This is because in the current formula, the kernels are embedded within the polynomials themselves. This embedding operation is performed at the beginning, after checking the database and extracting relevant information. Once the embedding is complete, the moments can be computed without the need to apply the kernel for each object (function).

In other words, the current method saves computational time because the convolution operation is performed only once, and the resulting orthogonal polynomials containing the embedded kernels are then used to calculate moments for multiple objects without the need for repeated convolution.

Note that the matrix $\mathbf{H}$ in the previous equation represents a Toeplitz matrix that is truncated to a size of $N\times N$ for the operator $\mathbf{h}$. Suppose $\mathbf{h}=[{\mathbf{h}}_0,h_1,\dots ,{\mathbf{h}}_m]$, then the Toeplitz matrix can be constructed as follows:

$$\begin{array}{c}\hfill \mathbf{H}=\left[\begin{array}{cccccc}{h}_0& 0& 0& \dots & 0& 0\\ h_1& h_0& 0& 0& \dots & 0\\ ⋮& h_1& h_0& 0& \dots & 0\\ h_m& ⋮& h_1& \ddots & \ddots & ⋮\\ 0& h_m& ⋮& \ddots & h_0& 0\\ 0& 0& h_m& \dots & h_1& h_0\end{array}\right].\end{array}$$

(17)

After presenting the mathematical model for moment computation, it can be applied for object recognition to demonstrate its advantages and importance. This process includes the following steps: generating the orthogonal polynomials, followed by constructing the Toeplitz matrix version of the kernel, and finally, embedding the kernel into the orthogonal polynomials. This approach has several advantages, such as efficient and fast moment computation, without the need to repeatedly apply the kernel for each object, which makes it ideal for object recognition systems.

Research Design

In this section, the design of the methodology is provided. The feature extraction process plays a crucial role in object recognition systems. Features extracted using orthogonal polynomials are considered robust. However, to improve the representation of feature, the selection of orthogonal polynomials is substantial. Therefore, in the proposed recognition system, we have utilized the squared Krawtchouk–Tchebichef polynomial (SKTP) due to its superior performance in signal representation. The SKTP is formed of Krawtchouk and Tchebichef polynomials using (5), which also can be written as follows:

$$R_S={(R_K\times R_T)}^2,$$

(18)

where $R_S$, $R_K$, and $R_T$ represent the SKTP, Krawtchouk polynomials, and the Tchebichef polynomials, respectively. To improve the robustness of the features, we embedded kernels in the orthogonal polynomials to perform feature extraction. This will speed up the feature extraction process compared with a traditional feature extraction process. The traditional process starts with processing the object using the image kernels, then the process of feature extraction is performed. However, for the proposed technique, the feature extraction process is performed directly on the object, i.e., the proposed technique eliminates extra process while maintaining its effect. To embed the kernel in the orthogonal polynomials, we follow Equation (12). For more illustration, Figure 1 and Figure 2 show the effect of gradient kernels on 3D object samples using conventional convolution and OP-based convolution.

To generate the kernel, first, the length of the kernel ($l_{kernel}$) is set to generate 1D kernel. Moreover, the object information is extracted from the object dataset, where the object information includes the size of the object $N_x$, $N_y$, and $N_z$. According to the extracted object information, the orthogonal polynomials (SKTP) are generated. After generating the orthogonal polynomials, the generated kernel is embedded into the orthogonal polynomials. The resulting polynomials $P_x$, $P_y$, $P_z$ are then used to compute the moments. Figure 3 shows the proposed technique described above.

After computing the moments, the feature vector is generated and it is used for classification. The features are set to a specific size, which is performed by setting up the order of the orthogonal polynomials. In other words, the moments size is limited to the order of the orthogonal polynomials. These orders are $Or{d}_x$, $Or{d}_y$, and $Or{d}_z$ for the polynomials $P_x$, $P_y$, and $P_z$, respectively. Therefore, the moment size will be $Or{d}_x\times Or{d}_y\times Or{d}_z$. After computing the moment, it is flattened to form the feature vector. Thereafter, the feature vector is normalized and used for classification. It is noteworthy that after obtaining the normalized feature vector, each normalized feature vector is associated with a label (ID) for each object. The labels are used for training and testing processes. In this paper, support vector machine (SVM) is employed for its ability to optimize the margin between two hyperplanes that separate the classes [52]. Moreover, SVM is widely used in recognition for its robustness against signal fluctuations compared to other classifiers [53]. Figure 3 shows the presented technique for embedding kernels. Moreover, Figure 4 shows the methodology using the proposed technique for 3D object recognition.

4. Results and Discussion

The performance of the recognition system based on the proposed technique is evaluated in this section. The evaluation is performed using the McGill dataset formed in [54]. Figure 5 shows samples of the object in the dataset. The dataset (McGill) serves as a benchmark dataset and includes nineteen classes expressed as 3D objects. These classes are categorized as planes, chairs, dinosaurs, fishes, cups, birds, spiders, spectacles, snakes, octopus, teddies, pliers, dolphins, fours, ants, humans, tables, and craps. For the SVM, we utilized the LIB-SVM version 3.24 [55]. It is noteworthy that the experiment is performed using Matlab 2019 on an 8-core core i7-4700MQ CPU with a frequency of 2.4 HGz and 16 GB RAM.

In this paper, we focused on 19 different objects and applied a range of translation effects to enrich the original dataset. The augmentation process starts by shifting each object within a range from −10 to 10 along the x, y, and z axes, using a step size of 5. This systematic shifting creates a diverse array of translations, which helps the recognition system generalize better across various object positions. This augmentation approach guarantee that the dataset captures a wide range of spatial arrangements. A total of 5902 samples are generated as a result of the utilized augmentation techniques. To evaluate the performance of the proposed technique, we implemented different evaluation metric, which are discussed in the following sections.

4.1. Analysis of Optimal Parameter for Orthogonal Polynomial

In this section, first, we performed an experimental analysis to evaluate the performance of the proposed system for different values of the orthogonal polynomial parameter (p). The goal of this analysis is to identify the optimal value that enhances the performance of the proposed system. Support vector machine (SVM) is utilized as a classifier for this analysis. SVM is a powerful tool in the field of machine learning which is widely employed for classification and regression tasks. Compared to other classifiers, SVM’s robustness against signal fluctuations makes it particularly effective for recognition applications [53].

In this paper, SKTP is applied to 3D objects that are chosen from the McGill dataset. Various values of the polynomial parameter (p) are tested for the nth order of the polynomial ($R_n^p(x;N)$), where (p) affects the polynomial’s shift. The maximum order of the polynomial, denoted as ($Ord$), is set to 8, 10, and 12, while the values of the polynomial parameter (p) include 0.2, 0.3, 0.4, 0.5, and 0.6.

The SVM model was trained using 4134 3D objects from the McGill dataset, and the testing phase involved 1768 3D objects. The details of the dataset are given in

Table 1. Details of the McGill dataset.

Class ID	Class Name	Number of Samples	Class ID	Class Name	Number of Samples
1	airplanes	26	11	hands	20
2	ants	30	12	humans	26
3	birds	21	13	octopus	25
4	chairs	23	14	pliers	20
5	crabs	30	15	snakes	25
6	cups	25	16	spectacles	25
7	dinosaurs	19	17	spiders	31
8	dolphins	12	18	tables	22
9	fishes	23	19	teddy	20
10	four	31
Total number of samples			454

We examined three different cases of the orthogonal parameter to determine which configuration yields the best fitting effect of SKTP, ultimately aiming to achieve the most accurate signal representation based on the information provided by the 3D objects.

First, the SVM model is trained and tested in clean environment with the results reported in

Table 2. Recognition accuracy for clean environment with different OP parameter p and order.

p	0.2	0.3	0.4	0.5	0.6	Average
Ord
8	69.853	83.258	85.294	83.088	76.471	79.593
10	81.109	83.824	86.765	85.249	82.353	83.971
12	77.941	82.353	86.029	84.559	78.676	81.912

.

The results shows that the highest performance score is 86.765, which is achieved with ($p=$ 0.4) and ($Ord=$ 10). This combination indicates that a moderate value of (p) paired with a polynomial order ($Ord$) of 10 yields optimal results. Furthermore, the results demonstrate that the accuracy increases as the polynomial parameter p increases from 0.2 to 0.4, and the recognition accuracy declines after the polynomial parameter p becomes greater than 0.4 (0.5 and 0.6).

Moreover, the analysis of the average recognition accuracy across different polynomial orders ($Ord$) is important to providing the effect of the polynomial order. For ($Ord=$ 8), the average recognition accuracy is 79.593, indicating a good ability to capture a relevant representation of the data. This recognition accuracy increases to 83.971 for ($Ord=$ 10), which shows that the model benefits from increasing the number of features by a higher polynomial order, which enhances the fitting capabilities of data distribution. However, as the polynomial order increases to ($Ord=$ 12), the average performance score decreases to 81.912. The decrease in average performance shows that as the order of the polynomial increases, the complexity is also increases, potentially resulting in overfitting. These findings show the importance of selecting an appropriate polynomial order, as the results indicate that while higher orders can improve performance, there exists an optimal threshold.

To investigate the performance of the proposed approach, an experiment is performed in different noisy environments, namely Gaussian, salt-and-pepper, and speckle noise. This experiment aims to examine the effects of these various noise types on the ability of the presented technique to generalize across different configurations of the orthogonal polynomial parameter (p) and polynomial orders ($Ord$). The obtained results are reported in

Table 3. Recognition accuracy for noisy environments with different OP parameter p and order ($Ord=$ 8).

Environment		p
		0.2	0.3	0.4	0.5	0.6
Clean		69.853	83.258	85.294	83.088	76.471
Gaussian	0.01	69.570	82.692	84.842	82.636	76.357
	0.02	67.986	80.826	83.937	81.844	75.452
	0.03	66.516	78.281	82.692	80.995	75.170
	0.04	64.649	77.149	80.713	80.373	72.455
	0.05	63.462	77.093	78.676	78.959	69.514
Salt and Pepper	0.01	69.344	82.523	84.785	82.692	75.848
	0.02	67.364	81.505	83.767	81.674	75.226
	0.03	66.346	80.769	82.862	80.486	74.717
	0.04	65.667	79.016	81.505	79.808	73.756
	0.05	64.593	78.281	80.147	79.412	72.794
Speckle	0.2	69.627	82.296	84.615	82.692	76.018
	0.4	69.061	80.939	83.767	82.523	75.622
	0.6	68.722	79.299	83.258	81.844	75.057
	0.8	68.382	77.771	81.957	81.222	73.416
	1	67.590	75.905	80.882	80.882	72.059
Average of both clean and noisy environments		67.421	79.850	82.731	81.321	74.371

,

Table 4. Recognition accuracy for noisy environments with different OP parameter p and order ($Ord=$ 10).

Environment		p
		0.2	0.3	0.4	0.5	0.6
Clean		81.618	83.824	86.765	85.294	82.353
Gaussian	0.01	81.109	82.862	85.464	84.446	82.070
	0.02	79.921	81.505	84.615	84.050	79.016
	0.03	78.054	80.600	83.993	83.484	78.281
	0.04	76.640	79.977	82.975	81.505	77.771
	0.05	75.735	77.602	82.127	80.147	77.206
Salt and Pepper	0.01	81.335	83.145	85.351	84.106	82.353
	0.02	79.808	82.014	84.333	83.484	81.505
	0.03	77.941	80.600	83.258	82.523	80.430
	0.04	76.867	79.355	81.618	81.957	79.299
	0.05	75.962	78.450	80.882	81.618	78.054
Speckle	0.2	81.165	83.428	85.238	84.389	82.127
	0.4	79.751	81.957	84.276	83.993	82.014
	0.6	78.054	80.373	84.219	82.975	81.222
	0.8	75.396	78.507	83.428	82.183	80.260
	1	74.434	76.471	83.088	81.448	79.412
Average of both clean and noisy environments		78.362	80.667	83.852	82.975	80.211

and

Table 5. Recognition accuracy for noisy environments with different OP parameter p and order ($Ord=$ 12).

Environment		p
		0.2	0.3	0.4	0.5	0.6
Clean		77.941	82.353	86.029	84.559	78.676
Gaussian	0.01	77.432	81.900	84.898	84.276	77.941
	0.02	75.396	80.826	83.880	83.484	75.905
	0.03	74.095	78.507	83.258	82.127	75.622
	0.04	73.586	77.771	82.523	81.052	75.113
	0.05	72.738	76.980	80.769	78.959	74.717
Salt and Pepper	0.01	77.489	82.127	84.842	84.333	78.563
	0.02	76.131	81.165	84.219	83.428	77.602
	0.03	75.057	79.242	83.032	82.070	76.414
	0.04	74.095	78.394	82.579	81.448	74.038
	0.05	73.190	77.206	81.957	79.412	73.529
Speckle	0.2	77.206	81.165	84.729	84.106	77.941
	0.4	74.717	79.129	83.767	83.258	77.262
	0.6	73.020	76.867	82.975	82.975	75.962
	0.8	71.946	74.943	82.353	81.731	75.170
	1	70.928	74.887	81.618	80.995	74.265
Average of both clean and noisy environments		74.685	78.966	83.339	82.388	76.170

.

In Table 3, a comprehensive evaluation of 3D object recognition based on the proposed technique for polynomial order ($Ord=$ 8) is presented across various environments with different noise parameters. The Gaussian noisy environment reveals a decline in recognition accuracy as the noise level increases. At a Gaussian noise level of 1%, the recognition accuracy is 84.842 at $p=$ 0.4, indicating that the performance can be considered good under low noise conditions. However, as the noise level increases to 5%, the recognition accuracy drops to 78.676. The recognition accuracy in the salt and pepper noisy environment follows a comparable trend when compared to the Gaussian noisy environment, with a maximum recognition accuracy of 84.785 at $p=$ 0.4 and a noise density of 1%. As the noise level increases, the recognition accuracy declines, reaching a score of 80.147 at $p=$ 0.4 and a noise density of 5%. The analysis of speckle noise further emphasizes the challenges posed by noise in maintaining recognition accuracy. The results show that the recognition accuracy is 84.615 at $p=$ 0.4 and a noise variance of 0.2, but recognition accuracy decreases as the noise level increases, with a score of 80.882 at $p=$ 0.4 and a noise variance of 1.

In Table 4, we present a detailed assessment of 3D object recognition performance using the proposed technique for polynomial order ($Ord=$ 10) across various environments with differing noise parameters. In the clean environment, the system exhibits a high recognition accuracy, achieving a peak score of 86.765 at $p=$ 0.4. This high accuracy indicates that the system effectively captures the underlying features of the data without the interference of noise. The performance remains commendable across other parameter settings, with scores of 85.294 at $p=$ 0.5 and 83.824 at $p=$ 0.3. However, the lowest score of 81.618 is observed at $p=$ 0.2. When Gaussian noise is applied to the objects, the recognition accuracy shows a gradual decline as the noise level increases. At a noise level of 1%, the system maintains a recognition accuracy of 85.464 at $p=$ 0.4, indicating that it performs well under low noise conditions. However, as the noise level rises to 5%, the accuracy decreases to 82.127. The recognition accuracy for Gaussian noise at different levels demonstrate a consistent downward trend, with accuracy values of 84.615 at $p=$ 0.4 for a noise level of 2% and 83.993 at the same parameter for a noise level of 3%. The performance in the salt and pepper noisy environment reveals the same trends observed in the Gaussian noise scenario. The system achieves a maximum recognition accuracy of 85.351 at $p=$ 0.4 and a noise density of 0.01. As the noise density increases, the recognition accuracy declines, reaching 80.882 at $p=$ 0.4 and a noise density of 0.05. This decline highlights that the system is sensitive to high levels of salt and pepper noise. The recognition accuracy for salt and pepper noise also reflect a gradual decrease, with values of 84.333 at $p=$ 0.4 for a noise density of 0.02 and 83.258 at the same parameter for a noise density of 0.03. The analysis of speckle noise further illustrates the challenges associated with maintaining recognition accuracy in the presence of noise. The system achieves a recognition accuracy of 85.238 at $p=$ 0.4 and a noise variance of 0.2. However, as the noise variance increases, the recognition accuracy declines, with a score of 83.088 at $p=$ 0.4 and a noise variance of 1.

In Table 5, we present a thorough evaluation of 3D object recognition performance using the proposed technique for polynomial order ($Ord=$ 12) across various environments with differing noise parameters. In the clean environment, the system demonstrates comparable performance, achieving a peak recognition accuracy of 86.029 at $p=$ 0.4. When Gaussian noise is applied to 3D objects, the recognition accuracy exhibits a decline as the noise level increases. At a noise level of 1%, the system maintains a recognition accuracy of 84.898 at $p=$ 0.4, indicating that it performs well under low noise conditions. However, as the noise level rises to 5%, the accuracy decreases to 80.769. The accuracy for Gaussian noise at different levels shows a consistent downward trend, with accuracy values of 83.880 at $p=$ 0.4 for a noise level of 2% and 83.258 at the same parameter for a noise level of 3%. The performance in the salt and pepper noisy environment follows a similar performance to that observed with Gaussian noise. The model achieves a maximum recognition accuracy of 84.842 at $p=$ 0.4 and a noise density of 0.01. As the noise density increases, the recognition accuracy decreases, reaching 81.957 at $p=$ 0.4 and a noise density of 0.05. The scores for salt and pepper noise also reflect a gradual decrease, with values of 84.219 at $p=$ 0.4 for a noise density of 0.02 and 83.032 at the same parameter for a noise density of 0.03. The results of speckle noise illustrate the challenges associated with maintaining recognition accuracy in the presence of noise. The model achieves a recognition accuracy of 84.729 at $p=$ 0.4 and a noise variance of 0.2. However, as the noise variance increases, the recognition accuracy declines, with a score of 81.618 at $p=$ 0.4 and a noise variance of 1.

To this end, the results indicate that while the proposed technique performs well in clean environments, its slightly affected in the presence of noise, especially for OP parameter $p=$0.4. The findings highlight that the recognition system based on the proposed technique is able to tackle the problem of noisy environments.

4.2. Comparison Between the Proposed System and Existing Works

To assess the effectiveness of the presented recognition system based on the proposed technique, we conducted a comparative analysis of its recognition accuracy against several existing methods. The algorithms included in this comparison are direct Krawtchouk moment invariants (DKMI), Tchebichef moment invariants (TMI), Krawtchouk moment invariants (KMI), Hahn moment invariants (HMI), Tchebichef–Tchebichef–Tchebichef moment invariants (TTTMI), Krawtchouk–Krawtchouk–Krawtchouk moment invariants (KKKMI), Tchebichef–Krawtchouk–Krawtchouk moment invariants (TKKMI), Tchebichef–Tchebichef–Krawtchouk moment invariants (TTKMI), geometric moment invariants (GMI), and overlapped block processing (OBP). The average recognition accuracy for both the presented recognition system and the existing methods are shown in

Table 6. Comparison between the presented recognition system and existing methods using the McGill database.

Method Name	Average Recognition Accuracy	Average of Recognition Accuracy for Noisy Environment
DKMI [56]	62.01%	57.92%
HMI [56]	60.89%	56.69%
KMI [56]	60.32%	56.44%
TMI [56]	60.54%	56.40%
TTTMI [57]	71.57%	67.30%
KKKMI [57]	71.11%	66.97%
TKKMI [57]	72.19%	67.64%
TTKMI [57]	72.87%	68.20%
GMI [57]	70.26%	65.49%
OBP [50]	80.21%	80.22%
Proposed System ($p=0.4$ and $Ord=8$)	82.73%	82.56%
Proposed System ($p=0.4$ and $Ord=10$)	83.85%	83.66%
Proposed System ($p=0.4$ and $Ord=12$)	83.33%	83.16%

.

The comparison presented in Table 6 highlights the performance of the proposed recognition system against several existing methods using the McGill database. The average recognition accuracy of each method is reported, providing a clear perspective on the effectiveness of the proposed approach.

The existing methods, including DKMI, HMI, KMI, and TMI, exhibit relatively low recognition accuracy, ranging from 60.32% to 62.01%. These results indicate that they are not too robust for the complexities presented in the McGill database. Moreover, the Tchebichef-based methods, which are TTTMI, KKKMI, TKKMI, and TTKMI, show improved performance, with an accuracy between 71.11% and 72.87%. This indicates that the incorporation of Tchebichef moments enhances the recognition capabilities compared to the earlier methods. However, even the best-performing Tchebichef-based method, TTKMI, achieves only 72.87%, which still falls short of optimal performance. In contrast, the proposed system demonstrates significantly higher recognition accuracy across all tested configurations. The system achieves an accuracy of 82.73% at polynomial order 8, which surpasses the best existing methods by a notable margin. When the polynomial order is increased to 10, the accuracy improves further to 83.85%, indicating that the proposed system benefits from higher polynomial orders, likely due to its enhanced ability to capture complex features in the data. In addition, for polynomial order of 12, the proposed system shows robust performance with an accuracy of 83.33% This stability of performance across different polynomials orders demonstrates that the proposed approach is robust and adaptable. thus, the variations in the dataset are effectively handled by the proposed approach.

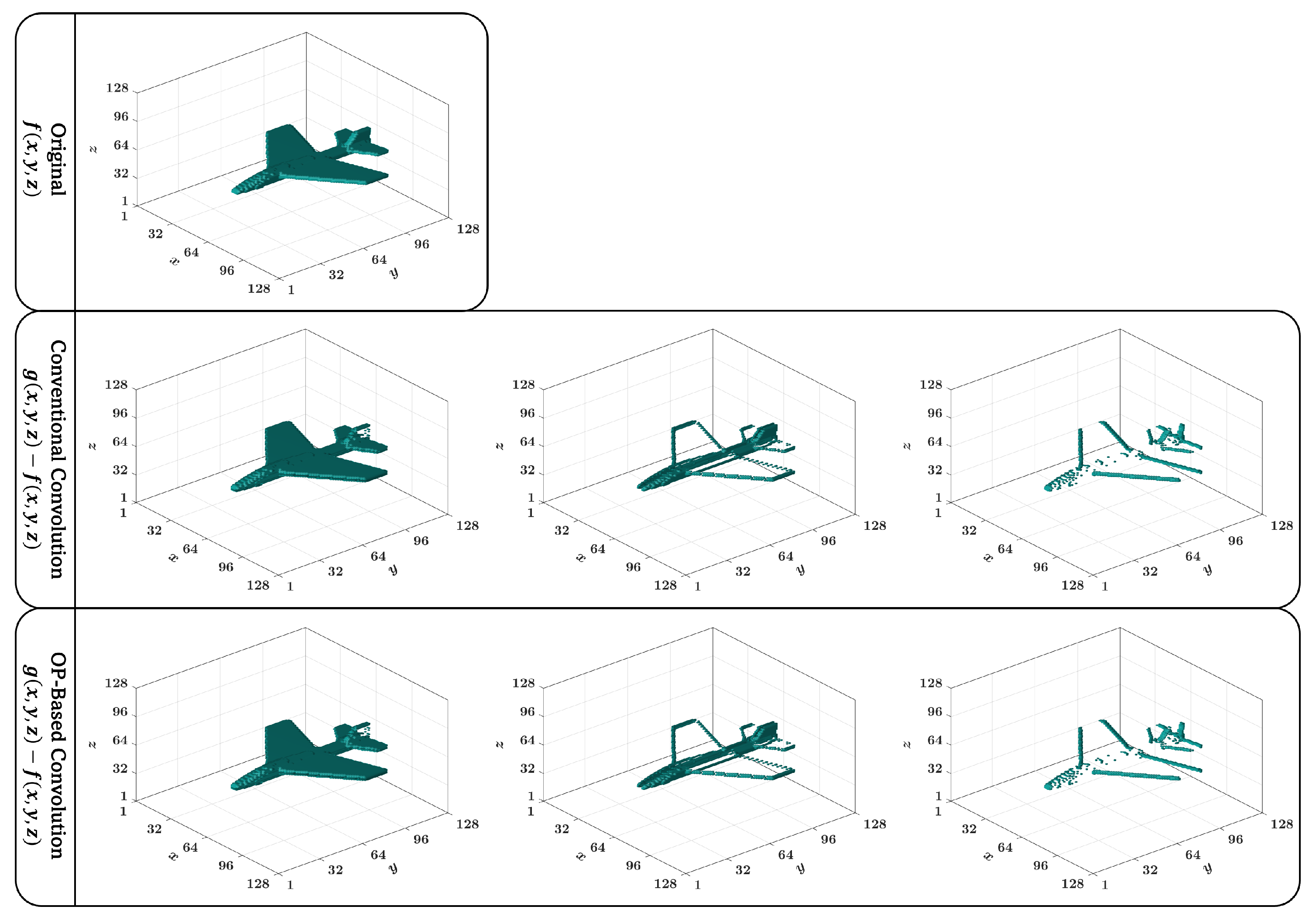
The performance of the proposed approach is further evaluated by benchmarking the proposed approach with the traditional method in terms of computational cost. In the traditional method, the 3D object is convolved by the kernel and then the moments are computed. It is noteworthy that the kernel utilized in the experiment is the averaging kernel with a length of 7.

For this purpose, the computation cost is evaluated by performing five runs for all 3D objects across different classes. Then, the average computation time is recorded for each 3D object. The comparison is conducted for three different polynomial orders ($Ord=$ 8, 10, and 12), and the results are summarized in

Table 7. Computation time (in seconds) comparison between the proposed approach (Our) and traditional method (Trad).

	$\mathit{Ord}=8$			$\mathit{Ord}=10$			$\mathit{Ord}=12$
Class ID	Time (Trad)	Time (Ours)	Imp	Time (Trad)	Time (Ours)	Imp	Time (Trad)	Time (Ours)	Imp
1	1.446	0.722	50.0	1.554	0.750	51.7	1.572	0.805	48.8
2	1.790	0.824	53.9	1.855	0.866	53.3	1.995	0.916	54.1
3	1.198	0.580	51.6	1.239	0.604	51.2	1.263	0.641	49.3
4	1.302	0.638	51.0	1.361	0.669	50.9	1.490	0.717	51.9
5	2.210	0.831	62.4	2.258	0.870	61.5	2.286	0.925	59.5
6	2.068	0.715	65.4	2.148	0.718	66.6	2.191	0.778	64.5
7	1.073	0.527	50.9	1.153	0.548	52.5	1.173	0.585	50.2
8	0.661	0.331	49.9	0.734	0.346	52.9	0.762	0.368	51.8
9	1.318	0.631	52.1	1.397	0.669	52.1	1.424	0.707	50.3
10	1.834	0.856	53.3	1.921	0.902	53.1	2.030	0.957	52.9
11	1.245	0.547	56.1	1.300	0.578	55.5	1.354	0.614	54.6
12	1.445	0.714	50.5	1.509	0.749	50.3	1.549	0.803	48.1
13	1.499	0.690	53.9	1.556	0.725	53.4	1.605	0.771	52.0
14	1.067	0.553	48.2	1.142	0.577	49.4	1.198	0.615	48.7
15	1.481	0.683	53.9	1.565	0.723	53.8	1.595	0.766	52.0
16	1.289	0.683	47.0	1.371	0.717	47.7	1.425	0.768	46.1
17	1.838	0.848	53.9	1.929	0.888	54.0	1.978	0.958	51.6
18	1.393	0.606	56.5	1.420	0.635	55.3	1.459	0.696	52.3
19	1.545	0.553	64.2	1.616	0.579	64.1	1.714	0.617	64.0
Average	27.70	12.535	54.7	29.03	13.11	54.8	30.06	14.00	53.4
Avg for 3D object 1	0.061	0.028	54.7	0.064	0.029	54.8	0.066	0.031	53.4

¹ Avg per 3D object represents the average computation time for one 3D object. It is computed by summing all the computation time and dividing it by the number of objects (454)—the test is performed on the original dataset without augmentation.

. The table includes the computation time for both the proposed approach (Time (ours)) and the traditional method (Time (Trad)), as well as the percentage improvement (Imp) achieved by the proposed method over the traditional method. The percentage improvement is calculated using the following formula:

$$PercentageImprovement\left(Imp\right)=\left({\displaystyle \frac{T_{Trad}-T_{Ours}}{T_{Trad}}}\right)\times 100\%$$

(19)

The minimum percentage improvement is observed for Class 16, with improvements of 47.0% at $Ord=8$, 47.7% at $Ord=$ 10, and 46.1% at $Ord=$ 12. In contrast, the highest percentage improvement is achieved for Class 19, where the proposed method attains improvements of 64.2% at $Ord=8$, 64.1% at $Ord=$ 10, and 64.0% at $Ord=$ 12.

The results demonstrate that the proposed algorithm significantly outperforms the traditional algorithm across all polynomial orders and classes. For instance, at $Ord=8$, the average percentage improvement across all classes is 54.7%, while at $Ord=10$ and $Ord=12$, the average improvements are 54.8% and 53.4%, respectively. This indicates that the proposed method consistently reduces computation time by more than half compared to the traditional approach. This clearly signifies the robustness and efficiency of the proposed algorithm, particularly when dealing with higher polynomial orders and complex 3D objects. The last row of the table provides the average computation time and improvement per 3D object, further confirming the superiority of the proposed method in terms of computational efficiency.

5. Conclusions

Signal preprocessing plays a crucial role in computer vision applications, as it directly enhances the performance of computer vision algorithms. OMs are considered as robust descriptors for signal analysis and recognition. Convolving kernels with the signal and precomputing OMs increases computational demands. Therefore, this paper introduced a novel mathematical model that embeds the kernel directly into the OPs functions by integrating the processes into a single, streamlined framework. By computing the OMs of smoothed 3D signals directly, the model achieved a substantial reduction in computational overhead while maintaining high accuracy. Our experimental work on 3D objects demonstrated that the proposed algorithm outperforms traditional methods. When the polynomial order is equal to 10, the accuracy improves further to 83.85%, indicating that the proposed work benefits from higher polynomial orders, likely due to its enhanced ability to capture complex features. In the future, we plan to further enhance the performance of the proposed method and apply it to various applications, such as medical imaging and robotics.