Abstract
In contextual multi-armed bandits, the relationship between contextual information and rewards is typically unknown, complicating the trade-off between exploration and exploitation. A common approach to address this challenge is the Upper Confidence Bound (UCB) method, which constructs confidence intervals to guide exploration. However, the UCB method becomes computationally expensive in environments with numerous arms and dynamic contexts. This paper presents an adaptive noise exploration framework to reduce computational complexity and introduces two novel algorithms: EAD (Exploring Adaptive Noise in Decision-Making Processes) and EAP (Exploring Adaptive Noise in Parameter Spaces). EAD injects adaptive noise into the reward signals based on arm selection frequency, while EAP adds adaptive noise to the hidden layer of the neural network for more stable exploration. Experimental results on recommendation and classification tasks show that both algorithms significantly surpass traditional linear and neural methods in computational efficiency and overall performance.
1. Introduction
The contextual Multi-Armed Bandit (MAB) framework is a critical model for sequential decision making under uncertainty with broad applications in online recommendation systems [1,2] and clinical trials [3,4]. Agents aim to maximize cumulative rewards through iterative interactions with the environment. Each round’s observed reward depends on the chosen arm, and only the selected arm’s reward can be observed. Thus, agents must identify the intrinsic relationship between arms and their rewards to optimize expected outcomes [5]. The main challenge in this domain is to strike an optimal balance between exploration and exploitation: exploration involves trying arms that must be sufficiently investigated. In contrast, exploitation focuses on selecting the best arm based on existing historical data [6,7].
The Upper Confidence Bound (UCB) algorithm is a classic method for balancing exploration and exploitation [8]. The UCB algorithm assigns a confidence interval to each arm and uses the upper bound of this interval for subsequent selections. Specifically, the algorithm integrates both the historical average reward and the current uncertainty of each arm to balance exploration and exploitation.
Most MAB algorithms, such as LinUCB, ConUCB, and KNNConUCB, assume a linear relationship between each arm’s reward and its corresponding context vector [9,10]. While these algorithms have achieved significant research results, this assumption may only partially capture the natural world’s complex relationships between rewards and context vectors. To address this limitation, neural bandit algorithms utilize neural networks to capture intricate nonlinear relationships, enabling more accurate predictions of arm rewards [11,12]. NeuralUCB [13] and NeuralTS [14] are two prominent algorithms in the neural bandit framework. NeuralUCB extends the traditional UCB algorithm by predicting rewards through neural networks and constructing confidence intervals based on the output gradient to select arms. NeuralTS (Neural Thompson Sampling) treats each arm as a normal distribution, with the mean being the neural network’s output and the standard deviation calculated from the output’s gradient, using the Thompson sampling strategy to select arms. These algorithms leverage the representational power of neural networks to handle complex nonlinear relationships [15,16].
In neural bandit algorithms, UCB and TS-based methods require inverting the induced covariance matrix of numerous parameters to construct confidence intervals [13,14,17]. To reduce computational complexity, approximate methods are often employed in practice, such as using only the diagonal of the covariance matrix, although this diagonal approximation lacks theoretical justification [13]. The Neural Perturbed Rewards (NPR) algorithm replaces confidence interval calculation with noisy perturbed rewards for exploration. While this method increases randomness to facilitate exploration and reduces computational resource consumption, the fixed noise variance as a hyperparameter means that the exploration rate does not automatically adjust as the model learns [5].
Specifically, we propose an adaptive noise exploration framework that dynamically adjusts the noise level based on the selection frequency of each arm. We have developed two novel neural contextual multi-armed bandit algorithms within this framework: Exploring Adaptive Noise in Decision-Making Processes (EAD) and Exploring Adaptive Noise in Parameter Spaces (EAP). The EAD algorithm adds adaptive noise to the reward of each selected arm. It adjusts the noise based on the arm’s selection frequency, achieving a finer balance between exploration and exploitation. The EAP algorithm introduces adaptive noise directly to the network parameters at the neural network’s hidden layers. This approach results in more stable exploration and allows for a flexible adjustment of exploration intensity throughout the learning process.
The principal contributions of this paper are summarized as follows:
- We propose an adaptive dynamic noise exploration framework to address the general contextual bandit problem. Based on this framework, we develop two novel neural contextual multi-armed bandit algorithms: EAD and EAP.
- EAD algorithm: Adjust the variance of the added noise adaptively based on the arms’ selection frequencies and incorporate this adjusted noise into the rewards of the selected arms. With adaptive noise, these rewards are used to construct the loss function.
- EAP Algorithm: This algorithm introduces adaptive dynamic noise directly into the network parameters at the neural network’s hidden layers. Continuously interacting with the environment using these noisy parameters achieves more stable exploration.
- To validate the effectiveness of our framework, we conducted empirical evaluations on two recommendation system datasets and six classification datasets. Compared to existing baseline methods, our adaptive dynamic noise exploration strategies demonstrate significant advantages in improving long-term cumulative rewards and exploration time.
2. Related Work
Neural contextal bandit: To learn nonlinear reward functions [18,19], deep neural networks have been adapted to bandit problems through various modifications [20]. For instance, NeuralUCB employs random feature mappings from deep neural networks to establish upper confidence bounds for exploration [13], while NeuralTS uses a comparable approach to derive samples from posterior distributions [14]. Additionally, BatchNeuralUCB explored the effectiveness of batch learning, which calculates rewards under both fixed and adaptive batch size conditions [21]. To address the high computational demands, Neural-LinUCB implements UCB-based exploration in the neural network’s final layer, significantly reducing the computational load associated with gradient-based UCB [17]. EE-Net constructs a neural network similar to NeuralUCB to estimate expected rewards for each arm and creates an exploration network that predicts potential rewards for each arm based on current evaluations [22].
Bandit with Noisy Data: In the realm of multi-armed bandit problems, managing noise is equally critical. Here, noise is not only seen as a challenge but also as a means to enhance the algorithms’ exploratory capabilities. This exploration mechanism involves integrating noise into the decision-making process, thus promoting learning and adaptation in uncertain environments [23]. Ref. [23] were the first to explore context-free multi-armed bandits using noise-perturbed observations to estimate arm rewards and select the arm with the highest estimated reward. The advantage of their approach lies in its minimal modifications, thereby reducing computational complexity. Refs. [24,25,26,27] proposed two main strategies to induce exploration through perturbation. The first strategy involves adding a fixed number of copies for each observation and replacing the rewards with randomly selected values. This method promotes exploration by increasing the data volume and diversifying the reward structure. The second strategy perturbs the observed rewards without expanding the data volume. Ref. [5] combined this strategy with deep neural networks by injecting noise into the observed reward history and training the models using these noisy rewards.
3. Problem Definition
In the contextual multi-armed bandit problems, in each round , the user needs to interact with the contextual multi-armed bandit. The bandit presents the user with K arms, which are each represented by a feature vector . After choosing an arm , its reward is assumed to be generated by the following function:
The reward function is unknown. is random noise with a mean of 0 [17,21].
We aim to design a strategy that minimizes cumulative regret, which is equivalent to maximizing the expected cumulative rewards [28]. is the reward brought by always choosing the optimal strategy in a given context. Thus, the definition of cumulative regret is
Our algorithm models the reward distribution using a neural network and integrates a dynamic noise adjustment mechanism to balance exploration and exploitation. This mechanism enhances early exploration and gradually shifts focus to exploiting high-reward arms, effectively reducing regret and improving long-term returns. An inverse relationship exists between long-term returns and regret: higher long-term returns correspond to lower regret. Regret serves as a complementary metric to long-term return, representing the gap between achieved and optimal returns over time.
To reflect the potential nonlinear relationships of the reward function , we use a deep neural network
as a function approximator to learn the unknown reward function . Here, , m is the width of the neural network, , , , is the collection of parameters of the neural network, and .
4. Proposed Method
NeuralUCB employs neural networks to estimate the expected reward and uncertainty of each action. The formula for calculating the confidence interval is given by
where . Since NeuralUCB exploration covers the entire network parameter space, the dimensionality involved is [29].
Although this method is theoretically effective, its computational cost is extremely high in high-dimensional feature spaces or large datasets. To reduce the computational burden and improve efficiency, NPR introduces a randomization strategy in neural network updates, demonstrating that the added noise leads to optimistic estimates of rewards [5] with the model’s predicted values having a probability of falling within the error term of the actual rewards in each round . The formula is as follows:
In this context, is generally a small constant. This noisy reward perturbation ensures that the model makes optimistic estimates of rewards with high probability, thereby encouraging sufficient exploration. Building on this, we introduce a dynamic noise strategy to facilitate more effective prospecting and reduce dependence on traditional confidence interval estimates.
In the multi-armed bandit model, consistent exploration–exploitation interactions indicate that for arms selected frequently, their underlying reward distributions are sufficiently explored, and thus the exploration level should be reduced by injecting less noise during reselection. Conversely, if an arm is chosen infrequently, it signals insufficient exploration, requiring an increase in noise injection to encourage further exploration. To address this, we propose a formula that dynamically adjusts the noise intensity:
The formula dynamically adjusts the noise intensity for each arm to balance the trade-off between exploration and exploitation. Specifically, the maximum term ensures that the noise intensity does not fall below a minimum threshold , thus preventing the noise from becoming too small and avoiding insufficient exploration. The minimum term ensures that the noise intensity decreases as the selection count for a specific arm increases but does not fall below . Here, represents the upper bound of the noise scale, preventing the noise from becoming excessively large and compromising the model’s stability. The term is designed to ensure that the noise scale decreases at a logarithmic rate as increases. Compared to other decay forms, such as polynomial or exponential decay, logarithmic decay was chosen primarily for its characteristic of slow attenuation. Logarithmic decay causes the noise scale to decrease gradually with increasing time steps but at a slower rate. This slower decay helps maintain a relatively high level of exploration over a longer period, which is particularly beneficial in reducing the risk of premature convergence to suboptimal solutions. This advantage becomes especially significant in complex or high-dimensional environments, where sufficient exploration is critical for the algorithm to discover and exploit globally optimal solutions.
Figure 1 illustrates the adaptive noise exploration framework we propose. After a user selects an arm using the algorithm, the selection count of that arm is reviewed to calculate the variance of the input noise. If the arm has been selected frequently, indicating extensive exploration, the noise input is decreased. Conversely, if the arm has been underselected, the noise input is increased to enhance exploration.
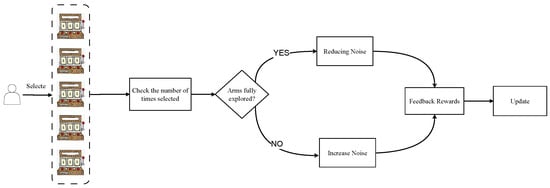
Figure 1.
Adaptive noise exploration framework.
We facilitate adaptive noise exploration through two approaches: integrating noise into the decision-making process and incorporating noise into the model’s parameter space. This continual interaction learning with noise-augmented parameters enables more stable exploration.
4.1. Exploring Adaptive Noise in Decision-Making Processes
In each decision-making round, the model selects the arm with the highest predicted reward using
where k represents the number of available arms per round. After choosing the arm with the highest predicted reward, the model receives a reward. Each round, to foster exploration, introduces newly sampled noise into the reward with drawn from a normal distribution with mean 0 and variance . The variance is calculated by Equation (6). We have named this approach Exploring Adaptive Noise in Decision-Making Processes or EAD for short.
Figure 2 illustrates the complete process of integrating adaptive noise into the decision-making procedure. The algorithm selects the arm predicted to have the highest reward. After receiving reward, the noise variance is calculated based on the arm’s previous selections, and sampled noise is added to the feedback. The model is updated using the following loss function:
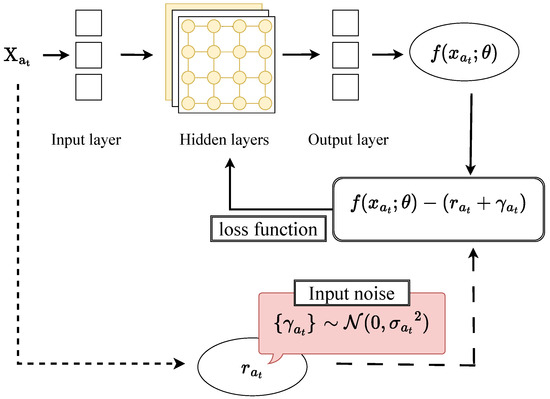
Figure 2.
Adaptive noise exploration framework.
4.2. Exploring Adaptive Noise in Parameter Spaces
In the neural bandit algorithm, besides introducing noise into the decision-making process to encourage exploration, another approach involves directly adding noise to the parameters of the neural network. At the beginning of each iteration, noise is added to the parameters to generate perturbed parameters , where denotes a multivariate normal distribution with mean 0 and variance , and I is the identity matrix. This ensures noise is adaptively and independently added to each data point of based on arm selection frequency. We have named this method Exploring Adaptive Noise in Parameter Spaces or EAP in short.
Figure 3 illustrates the entire process of integrating adaptive noise within the parameter space. After selecting the arm with the highest predicted reward, the algorithm receives reward feedback and uses gradient descent to update neural network parameters based on the observed data . Unlike conventional approaches, this algorithm adds newly sampled noise to post-update and continues training with these noise-enhanced parameters , facilitating a more stable and effective exploration.
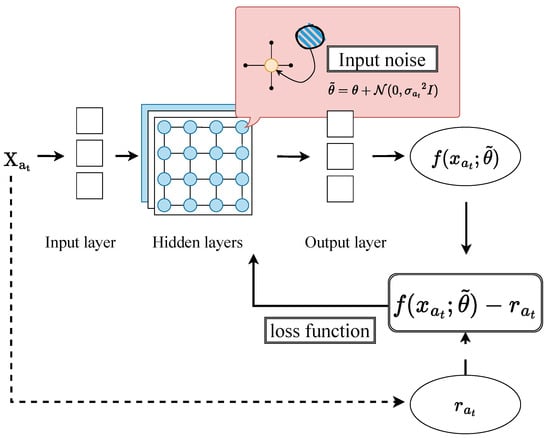
Figure 3.
Adaptive noise exploration framework.
Comparison with other algorithms: Algorithms 1 and 2 detail the procedures for EAD and EAP, respectively. Unlike NeuralUCB, these algorithms do not use confidence intervals to select arms; instead, they rely solely on the neural network’s output, determining the arm with the highest predicted reward. For exploration, the objective is achieved by adding noise. Unlike the fixed noise variance in the NPR algorithm, our algorithm dynamically adjusts the noise variance according to the frequency of arm selections. Our algorithm enhances exploration flexibility by adaptively adding noise to both the decision-making process and parameter space, thereby increasing exploration efficiency and reducing computational overhead.
| Algorithm 1 Exploring Adaptive Noise in Parameter Spaces (EAD) |
|
| Algorithm 2 Exploring Adaptive Noise in Parameter Spaces (EAP) |
|
4.3. Real-World Application Analysis
Both EAD and EAP are well-suited for “online learning” scenarios, where only a small amount of data (context and reward) are acquired with each interaction, and the model is updated immediately based on these data. EAD introduces noise into the rewards to increase the model’s perceived uncertainty during training, encouraging better exploration. The key idea behind EAD is that when the external environment provides rewards with significant random fluctuations (e.g., advertising click-through rates varying over time or across demographic groups), adding noise amplifies this inherent randomness. This enables the model to continue learning and adapting to the dynamic environment without frequent updates to its internal parameters. Therefore, EAD is better suited for applications where rewards are influenced by random factors, such as advertising click rates or recommendation systems, enabling the model to self-adapt and generalize under time-varying uncertainty.
In contrast, EAP adds noise to the model’s internal parameters without modifying the reward data. The core concept of EAP is that when reward data are particularly valuable (e.g., high-cost experimental data, medical data, or financial transactions), adding noise directly to the model’s parameters is more appropriate. This approach maintains exploration during training while preserving the authenticity and traceability of the original reward data. As a result, EAP is better suited for applications where the stability and accuracy of reward data are crucial, allowing the model to explore sufficiently without altering the valuable data.
5. Experiments
This paper presents an adaptive noise detection mechanism that adjusts the noise level dynamically based on arm selection frequency. In this framework, the noise intensity decreases logarithmically as the number of rounds increases. The logarithmic decay is characterized by slow attenuation, enabling prolonged high levels of exploration. This helps reduce the risk of premature convergence to suboptimal solutions, which is especially important in complex or high-dimensional environments. To validate the framework’s effectiveness, we conducted a small experiment using a simple synthetic dataset, comparing three noise strategies: fixed, decreasing, and adaptive noise. The average rewards for each arm were as follows: [0.2, −0.85, 1.55, 0.3, 1.2, −1.5, −0.2, −1.0, 0.9, −0.6]. As shown in Figure 4a, the logarithmic adaptive noise strategy outperforms the other two strategies in terms of the proportion of optimal actions, suggesting that dynamically adjusting the noise more effectively aids in selecting high-reward arms. Furthermore, Figure 4b shows that the logarithmic adaptive noise strategy also performs well in terms of average reward [30,31].
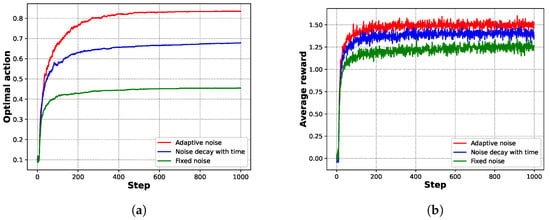
Figure 4.
Effect comparison of different noise adjustment strategies in stochastic multi-armed bandits. (a) Optimal action proportion. (b) Average reward.
Next, we evaluate our algorithm on two recommendation and six classification datasets, comparing it against several benchmark contextual bandit algorithms, including the six most recent neural contextual multi-armed bandit algorithms. We first introduce the experimental setup, which is followed by a regret comparison. We run 15,000 rounds for all algorithms, repeat the experiment 5 times, and compare their average results.
Baseline: We selected four neural network-based bandit algorithms and one linear algorithm to evaluate our algorithm comprehensively.
- LinUCB [9]: This approach explicitly assumes a linear relationship between the reward and the arm’s context vector. Unknown parameters are estimated using ridge regression, which is integrated with the UCB strategy to select the arm.
- Neural-Epsilon [32]: Utilizes a neural network to learn the reward function of pulling an arm. It selects the arm with the highest predicted reward with a probability of , i.e., , and randomly selects an arm with a probability of .
- NeuralUCB [13]: A neural network is employed to learn the reward function from the exploration strategy based on UCB.
- NeuralTS [14]: It uses a neural network to learn the reward function derived from the Thompson Sampling exploration strategy.
- NPR [5]: Utilizes a neural network to learn the reward function by exploring through the addition of perturbed rewards.
- DQN [33]: A reinforcement learning approach that combines deep learning and Q-learning leverages neural networks to approximate the Q-value function, enabling agents to efficiently learn optimal policies in high-dimensional state spaces.
- EE-Net [22]: A dual neural network architecture is adopted. One neural network learns the real reward function, and the other neural network learns the potential reward value, and the architecture combines the output of the two to make a comprehensive decision, so as to improve the effect of exploration and utilization.
5.1. Experiments on the Recommendation Dataset
Dataset Introduction: The Yelp dataset, released by Yelp as part of a data challenge, includes 4.7 million ratings from 1.18 million users for 157,000 restaurants [34]. The MovieLens dataset, on the other hand, contains approximately 25 million ratings from about 160,000 users for approximately 60,000 movies [35]. In these datasets, restaurants and movies are considered arms. We selected the 2000 most active users and the top 10,000 highest-rated arms. SVD was then used to extract 10-dimensional feature vectors for each user and arm from the rating data. In this study, the algorithm aims to select arms with lower ratings. Specifically, the algorithm’s rewards are based on the star ratings users give to arms. In each round, 10 arms are set up with 1 arm randomly selected for a reward of 1 and the remaining 9 arms selected to have a reward of 0. The context for each arm is the concatenation of the corresponding user’s feature vector and the arm’s feature vector.
Cumulative regret comparison: In Figure 5, we compare the cumulative regrets of various algorithms, where the arms are implemented by randomly drawing from a candidate pool. The results show that the two neural bandit learning algorithms, EAD and EAP, expanded under our proposed Adaptive Dynamic Noise Exploration framework, successfully learned the mapping of potential nonlinear reward functions on two real-world datasets. In contrast, the LinUCB algorithm, relying on simple linear reward functions, failed to capture the complex reward structures present in real-world datasets effectively. Meanwhile, the Neural-Epsilon and NPR algorithms face challenges in compelling exploration due to their fixed exploration probabilities, which are difficult to adjust to complex environments. In our framework, the exploration mechanism can dynamically change the noise level based on the frequency of arm selection, thus more flexibly adapting to complex environments.
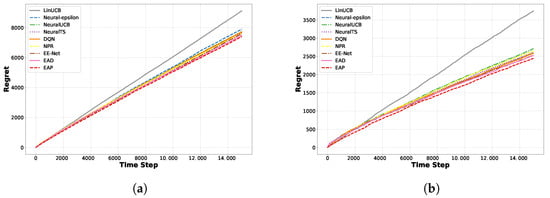
Figure 5.
Regret comparison on Yelp and Movielens. (a) Yelp. (b) Movielens.
Accuracy of learned parameters: Next, we compared the parameter estimation accuracy among six different neural bandit algorithms, including our own. Precisely, we measure the performance of each algorithm by calculating the average Euclidean distance between the learned parameter vector and the real parameter vector , using the formula . Here, represents the estimated parameter vector of user u after each iteration, and is the actual parameter vector obtained by averaging the results of five experiments on each dataset. A smaller average Euclidean distance indicates greater accuracy in parameter learning. In Figure 6, we display the changes in average distance every 50 iterations. The results show that across all the neural bandit algorithms examined, the average Euclidean distance gradually decreases as the number of iterations increases. This indicates that by increasing user interactions, all algorithms can gradually improve the accuracy of parameter learning. Notably, our EAP algorithm significantly outperforms the other algorithms examined regarding parameter learning accuracy.
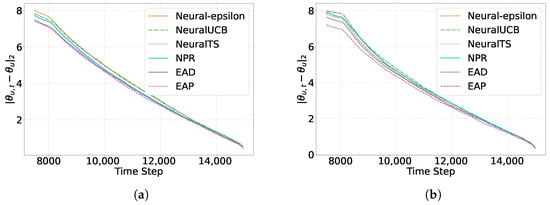
Figure 6.
Learned parameters comparison on Yelp and Movielens. (a) Yelp. (b) Movielens.
Comparison of exploration time: The central challenge in the context-aware multi-armed bandit problem is finding the right balance between exploration and exploitation. Excessive exploration could cause the system to spend too much time on new actions and need more on utilizing available information, thereby diminishing long-term rewards. On the other hand, excessive exploitation might lead the system to prematurely concentrate on a few known high-return actions, overlooking other potential high-return opportunities and resulting in suboptimal long-term rewards. Our algorithm dynamically balances exploration and exploitation, automatically computing this based on how frequently an arm is selected, eliminating the need to define exploration time explicitly. Hence, in this paper, we define exploration time as the total time the system spends from the selection of the first arm to the end of the round.
Figure 7 shows the average exploration time of all slot machine models on two recommendation datasets. Since NeuralUCB and NeuralTS models require more time to build the covariance matrix based on historically selected arms, although the diagonal matrix approximation can alleviate the computational burden, NeuralUCB and NeuralTS still need more time for exploration compared to noise-based exploration algorithms. In the experiment, we gradually increased the number of arms per round from 10 to 100. We observed that as the number of arms increased, the time difference between noise-based and covariance matrix-based exploration methods also gradually increased. The exploration time is shown in Figure 8.
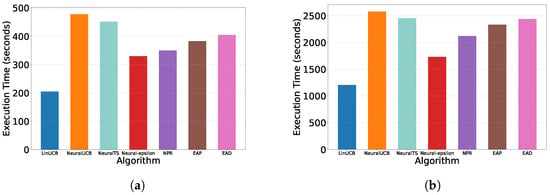
Figure 7.
Exploration time comparison on Yelp and Movielens. (a,b) The average exploration time per round with 10 arms: (a) Yelp. (b) Movielens.
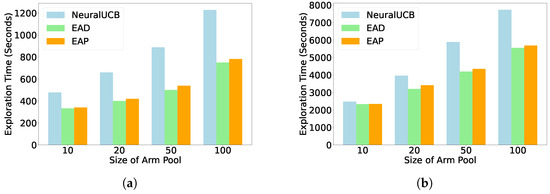
Figure 8.
Effect of the number of candidate arm sets on exploration time. (a,b) Comparison of exploration times between the EAD and EAP algorithms and the NeuralUCB algorithm with arm numbers of 10, 20, 50, and 100: (a) Yelp. (b) Movielens.
Dynamic Environment Evaluation: The experiment simulates a dynamic environment where users are randomly selected for interaction in each round. A Zipf distribution with parameter was applied to generate user visit frequencies, which were normalized to obtain the user visit probability distribution. Users were randomly selected in each round based on this weighted probability, simulating the real-world “long-tail phenomenon”, where a few active users have high visit frequencies, while most users have low visit frequencies.This setup replicates the dynamic changes in user preferences observed in real-world scenarios. The algorithm operates in this dynamic environment, continuously making decisions and adjusting its strategy based on feedback [36].
As depicted in Figure 9, the experimental results demonstrated that noise-based exploration strategies outperformed confidence interval-based strategies. In the dynamic environment, both the EAD and EAP algorithms could adaptively adjust noise variance based on the frequency of arm selections, thereby enhancing exploration capabilities and facilitating quicker adaptation to changes in user preferences. This study underscores the significant advantage of our proposed adaptive noise mechanisms in dynamic environments, particularly in coping with frequent changes in user preferences.
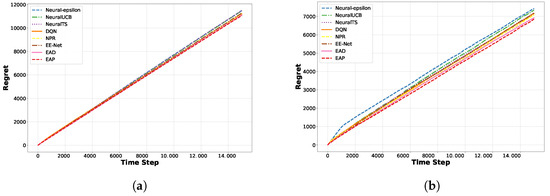
Figure 9.
Dynamic environment evaluation on Yelp and Movielens: (a) Yelp. (b) Movielens.
Analysis on Hyperparameter Sensitivity: In the adaptive noise addition method we propose, we need to maintain the noise level within a specified range to prevent either too high or too low noise levels from negatively impacting the algorithm’s performance. In the initial 1000 rounds, a grid search was conducted for parameters , , and , within the range of , with an increment of . For each algorithm, the best hyperparameter combination was applied to a full simulation of 15,000 rounds with the trial continuing for the additional 14,000 rounds.
To analyze parameter impacts on model performance, we explored a range from 0.0001 to 1 and visualized regret values in a heatmap (Figure 10). The heatmap shows the regret of EAD and EAP algorithms on the Yelp dataset under varying parameter configurations with the x-axis representing (the upper bound of noise) and the y-axis showing its lower bound, which was set to 0.01 of . The heatmap analysis shows that selecting an appropriate parameter range is crucial for optimal performance. When the noise range is too large or too small, the algorithm fails to achieve optimal performance. This emphasizes the need to carefully select parameter boundaries to manage noise effectively and balance exploration with exploitation.
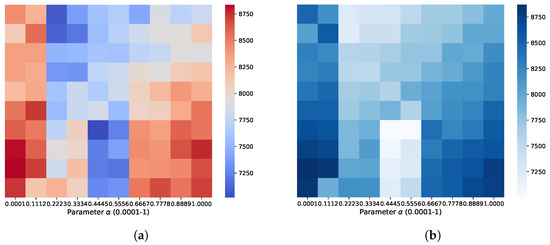
Figure 10.
Unfortunately for the different parameters of EAD and EAP on the yelp dataset: (a) EAD. (b) EAP.
Figure 11 and Figure 12 illustrate the impact of five parameter settings on regret for the EAP and EAD algorithms across the Yelp and Movielens datasets, offering an intuitive understanding of how parameter settings affect performance. When the noise parameter is set to 1 or 0.5, the large noise range causes persistently high noise levels. Despite multiple choices, the algorithms struggle to reduce interference, resulting in greater performance fluctuations and higher cumulative regret on both datasets. When the noise ratio is reduced to 0.01, it minimizes interference during updates but also limits the algorithm’s exploration capacity. This can cause premature convergence to suboptimal solutions, negatively impacting overall performance. Thus, setting an appropriate noise ratio—and balancing the trade-off between exploration and exploitation—is crucial for optimizing the algorithm. Achieving this balance ensures that the algorithm explores adequately in the early stages while exploiting high-reward choices effectively in later stages, leading to better long-term reward.
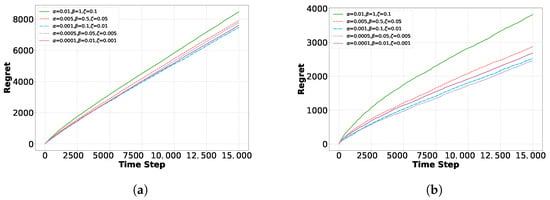
Figure 11.
Effect of different noise scales on EAD in Yelp and Movielens datasets: (a) Yelp. (b) Movielens.
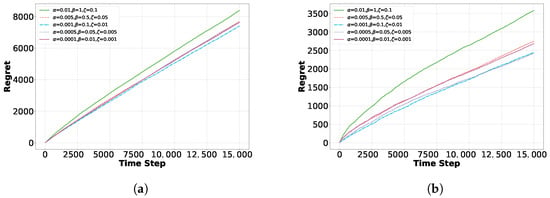
Figure 12.
Effect of different noise scales on EAP in Yelp and Movielens datasets: (a) Yelp. (b) Movielens.
5.2. Regret Comparison Experiments on Classification Datasets
Introduction to Classification Datasets: The K-class classification datasets are transformed into contextual multi-armed bandit problems using the MNIST dataset and five classification datasets from the UCI Machine Learning Repository (Table 1). Each context vector is transformed into k vectors [14]. If the agent correctly classifies, it receives a reward of 1; otherwise, it is 0.

Table 1.
Summary of the classification dataset used for the experiment.
Experiment Results Analysis:Figure 13, Figure 14 and Figure 15 shows the regret comparison on these six datasets with our algorithm outperforming all baselines. Improving the neural bandit algorithm depends on the dataset’s nonlinear relationship between the arms and rewards. For example, there was a notable improvement in the Mushroom and Shuttle datasets. However, in datasets like Mnist, the cumulative regret did not achieve sublinear growth. Our algorithm improves cumulative regret and operational efficiency across all datasets, making it more advantageous in practical applications.
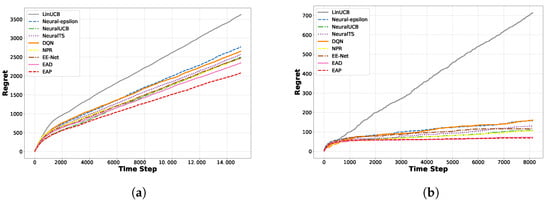
Figure 13.
Regret comparison on MNIST and Mushroom datasets: (a) MNIST. (b) Mushroom.
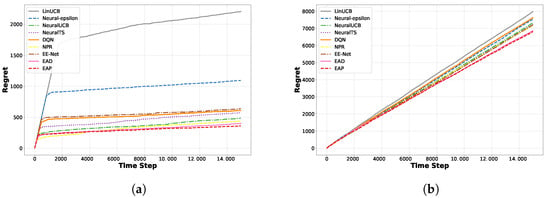
Figure 14.
Regret comparison on Shuttle and Covertype datasets: (a) Shuttle. (b) Covertype.
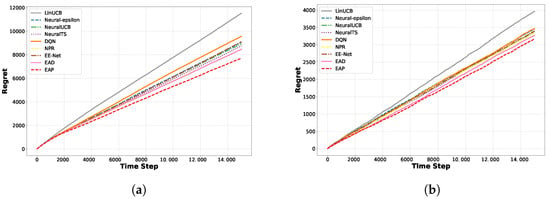
Figure 15.
Regret comparison on Letter and MagicTelescope datasets: (a) Letter. (b) MagicTelescope.
5.3. Scalability of the Methods
In this experiment, we evaluated model performance under conditions with 10 and 20 arms to examine the impact of arm count on performance. With 10 arms per round, the EAD and EAP algorithms quickly identified the high-reward arms, accelerating convergence to the optimal solution. In contrast, with 20 arms, sparse feedback led to inaccurate reward estimates, which negatively impacted the algorithm’s overall performance. Figure 16 and Figure 17 illustrate the regret of the EAD and EAP algorithms with 10 and 20 arms, respectively. The results show significant performance differences as the number of arms increases. With fewer arms (e.g., 10), denser reward feedback allows the model to quickly identify high-reward arms, accelerating convergence to the optimal solution. However, with more arms (e.g., 20), sparse feedback increases reward estimation error, reducing overall performance. Based on these findings, we identify limitations in the current arm selection strategy when handling a large number of arms. Our future research will focus on two main optimization directions: (1) Dynamic Exploration Strategy: This strategy will adapt to the increasing number of arms and adjust the exploration intensity accordingly. (2) Sparse Reward Estimation: We will employ more robust reward estimation methods to reduce the errors caused by sparse rewards in high-dimensional arm spaces.
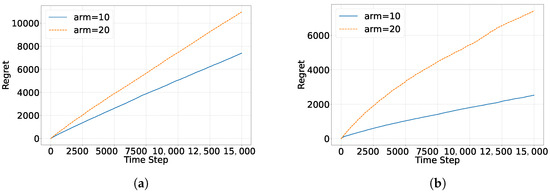
Figure 16.
The impact of the number of arms faced per round on EAD regret: (a) Yelp. (b) Movielens.
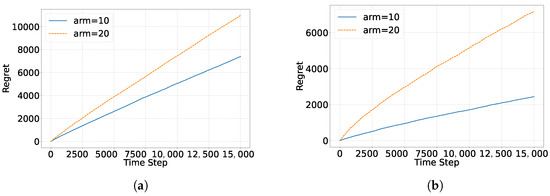
Figure 17.
The impact of the number of arms faced per round on EAP regret: (a) Yelp. (b) Movielens.
6. Conclusions
In this paper, we introduce two novel exploration strategy algorithms that adaptively add noise based on each arm’s selection frequency. This adaptive noise is separately added to the reward and input sides. Our method provides greater dynamism and flexibility in noise adjustment, allowing the noise intensity to be tuned according to the arms’ selection frequency. This improves exploration efficiency and reduces computational load. Extensive empirical results on recommendation and classification datasets support our analysis.
Author Contributions
J.L. was the advisor. C.W. designed the scheme. C.W. carried out the implementation. C.W. wrote the manuscript. J.L. and L.S. revised the final version of the text. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no grant or funding from any funding agency in the public, commercial, or not-for-profit sectors.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhao, Y.; Yang, L. Constrained contextual bandit algorithm for limited-budget recommendation system. Eng. Appl. Artif. Intell. 2024, 128, 107558. [Google Scholar] [CrossRef]
- Xia, Y.; Xie, Z.; Yu, T.; Zhao, C.; Li, S. Toward joint utilization of absolute and relative bandit feedback for conversational recommendation. User Model. User-Adapt. Interact. 2024, 34, 1707–1744. [Google Scholar] [CrossRef]
- Yu, C.; Liu, J.; Nemati, S.; Yin, G. Reinforcement learning in healthcare: A survey. ACM Comput. Surv. 2021, 55, 5. [Google Scholar] [CrossRef]
- Aguilera, A.; Figueroa, C.A.; Hernandez-Ramos, R.; Sarkar, U.; Cemballi, A.; Gomez-Pathak, L.; Miramontes, J.; Yom-Tov, E.; Chakraborty, B.; Yan, X.; et al. mHealth app using machine learning to increase physical activity in diabetes and depression: Clinical trial protocol for the DIAMANTE Study. BMJ Open 2020, 10, e034723. [Google Scholar] [CrossRef] [PubMed]
- Jia, Y.; Zhang, W.; Zhou, D.; Gu, Q.; Wang, H. Learning Neural Contextual Bandits through Perturbed Rewards. In Proceedings of the International Conference on Learning Representations, Virtual, 25–29 April 2022. [Google Scholar]
- Saber, H.; Pesquerel, F.; Maillard, O.A.; Talebi, M.S. Logarithmic regret in communicating MDPs: Leveraging known dynamics with bandits. In Proceedings of the 15th Asian Conference on Machine Learning, İstanbul, Turkey, 11–14 November 2024; Yanıkoğlu, B., Buntine, W., Eds.; PMLR: Cambridge, MA, USA, 2024; Volume 222, pp. 1167–1182. [Google Scholar]
- Letard, A.; Gutowski, N.; Camp, O.; Amghar, T. Bandit algorithms: A comprehensive review and their dynamic selection from a portfolio for multicriteria top-k recommendation. Expert Syst. Appl. 2024, 246, 123151. [Google Scholar] [CrossRef]
- Auer, P.; Cesa-Bianchi, N.; Fischer, P. Finite-time analysis of the multiarmed bandit problem. Mach. Learn. 2002, 47, 235–256. [Google Scholar] [CrossRef]
- Li, L.; Chu, W.; Langford, J.; Schapire, R.E. A contextual-bandit approach to personalized news article recommendation. In Proceedings of the 19th International Conference on World Wide Web, Raleigh, NC, USA, 26–30 April 2010; pp. 661–670. [Google Scholar]
- Zhang, X.; Xie, H.; Li, H.; CS Lui, J. Conversational contextual bandit: Algorithm and application. In Proceedings of the Web Conference 2020, Taipei, Taiwan, 20–24 April 2020; pp. 662–672. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Zhou, D.; Li, L.; Gu, Q. Neural contextual bandits with ucb-based exploration. In Proceedings of the International Conference on Machine Learning, Virtual, 13–18 July 2020; PMLR: Cambridge, MA, USA, 2020; pp. 11492–11502. [Google Scholar]
- Zhang, W.; Zhou, D.; Li, L.; Gu, Q. Neural thompson sampling. arXiv 2020, arXiv:2010.00827. [Google Scholar]
- Zhang, H.; He, J.; Righter, R.; Shen, Z.J.; Zheng, Z. Contextual Gaussian Process Bandits with Neural Networks. In Proceedings of the 38th Annual Conference on Neural Information Processing Systems (NeurIPS 2024), Vancouver, BC, Canada, 10–15 December 2024. [Google Scholar]
- Lin, Y.; Endo, Y.; Lee, J.; Kamijo, S. Bandit-NAS: Bandit sampling and training method for Neural Architecture Search. Neurocomputing 2024, 597, 127684. [Google Scholar] [CrossRef]
- Xu, P.; Wen, Z.; Zhao, H.; Gu, Q. Neural Contextual Bandits with Deep Representation and Shallow Exploration. In Proceedings of the International Conference on Learning Representations, Virtual, 25–29 April 2022. [Google Scholar]
- Ban, Y.; He, J. Local clustering in contextual multi-armed bandits. In Proceedings of the Web Conference 2021, Ljubljana, Slovenia, 19–23 April 2021; pp. 2335–2346. [Google Scholar]
- Chaudhuri, A.R.; Jawanpuria, P.; Mishra, B. ProtoBandit: Efficient Prototype Selection via Multi-Armed Bandits. In Proceedings of the 14th Asian Conference on Machine Learning, Hyderabad, India, 12–14 December 2022; Khan, E., Gonen, M., Eds.; PMLR: Cambridge, MA, USA, 2023; Volume 189, pp. 169–184. [Google Scholar]
- Feng, Z.; Wang, P.; Li, K.; Li, C.; Wang, S. Contextual MAB Oriented Embedding Denoising for Sequential Recommendation. In Proceedings of the 17th ACM International Conference on Web Search and Data Mining, Merida, Mexico, 4–8 March 2024; pp. 199–207. [Google Scholar]
- Gu, Q.; Karbasi, A.; Khosravi, K.; Mirrokni, V.; Zhou, D. Batched neural bandits. ACM/IMS J. Data Sci. 2024, 1, 1–18. [Google Scholar] [CrossRef]
- Ban, Y.; Yan, Y.; Banerjee, A.; He, J. EE-Net: Exploitation-Exploration Neural Networks in Contextual Bandits. In Proceedings of the Tenth International Conference on Learning Representations, Virtual, 25–29 April 2022. [Google Scholar]
- Kveton, B.; Szepesvari, C.; Vaswani, S.; Wen, Z.; Lattimore, T.; Ghavamzadeh, M. Garbage in, reward out: Bootstrapping exploration in multi-armed bandits. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; PMLR: Cambridge, MA, USA, 2019; pp. 3601–3610. [Google Scholar]
- Kveton, B.; Szepesvári, C.; Ghavamzadeh, M.; Boutilier, C. Perturbed-history exploration in stochastic multi-armed bandits. In Proceedings of the 28th International Joint Conference on Artificial Intelligence, Macao, China, 10–16 August 2019; pp. 2786–2793. [Google Scholar]
- Kveton, B.; Szepesvári, C.; Ghavamzadeh, M.; Boutilier, C. Perturbed-History Exploration in Stochastic Linear Bandits. In Proceedings of the Uncertainty in Artificial Intelligence, Virtual, 3–6 August 2020; PMLR: Cambridge, MA, USA, 2020; pp. 530–540. [Google Scholar]
- Kveton, B.; Zaheer, M.; Szepesvari, C.; Li, L.; Ghavamzadeh, M.; Boutilier, C. Randomized exploration in generalized linear bandits. In Proceedings of the International Conference on Artificial Intelligence and Statistics, Online, 26–28 August 2020; PMLR: Cambridge, MA, USA, 2020; pp. 2066–2076. [Google Scholar]
- Janz, D.; Liu, S.; Ayoub, A.; Szepesvári, C. Exploration via linearly perturbed loss minimisation. arXiv 2023, arXiv:2311.07565. [Google Scholar]
- Audibert, J.Y.; Munos, R.; Szepesvári, C. Exploration–exploitation trade-off using variance estimates in multi-armed bandits. Theor. Comput. Sci. 2009, 410, 1876–1902. [Google Scholar] [CrossRef]
- Su, Y.; Lu, H.; Li, Y.; Liu, L.; Bi, S.; Chi, E.H.; Chen, M. Multi-Task Neural Linear Bandit for Exploration in Recommender Systems. In Proceedings of the 30th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Barcelona, Spain, 25–29 August 2024; pp. 5723–5730. [Google Scholar]
- Park, H. Partially Observable Stochastic Contextual Bandits. Ph.D. Thesis, University of Georgia, Athens, GA, USA, 2024. [Google Scholar]
- Min, D.J.; Stolcke, A.; Raju, A.; Vaz, C.; He, D.; Ravichandran, V.; Trinh, V.A. Adaptive Endpointing with Deep Contextual Multi-Armed Bandits. In Proceedings of the ICASSP 2023—2023 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Rhodes Island, Greece, 4–10 June 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Langford, J.; Zhang, T. The Epoch-Greedy algorithm for contextual multi-armed bandits. In Proceedings of the Neural Information Processing Systems, Vancouver, BC, Canada, 3–6 December 2007. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M.A. Playing Atari with Deep Reinforcement Learning. arXiv 2013, arXiv:1312.5602. [Google Scholar]
- Wu, J.; Wang, X.; Feng, F.; He, X.; Chen, L.; Lian, J.; Xie, X. Self-supervised graph learning for recommendation. In Proceedings of the 44th International ACM SIGIR Conference on Research and Development in Information Retrieval, Virtual, 11–15 July 2021; pp. 726–735. [Google Scholar]
- Harper, F.M.; Konstan, J.A. The movielens datasets: History and context. ACM Trans. Interact. Intell. Syst. 2015, 5, 19. [Google Scholar] [CrossRef]
- Alami, R. Bayesian Change-Point Detection for Bandit Feedback in Non-stationary Environments. In Proceedings of the 14th Asian Conference on Machine Learning, Hyderabad, India, 12–14 December 2022; Khan, E., Gonen, M., Eds.; PMLR: Cambridge, MA, USA, 2023; Volume 189, pp. 17–31. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).