Abstract
Deep learning-based medical image classification models have been shown to exhibit race-, gender-, and age-related biases towards certain demographic attributes. Existing bias mitigation methods primarily focus on learning debiased models, which may not guarantee that all sensitive information is removed and usually targets discrete sensitive attributes. In order to address age-related bias in these models, we introduce a novel method called Mitigating Digital Ageism using Adversarially Learned Representation (MA-ADReL), which aims to achieve fairness for age as a sensitive continuous attribute. We propose controlling the mutual information penalty term to reduce the bias for age as a sensitive continuous attribute, and we seek to enhance the fairness without compromising the accuracy. We also employ the fusion of low- and high-resolution inputs to improve the transferable latent representation of medical images. Our method achieves an AUROC of 0.942, significantly outperforming the baseline models while reducing the bias, with an MI score of 1.89. Our experiments on two skin lesion analysis datasets indicate that MA-ADReL can significantly improve the fairness with respect to age-related bias while maintaining high accuracy.
1. Introduction
In recent years, the success of deep learning models across a wide range of application domains has spurred the creation of numerous large datasets. However, these datasets often exhibit various forms of bias [1], which can broadly be categorized as operational or systemic. Operational biases stem from factors like the instruments used for data collection, the labeling strategies, and the definition of different data classes [2]. On the other hand, systemic biases in AI can be attributed to data collection that inadvertently reinforces societal prejudices, including those related to sexism, racism, and ageism. To address these issues, the field of fairness [3] and ethical artificial intelligence (AI) [4] approaches are becoming mainstream, aiming to mitigate some of the biases persisting in datasets. The general idea in many of these approaches is to learn a ‘sensitive attribute’ agnostic representation that can be generalized to the rest of the data [5]. While many of these approaches are designed as classification problems, dealing with binary or multi-class scenarios like sex or ethnicity, they often overlook the consideration of numerical attributes, particularly in the context of age, when developing fair AI models.
In the context of skin lesion detection, addressing age-related bias and digital ageism is critical [3,6,7] in developing fair AI models. Unfair models with respect to age could result in multiple issues. One major issue is the difficulty in collecting sufficient data from older adults, which limits the model’s ability to generalize across different age groups. Chu et al. [8] describe the presence of sampling bias in several databases containing very few data from older people. The other crucial aspect is the misrepresentation of age as a category, the reinforcement of stereotypes, a lack of awareness, and the neglect of the older population. These factors, in most cases, lead to the predominance of training data from younger people [9]. In a health-sensitive application, such as skin lesion detection, this systemic data imbalance could lead to algorithms that are less sensitive to the nuances of skin lesions in older demographics, potentially resulting in higher misdiagnosis rates. Another significant issue is the deployment of medical devices using unfair AI algorithms. As an example, if a medical treatment requires the use of a digital device (i.e., a mobile phone, web services) and the digital literacy and education of older adults is not considered, such devices risk producing discriminatory results regarding older people and may have negative impacts on their health [10].
For skin lesion detection problems, it appears that older people who are more exposed to sunlight may have a higher likelihood of developing skin cancer [11]. However, an important question is whether the publicly available datasets on skin lesions contain equal or larger numbers of older people in their cohorts. To test this, we plotted the age distributions of the PAD20 [12] and ISIC2019 [13] datasets (more details are given in Section 3.5). Figure 1 shows the combined age distribution in the ISIC2019 and PAD20 datasets. It can be seen that the representation of older adult people (more than 65 years) is small. In the PAD20 dataset, the age distribution of people above 80 is very small. Therefore, it is not clear if the skewed age distribution in these datasets reflects the prevalence of skin lesions in the older population. This could potentially lead to age-biased AI models. Furthermore, it is not clear whether the models trained on these datasets, predominately comprising younger people, generalize well to older people.
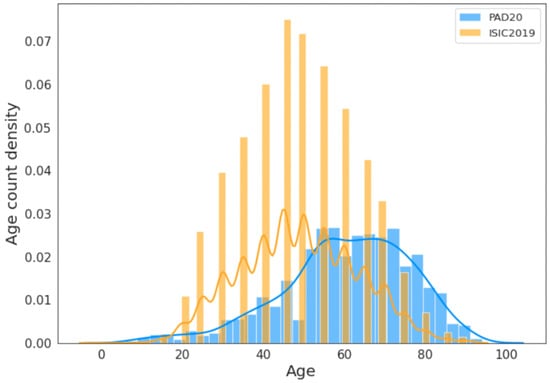
Figure 1.
Histogram of age distribution across PAD20 (blue) and ISIC2019 (yellow) skin lesion datasets. Both datasets show considerably fewer samples from older patients, who may have a high likelihood of skin lesions. The solid lines show the fitting of the curves and are only included for visualization purposes.
Adversarial learning is one of the most commonly used techniques to mitigate general biases, and it can achieve fair and transferable performance [14]. In this setting, an adversarial network can be employed as an encoder before or after the classifier to learn a fair latent representation for sensitive attributes [14,15,16]. While effective for tabular data, this approach is not well suited to handle image inputs. On the other hand, an adversarial network can also be appended to the end of an encoder or classifier to forecast protected or sensitive attributes (e.g., age, sex), creating a minimax game (see Section 3.5). This game aims to maximize the network’s performance in predicting the class label, while simultaneously minimizing the ability of the adversarial network to predict the sensitive attributes [15,16]. However, if a model is required to ignore features pertaining to a protected attribute, this may have a negative impact on its classification accuracy, as those features could potentially contain vital information necessary for accurate predictions. Furthermore, most related works consider sex, gender, or race as the selected (binary) sensitive attribute [14,17]. These models are limited in their ability to handle continuous sensitive variables, such as age, which cannot be arbitrarily divided into categories as there is a lack of consistency in the labeling of age groups [18]. Manually binning data into age groups can also introduce human biases and inconsistent categorization [19]; thus, previous approaches are not suitable for this problem. Age as a continuous attribute could be incorporated into an adversarial loss function for bias mitigation purposes (e.g., BR-Net [20], AMAT-Net [21]); these are based on Pearson and/or cosine correlations between the true and predicted values of a protected variable. Furthermore, it is challenging to directly use the previous fairness criteria for continuous attributes (e.g., age). Therefore, alternative approaches are required to address fairness concerns related to continuous attributes.
In this paper, we present a new method, called Mitigating Digital Ageism using Adversarially Learned Representation (MA-ADReL), to handle a continuous sensitive attribute in an adversarial learning setting for the mitigation of age-related bias in skin lesion problems. We introduce a mutual information penalty term that can mitigate bias for sensitive continuous attributes to improve the fairness while maintaining the accuracy. To further improve the performance, we utilize the information fusion of both low- and high-resolution inputs for medical image encoding in order to learn a more transferable latent representation. Various experiments on two skin lesion datasets demonstrate the consistent effectiveness of our method in mitigating bias and achieving comparable performance.
2. Related Work
Several studies have focused on mitigating bias in training their predictive models. From a dataset perspective, a commonly used method is data augmentation. Georgopoulos et al. [22] used a generative adversarial network (GAN) that included a style-based generator and discriminator. Images were categorized into four age groups, and the GAN was employed to produce digitally aged images to balance the training dataset among each group. In another study, Smith and Ricanek [23] utilized two augmentation methods, random Gaussian tinting and random cropping, to expand their training dataset for a deep neural network model. However, the effectiveness of data augmentation in mitigating bias is impacted by the quality and diversity of the original data augmentation techniques employed; it could also lead to overfitting problems.
From a model learning perspective, bias mitigation methods usually involve modifying the training loss function to regularize the model for fairness. Corral et al. [24] added a task-specific prior to implicitly regularize the model to not pay attention to the sensitive attribute-related information for its prediction. Adversarial training has been applied in several works ([20,25,26]) to achieve fairness by removing sensitive information with an adversarial learner or calculating correlations between actual and predicted protected variables. Bevan and Amir [27] proposed a method for the mitigation of skin tone bias in skin lesion classification. They first detected the skin tones of the lesion images and then debiased the feature representations to reduce the impact of the skin tone on the final prediction. However, it addressed bias related to skin tone and did not consider age-related bias. In this paper, we present a new adversarial method that accounts for age as a continuous attribute and reduces the bias while maintaining the classification performance.
3. Methods
3.1. Fair Skin Lesion Detection
Consider a medical image with metadata consisting of tuples in , , where is the input skin lesion image, denotes the metadata, is the class label from the set X, Y, and A, and a pretrained encoder yields the representations Z. Each is a high-resolution image represented as a 3-dimensional matrix of dimensions , where W, H, and C are the width, height, and the number of color channels (typically C = 3 for RGB images). The metadata consist of vectors of real-valued attributes associated with each image. They are represented as , where M is the number of metadata attributes, such as age, gender, weight, and height. The class label is a binary indicator representing the diagnosis of a skin lesion in the image . It takes values from the set A 0,1, where 0 corresponds to ‘benign’ and 1 to ‘malignant’. The classifier learns to predict based on the representation Z from the input image. In the context of mitigating age-related bias in skin lesion detection, the encoder , decoder , and classifier work together to minimize both the classification loss and the reconstruction error, while also minimizing the objective of the adversary .
In the adversarial framework, we establish a competitive yet collaborative environment between the classifier and the adversary. The classifier aims to maximize its predictive accuracy to detect skin lesions, while the adversary strives to minimize the classifier’s ability to discern sensitive attributes, such as age, from the latent representation. This dynamic creates a minimax game, where the objective is to find a balance where the classifier performs well on the primary task without relying on sensitive attributes that the adversary is trying to ‘protect’ from being predictive. However, there are several operational challenges when working with adversarial networks that should be proactively considered, including vanishing gradients, mode collapse, and convergence problems [28]. Furthermore, data poisoning and other malicious data injections can severely undermine the predictive abilities of adversarial networks [29].
Unlike Madras et al. [14], in our problem, input is not a tabular dataset [30] but skin lesion images with metadata. Moreover, our sensitive attribute is age, which is a continuous variable rather than a discrete variable (e.g., ethnicity, sex, or gender). We aim to maximize the prediction performance while minimizing the bias against sensitive attributes:
In this equation, represents the encoder that extracts features from the input images , g is the classifier that predicts the class labels , and is an optional decoder that may reconstruct the images from the latent features. The adversary h attempts to predict the sensitive attribute (such as age) from the features to ensure fairness. The expectation is taken over the input images X, labels Y, and sensitive attributes A, while is the loss function that balances both prediction accuracy and fairness.
Our objective function is expressed as
The classification loss ensures accurate classification; the reconstruction loss enhances the accuracy of data reconstruction by the deep variational autoencoder (VAE), promoting meaningful representation learning and improving the data quality. The adversarial loss promotes fairness. The hyperparameters , , and are used to control the trade-off in the performance of the model in detecting skin lesions, reconstructing the input images, and achieving fairness in the prediction results, respectively. In the following section, we investigate different values to balance model performance and fairness. The overall framework is shown in Figure 2. Following the framework from [13], the metadata undergo processing through two fully connected layers before being combined with the CNN features from the skin lesion image. Training with the adversary, we then input the latent representations Z into the classifier.
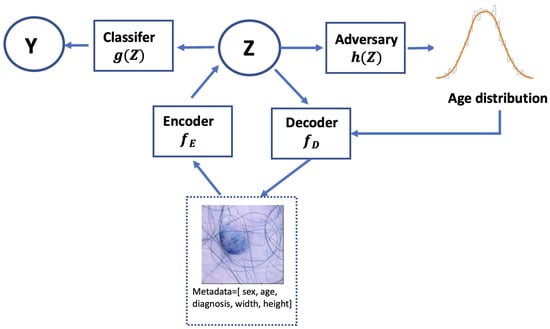
Figure 2.
The process of learning a fair representation with MA-ADReL. An adversarial minimax game is established between a classifier and adversary based on the representation Z from an input image learned through a pretrained encoder . Together with a decoder , the architecture minimizes the classification, reconstruction, and adversarial losses.
3.2. Fairness Criteria Definitions
In the context of skin lesion detection, the fairness criteria proposed by Madras et al. [14] are as follows.
Demographic Parity: This criterion ensures that the probability of positive predictions is approximately equal across different sensitive attribute groups. In other words, the model should not favor one group over another. The difference in the true positive rates for the sensitive () and non-sensitive () groups should be within a specified bound . This can be formulated as follows:
where is the predicted class label, A is the sensitive attribute (e.g., race, gender), and is the maximum allowed difference.
Equalized Odds: This criterion ensures that the probability of false positives and true positives is similar across the sensitive and non-sensitive groups. The idea is to ensure that the model’s error rates (false positives or negatives) are evenly distributed across the groups. The difference in the false positive rates for the sensitive and non-sensitive groups should be within a certain bound. This can be formulated as follows:
where Y is the true class label (e.g., indicates a benign lesion, indicates a malignant lesion). is the predicted class label (e.g., is a prediction of malignancy). A represents the sensitive attribute (e.g., gender, where might represent male and female). again represents the acceptable difference between the false positive rates, ensuring equalized odds across groups.
The fairness criteria defined in Equations (3) and (4) are straightforward to integrate for gender or racial bias mitigation by labeling them in discrete categories. However, dealing with continuously protected attributes, such as age, can be more challenging than with categorical attributes, because the fairness constraint needs to be defined over a continuous range of values. Manually classifying a continuous age distribution into different groups will also induce bias [1].
3.3. Protecting Continuous Sensitive Attributes with Mutual Information Penalty
To address bias related to continuous sensitive attributes such as age, we propose incorporating a mutual information loss term in the objective function of the learning algorithm. The core idea is that, by minimizing the mutual information between the sensitive attribute (age) and the latent representation, we can reduce the model’s dependence on age when making predictions. This ensures that the model focuses more on relevant skin lesion features rather than age, thus mitigating the impact of age-related bias in skin lesion detection. Given the input features, which include the skin image and metadata X, the target label Y, and the continuous sensitive attribute A (in this case, age), we can calculate the mutual information between X and A as
where is the entropy of X and is the conditional entropy of X given A. To mitigate the bias, we wish to minimize the mutual information between A and the hidden representation Z, while preserving the mutual information between X and Z, Y, and Z. This can be formulated as the following optimization problem:
where is the mutual information between the latent representation Z and the sensitive attribute A. Minimizing this term helps to reduce age bias. is the mutual information between the latent representation Z and the input X. This term should be maintained above a certain threshold , ensuring that the representation Z retains enough information from the input X for accurate classification. is the mutual information between the latent representation Z and the target label Y, and it should also be above a threshold to ensure that Z contains enough information to make correct predictions. and are constants that define the minimum acceptable levels of mutual information, balancing the model’s ability to use the input and target label information.
As a result, we can formulate the adversarial loss term; this is achieved by minimizing the following objective function:
where and are hyperparameters that balance the trade-off between the classification and reconstruction accuracy and the fairness of the model from the level of mutual information. Finally, we can integrate Equation (7) into Equation (2).
3.4. Training Deep VAE Model for Fairness
Previous works aimed at learning fair representations via adversarial learning primarily focused on tabular data [14,31] or low-resolution images [25,32]. However, when dealing with high-resolution medical images, such as those used in skin lesion detection, directly applying traditional variational autoencoders (VAE) can introduce several challenges. First, high-resolution images typically contain a large amount of pixel-level detail, resulting in a high-dimensional input space. Training a model on such data can become computationally expensive and difficult due to the increased complexity and dimensionality of the input [33]. Second, traditional VAE architectures often struggle to capture the fine-grained details that are critical for the accurate classification and diagnosis of skin lesions. The loss of this crucial information during encoding can negatively impact the model’s performance, leading to suboptimal predictions. Therefore, specialized architectures and techniques are required to effectively encode high-resolution medical images in a way that preserves essential details while ensuring fairness in the model’s predictions. To address these issues, we propose using a deep hierarchical VAE architecture. A deep hierarchical VAE is capable of learning more complex and structured representations of the data by encoding the input at multiple levels of abstraction. This allows the model to capture both coarse- and fine-grained details of the image by progressively refining the latent representation across different layers. By encoding at multiple abstraction levels, the VAE can generate data at different levels of detail by sampling from different layers of the latent representation [33]. This hierarchical structure is particularly beneficial for high-resolution medical images, as it allows for the effective capture of both global and local image features. The Very Deep VAE (VDVAE) uses the hierarchical factorization of the prior and approximate posterior distributions, where K stochastic layers are employed to progressively capture more complex information from the input data. The factorization of the prior distribution and the approximate posterior distribution for a model with K layers are expressed as follows:
where is the prior distribution for the latent variable at the first layer, and is the conditional prior for each subsequent latent variable, conditioned on the latent variables from previous layers. K represents the total number of stochastic layers in the model, with each layer refining the latent representation learned by the model. represents all latent variables from the layers before layer K, capturing hierarchical information.
As depicted in Figure 3, the model comprises both a high-resolution (HR) branch, with dimensions , and a low-resolution (LR) branch, with dimensions . The pooling layer is employed for the downsampling of the HR input and upsampling of the LR input. The distribution is modeled as a diagonal Gaussian, is sampled from , and the group of latent variables is positioned at the top layer, featuring a smaller number of variables for the low-resolution input. Conversely, resides at the bottom of the network, encompassing a greater number of latent variables for the high-resolution input. This hierarchical arrangement offers enhanced flexibility in capturing intricate relationships between the input and the latent variables.
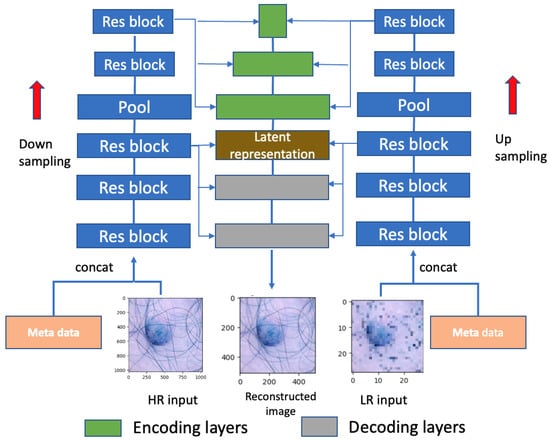
Figure 3.
Network architecture for high-resolution medical image processing, consisting of an encoding phase with downsampling, followed by residual blocks, and a decoding phase with upsampling. The network also incorporates concatenation layers to integrate additional metadata, enhancing the model’s representational capacity.
To be more specific, as shown in Figure 4, we follow a similar procedure to that proposed by [13] to conduct information fusion for the image and metadata. After passing through the fully connected layers, the metadata are combined with the CNN features extracted from the raw images through concatenation and then forwarded to the final fully connected layer. The CNN model has a 7 × 7 kernel with stride 2 for broad feature extraction, followed by 3 × 3 residual blocks with 64, 128, and 256 filters; global average pooling; and a 128-neuron fully connected layer. Batch normalization ensures stable and efficient training, with outputs via softmax for binary classification. To train our model, we used 5-fold cross-validation to select the optimal subsets of models based on the cross-validation performance. We tuned different parameters of , as shown in Equation (2), to achieve the best outcomes in balancing the prediction performance and fairness.
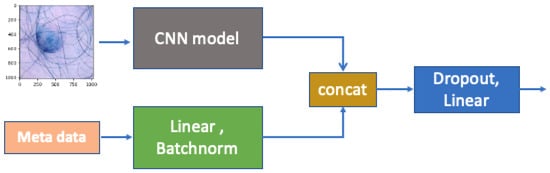
Figure 4.
Concatenation of images and metadata, which involves concatenating linear and batch-normalized features, enhancing the model’s ability to learn from both the visual content and associated metadata.
3.5. Datasets
We implement our framework on the ISIC2019 challenge’s Skin Lesion Classification dataset [34], which is a compilation of skin lesion images utilized for the identification and categorization of melanoma. The dataset comprises 33,126 images with dimensions of pixels, with binary labels indicating whether each lesion is benign (0) or malignant (1). Additional metadata are also provided with other information, including the approximate ages of the participants. We performed 5-fold cross-validation on the dataset and report the mean and standard deviation. To demonstrate the transferability of MA-ADRel, we also used the PAD20 dataset for testing [35], which contains dermatoscopic images of skin lesions collected from a public health center in Brazil using smartphones. It contains 2298 images with various metadata, including age.
3.6. Dataset Exploration
First, we analyzed the age distribution of the images within these datasets. Figure 1 shows that the age distributions in these two datasets follow normal distributions. The blue curve represents the distribution of PAD20, while the yellow curve represents the distribution of ISIC2019. The median age from the ISIC2019 dataset is 43 years old, while the median age from PAD20 is 63 years old. It appears that ISIC2019 comprises a greater number of middle-aged adults, whereas PAD20 has a larger sample of older adults.
Furthermore, we analyzed the disease rate among each age group. Consider n as the total number of individuals in the age group, and consider d as the number of individuals in the age group who have the disease. We define the disease rate for the age group as
For example, if there are 100 individuals in the age group and 10 of them have the disease, the disease rate would be . We plotted the disease rate among each age sample for these datasets. As shown in Figure 5 and Figure 6, the disease rate is not equally distributed within each dataset. For the ISIC2019 dataset, older adults have higher disease rates, whereas they are less represented in the data. For the PAD20 dataset, middle-aged adults have higher disease rates and there is better representation of older adults. Therefore, the distributions of the age and disease rates are not consistent in these datasets; as a result, age-related biases may be introduced when developing predictive models.
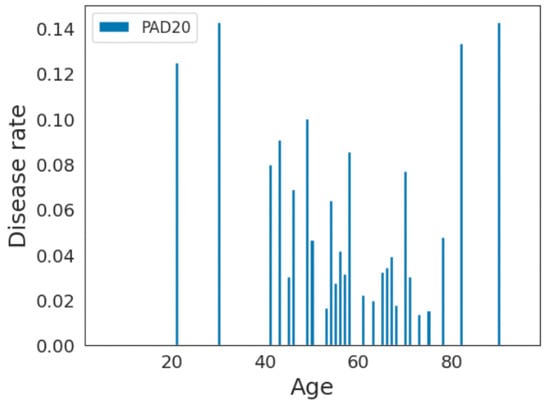
Figure 5.
Disease rate distribution in PAD20 dataset.
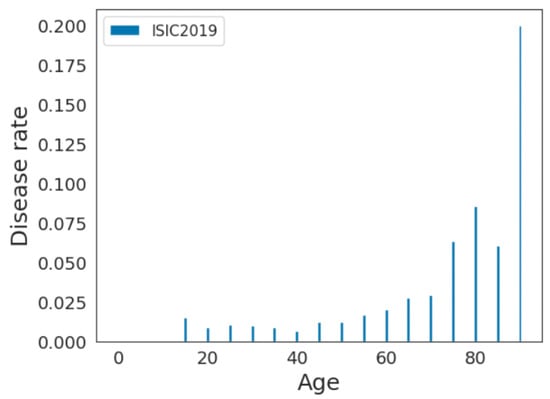
Figure 6.
Disease rate distribution in ISIC2019 dataset.
As pointed out by Mehrabi et al. [1], different data collection protocols can induce measurement biases. According to Wu et al. [17], the target prediction in skin lesion diagnosis should not depend on sensitive attributes, such as age. Furthermore, the training data should not be biased in terms of the disease samples per age category. As demonstrated in Figure 6 and Table 3, age-related bias exists in these two datasets. As a result, the investigation of bias mitigation strategies for the continuous sensitive attribute is necessary before developing predictive models.
3.7. Baseline Setup
We compared MA-ADReL with several baselines, including (i) LAFTR learning [14] and (ii) EfficientNet Ensemble, which is a vanilla training method without fairness constraints that achieved the best performance in the IIM-ISIC Melanoma Classification Challenge (i.e., the ISIC2019 dataset [13]). We built upon their framework’s main classification backbone network.
We trained our model on 4 NVIDIA Tesla V100 GPUs with batch size 64 for all models using 5 random seeds. To schedule the training process, we employed cosine annealing with a single warm-up epoch [36]. All models were trained for a total of 30 epochs. We report the average and standard deviation using the models with 5 random seeds on the test set. The performance metrics for evaluation are defined below.
3.8. Evaluation Criteria
We utilized the AUROC and AUPRC to evaluate the prediction performance, and we also utilized the MI score (as defined in Equation (5)). To be more specific, the AUROC and AUPRC are defined as follows.
AUROC (Area Under the Receiver Operating Characteristic Curve). This is formulated as follows:
where TPR and FPR are the true positive rate and false positive rate at a threshold t. The AUCROC is an integral of the TPR and FPR at all thresholds and quantifies the model’s ability to distinguish between the two classes (e.g., positive and negative) by calculating the area under the ROC curve. The AUCROC represents the probability that, if given a randomly chosen positive and negative sample, the model will rank the positive higher than the negative. The AUCROC of a perfect classifier is 1 and that of a random classifier is .
AUPRC (Area Under the Precision–Recall Curve).
The precision–recall curve is another graphical representation of the model’s performance, particularly suitable for imbalanced datasets. It plots the precision against the recall at various classification thresholds t and can be expressed mathematically as
The AUPRC quantifies the trade-off between the precision and recall across different classification thresholds, i.e., in terms of both not labeling negative samples as positive (precision) and correctly labeling the positive samples (recall). A higher AUCPR signifies a better-performing classifier. A perfect classifier will have an AUCPR of 1, and a random classifier’s AUCPR will be equal to the proportion of the number of positive samples in the data. As our dataset’s target variables are severely imbalanced, this can demonstrate the prediction performance from another perspective. We used Scikit-learn to calculate the AUROC and AUPRC criteria [37].
4. Results
From Figure 7, it is evident that the validation loss closely follows the training loss, without significant divergence, indicating that the model generalizes well to unseen data. The consistent improvement in the validation loss supports the claim that the classifier is pretrained adequately. Additionally, the pretraining was validated by comparing the pretrained model’s performance (AUROC: 0.942) to a model trained from scratch (AUROC: 0.876), showcasing the effectiveness of pretraining.
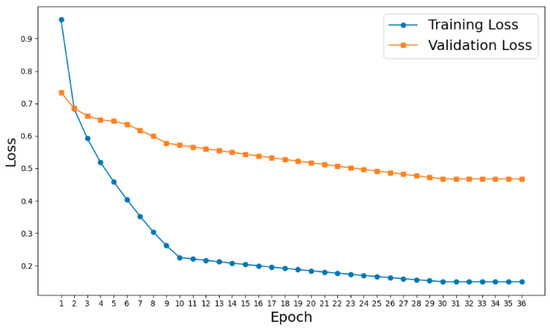
Figure 7.
Training and validation loss curve visualization.
4.1. ISIC2019 Dataset
Firstly, we compare different regularization factors in Equation (2) on the ISIC2019 dataset. From the results in Figure 8, we can deduce the trade-off between the fairness ratio and the AUC ROC score. With , we can achieve consistently better performance than LAFTR. With varying fairness ratios, we can achieve better fairness than EfficientNet Ensemble and LAFTR. From Figure 9, we can see that when the fairness ratio increases, the MI score will decrease, which indicates that the fairness has improved. Comparing the results between LAFTR and MA-ADRel, we can also see that, with the help of the proposed network structure in Figure 3, it can be better applied in image settings. It should be noted that the proposed MA-ADRel approach has the capability to vary the fairness ratio, , to regulate the fairness and performance of the model (see Figure 8). The other state-of-the-art models investigated in this work do not have this capability; they only give one performance value for a given dataset and can be seen as singular points in Figure 8.
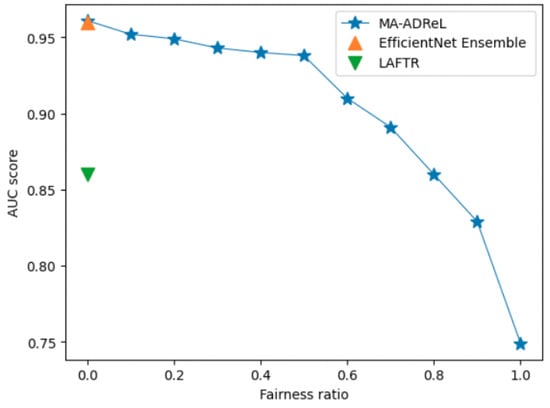
Figure 8.
Ablation study on hyperparameter for AUC score on ISIC2019 validation dataset for MA-ADRel, along with two state-of-the-art models. While MA-ADRel shows varied performance at different fairness ratios, the state-of-the-art models show singular performance for an unfair model.
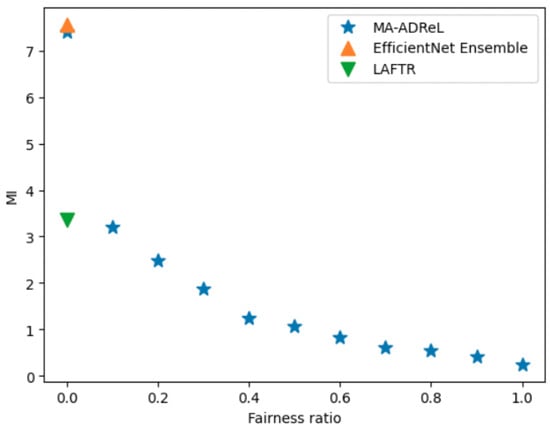
Figure 9.
Ablation study on hyperparameter for MI score on ISIC2019 validation dataset.
Moreover, from Figure 10, we can observe that there is a trade-off between the learning of fairness representations and the prediction performance. During deployment, we can control to control the amount of desired fairness in the model. We further utilize the best and compare the results in Table 1. Our proposed method balances the trade-off between accuracy and fairness. Moreover, a vanilla MA-ADReL without fairness incorporated (i.e., ) can also achieve comparable performance against the best solution, EfficientNet Ensemble.
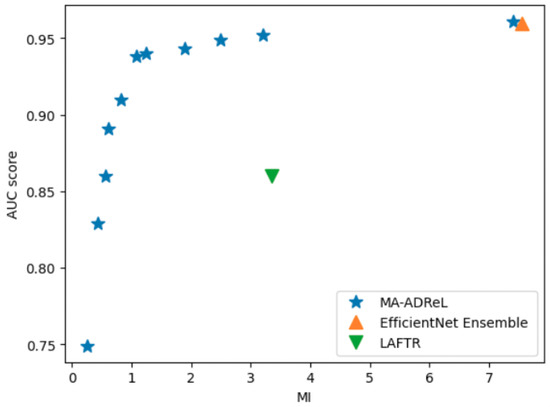
Figure 10.
Trade-off between fairness representation (MI) and prediction performance (AUC score).

Table 1.
Performance comparison on ISIC2019 dataset. The methods above the dash line are without fairness constraints. The higher the AUROC, the better the prediction performance as represented by the AUPRC, while a lower MI score indicates lower age-related bias.
4.2. PAD20 Dataset
As shown in Table 2, we directly applied the MA-ADReL framework to the PAD20 dataset with the best . We can see that MA-ADRel without an adversary can achieve the best . Secondly, focusing on the transfer learning performance, we compared different regularization factors on the PAD20 dataset. Following the transfer learning algorithm as proposed by Madras et al. [14], we trained an encoder (with ) using data X on the ISIC2019 dataset, and then we froze the encoder and trained a classifier on top of the pretrained encoder using data on the PAD20 dataset. Then, we evaluated the fairness and performance of the classifier.

Table 2.
Direct application performance comparison on PAD20 dataset. The methods above the dash line are without fairness constraints. The higher the AUROC, the better the prediction performance as represented by the AUPRC, while a lower MI score indicates lower age-related bias.
Table 3 shows a comparison of the accuracy and fairness results on the PAD20-transfer dataset. We observed that MA-ADReL () achieved significantly better fairness while maintaining relatively good performance. Our method can achieve MI = 5.51, which is better than the MA-ADReL without any constraints (). Additionally, our findings demonstrate that learning latent representations can lead to better transfer performance. We also find that, when using the transfer encoder, the MI score is usually lower. This suggests that the transferred knowledge from the source domain helps to reduce age-related bias in the target domain. This reduction in bias is desirable as it indicates that our model’s performance is less influenced by age-related factors, making it more equitable and applicable to a broader range of patients, regardless of age.

Table 3.
Transfer performance comparison on PAD20 dataset. The methods above the dash line are without fairness constraints. The higher the AUROC, the better the prediction performance as represented by the AUPRC, while a lower MI score indicates lower age-related bias.
4.3. Evaluation of the Deep Fusion VAE Model
To evaluate the effectiveness of capturing more fine-grained features with the deep fusion VAE model, as shown in Figure 3, we conducted an ablation study using the ISIC2019 dataset. Firstly, for the ISIC2019 dataset, we compared different backbones for the VAE’s encoder and decoder, as utilized in Ha et al. [13]. To compare all models fairly, we used the same size of input. If we only use higher-resolution inputs, i.e., , this would be equal to only using the left branch in Figure 3. On the other hand, if we only use lower-resolution inputs, i.e., , this would be equal to only using the right branch in Figure 3. For the backbones, we consider SE-ResNeXt-101 [38] and ResNeSt-101 [39], which are some representative backbones from [13]. All models are trained with the same adversary learning framework in Figure 2, and all models’ fairness regulation parameters are set to . From Table 4, we can observe that the higher-resolution inputs performed better (higher AUROC and AUPRC) than the lower-resolution inputs, and our fusion network performed the best, with the highest AUROC score and the lowest MI score. We also observed that the lower-resolution inputs gave a lower AUC score and a higher MI score. Note that our classification model learns a combination of the reconstructed image and metadata. If the model’s reconstructed image contains less representative information, then the classification module tends to learn more about the information from the metadata, so it is more likely to capture the existing bias from the metadata.

Table 4.
Performance comparison on ISIC2019 dataset using different backbones.
5. Discussion and Future Work
Aimed at advancing the field of fair AI, our study presents MA-ADReL, a novel approach to counteracting age-related bias in skin lesion detection. Through the combination of adversarial learning and mutual information optimization, we have optimized the interplay between bias mitigation and performance retention. Nonetheless, our work is not without its limitations, which we acknowledge and discuss below.
One of the primary limitations of our study is the reliance on existing datasets, which, despite their utility, are not representative of the full demographic spectrum. The underrepresentation of certain age groups, particularly the elderly, in the ISIC2019 dataset poses a challenge in training and validating models that are equitable across all ages. This limitation is not unique to our study but is a common constraint in medical imaging research, which we hope that future data collection efforts will address. Future research could focus on training fair (and unfair) models on data from various younger age groups and testing them on various older age groups to develop an understanding of their performance. These experiments could establish the generalization capacities and limitations of models trained on younger patients’ skin lesions to detect older patients’ skin lesions.
Additionally, while our method has been effective in reducing age-related bias, it is possible that other forms of bias, such as those related to ethnicity, sex, or gender, may not be as effectively mitigated. Other types of bias, beyond age and demographics, may also be present in datasets due to selection bias, negative set bias, and category or labeling bias [1,2]. Therefore, it is very difficult to obtain a completely unbiased dataset in practical settings, especially those using human participants and different data collection protocols, instruments, and labeling strategies. Hypothetically, if a completely unbiased dataset existed, MA-ADRel would still perform comparably, with an additional functionality to manage future (age-related) bias. Our focus on age as a continuous attribute was intentional given the spotlight on digital ageism; however, a comprehensive assessment of all potential biases was beyond the scope of this study. We recommend that future research in this area should attempt to develop skin lesion models that can address different types of demographics and other data biases in one inclusive model. Other potential directions for research, besides adversarial learning to mitigate continuous variable-related bias (e.g., age), are to investigate deep imbalanced regression [40] and supervised contrastive regression approaches [41].
Lastly, our study focused on the technical aspects of bias mitigation and did not delve into the ethical and societal implications of deploying AI in healthcare. Future work should consider the broader ethical frameworks within which these technologies operate, including issues of consent, transparency, and accountability.
6. Conclusions
In this work, we introduced MA-ADReL, an innovative approach that utilizes adversarial learning to address the critical issue of age-related bias in the context of skin lesion detection. Our method differs from existing bias mitigation techniques, which predominately addresses discrete attributes (e.g., gender or race), by extending the focus to continuous attributes—specifically, age. By controlling the mutual information penalty term, MA-ADReL not only improves the fairness but also maintains high predictive accuracy, a delicate balance in the realm of AI fairness and performance. Our method’s innovation lies in its ability to manage continuous variables, which are often more complex to handle due to their inherent lack of natural categorization. This dual achievement is a significant milestone in the quest for fair AI. The implications of our research extend beyond technical advancements. As AI becomes increasingly integrated into healthcare, the need for algorithms that are fair, unbiased, and sensitive to demographic variables is important. The successful application of MA-ADReL on the ISIC2019 and PAD20 datasets illustrates its potential to transform the field of medical image analysis, ensuring that AI systems treat all patients equitably, regardless of age. Our work contributes to this critical discourse by providing a viable solution that can be potentially applied to other areas of medical diagnosis and beyond.
Author Contributions
S.S.K. conceived the original idea, prepared the manuscript with support from the other authors, and prepared subsequent revisions. C.H.C. supervised T.S. in developing the AI models and performing the various experiments. S.D.-W. and C.H.C. helped with proofreading. All authors have read and agreed to the published version of the manuscript.
Funding
Social Sciences and Humanities Research Council grant, Grant Number: 2020-00360.
Data Availability Statement
The data used in this research paper is available publicly.
Acknowledgments
This research is supported by the Social Sciences and Humanities Research Council, Canada.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of the data; in the writing of the manuscript; or in the decision to publish the results.
References
- Mehrabi, N.; Morstatter, F.; Saxena, N.; Lerman, K.; Galstyan, A. A survey on bias and fairness in machine learning. ACM Comput. Surv. (CSUR) 2021, 54, 1–35. [Google Scholar] [CrossRef]
- Torralba, A.; Efros, A.A. Unbiased look at dataset bias. In Proceedings of the CVPR 2011, Colorado Springs, CO, USA, 20–25 June 2011; pp. 1521–1528. [Google Scholar]
- Fan, D.; Wu, Y.; Li, X. On the fairness of swarm learning in skin lesion classification. In Proceedings of the Clinical Image-Based Procedures, Distributed and Collaborative Learning, Artificial Intelligence for Combating COVID-19 and Secure and Privacy-Preserving Machine Learning: 10th Workshop, CLIP 2021, Second Workshop, DCL 2021, First Workshop, LL-COVID19 2021, and First Workshop and Tutorial, PPML 2021, Held in Conjunction with MICCAI 2021, Strasbourg, France, 27 September and 1 October 2021; Proceedings 2. Springer: Berlin/Heidelberg, Germany, 2021; pp. 120–129. [Google Scholar]
- Rigby, M.J. Ethical dimensions of using artificial intelligence in health care. AMA J. Ethics 2019, 21, 121–124. [Google Scholar]
- Ashraf, A.; Khan, S.; Bhagwat, N.; Chakravarty, M.; Taati, B. Learning to unlearn: Building immunity to dataset bias in medical imaging studies. In Proceedings of the Machine Learning for Health (ML4H), Workshop at NeurIPS 2018, Montréal, Canada, 3–8 December 2018. [Google Scholar]
- Bissoto, A.; Valle, E.; Avila, S. Debiasing skin lesion datasets and models? Not so fast. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Seattle, WA, USA, 14–19 June 2020; pp. 740–741. [Google Scholar]
- Rosales, A.; Fernández-Ardèvol, M.; Svensson, J. Digital Ageism: How It Operates and Approaches to Tackling It; Taylor & Francis: Oxfordshire, UK, 2023. [Google Scholar]
- Chu, C.H.; Donato-Woodger, S.; Khan, S.S.; Nyrup, R.; Leslie, K.; Lyn, A.; Shi, T.; Bianchi, A.; Rahimi, S.A.; Grenier, A. Age-related bias and artificial intelligence: A scoping review. Humanit. Soc. Sci. Commun. 2023, 10, 1–17. [Google Scholar] [CrossRef]
- Chu, C.; Donato-Woodger, S.; Khan, S.S.; Shi, T.; Leslie, K.; Abbasgholizadeh-Rahimi, S.; Nyrup, R.; Grenier, A. Strategies to Mitigate Age-Related Bias in Machine Learning: Scoping Review. JMIR Aging 2024, 7, e53564. [Google Scholar] [CrossRef] [PubMed]
- van Kolfschooten, H. The AI cycle of health inequity and digital ageism: Mitigating biases through the EU regulatory framework on medical devices. J. Law Biosci. 2023, 10, lsad031. [Google Scholar] [CrossRef]
- Baumann, L. Skin ageing and its treatment. J. Pathol. A J. Pathol. Soc. Great Br. Irel. 2007, 211, 241–251. [Google Scholar] [CrossRef]
- Pacheco, A.G.; Lima, G.R.; Salomao, A.S.; Krohling, B.; Biral, I.P.; de Angelo, G.G.; Alves Jr, F.C.; Esgario, J.G.; Simora, A.C.; Castro, P.B.; et al. PAD-UFES-20: A skin lesion dataset composed of patient data and clinical images collected from smartphones. Data Brief 2020, 32, 106221. [Google Scholar] [CrossRef]
- Ha, Q.; Liu, B.; Liu, F. Identifying melanoma images using efficientnet ensemble: Winning solution to the siim-isic melanoma classification challenge. arXiv 2020, arXiv:2010.05351. [Google Scholar]
- Madras, D.; Creager, E.; Pitassi, T.; Zemel, R. Learning adversarially fair and transferable representations. In Proceedings of the International Conference on Machine Learning, PMLR, Stockholm, Sweden, 10–15 July 2018; pp. 3384–3393. [Google Scholar]
- Wang, T.; Zhao, J.; Yatskar, M.; Chang, K.W.; Ordonez, V. Balanced datasets are not enough: Estimating and mitigating gender bias in deep image representations. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 5310–5319. [Google Scholar]
- Zhang, B.H.; Lemoine, B.; Mitchell, M. Mitigating unwanted biases with adversarial learning. In Proceedings of the 2018 AAAI/ACM Conference on AI, Ethics, and Society, New Orleans, LA, USA, 2–3 February 2018; pp. 335–340. [Google Scholar]
- Wu, Y.; Zeng, D.; Xu, X.; Shi, Y.; Hu, J. Fairprune: Achieving fairness through pruning for dermatological disease diagnosis. In Proceedings of the Medical Image Computing and Computer Assisted Intervention–MICCAI 2022: 25th International Conference, Singapore, 18–22 September 2022; Proceedings, Part I. Springer: Berlin/Heidelberg, Germany, 2022; pp. 743–753. [Google Scholar]
- Drysdale, C. Ageism Is a Global Challenge: UN. 2021. Available online: https://www.who.int/news/item/18-03-2021-ageism-is-a-global-challenge-un (accessed on 8 March 2023).
- Chu, C.; Nyrup, R.; Donato-Woodger, S.; Leslie, K.; Khan, S.; Bernett, C.; Grenier, A. Examining the technology-mediated cycles of injustice that contribute to digital ageism: Advancing the conceptualization of digital ageism: Evidence and implications. In Proceedings of the 15th International Conference on PErvasive Technologies Related to Assistive Environments, Corfu Greece, 29 June–1 July 2022; pp. 545–551. [Google Scholar]
- Adeli, E.; Zhao, Q.; Pfefferbaum, A.; Sullivan, E.V.; Fei-Fei, L.; Niebles, J.C.; Pohl, K.M. Representation learning with statistical independence to mitigate bias. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Virtual, 5–9 January 2021; pp. 2513–2523. [Google Scholar]
- Feng, F.; Wang, K.; Liu, X.; Gu, Q.; Wang, G. AMAT-Net: An Unbiased Network with High Performance for Metabolic Diseases Prediction Using Facial Images. In Proceedings of the 2022 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), Las Vegas, NV, USA, 6–8 December 2022; pp. 2074–2079. [Google Scholar]
- Georgopoulos, M.; Oldfield, J.; Nicolaou, M.A.; Panagakis, Y.; Pantic, M. Enhancing facial data diversity with style-based face aging. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Seattle, WA, USA, 14–19 June 2020; pp. 14–15. [Google Scholar]
- Smith, P.; Ricanek, K. Mitigating algorithmic bias: Evolving an augmentation policy that is non-biasing. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision Workshops, Waikoloa, HI, USA, 4–8 January 2020; pp. 90–97. [Google Scholar]
- Corral, A.; Saralegi, X. Gender Bias Mitigation for NMT Involving Genderless Languages. In Proceedings of the Seventh Conference on Machine Translation (WMT), Abu Dhabi, United Arab Emirates, 7–8 December 2022; pp. 165–176. [Google Scholar]
- Reimers, C.; Bodesheim, P.; Runge, J.; Denzler, J. Conditional adversarial debiasing: Towards learning unbiased classifiers from biased data. In Proceedings of the Pattern Recognition: 43rd DAGM German Conference, DAGM GCPR 2021, Bonn, Germany, 28 September–1 October 2021; Springer: Berlin/Heidelberg, Germany, 2022; pp. 48–62. [Google Scholar]
- Rajotte, J.F.; Mukherjee, S.; Robinson, C.; Ortiz, A.; West, C.; Ferres, J.M.L.; Ng, R.T. Reducing bias and increasing utility by federated generative modeling of medical images using a centralized adversary. In Proceedings of the Conference on Information Technology for Social Good, Roma, Italy, 9–11 September 2021; pp. 79–84. [Google Scholar]
- Bevan, P.J.; Atapour-Abarghouei, A. Detecting melanoma fairly: Skin tone detection and debiasing for skin lesion classification. In Proceedings of the Domain Adaptation and Representation Transfer: 4th MICCAI Workshop, DART 2022, Held in Conjunction with MICCAI 2022, Singapore, 22 September 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 1–11. [Google Scholar]
- Ding, Z.; Jiang, S.; Zhao, J. Take a close look at mode collapse and vanishing gradient in GAN. In Proceedings of the 2022 IEEE 2nd International Conference on Electronic Technology, Communication and Information (ICETCI), Changchun, China, 27–29 May 2022; pp. 597–602. [Google Scholar]
- Hassanin, M.; Radwan, I.; Moustafa, N.; Tahtali, M.; Kumar, N. Mitigating the impact of adversarial attacks in very deep networks. Appl. Soft Comput. 2021, 105, 107231. [Google Scholar] [CrossRef]
- Frank, A. UCI Machine Learning Repository; School of Information and Computer Science, University of California: Irvine, CA, USA, 2010; Available online: http://archive.ics.uci.edu/ml (accessed on 13 December 2024).
- Louizos, C.; Swersky, K.; Li, Y.; Welling, M.; Zemel, R. The variational fair autoencoder. arXiv 2015, arXiv:1511.00830. [Google Scholar]
- Li, X.; Cui, Z.; Wu, Y.; Gu, L.; Harada, T. Estimating and improving fairness with adversarial learning. arXiv 2021, arXiv:2103.04243. [Google Scholar]
- Child, R. Very deep vaes generalize autoregressive models and can outperform them on images. arXiv 2020, arXiv:2011.10650. [Google Scholar]
- Combalia, M.; Codella, N.C.; Rotemberg, V.; Helba, B.; Vilaplana, V.; Reiter, O.; Carrera, C.; Barreiro, A.; Halpern, A.C.; Puig, S.; et al. Bcn20000: Dermoscopic lesions in the wild. arXiv 2019, arXiv:1908.02288. [Google Scholar]
- Dai, W.; Liu, R.; Wu, T.; Wang, M.; Yin, J.; Liu, J. Deeply Supervised Skin Lesions Diagnosis with Stage and Branch Attention. arXiv 2022, arXiv:2205.04326. [Google Scholar] [CrossRef] [PubMed]
- Loshchilov, I.; Hutter, F. Sgdr: Stochastic gradient descent with warm restarts. arXiv 2016, arXiv:1608.03983. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7132–7141. [Google Scholar]
- Zhang, H.; Wu, C.; Zhang, Z.; Zhu, Y.; Lin, H.; Zhang, Z.; Sun, Y.; He, T.; Mueller, J.; Manmatha, R.; et al. Resnest: Split-attention networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 2736–2746. [Google Scholar]
- Yang, Y.; Zha, K.; Chen, Y.; Wang, H.; Katabi, D. Delving into deep imbalanced regression. In Proceedings of the International Conference on Machine Learning, PMLR, Virtual, 18–24 July 2021; pp. 11842–11851. [Google Scholar]
- Zhou, Z.; Zhao, Y.; Zuo, H.; Chen, W. Ranking Enhanced Supervised Contrastive Learning for Regression. In Proceedings of the Pacific-Asia Conference on Knowledge Discovery and Data Mining, Taipei, Taiwan, 7–10 May 2024; Springer: Berlin/Heidelberg, Germany, 2024; pp. 15–27. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).