An Improved Bi-RRT Algorithm for Optimal Puncture Path Planning

Abstract

Percutaneous puncture has become one of the most widely used minimally invasive techniques in clinical practice due to its advantages of low trauma, quick recovery and easy operation. However, incomplete needle tip movement, tissue barriers and complex distribution of sensitive organs make it difficult to balance puncture accuracy and safety. To this end, this paper proposes a new puncture path planning algorithm for flexible needles, which integrates gravitational guidance, bi-directional adaptive expansion, optimal node selection based on the A* algorithm, and path optimization strategies, with Bi-Rapid-Research Random Trees (Bi-RRTs) at its core, to significantly improve obstacle avoidance capability and computational efficiency. The simulation results of 2D and 3D complex scenes in MATLAB show that compared with the traditional RRT algorithm and Bi-RRT algorithm, the GBOPBi-RRT algorithm achieves significant advantages in terms of path length, computation time and node size. In particular, in the 3D environment, the GBOPBi-RRT algorithm shortens the planning path by 43.21% compared with RRT, 27.47% compared with RRT* and 30.33% compared with Bi-RRT, which provides a reliable solution for efficient planning of percutaneous puncture with flexible needles.

1. Introduction

With good flexibility, obstacle avoidance ability, high dexterity and variable curvature, the trocar flexible needle can avoid some obstacles like bones or blood vessels to realize the targeted puncture of the lesion. Compared with rigid needles, the form of the puncture path of cannulated flexible needles is particularly complicated. Therefore, it is necessary to conduct a more in-depth study on the path planning algorithm for flexible cannulated needles. The path planning solution algorithms for flexible needles can be broadly categorized into mathematical algorithms, inverse kinematics algorithms, intelligent algorithms and search algorithms [1,2,3].

The numerical method can simplify the complex path planning problem into a mathematical problem by establishing and calculating an optimization function to find the optimal solution of the path [4]. The algorithm can obtain global or local optimal solutions, but its solutions are often affected by the initial settings and suffer from slow computation speed and mathematical non-convergence.

In 2005, Alterovitz et al. [5] proposed a puncture path planning algorithm for flexible needles in conjunction with a single-wheel kinematic model, which discretizes the state space of the needle tip position and orientation by using a Markov decision process to compute the optimal steering point that maximizes the probability of the flexible needle tip reaching the target, and gives Bellman’s equation for the stochastic shortest path. In 2007, Alterovitz et al. [6] proposed a stochastic motion wayfinding algorithm based on the previous theory. The algorithm can plan the motion trajectory of a flexible needle under uncertain image navigation conditions.

A search method involves randomly selecting points in the state space and then connecting the appropriate sampled points in some way to create paths. There are three typical search methods: the Artificial Potential Field (APF) method, the Probabilistic Roadmap (PRM) algorithm, and the Rapid Exploration Random Tree (RRT) algorithm. A* and RRT algorithms are among the more typical search algorithms. Many hybrid algorithms based on A* utilize metaheuristic techniques, such as the multiagent hybrid clustering-assisted genetic algorithm (MA-HCAGA) and the A*-PSO hybrid algorithm. The MA-HCAGA algorithm was proposed by Andranik S. Akopov et al. [7] This algorithm, by integrating multi-agent systems, fuzzy clustering, genetic operators, and particle swarm mechanisms, demonstrates superior Pareto front quality in bi-objective optimization. However, it faces challenges such as random evolution failing to guarantee a global optimum, sensitivity to key frequency parameters, and slow convergence due to improper parameter tuning. The APSO algorithm, proposed by Huang et al. [8] in 2023, combines A* with an improved PSO, eliminating redundant nodes and introducing random inertia weights and reverse learning. It offers advantages such as fast search, smooth paths, and short runtime. However, its drawbacks include relatively high algorithm complexity and the inability to theoretically guarantee a global optimal path due to random initialization and the evolutionary mechanism. The RRT algorithm was proposed by Edsger Wybe Dijkstra [9,10]. the advantages of the search method are easy convergence and fast search, its disadvantage is that the nature of random sampling makes it possible to find feasible paths without ensuring the best route.

Bidirectional RRT (Bi-RRT) reduces the search time by more than 30% in complex environments by simultaneously growing two trees from the starting point and the goal point, but it still follows the stochastic expansion mechanism without goal bias, and the problems of redundant nodes and tortuous paths are still prominent [11]. In 2025, Huang Bo et al. [12] introduced a hierarchical sampling strategy within the Bi-RRT framework, which significantly improved the path smoothing, but accompanied by a surge in computation and a decrease in real-time performance instead.

Aiming at the problems of the traditional bidirectional rapidly expanding random tree (Bi-RRT) in flexible needle puncture path planning, this paper proposes an improved Bi-RRT algorithm for flexible needle puncture, which aims to improve the efficiency and quality of flexible needle path planning.The GBOPBi-RRT algorithm reduces the blindness of the search, improves the convergence speed, eliminates the redundant nodes, reduces the path length, and improves the search efficiency and effectiveness by introducing the gravitationally oriented, bi-directionally adaptive expansion, the optimal node selection based on the A* algorithm and the path optimization strategy.

2. Related Work

2.1. Two-Dimensional Puncture Path Planning

Addressing the multiple challenges posed by flexible needles in soft tissue—including susceptibility to deformation, high real-time requirements, and the need to balance puncture accuracy with damage control, in 2012, Zhao et al. [13] pioneered a flexible needle path planning method. By simultaneously optimizing the entry point, needle posture, and manipulation parameters based on an improved loop model, they significantly improved puncture performance. Addressing the challenge of balancing multiple objectives (real-time performance, accuracy, and tissue damage) that are difficult to balance online, Bobrenkov et al. and Huo et al. developed a multi-objective optimization framework, achieving high-fidelity online planning [14,15]. Addressing the issues of blind sampling and single evaluation dimension in complex soft tissue environments with traditional RRT, in 2017, Li et al. [16] improved the RRT algorithm based on environmental features, redefined the path evaluation function, and assigned weights based on obstacle risk levels, while comprehensively considering multiple indicators such as path length, arc segment count, and safety. To address the challenges of low initial path quality and optimization getting stuck in local optima during the iterative learning process of flexible needle trajectories, in 2021, Li et al. [17] proposed an iterative learning trajectory planning algorithm: first generate an initial path set in rigid body space, then select the optimal path using a genetic-simulated annealing hybrid optimization method. To address the issue of large prediction errors caused by the heterogeneity of soft tissue affecting the trajectory of flexible needles, in 2022, Xiong et al. [18] and other researchers combined the Fokker–Planck equation with an analytical Kriging model to predict the trajectory of flexible needles, and further improved prediction accuracy through data-driven post-processing.

However, the traditional RRT and Bi-RRT still have obvious shortcomings, random sampling makes the path tortuous and redundant, especially in the narrow space; although Bi-RRT is bi-directionally parallel, the proportion of invalid sampling is still high; and both lack cost function guidance. To this end, this paper proposes the GBOPBi-RRT algorithm, which uses the target gravitational field potential function to guide the sampling and increase the effective sampling rate; then uses the adaptive step size to avoid obstacles, so that the number of iterations can be effectively reduced; introduces the cost function based on the A* algorithm to optimize nodes in the bi-directional tree connecting phase, so as to reduce the cost of the path; and finally, through the pruning of the redundant nodes to shorten the length of the path to achieve the simultaneous improvement in real-time performance and optimality [19,20].

2.2. Three-Dimensional Puncture Path Planning

Puncture accuracy is affected by a variety of factors, such as needle–tissue interaction, patient movement and physiological changes. In recent years, dynamic path planning has attracted much attention because it is more compatible with human physiology and has more advantages over static planning.

Wang et al. [21] proposed a dynamic path planning and tracking control method based on curve fitting for needle insertion. They constructed a three-dimensional needle–tissue interaction deformation model using the local constraint method, which can simultaneously predict the needle–tissue interaction force and the needle–tissue deformation. Based on this model, the targeting error due to tissue deformation and needle deflection is corrected by iterative learning control, and the results show that the method can significantly improve the accuracy of needle tip localization.

Lei et al. [22] proposed a needle puncture path planning method based on a needle–tissue interaction model and designed a patient-specific parameter identification algorithm. They first used a fast exploratory random tree algorithm to generate static paths, then applied a complete computational model to calculate the forces and deformations of the static paths, and proposed an intraoperative patient-specific parameter identification algorithm to identify patient-specific parameters. Simulation experiment results show that the method can reduce the targeting error from a maximum of 3.89 mm to less than 1 mm.

3. Method Construction

In recent years, flexible needle path planning techniques based on RRT (Rapidly-exploring Random Tree) algorithm have received much attention. As an important improvement, Bi-RRT (Bidirectional rapidly-exploring random tree) algorithm has made significant progress in improving the efficiency of path planning [23]. However, the traditional Bi-RRT algorithm lacks a clear goal orientation during the random tree growth process, leading to the generation of a large number of redundant nodes, which not only significantly reduces the search efficiency, but also increases the computational cost, limiting its application in complex environments. In order to overcome this limitation of the traditional Bi-RRT algorithm, an improved GBOPBi-RRT algorithm is proposed in this paper. The algorithm significantly improves the efficiency of path planning and path quality by introducing the optimal node selection strategy of the gravity-oriented strategy, the bidirectional adaptive step-size strategy, the optimal node selection strategy based on A* heuristic algorithm, and the path optimization technique. Due to the fact that the path generated by the flexible needle within the tissue is an arc-shaped path with a variable radius and is affected by the material and curvature characteristics of the flexible needle, it may lead to the planned path being unreachable. Therefore, it is necessary to conduct kinematic modeling and reachable space analysis of the flexible needle puncture process and correct the unreachable paths. The overall system architecture is illustrated in Figure 1.

In Figure 1, the puncture path is first obtained through simulation and subsequently validated by physical experiments. The puncture experiments are carried out by mounting a puncture execution mechanism—with two degrees of freedom (rotation and feed)—at the end effector of a dual-arm robot and applying a duty-cycle control strategy. The Fiber Bragg Grating (FBG) sensor offers advantages such as high sensitivity, fast response, and good compatibility; therefore, it was selected for this design. Three optical fibers were used, arranged at ${120}^{°}$ intervals. Triangular grooves were created, and the fibers were embedded within them to form the core structure of the flexible needle. Based on the FBG sensing principle, the wavelength information is transmitted to the host computer via an FBG demodulator (model MOI si155) for real-time perception of the flexible needle’s shape and tip position, providing closed-loop feedback for the puncture robot’s path planning and puncture control. The sensor features a wavelength resolution of $1\mathrm{pm}$, a strain resolution of 1.2 $\mu \epsilon$, and a spatial resolution of $30\mathrm{mm}$, with an expected shape reconstruction accuracy at the sub-millimeter level. Regarding the puncture execution mechanism, the feed unit employs a two-phase stepper motor with a step angle of ${1.8}^{°}$, driving the needle tube axially via a 0601 ball screw pair. The rotation unit utilizes a brushless DC motor (BLDC) controlled by field-oriented control (FOC) and is equipped with a 12-bit absolute encoder (resolution: 4096 counts/rev). After integration with the UR3 robotic arm, the actuator achieves an end-effector positioning accuracy within $0.1\mathrm{mm}$. The current and velocity control loops can operate at high frequency, and considering the mechanical inertia and resonance of the screw, coupler, and needle, the system bandwidth reaches 20–$50\mathrm{Hz}$. The core contribution of this work lies in planning a puncture trajectory through simulation that conforms to the material characteristics of the flexible needle in a simulated puncture environment.

3.1. Brief Description of Bi-RRT Algorithm

The algorithm abandons the traditional completely randomized expansion method and adopts the greedy expansion idea instead. Given that the start point and the target point are both in the restricted space surrounded by obstacles, this heuristic expansion strategy can effectively motivate the two search trees to grow with each other quickly, so that they can quickly get rid of their respective constraint space limitations, thus significantly shortening the convergence time of the algorithm and improving the overall efficiency. The extension process of the Bi-RRT algorithm is shown in Figure 2.

In Figure 2, the left side shows the random tree $T_a$, while the right side shows the random tree $T_b$. In the random tree $T_a$, Pinit denotes the starting point of the path planning. $P_{rand}$ is the random sampling point, and $P_{near}$ is the node with the closest distance to $P_{rand}$ in the random tree $T_a$. and $P_{new}$ is the new node that is generated by expanding along the fixed search step from $P_{near}$. In the random tree $T_b$, $P_{nea{r}^{\prime }}$ is the node with the closest distance to $P_{ne{w}^{\prime }}$, while $P_{ne{w}^{\prime }}$ is a new node generated by expanding along a fixed search step from $P_{nea{r}^{\prime }}$.

3.2. Improved Bi-RRT Method: GBOPBi-RRT

3.2.1. Gravity-Oriented Strategy

The artificial potential field method is a path planning method based on virtual force field, which belongs to the category of local path planning. Its core idea is to equate the motion environment where the flexible needle is located to a virtual artificial potential field [24]. In the field of path planning, the artificial potential field method can provide heuristic information for the Bi-RRT algorithm, thus effectively guiding its exploration process. In this way, Bi-RRT algorithm can traverse the nodes more intelligently and choose the exploration direction, thus significantly improving the speed of path search and finding the global optimal path faster. At the same time, the Bi-RRT algorithm can provide strong support for the artificial potential field method by virtue of its fast searching characteristics, helping it to overcome the dilemma of local minima, thus significantly improving the robustness of the path planning algorithm.

In the traditional Bi-RRT algorithm, the expansion process of the random tree has a high degree of randomness, which leads to low search efficiency, especially in complex environments where the problem of blind search is prone to occur. In order to improve the search efficiency and goal orientation of the algorithm, this paper introduces the gravitational orientation strategy, which guides the growth direction of the random tree to approach the goal point more quickly by simulating the action of the gravitational field, as shown in Figure 3.

In Figure 3, the dots indicate the nodes of the Bi-RRT tree. Take one of the trees as an example, its start point is the root node. Suppose the start point is $P_{init}$, the target point is $P_{goal}$, and the direction pointed by the arrow is the direction of the force. During the spatial search, the random tree generates a random point $P_{rand}$, and then it expands at the closest node $P_{near}$ to $P_{rand}$ in the direction from $P_{near}$ to $P_{rand}$ in steps of fixed length s to generate a new node $P_{new}$.

The design of the gravitational field function is inspired by the artificial potential field method, and its core idea is to direct the growth direction of the random tree by applying a gravitational-like effect of the target point on the random tree growth process [25,26]. Specifically, for the current node $P_{near}$ on the random tree, its gravitational force $H_{att}\left(P\right)$ from the target point $P_{goal}$ can be expressed as:

$$H_{att}\left(P\right)=s·\lambda ·{\displaystyle \frac{P_{goal}-P_{near}}{\parallel P_{goal}-P_{near}\parallel }}$$

(1)

where: s is the extension step size, which controls the distance of each node extension; $\lambda$ is the gravitational coefficient, which is used to adjust the magnitude of the gravitational force; $P_{goal}-P_{near}$ is the direction vector pointing from the current node to the target point; ∥$P_{goal}-P_{near}$∥ is the Euclidean distance between the current node and the target point, which is used to normalize the gravitational direction vector.

In each expansion of the random tree, the original expansion direction vector $R\left(P\right)$ is first computed from the random sampling point $P_{rand}$ and the nearest node $P_{near}$:

$$R\left(P\right)=s·{\displaystyle \frac{P_{rand}-P_{near}}{\parallel P_{rand}-P_{near}\parallel }}$$

(2)

The gravitational $H_{att}\left(P\right)$ is then superimposed with the original extended direction vector $R\left(P\right)$ to obtain the final extended direction vector $H_{final}\left(P\right)$:

$$H_{final}\left(P\right)=H_{att}\left(P\right)+R\left(P\right)$$

(3)

Eventually, the position of the new node $P_{new}^{\prime }$ can be calculated by the following equation:

$$P_{new}^{\prime }=P_{near}+H_{final}\left(P\right)$$

(4)

By introducing the gravity-oriented strategy, the growth direction of the random tree is influenced by the gravitational force of the target point, which enables the random tree to expand toward the target point more efficiently, reduces the blindness during the search process, and improves the search efficiency of the algorithm and the success rate of path planning.

The size of the gravitational coefficient $\lambda$ has an important effect on the growth direction and search efficiency of the random tree [27]. When $\lambda$ is large, the random tree is subject to stronger gravitational force, and the growth direction is more inclined to point directly to the target point, which helps to approach the target point quickly, but may lead to the random tree’s search range near the target point is too narrow, and is easy to fall into the local optimum. On the contrary, when $\lambda$ is small, the growth direction of the random tree is more flexible and can search in a wider range, which is conducive to avoiding obstacles, but may increase the search time. Therefore, in practical applications, the size of the gravitational coefficient $\lambda$ needs to be reasonably adjusted according to the complexity of the environment and the specific requirements of path planning, in order to achieve the best search effect.

3.2.2. Bidirectional Adaptive Scaling Strategy

In the traditional two-way fast exploration randomized tree algorithm, the expansion step size of nodes is usually fixed. This fixed step-size strategy has certain limitations in complex environments. When the search space is large, a larger step-size can accelerate the search speed, but it may lead to an insufficiently smooth path; meanwhile, when approaching the target point or the dense region of obstacles, a smaller step-size can improve the smoothness and safety of the path, but it will significantly increase the search time. Compared with the fixed step size, the dynamic step size can fully exploit and utilize the known environmental information to adjust the current extended step size to a more appropriate size, thus realizing a more efficient and adaptive optimization process [28]. In order to overcome these shortcomings, this paper proposes an adaptive expansion strategy that dynamically adjusts the step length according to the distance between the current node and the target point.

The core of the adaptive expansion strategy lies in dynamically adjusting the step size according to the distance between the current node and the target point. Specifically, for each node of the forward and reverse trees, the expansion step size s is defined as:

$$s=\max \left(s_{\min },\min \left(s_{\max },{\displaystyle \frac{d}{\sqrt{c}}}\right)\right)$$

(5)

where: $s_{\min }$ and $s_{\max }$ are the minimum and maximum values of the step size, respectively, which are used to limit the range of the step size; d is the Euclidean distance between the current node and the target point; c is the number of nodes in the current tree, which is used to dynamically adjust the size of the step size.

When the search space is large, the distance d between the current node and the target point is large, so the step size s approaches $s_{\max }$. This allows the search tree to expand quickly towards the target point and speeds up the search. As the search tree is being formed, the distance d between the current node and the target gradually decreases, while the number of nodes c increases. At this time, the step size s will be dynamically adjusted according to ${\displaystyle \frac{d}{\sqrt{c}}}$, which not only ensures the search efficiency, but also avoids the path being too rough. When the search space is small, the step size s approaches $s_{\min }$. This enables the search tree to perform fine search when approaching the target point or dense obstacle area, and improves the smoothness and safety of the path.

3.2.3. Optimal Node Selection Based on A* Algorithm

In the expansion process of the bidirectional random tree, the selection of the nearest node $P_{near}$ plays a crucial role in the generation of the new node $P_{new}$. Specifically, the nearest node $P_{near}$ is selected by calculating the Euclidean distance between each node $P_i$($x_i$,$y_i$) in the random tree $T_a$ and the new random point $P_{new}$($x_{\mathrm{j}}$,$y_{\mathrm{j}}$) generated based on the direction of the ensemble force; however, this Euclidean distance-based selection makes the random tree $T_a$ significantly more dependent on the new random point $P_{new}$. A potential problem is that the selected nearest node $P_{near}$ is not necessarily the optimal node from a global path planning perspective, which may impose some limitations on the optimization of the path. Euclidean distance is:

$$l=\sqrt{{\left(x_i-x_{\mathrm{j}}\right)}^2+{\left(y_i-y_{\mathrm{j}}\right)}^2}$$

(6)

in the above equation, i denotes the node index in the random tree $T_a$ and its value range is [1, length($T_a$)], where length($T_a$) denotes the total number of nodes in the random tree $T_a$.

After generating a new node $P_{new}$ by the bi-directional adaptive expansion strategy, the idea of cost estimation in the A* algorithm is introduced, and a heuristic method is used to select the node with the smallest cost in the random tree $T_a$ as the nearest node $P_{near}$. This improvement enables the bidirectional random tree to expand the path towards the goal more efficiently. The cost estimation function of the A* algorithm is:

$$G\left(n\right)=g\left(n\right)+h\left(n\right)$$

(7)

where $g\left(n\right)$ is the actual cost from each point $P_i$ on the random tree $T_a$ to the new random point $P_{new}$; $h\left(n\right)$ is the estimated cost from $P_i$ to the target point $P_{goal}$. Where the actual cost is the cumulative path length from the starting point to $P_i$ and the estimated cost is the Euclidean distance from $P_i$ to the goal point.

By introducing the optimal node selection strategy based on the A* algorithm, the improved Bi-RRT algorithm pays more attention to goal orientation in the path planning process, which can effectively reduce the path length and planning time and improve the efficiency and quality of path planning.

3.2.4. Path Optimization Strategy

In the bidirectional fast expanding random tree algorithm, the generated path usually contains a large number of redundant nodes, resulting in a jagged path, which not only increases the path length, but also reduces the smoothness of the path and the efficiency of the motion of the flexible needle. In order to improve the quality of the path, this paper proposes a path optimization strategy, by pruning and interpolating the redundant nodes of the generated path to smooth the path, so that the path is more concise and smooth, which is closer to the kinematics of flexible needle puncture. The pruning process is shown in Figure 4, where the black dotted lines represent the original path, clearly depicting the initial traveling trajectory. The green lines, on the other hand, mark the regions in the path that are at risk of collision. After optimization, the final red solid path is obtained, which is a safe and efficient path after trimming and adjustment.

Starting from the beginning of the path, each node is traversed along the path sequentially. For the current node and its subsequent nodes, check whether the connecting line between the two has collided with an obstacle. If the connecting line between the current node and the subsequent node has no collision, all intermediate nodes between the current node and the subsequent node are deleted; if a collision is detected, the previous node of the subsequent node is retained and the checking of the subsequent nodes continues.

3.2.5. Algorithms Run Pseudo-Code

Based on the preceding theoretical framework, the enhanced Bi-RRT algorithm is employed to efficiently plan the puncture path, as outlined in the pseudocode below.

Algorithm 1 describes the proposed GBOPBi-RRT algorithm, developed based on the following principles.

• (Lines 1–3) Initialize the forward tree $T_{\mathrm{forward}}$ rooted at $P_{\mathrm{init}}$ and the backward tree $T_{\mathrm{backward}}$ rooted at $P_{\mathrm{goal}}$. Set the algorithm parameters ${\eta }_{\min }$, ${\eta }_{\max }$, $k_{\mathrm{gravity}}$, and $MaxIter$, and set the expansion direction flag forward_to_backward to true.
• (Lines 4 and 5) Randomly sample a point $P_{\mathrm{rand}}$ within the search space at each iteration to guide the bidirectional expansion.
• (Line 6) Select the optimal node $P_{\mathrm{near}}$ in the current tree using an A*-inspired cost function that balances exploration efficiency and convergence toward the goal.
• (Lines 7–10) Compute an adaptive step size based on the distance between $P_{\mathrm{near}}$ and the goal. Determine the expansion direction by combining the random sampling direction with a gravity term that biases the search toward the goal. Generate a new node $P_{\mathrm{new}}$ from $P_{\mathrm{near}}$ along this direction.
• (Lines 11 and 12) If the segment between $P_{\mathrm{near}}$ and $P_{\mathrm{new}}$ is collision-free, add $P_{\mathrm{new}}$ to the current tree as a child of $P_{\mathrm{near}}$; otherwise, skip to the next iteration.
• (Lines 13–17) Check whether the newly expanded node can connect the two trees. If a valid connection is found, reconstruct the complete path by merging the forward and backward trees, and terminate the loop. Alternate the expansion direction after each iteration to ensure balanced bidirectional growth.
• (Lines 19 and 20) Optimize the resulting path to remove redundant nodes and improve trajectory continuity. Return the optimized path $Pat{h}_{\mathrm{opt}}$ as the final output.

Algorithm 1 GBOPBi-RRT($P_{\mathrm{init}}$, $P_{\mathrm{goal}}$, Path)

1: Initialize $T_{\mathrm{forward}}\leftarrow \left\{P_{\mathrm{init}}\right\}$, $T_{\mathrm{backward}}\leftarrow \left\{P_{\mathrm{goal}}\right\}$ 2: Set ${\eta }_{\min }$, ${\eta }_{\max }$, $k_{\mathrm{gravity}}$, Maxiter 3: $forward\_to\_backward\leftarrow \mathrm{true}$ 4: for iter = 1 : Maxiter do 5:  $P_{\mathrm{rand}}\leftarrow$ RandomSample(Map) 6:  $P_{\mathrm{near}}\leftarrow argmin(\cos \mathrm{t}\left(V_i\right)=dist(V_i,root)+\alpha ·dist(V_i,goal))$ 7:  $S\leftarrow \mathrm{clamp}\left({\displaystyle \frac{dist(P_{\mathrm{near}},goal)}{|T_{\mathrm{current}}|}},{\eta }_{\min },{\eta }_{\max }\right)$ 8:  $gravityDir\leftarrow normalize(goal-P_{\mathrm{near}})$ 9:  $expandDir\leftarrow normalize((P_{\mathrm{rand}}-P_{\mathrm{near}})+k_{\mathrm{gravity}}·gravityDir)$ 10:  $P_{\mathrm{new}}\leftarrow P_{\mathrm{near}}+S·expandDir$ 11:  if not CollisionFree($P_{\mathrm{near}}$, $P_{\mathrm{new}}$) then continue 12:  AddNode($T_{\mathrm{current}}$, $P_{\mathrm{new}}$, $P_{\mathrm{near}}$) 13:  if Connectable($T_{\mathrm{forward}}$, $T_{\mathrm{backward}}$, $P_{\mathrm{new}}$, S) then 14:   Path ← Reconstruct($T_{\mathrm{forward}}$, $T_{\mathrm{backward}}$) 15:   break 16:  end if 17:  $forward\_to\_backward\leftarrow \neg forward\_to\_backward$ 18: end for 19: $Pat{h}_{\mathrm{opt}}\leftarrow$ OptimizePath(Path) 20: return$Pat{h}_{\mathrm{opt}}$

3.3. Puncture Path Analysis

3.3.1. Unicycle Kinematic Model

Flexible needles with asymmetric beveled tips are highly flexible. During puncture, the needle axis bends in the direction of the beveled tip due to the reaction forces generated by the soft tissue, thus creating a circular path of variable radius inside the tissue. The puncturing principle of flexible needles is very different from that of conventional rigid needles. Flexible needles are controlled by two degrees of freedom: a feed motion that includes forward and backward movement of the needle and a rotary motion that changes the direction of bending, which can be compared to the motion of a bicycle [29,30] and can be simplified as a one-way valve.

In this paper, a uniaxial puncture kinematic model is developed, as shown in Figure 5, in which the fixed inertial reference system AXYZ and the follower coordinate systems A₁Y₁Z₁ and A₂Y₂Z₂, which are solidly attached to the tip of the needle, are defined. In the needle body coordinate system, the Z₁-axis is along the direction of needle body insertion, and the Y₁-axis is perpendicular to the Z₁-axis and in the direction opposite to the direction of needle body bending [31]. During the puncture process, the needle body produces a compound motion under the effect of tissue interaction force, including translational motion with velocity along the Z₁-axis and rotational motion with angular velocity $\omega$ around the X₁-axis, and the relationship between linear velocity v and angular velocity $\omega$ can be expressed as:

$$\omega ={\displaystyle \frac{v}{r_1}}$$

(8)

where $r_1$ represent the radius of penetration determined by the mechanical properties of the needle. Equation (1) clearly shows that the trajectory of the flexible needle is a circular path with radius $r_1$. According to the relevant literature, the trajectory of the needle is jointly determined by the feed motion and the rotational motion of the needle, and the velocities of these two motions are denoted by $\mathit{u}$₁ and $\mathit{u}$₂, respectively [32,33,34]. Therefore, v and $\omega$ can be expressed as:

$$v={\left[00u_1\right]}^{\mathrm{T}}$$

(9)

$$\omega ={\left[{\displaystyle \frac{u_1}{r_1}}0u_2\right]}^{\mathrm{T}}$$

(10)

The kinematic trajectory function and the kinematic model can be expressed as:

$$G=f(r,u_1,u_2)$$

(11)

$$q=\left[\begin{array}{c}v\\ \omega \end{array}\right]=\left[\begin{array}{c}0\\ 0\\ u_1\\ {\displaystyle \frac{u_1}{r_1}}\\ 0\\ u_2\end{array}\right]$$

(12)

where $r_1$ can be the radius of the first segment of the circular trajectory of the flexible needle into the tissue and q is the state of motion of the needle during the movement of the flexible needle. The coordinate transformation matrix $B_{WF}$ from the flexible needle coordinate system to the world coordinate system is described as:

$$B_{WF}=\left[\begin{array}{cc}{R}_{WF}& X_{WF}\\ 0& 1\end{array}\right]\in \mathrm{SE}\left(3\right)$$

(13)

$$\mathrm{SE}\left(3\right)=R_3\times \mathrm{SO}\left(3\right)$$

(14)

where $B_{WF}$∈ SO (3) (SO (3) denotes the three-dimensional rotation group) and $X_{WF}$ ∈ $R_3$ denote the rotation matrix and the position vector of the coordinate system A₁ with respect to the coordinate system A₂, respectively. Moreover, SE (3) denotes the special Euclidean group, also known as the rigid body transformation group. Thus, the motion of the needle tip can be described as follows:

$$P^{\wedge }={\left[\begin{array}{c}v\\ \omega \end{array}\right]}^{\wedge }=\left[\begin{array}{cccc}0& {\displaystyle \frac{-u_2}{r_2}}& 0& 0\\ u_2& 0& {\displaystyle \frac{-u_1}{r_1}}& 0\\ 0& {\displaystyle \frac{u_1}{r_1}}& 0& u_1\\ 0& 0& 0& 0\end{array}\right]$$

(15)

where ∧ is the wedge operator for generating matrices in the special Euclidean group SE (3) and $r_2$ represent the radius of penetration determined by varying the ratio of the angle of rotation of the needle to the depth of penetration. And the term SE (3) is the Lie algebra expression of SE (3), which in a physical sense represents the generalized instantaneous velocity. The chi-square transformation matrix can be represented by means of an exponential mapping in the following form:

$$B_{WF}\left(t\right)=B_{WF}\left(0\right)exp\left(q^t\right)$$

(16)

In Equation (9), $B_{WF}$(0) denotes the initial configuration of the flexible needle, i.e., the starting position and orientation of the needle tip in 3D space. t denotes the time, which represents the motion state of the needle tip after a time t from the initial configuration. This time t, together with q, is used to calculate the position and orientation of the needle at time t by the exponential form exp(qt). Equation (9) is an element of the Lie algebra expression of SE (3) that describes rigid-body transformation, i.e., translation and rotation of a rigid body.

3.3.2. Reachable Space Analysis for Flexible Needles

During flexible needle puncture, the interaction between the needle and tissue causes the puncture path to be strongly influenced by the needle’s material properties and intrinsic curvature. Consequently, the planned path may not be achievable due to limited spatial accessibility. Therefore, path planning must consider the actual reachable workspace of the flexible needle and optimize inaccessible regions to ensure path smoothness, safety, accessibility, and optimality (i.e., minimal length). Owing to its structural characteristics, the flexible needle exhibits a maximum and minimum spatial bending radius, $r_{max}$ and $r_{min}$, respectively, as shown in Figure 6. To guarantee path accessibility, the bending radius between any two consecutive puncture points, $r_i$, must satisfy the following constraint:

$$r_{min}\le r_i\le r_{max}$$

(17)

The emergence of unreachable paths is an urgent problem in flexible needle puncture path planning. In order to solve this problem, this paper proposes a puncture path optimization function, through which the path is corrected to effectively guarantee the accessibility of flexible needle puncture. The optimization function integrally considers key factors such as the bending curvature characteristics of the flexible needle, the degree of damage to the tissue by the flexible needle and the safety level of the puncture path, aiming to achieve the science and safety of path planning. The following is the definition of the optimization function:

$$PO{F}_{\min }=\min \left\{\begin{array}{ccccc}{k}_{1}L& +& k_{2}D& +& k_{3}C\end{array}\right\}$$

(18)

where $k_1$, $k_2$ and $k_3$ denote the weight coefficients of the corresponding subfunctions, respectively, which are used to balance the influence of each factor on the path planning; L denotes the total length of the puncture path; D denotes the shortest distance between the tip point of the needle and the obstacle; and C denotes the degree of bending of the flexible needle in the tissues. By adopting the flexible needle characterization strategy, a significant improvement in the performance of path planning is achieved. These improvements make the puncture path of the flexible needle more closely match the real puncture environment, thus ensuring that the flexible needle can reach the target position safely and reliably.

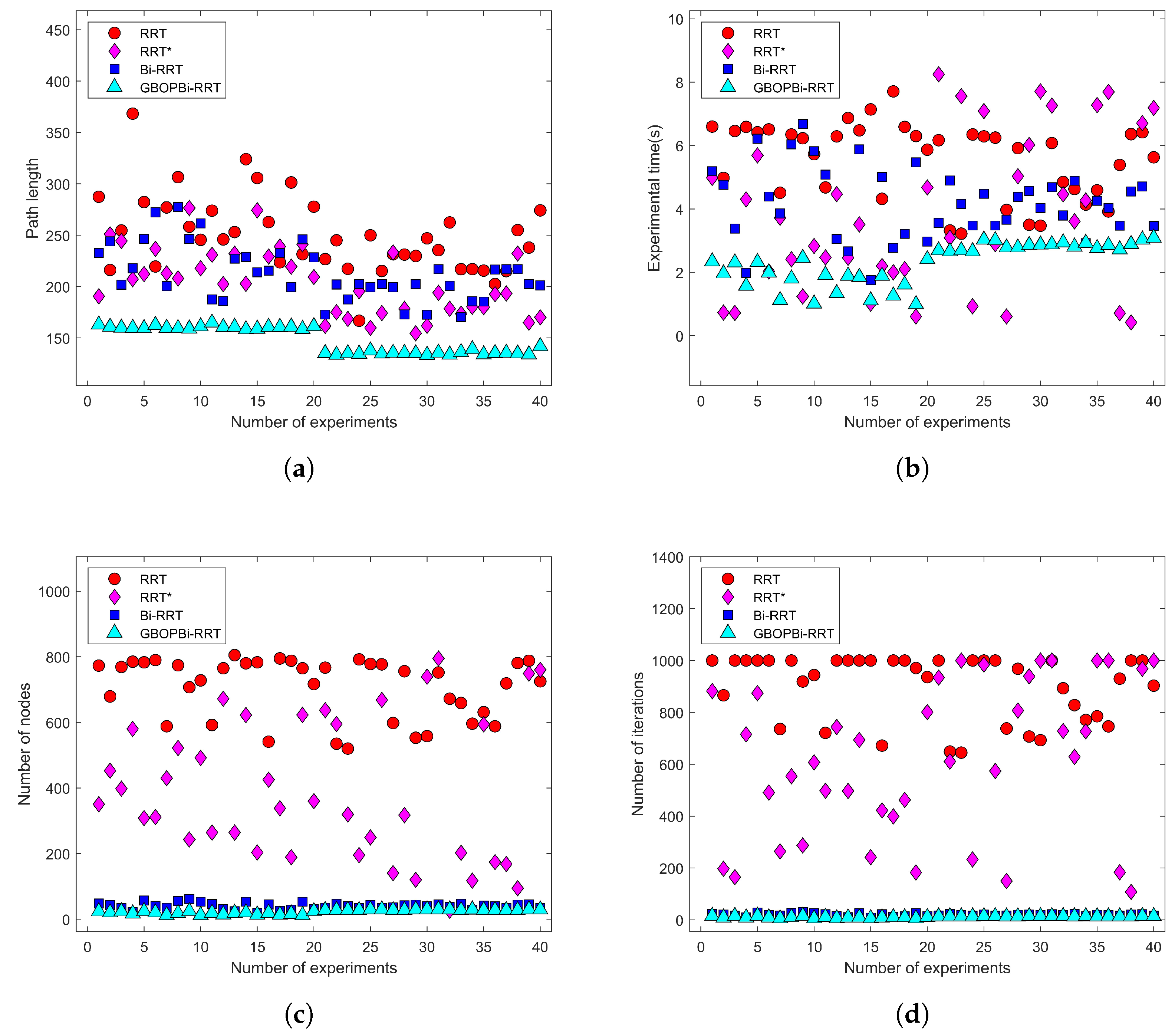
4. Results

4.1. Simulation Results of Flexible Needle Two-Dimensional Path Planning

In order to verify the rationality and feasibility of the improved algorithm in this paper, a series of comparative simulation experiments are designed and implemented. The experimental platform is MATLAB R2022b, the hardware configuration is AMD Ryzen 9 8940HX with Radeon Graphics CPU, 8 GB RAM, and the operating system is 64-bit Windows 11. Considering the effect of randomness on the results, each algorithm is run independently for 20 times under the same experimental environment, so as to ensure the reliability of the conclusions by the statistical mean value. The reliability of the conclusions is guaranteed by the statistical mean value. Simulation studies were first performed in the first two-dimensional environment, the simulation scenario is set as an 800 × 800 square area: the starting point is located in the lower right corner (500, 700) and the target point is placed in the upper left corner (50, 50). The multi-obstacle environment consists of three circular obstacles with centroid coordinates (150, 550), (375, 425), and (550, 200), and corresponding radii of 60, 90, and 70, respectively. Subsequently, simulation studies were conducted in the second two-dimensional environment, the simulation scenario is set as an 800 × 800 square area: the starting point is located in the upper left corner (1, 1) and the target point is placed in the lower right corner (750, 750). The multi-obstacle environment consists of five circular obstacles with centroid coordinates (200, 200), (300, 600), (400, 400), (600, 300), and (600, 600), and corresponding radii of 50, 60, 80, 40, and 30, respectively. For all four comparison algorithms, the goal threshold was set to 30, and the maximum number of search iterations was limited to 3000. In the proposed improved algorithm, the maximum and minimum expansion step sizes were set to 40 and 25, respectively, while the expansion step size for the other algorithms was fixed at 32.5. The connection threshold between the two search trees was set to 40. And the radius of each obstacle is uniformly doubled to simulate the possible localization bias in the puncture process and to ensure safety. The radius of each obstacle is uniformly doubled to simulate possible positioning deviations during puncture and to ensure safety. This diagonal start-end layout can comprehensively test the algorithm’s ability to search and avoid obstacles in any direction, and at the same time facilitates a visual comparison of the smoothness and length of the paths obtained by different algorithms. This standardized environment not only ensures the fairness of the algorithm evaluation, but also provides a reliable experimental basis for the further optimization of the algorithm.

The RRT, RRT*, Bi-RRT, and the proposed improved algorithms were each evaluated through 20 repeated simulations in two distinct environments, with all resulting data recorded and analyzed. The path planning outcomes of the four algorithms in the two simulated map environments are illustrated in Figure 7 and Figure 8.

In the path expansion process, the traditional RRT algorithm lacks directionality due to random sampling, and the search tree is in the form of “unordered spreading”, with serious branch redundancy, which leads to low node utilization and significant iteration time; building upon the RRT framework, the RRT* algorithm introduces a rewiring and path optimization mechanism to achieve asymptotic optimality. However, it still relies on global random sampling, which can lead to invalid extensions and inefficient rewiring in simulation environments, resulting in slow convergence and high computational cost; the standard Bi-RRT algorithm mitigates the problem of slow convergence through bidirectional parallel expansion, but the two trees still rely on purely random sampling, and are prone to form “cross-redundant branches” in the obstacle-dense region, as shown in Figure 7a–d and Figure 8a–d. The GBOPBi-RRT algorithm proposed in this paper embeds an artificial potential field guidance mechanism in the traditional Bi-RRT framework, and through the synergistic effect of the target gravitational force and the starting point retrospective force, the random sampling direction is modified to the direction of the combined force of the target and the random guidance, which significantly compresses the ineffective search space; and adopts a dynamic step-size strategy, which is based on the current node density and the target distance to adapt to the current node density and the target distance. Dynamic step size strategy is adopted to adaptively adjust the expansion step size according to the current node density and target distance to avoid over-branching; combined with the A* heuristic cost function to optimize the selection of nearest-neighbor nodes, the expansion efficiency is improved.

In order to more intuitively and fully verify the reasonableness and superiority of GBOPBi-RRT algorithm with the introduction of smooth fitting, we designed 40 sets of comparison experiments in the simulation environment and systematically collected four key indexes, namely, path length, running time, node size and iteration number. Figure 9a–d show the quantitative comparison results between GBOPBi-RRT and the other three mainstream algorithms in the above dimensions.

Table 1. Experimental data in two circular obstacle environment.

Arithmetic	Path Length	Experimental Time (s)	Number of Nodes	Number of Iterations
RRT	1264.55	12.17	400	448
RRT*	1109.82	4.56	384	421
Bi-RRT	1234.67	2.38	80	94
GBOPBi-RRT	947.33	1.50	48	108

presents the comparative results of the average values for four metrics—path length, computation time, number of generated nodes, and number of iterations—obtained from 40 independent experiments conducted in two different environments using the RRT, RRT*, Bi-RRT, and the proposed GBOPBi-RRT algorithms.

As shown in Table 1 and Figure 7 and Figure 8a–e, the GBOPBi-RRT algorithm demonstrates significantly better performance in terms of path length and planning time compared with the other algorithms in both circular environments. Compared with RRT, the path length is shortened by 25.09%, the planning time is shortened by 87.67%, and the number of nodes and iterations are reduced by 88% and 75.89%, respectively; compared with RRT*, the path length is shortened by 14.64%, the planning time is shortened by 67.11%, and the number of nodes and iterations are reduced by 87.5% and 74.35%, respectively; compared with Bi-RRT, the path length and planning time are reduced by 23.27% and 36.97%, respectively, and the number of nodes decreases by 40%, but the number of iterations increases by 14.89%. Comprehensively, GBOPBi-RRT achieves significant improvement in path quality, planning efficiency and node utilization compared with traditional RRT and Bi-RRT in both circular scenarios.

4.2. Simulation Results of Flexible Needle Three-Dimensional Path Planning

In order to further verify the feasibility of GBOPBi-RRT in 3D complex scenes, this paper carries out comparative simulation experiments in a 100 × 100 × 100 cube space (x, y, z ∈ [0, 100]). Simulation studies were first performed in the first three-dimensional environment, a total of 10 spherical obstacles are arranged in the environment, and the coordinates of the spherical centers are (67, 89, 47), (35, 83, 84), (54, 58, 78), (81, 17, 68), (80, 72, 41), (77, 71, 79), (24, 85, 40), (40, 73, 74), (74, 69, 10) and (50, 50, 50), and the radii are all 10. The radius is 10. The starting point is (5, 5, 5) and the target point is (95, 95, 95). Subsequently, simulation studies were conducted in the second three-dimensional environment, a total of 10 spherical obstacles are arranged in the environment, and the coordinates of the spherical centers are (70, 30, 50), (80, 10, 70), (20, 90, 65), (40, 40, 40), (60, 60, 60), (20, 10, 70), (30, 50, 50), (20, 20, 70), (41, 79, 40) and (74, 10, 50), and the radii are all 10. The radius is 10. The starting point is (10, 90, 90) and the target point is (75, 10, 10). For all four comparison algorithms, the goal threshold was set to 8, and the maximum number of search iterations was limited to 1000. In the proposed improved algorithm, the maximum and minimum expansion step sizes were set to 5 and 25, respectively, while the expansion step size for the other algorithms was fixed at 15. The connection threshold between the two search trees was set to 8. Typical simulation results in a 3D scenario are shown in Figure 10 and Figure 11.

In order to eliminate the bias caused by random fluctuations, in this study, the GBOPBi-RRT algorithm and three mainstream algorithms were each independently executed 20 times under identical conditions in two three-dimensional scenarios and this paper compares them in four dimensions, namely, path length, running time, number of nodes, and number of iterations, and the statistical results are shown in Figure 12a–d.

Table 2. Experimental data in two spherical obstacle environment.

Arithmetic	Path Length	Experimental Time (s)	Number of Nodes	Number of Iterations
RRT	260.47	5.88	562	728
RRT*	203.95	3.83	393	614
Bi-RRT	212.31	4.19	40	19
GBOPBi-RRT	147.92	2.31	23	12

summarizes the performance comparison between RRT, RRT*, Bi-RRT and the GBOPBi-RRT algorithm proposed in this paper in 3D space.

From Table 2, Figure 10 and Figure 11, it can be seen that in the spherical environment, GBOPBi-RRT significantly outperforms RRT, RRT*, and Bi-RRT in terms of path length, running time, number of generated nodes and number of iterations. Compared with RRT, the path length is reduced by 43.21%, the planning time by 60.71%, and the number of nodes and iterations by 95.91% and 98.35%, respectively; compared with RRT*, the path length and planning time are reduced by 27.47% and 39.69%, and the number of nodes and iterations are reduced by 94.15% and 98.05%, respectively; compared with Bi-RRT, the path length and planning time are reduced by 30.33% and 44.87%, and the number of nodes and iterations are reduced by 42.5% and 36.84%, respectively. Comprehensively, GBOPBi-RRT can search for feasible puncture paths more efficiently and stably, which fully verifies the effectiveness and rationality of the strategy in this paper.

5. Conclusions

In this paper, we study the flexible needle puncture path planning problem based on the single-wheeled vehicle model and the flexible needle reachable space, systematically analyze the geometry of the feasible trajectory of the flexible needle, and carry out a systematic experimental study, which lays a theoretical foundation for circular arc fitting. On this basis, the GBOPBi-RRT algorithm is proposed in the framework of Bi-RRT: it incorporates gravitational guidance, bi-directional adaptive expansion, optimal node selection based on A* and path optimization strategy, which significantly improves the search efficiency and path quality. The theoretical analysis verifies the completeness and asymptotic optimality of GBOPBi-RRT. Comparison with RRT, RRT* and Bi-RRT in various complex environments through MATLAB simulation shows that GBOPBi-RRT significantly outperforms the comparative algorithms in terms of path length, computation time and the number of nodes, and in particular, in the three-dimensional environment, the length of the planned paths of the improved GBOPBi-RRT algorithm is 43.21%, 27.47% and 30.33% less than that of RRT, RRT* and Bi-RRT, respectively. Additionally, if appropriate parameters are set, this algorithm can be applied to fields such as transportation problems, robot motion control, and other areas. This study has several limitations. First, the proposed method mainly addresses path planning in static environments. During actual puncture procedures, factors such as model parameter deviations, limited sensor accuracy, and variations in biological tissue properties may lead to discrepancies between the planned and actual paths. In complex anatomical environments, the proposed algorithm may still fall into local minima. In addition, this work does not incorporate real-time control for intraoperative path adjustment based on navigation feedback or information from the flexible needle tip, obstacles, and target positions within tissue. These factors further increase the difficulty of flexible needle path planning and control. Even so, the proposed algorithm establishes a solid basis for future studies on real-time intraoperative path optimization, which will be an important direction of subsequent research.