Abstract
This paper presents a fault diagnosis model for rolling bearings that addresses the challenges of establishing long-sequence correlations and extracting spatial features in deep-learning models. The proposed model combines SENet with an improved Informer model. Initially, local features are extracted using the Conv1d method, and input data is optimized through normalization and embedding techniques. Next, the SE-Conv1d network model is employed to enhance key features while suppressing noise interference adaptively. In the improved Informer model, the ProbSparse self-attention mechanism and self-attention distillation technique efficiently capture global dependencies in long sequences within the rolling bearing dataset, significantly reducing computational complexity and improving accuracy. Finally, experiments on the CWRU and HUST datasets demonstrate that the proposed model achieves accuracy rates of 99.78% and 99.45%, respectively. The experimental results show that, compared to other deep learning methods, the proposed model offers superior fault diagnosis accuracy, stability, and generalization ability.
1. Introduction
Rotating machinery plays an instrumental role in modern industry and technology, with broad applications across various sectors, including aerospace, automotive, wind energy production, and railway systems [1]. In some equipment, bearing faults are responsible for as much as 44% of total failures [2]. Consequently, investigating fault diagnosis in rolling bearings is essential for maintaining the safe and reliable operation of equipment.
Signal processing techniques and deep learning-based approaches are two widely employed methods for diagnosing rolling bearing faults [3]. Conventional fault diagnosis techniques based on signal processing mainly depend on the collection and analysis of bearing vibration signals. In the fault diagnosis process, the bearing fault type is established by extracting features from the time-frequency domain [4]. These methods yielded favorable results in early applications, utilizing standard techniques such as envelope analysis, the Fourier transform, and the wavelet transform. These methods are capable of efficiently extracting the distinctive features of bearings under fault conditions [5]. Nevertheless, these conventional methods necessitate extensive signal preprocessing and feature extraction, heavily relying on manual techniques, which leads to reduced accuracy and robustness in fault diagnosis. Additionally, they are challenging to apply to complex fault patterns and changing operating environments.
With the increasing volume of data and advancements in computational capabilities, deep learning-based fault diagnosis methods have become a growing area of research focus. In contrast to signal processing methods, deep learning-based diagnostic approaches do not rely on intricate feature extraction processes, yet they are capable of performing efficient fault diagnosis. Instead, they achieve fault classification by automatically learning the implicit information within the signals [6]. Convolutional neural networks (CNNs) are regarded as robust deep learning algorithms and have found extensive application in the domain of fault diagnosis [7]. Traditional signal processing approaches in bearing fault diagnosis are based on manual feature extraction. In contrast to these methods, CNN-based diagnostic techniques autonomously extract relevant local features from raw data. This capability eliminates the need for manual feature extraction, significantly enhancing both the efficiency and accuracy of fault diagnosis [8]. Wang et al. [9] introduced a fault diagnosis model, Squeezed and Enabled Convolutional Neural Network (SE-CNN), which combines the CNN architecture with Symmetric Dot Pattern (SDP) to enable the automatic extraction and visualization of fault features. While CNN models do not encounter issues related to sequence dependency, they struggle to effectively capture long-term features when processing extended sequence data [10]. After the pooling layer process in CNNs, the connections between local and global features are ignored, resulting in the loss of valuable information. Bearing failures typically manifest as temporal variations in vibration signals. Recurrent Neural Networks (RNNs) are capable of effectively handling continuous time-series data and identifying latent failure patterns by learning the dynamic features embedded in the signals [11]. Based on this, Liu et al. [12] presented a method that merges an autoencoder with an RNN (recursive neural network) for bearing fault detection. This method effectively extracts high-dimensional potential features from the original vibration signal and reduces redundant information by using an autoencoder as a feature extractor.
Nevertheless, conventional RNNs are susceptible to issues such as vanishing or exploding gradients during the fault diagnosis training process, resulting in suboptimal performance when processing long sequences. Long Short-Term Memory (LSTM) networks, a variant of Recurrent Neural Networks (RNNs), overcome the everyday challenges of gradient vanishing and explosion during training. This is achieved through the integration of memory cells and gating mechanisms. LSTM models exhibit superior performance in handling long-sequence dependency problems [13]. Recent research has proposed hybrid models by several authors [14,15], which integrate the feature extraction advantages of CNNs combined with the temporal modeling abilities of LSTMs, demonstrating promising results in fault diagnosis. Although the CNN-LSTM model addresses the long-term dependency problem in time series to some extent, it still faces challenges in fully resolving long-term dependencies when handling long-time sequences. The Temporal Convolutional Network (TCN), utilizing dilated convolution and causal convolution techniques, effectively captures dependencies in long time series, thereby enhancing the model’s expressive power. Compared to LSTMs, TCNs offer higher parallelism and lower computational costs [16]. The authors [17] proposed a network architecture that combines Temporal Convolutional Networks (TCN) with an attention mechanism, termed TCAN, which efficiently captures both local and global dependencies within sequences, thereby enhancing the precision and reliability of time series forecasting. While TCNs perform well in capturing long-term dependencies, they require significant computational resources and exhibit high computational complexity.
To efficiently model dependencies within time series data, Vaswani et al. [18] introduced the Transformer model, which integrates the self-attention mechanism, effectively mitigating the everyday challenges of gradient vanishing and explosion that arise during long sequence training with LSTMs and CNNs. This advantage makes the Transformer particularly effective in modeling large-scale time series data. Nevertheless, the application of the Transformer model in fault diagnosis remains in the early phase of exploration [19]. Pei et al. [20] integrated convolution procedures with the Transformer model for the fault recognition in rotating machinery. Nath et al. [21] tackled the issue of rotor fault (SRF) imbalance by employing a Transformer-based framework. These approaches largely depend on the capabilities of the Transformer model. When processing long-time series data, the model may struggle to capture both global and local dependencies efficiently. Additionally, challenges such as increased computational costs and substantial memory usage may arise. Zhuo et al. [22] proposed the Informer model to enhance the potential of the Transformer model in time series analysis. By incorporating an enhanced self-attention mechanism, the model improves the processing efficiency of extended sequence data, leading to a significant enhancement in its performance. Zhen et al. [23] utilized the Informer model for time series prediction of motor bearing vibrations. They proposed an optimized Informer model based on the GELU activation function, which addresses the issue of error accumulation in long sequence predictions encountered by traditional methods. However, the application of Informer in fault detection and associated areas remains in the early stages of investigation, with limited research and applications in this field.
To enhance the extraction of sequence features and establish long-sequence dependencies, this study integrates SENet with the enhanced Informer, suggesting a more powerful model for fault detection in rolling bearings. This method alleviates computational complexity and training challenges by extracting both local and global features from fault data.
2. Related Work
This study provides the following key contributions:
- (1)
- First, we designed a fault diagnosis model based on SENet and the improved Informer. By effectively combining the spatial feature extraction capability of convolutional neural networks with the time series modeling ability of Informer, the model enables efficient and accurate fault diagnosis in different operating conditions.
- (2)
- Subsequently, during the data processing stage, we employed the Conv1D method to extract local features and handle the local dependencies of sequence data. By utilizing Positional Embedding and Token Embedding, we preserved the sequential information and semantic representations of the data, providing high-quality input for subsequent operations. This approach enables the model to capture global dependencies, thus improving the performance of subsequent stages.
- (3)
- Finally, the fault diagnosis model presented in this study was empirically validated using two distinct datasets: the CWRU and HUST public datasets. According to the experimental results, the fault diagnosis model suggested in this study attains over 99% detection accuracy on both datasets. This demonstrates its effective fault diagnosis performance. Furthermore, this model shows better fault diagnosis performance and consistency when compared to other deep learning models.
The paper follows this structure: Section 2 depicts the primary network architectures of Informer and SENet. Section 3 outlines the overall framework and experimental workflow of the SENet based and modified Informer models. Section 4 evaluates the performance of the proposed model using the CWRU and HUST-bearing datasets. Finally, Section 5 provides the conclusion of the paper and suggests potential avenues for future research.
3. Basic Theory
3.1. Informer
Informer is an optimized Transformer model designed for processing long-time series data. With its ProbSparse Attention technique and improved encoder–decoder structure, it efficiently handles long-time series forecasting tasks, overcoming the computational bottleneck of traditional self-attention mechanisms [24]. Figure 1 below illustrates the structure of the Informer. On the left side, the encoder processes a substantial input of long sequences (represented by the green series), where the ProbSparse self-attention mechanism is employed to substitute the conventional self-attention. The blue trapezoid illustrates the self-attention distillation operation, which extracts the most relevant attention and significantly reduces the network size. Additionally, the stacked layers improve the model’s robustness. On the right side, the decoder processes long sequence inputs (depicted by the green series), calculates the weighted feature map attention components, and generates the output components (represented by the orange sequence).
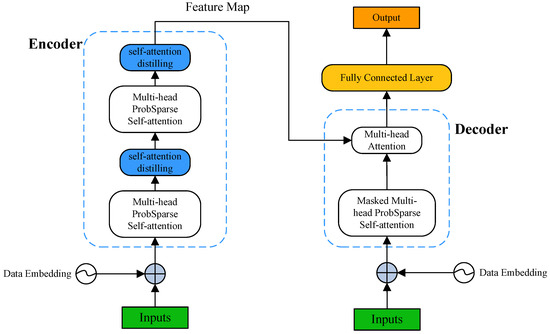
Figure 1.
Informer structure.
3.1.1. Data Embedding
Data embedding consists of two components: Positional Embedding and Token Embedding. By integrating these components, data embedding is achieved. In the Informer model, the incorporation of positional encoding allows the model to differentiate elements at various positions within long sequences and effectively capture sequential information. The expression formula for the positional encoding is as follows:
corresponds to the location of the fault data at the -th position in the sequence, where 2 and 2 + 1 are its two components. The formula consists of sine and cosine functions, allowing the positional encoding to be applied in the training of long sequences, enabling the model to compute the relationships between different positions efficiently.
In the Informer model, token embedding is generally performed by mapping the input discrete data into a higher-dimensional space. The following formula can represent this:
is composed of the weight matrix and the bias term , while represents the input data corresponding to time step . This process is achieved through a linear layer composed of the weight matrix and the bias term , which modifies the input data from a low-dimensional space to a high-dimensional embedding space, enabling the network to more precisely capture the data’s traits.
In the Informer model, the Data Embedding, which combines both Positional Embedding and Token Embedding, leverages the advantages of these two encodings to provide a better understanding of the sequentiality and dependencies inherent in time series data, thereby improving prediction accuracy.
3.1.2. ProbSparse Self-Attention
The self-attention mechanism in the Transformer model accepts three inputs—query, key, and value—and computes the scaled dot product according to the equation below:
where and selects the asymmetric exponential kernel . The self-attention mechanism involves the weighted summation of all values by computing , a process that demands in both time complexity and memory usage, which significantly enhances predictive performance.
Previous studies have demonstrated that weight distributions in self-attention mechanisms typically exhibit sparsity [25]. The Informer model investigates this sparsity by employing the Kullback–Leibler divergence, which quantifies the difference between the query distribution and the uniform distribution through KL divergence:
The initial term represents the Log-Sum-Exp (LSE) operation applied to for all keys, while the second element corresponds to the arithmetic mean of these values. If the th query produces a larger , it suggests a more diverse distribution of attention weights, increasing the likelihood of capturing significant dot product pairs. Consequently, for all queries, a subset of queries ranked among the top by are selected as , where and refers to the consistent sampling parameter. The ProbSparse self-attention mechanism is subsequently defined as:
Accordingly, ProbSparse Self-attention requires c computing only dot products for each query-key lookup while using memory. By employing multiple heads, this attention mechanism produces unique sparse query-key pairs for each head, thus minimizing the risk of considerable information loss.
3.1.3. Self-Attention Distilling
Self-attention distillation represents a crucial innovation in the Informer model, effectively mitigating the memory challenges linked to long sequence inputs. As shown in Figure 2, the entire distillation process is composed of components such as the Attention block, Conv1D, ELU Activation, and Max Pooling, all of which are located within the Encoder. By compressing the attention feature maps, the amount of data transmitted between encoder layers is reduced, thereby decreasing overall memory consumption. Its mathematical expression is given by:
where represents the attention module, which includes multi-head Probsparse self-attention and the essential procedures. The applies a 1-D convolution filter (kernel width = 3) along the temporal axis, and the activation mechanism is utilized. By reducing the input sequence length by half from the previous layer, the problem of high memory usage resulting from lengthy input sequences is alleviated.
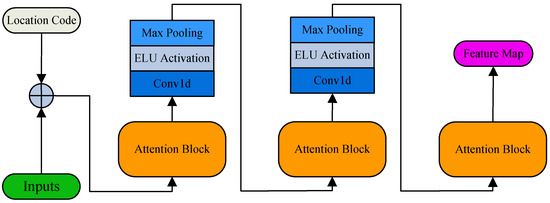
Figure 2.
Self-attention distilling.
3.2. SENet
SENet is a channel attention mechanism [26] that selectively captures important feature information. It achieves this by examining and processing the correlations between feature channels. As a result, it dynamically modulates the dependencies across distinct attribute channels in convolutional neural networks. This makes it possible for the diagnostic model to modify the importance of each channel flexibly. It suppresses irrelevant channels, thereby improving the model’s diagnostic and representational capabilities. As illustrated in Figure 3, the core architecture of SENet is primarily built upon two essential operations: squeeze and excitation.
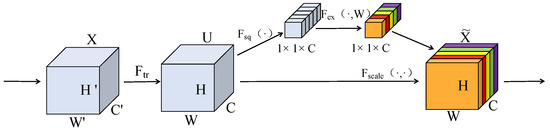
Figure 3.
Squeeze-and-Excitation block.
As shown in Figure 3, the matrix is obtained by applying the excitation function , to the matrix through a mapping transformation, and is derived from matrix . In this context, and correspond to the height, width, and the number of feature channels in matrices and , respectively. The equation is expressed as:
here, indicates the th convolution matrix, while denotes the submatrix in the th matrix. Additionally, refers to the th input of the th convolution kernel, and stands for the th input.
Global average pooling is applied to matrix in the squeeze operation, reducing the spatial size of the output maps along the axes. This process generates a unique value that represents the global consolidation of information by averaging across all channels, yielding a one-dimensional feature vector of size . The mathematical expression is as follows:
In this context, denotes the squeezed feature in channel . The value corresponds to the mapped value at the th and th positions in the th channel.
The motivation process analyzes the nonlinear correlations among the feature vectors generated by the squeezing process. The importance of individual channel weights is then adaptively adjusted to prioritize the most relevant feature information. The activation process comprises a concise and complete connection series. The following expression gives the mathematical representation of the interactions among its internal components:
where denotes the ReLU activation mechanism following dimensionality decreases, and is the Sigmoid response function applied once dimensionality is expanded. The two fully connected layers are defined by the parameters and . The serves as the scaling parameter, while shows the channel result after the activation.
The outcome of the activation process is a 1 × 1 × C channel weight vector, which encapsulates the importance of each channel. Subsequently, the scaling step is performed through individual multiplication of the channel parameter vector and the primary matrix . The mathematical formulation for this operation is:
where denotes the final activation map output of the SENet network.
4. Proposed Method
4.1. The Overall Architecture of SENet-Informer Diagnosis Model
This section provides a formal description of the diagnostic model’s overall architecture and its key components. The model includes data processing, the SENet-Informer encoder, and the classification head. A schematic representation of the SENet-Informer diagnosis model is presented in Figure 4. This study presents a fault diagnosis approach for rolling bearings using an improved Informer model integrated with SENet. The data preprocessing is split into two components: Scalar and Position, aimed at extracting local features and preserving sequence order, respectively. The enhanced Informer encoder employs a combination of the ProbSparse Self-attention and Full Attention mechanisms, allowing it to effectively capture both local and global dependencies within the input sequence. To further improve feature extraction, Conv1d convolutional layers, Max Pool1d pooling layers, and the SENet module are used. The SENet module’s adaptive adjustment mechanism significantly enhances the precision and discriminative capability of the extracted features.
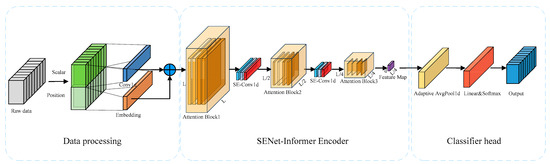
Figure 4.
The overall architecture of SENet-Informer diagnosis model.
Additionally, Self-attention Distilling technology is introduced to reduce computational complexity while maintaining the model’s efficiency in processing sequences. During classification, the feature map is resized via an Adaptive AvgPool1d pooling layer and mapped to the classification space through a Linear layer. Finally, a Softmax layer is used for fault category prediction.
4.1.1. Data Processing
During the data processing phase, the raw data is first preprocessed through two components: Scalar and Position. In the Scalar component, the Conv1d technique is employed to extract local features and address the local dependencies within sequential data. In the Position component, positional embedding and token embedding are employed to retain the sequential information and semantic representations of the data.
4.1.2. The Structure of SE-Conv1d
The SE-Conv1d network model is a deep learning architecture that integrates the Conv1d and SENet modules, with the core feature enhancement achieved through a channel attention mechanism. As shown in Figure 5, the SE-Conv1d network structure consists of both the Conv1d and SENet modules. In the Conv1d module, the local features of the input data are extracted primarily through Conv1d convolutional layers, with an output dimension of . In the SENet module, the channel weights are dynamically adjusted via the “squeeze-excitation” mechanism. This involves global pooling to aggregate channel-wide information, followed by a fully connected layer with a Sigmoid activation function to generate the channel weights. Finally, the original feature map is scaled, achieving key feature enhancement and redundancy suppression.
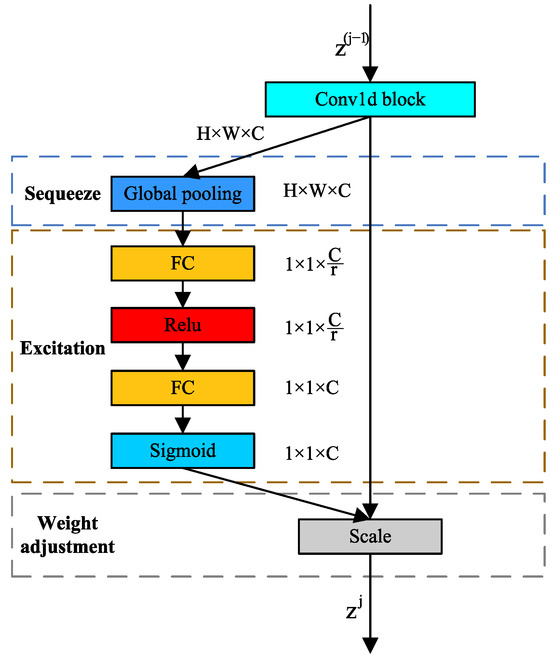
Figure 5.
The structure of SE-Conv1d.
4.1.3. The Encoder Structure of SENet-Informer Model
As presented in Figure 6, the Encoder of the SENet-Informer model extracts high-quality features through various mechanisms. First, an Attention Block composed of ProbSparse Self-attention and Full Attention is employed to extract both local and global dependencies, thereby enhancing the efficiency of long-sequence processing and alleviating computational burden. Subsequently, the SE-Conv1d, which consists of Conv1d, Max Pool1d, and the SENet module, is employed to extract local features and adaptively recalibrate their significance through the SENet module. Finally, the Self-attention Distilling approach, which integrates the previously discussed techniques, is applied to shorten the input sequence length, thus further enhancing storage and computational efficiency. This enables the proposed model to maintain high efficiency when processing long-time series data and output feature maps with rich information.
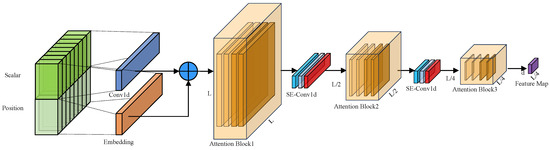
Figure 6.
The encoder structure of SENet-Informer model.
4.1.4. Classifier Head
As shown in Figure 4, the final output of the model is determined by the Classifier head, which consists of three key components: Adaptive AvgPool1d, Linear, and Softmax. After the data is processed by the SE-Net-Informer model’s Encoder, a rich feature map is produced. The Classifier head’s primary function is to perform the final classification decision based on these features. The Adaptive AvgPool1d layer ensures a uniform output size by pooling the feature map. Subsequently, the Linear layer maps the features to the classification space, and the Softmax layer generates a probability distribution for each class, providing the final classification results. This architecture allows the model to effectively classify based on the feature map, outputting the predicted probability for each class.
4.2. Overall Process of the SENet-Informer Method
Figure 7 presents the comprehensive diagram of the fault diagnosis study. The entire procedure can be categorized into three phases. During the sample processing phase, the bearing vibration signals are initially preprocessed to remove noise and normalize the data. Following preprocessing, the samples are divided into subsets. This partitioning ensures that the data from both healthy and faulty bearing states are distributed across the training, validation, and test sets in distinct proportions, facilitating robust model training and evaluation. The diagnostic model is optimized during the training process using the Sparrow Search Algorithm (SSA) to identify the optimal hyperparameters [27].
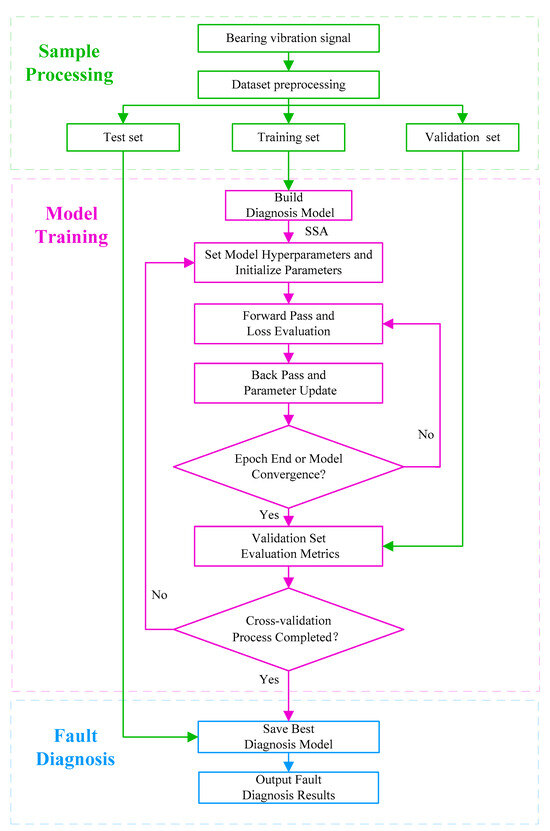
Figure 7.
The overall diagram of fault diagnosis research.
Subsequently, the hyperparameters are set, and the network weights are initialized. Subsequently, forward propagation is performed, and the loss function value is computed. The gradient is subsequently computed via the backpropagation algorithm, and the model’s weights or parameters are iteratively updated until convergence is achieved or the predetermined number of epochs is reached. Finally, continuous cross-validation is performed on the validation set. During this phase, the process is iteratively carried out by manually adjusting the hyperparameters, ultimately resulting in a model with the best diagnostic performance. At the fault diagnosis stage, the model that performs the best, according to metrics from the test set during training, is selected. The model is then validated and evaluated using the test set, generating the fault diagnosis results.
5. Experimental Verification
To assess the performance and applicability of the proposed diagnostic method for bearing fault detection, measurement data from the CWRU and HUST bearing datasets were utilized to evaluate the model. All models were trained on an AMD Ryzen 9 7945HX with Radeon Graphics, applying the PyTorch 2.1.1 deep learning framework.
5.1. CWRU Bearing Dataset
5.1.1. CWRU Dataset Description
The CWRU bearing dataset is one of the most classical open-source datasets in the field of mechanical fault diagnosis, collected by Case Western Reserve University through an electrical machine testing platform [28]. The experimental platform, as shown in Figure 8, mainly consists of a motor, a torque sensor, a power meter, and an electronic controller. The bearing model tested in this study is the SKF-6205-2RS deep groove ball bearing, with simulated fault diameters of 0.007 inches, 0.014 inches, 0.021 inches, and 0.028 inches. The fault types considered include inner race fault, outer race fault, and rolling element fault. Data for this analysis were captured from the drive end, where the motor speed was 1750 rpm, the load was two hp, and the sampling frequency was 12 kHz.

Figure 8.
CWRU platform.
Bearing status is organized into 10 categories, depending on the fault’s position and degree. Among these, one category represents the healthy condition, while the remaining nine categories represent different fault conditions. To extract the maximum correlation from the time-series samples, an overlapping sampling method was employed in this research [29]. The dataset is split into training, validation, and test sets in a 6:2:2 ratio, corresponding to sample sizes of 1400, 466, and 466, respectively. The details of the experimental dataset are presented in Table 1.

Table 1.
Table of parameters for various fault types.
5.1.2. Selection of Model Parameters and Experimental Analysis
The parameters of the fault diagnosis model based on SENet and the improved Informer are shown in Table 2. These include the model dimension , the number of attention heads , the number of encoder layers , and the dimension of the fully connected network . These four parameters were globally optimized using the Sparrow Search Algorithm (SSA). Other parameters were set using the control variable method, in conjunction with prior knowledge from the fault diagnosis field. All parameters were validated through multiple repeated experiments and demonstrated good stability.

Table 2.
Parameters of fault diagnosis models.
To validate the effectiveness of the SENet channel attention mechanism, ProbSparse sparse attention mechanism, and the Distil operation in the proposed model, four ablation experiments were designed, as shown in Table 3. Classification accuracy and inference time were compared under the same training parameters and test dataset. The experimental results demonstrate that the classification accuracy of the SENet and the improved Informer-based model reached 99.78%, confirming the complementary roles of the three modules in feature extraction. Specifically, the SENet module effectively enhanced the fault channel weights, improving the fault diagnosis accuracy; the ProbSparse attention mechanism reduced the complexity of temporal modeling, optimizing the computational efficiency of the model; and the Distil module improved the model’s robustness through feature dimensionality reduction, thereby enhancing the model’s generalization ability when handling complex data.

Table 3.
Ablation study.
5.1.3. Experimental Comparison and Result Analysis
A comparative experiment was conducted to assess the performance of the proposed model, utilizing several machine learning models commonly applied in bearing fault diagnosis. The experiment includes six methods in total: CNN, TCN, LSTM, Transformer, CNN-LSTM, and SENet-Informer. These comparison methods utilize the widely adopted Convolutional network model in deep learning, with parameters configured based on the recommended settings. Table 4 illustrates the results of the experiment. As illustrated in the table, the SENet-Informer model achieves the highest diagnostic accuracy, reaching 99.78%. The model’s recall rate and F1-score are consistent with its accuracy, and the corresponding values are higher than those of other models. This further validates the superior classification performance of the proposed model in fault diagnosis. Furthermore, compared to the other models, the presented model exhibits a lower standard deviation (Std) and variance, indicating that its fault diagnosis results are the most consistent across all samples.

Table 4.
Performance of various models.
As illustrated in Figure 9, the confusion matrix results for each method on the CWRU dataset test set are presented, with the horizontal axis representing the predicted labels and the vertical axis corresponding to the actual labels. An analysis of the figure reveals that the classification performance of the SENet-Informer model outperforms the other models. Figure 10 illustrates the accuracy and training loss curves for the presented approach, shown for the training and validation datasets. Upon analyzing the figure, it is evident that after over 50 iterations, the model starts to converge and steadily stabilize, demonstrating the robust convergence capabilities of the presented model. Figure 11 presents the t-SNE visualization of the results. It clearly shows the diagnostic model’s capability to distinguish between the ten fault categories. The visualization highlights the model’s superior clustering performance, indicating its effectiveness in classifying diverse fault types with high accuracy. This suggests that the model has robust feature extraction capabilities.
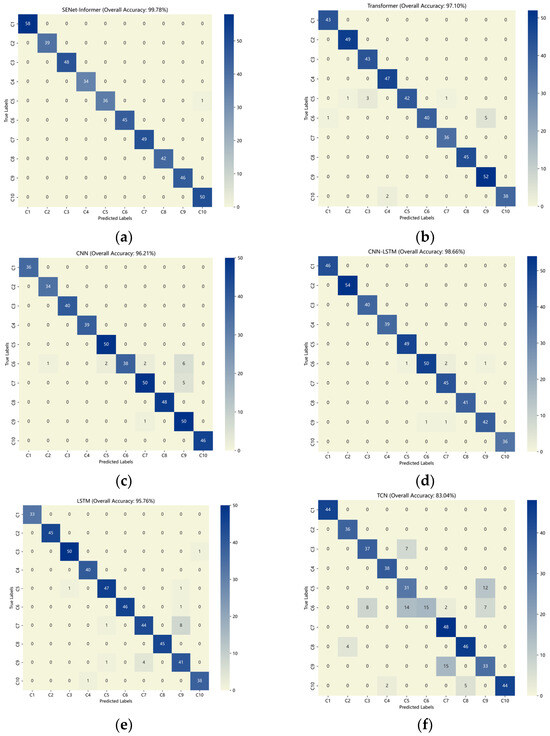
Figure 9.
Confusion matrix results of the CWRU dataset for (a) SENet-Informer; (b) Transformer; (c) CNN-LSTM; (d) CNN; (e) LSTM; (f) TCN.
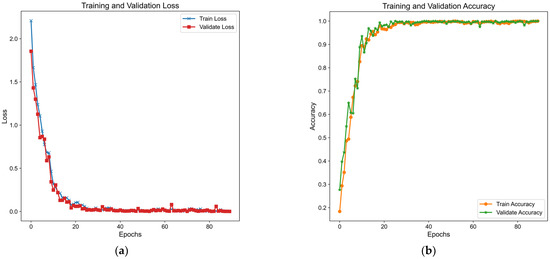
Figure 10.
(a) The loss curves for the CWRU bearing dataset. (b) The training accuracy for the CWRU bearing dataset.
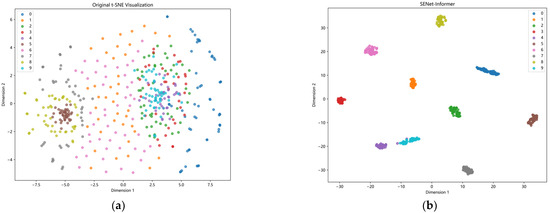
Figure 11.
Two-dimensional visualization results of CWRU bearing dataset. (a) Original t-SNE visualization. (b) t-SNE visualization results of SENet-Informer.
5.2. HUST Bearing Dataset
5.2.1. HUST Dataset Description
Figure 12 illustrates the HUST bearing dataset [30], which encompasses bearing fault tests performed using the Spectra-Quest mechanical fault simulator. From left to right on the test rig, the components include the speed controller, electric motor, shaft, accelerometer, bearing, and data acquisition board. The test bench does not incorporate a loading device. The ER-16K bearing model, presently under analysis, features a shaft diameter of 38.52 mm and a ball diameter of 7.94 mm and is employed to simulate bearing faults. As depicted in Figure 13, nine distinct bearing conditions are considered: (1) normal, (2) moderate internal fault, (3) severe internal fault, (4) moderate external fault, (5) severe external fault, (6) moderate ball fault, (7) severe ball fault, (8) moderate combined fault, and (9) severe combined fault. The combined fault involves both internal and external faults. The data used in this experiment were collected at a sampling frequency of 25.6 kHz under time-varying operating conditions with a bearing rotational speed of 0-40-0 Hz.

Figure 12.
Test rig of HUST bearing dataset.

Figure 13.
Photographs of the failure bearings.
The bearing health condition is categorized into nine groups based on the fault location and severity. Among these, one category represents the healthy condition, while the remaining eight categories correspond to different fault conditions. The dataset is divided into training, validation, and test sets with proportions of 6:2:2, corresponding to sample sizes of 1680, 560, and 560, respectively. Table 5 outlines the experimental dataset in detail.

Table 5.
Table of parameters for various fault types.
5.2.2. Experimental Comparison and Result Analysis
To assess the efficacy of the proposed model, a comparative experiment was performed using various machine learning models commonly employed in bearing fault diagnosis. The experiment includes six methods in total: CNN, TCN, LSTM, Transformer, CNN-LSTM, and SENet-Informer. The comparison strategies utilize the widely accepted CNN model in deep learning, with parameters set according to the suggested guidelines. The experimental results are summarized in Table 6. As shown in the table, the fault classification accuracy of most other methods decreases under time-varying operating conditions.

Table 6.
Performance of various models.
In contrast, the SENet-Informer model achieves the highest diagnostic accuracy, with a value of 99.45%. The model’s recall rate and F1-score are consistent with its accuracy, and the corresponding values are higher than those of other models. This further validates the superior classification performance of the proposed model in fault diagnosis. Furthermore, in comparison to other models, the proposed model in this study demonstrates a minimal standard deviation (Std-Variance), suggesting that its fault diagnosis outcomes are the most consistent across all samples. This suggests that the model possesses good generalizability.
Figure 14 presents the confusion matrix results for each method on the test set. The predicted labels are represented on the horizontal axis, whereas the actual labels are shown on the vertical axis. As shown in the figure, the SENet-Informer model demonstrates superior classification performance compared to the other models. Figure 15 illustrates the t-SNE-based visualization results for the HUST dataset. The figure clearly illustrates that the diagnostic model proposed in this study effectively differentiates the nine fault classes, exhibiting enhanced clustering performance. This suggests that the diagnostic model possesses strong feature extraction capabilities and exhibits good generalizability.
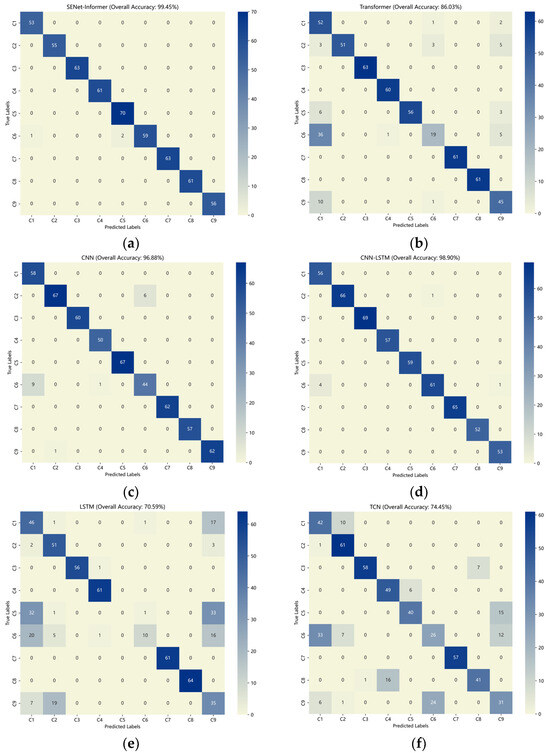
Figure 14.
Confusion matrix results of the HUST dataset for (a) SENet-Informer; (b) Transformer; (c) CNN-LSTM; (d) CNN; (e) LSTM; (f) TCN.
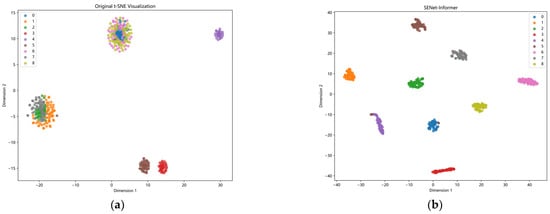
Figure 15.
Two-dimensional visualization results of HUST bearing dataset (a) Original t-SNE visualization (b) t-SNE visualization results of SENet-Informer.
6. Conclusions
This research presents the SENet-Informer model for rolling bearing fault diagnosis, which efficiently extracts essential features from bearing faults and demonstrates outstanding performance in time series prediction tasks. In data preprocessing, a combination of Conv1d and Positional Embedding is employed to extract local features. This approach also preserves temporal information, enabling the effective handling of long-time series data. Through the addition of the ProbSparse Self-attention mechanism and the SE-Conv1d convolution module, the SENet-Informer model improves feature extraction capabilities and minimizes computational overhead. The classification head efficiently performs classification decisions through the Adaptive AvgPool1d and Softmax layers. Finally, experiments were conducted on the CWRU bearing dataset and the HUST bearing dataset, achieving fault diagnosis accuracies of 99.78% and 99.45%, respectively, which represents an improvement of approximately 5–8% compared to traditional methods such as CNN and LSTM. This demonstrates that the proposed model achieves higher accuracy and stability in rolling bearing fault diagnosis, with good generalization ability, and performs effectively across different datasets.
However, given the reliance on labeled data in this study, future work could incorporate transfer learning or domain adaptation techniques to reduce the dependency on labeled data and enhance the model’s adaptability to various scenarios. In the future, improving the generalization capability of deep learning models will become a key research focus. To expand the applicability of these models, further exploration will be conducted using datasets such as SEU, Paderborn, and PHM under different operating conditions.
Author Contributions
Conceptualization, B.Y. and Y.D.; methodology, B.Y.; software, Y.D.; validation, Y.D.; formal analysis, B.Y.; investigation, Y.D.; resources, S.C.; data curation, Z.X.; writing—original draft preparation, B.Y. and Y.D.; writing—review and editing, B.Y. and Y.D.; visualization, Y.D.; supervision, S.C.; project administration, Z.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was conducted without external funding.
Data Availability Statement
CWRU-bearing dataset. (2009). Available online: https://engineering.case.edu/bearingdatacenter (accessed on 20 November 2024). HUST-bearing dataset. Available online: https://github.com/CHAOZHAO-1/HUSTbearing-dataset (accessed on 20 November 2024).
Conflicts of Interest
The authors state that they have no conflicts of interest.
References
- Ni, Q.; Ji, J.C.; Halkon, B.; Feng, K.; Nandi, A.K. Physics-Informed Residual Network (PIResNet) for rolling element bearing fault diagnostics. Mech. Syst. Signal Process. 2023, 200, 110544. [Google Scholar] [CrossRef]
- Cerrada, M.; Sánchez, R.V.; Li, C.; Pacheco, F.; Cabrera, D.; De Oliveira, J.V.; Vásquez, R.E. A review on data-driven fault severity assessment in rolling bearings. Mech. Syst. Signal Process. 2018, 99, 169–196. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, S.; Wang, B.; Habetler, T.G. Deep learning algorithms for bearing fault diagnostics—A comprehensive review. IEEE Access 2020, 8, 29857–29881. [Google Scholar] [CrossRef]
- Magar, R.; Ghule, L.; Li, J.; Zhao, Y.; Farimani, A.B. FaultNet: A deep convolutional neural network for bearing fault classification. IEEE Access 2021, 9, 25189–25199. [Google Scholar] [CrossRef]
- Aburakhia, S.A.; Myers, R.; Shami, A. A hybrid method for condition monitoring and fault diagnosis of rolling bearings with low system delay. IEEE Trans. Instrum. Meas. 2022, 71, 3519913. [Google Scholar] [CrossRef]
- Saufi, S.R.; Ahmad, Z.A.B.; Leong, M.S.; Hee, L.M. Bearing fault diagnosis using deep sparse autoencoder. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Suzhou, China, 17–19 March 2021; Volume 1062, p. 012002. [Google Scholar]
- Vashishtha, G.; Chauhan, S.; Sehri, M.; Hebda-Sobkowicz, J.; Zimroz, R.; Dumond, P.; Kumar, R. Advancing machine fault diagnosis: A detailed examination of convolutional neural networks. Meas. Sci. Technol. 2024, 36, 022001. [Google Scholar] [CrossRef]
- Sinitsin, V.; Ibryaeva, O.; Sakovskaya, V.; Eremeeva, V. Intelligent bearing fault diagnosis method combining mixed input and hybrid CNN-MLP model. Mech. Syst. Signal Process. 2022, 180, 109454. [Google Scholar] [CrossRef]
- Wang, H.; Xu, J.; Yan, R.; Gao, R.X. A new intelligent bearing fault diagnosis method using SDP representation and SE-CNN. IEEE Trans. Instrum. Meas. 2019, 69, 2377–2389. [Google Scholar] [CrossRef]
- Cui, W.; Meng, G.; Wang, A.; Zhang, X.; Ding, J. Application of rotating machinery fault diagnosis based on deep learning. Shock Vib. 2021, 2021, 3083190. [Google Scholar] [CrossRef]
- Hewamalage, H.; Bergmeir, C.; Bandara, K. Recurrent neural networks for time series forecasting: Current status and future directions. Int. J. Forecast. 2021, 37, 388–427. [Google Scholar] [CrossRef]
- Liu, H.; Zhou, J.; Zheng, Y.; Jiang, W.; Zhang, Y. Fault diagnosis of rolling bearings with recurrent neural network-based autoencoders. ISA Trans. 2018, 77, 167–178. [Google Scholar] [CrossRef] [PubMed]
- Qiao, M.; Yan, S.; Tang, X.; Xu, C. Deep convolutional and LSTM recurrent neural networks for rolling bearing fault diagnosis under strong noises and variable loads. IEEE Access 2020, 8, 66257–66269. [Google Scholar] [CrossRef]
- Pan, H.; He, X.; Tang, S.; Meng, F. An improved bearing fault diagnosis method using one-dimensional CNN and LSTM. J. Mech. Eng./Stroj. Vestn. 2018, 64, 443–452. [Google Scholar]
- Sun, H.; Fan, Y. Fault diagnosis of rolling bearings based on CNN and LSTM networks under mixed load and noise. Multimed. Tools Appl. 2023, 82, 43543–43567. [Google Scholar] [CrossRef]
- Wang, M.; Qin, F. A TCN-Linear Hybrid Model for Chaotic Time Series Forecasting. Entropy 2024, 26, 467. [Google Scholar] [CrossRef]
- Hao, H.; Wang, Y.; Xue, S.; Xia, Y.; Zhao, J.; Shen, F. Temporal convolutional attention-based network for sequence modeling. arXiv 2020, arXiv:2002.12530. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Tama, B.A.; Vania, M.; Lee, S.; Lim, S. Recent advances in the application of deep learning for fault diagnosis of rotating machinery using vibration signals. Artif. Intell. Rev. 2023, 56, 4667–4709. [Google Scholar] [CrossRef]
- Pei, X.; Zheng, X.; Wu, J. Rotating machinery fault diagnosis through a transformer convolution network subjected to transfer learning. IEEE Trans. Instrum. Meas. 2021, 70, 2515611. [Google Scholar] [CrossRef]
- Nath, A.G.; Udmale, S.S.; Raghuwanshi, D.; Singh, S.K. Structural rotor fault diagnosis using attention-based sensor fusion and transformers. IEEE Sens. J. 2021, 22, 707–719. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond efficient transformer for long sequence time-series forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 2–9 February 2021; Volume 35, pp. 11106–11115. [Google Scholar]
- Yang, Z.; Liu, L.; Li, N.; Tian, J. Time series forecasting of motor bearing vibration based on informer. Sensors 2022, 22, 5858. [Google Scholar] [CrossRef]
- Tepetidis, N.; Koutsoyiannis, D.; Iliopoulou, T.; Dimitriadis, P. Investigating the Performance of the Informer Model for Streamflow Forecasting. Water 2024, 16, 2882. [Google Scholar] [CrossRef]
- Wei, H.; Wang, W.-S.; Kao, X.X. A novel approach to ultra-short-term wind power prediction based on feature engineering and informer. Energy Rep. 2023, 9, 1236–1250. [Google Scholar] [CrossRef]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 7132–7141. [Google Scholar]
- Appel, A.W. SSA is functional programming. ACM Sigplan Not. 1998, 33, 17–20. [Google Scholar] [CrossRef]
- Smith, W.A.; Randall, R.B. Rolling element bearing diagnostics using the Case Western Reserve University data: A benchmark study. Mech. Syst. Signal Process. 2015, 64, 100–131. [Google Scholar] [CrossRef]
- Xiong, F.; Wen, H.; Zhang, C.; Song, C.; Zhou, X. Semantic segmentation recognition model for tornado-induced building damage based on satellite images. J. Build. Eng. 2022, 61, 105321. [Google Scholar] [CrossRef]
- Zhao, C.; Zio, E.; Shen, W. Domain generalization for cross-domain fault diagnosis: An application-oriented perspective and a benchmark study. Reliab. Eng. Syst. Saf. 2024, 245, 109964. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).