Research on Energy Storage Configuration Optimization Method for Wind Farm Substations Based on Wind Power Fluctuation Prediction Integrating Chaotic Features and Bidirectional Gated Recurrent Units

Abstract

To address wind power fluctuations causing curtailment and high costs, this study proposes an integrated method combining wind power forecasting with substation optimization. An enhanced Bidirectional Gated Recurrent Unit (BiGRU) model is developed by incorporating chaotic features (maximum Lyapunov exponent) and sliding-window statistical features (mean, standard deviation), significantly improving short-term prediction accuracy. Based on these high-precision forecasts, a dynamic transformer switching optimization model is established to maximize the wind farm’s net profit. This model finely balances power generation revenue, wind curtailment penalties, and transformer losses (no-load and load) at a 15 min timescale. Experimental results from a wind farm in Xinjiang demonstrate that the proposed method effectively enhances the economic efficiency of wind farm operations. The study provides a valuable framework for optimizing energy storage configuration and improving profitability by leveraging accurate forecasting.

1. Introduction

As wind power installations in the grid continue to grow, the inherent randomness, intermittency, and volatility of wind energy pose significant challenges to the safe and stable operation of power systems [1]. The unpredictability of wind output forces grids to deploy substantial reserve capacities to address power fluctuations, leading to increased operational costs [2]. When wind generation surges outpace grid absorption capacity, forced wind curtailment occurs, severely limiting the efficient utilization and economic viability of wind energy [3]. High-precision wind power forecasting is key to mitigating these issues. Accurate predictions provide decision-making support for grid dispatchers, optimize output planning for conventional units, reduce system reserve requirements, and enable wind farms to actively participate in grid regulation [4,5]. However, constrained by meteorological forecast accuracy and limitations in current forecasting methods, current predictions still exhibit considerable errors, failing to fully meet the demands of refined dispatching.

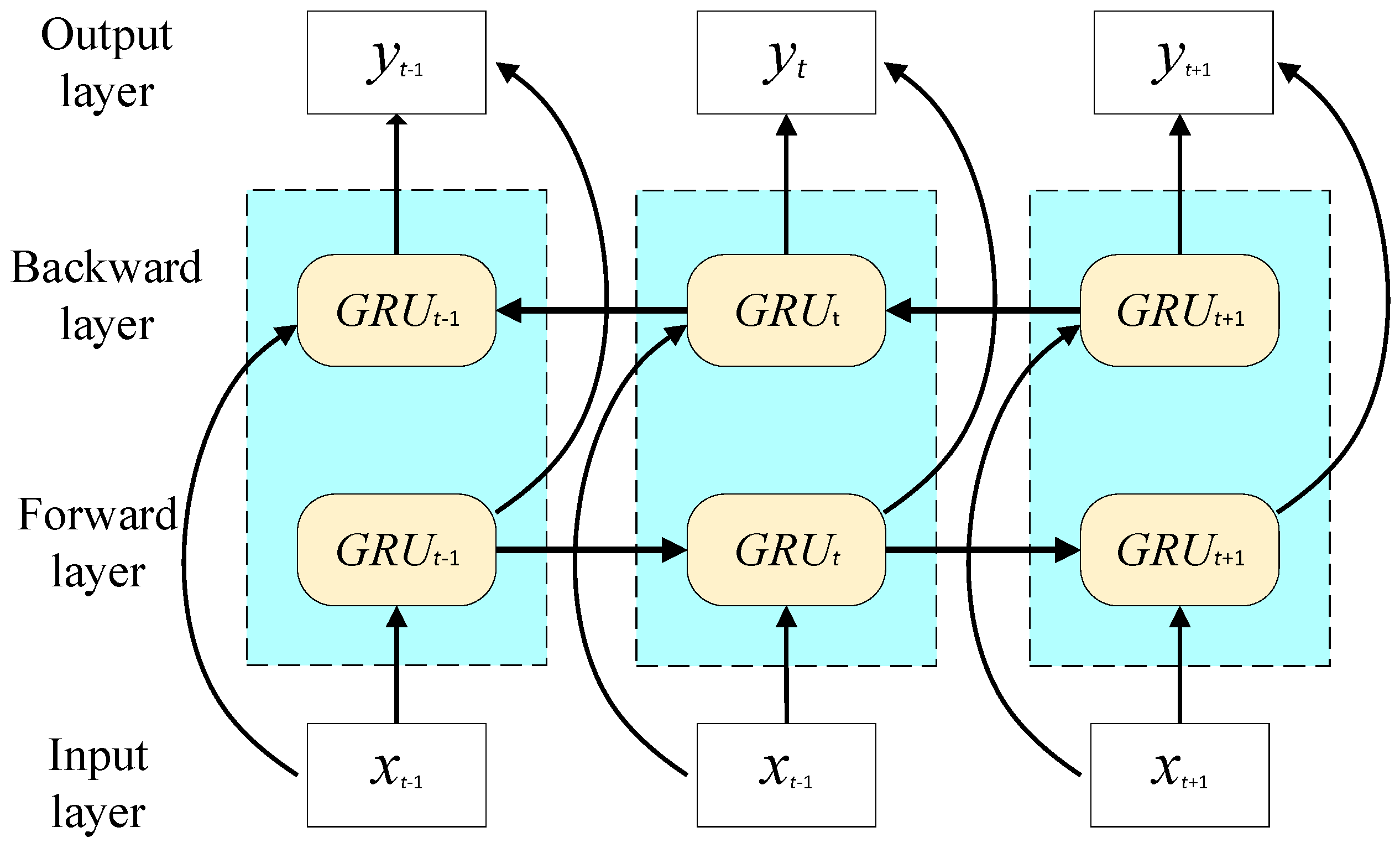
In recent years, deep learning models have been increasingly applied in the field of wind power forecasting [6]. Mainstream deep learning models for wind power prediction primarily include the Recurrent Neural Network (RNN) [7], Long Short-Term Memory Network (LSTM) [8], Gated Recurrent Unit (GRU) [9], and its bidirectional variant (Bidirectional GRU, BiGRU) [10]. RNN, a neural network specifically designed for sequential data, has been widely used in wind power forecasting [11]. However, standard RNNs are prone to the problems of gradient vanishing or explosion when processing long sequences, making it difficult to effectively capture the long-term dependencies inherent in wind speed series. To address this limitation, the LSTM mitigates gradient issues by introducing gating mechanisms—such as input, forget, and output gates—significantly enhancing the model’s ability to learn long-range temporal dependencies [12]. For instance, in [13], a novel intelligent granular model combined with LSTM is proposed to comprehensively assess precise data distribution for wind power system reliability. The GRU, a simplified variant of the LSTM, merges the forget and input gates into a single update gate and introduces a reset gate, thereby reducing model complexity and improving computational efficiency while maintaining comparable performance. In [14], a hybrid model based on GRU and stationary wavelet transform is proposed for short-term wind speed forecasting. To further exploit contextual information within sequences, the Bidirectional GRU (BiGRU) was proposed. It employs two separate GRU networks—one processing the sequence forward and the other backward—enabling the model to simultaneously capture information from both past and future states. This architecture demonstrates superior feature extraction capability when handling wind power data with strong temporal correlations. In [15], a short-term wind power forecasting model is developed using a multi-layer stacked architecture that integrates CNN and BiGRU.

Meanwhile, with the deepening implementation of China’s energy strategy, wind power, as a vital component of the clean energy system, has seen continuous growth in installed capacity [16]. However, the inherent intermittency and volatility of wind power generation necessitate the operation of a large number of electrical devices at wind farms even during low-load periods, resulting in unnecessary energy losses and operational costs [17]. Among these, the step-up transformers, which are critical equipment connecting wind turbine generators to the power grid, constitute a significant portion of the station’s auxiliary power consumption through their no-load and load losses.

Traditional operational strategies typically employ a fixed-number operation mode, which ensures power supply reliability [18]. However, during periods of low wind speed or at night, when power output is low, transformers often operate under light load for extended durations, leading to low energy efficiency [19]. Therefore, dynamically adjusting the number of operational transformers based on real-time wind power output can minimize system losses and operational costs while satisfying transmission capacity constraints. This approach has become a key issue in enhancing the economic operation of wind farms [20].

Nevertheless, most models oversimplify the loss characteristics or neglect operational costs, and lack an assessment of scheduling robustness under power forecast uncertainty. To address these limitations, this paper establishes a Mixed Integer Programming (MIP)-based optimization model for wind farm transformer operation. The model comprehensively considers power generation revenue, wind curtailment penalties, transformer losses, and switching operational costs to achieve multi-objective synergistic optimization. To enhance the robustness of the scheduling decisions under uncertainty, high-precision short-term wind power forecasting is essential. In this study, a Bidirectional Gated Recurrent Unit (BiGRU) model is employed and enhanced by incorporating chaotic features—specifically the maximum Lyapunov exponent—and sliding-window statistical features (mean and standard deviation) into the input layer. These features help characterize the intrinsic instability of wind dynamics and capture local fluctuation patterns, enabling the model to achieve superior forecasting accuracy compared to standard GRU and LSTM models.

This study addresses two critical limitations in the existing literature. First, to overcome the insufficient accuracy of conventional wind power forecasting models (e.g., standard GRU, LSTM, BiGRU) which often fail to capture the inherent chaotic nature and local fluctuation patterns of wind power, we propose an enhanced Bidirectional Gated Recurrent Unit (BiGRU) model. This model innovatively integrates chaotic features—specifically the maximum Lyapunov exponent (a measure of system instability)—and sliding-window statistical features (mean and standard deviation) into its input layer, thereby significantly improving short-term prediction fidelity. Second, to mitigate the oversimplification of operational costs and the lack of integration between prediction and decision-making in current optimization frameworks, we establish a Mixed Integer Programming (MIP)-based dynamic transformer switching model. This model operates on a 15 min timescale and comprehensively optimizes net profit by balancing power generation revenue, wind curtailment penalties, transformer losses (no-load and load), and switching operation costs. The integration of the high-accuracy BiGRU forecasts into the MIP optimization framework forms a closed-loop system, effectively bridging the gap between prediction and economic dispatch and providing a robust decision-support tool for wind farm energy management.

2. Materials and Methods

2.1. Chaos Features and Lyapunov

Chaotic system refers to the complex phenomenon of extreme sensitivity to initial conditions and unpredictable long-term behavior of deterministic nonlinear dynamic system under specific parameters, namely “butterfly effect” [21]. Although its behavior seems random, its evolution is governed by deterministic equations. The Lyapunov exponent (LE) quantitatively describes the average rate of divergence or convergence of adjacent trajectories in phase space [22]. For a dynamical system, its maximum Lyapunov exponent (MLE) is defined as:

$$\lambda =\underset{t\to \infty }{\lim }\underset{\parallel \delta Z_0\parallel \to 0}{\lim }{\displaystyle \frac{1}{t}}\ln {\displaystyle \frac{\parallel \delta Z(t)\parallel }{\parallel \delta Z_0\parallel }}$$

(1)

where $\delta Z_0$ is the small distance between two adjacent trajectories at the initial moment, $\delta Z(t)$ is the distance between the two trajectories after the elapsed time $t$, and is the Lyapunov index.

If $\lambda >0$, it means that the adjacent trajectory exponents diverge, and the system has chaotic characteristics. If $\lambda <0$, the trajectory converges and the system tends to be stable; If $\lambda =0$, the system is periodic or quasi-periodic motion.

In practical calculations, since the limit cannot be taken, it is usually estimated by linear regression:

$$\ln \parallel \delta Z(t)\parallel \approx \lambda t+\ln \parallel \delta Z_0\parallel$$

(2)

The linear fitting of the average distance to time t is the estimate of its slope.

However, for the univariate time series $x(t)$, the trajectories in high-dimensional phase space cannot be directly observed. The Takens embedding theorem provides a method to reconstruct phase space from a one-dimensional time series. The reconstructed phase space vector is:

$$Z(i)=[x(i),x(i+\tau ),x(i+2\tau ),\dots ,x(i+(m-1)\tau )]$$

(3)

where $m$ is the embedding dimension and $\tau$ is the time delay.

The reconstructed phase space trajectory is topologically equivalent to the original system, and the Lyapunov exponent can be calculated on it.

In this paper, a simplified version of Wolf method is used to calculate the Lyapunov index. The process is as follows:

(1)

Phase space reconstruction: For the normalized time series $x(t)$, construct the phase space trajectory using the embedding dimension $m=3$ and time delay $\tau =1$:

$$Z(i)=[x(i),x(i+1),x(i+2)],\hspace{1em}i=1,2,\dots ,N-2\tau$$

(4)

(2)

Calculate the distance evolution of nearest neighbor: For each point $Z(i)$, calculate the distance between it and subsequent points, select the nearest $k=1$ neighbors, and record their average distance $d(i)$.

(3)

Linear fitting to find LE: Perform linear regression on time $t=1,2,...,T$ and $\ln d(t)$:

$$\ln d(t)=\lambda t+b$$

(5)

where the regression slope $\lambda$ is the estimated value of Lyapunov exponent.

In addition, the mean $\mu$ and standard deviation $\sigma$ in the sliding window are extracted as auxiliary features:

$$\mu ={\displaystyle \frac{1}{W}}\sum _{i=1}^W{x}_i,\hspace{1em}\sigma =\sqrt{{\displaystyle \frac{1}{W-1}}\sum _{i=1}^W{(x_i-\mu )}^2}$$

(6)

2.2. Bi-Directional Gated Recurrent Unit

The Bidirectional Gated Recurrent Unit (BiGRU) is an advanced recurrent neural network architecture designed to model sequential data by capturing dependencies from both past and future contexts [23]. Unlike standard unidirectional GRUs, which process sequences in a single forward direction, the BiGRU consists of two parallel GRU layers: one processes the input sequence in the forward (temporal) direction, while the other processes it in the reverse direction. The final hidden state at each time step is obtained by concatenating or summing the outputs of both the forward and backward GRUs. This dual-path structure enables the model to simultaneously access historical information and future context, making it particularly effective in capturing complex temporal patterns in time series data such as wind power generation.

In this study, the BiGRU serves as the core forecasting engine, enhanced with domain-specific features to better model the nonlinear and chaotic characteristics of wind power. Specifically, the input vector is augmented with the maximum Lyapunov exponent—a measure of system chaos derived from phase space reconstruction—and sliding-window statistical features (mean and standard deviation) to capture local volatility. This integration allows the BiGRU to more accurately represent the dynamic behavior of wind power, thereby improving short-term prediction accuracy. The enhanced BiGRU model is then utilized to generate high-precision forecasts, which serve as critical inputs for the downstream transformer operation optimization model.

Conventional neural networks process sequential data in a unidirectional manner, where each state is computed based only on past and present inputs, thus lacking access to future contextual information. To address this constraint, the Bidirectional Gated Recurrent Unit (BiGRU) is adopted, which enhances modeling capability by processing the input sequence in both forward and reverse temporal directions. The BiGRU architecture consists of two parallel GRU layers. At each time step $t$, the input $x_t$ is simultaneously fed into the forward GRU unit and the backward GRU unit. The forward GRU processes the sequence in chronological order, allowing the model to capture dependencies from previous inputs (e.g., $x_{t-1}$) to the current time step $t$. In contrast, the backward GRU processes the sequence in reverse order, enabling it to capture dependencies from subsequent inputs (e.g., $x_{t+1}$) to $t$. The outputs of both GRU units at time step $t$ are combined (e.g., by concatenation or summation) to form the output $y_t$. This bidirectional mechanism enables the model to integrate both past and future contextual information into the hidden state at the current time step $t$, thereby enhancing its ability to understand the temporal structure of the sequence. As a result, the BiGRU is particularly suitable for tasks requiring rich contextual modeling, such as wind power forecasting. The structure of the BiGRU is illustrated in Figure 1.

2.3. Optimization Model for Dynamic Switching of Transformers in Wind Farms

To enhance the economic efficiency of wind farm operations, this study establishes a dynamic capacity allocation optimization model on the substation side, based on high-precision power forecasting. The model aims to maximize the net profit of the wind farm by dynamically adjusting the number of operational transformers within the substation, thereby enabling fine-grained management of transmission capacity. This approach balances power generation revenue, wind curtailment costs, and equipment operating expenses while ensuring safe and reliable power delivery.

2.3.1. Variables and System Parameters

The model performs optimization decisions on a 15 min time step. The decision variable is defined as, representing the number of transformers in operation at each time period t.

The main parameters involved in the model are shown in

Table 1. Model parameters for dynamic transformer switching optimization.

Parameter	Symbol	Value	Unit
Rated capacity per transformer	C	50.0	MVA
No-load loss per transformer	p0	34	kW
Full-load loss per transformer	pk	180	kW
Optimization time step	Δt	0.25	h
Grid electricity price for wind power	πe	0.50	CNY/kWh
Wind curtailment penalty price	πc	0.61	CNY/kWh
Energy loss cost	πl	0.50	CNY/kWh

.

2.3.2. Constraints and Objective Function

• Objective Function

The overall objective of the model is to maximize the total net profit over the optimization horizon. The mathematical expression is as follows:

$$\max \hspace{1em}{\mathrm{N}}_{\mathrm{Benefit} }=R-L_c-L_{\mathrm{loss}}-C_{\mathrm{op}}-C_{\mathrm{penalty}}$$

(7)

where each component is defined below:

(1)

Wind Power Generation Revenue

$$R=\sum _{t=0}^{T-1}(P_t\times {\pi }_e)\Delta t$$

(8)

Revenue is calculated based on the actual grid-connected power.

(2)

Wind Curtailment Cost

$$L_c=\sum _{t=0}^{T-1}{\pi }_c\times \max (0, P_{\mathrm{t}}-n_t\ast C)\Delta t$$

(9)

When the wind power output $P_{\mathrm{t}}$ exceeds the total capacity of the operational transformers $n_t\ast C$, the excess power is curtailed and incurs a penalty cost.

(3)

Transformer Loss Cost

$${\mathrm{L}}_{loss}={\displaystyle \sum _{t=0}^T{\pi }_l}\times (n_t\times p_0+p_k\times {\displaystyle \frac{{P_t}^2}{n_t\cdot C^2}})\Delta t$$

(10)

The total loss cost includes the no-load loss cost and the load loss cost, which is proportional to the square of the load. $P_t$ represents the actual power transmitted through the transformers.

(4)

Operating Cost

This term can include maintenance costs associated with transformer switching operations.

$$C_{\mathrm{op}}=S\times c_{op}$$

(11)

where $S$ represents the number of operation times, $c_{op}$ represents the cost per operation, $C_{\mathrm{op}}$ represents the total operation cost.

2.

Constraints

(1)

Mutually Exclusive Operation Mode Constraint

Ensures that only one specific $n_t$ value (1, 2, or 3) is selected for each time period t.

(2)

Initial State Constraint

Sets the initial number of operational transformers to two at the start of the optimization period ($t=2$).

(3)

Power Balance and Wind Curtailment Constraint

$$P_t=\min (P_t,n_t\ast C)$$

(12)

The actual transmitted power is limited by the minimum of the wind power output and the total capacity of the operational transformers. Any excess power constitutes wind curtailment.

2.4. Proposed Method and Procedures

Based on the integration of enhanced wind power forecasting and dynamic transformer optimization, this study proposes a two-stage framework for improving the economic operation of wind farm substations. The overall methodology, illustrated in Figure 2, consists of the following sequential steps:

Stage 1: Enhanced Short-Term Wind Power Forecasting

First, historical wind power and meteorological data are preprocessed and normalized. Using the Takens embedding theorem, phase space reconstruction is performed on the wind power time series to extract chaotic characteristics. The maximum Lyapunov exponent (MLE) is computed using a simplified Wolf method to quantify the system’s sensitivity to initial conditions. Concurrently, sliding-window statistical features—including the mean and standard deviation—are calculated over a moving window to capture local volatility patterns. These domain-specific features (MLE, mean, standard deviation) are then fused with the original meteorological and power data to form an enriched input vector. This enhanced input is fed into the Bidirectional Gated Recurrent Unit (BiGRU) network, which processes the sequence in both forward and backward directions to capture comprehensive temporal dependencies. The trained BiGRU model outputs high-precision 15 min ahead wind power forecasts.

Stage 2: Dynamic Transformer Switching Optimization

The predicted wind power series from Stage 1 serves as a critical input to the downstream Mixed Integer Programming (MIP) optimization model. The objective is to maximize the wind farm’s net profit over a 24 h horizon, discretized into 15 min intervals. The decision variable is the number of operational transformers at each time step. The optimization model comprehensively evaluates power generation revenue, wind curtailment penalties, transformer no-load and load losses, and switching operation costs, subject to technical constraints such as transmission capacity limits and mutually exclusive transformer states. The MIP solver determines the optimal transformer switching schedule that balances economic benefits with operational reliability.

This integrated approach ensures that operational decisions are based on accurate predictions of wind power fluctuations, thereby enhancing the robustness and profitability of substation management. The entire procedure enables fine-grained, data-driven decision-making for wind farm energy management systems.

3. Results

The wind farm topology under study is illustrated in Figure 3, which depicts a typical centralized wind power station structure. Wind turbines generate electricity at a low voltage level, which is then stepped up by individual pad-mounted transformers to the medium voltage level. The output from multiple turbines is collected via collection lines and fed into the medium voltage busbar.

From the MV busbar, the aggregated power is transmitted through one or more step-up transformers to the high voltage busbar, where the voltage is further increased for connection to the external power grid. In this study, each step-up transformer has a rated capacity of 50.0 MVA, and multiple units are operated in parallel. The proposed optimization model focuses specifically on the dynamic switching strategy of these step-up transformers, aiming to determine the optimal number of transformers to operate at any given time based on predicted wind power output.

Additionally, an energy storage system (ESS), such as a battery energy storage system (BESS), can be integrated into the substation. Its primary functions include smoothing power fluctuations, providing ancillary services, and enhancing grid stability. It is important to note that the term “energy storage” used in the context of “energy storage configuration optimization” in this paper is employed in a broad, functional sense. It does not refer exclusively to physical ESS devices like batteries. Instead, it denotes the operational flexibility achieved by optimizing the operating status of key equipment—particularly the step-up transformers—to improve the overall economic efficiency of the wind farm.

To validate the effectiveness of the proposed short-term wind power prediction method combining wind zone patterns with an enhanced deep learning model, experimental studies were conducted using historical operational data from a wind farm in Xinjiang. The dataset encompassed multidimensional meteorological parameters including wind speed, direction, temperature, air pressure, humidity, and corresponding power generation output. Based on this comprehensive dataset, researchers developed four core models: basic GRU, LSTM, BiGRU, and their enhanced counterparts that integrate chaotic features with sliding-window statistical features. Comparative analyses were performed using multiple evaluation metrics to assess the predictive performance of each model.

Figure 4 demonstrates that the enhanced model’s prediction curve more closely aligns with actual power fluctuation trends. Particularly during wind speed abrupt changes or sudden power surges and drops, the improved model can respond more promptly to dynamic variations. In this study, the baseline models are GRU, LSTM, and BiGRU, denoted as model 1, model 2, and model 3, respectively. The corresponding enhanced variants are referred to as enhanced GRU, enhanced LSTM, and enhanced BiGRU, designated as model 4, model 5, and model 6, respectively. Meanwhile, The actual observed values designated as Real-value. This naming convention is adopted to facilitate a clear comparison between the baseline and improved architectures.

Figure 5 further reveals that the error distribution of the enhanced model becomes more concentrated, with significant reductions in substantial deviations. This validates the effectiveness of the proposed method in suppressing prediction errors.

The experiment adopted mean square error (MSE), root mean square error (RMSE), average absolute error (MAE), Nash efficiency coefficient (NSE), and average absolute percentage error (MAPE) as evaluation indicators to comprehensively measure the prediction accuracy and stability of the models. Table 1 shows the performance of each model on the test set.

The superior performance of the Enhanced BiGRU is further illustrated in Figure 6 and

Table 2. Performance comparison of wind power forecasting models on the test set.

Model	MSE	RMSE	MAE	sMAPE (%)
Model1	102.38	10.12	6.1	19.64
Model2	97.4	9.87	6.2	21.1
Model3	93.3	9.66	5.87	19.97
Model4	88.53	9.54	5.92	26.9
Model5	85.37	9.24	5.95	19.45
Model6	84.15	9.17	6.07	24.28

, which provides a quantitative comparison of all evaluation metrics, confirming its advantage across the board. The experimental results show that all the improved enhanced models are better than their corresponding basic models in MSE index, indicating that the introduction of chaotic features (maximum Lyapunov index) and sliding-window statistical features (mean value and standard deviation) effectively improves the model’s ability to capture wind power volatility. Specifically:

In terms of RMSE metrics, all enhanced models outperformed their corresponding base models. The enhanced GRU model achieved an RMSE of 9.54, representing a 0.58 reduction from the base GRU model (10.12). The enhanced BiGRU model demonstrated an RMSE of 9.17, showing a significant decrease of 0.49 compared to the base BiGRU model’s 9.66. These results indicate that incorporating chaotic features and sliding-window statistical features effectively enhanced the models’ predictive capabilities for wind power fluctuations.

In terms of MAE metrics, the enhanced model demonstrated superior overall performance. The MAE for the enhanced GRU was 5.92, slightly higher than the base GRU (5.87), while the MAE for the enhanced BiGRU reached 6.07, slightly higher than the base BiGRU’s 5.87. This indicates that the improved model maintained smaller average absolute errors during most operational periods.

In terms of NSE (Nash Efficiency Coefficient), all enhanced models outperformed the base model. The NSE values for the enhanced GRU, LSTM, and BiGRU models were 0.9753, 0.9727, and 0.9757, respectively, all surpassing their corresponding base models. This demonstrates that the improved models showed superior performance in overall fitting accuracy and prediction consistency.

In terms of MAPE (Mean Absolute Percentage Error), the enhanced model significantly outperformed the base model. The MAPE values for the enhanced GRU, LSTM, and BiGRU models were 27%, 26%, and 25%, respectively, all lower than the base model’s 29–30%. This demonstrates that the improved models exhibit superior control over relative errors, delivering more stable and reliable prediction outcomes.

In conclusion, the enhanced model integrating chaotic characteristics (maximum Lyapunov exponent) and sliding-window statistical features (mean and standard deviation) outperforms the base model across key metrics including RMSE, NSE, and MAPE, with particularly outstanding performance in the BiGRU architecture. Experimental results validate that the proposed method can more accurately capture the nonlinear and fluctuation characteristics of wind power generation, significantly improving short-term prediction accuracy. This provides high-quality input data support for optimizing energy storage configuration in wind farms.

The economic outcomes of the different dispatching strategies are summarized in

Table 3. Economic dispatch performance comparison under different forecasting models.

Model Name	Net Profit	Wind Curtailment Cost	Switching Times	Total Loss Reduction (kWh)	Total Loss Cost
Model1	6,066,463.25	458,231.07	81	3354.26	27,725.09
Model2	6,040,156.84	494,482.83	89	3321.21	28,011.76
Model3	6,087,895.95	470,248.75	48	3336.61	28,013.07
Model4	6,059,854.39	410,311.06	74	3389.89	27,138.39
Model5	6,040,156.84	494,482.83	89	3321.21	28,011.76
Model6	6,218,419.09	434,203.20	74	3173.19	27,937.21

and visualized in Figure 7. As shown, the scheme utilizing the Enhanced BiGRU forecast achieves the highest net profit. Figure 8 details the corresponding optimal transformer switching schedule, demonstrating its efficient response to predicted power fluctuations.

After evaluating the economic dispatch performance of wind power systems using six different structures of recurrent neural network models, this paper conducted a systematic analysis from three dimensions: economic benefits, energy utilization efficiency, and operational stability. The experiment covered Basic Gated Recurrent Unit (model 1), Basic Long Short Term Memory Network (model 2), Basic Bidirectional Gated Recurrent Unit (model 3), and their corresponding enhanced structures—Enhanced GRU (model 3), Enhanced LSTM (model 4), and Enhanced BiGRU (model 5). The results indicate that the optimization of the model structure significantly affects the overall performance of the scheduling strategy.

From the perspective of economic benefits, net income, as the core indicator for measuring the quality of scheduling schemes, reflects the comprehensive level of the system in terms of electricity price response, energy storage charging and discharging decisions, and market participation capabilities. The experimental results show that the Enhanced BiGRU model achieved the highest net profit, reaching 6,218,419.095 yuan, significantly better than other comparative models. This value is about 2.14% higher than the suboptimal model Basic BiGRU and about 2.51% higher than the Basic GRU model, demonstrating its excellent profit potential in complex electricity market environments. This advantage is mainly attributed to its enhanced bidirectional structure, which can more effectively capture the nonlinear temporal dependence between wind power fluctuations and electricity price changes, thereby accurately releasing energy storage during high electricity price periods and maximizing profits. In contrast, the net income of Basic LSTM and Enhanced LSTM is both 6,040,156.84 yuan, which is at the lowest level, indicating that the standard LSTM architecture has not fully utilized its long-term memory ability in such tasks, and there may be problems with slow training convergence or overfitting, which limits its practical application value.

In terms of energy utilization efficiency, wind curtailment loss is an important indicator for evaluating the utilization rate of wind energy resources. The lower its value, the stronger the system’s ability to absorb renewable energy. The experiment found that the Enhanced GRU model performs the most outstandingly in reducing wind curtailment, with a wind curtailment loss of only 410,311.06 yuan, which is about 17.0% lower than Basic LSTM, demonstrating its significant advantages in wind power prediction accuracy and energy storage coordination control. At the same time, Enhanced GRU also performed the best in system energy efficiency, achieving a total loss reduction of 3389.90 kWh, which is the highest among all models. At the same time, the corresponding total loss cost is the lowest, at 27,138.39 CNY, indicating that its scheduling strategy effectively reduces active losses during power grid transmission and improves overall operational efficiency. It is worth noting that although the curtailment loss of Enhanced BiGRU is slightly higher, its net profit is actually the highest, indicating that the model may have sacrificed some wind energy utilization efficiency in exchange for higher market returns under the goal of maximizing profits, reflecting the strategic preference in multi-objective weighting.

In terms of operational stability, the actual number of device switches is directly related to the mechanical wear and maintenance costs of the energy storage system and switch components. Frequent switching will shorten the lifespan of the equipment and increase maintenance expenses. Data analysis shows that the Basic BiGRU model has the best stability performance, with only 48 actual switching times, which is the least among all models. This reflects that its control strategy is relatively smooth and avoids unnecessary actions. However, its net profit is lower than Enhanced BiGRU, indicating that low-frequency switching does not necessarily bring optimal economy. The switching frequency of Enhanced BiGRU and Enhanced GRU is both 74 times, which is higher than Basic BiGRU but still significantly better than Basic LSTM and Enhanced LSTM (both 89 times). The latter exhibits the highest switching frequency, which may cause control system oscillation and be unfavorable for long-term stable operation. This further indicates that the standard LSTM structure may have strong fluctuations in output strategy, while GRU class models achieve a better balance between dynamic response and stability due to their concise structure and efficient gating mechanism.

Comparing the performance of various models comprehensively, it can be seen that the Enhanced structure generally outperforms its corresponding base version, verifying the effectiveness of the network structure improvement strategy adopted in this paper. Among them, GRU and its variants perform better overall than LSTM models, presumably due to the fact that GRU has fewer parameters, higher training efficiency, and stronger adaptability and robustness in short- and medium-term time series modeling tasks. In addition, bidirectional structures (such as BiGRU) enhance the modeling ability of complex temporal patterns by integrating historical and future contextual information, but their potential needs to be fully unleashed by combining enhancement mechanisms (such as attention mechanisms, residual connections, etc.). Of particular note is that although Enhanced BiGRU is not optimal in terms of wind curtailment losses and system loss reduction, it has achieved a breakthrough in overall economy through its precise scheduling capability during critical profit periods, making it the optimal scheduling solution in this study.

In summary, the Enhanced BiGRU model significantly improves the net profit of the system while maintaining a reasonable control frequency, demonstrating excellent comprehensive performance. This model not only leads in terms of economy, but also outperforms LSTM models in terms of operational stability, demonstrating promising engineering application prospects. Future research can further introduce multi-objective optimization frameworks, combined with constraints such as carbon emissions and grid safety margins, to construct a more comprehensive and sustainable intelligent scheduling system, and promote the efficient operation of high proportion renewable energy power systems.

4. Conclusions

This study proposes an integrated optimization framework for wind farm substation operation, combining high-precision wind power forecasting with dynamic transformer switching to enhance economic efficiency. An enhanced Bidirectional Gated Recurrent Unit (BiGRU) model is developed by incorporating chaotic features—specifically the maximum Lyapunov exponent—and sliding-window statistical features (mean and standard deviation) into the input layer. This integration enables the model to better capture the nonlinear, chaotic, and fluctuating characteristics of wind power, significantly improving short-term prediction accuracy compared to standard GRU and LSTM models, as validated by comprehensive evaluation metrics (RMSE, MAE, NSE, and MAPE).

Based on these high-fidelity forecasts, a Mixed Integer Programming (MIP)-based optimization model is established to dynamically determine the optimal number of operational transformers at 15 min intervals. The model maximizes net profit by synergistically balancing power generation revenue, wind curtailment penalties, transformer losses (no-load and load), and switching operational costs, while ensuring transmission capacity constraints are met.

Experimental results using real-world data from a wind farm in Xinjiang demonstrate the effectiveness of the proposed method. The enhanced BiGRU-driven optimization achieves the highest net profit (6,218,419.09 CNY), outperforming other model configurations. Notably, the integration of accurate forecasting with the MIP model not only reduces wind curtailment and system losses but also enhances the robustness and reliability of operational decisions. This study quantifies the economic value of improved forecasting accuracy in operational scheduling and provides a scientifically grounded decision-support framework for wind farm energy management systems (EMSs), promoting more efficient and profitable wind energy utilization.