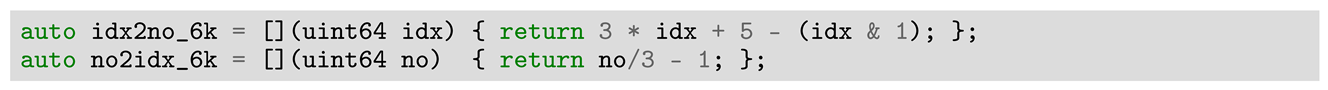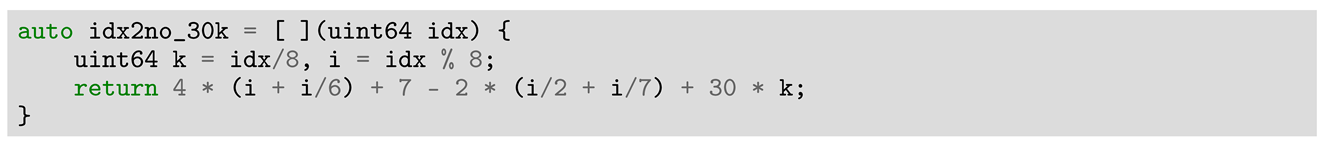3.1. Generic Considerations
Figure 2 depicts the generic sieving process for a modern, fast sieve. First, the pre-sieving phase initializes the list of root primes and the pre-sieved bit pattern. Then, the sieving continues segment by segment, in parallel. There is much to discuss for each component involved in this process. We have already covered the main data structures (seed and root primes, pre-sieved pattern, sieve buffer). This section will focus on the primary tasks involved in the sieving process.
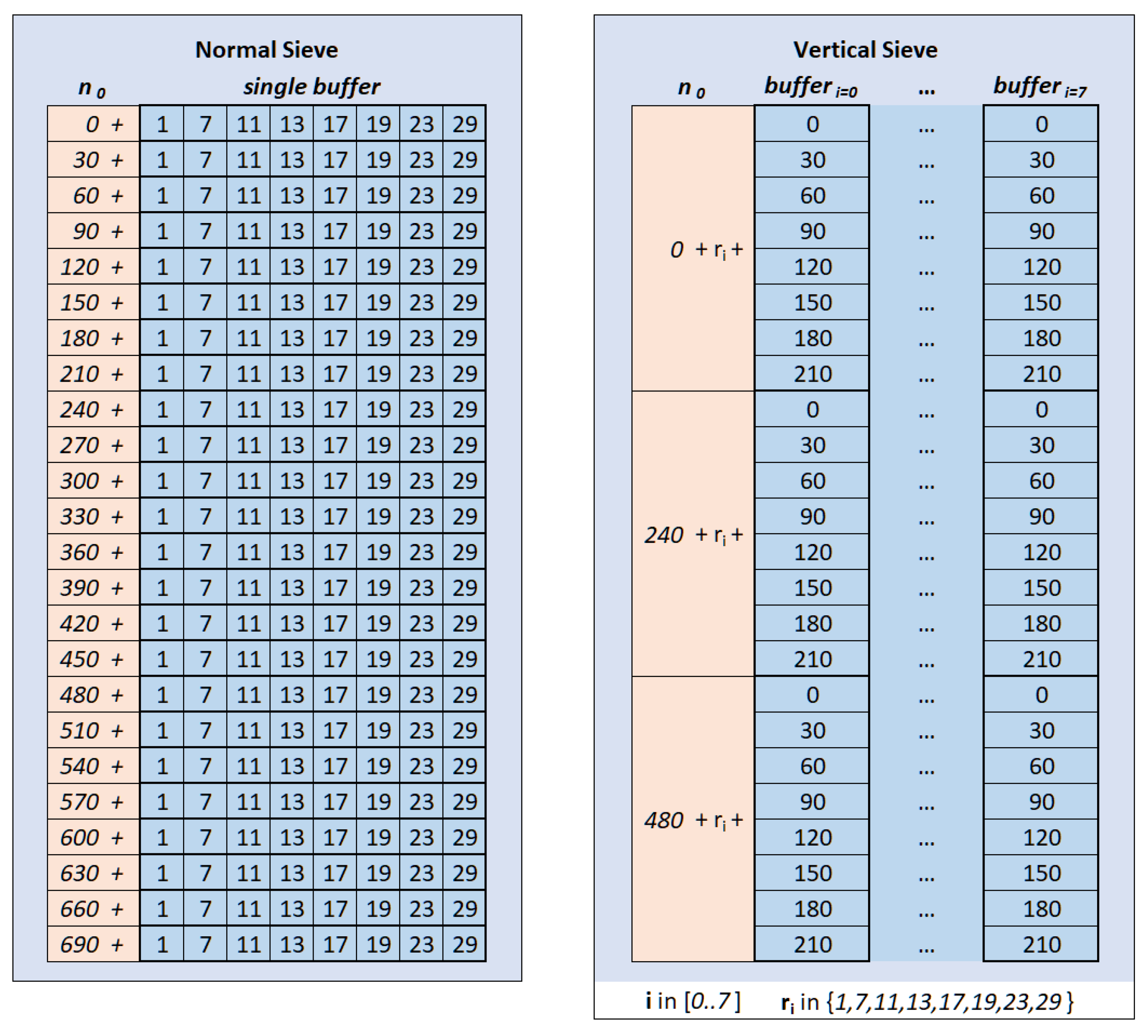
The simplest tasks might seem to be generating the bit pattern and initializing the sieve buffer with it. However, the initialization is not straightforward, especially when using more complex bit compression schemes, such as the pattern. The approach shown earlier is still viable but somewhat heavier. Ideally, one should superimpose the pre-sieved pattern by copying the bit pattern memory block onto the sieve, over and over, until the end of the sieve buffer. But, with bit compression and such a non-uniform pattern, there are eight pattern variants (each shifted 1 per bit), leading to a performance gain when replacing numerous bitwise operations with relatively few contiguous memory copies.
Nevertheless, this gain comes at the cost of increasing the memory footprint of the bit buffer by eight times. While this increased memory usage might be negligible up to prime 13, it becomes substantial with larger primes. For instance, adding prime 17 increases the memory footprint to 2 GB, and prime 19 to 4 GB. Despite this, the performance gains typically justify the increased memory usage, and it should not pose a problem with a segmented algorithm on modern computers.
The other part of the pre-sieving process, the small sieve, can also be implemented in a variety of ways. Sieving for those 203+ million primes is not immediate. Some implementations handle the small sieve separately from the main sieve, potentially using different algorithms or parallelization strategies. They may even restart the main sieve from scratch, although the sieving is already performed up to . Others may use the exact same sieve for both stages, dealing with the added complexity required to differentiate root primes from the rest of the output.
The bulk of the process occurs during the segment sieving phase. This phase is typically executed using a combined parallel–incremental approach; segments are allocated to execution threads and processed in parallel. Within an execution thread, the segment is divided into chunks according to L1 and L2 cache sizes and processed iteratively, sequentially, chunk by chunk. Segmentation is employed for parallelization, while incremental processing is used to maximize cache intensity.
Since sieving is highly sensitive to cache efficiency, maintaining an optimal cache-to-thread ratio is crucial. Usually, implementations employ a 1:1 ratio relative to the available native threads. However, it can be experimentally determined that a slightly higher ratio may be optimal, as modern CPUs employ sophisticated cache management strategies.
After sieving, each thread processes its sieved chunk to generate or count the primes. This is a uniform, linear process and is less dependent on intentional cache strategies because it parses the buffer unidirectionally in read and write operations. Prefetch mechanisms for sequential memory access will almost always keep the relevant data in cache, resulting in minimal latency.
If the goal is solely to count the primes, additional threads can be launched to process smaller pieces of the chunk. This approach can be significantly faster than having the main segment thread perform the task single-threadedly. To reduce overhead, counting threads can be kept idle and then released simultaneously for counting using a simple synchronization mechanism.
If the primes need to be generated in order, a multi-threaded approach introduces some complications, but the overall performance can still be improved with the use of extra threads.
The method described here alternates between sieving and counting. However, these two tasks differ significantly in how they utilize CPU pipelines and their data access patterns. Therefore, overlapping them may lead to better utilization of CPU resources. By concurrently performing sieving and counting, the CPU can be more efficiently exploited, as it can handle the distinct demands of each task in parallel, potentially reducing idle times and improving overall performance. Such a strategy is exemplified in [
24], using a so-called tic-toc mechanism which involves two distinct sieving buffers that are processed alternately by the working threads; while one buffer is being sieved, the other buffer is being counted (tic), then the buffers are switched (toc). Here is the gist of the main loop in such an implementation:
![Algorithms 17 00291 i009 Algorithms 17 00291 i009]()
The counting loop is practically identical, except its states are initialized with 1. Overlapping the two working patterns and fine-tuning the number of sieving and counting threads may result in a better utilization of CPU pipelines.
To conclude the process, the final task is to collect and organize the many lists of primes (one for each segment), which are not necessarily produced in order. This problem is essentially identical to the one encountered within an individual segment if parallel counting is employed. Given that we may need to address the same issue here, it is straightforward to use the same solution in both places.
One effective solution is to have an additional parallel thread that waits for segments/chunks to produce their results and then processes them in the correct order as they become available. This approach ensures that the primes are gathered and ordered efficiently, leveraging parallel processing to maintain performance.
Finally, for testing or benchmarking, there arises the question of how to handle each generated prime. The task must be lightweight enough to avoid skewing the performance metrics, yet substantial enough to ensure the compiler actually computes the prime and passes it to a designated location. Here is our solution of choice for this problem; it works without congestion in a multi-threaded execution, the index does not require any limit check (255 + 1 = 0), and it allows visibility of the last 256 primes generated and facilitates prime validation when single-threaded:
3.2. Massive Parallel Sieving
A highly effective strategy for managing the immense computational demands of sieving is to employ a GPGPU paradigm, leveraging the substantial throughput capabilities of GPU devices. To achieve this, it is essential to utilize a framework or SDK that abstracts the complexities and diversity of specific GPUs, providing a generic API. Prominent options include CUDA (perhaps the most widely used framework today, but limited to NVIDIA hardware), Metal (specific to Apple devices), Vulkan (a newer contender in the GPGPU area, though not yet widely adopted), and OpenCL.
OpenCL is a mature platform currently at version 3, supported by major vendors such as NVIDIA, AMD/Xilinx, and Intel, as well as many smaller players. OpenCL also targets devices like FPGAs and various niche hardware from companies like Qualcomm, Samsung, and Texas Instruments. Its practical utility is significant, given that an OpenCL program can run on any OpenCL platform, including most CPUs. Due to its extensive support and versatility, OpenCL is particularly useful. Many professionals are already familiar with CUDA, so this approach will not be used here; instead, GPGPU algorithms will be exemplified using the C++ wrapper (
https://www.khronos.org/opencl/assets/CXX_for_OpenCL.html, accessed on May 2024) of OpenCL (
https://www.khronos.org/opencl/, accessed on May 2024).
For those familiar with CUDA, we must emphasize that OpenCL and CUDA are quite similar in essence; both are parallel computing platforms designed to harness the computational power of GPUs for general-purpose computing tasks, providing frameworks for parallel computing on GPUs. They allow developers to write programs that execute in parallel on the GPU, taking advantage of the massive parallelism inherent in GPU architectures. Both OpenCL and CUDA use a similar programming model based on kernels (small functions that are executed in parallel across many threads on the GPU) and provide memory models tailored for GPU architectures (different types of memory, e.g., global, local, constant, with specific access patterns optimized for parallel execution). Both platforms organize computation into threads and thread blocks (CUDA) or work-items and work-groups (OpenCL). These units of parallelism are scheduled and executed on the GPU hardware.
The initial tendency when addressing a sieving problem using GPGPU might be to adopt a simple method, where a kernel is launched for each value to be processed. Typically, this is not advisable, because such an approach struggles to handle race conditions effectively: when multiple threads execute simultaneously without proper synchronization, race conditions occur, where the threads attempt to modify the same variable concurrently (in the context of sieving algorithms, if each GPU thread is assigned to mark multiples of a specific prime number, threads may interfere with each other when updating shared data structures like arrays, which can lead to errors or inconsistent results).
Such approach also fails to make use of the GPU’s local data cache: GPUs are most efficient when they can leverage their fast, local memory (like shared memory among threads in a block) instead of relying on global memory, which is slower to access. A simplistic approach where each thread deals independently with marking composites may not effectively utilize this local memory. Algorithms optimized for GPUs often try to maximize data locality to reduce memory access times and increase throughput.
Moreover, launching a separate kernel for each composite to be marked is typically inefficient. It involves considerable overhead in terms of kernel launch and execution management. Efficient GPGPU algorithms usually minimize the number of kernel launches and maximize the work performed per thread, often by allowing each thread to handle multiple data elements or by intelligently grouping related tasks.
To optimally exploit the hardware resources we should implement the sieving algorithm at hand with non-trivial kernels and split the sieving process between the host CPU and device GPU, as in Algorithm 1.
| Algorithm 1 Generic CPU-GPU cooperation for sieving |
This algorithm splits work between host and device(s), using the GPU(s) mainly for sieving itself.Initialization • Initialize the GPU device, create a context, allocate memory buffers, and compile/load the kernel code onto the GPU. • Set up any necessary data structures and parameters for the sieve algorithm. • Presieve both host- and device-side tasks. Splitting presieve tasks between the CPU and GPU is not trivial: in the early days, transferring data from the host to the device was slow, so it was often faster to generate, for example, root primes directly on the device; new hardware minimizes such issues, so it is best to conduct some benchmarking before deciding where to perform each task. Launching Parallel Threads • The main thread will coordinate the sieving process and handle communication between the CPU and GPU. This thread will manage the overall control flow of the algorithm and coordinate the execution of kernels on the GPU. • Start a parallel thread or process on the host for generating and counting the primes. This thread will work on buffers sieved by the kernel; the thread is initially idle, waiting for the first buffer to process the primes. Loop Kernel Executions • Divide the range of numbers into segments or chunks, each corresponding to a separate interval to sieve for prime numbers. • Iterate over each segment and perform the following steps: a. Launching the Kernel: - Prepare any necessary parameters or buffers to the kernel. - Launch the GPU kernel responsible for sieving prime numbers within the current segment. b. Waiting for the Kernel to complete the sieving: - Wait for the GPU kernel to complete its execution. c. Downloading Sieved Buffer: - Wait for the previous counting step (if any) to finish. - Transfer the results (sieved buffer) from the GPU back to the CPU. - This buffer contains information about which numbers in the current segment are primes. - Release the semaphore or whatever sync mechanism in place, in order to signal the parallel counting thread that it can start counting. d. Generating Primes (this step is executed in parallel with all others): - On the parallel CPU thread(s), wait to receive a new sieved buffer. - Process the sieved buffer to identify and generate the prime numbers within the current segment. - This step involves parsing the buffer and extracting the prime numbers based on the sieve results. - At the end of counting, release the semaphore or whatever sync mechanism to signal the main thread that it can download the new buffer from the GPU. - Go back to waiting for the new buffer or exit if finished. e. Repeating the Process: - Repeat steps a–c and d for each remaining segment until the entire interval is exhausted. Completion and Cleanup • Once all segments have been processed and the prime numbers have been generated, finalize any necessary cleanup tasks. • Release GPU resources, free memory buffers, and perform any other necessary cleanup operations.
|
To exemplify a non-trivial kernel, in Algorithm 2, we have a straightforward kernel for a basic OpenCL implementation of the Sieve of Sundaram on a GPU.
| Algorithm 2 Sieve of Sundaram—basic kernel |
|
This basic implementation still uses only global memory, but what is particularly interesting is that, inserting before the kernel code some header code like the following:
We can also compile and use this kernel on the normal CPU, thus helping with the development process, as compile errors are signalled immediately and most of the logical errors can be debugged using the IDE debugger, which is much easier; of course, more subtle bugs that are specific to a GPU environment will still have to be investigated natively, but in any case, the development process may accelerate significantly. Here is an example for such simulation code using the kernel above as such, but also prepared to use other experimental kernels:
![Algorithms 17 00291 i014 Algorithms 17 00291 i014]()
The problem with such non-trivial but basic implementations of sieving algorithms is that the internal mechanics of sieving are not linear. Practically all sieves are executed in a nested loop technique; the outer loop iterates a primary parameter, while the inner will iterate a second parameter and the number of iterations varies significantly, usually non-linearly. Yet, while the kernel code exemplified above tries to obey the basic rules of GPU programming—avoid complex operations and 64-bit data whenever possible, and do not count too much on the optimizer—the resulting performance is horrendous; although we exploit thousands of native GPU threads, the performance may very well be worse than a similar basic one-threaded incremental CPU implementation.
There are some generic explanations involving the lower frequency of the GPU cores, the overall cache efficiency of a CPU, and generally speaking, the huge differences in performance when comparing one-to-one a CPU thread to a GPU one, but the fundamental explanation comes from the fact that those thousands of GPU “threads” are not really independent threads; they correspond with the work-items in OpenCL and are grouped in wavefronts (or warps for CUDA), each consisting of 32 or 64 threads that run in sync. Each thread in the wave will not end until the last thread in the wave has finished all the work, thus keeping the whole CU (compute unit) occupied. Because we are using a stripping approach for domain segmentation, the thread lengths vary significantly within a warp, so the result is that, although the vast majority of threads have finished, a very small number of threads keep everything stalled, and those are the work-items that include
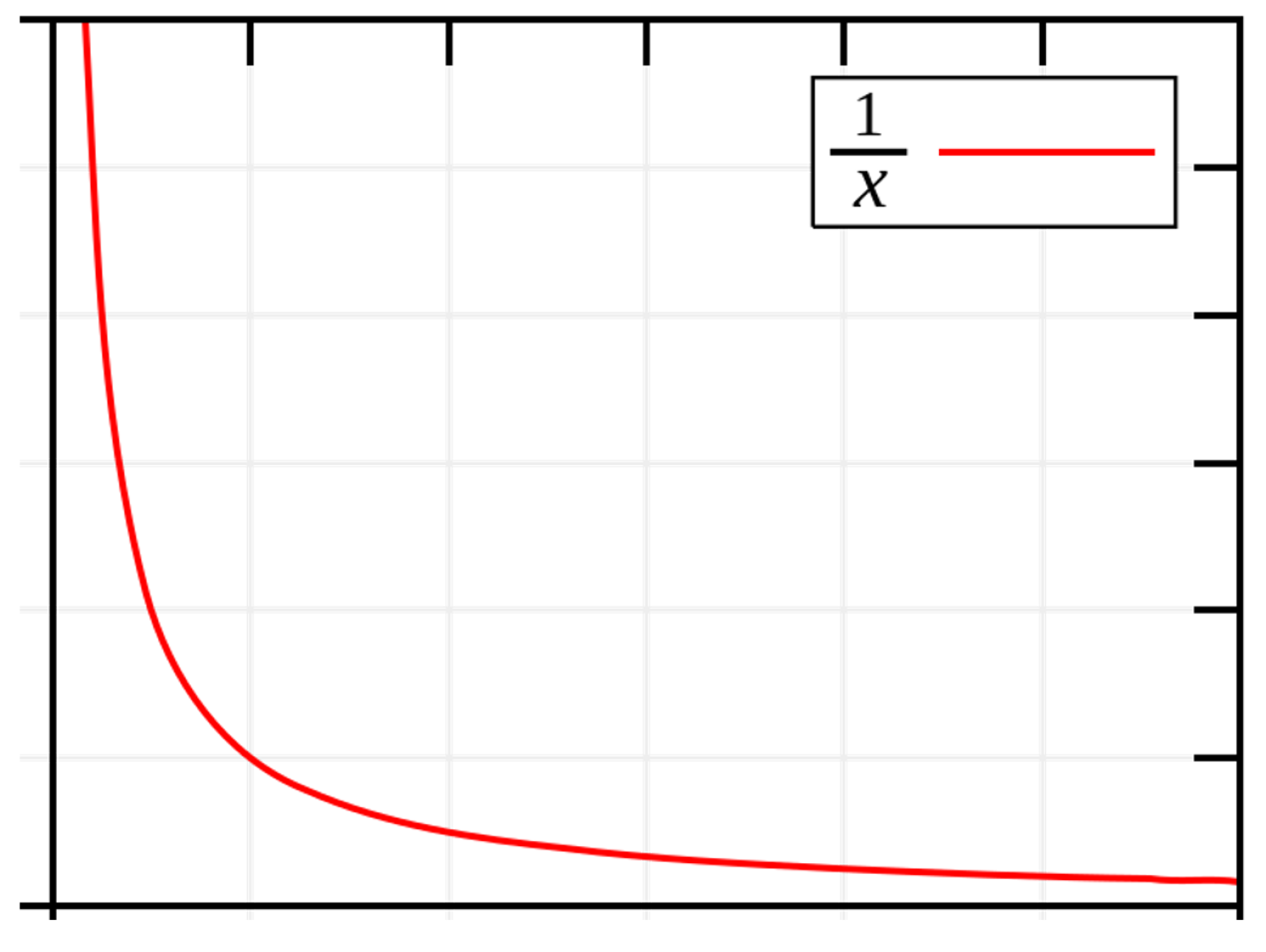
is with very small values. While for
i above 100, there are only several hundred iterations in the inner loop, for values bellow 10, there are many thousands, something qualitatively similar to function
, as in
Figure 3. (This particular function—
—is chosen simply because it is the most well known among those with a similar profile, only to provide an idea of the curve’s profile. The actual function is more complex, but qualitatively, the profile is similar).
Although most of the work is completed in the first hundred milliseconds, a small number of threads will keep working to process all the js for those small is; thus, because the GPU thread is significantly weaker than a CPU thread, we obtain lower performance overall.
The real art in devising a parallel algorithm is to find a segmentation method for the problem domain that is able to evenly distribute the computation effort between segments; basically the goal is to flatten the curve, in order to achieve the best possible occupancy of the GPU. One solution here is to create two different kernels: one very similar to the simple one used above, which works quite well for big values of
i, and another one for very small
is. The second kernel will transpose the problem, iterating on
j in the outer loop, thus surfacing the depth of the inner loop and flattening the curve like in
Figure 4. Such a dual big–small-transposed approach will have significantly better results.
Most of the time, a better solution is to use an approach similar to the one for the corresponding incremental/segmented sieve and exploit the local data cache of the GPU CU; mapping each CU to a segment and targeting the local data cache size for the segment buffer size, the curve will be relatively leveled naturally. The overhead for positioning in each segment is mitigated by the fast access of the cache, resulting normally in even better timings. The gist of such a segmented kernel that exploits local a CU cache is exemplified for Sundaram in Algorithm 3.
| Algorithm 3 Sieve of Sundaram—segmented kernel |
Barriers are used to guard local buffer initialization and upload. Optimizing the positioning component (determining the initial i and j values for each segment) was very important. The outer loop is descending for simplified logic.
|
Once we have a decent kernel, the last step in optimizing the sieve is to parallelize the final phase of the sieving process, the actual counting/generation of primes, so that the counting is not longer that the sieving, which should not be difficult; final timings of such an implementation will be driven exclusively by the duration of sieving itself, as executed on the GPU, plus the transfer of data buffers between host and device, which is not negligible. Sometimes, it may be faster to generate initial data directly on the GPU and avoid any data transfer from the host to the device, although modern technologies like PCIe 4/5 and Base Address Register (BAR) Resizing (or Resizable BAR) have improved this issue a lot.
The performance may be further improved by flattening the curve inside each segment using the cutoff–transpose technique, as described above, or avoiding unnecessary loops because, for larger
is, only a small number of
js will actually impact a certain segment, and a bucket-like algorithm [
26] may benefit the implementation.
But perhaps the hardest problem is to avoid collisions between local threads, especially when using on the GPU buffer a 1bit approach for data compression, as we use on the normal CPU; on the GPU, this is particularly difficult, as one has to be sure that in the same workgroup cycle there are not two work items (local threads) that will try to update the same byte, as this will result in memory races that will keep only the last data value and lose the others.
When working with uncompressed buffers (1 byte per value), this issue is not important anymore for Eratosthenes and Sundaram families of sieves, because here, if the values are updated, they are always updated in the same direction: changing from 0/false to 1/true (or vice versa); memory races are not an issue here, as the final result will be correct irrespective of which thread managed to make the update.
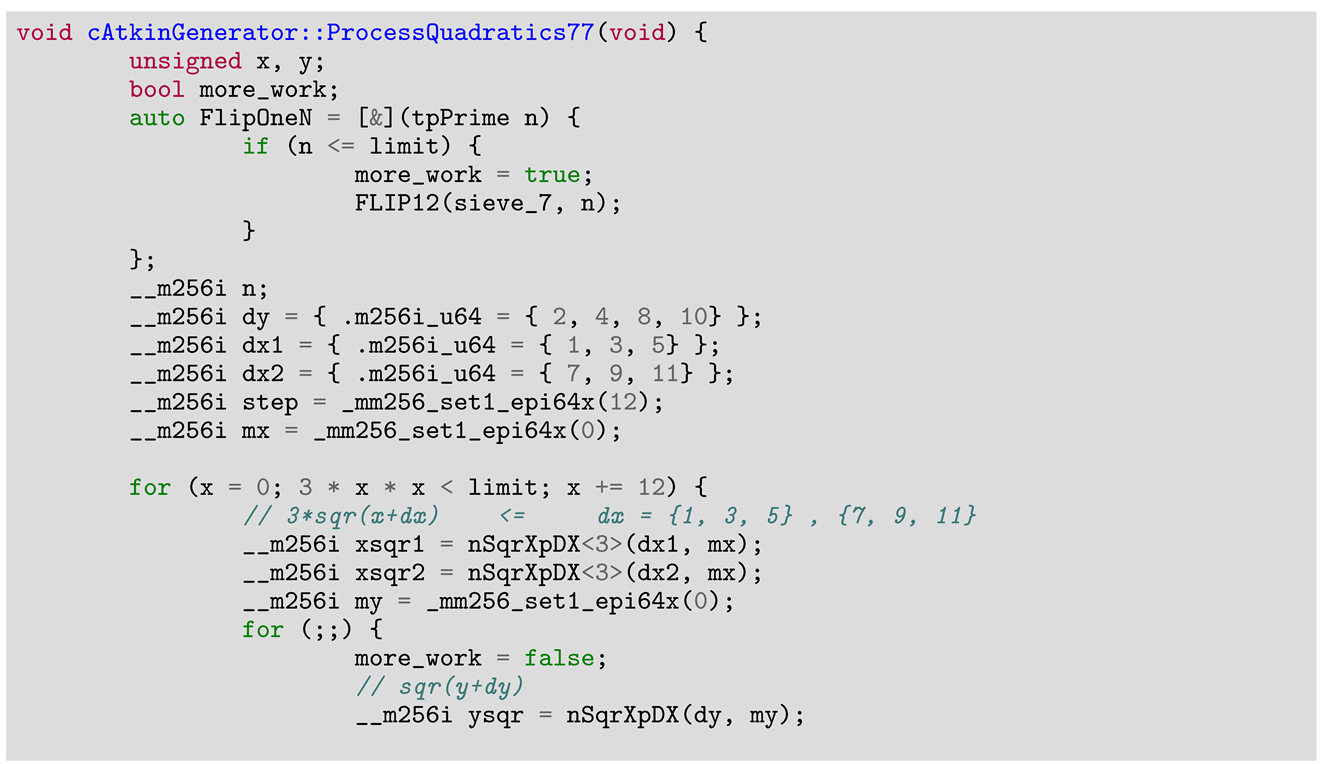
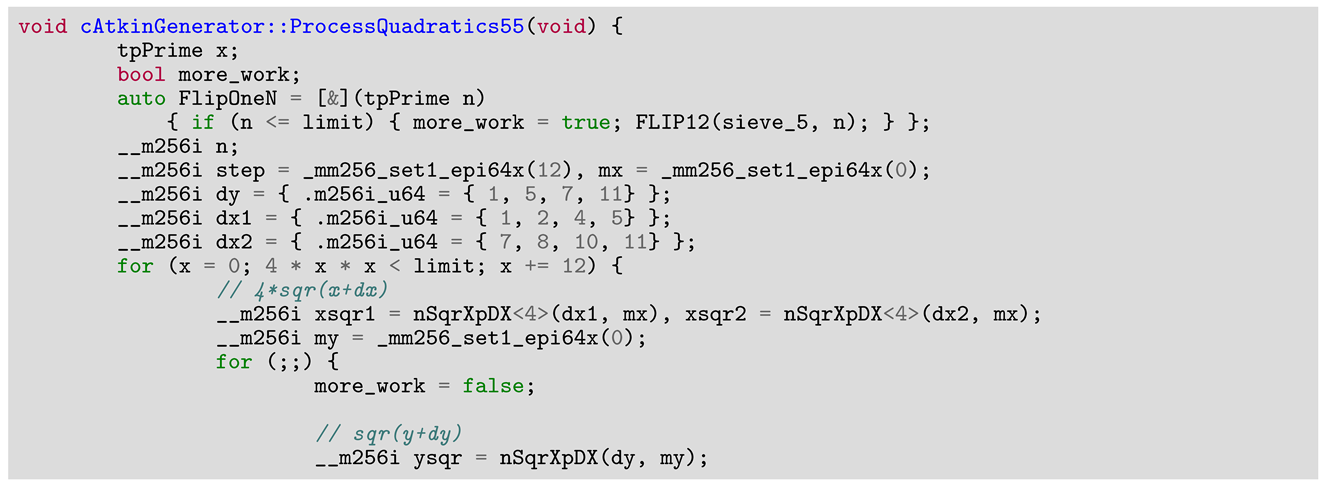
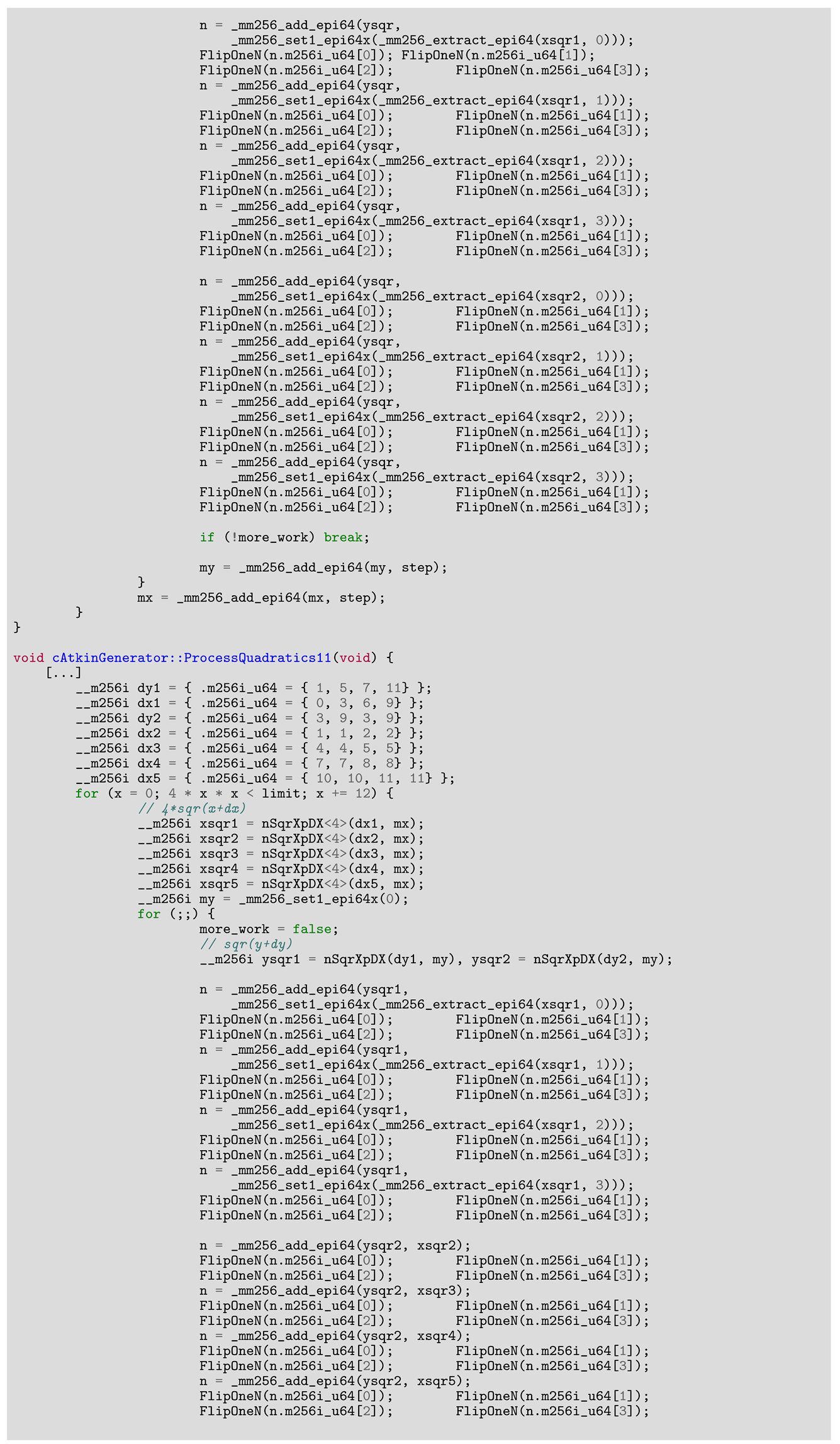
For the Atkin algorithm, the outcome is contingent on the starting value, and concurrent operations by two or more threads can lead to incorrect results. For instance, in Atkin, if the initial value is 0 and two threads modify it one after the other, the first thread will read 0 and change it to 1, while the second thread will read 1 and switch it back to 0. However, if both threads operate at the same time, each will read the initial value of 0 and both will write back 1, resulting in an erroneous final outcome. And this problem is valid for all sieve families when dealing with bit compression.
For non-segmented variants the problem is relatively easier to solve, for example, using larger strides (as in Buchner’s example mentioned earlier), thus ensuring that each thread will work on a separate byte. The solutions for this problem are not at all trivial. One illustration of such an efficient approach is given in
CUDASieve, a GPU-accelerated C++/CUDA C implementation of the segmented sieve of Eratosthenes [
27]; unfortunately, we could not find other detailed examples of such mechanisms.