3D Reconstruction Based on Iterative Optimization of Moving Least-Squares Function

Abstract

Three-dimensional reconstruction from point clouds is an important research topic in computer vision and computer graphics. However, the discrete nature, sparsity, and noise of the original point cloud contribute to the results of 3D surface generation based on global features often appearing jagged and lacking details, making it difficult to describe shape details accurately. We address the challenge of generating smooth and detailed 3D surfaces from point clouds. We propose an adaptive octree partitioning method to divide the global shape into local regions of different scales. An iterative loop method based on GRU is then used to extract features from local voxels and learn local smoothness and global shape priors. Finally, a moving least-squares approach is employed to generate the 3D surface. Experiments demonstrate that our method outperforms existing methods on benchmark datasets (ShapeNet dataset, ABC dataset, and Famous dataset). Ablation studies confirm the effectiveness of the adaptive octree partitioning and GRU modules.

1. Introduction

Three-dimensional reconstruction is a fundamental task in computer vision and computer graphics, with applications spanning virtual reality, autonomous driving, and many other fields. Point clouds, as one of the common input representations in 3D reconstruction tasks, offer flexibility and ease in expressing the surface information of target shapes. However, point clouds may exhibit noise interference, which makes it more difficult to generate accurate 3D surfaces from sparse point clouds compared to dense ones. Therefore, a key challenge in 3D reconstruction is how to utilize sparse point clouds to generate accurate 3D surfaces.

To effectively enhance the accuracy of 3D surface generation from sparse point clouds, recent research has primarily focused on deep-learning approaches. For instance, as a typical 3D reconstruction method, deep-learning signed distance function (DeepSDF) [1] regards the target shape as a whole, obtains the feature information of the global shape through the automatic encoder, and obtains the triangular surface under the mesh extraction of marching cubes [2]. This method is better at dealing with simple shapes that are similar to smooth shapes, but it is difficult to deal with complex shapes with fine structures, such as shapes in the Famous dataset; deep-learning local shapes (DeepLS) [3], unlike DeepSDF, utilizes an autoencoder to extract local shape features, effectively mitigating the limitations of DeepSDF. This method can effectively alleviate the disadvantages of DeepSDF. However, the autoencoder is executed within the voxel, and it is difficult to deal with the situation of the voxel boundary, resulting in the discontinuity of the generated three-dimensional surface. Recently, DeepMLS [4] approximates the moving least-squares function (MLS) [5] as an implicit function to obtain the signed distance function (SDF). Using the data structure of the octree, the global shape is divided into multiple voxels (octrees) of the same unit size. The convolutional neural network is performed in the least octree to extract features. The MLS point set is obtained by the shallow multi-layer perceptron (MLP), and the SDF is obtained under the action of the moving least-square function. This method transforms the uneven point cloud into a uniform MLS point cloud distributed near the shape surface, which effectively alleviates the problem of unevenness and noise of the original point cloud. However, the octree partitioning method employed in this approach leads to storage memory inefficiency, and local voxel features may induce discontinuities in the generated surface.

In the paper, we present further enhancements to the DeepMLS method. Firstly, we leverage an adaptive octree based on cosine similarity to partition the target shape point cloud from global to local, obtaining local shapes at different scales. Secondly, by introducing the gated recurrent unit (GRU) [6] module, voxel features of different scales are inherited in octrees of different depths. This crucial step facilitates the iterative optimization of local shape features and integrates local and global feature information. Under the guidance of this iteratively optimized GRU module, optimized shape features are generated. Subsequently, accurate and interpretable MLS point clouds are generated through the processing of an MLP. Finally, the signed distance function is approximated by the moving least-square function, and the 3D surface is extracted by the marching-cubes method. In summary, our method implements GRU modules in octrees of different depths so that the final shape features contain local information and global information. Through the feature iteration and optimization of different scales, the MLS point set generated after entering the MLP is more suitable for the shape surface and easier to express the details of the shape.

Our method offers several key advantages:

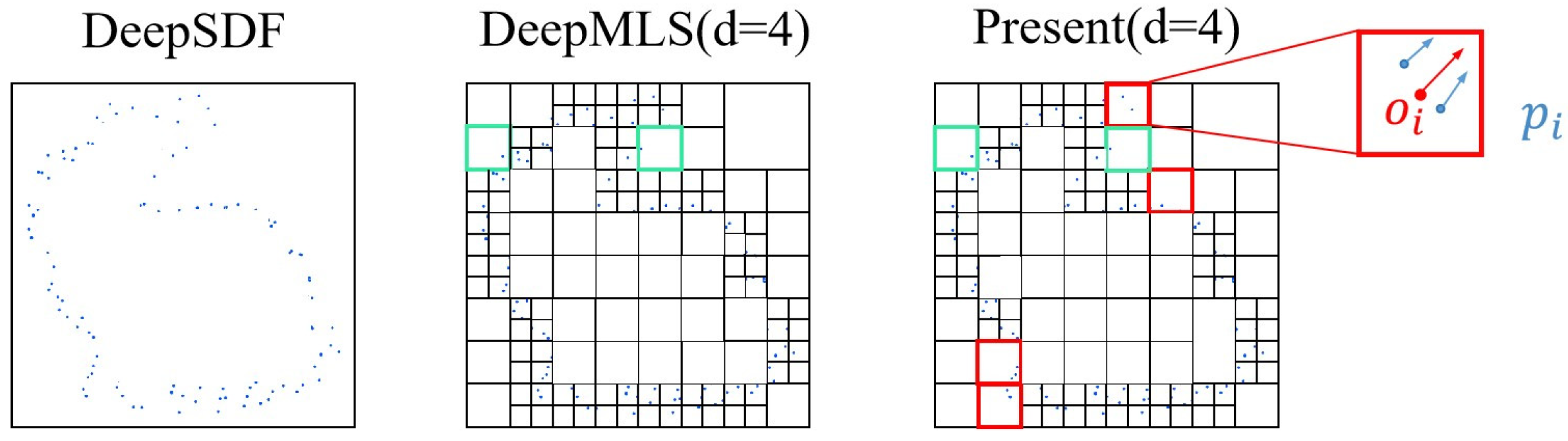
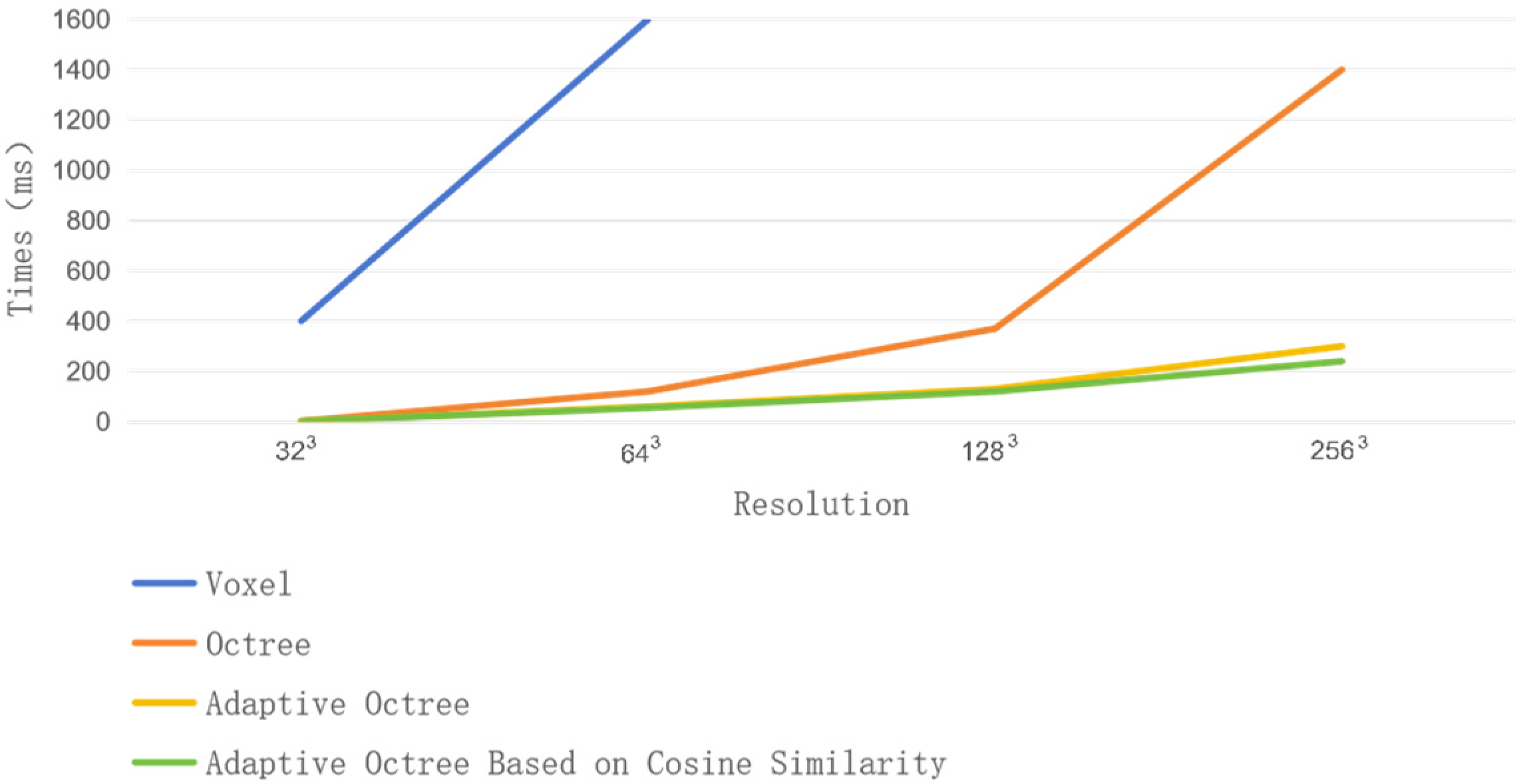
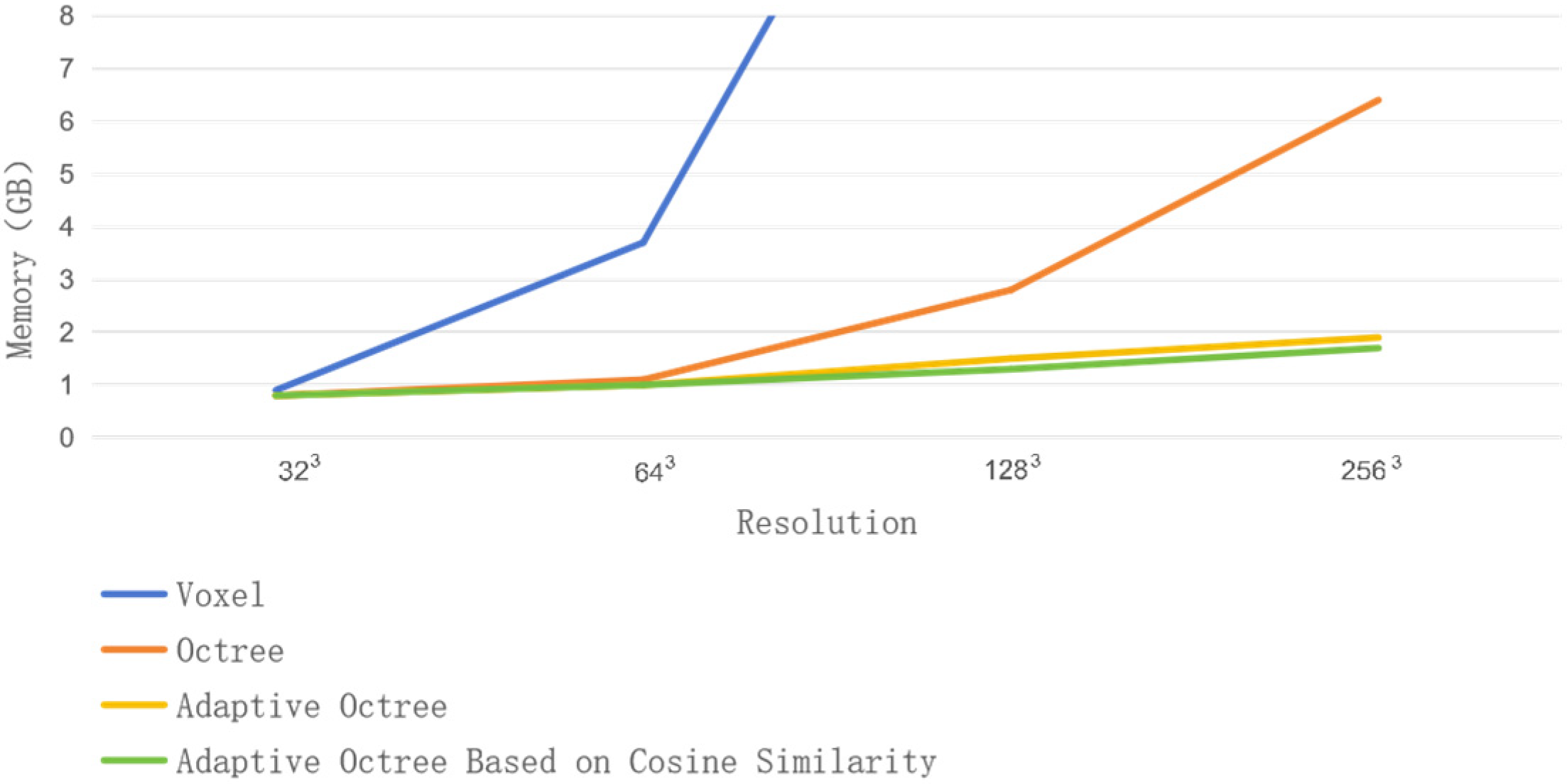
• Adaptive octree partitioning: This scheme speeds up iteration and saves memory space by dynamically adjusting the partitioning based on local shape characteristics;
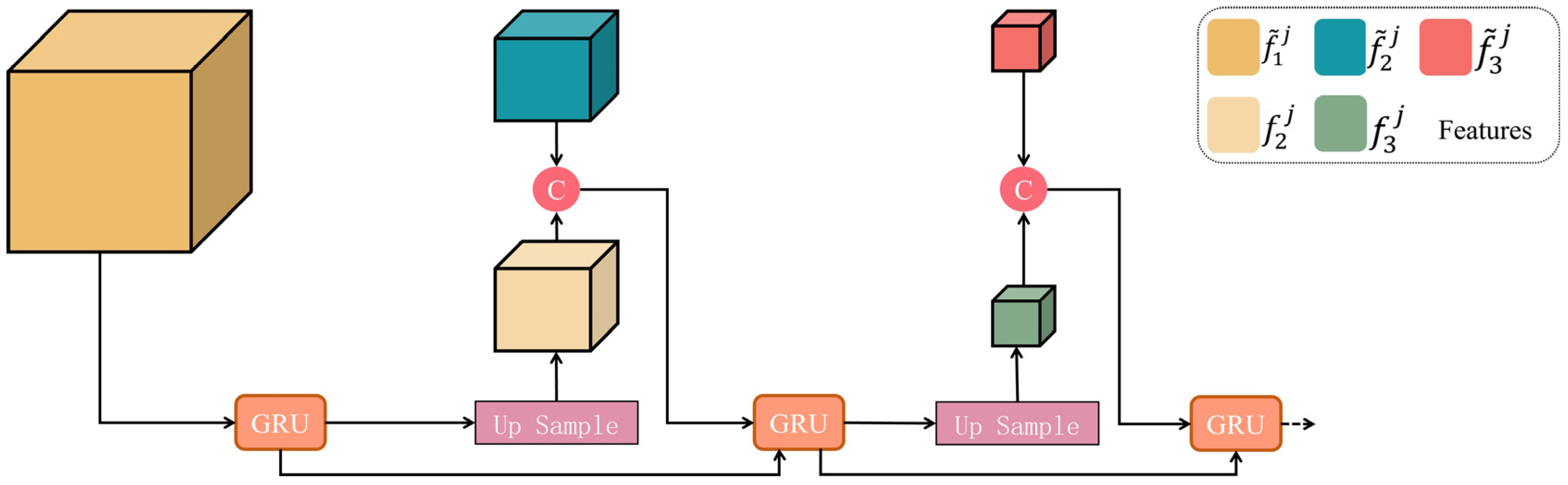
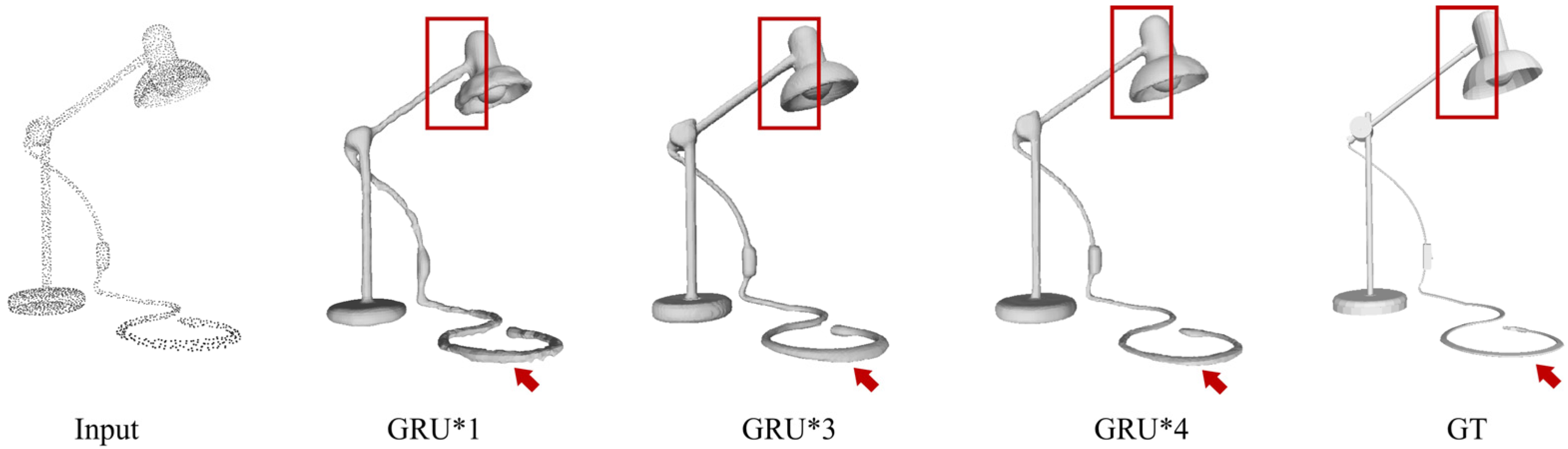
• GRU-based feature optimization: The GRU module iteratively optimizes local features, capturing the correlation and contextual information between shape features and achieving dynamic learning of feature changes;
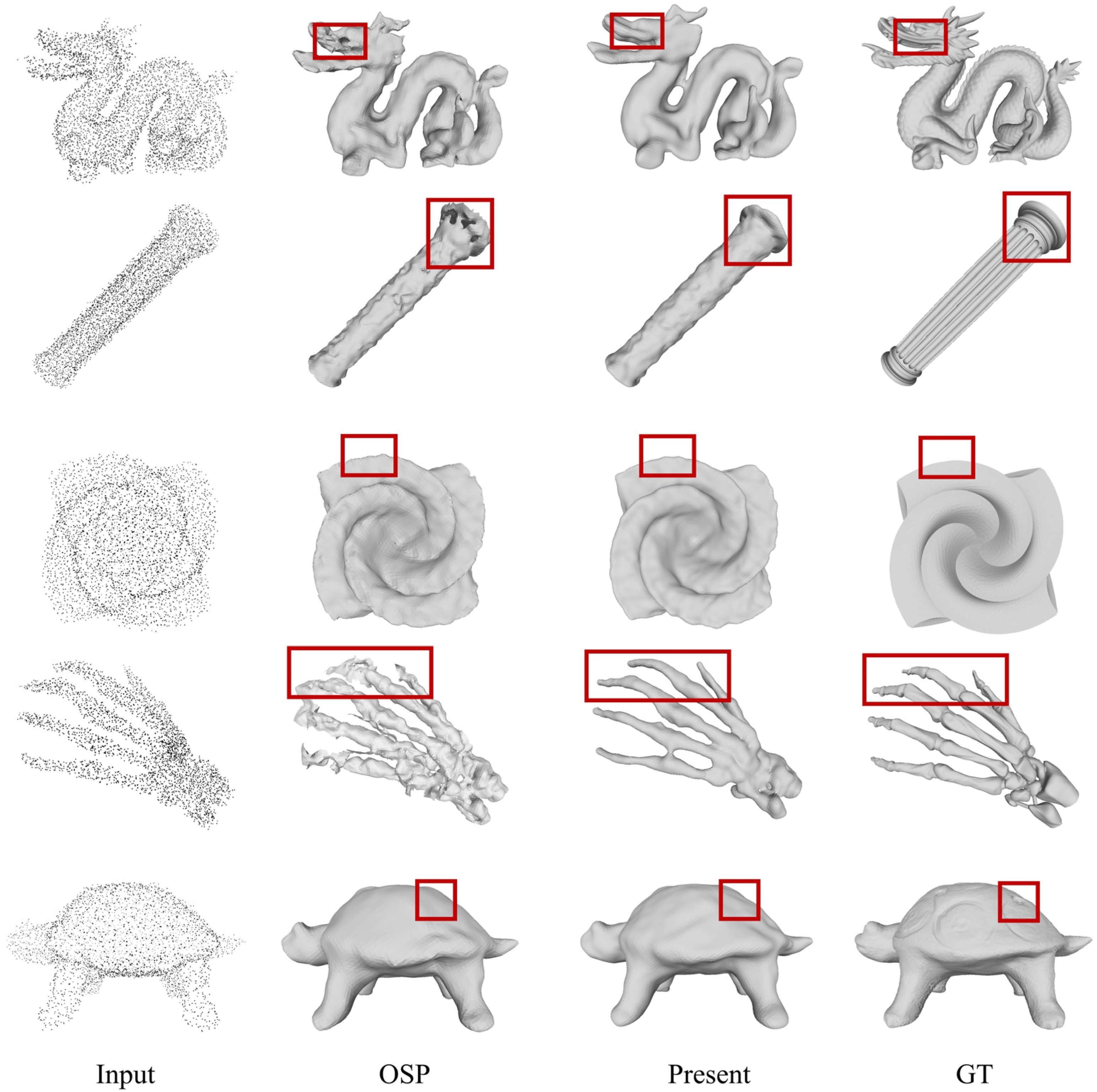
• Excellent visualization results: Our method achieves state-of-the-art results on ShapeNet, ABC, and Famous datasets, demonstrating its effectiveness in generating high-quality 3D surfaces.

2. Related Work

At present, there are many 3D reconstruction methods for point clouds based on deep learning [7,8], which use auto-encoder to obtain the feature information of shapes, and although the output forms are different (occupancy values [9], SDF [10], neural unsigned distance fields (UDF) [11]), the surface can be extracted by marching cubes and back projection algorithms [12].

Three-dimensional reconstruction based on octree structure. At present, the most typical 3D reconstruction method based on octree is octree-based convolutional neural networks (O-CNN) [13]. This method first combines the target shape, then divides it into eight equal parts and performs convolutional neural network extraction of voxel features within each octant; based on O-CNN, adaptive O-CNN [14] proposed a planar fitting method for three-dimensional surfaces, in addition to using the pre-set depth of the octree and whether the number of point clouds within the octree reaches a threshold as the partition conditions for the octree, and using the ability to fit the current shape within the octree as an additional partition condition; based on O-CNN, DeepMLS proposed to perform convolutional neural network feature extraction in each smallest octant, and output MLS point cloud through MLP. The moving least-square function is used to approximate the signed distance function, which is used as an implicit function to extract three-dimensional surfaces; dual graph neural networks (GNN) [15] utilized graph convolution to combine voxel features of different scales and transmit octahedral feature information of different depths; Neural-IMLS [16] proposed different weight functions based on DeepMLS and learns SDF directly from the original point cloud in a self-supervised manner. Towards implicit text-guided 3D-shape generation (TISG) [17] generated 3D shapes from text based on an octree; dynamic code cloud-deep implicit functions (DCC-DIF) [18] discretized the space into regular 3D meshes (or octree) and store local codes in grid points (or octant nodes) to calculate local features by interpolating their adjacent local codes and their positions.

Three-dimensional surface generation based on local and global integration. Points2surf [19] used autoencoders to obtain more accurate distance values from local sources and more accurate sign values from global sources. The combination of the two has both local and global information, which can quickly and conveniently obtain sign distance values and improve reconstruction efficiency; latent partition implicit (LPI) [20] combined local regions into global shapes in implicit space, and the use of affinity vectors allowed the reconstruction results to include both local region features and cleverly integrate global information, resulting in currently outstanding reconstruction results; implicit functions in reconstruction and completion (IFRC) [21] proposed an implicit feature network that does not use a single vector to encode three-dimensional shapes. Instead, it extracts a learnable deep feature tensor for three-dimensional multi-scale deep features and aligns it with the original Euclidean space of the embedded shape, allowing the model to make decisions based on global and local shape structures; Octfield [22] proposed adaptive decomposition in 3D scenes, which only distributes local implicit functions around the surface of interest, connects the shape features of different layers, and possesses both local and global information, achieving excellent reconstruction accuracy. Learning consistency-aware unsigned distance functions (Learning CU) [23] used a cyclic optimization approach to reconstruct sparse point clouds into dense point clouds surrounding the shape, while maintaining the normal consistency of the point cloud; learning local pattern-specific deep implicit function (LP-DIF) [24] proposed a new local pattern-specific implicit function that simplifies the learning of fine geometric details by reducing the diversity of local regions seen by each decoder. A kernel density estimator is used to introduce region reweighting modules to each specific pattern decoder, which dynamically reweights regions during the learning process; neural galerkin solver [25] discretized the interior of the target implicit field into a linear combination of spatially varying basis functions inferred by an adaptive sparse convolutional neural network.

Three-dimensional reconstruction based on loop optimization. To generate higher precision surfaces, current methods revolve around the iterative strategy of “loops” for network optimization or feature optimization. For example, alternately denoising and reconstructing (ADR) unoriented point sets [26] used iterative poisson surface reconstruction (iPSR) [27] to support undirected surface reconstruction, iteratively executing iPSR as an outer loop of iPSR. Considering that the depth of the octree significantly affects the reconstruction results, an adaptive depth-selection strategy is proposed to ensure appropriate depth selection; deep-shape representation (DSR) [28] first extracted edge points from input points using an edge detection network and then preserved the sharp features of the real model while restoring the implicit surface. The two-stage training process ensures that the sharp features of the input points are learned while fitting surface details; USR [29] proposed generating target objects through part assembly, which iteratively retrieves parts from the shape parts library through a self-supervised method, improves their positions, and combines parts into the surface of the target object; octree-guided unoriented surface reconstruction (OGUSR) [30] constructed a discrete octree with inner and outer labels, and optimized the continuous and high fidelity shape using an implicit neural representation guided by the octree labels. This method generates a three-dimensional surface using an unoriented point cloud as input, achieving results comparable to those generated by directed point clouds; unsupervised single sparse point (USSP) [31] used parameterized surfaces as coarse surface samplers to provide many coarse surface estimates during training iterations. Based on these estimates, the SDF was statistically inferred as a smooth function using a thin plate spline (TPS) network. This significantly improved the generalization ability and accuracy in invisible point clouds; real-time coherent 3D reconstruction from monocular video (NeuralRecon) [32] used gated recurrent units to capture local smoothing priors and global shape priors of three-dimensional surfaces during sequential surface reconstruction, thereby achieving accurate, coherent, and real-time surface reconstruction of images. Towards better gradient consistency (TBGC) for neural signed [33] adaptively constrained the gradient at the query and its projection on the zero level set, cyclically aligning all level sets to the zero level set, minimizing the level set alignment loss to obtain more accurate signed distance function, and, thus, generating a three-dimensional surface. A new iPSR [34] showed that, in each iteration, the surface obtained from the previous iteration directly calculates the normal vector as input sample points, generating a new surface with better quality.

Based on adaptive octree based on cosine similarity, we achieve iterative optimization of information through GRU. In the paper, we describe the method in detail in Section 3 and analyze the experimental results in Section 4.

3. Methods

Our method presents an end-to-end 3D surface-generation algorithm. As depicted in Figure 1, the algorithm involves the following steps:

• Adaptive Octree Voxel Partitioning: The input point cloud undergoes adaptive octree voxel partitioning based on cosine similarity, as detailed in Section 3.1;
• Contextual Information Encoding: A convolutional neural network (CNN) is employed to extract local features within the smallest octant voxel. Subsequently, a GRU transmits contextual information across different scales, as described in Section 3.2;
• Moving Least Squares Surface Generation: Following MLP processing, the accumulated contextual information from voxels of various scales is utilized to generate a moving least squares point set. This enables the approximation of locally smooth and coherent surface geometry on a large scale, as elaborated in Section 3.3;
• Model Optimization: The network parameters are optimized by minimizing the loss function defined in Section 3.4.

Figure 1. Structure diagram of the 3D reconstruction based on iterative optimization of MLS.

Figure 1. Structure diagram of the 3D reconstruction based on iterative optimization of MLS.

3.1. Adaptive Octree Voxel Partitioning

In conventional 3D reconstruction methods, autoencoders were widely employed to extract global or local shape features, which were subsequently used to generate the 3D surface. For instance, DeepSDF generates an implicit encoding for each shape, representing its global features. However, the shape surfaces generated by this method often lack detail and struggle to effectively capture intricate information. Consequently, methods have been proposed to transform the target shape from global to local, utilizing local features to express shape details. Among the partitioning methods, the octree data structure has proven to be the most effective, as exemplified by the O-CNN. O-CNN first normalized the target shape to a unit voxel and then performed octree division. Each voxel after division is termed an “octant”. This octree partition operation is repeated until the specified depth is reached or the number of point clouds within the octant is less than the specified threshold. DeepMLS is a 3D reconstruction based on O-CNN; adaptive O-CNN proposed an adaptive octree partitioning method. Unlike O-CNN, this paper added a partitioning criterion based on O-CNN; that is, whether the point cloud within the octree can be fitted by a plane. When the plane can fit the point cloud within the octant, it indicates that the local area is sufficiently flat and does not need to be further partitioned. However, according to the planar fitting results of adaptive O-CNN, the generated shape surface is not smooth enough.

We propose a novel shape-adaptive partitioning method that utilizes the correlation between normal vectors of the input point cloud to achieve a more refined division from global to local representations. The input point cloud $\mathcal{P}$ ($p_i\in \mathcal{P}$, each $p_i$ with a normal $n_i$) is normalized to a unit voxel and undergoes octree partitioning, where each voxel is recursively subdivided into eight equal parts. In the example of an octree with a depth of 4 (Figure 2), DeepMLS terminates the partitioning process due to the number of points in each octant falling below the smallest threshold. Our method retains this condition but introduces an additional criterion: the average cosine of the angle between the normal of each point in the input cloud and the average normal of the smallest octant containing that point must exceed a predefined threshold.

This additional criterion ensures that regions with highly similar surface normals, indicating relatively smooth surfaces are not further subdivided, result in a more efficient and detail-preserving partitioning, which reduces computational cost while preserving important geometric features. The cosine mean is calculated as follows:

$$\overline{c}=\frac{1}{m}{\displaystyle \sum _{i=1}^m(cos(}{n}_{i,d},n_{c,d})),$$

(1)

where $\overline{c}$ represents the mean of the cosine, $m$ represents the total number of points within the smallest octant with depth $d$ in the input point cloud, $cos\left(n_{i,d},n_{c,d}\right)$ shows the cosine value of the angle between the normal $n_{i,d}$ of each point and the normal $n_{c,d}$ of the smallest octant with depth $d$. In our experiment, the threshold is set to 0.8. (When $\overline{c}$ is smaller than 0.8, it indicates that the direction of the point cloud normal in the octant is uneven; that is, the octant may contain a complex geometric feature, requiring further subdivision). $cos\left(n_{i,d},n_{c,d}\right)$ is calculated as:

$$cos(n_{i,d},n_{c,d})=\frac{n_{i,d}{n}_{c,d}}{\left|n_{i,d}\right|\left|n_{c,d}\right|},$$

(2)

$$n_{c,d}=\frac{1}{m}{\displaystyle \sum _{i=1}^m{n}_{i,d}},$$

(3)

where $n_{i,d}$ represents the normal vector of the point cloud in depth $d$, while $n_{c,d}$ represents the mean normal of the point cloud in the smallest octant in depth $d$ where $p_i$ is located.

3.2. Contextual Information Encoding

To extract local information about the shape, we apply convolutional neural networks on the smallest octant at various depths, which incorporate residual blocks and output-guided skip connections, helping to preserve the details and semantic information in the original input data and avoid information loss. During the processing, each down-sampling generates a shallower octree, while each up-sampling generates a deeper octree. When reaching the shallowest octree, each residual block is connected to the GRU module, allowing the reconstruction process within the current octree to be conditional on the previously reconstructed parent octant, thus achieving joint reconstruction and fusion.

The GRU module is shown in Figure 3. After data partitioning through adaptive octree and processing with convolutional neural networks, feature representations of different depths were obtained, such as ${\tilde{f}}_1^j$, ${\tilde{f}}_2^j$, ${\tilde{f}}_3^j$. ${\tilde{f}}_1^j$ corresponds to the relatively shallow octant, where $j$ represents all octants at the same octree depth. ${\tilde{f}}_2^j$ is a sub octant of ${\tilde{f}}_1^j$, and ${\tilde{f}}_3^j$ represents the deeper octant. ${\tilde{f}}_1^j$ is input into the GRU module and then up-sampled to obtain the deformed feature $f_2^j$. The purpose of up-sampling is to maintain the same number of channels for $f_2^j$ and ${\tilde{f}}_2^j$, facilitating concatenation and transfer to the next GRU. $f_3^j$ is then obtained through GRU and up-sampling, matching the number of channels of ${\tilde{f}}_3^j$. They are then concatenated and passed to the next GRU. This process continues sequentially to achieve the transmission and fusion of features across different octant depths. In Figure 3, information flows from left to right (from shallow octants to deep octants) within the GRU module. This ensures that feature information and contextual information between different scales are fully exchanged and integrated, ultimately enhancing the learning and representation capabilities of the entire network and further optimizing the 3D shape-reconstruction process.

The calculation method for feature $f_h^j$ after passing through the GRU module is:

$$f_h^j=(1-z_h)f_{h-1}^j+z_h{\tilde{f}}_h^j.$$

(4)

Here, $h$ represents the current octree depth, and $j$ represents the octant node at $h$ depth. $f_{h-1}^j$ represents the feature information of $f_h^j$ after GRU and up-sampling, while ${\tilde{f}}_h^j$ represents the feature information after passing through a convolutional neural network. In the use of GRU [6], the calculation method for the update gate $z_h$ is:

$$z_h=\sigma \left(W_z{x}_h+U_z{f}_{h-1}^j\right),$$

(5)

$${\tilde{f}}_h^j=tanh\left(W_{\mathrm{c}}{x}_h+U_{\mathrm{c}}\left(r_h\odot f_{h-1}^j\right)\right).$$

(6)

The calculation method for reset gate $r_h$ is:

$$r_h=\sigma \left(W_r{x}_h+U_r{f}_{h-1}^j\right),$$

(7)

where $\mathsf{\sigma }$ means the sigmoid activation function, and $x_h$ represents the octant center coordinates at depth $h$ in the octree. The update gate $z_h$ and reset gate $r_h$ in GRU determine how much information from the previous reconstructions of the octant will be integrated into the geometric features of the current octant node, and how much information from the current octant node will be integrated into the next round of GRU module. In Formulas (5)–(7), $\mathrm{W}$ (include $W_z$, $W_c$, $W_r$) and $\mathrm{U}$ (include $U_z$, $U_c$, $U_r$) are the matrices of the values (also known as the GRU network weights) learned at different stages of the training process. In this method, by predicting the post-GRU features, the MLP network can make full use of the contextual information accumulated from the historical multi-scale octant voxels. This mechanism enables the generation of consistent surface geometry between parts at different scales, thus facilitating the integration of shape features.

Under the action of the GRU module, local feature information from different scales is transmitted unidirectionally, effectively capturing the correlations and contextual relationships between shape features. This enables the model to dynamically learn and adapt to changes in features, ensuring the continuity of features at different depths. This mechanism facilitates the transmission and integration of information, enhancing the model’s understanding and modeling capabilities of shape features. By promoting information exchange and integration across the entire network at different levels, this method of feature transmission and fusion improves the accurate reconstruction ability of three-dimensional shapes.

3.3. Moving Least-Squares Surface Generation

After the GRU module described in Section 3.2, shape features $f$ with contextual information can be obtained. Where $f$ is calculated as $f=MLP\left\{ f_h^j⨁{\tilde{f}}_h^j\right\}$, and ⨁ represents the feature concatenation of each channel, $f_h^j$ and ${\tilde{f}}_h^j$ are calculated as described in Section 3.2. $h$ represents the current octree depth, and $j$ represents the octree node at depth $h$.

We generate MLS point cloud $Q\in R^3$ through a shallow MLP, where $q_i\in Q$ represents the MLS point within the octant and $o_i$ represents the smallest octant center point where $q_i$ is located. Through the above steps, a collection of MLS point clouds can be obtained, denoted as $\left\{q_i,n_c\right\}$.

To approximate the signed distance function, we employ the classic moving least-squares (MLS) function, treating it as an implicit signed distance function for 3D shape surfaces. (We adopt a sampling strategy like DeepMLS, which makes the sampling points dense enough and the distance between the sampling points small enough to make MLS approach SDF). This method effectively applies the moving least-squares technique to three-dimensional shape analysis, enabling the estimation and calculation of implicit signed distance functions on surfaces. This provides crucial support for further geometric calculations and surface reconstruction. By constructing and applying MLS functions, we can more accurately describe and represent the features and topological structures of three-dimensional shapes. In the paper, the function $F\left(·\right)$ is defined to represent the moving least-square function, which is used to estimate the signed distance value of the point cloud:

$$F(x)=\frac{{\displaystyle {\sum }_{q_i\in {\mathbb{Q}}_{mls}}\omega \left(x-q_i\right)\cdot 〈x-q_i,n_c〉}}{{\displaystyle {\sum }_{q_i\in {\mathbb{Q}}_{mls}}\omega (x-q_i)}},$$

(8)

$$\omega (x)=e^{-\frac{x^2}{{\sigma }^2}},$$

(9)

where $a,b$ denotes the inner product of $a$ and $b$, $Q_{mls}$ represents all MLS points of the local patch contained in the sphere with $x$ as the center and $r$ as the radius, where $r$ is 1.8 times the width of the octant where $x$ is located. $\sigma$ is defined as:

$$\sigma =\sqrt{\frac{d_{Qmls}}{\left|Q_{mls}\right|}},$$

(10)

where $d_{Q_{mls}}$ indicates the length of the bounding box of the local patch where $Q_{mls}$ is located. And $\left|Q_{mls}\right|$ is defined as 200.

3.4. Model Optimization

In scenarios where the point cloud is evenly distributed within an octant, resulting in a flat and continuous surface, a corresponding division loss function, $L_1$, is proposed to minimize unnecessary divisions. This loss function dynamically adjusts the partitioning strategy based on the local morphology and characteristics of the point cloud, thereby reducing redundant partitioning operations while maintaining accuracy.

$$L_1={\displaystyle \sum _{d=1}^7\left[1-\frac{1}{m}{\displaystyle \sum _{i=1}^{m}cos(n_{i,d},n_{c,d})}\right]}.$$

(11)

The paper uses supervised deep-learning techniques to enhance the method’s performance. We train on each shape on the ShapeNet dataset and use the result of voxel partitioning of a ground-truth octree with an output depth of $d$, $O_d$, to supervise shape partitioning. By introducing a loss constraint between the results of the network-generated octree partition and the ground-truth partition results, the learned partition results are infinitely close to the true partitions. Define the loss function as the structural loss, $L_2$:

$$L_2=\frac{1}{\left|O_d\right|}{\displaystyle {\sum }_{o\in O_d}E(o,o_{gt})}.$$

(12)

In the paper, we use the binary cross-entropy function (denoted as $E\left(·\right)$) to measure the difference between the predicted octree structure (denoted as $o$) and the real octree structure (denoted as $o_{gt}$). Moreover, we use the SDF loss $L_{sdf}$, point repulsion loss $L_{rep}$, projection-smoothing loss $L_{proj}$, and radius-smoothing loss $L_{rad}$, which are performed using the same computational method as described in DeepMLS [4].

The optimized feature $f$ after GRU iteration can generate an MLS point cloud (denoted as $x_i\in S_1$), and the real point cloud extracted from the shape surface (denoted as $y_i\in S_2$) needs to be highly approximate in position. Therefore, using the chamfer distance (CD1) between the two as a loss function, $L_3$. constrains the accuracy of the generated MLS point cloud:

$$L_3=\frac{1}{\left|S_1\right|}{\displaystyle \sum _{x_i\in S_1}mi{n}_{y_i\in S_2}}\Vert x_i-y_i\Vert +\frac{1}{\left|S_2\right|}{\displaystyle \sum _{y_i\in S_2}mi{n}_{x_i\in S_1}}\Vert y_i-x_i\Vert .$$

(13)

In the paper, the surface generated during the reconstruction process is denoted as $S_Q$, while the GT surface is denoted as $S_T$. Point clouds are randomly sampled from two surfaces to obtain N $=10k$ points. And $S_1={\left\{x_i\right\}}_{i=1}^N$ represents the point cloud extracted from $S_Q$, while $S_2={\left\{y_i\right\}}_{i=1}^N$ is the point cloud extracted from the GT surface $S_T$. $\left|S_1\right|$ and $\left|S_2\right|$ mean the number of point clouds in $S_1$ and $S_2$, respectively. In Formula (13), the first term represents the sum of the smallest distances of any point $x_i$ in $S_1$ to $S_2$, and the second term represents the sum of the smallest distances of any point $y_i$ in $S_2$ and $S_1$. Combining these two terms ensures that the point cloud extracted from the reconstructed surface is closer to the point cloud extracted from the ground truth surface.

In summary, the total loss is defined as L:

$$L=L_1+L_2+L_3+L_{sdf}+L_{rep}+L_{proj}+L_{rad}.$$

(14)

We train our model in an end-to-end fashion by using gradient descent. This involves back-propagating through the sum of all these loss functions to update the model parameters iteratively.

4. Experiments

4.1. Dataset

We conduct experiments on publicly available datasets, including ShapeNet, ABC, and Famous. These datasets are described in detail below:

ShapeNet [35]: The ShapeNet dataset is widely used in the field of 3D shape point cloud modeling and is a large-scale comprehensive dataset for 3D shape recognition and modeling research. The dataset contains a single clean 3D model and manually validated category and alignment annotations, with more than 50,000 3D models covering 13 different shape categories, such as furniture, bags, airplanes, etc.

ABC [36]: The ABC dataset is a collection of computer-aided design (CAD) models designed for studying geometric deep learning. The collection contains 1 million models, each with an explicitly parameterized collection of curves and surfaces, and provides data related to accurate ground truth information. These real-world CAD models provide benchmarks and basic facts for tasks such as differential components, patch segmentation, geometric feature detection, and shape reconstruction, and they provide important support and reference for in-depth study of the performance and effectiveness of geometric deep-learning algorithms.

Famous [19]: The Famous dataset was released in 2020 and contains 22 well-known geometric shapes, including the Stanford University’s Bunny and Utah Teapot, among others. Points2surf combined these famous shapes in their study and named it the Famous dataset. In this study, the dataset is used to test the generalization performance of the proposed method and to verify the applicability and effectiveness of the method on different well-known geometries.

4.2. Evaluation Metrics

In the paper, we use three commonly used evaluation metrics to evaluate the results of our experiments. The evaluation metrics are described in detail as follows:

Chamfer Distance (CD2): As one of the most frequently used metrics in 3D surface generation, the chamfer distance between point clouds provides a simple and intuitive way to compare the similarity between two sets of point clouds. A higher CD2 indicates a larger difference between the two point clouds, potentially signifying poor reconstruction or significant shape deviations. When the CD2 is small, it indicates that the geometry of the reconstruction is closer to the original model, and the reconstruction effect is relatively better.

$$CD2=\frac{1}{\left|S_1\right|}{\displaystyle \sum _{x_i\in S_1}mi{n}_{y_i\in S_2}}\Vert x_i-y_i{\Vert }_2^2+\frac{1}{\left|S_2\right|}{\displaystyle \sum _{y_i\in S_2}mi{n}_{x_i\in S_1}}\Vert y_i-x_i{\Vert }_2^2.$$

(15)

Normal Consistency (NC):

$$NC=\frac{1}{\left|S_1\right|}{\displaystyle \sum _{i=1}^{\left|S_1\right|}\left|n(x_i)\cdot n(S_T(x_i))\right|}+\frac{1}{\left|S_2\right|}{\displaystyle \sum _{i=1}^{\left|S_2\right|}\left|n(y_i)\cdot n(S_Q(y_i))\right|},$$

(16)

where $n\left(x_i\right)$ represents the normal of point $x_i$, $n\left(y_i\right)$ represents the normal of point $y_i$, $n\left(S_T\left(x_i\right)\right)$ represents the normal of the point $x_i$ in the generated surface at the nearest neighbor of the ground truth surface, and $n\left(S_Q\left(y_i\right)\right)$ represents the normal of the point $y_i$ in the ground truth surface at the nearest neighbor of the generated surface. Based on the quantification results of the NC, the consistency between the model output normal and the GT normal is evaluated.

F-score: Expressed as a combination of accuracy and recall, it is the harmonic average of precision and recall at a particular threshold $t$.

$$F-Score=\frac{2P(t)R(t)}{P(t)+R(t)},$$

(17)

where $P\left(t\right)$ represents the precision, and the distance from the threshold $t$ is generally 0.40. $R\left(t\right)$ represents the recall.

$$P(t)=\frac{100}{\left|\begin{array}{c}{S}_1\end{array}\right|}{\displaystyle \sum _{x_i\in S_1}\left[\begin{array}{c}mi{n}_{y_i\in S_2}‖\begin{array}{c}{x}_i-y_i\end{array}‖\end{array}\right]},$$

(18)

$$R(t)=\frac{100}{\left|\begin{array}{c}{S}_2\end{array}\right|}{\displaystyle \sum _{y_i\in S_2}\left[\begin{array}{c}mi{n}_{x_i\in S_1}‖\begin{array}{c}{y}_i-x_i\end{array}‖\end{array}\right]}.$$

(19)

where $t$ is the distance from the reconstructed point set to the real point set (that is, the threshold t is 0.40).

4.3. Implementation Details

The experimental results in the paper are trained and tested on their respective datasets. Specifically, the method’s surface generation results on the ShapeNet dataset are tested after training on the same dataset. Similarly, the surface generation results on the ABC dataset are tested after training on the ABC dataset, and the surface generation results of the method on the Famous dataset are tested after training on the Famous dataset. During the testing stage, the number of input point clouds for each shape is controlled at 3k to verify the modeling effect of the proposed method on sparse point clouds.

Based on the experience of DeepMLS, the depth of the octree tree with set inputs and outputs is controlled at seven layers.

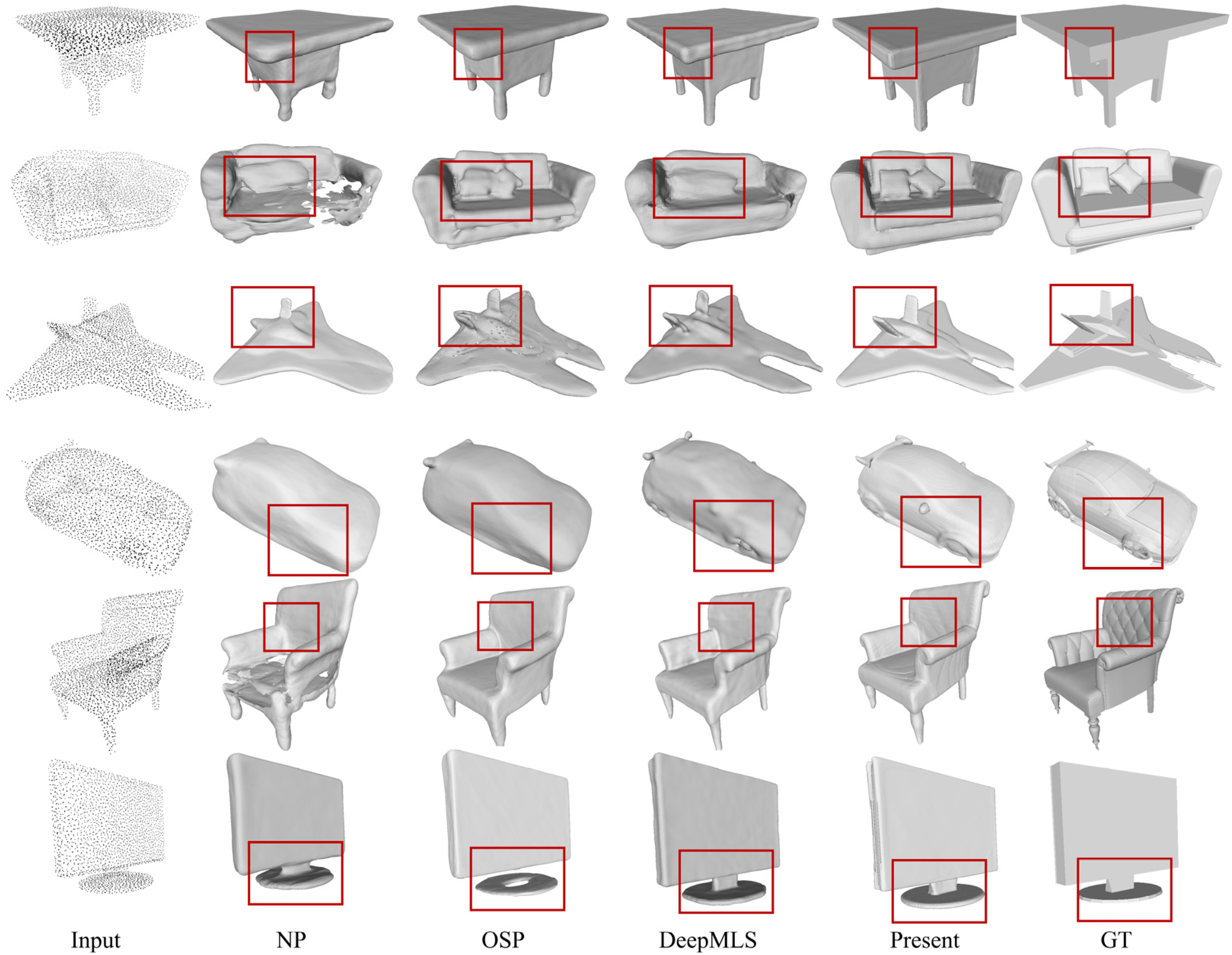
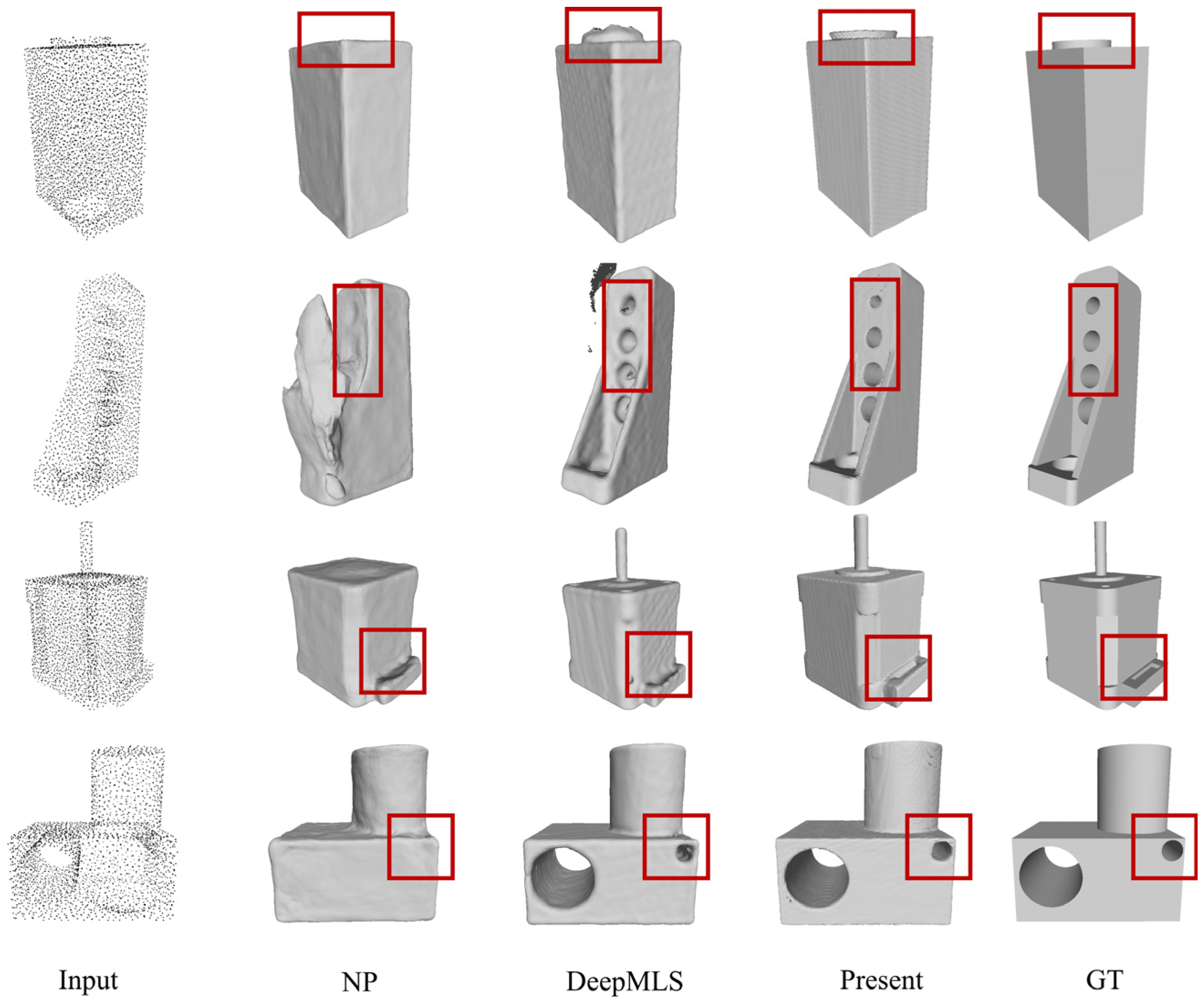
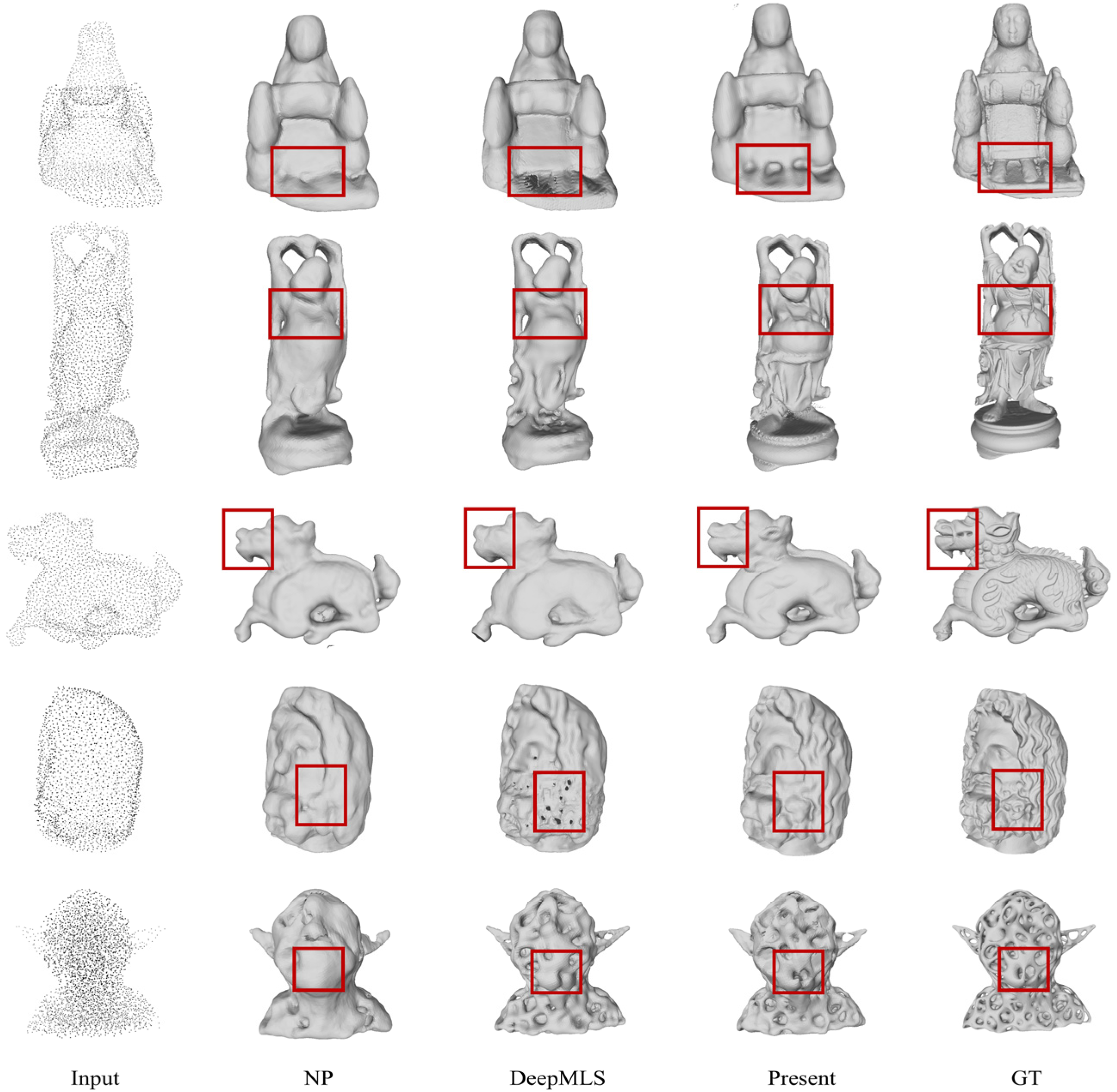
4.4. Result

To verify the effectiveness of this method, comparative experiments were conducted with the NP [37], OSP [38], and DeepMLS methods.

In Figure 4, the surface generation of sofas and chairs demonstrates that the NP method causes the anomaly of surface loss. When dealing with airplane classes, airplane surfaces conjoin in unintended areas. In the surface generation of the sofa, the OSP method results in cushions incorrectly linked in certain areas, and the vehicle lacks detail, causing a loss of shape details and feature information. The modeling effect of DeepMLS in the table shape is finer than that of NP and OSP, but there are abnormal holes in the surface generation of the chair, resulting in discontinuity of the surface. In contrast, the method proposed in the paper avoids the aforementioned problems. Not only is there no adhesion on the sofa, but also the surface generation results of the chair show that the proposed method can effectively model the texture details of the chair rest. Through the visualization results in Figure 4, the proposed method has certain advantages over other deep-learning methods, showing better modeling accuracy and surface continuity, which brings breakthroughs and improvements to the object shape generation task.

Several deep-learning-based surface-generation methods (DeepSDF, MeshP [39], LIG [40], IMNET [41], NP, DeepMLS) were quantitatively compared on the ShapeNet dataset. (↑ and ↓ indicate that either larger data values are better or smaller data values are better, respectively).

Table 1. Results of NC (↑) of each method in the ShapeNet dataset. (The bold font indicates that it is the optimal result).

Class Name	DeepSDF	MeshP	LIG	IMNET	NP	DeepMLS	Present
Display	0.932	0.974	0.926	0.574	0.964	0.973	0.988
Lamp	0.864	0.963	0.882	0.592	0.930	0.922	0.963
Airplane	0.872	0.955	0.817	0.550	0.947	0.937	0.964
Cabinet	0.872	0.957	0.948	0.700	0.930	0.955	0.986
Vessel	0.841	0.953	0.847	0.574	0.941	0.932	0.964
Table	0.901	0.962	0.936	0.702	0.908	0.962	0.977
Chair	0.886	0.962	0.920	0.820	0.937	0.950	0.955
Sofa	0.906	0.971	0.944	0.818	0.951	0.963	0.982
Mean	0.884	0.962	0.903	0.666	0.939	0.949	0.972

shows the comparison results of the above methods on NC evaluation indexes. The comparative experimental results show that the proposed method achieves a high score in the NC evaluation index, which means that the surface generated by the proposed method is closer to the ground truth surface in terms of accuracy and fidelity. Compared with other methods, this method can better restore the details and overall characteristics of the target shape to provide more accurate and reliable surface-generation results.

Table 2. Results of F-Score (↑) of each method in the ShapeNet dataset. (The bold font indicates that it is the optimal result).

Class Name	DeepSDF	MeshP	LIG	IMNET	NP	DeepMLS	Present
Display	0.632	0. 903	0.551	0.601	0.989	0.994	0.998
Lamp	0.268	0.855	0.624	0.836	0.891	0.979	0.990
Airplane	0.350	0.844	0.564	0.698	0.996	0.992	0.998
Cabinet	0.573	0.860	0.733	0.343	0.980	0.981	0.987
Vessel	0.323	0.862	0.467	0.147	0.985	0.987	0.996
Table	0.577	0.880	0.844	0.425	0.922	0.987	0.975
Chair	0.447	0.875	0.710	0.181	0.954	0.982	0.985
Sofa	0.577	0.895	0.822	0.199	0.968	0.987	0.994
Mean	0.468	0.872	0.664	0.429	0.961	0.986	0.990

shows the comparison results of various methods on F-Score evaluation indicators. After data analysis, our method shows good quantitative results in various shape categories. Especially in the two categories of Display and Airplane, the method achieved the best score of 0.998. These results demonstrate the excellent performance of the proposed method in surface-generation tasks and the advantages of different shape classes.

Table 3. Results of CD2 (×100) (↓) of each method in the ShapeNet dataset. (The bold font indicates that it is the optimal result).

Class	DeepSDF	MeshP	NUD	SALD	NP	DeepMLS	Present
Display	0.317	0.069	0.077	-	0.039	0.012	0.007
Lamp	0.955	0.053	0.075	0.071	0.080	0.015	0.012
Airplane	1.043	0.049	0.076	0.054	0.008	0.008	0.006
Cabinet	0.921	0.112	0.041	-	0.026	0.024	0.015
Vessel	1.254	0.061	0.079	-	0.022	0.011	0.014
Table	0.660	0.076	0.067	0.066	0.060	0.014	0.012
Chair	0.483	0.071	0.063	0.061	0.054	0.027	0.010
Sofa	0.496	0.080	0.071	0.058	0.012	0.014	0.017
Mean	0.766	0.071	0.069	0.062	0.038	0.016	0.014

shows the results of a comparison of the CD2 indicator between the various methods. Through data analysis, the proposed method performs well in multiple shape categories. Although it is inferior to DeepMLS in vessel and sofa categories, it is better than other methods in other categories and the mean of all categories, indicating that the proposed method has good performance in the surface generation task under the evaluation of CD2 index and has good effect and superior performance.

To verify the effectiveness of the proposed method, comparative experiments are carried out on the ABC dataset and the Famous dataset, and the specific results are shown in Figure 5 and Figure 6. By comparing the performance of each method on the ABC dataset, it can be observed that the proposed method can generate continuous surfaces and avoid abnormal surface phenomena such as shape “hyperplasia”, adhesion, and “ectopia”. This shows that the proposed method can maintain stable and excellent performance in processing different datasets.

Compared with the ABC dataset, the Famous dataset is more complex in shape, contains more shape details, and is usually presented as an irregular surface, making it more challenging for 3D surface generation. In the paper, a visual comparison is performed on the Famous dataset, and the results are shown in Figure 6. By comparing the NP and DeepMLS methods, it can be observed that the proposed method successfully avoids the adhesion of the shape surface (such as the leg area of the first-row shape), can generate fine surface details (such as the hem of the character in the second row, the face of the shape of the third row), and avoids the generation of “holes” (such as the beard in the shape of the fourth row), which further verifies the ability of the proposed method to deal with complex shapes and details, and demonstrates its robustness and superiority in challenging scenarios.

4.5. Ablation Studies

4.5.1. Adaptive Partitioning

As we all know, the number of elements involved in the calculation is directly related to the efficiency of the CNN. For full voxel representation if the voxel resolution is $N$, the overall prime number is $N^3$. In the paper, the adaptive octree based on cosine similarity is compared with the full voxel (that is, DeepSDF), octree (that is, O-CNN), and adaptive octree (that is, adaptive O-CNN) in the same operating environment. Calculate the average run time of a forward and backward iteration, as shown in Figure 7. Adaptive octree trees are 10-to-100 times faster than voxel-based CNN. When the input resolution exceeds, ${128}^3$, it is even three-to-five times faster than O-CNN. The adaptive octree based on cosine similarity proposed in the paper is faster than that of adaptive O-CNN. At the same time, Figure 8 also records the GPU memory consumption, and the adaptive octree based on cosine similarity proposed in the paper consumes less memory than the Voxel, Octree, and Adaptive Octree.

The ablative experiment demonstrates that the cosine similarity-based adaptive octree partitioning method accelerates the overall training speed and reduces the storage overhead, resulting in improved efficiency.

4.5.2. GRU

To verify the effectiveness of the GRU module in the paper, an ablation experiment was performed, and the visualization results are presented in Figure 9. In the experiment, “GRU*1” indicates that only one GRU module is connected after the shallowest octant (third layer). From the results of observation, when there is only one GRU module, it is difficult to keep the generated surface smooth and continuous. In contrast, “GRU*3” refers to the insertion of three GRU modules after the octant of the third-to-fifth layers. By observing the experimental results, compared with “GRU*1”, the surface quality generated by “GRU*3” is significantly improved, and although the GRU is not connected to the deepest octant node, the generated surface still maintains good continuity and avoids sharp edges. In addition, “GRU*4” means that four GRU modules are connected after the octant of the third to sixth layers. According to the results, “GRU*4” is more accurate than “GRU*3” in the expression of wires, and at the same time, it can better show the sharp features of the edge of the lampshade, making it closer to the ground truth surface. This shows that adding the GRU module can effectively extract the relationship between local and global features, which helps to improve the quality of generated surfaces, especially when dealing with complex structures and details.

The effect of different numbers of GRU modules on the generated surface can be observed through the ablation experiments on GRU, and the gradual increase of the number of GRU modules can improve the continuity and fineness of the surface, which provides strong support for the effectiveness of the proposed method and further verifies the important role and superiority of GRU modules in the 3D surface generation task.

4.5.3. Robustness Test on Noise

We train on a clean point cloud while adding a value of 0.01 ($\mathsf{\sigma }=0.01$) Gaussian noise to the input point cloud during testing, which is to simulate the noise of the data in the actual scene, and then verify the surface-generation ability of the network model for the noisy point cloud. By inputting the noise point clouds into the network and comparing the surface-generation capabilities of the proposed method with the advanced OSP method, the adaptability of the proposed method to the noisy point clouds can be more clearly evaluated, as shown in Figure 10. To ensure the comparability of the experiments on OSP and the method in the paper, a control experiment on OSP was conducted in the paper, and the experimental settings of the two methods were optimally adjusted according to the experimental needs. For example, for the OSP method, set the number of input point clouds to 2 k and perform 30 k iterations. For the proposed method, 3 k input point clouds were used, and GPU*4 (such as Figure 9) was used for experiments.

According to the analysis of the experimental results, it can be observed that the OSP method performs the worst in the surface generation of column and hand shapes, and there are holes and unevenness anomalies in the generated results. This indicates that the OSP method has certain limitations when dealing with shapes with complex structures and detailed features in the presence of noise, and it is difficult to effectively capture and reconstruct the features of these complex shapes, resulting in a poor quality of the generated results. In contrast, the method proposed in the paper is slightly superior to OSP in the surface generation of the two shapes, especially in the modeling of the hand region, and avoids the formation of adhesions or holes. This method is of great significance in practical application because it can better deal with complex shapes and can still generate 3D surfaces close to the real situation for various shapes in a noisy environment. In the real world, the shapes of many objects have complex structural and detailed features, such as hand shapes, so the performance advantages of this method will have a positive impact on the 3D shape-surface-generation task of realistic scanning.

To verify the effectiveness of the proposed method in a noisy environment, a comparative experiment on the 3D surface-generation method NKSR [42], based on deep learning, is presented in Figure 11. NKSR is a new method for reconstructing 3D implicit surfaces from large-scale, sparse, and noisy point clouds using a linear combination of learned kernel basis functions to evaluate the value of the function at the corners of the voxels and then extracting the 3D surface using double-marching cubes. In the face of a noisy environment, compared with NKSR, which uses hierarchical sparse data structures to achieve feature mapping, the cyclic iterative optimization method based on GRU in the paper is more advantageous. In Figure 11, it can be observed that the surface generation results of the two are not much different in the plane region (e.g., the “package” in the second row), but in the face of shapes with fine structures (such as the “chair” in the fourth row), this paper can better model the shape surface, which effectively alleviates the influence of noise on the 3D surface generation.

5. Discussion

In the paper, we present comparative experiments conducted on the ShapeNet, ABC, and Famous datasets, as well as ablation experiments on adaptive partitioning and GRU modules. Moreover, we conducted a comparative experiment in a noisy environment. The results show that the adaptive partitioning method can reduce storage space and improve running speed. GRU is connected after different depths of octets, and the update and reset mechanisms of GRU are used to fuse features at different scales, improving the experimental effect. In addition, the method proposed in the paper can have a certain level of noise resistance; that is, it generates three-dimensional surfaces in noisy environments. While the proposed method exhibits a certain level of noise resistance, generating three-dimensional surfaces in noisy environments, the results may exhibit adhesive situations on the generated surfaces. Therefore, further research is necessary to explore more optimal shape partitioning and feature-fusion methods.

6. Conclusions

We present a novel 3D reconstruction method based on iterative optimization of the Moving Least-Squares function. Our method employs an adaptive octree partitioning scheme and a GRU-based feature-optimization module to generate smooth and detailed 3D surfaces from point clouds, which solves the problem of generating accurate 3D surfaces from sparse point clouds. Extensive experiments on benchmark datasets demonstrate that our method is superior to several deep-learning methods in terms of reconstruction accuracy and visual quality. Ablation studies confirm the effectiveness of both the adaptive octree partitioning and GRU modules. Our method provides a valuable tool for generating high-quality 3D surfaces from point clouds.

In future work, we aim to explore a more optimal shape-partitioning method that is resistant to noise interference, as, in some cases, existing adaptive octree partitioning methods unnecessarily partition the voxels of noisy point clouds, resulting in jagged 3D surfaces generated in noisy environments. Then, we will set different weights for different losses in the calculation of total losses to achieve better experimental results. Additionally, we will introduce the neural nuclear field to improve the network’s generalization ability.