Univariate Outlier Detection: Precision-Driven Algorithm for Single-Cluster Scenarios

Abstract

This study introduces a novel algorithm tailored for the precise detection of lower outliers (i.e., data points at the lower tail) in univariate datasets, which is particularly suited for scenarios with a single cluster and similar data distribution. The approach leverages a combination of transformative techniques and advanced filtration methods to efficiently segregate anomalies from normal values. Notably, the algorithm emphasizes high-precision outlier detection, ensuring minimal false positives, and requires only a few parameters for configuration. Its unsupervised nature enables robust outlier filtering without the need for extensive manual intervention. To validate its efficacy, the algorithm is rigorously tested using real-world data obtained from photovoltaic (PV) module strings with similar DC capacities, containing various outliers. The results demonstrate the algorithm’s capability to accurately identify lower outliers while maintaining computational efficiency and reliability in practical applications.

1. Introduction

Anomaly detection is pivotal across various sectors, such as finance, healthcare, and industrial monitoring, where accurately identifying anomalies is vital for operational efficiency and risk mitigation [1,2]. In many applications, achieving high precision in anomaly detection is paramount, particularly in scenarios with a single cluster of data points where anomalies are less common but their detection holds significant consequences. In such contexts, false positives can result in costly disruptions or erroneous decisions, highlighting the importance of algorithms prioritizing precision.

Univariate outlier detection techniques, such as the three-sigma rule and boxplot, rely on statistical assumptions regarding the normal distribution of dat a [3]. While these methods offer a simple approach, their effectiveness can be limited in real-world scenarios where data often deviate from perfect normality. Additionally, these techniques are overly sensitive to outliers, leading to an increased number of false positives [4].

Alternative tests or criteria for univariate outlier detection, such as Grubbs’ test or Chauvenet’s criterion [5], offer more effective solutions in our context. These methods are less reliant on the assumption of a perfectly normal distribution and might provide better specificity, meaning they are less likely to flag normal data points as anomalies.

As the complexity and dimensionality of data increase, even the improved techniques mentioned above encounter challenges in capturing the intricacies of the underlying data distribution [6]. Unsupervised anomaly detection algorithms emerge as a powerful solution in such cases. These algorithms offer a fundamentally different approach compared to traditional univariate methods. Unlike techniques relying on statistical assumptions or predefined thresholds, unsupervised algorithms can learn the inherent structure of the data itself. This allows them to identify anomalies that deviate significantly from the normal patterns within the data, making them particularly well-suited for scenarios with complex and multifaceted anomalies (e.g., Support Vector Data Description (SVDD) [7], autoencoders [8], and isolation forests [9]).

In this paper, we focus on anomaly detection in univariate data with a singular positive cluster. This refers to data that has a single, distinct group of positive values. Examples of such data include sensor readings, financial transactions, or customer engagement metrics. We will use the terms “outlier” and “anomaly” interchangeably throughout this paper to denote these data points.

Anomaly detection in univariate data with a singular positive cluster is crucial for various applications, particularly where high precision is paramount. Existing methods like simple thresholding or statistical techniques often struggle with skewed distributions and lack sensitivity to subtle outliers. This can lead to a high number of false positives, hindering decision making and operational integrity.

To address these challenges, we propose a novel unsupervised outlier detection algorithm specifically designed for this scenario, focusing on the precise identification of lower outliers. Our approach leverages three key innovations:

• Dynamic Threshold-Based Filtration: This technique utilizes a threshold derived from the median and mean of the normalized data, offering greater robustness in handling skewed distributions compared to static thresholds.
• Modified Hyperbolic Tangent Transformation: This non-linear transformation amplifies the differences between normal data points and outliers, enhancing the algorithm’s ability to identify outliers with high precision, minimizing false positives, and ultimately improving decision making in real-world applications.
• Empirical Evaluation: We extensively evaluate our algorithm on real-world data, showcasing its superior precision and effectiveness in detecting anomalies in univariate data with a single positive cluster. The results underscore the practical applicability and advantages of our approach over existing methods.

In this paper, we introduce a precision-focused anomaly detection algorithm tailored for univariate data with a single cluster. We begin by reviewing existing anomaly detection methods, highlighting their limitations, particularly in interpretability and parameter tuning for machine learning and deep learning approaches. Our methodology section details the proposed algorithm, emphasizing preprocessing steps like normalization and filtration, and introducing a modified hyperbolic tangent transformation combined with the Interquartile Range (IQR) method for outlier detection [10]. The results section evaluates the algorithm on real-world data, demonstrating its superior precision and discussing the trade-offs with other metrics due to threshold selection. We compare its performance with other methods, acknowledging limitations from the single case study. In conclusion, we summarize the algorithm’s success, underscore its critical application significance, and suggest future work on diverse datasets to further validate its effectiveness.

2. Related Works

Outlier detection in univariate data has been a well-studied area with various approaches proposed over the years. Carling [11] proposed improvements for non-Gaussian data, addressing the need for robustness in skewed distributions. However, this approach might not be suitable for high-dimensional datasets. Solak [12] discussed methods like Grubbs’ and Dixon’s tests, which can handle some outliers but may struggle with complex outlier patterns or noisy data. Maciá-Pérez et al. [13] presented an efficient algorithm based on Rough Set Theory, but its effectiveness can be limited by the quality of the knowledge base used for rule generation. Jiang et al. [14] proposed outlier-based initialization for K-modes clustering, highlighting the importance of accurate cluster centers. However, this method relies on the underlying clustering algorithm’s ability to handle outliers itself. Sandqvist [15] investigated non-parametric approaches for survey data, which is crucial due to their inherent skewness and heavy-tailed distributions. However, such methods might not be as efficient for very large datasets. Building on this, Walker [16] proposed modifications to the traditional boxplot method for better handling skewed distributions. While effective for univariate data, this approach might not extend well to multivariate outlier detection. These studies provide valuable foundations for outlier detection in univariate data. Marsh and Seo [17] offered a comprehensive review comparing various methods, aiding in selecting appropriate techniques for different data characteristics. Zhu et al. [18] emphasized the importance of handling outliers in industrial process modeling, highlighting the need for robust data mining approaches. This aligns with the growing focus on robust machine learning algorithms, as exemplified by Frenay et al.’s [19] work on reinforced Extreme Learning Machines for robust regression. While these approaches offer diverse methodologies, they might have limitations in areas like handling complex outlier patterns, high dimensionality, or noisy data. Additionally, some methods rely on the underlying assumptions of the chosen technique. Blazquez et al. [20] provide a structured overview of techniques applicable to univariate time series data, highlighting the need for the further exploration of methods for various data types and outlier scenarios.

Recent research explores alternative approaches beyond statistical methods. Machine learning techniques like Support Vector Machines and Support Vector Data Description (SVDDs)have shown promise in outlier detection. However, SVMs might require careful parameter tuning [21]. Additionally, deep learning approaches like autoencoders and Variational Autoencoders (VAEs) [22] can learn complex data representations for anomaly detection. However, their interpretability and black-box nature can be limitations compared to traditional methods [23].

Our proposed algorithm addresses these limitations by prioritizing high-precision anomaly detection through a data transformation process utilizing a customized tanh function. This function enhances the separation between normal and anomalous data points, facilitating the identification of complex outlier patterns. Furthermore, compared to black-box deep learning approaches, our method offers a balance between interpretability and achieving high precision in anomaly detection.

3. Methodology

In this study, we propose a novel algorithm designed for anomaly detection in univariate datasets, particularly when a singular cluster is expected. We assume that the data consist of positive real values.

• The Algorithm Steps:

• Step 1: Normalization

The initial step involves addressing the filtration of zero values from the dataset, considering their potential status as outliers contingent upon contextual considerations. Subsequently, the data are normalized to the range $[0,1]$ This is typically achieved using techniques such as Min–Max scaling.

The formula for Min–Max scaling can be expressed as shown below:

$$X_{\mathrm{scaled}}=\frac{X-X_{\min }}{X_{\max }-X_{\min }}$$

(1)

where: X is the original data point, $X_{\mathrm{scaled}}$ is the scaled data point, $X_{\min }$ is the minimum value in the dataset, and $X_{\max }$ is the maximum value in the dataset.

• Step 2: Lower Value Filtration

To establish a decisive boundary for anomaly identification, we filter out higher normalized values. The filtration threshold is set as the greater of either the median or the mean of the normalized values. This choice takes into account the positioning of the median and mean in positively or negatively skewed distributions. Values greater than the threshold are set to 0, while values below the threshold are replaced by the difference between the value and the reference value.

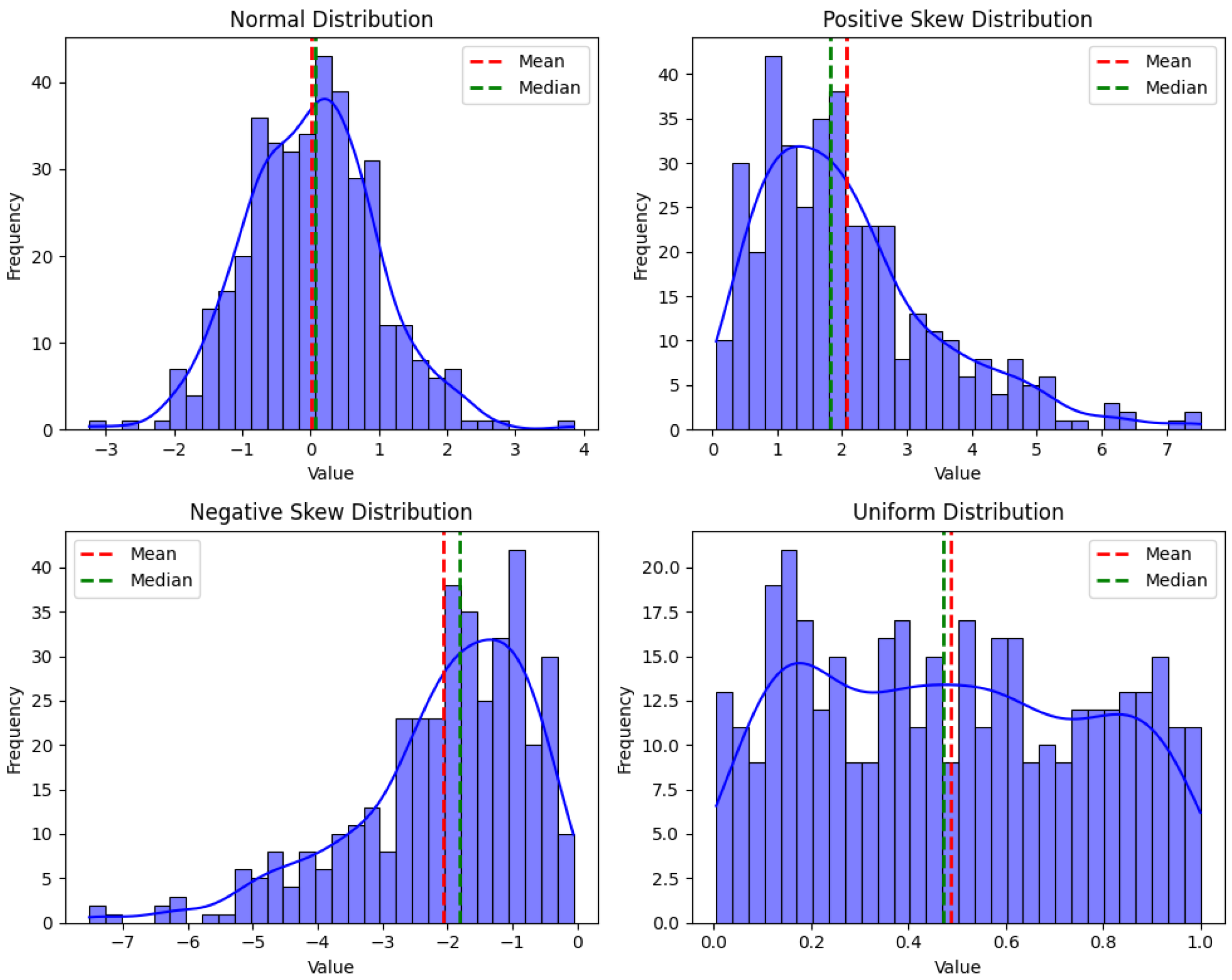
Figure 1 illustrates four distinct probability distributions: a normal distribution characterized by a symmetrical bell curve; a negatively skewed distribution, where the mean is typically less than the median and the tail extends toward lower values; a positively skewed distribution, where the mean is typically greater than the median and the tail extends toward higher values; and a uniform distribution, featuring constant probability density across the range of values. The same principle applies to other distributions, such as exponential, bimodal, and multimodal distributions, where the relationship between the mean and median may vary.

The filter used is as follows:

$$\sigma (s^{*},m,a)=\left\{\begin{array}{cc}{(s^{*}-max(m,a))}^2\hfill & \mathrm{if}{s}^{*}<max(m,a)\hfill \\ 0\hfill & \mathrm{if}{s}^{*}\ge max(m,a)\hfill \end{array}\right.$$

(2)

where $s^{*}$ is the normalized value, m is the median of the normalized values, and a is the average of the normalized values.

Since the data are scaled between 0 and 1, values below the threshold are replaced by the squared distance from the threshold. This distance also falls between 0 and 1 with values closer to 0 indicating greater proximity to the threshold. The squared function is used to emphasize the difference between values near 0 and those near 1. Squaring heavily compresses values closer to 0, bunching them together. Conversely, the effect on values closer to 1 is less pronounced. However, for high-sensitivity anomaly detection, Euclidean distance might be preferable because it avoids compressing small distances.

• Step 3: Hyperbolic Transformation

For a detailed exploration of our non-linear transformation strategy, Figure 2 presents the standard hyperbolic tangent transformation (tanh) curve, providing a benchmark for understanding subsequent modifications.

The formula for the modified hyperbolic tangent transformation is:

$$f\left(\sigma \right(s^{*},m,a))=tanh(\alpha ·\sigma (s^{*},m,a)-\beta )·\lambda +\eta$$

(3)

Parameters:

•

$\alpha$: Controls the slope of the transformation.

•

$\beta$: Shifts the center of the tanh curve.

•

$\lambda$: Scales the output to fit the desired range.

•

$\eta$: Shifts the entire graph vertically.

• Step 4: Detection of Outliers

The final result of the transformation splits outliers from the data with outliers having the highest transformed values. While visualizing the transformed data can provide a preliminary understanding of the outlier distribution, it is a subjective approach for identifying a threshold. To establish a more objective threshold, we propose employing a statistical approach: the Interquartile Range (IQR) method.

The IQR method focuses on the middle 50% of the data and identifies outliers as data points falling outside a specific range calculated based on the IQR value. This approach assumes that the majority of data points reside within the central area, and outliers deviate significantly beyond this range. We will utilize the IQR method to define the outlier threshold for our analysis.

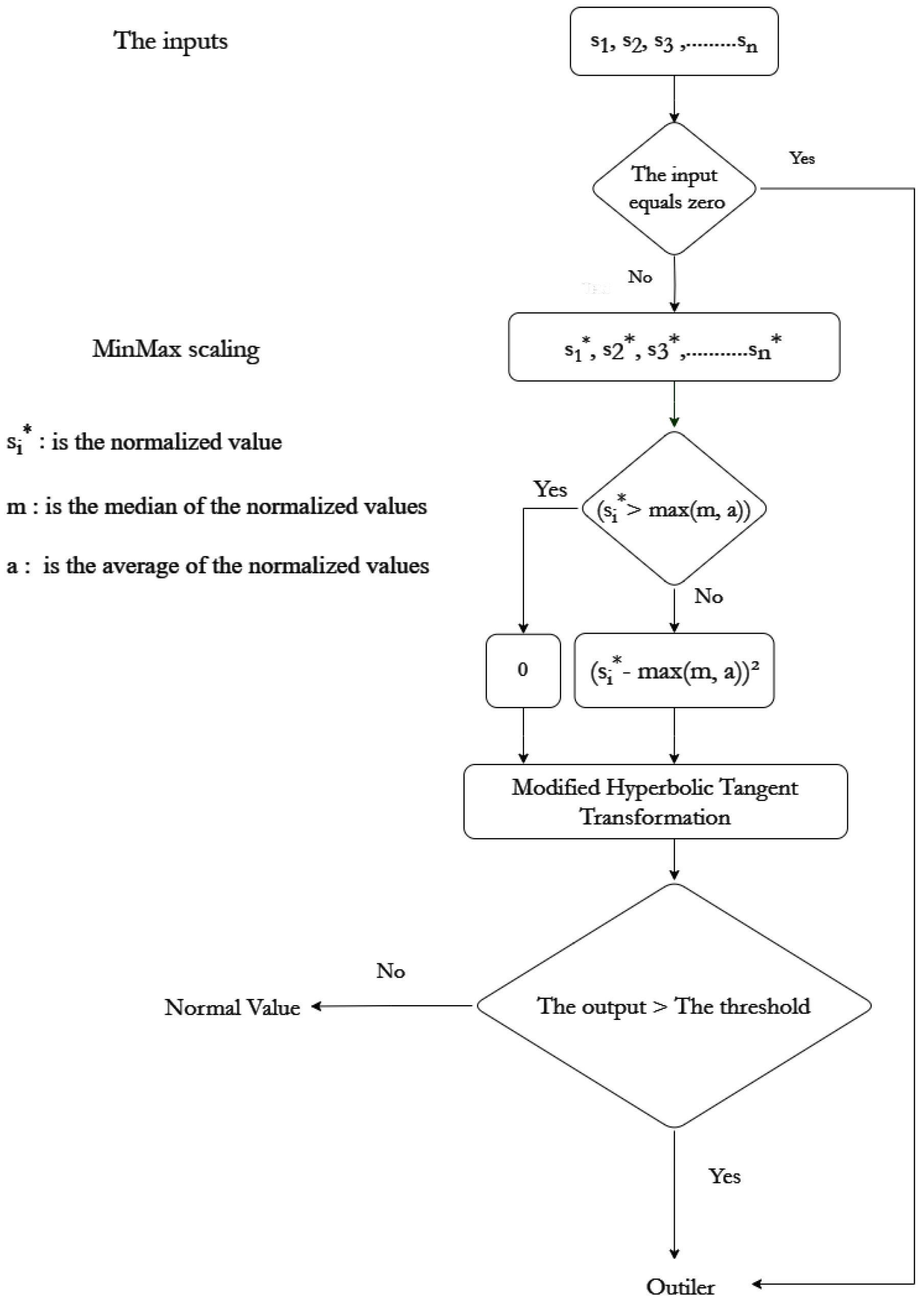
Figure 3 provides a visual representation of the algorithm’s flowchart, illustrating the interconnected steps involved in processing the data and identifying lower outliers.

4. Results and Discussion

In our study, we applied the proposed algorithm to real-world data collected from a photovoltaic (PV) plant located in Morocco, specifically the Noor PV Ouarzazate (55 MW), which has been in operation for six years. Our focus was on the strings’ current data of PV modules recorded over the course of a single day, where drops in current serve as indicators of anomalies. These anomalies encompass various faults such as hotspots, defective diodes, and degraded PV modules, all of which have been traditionally detected using tools like thermal imaging and I–V curve tests. Our objective was to leverage the proposed algorithm to precisely detect strings containing anomalies, thereby enhancing the efficiency of anomaly detection processes. Figure 4 provides a visual representation of the raw data before any processing, while Figure 5 illustrates the data after the application of our algorithm. Notably, the figure encapsulates the final stage of our algorithm, displaying the transformed data after the application of the customized tanh function. The plot effectively demonstrates how the non-linear transformation enhances the contrast between normal and anomalous data points, providing practical interpretability.

4.1. Results

Our findings indicate promising results with the algorithm achieving near-perfect precision across various threshold values as depicted in Figure 6. This high precision underscores the algorithm’s efficacy in accurately identifying true anomalies, rendering it suitable for scenarios where precision is paramount. However, we observed a sensitivity in recall and accuracy to threshold adjustments, emphasizing the inherent trade-off between precision and other metrics. This flexibility in prioritizing precision underscores the adaptability of the algorithm to accommodate different application requirements and preferences.

4.2. Discussion of Findings

The ability to achieve near-perfect precision renders the algorithm valuable in critical infrastructure monitoring and safety-critical systems. By minimizing false positives while maintaining high confidence in identifying true anomalies, the algorithm enhances operational efficiency and enables timely intervention in potential fault scenarios. However, it is crucial to acknowledge the trade-offs associated with threshold selection. Careful consideration of application-specific requirements is essential to optimize performance based on the desired balance between precision and other metrics [24].

4.3. Impact of Parameter Choices

It is important to acknowledge that the chosen parameters for the modified hyperbolic tangent transformation ($\alpha$ = 6, $\beta$ = 3, $\lambda$ = 3, $\eta$ = 3) might be data-dependent. These parameters influence the scaling, shifting, and stretching of the transformed data, impacting how effectively anomalies are distinguished from normal data points.

• Justification for Parameter Choices:

All parameters, namely $\alpha$, $\beta$, $\lambda$, and $\eta$, are set to positive values.

The parameter $\alpha$ is set to 6, while $\beta$, $\lambda$, and $\eta$ are all set to 3. The choice of 6 for scaling the input data (x) influences the horizontal stretching of the sigmoid curve (Figure 7). A higher $\alpha$ value results in the curve being more sensitive to variations in the data, making it more likely to detect even subtle anomalies. However, it is crucial to find the right balance:

• If $\alpha$ is too small: Many outliers will be closer to the normal data points in the transformed space, potentially leading to missed detections.
• If $\alpha$ is too large: Many normal data points might be shifted into the range of outliers, resulting in false positives.

Setting $\alpha$ to 6 effectively allows the curve to decrease values closer to 0 and increase values closer to 1, enhancing the separation between normal data and outliers. The parameter $\beta$ (set to 3 here) subtracts from the scaled input and shifts the center of the tanh curve horizontally. This adjustment impacts where the transformation focuses its attention within the data range.

Suppose x is an element in the range (0,1). The function $tanh(\alpha ·x-\beta )\times \lambda +\eta$, set with parameters $\alpha =6$, $\beta =3$, $\lambda =3$, and $\eta =3$, expands the range from (0,1) to (0,6), showcasing its transformative capability in data manipulation. In general, if $\lambda =\eta$, $\alpha -\beta$ is greater than 1, and $-\beta <-1$, the image range is the open interval $(0,2\eta )$.

Proof. 

For x within the range (0, 1), the following applies:

$$\alpha x-\beta \in [-\beta ,\alpha -\beta ]\Rightarrow tanh(\alpha x-\beta )\in [tanh(-\beta ),tanh(\alpha -\beta \left)\right]$$

Consequently, the range of $F\left(x\right)$ is within the interval:

$$[tanh(-\beta )·\lambda +\eta ,tanh(\alpha -\beta )·\lambda +\eta ]$$

Thus, under the condition where $\lambda =\eta$, $\alpha -\beta$ is greater than 1, and $-\beta <-1$, the range of $F\left(x\right)$ simplifies to the open interval $(0,2\eta )$.

Thus, the range of $F\left(x\right)$ becomes

$$(0,2\eta )=(0,6)$$

□

Transformation Steps:

• $tanh\left(x\right)$: The initial graph has a sigmoid shape, ranging from −1, rising gradually, reaching a maximum slope around 0, and then descending back to 1.
• $tanh(x·6)$: Scaling the input by a factor of 6 horizontally stretches the sigmoid curve, resulting in a more elongated shape compared to the original tanh function.
• $tanh(x·6-3)$: Shifting the scaled input to the right by 3 units horizontally relocates the curve to the right.
• $tanh(x·6-3)·3$: Multiplying the values vertically scales the graph, increasing the amplitude threefold.
• $tanh(x·6-3)·3+3$: Adding 3 shifts the entire graph vertically upwards by three units.

In summary, the parameter choices of 6 and 3 were obtained through experimentation and achieve a well-considered balance for this dataset. However, manually tuning these parameters might not be ideal for generalizability across different datasets. To address this limitation, future work will focus on incorporating an automated hyperparameter optimization technique, such as grid search or a more sophisticated algorithm, to select the most effective parameter settings for a given dataset.

4.4. Comparison of Outlier Detection Algorithms

To assess the efficacy of the proposed algorithm in achieving high-precision outlier detection, we compare its performance with established methods like the one-class SVM and autoencoders. This comparison utilizes a real-world dataset.

4.4.1. Baselines and Training Configurations

We employed careful hyperparameter tuning for both the one-class SVM and the autoencoder models to achieve optimal performance.

For the one-class SVM, we fine-tuned hyperparameters using grid search with k-fold cross-validation. This optimized parameters like $\nu$ (outlier fraction) and kernel type, ensuring model generalizability and prioritizing a balance between precision and recall (F1-score).

We employed a similar approach for hyperparameter tuning in the autoencoder model. Grid search was again utilized to optimize various settings, including the optimizer and the activation functions, and the number of neurons within the hidden layers. During this search, we prioritized minimizing the reconstruction error. A lower reconstruction error signifies the model’s better ability to capture the underlying structure of the data, which can be crucial for identifying anomalies that deviate from this structure.

4.4.2. Comparison Metrics and Calculations

The following metrics are used to compare the performance of the outlier detection algorithms:

F1 Score

The harmonic mean between precision and recall, combining both measures into a single metric. A higher F1 score indicates a better balance between correctly identifying outliers and minimizing false positives.

$$\mathrm{F}1\mathrm{Score}=2·\frac{\mathrm{Precision}·\mathrm{Recall}}{\mathrm{Precision}+\mathrm{Recall}}$$

(4)

Recall

The proportion of actual outliers correctly identified by the algorithm.

$$\mathrm{Recall}=\frac{\mathrm{True}\mathrm{Positives}}{\mathrm{True}\mathrm{Positives}+\mathrm{False}\mathrm{Negatives}}$$

(5)

Accuracy

The overall proportion of correct predictions (outliers and normal data points) made by the algorithm.

$$\mathrm{Accuracy}=\frac{\mathrm{True}\mathrm{Positives}+\mathrm{True}\mathrm{Negatives}}{\mathrm{Total}\mathrm{Samples}}$$

(6)

Precision

The proportion of predicted outliers that are actually outliers.

$$\mathrm{Precision}=\frac{\mathrm{True}\mathrm{Positives}}{\mathrm{True}\mathrm{Positives}+\mathrm{False}\mathrm{Positives}}$$

(7)

In addition to the previously mentioned metrics, we visualized the trade-off between correctly identifying outliers (True Positive Rate) and misclassifying normal data (False Positive Rate) using ROC curves for each algorithm. ROC curves provide a valuable comparison tool with algorithms closer to the top-left corner indicating superior performance.

Our proposed algorithm demonstrates significant advantages over one-class SVM and autoencoder algorithms in detecting outliers particularly those closer to the normal data. This advantage stems from the non-linear hyperbolic transformation, which effectively amplifies the separation between the main data and outliers, leading to improved detection accuracy.

The one-class SVM exhibits strong performance, which is particularly evident in its high recall and accuracy scores. However, its precision and F1-score, while respectable, are surpassed by the proposed algorithm. The autoencoder, though offering a competitive alternative, falls short in terms of precision and F1-score compared to both the SVM and the proposed algorithm (

Table 1. Comparison of outlier detection algorithms.

Algorithm	F1 Score	Recall	Accuracy	Precision
One-Class SVM	79.25%	95.45%	88.78%	67.74%
Autoencoder	73.08%	86.36%	85.71%	63.33%
Proposed	97.78%	100.00%	98.98%	95.65%

).

The proposed algorithm stands out with its remarkable F1-score of 97.78%, perfect recall of 100.00%, and near-perfect precision of 95.65% (Table 1). Such results signify its exceptional ability to accurately detect anomalies while minimizing false positives, which is a critical aspect in anomaly detection systems. The AUC score of 100% further solidifies its efficacy in distinguishing between normal and outlier instances compared to the SVM AUC score of 98% and the autoencoder AUC score of 89% (see Figure 8, Figure 9 and Figure 10).

While the proposed algorithm demonstrates strong performance in this specific context, its generalizability to diverse datasets can require further exploration. The non-linear hyperbolic transformation, although effective in separating outliers, can obscure their original distance from the reference point. This can be critical in certain scenarios where outliers farther from the reference point are more important than closer outliers. In such cases, the hyperbolic transformation might transform both types of outliers into a similar range, making it difficult to distinguish between them. However, it is important to note that for cases where precise deviation from the reference point is highly important, the proposed algorithm can still perform well. The one-class SVM and autoencoder, with further optimization and adaptability, might yield superior performance in different scenarios or data structures.

In conclusion, this comparison underscores the effectiveness of the proposed algorithm for anomaly detection in the present application. Its simplicity, interpretability, and outstanding performance metrics make it a compelling choice. However, future research should explore its robustness across diverse datasets to ascertain its broader utility in anomaly detection tasks.

5. Conclusions

In summary, our study introduces a novel algorithm designed for precise anomaly detection in univariate datasets, particularly in scenarios with a single cluster of data points. Applied to real-world data from the Noor PV Ouarzazate 55 MW plant in Morocco, our algorithm demonstrated near-perfect precision in identifying anomalies in photovoltaic module strings.

Through a combination of transformative techniques and advanced filtration methods, our algorithm effectively distinguishes anomalies from normal data points. This precision is crucial for applications where false positives can have significant consequences, highlighting the algorithm’s efficacy in scenarios where precision is paramount.

Despite achieving near-perfect precision, we acknowledge the trade-offs associated with threshold selection, emphasizing the need for careful consideration of application-specific requirements. Nevertheless, the algorithm’s ability to enhance operational efficiency and enable timely intervention in potential fault scenarios makes it invaluable for critical infrastructure monitoring and safety-critical systems.

In conclusion, our proposed algorithm represents a significant advancement in anomaly detection methodologies, offering a reliable and efficient solution for accurately identifying anomalies in various datasets. By prioritizing precision and adaptability, our algorithm holds promise for improving decision-making processes and ensuring operational integrity across different sectors.