A Comprehensive Brain MRI Image Segmentation System Based on Contourlet Transform and Deep Neural Networks
Abstract
1. Introduction
2. Literature Review
3. Method
3.1. Dataset and Pre-Processing
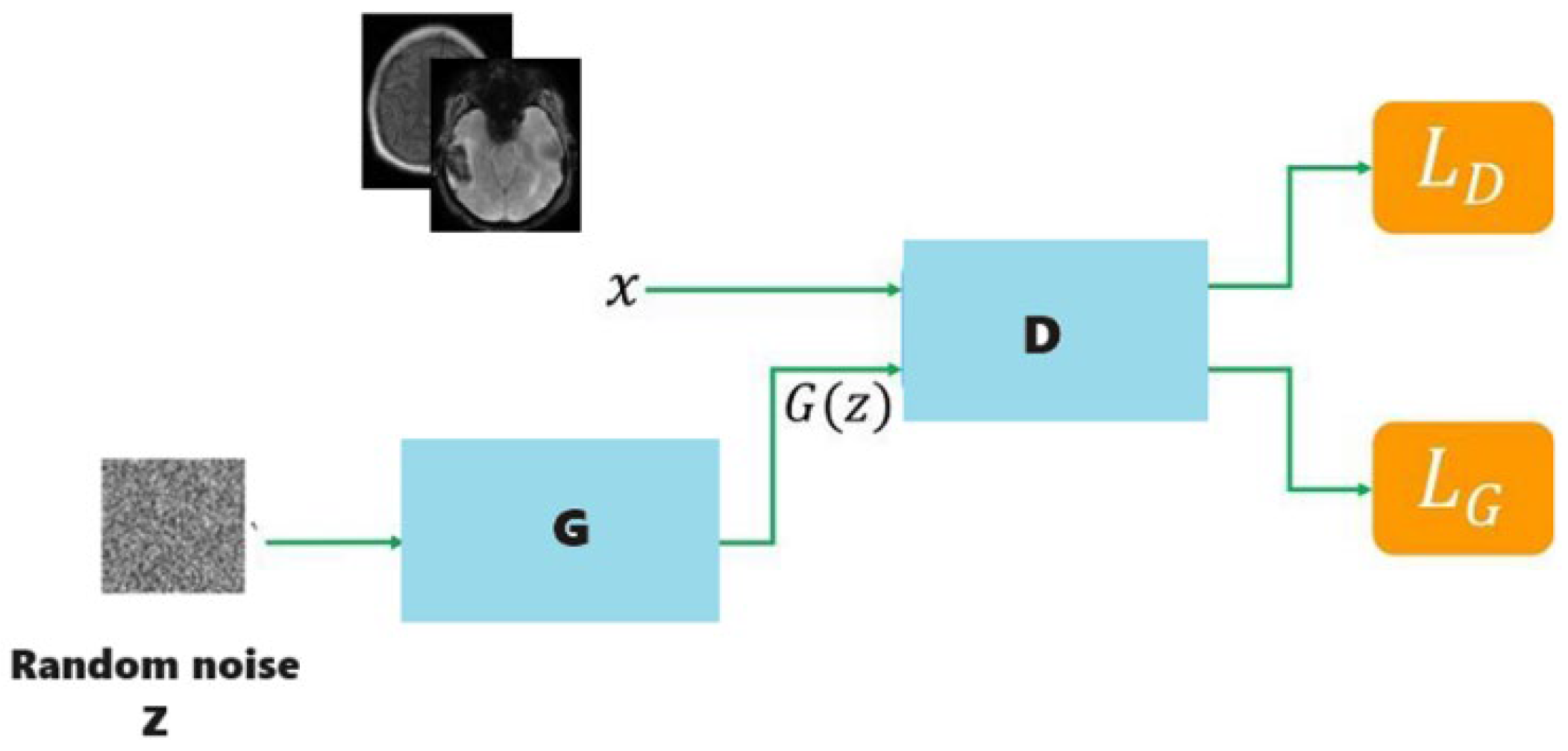
3.2. Data Augmentation and Generative Adversarial Networks
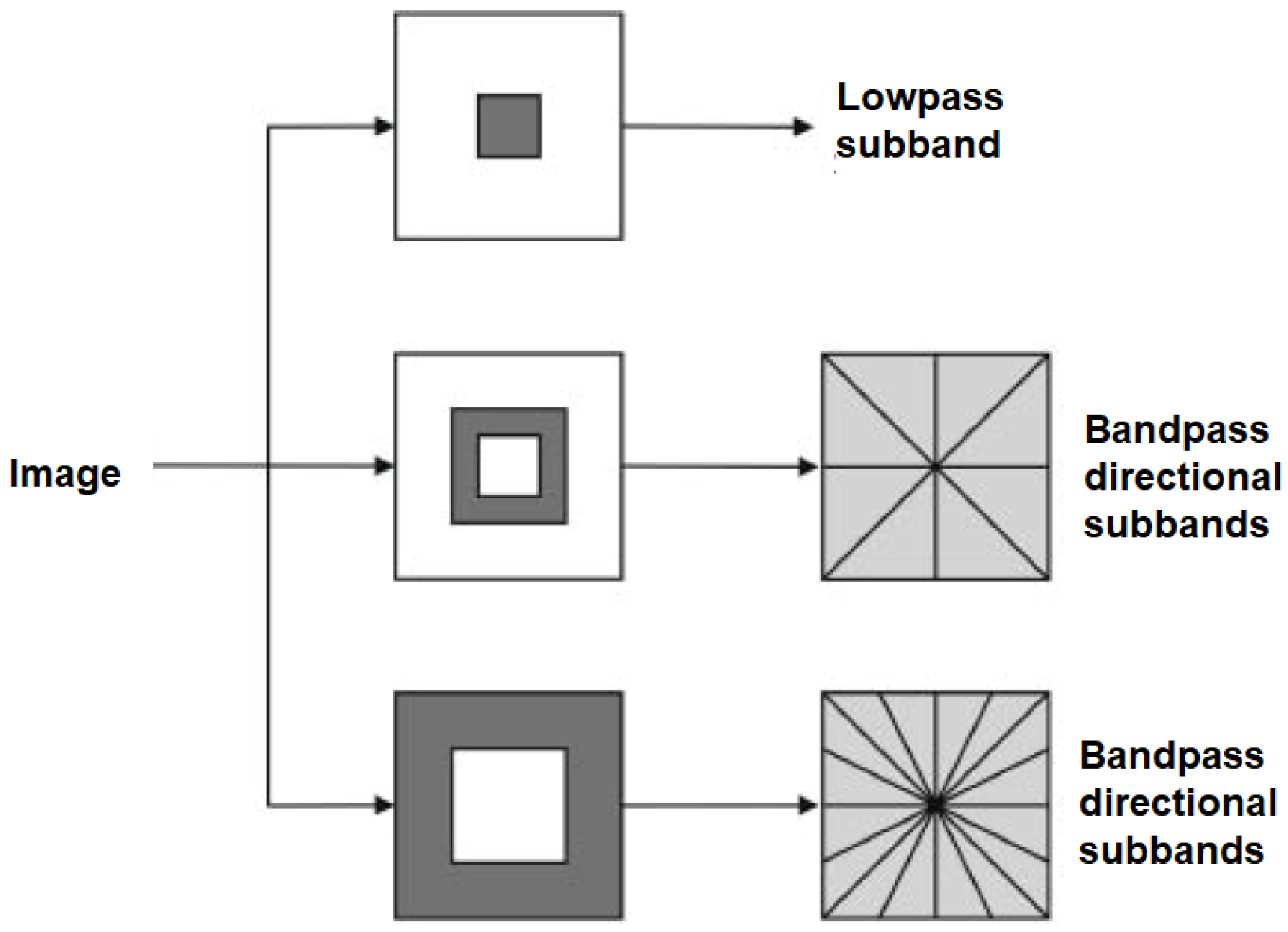
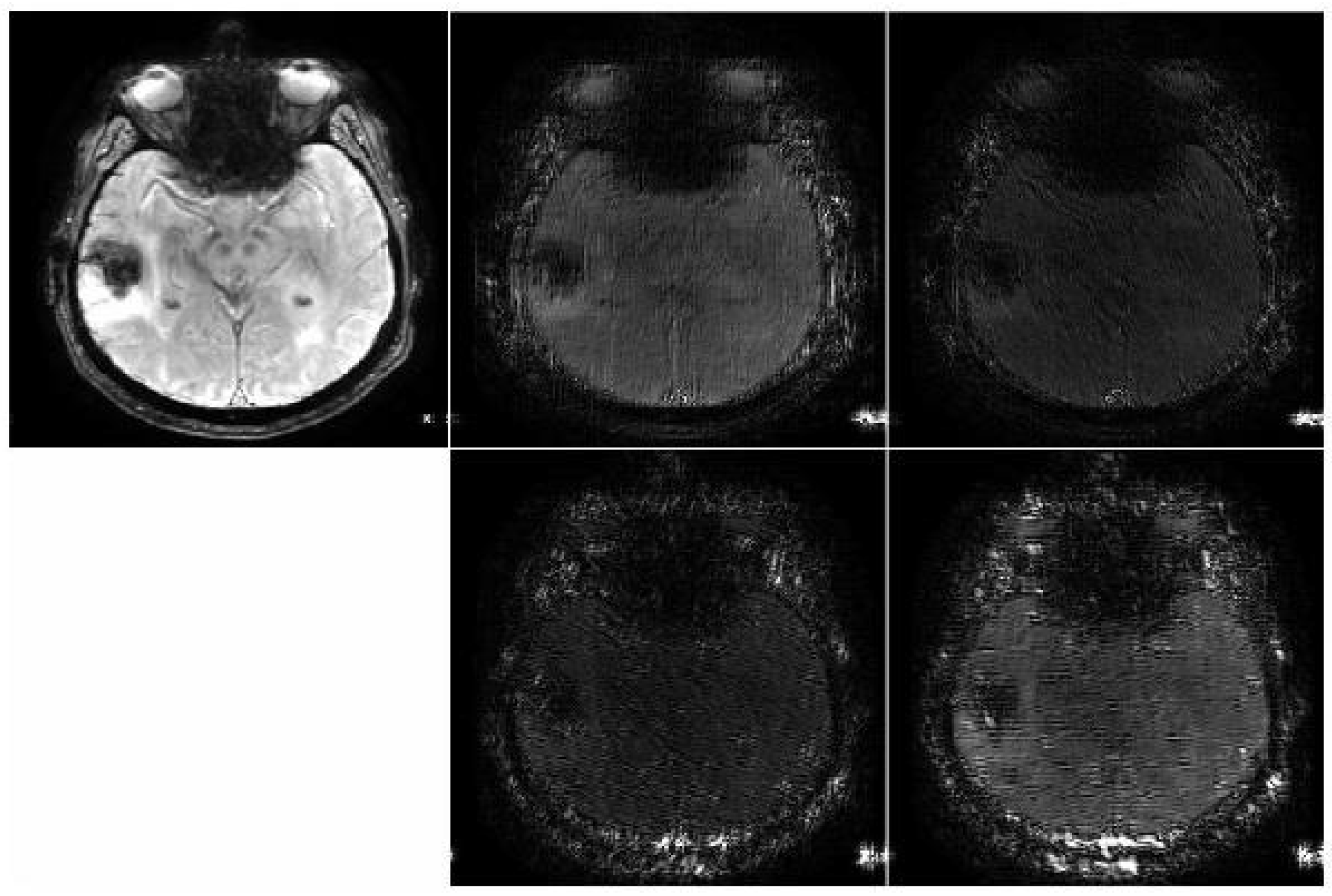
3.3. Data Processing and Contourlet Transform
3.4. Segmentation Network
4. Results and Discussion
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Abd-Ellah, M.K.; Awad, A.I.; Khalaf, A.A.; Hamed, H.F. A review on brain tumor diagnosis from MRI images: Practical implications, key achievements, and lessons learned. Magn. Reson. Imaging 2019, 61, 300–318. [Google Scholar] [CrossRef]
- Wadhwa, A.; Bhardwaj, A.; Verma, V.S. A review on brain tumor segmentation of MRI images. Magn. Reson. Imaging 2019, 61, 247–259. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.; Wu, Y.; Song, G.; Li, Z.; Zhang, Y.; Fan, Y. A deep learning model integrating FCNNs and CRFs for brain tumor segmentation. Med. Image Anal. 2018, 43, 98–111. [Google Scholar] [CrossRef] [PubMed]
- Ilunga–Mbuyamba, E.; Avina–Cervantes, J.G.; Cepeda–Negrete, J.; Ibarra–Manzano, M.A.; Chalopin, C. Automatic selection of localized region-based active contour models using image content analysis applied to brain tumor segmentation. Comput. Biol. Med. 2017, 91, 69–79. [Google Scholar] [CrossRef] [PubMed]
- Iqbal, S.; Ghani, M.U.; Saba, T.; Rehman, A. Brain tumor segmentation in multi-spectral MRI using convolutional neural networks (CNN). Microsc. Res. Tech. 2018, 81, 419–427. [Google Scholar] [CrossRef] [PubMed]
- Ker, J.; Wang, L.; Rao, J.; Lim, T. Deep Learning Applications in Medical Image Analysis. IEEE Access 2017, 6, 9375–9389. [Google Scholar] [CrossRef]
- Saman, S.; Narayanan, S.J. Survey on brain tumor segmentation and feature extraction of MR images. Int. J. Multimedia Inf. Retr. 2019, 8, 79–99. [Google Scholar] [CrossRef]
- Pereira, S.; Pinto, A.; Alves, V.; Silva, C.A. Brain tumor segmentation using convolutional neural networks in MRI images. IEEE Trans. Med. Imaging 2016, 35, 1240–1251. [Google Scholar] [CrossRef]
- More, S.S.; Mange, M.A.; Sankhe, M.S.; Sahu, S.S. Convolutional neural network based brain tumor detection. In Proceedings of the 2021 5th International Conference on Intelligent Computing and Control Systems (ICICCS), Madurai, India, 6–8 May 2021; pp. 1532–1538. [Google Scholar]
- Spinner, T.; Schlegel, U.; Schafer, H.; El-Assady, M. explAIner: A visual analytics framework for interactive and explainable machine learning. IEEE Trans. Vis. Comput. Graph. 2019, 26, 1064–1074. [Google Scholar] [CrossRef]
- Piccialli, F.; Di Somma, V.; Giampaolo, F.; Cuomo, S.; Fortino, G. A survey on deep learning in medicine: Why, how and when? Inf. Fusion 2021, 66, 111–137. [Google Scholar] [CrossRef]
- Ben Naceur, M.; Saouli, R.; Akil, M.; Kachouri, R. Fully automatic brain tumor segmentation using end-to-end incremental deep neural networks in MRI images. Comput. Methods Programs Biomed. 2018, 166, 39–49. [Google Scholar] [CrossRef] [PubMed]
- Raza, R.; Bajwa, U.I.; Mehmood, Y.; Anwar, M.W.; Jamal, M.H. dResU-Net: 3D deep residual U-Net based brain tumor segmentation from multimodal MRI. Biomed. Signal Process. Control 2023, 79, 103861. [Google Scholar] [CrossRef]
- Gull, S.; Akbar, S.; Shoukat, I.A. A Deep Transfer learning approach for automated detection of brain tumor through magnetic resonance imaging. In Proceedings of the 2021 International Conference on Innovative Computing (ICIC), Online, 15–16 September 2021; pp. 1–6. [Google Scholar]
- Karayegen, G.; Aksahin, M.F. Brain tumor prediction on MR images with semantic segmentation by using deep learning network and 3D imaging of tumor region. Biomed. Signal Process. Control 2021, 66, 102458. [Google Scholar] [CrossRef]
- Akbar, A.S.; Fatichah, C.; Suciati, N. Single level UNet3D with multipath residual attention block for brain tumor segmentation. J. King Saud Univ. Comput. Inf. Sci. 2022, 34, 3247–3258. [Google Scholar] [CrossRef]
- Ullah, Z.; Usman, M.; Jeon, M.; Gwak, J. Cascade multiscale residual attention CNNs with adaptive ROI for automatic brain tumor segmentation. Inf. Sci. 2022, 608, 1541–1556. [Google Scholar] [CrossRef]
- Zhou, X.; Li, X.; Hu, K.; Zhang, Y.; Chen, Z.; Gao, X. ERV-Net: An efficient 3D residual neural network for brain tumor segmentation. Expert Syst. Appl. 2021, 170, 114566. [Google Scholar] [CrossRef]
- Talo, M.; Baloglu, U.B.; Yıldırım, Ö.; Acharya, U.R. Application of deep transfer learning for automated brain abnormality classification using MR images. Cogn. Syst. Res. 2019, 54, 176–188. [Google Scholar] [CrossRef]
- Chawla, R.; Beram, S.M.; Murthy, C.R.; Thiruvenkadam, T.; Bhavani, N.; Saravanakumar, R.; Sathishkumar, P. Brain tumor recognition using an integrated bat algorithm with a convolutional neural network approach. Meas. Sensors 2022, 24, 100426. [Google Scholar] [CrossRef]
- Ghassemi, N.; Shoeibi, A.; Rouhani, M. Deep neural network with generative adversarial networks pre-training for brain tumor classification based on MR images. Biomed. Signal Process. Control 2020, 57, 101678. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Salimans, T.; Goodfellow, I.; Zaremba, W.; Cheung, V.; Radford, A.; Chen, X. Improved techniques for training gans. Adv. Neural Inf. Process. Syst. 2016, 2234–2242. [Google Scholar]
- Do, M.N.; Vetterli, M. Contourlets: A directional multiresolution image representation. In Proceedings of the International Conference on Image Processing, New York, NY, USA, 22–25 September 2002. [Google Scholar]
- Do, M.; Vetterli, M. The contourlet transform: An efficient directional multiresolution image representation. IEEE Trans. Image Process. 2005, 14, 2091–2106. [Google Scholar] [CrossRef] [PubMed]
- Mejía Muñoz, J.M.; de Jesús Ochoa Domínguez, H.; Ortega Máynez, L.; Vergara Villegas, O.O.; Cruz Sánchez, V.G.; Gordillo Castillo, N.; Gutiérrez Casas, E.D. SAR image denoising using the non-subsampled contourlet transform and morphological operators. In Proceedings of the Advances in Artificial Intelligence, 9th Mexican International Conference on Artificial Intelligence, MICAI 2010, Pachuca, Mexico, 8–13 November 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 337–347. [Google Scholar]
- Sadreazami, H.; Ahmad, M.O.; Swamy, M. A study on image denoising in contourlet domain using the alpha-stable family of distributions. Signal Process. 2016, 128, 459–473. [Google Scholar] [CrossRef]
- Bi, X.; Chen, X.; Li, X. Medical image compressed sensing based on contourlet. In Proceedings of the 2009 2nd International Congress on Image and Signal Processing, Tianjin, China, 17–19 October 2009; pp. 1–4. [Google Scholar]
- Sajedi, H.; Jamzad, M. A contourlet-based face detection method in color images. In Proceedings of the 2007 Third International IEEE Conference on Signal-Image Technologies and Internet-Based System, Shanghai, China, 16–18 December 2007; pp. 727–732. [Google Scholar]
- Khare, A.; Srivastava, R.; Singh, R. Edge preserving image fusion based on contourlet transform. In Proceedings of the International Conference on Image and Signal Processing, Agadir, Morocco, 28–30 June 2012; pp. 93–102. [Google Scholar]
- Xia, L.; Fangfei, Y.; Ligang, S. Image Edge Detection Based on Contourlet Transform Combined with the Model of Anisotropic Receptive Fields. In Proceedings of the 2014 Fifth International Conference on Intelligent Systems Design and Engineering Applications, Hunan, China, 15–16 June 2014; pp. 533–536. [Google Scholar]
- Fernandes, F.; van Spaendonck, R.; Burrus, C. A new framework for complex wavelet transforms. IEEE Trans. Signal Process. 2003, 51, 1825–1837. [Google Scholar] [CrossRef]
- Çiçek, Ö.; Abdulkadir, A.; Lienkamp, S.S.; Brox, T.; Ronneberger, O. 3D U-Net: Learning dense volumetric segmentation from sparse annotation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention–MICCAI 2016: 19th International Conference, Athens, Greece, 17–21 October 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 424–432. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, 5–9 October 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Identity mappings in deep residual networks. In Proceedings of the Computer Vision–ECCV 2016, Presented at the 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 630–645. [Google Scholar]











| Layer | Width | Hight | Depth | Stride | Layer Info |
|---|---|---|---|---|---|
| Dense | 1 | 1 | 262,144 | - | - |
| Activation | 1 | 1 | 262,144 | - | LeakyReLU |
| Reshape | 32 | 32 | 256 | - | - |
| ConVol-Transpose | 64 | 64 | 256 | 2 | - |
| Activation | 64 | 64 | 256 | - | LeakyReLU |
| ConVol-Transpose | 128 | 128 | 256 | 2 | - |
| Activation | 128 | 128 | 256 | - | LeakyReLU |
| ConVol | 128 | 128 | 1 | - | - |
| Activation | 128 | 128 | 1 | - | Tanh |
| Layer | Width | Hight | Depth | Stride | Layer Info |
|---|---|---|---|---|---|
| ConVol | 128 | 128 | 64 | - | - |
| Activation | 128 | 128 | 64 | - | LeakyReLU |
| ConVol | 64 | 64 | 128 | 2 | - |
| Activation | 64 | 64 | 128 | - | LeakyReLU |
| ConVol | 32 | 32 | 128 | 2 | - |
| Activation | 32 | 32 | 128 | - | LeakyReLU |
| ConVol | 16 | 16 | 256 | 2 | - |
| Activation | 16 | 16 | 256 | - | LeakyReLU |
| Flatten | 1 | 1 | 65,536 | - | - |
| Dropout | 1 | 1 | 65,536 | - | Rate 0.4 |
| Dense | 1 | 1 | 65,537 | - | - |
| Activation | 1 | 1 | 65,537 | - | Sigmoid |
| Layer | Encoder Block Structure | Decoder Block Structure |
|---|---|---|
| 1 | Add | Add |
| 2 | Activation | Activation |
| 3 | Max pooling | Up-sampling |
| 4 | ConVol | Concatenate |
| 5 | Batch Normalization | ConVol |
| 6 | Activation | Batch Normalization |
| 7 | ConVol | Activation |
| 8 | Batch Normalization | ConVol |
| 9 | ConVol | Batch Normalization |
| 10 | Batch Normalization | ConVol |
| 11 | Batch Normalization |
| EPOCH | Generator Loss | Discriminator Loss |
|---|---|---|
| 1 | 2.7882 | 0.2121 |
| 2 | 1.7463 | 1.5576 |
| 3 | 1.4884 | 0.7854 |
| 4 | 2.0414 | 0.0719 |
| 5 | 2.1013 | 0.2531 |
| 6 | 4.2882 | 0.0856 |
| 7 | 6.8006 | 0.0007 |
| 8 | 4.5135 | 0.0913 |
| 9 | 2.9847 | 0.1567 |
| 10 | 7.7373 | 0.0208 |
| 11 | 3.3118 | 0.0454 |
| 12 | 2.7657 | 0.0614 |
| Evaluation Criteria | DSC | IoU | Precision | Specificity | Sensitivity |
|---|---|---|---|---|---|
| With GAN | 0.9434 | 0.8928 | 0.9390 | 0.9390 | 0.9479 |
| Without GAN | 0.8070 | 0.6764 | 0.7863 | 0.7807 | 0.8288 |
| Criteria | DSC | IoU |
|---|---|---|
| Our segmentation model | 0.9434 | 0.8928 |
| Standard U net | 0.9281 | 0.8658 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khalili Dizaji, N.; Doğan, M. A Comprehensive Brain MRI Image Segmentation System Based on Contourlet Transform and Deep Neural Networks. Algorithms 2024, 17, 130. https://doi.org/10.3390/a17030130
Khalili Dizaji N, Doğan M. A Comprehensive Brain MRI Image Segmentation System Based on Contourlet Transform and Deep Neural Networks. Algorithms. 2024; 17(3):130. https://doi.org/10.3390/a17030130
Chicago/Turabian StyleKhalili Dizaji, Navid, and Mustafa Doğan. 2024. "A Comprehensive Brain MRI Image Segmentation System Based on Contourlet Transform and Deep Neural Networks" Algorithms 17, no. 3: 130. https://doi.org/10.3390/a17030130
APA StyleKhalili Dizaji, N., & Doğan, M. (2024). A Comprehensive Brain MRI Image Segmentation System Based on Contourlet Transform and Deep Neural Networks. Algorithms, 17(3), 130. https://doi.org/10.3390/a17030130







